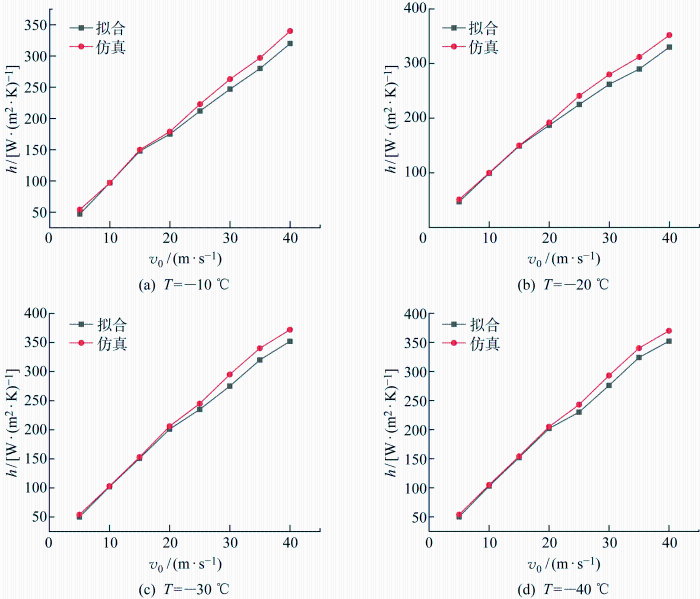随着各国可开采海洋资源的不断减少,极地蕴藏的丰富资源被持续发现,各国逐步加大了对北极资源的勘探和开发力度[1 ] .极地海洋环境复杂,低温、强风及潮湿等恶劣气候极易导致海洋工程装备上部的设施结冰.极地船舶覆冰会影响船舶结构稳性与功能性,表现为增加船舶质量,改变整体结构应力[2 ] ,造成设备不同程度的损坏,影响其使用性能,甚至会危害到作业人员自身安全[3 ] .因此,开展极地装备的防寒研究具有重要意义.极地装备上部设施复杂,从结构外形特征上可分为平板类、圆管类等规则构件和不规则类型构件,如带有花纹的踏步板构件.目前,极地装备上部设施各类部件的防寒措施主要采用电伴热方式[4 ] .
在电伴热加热过程中,因热源与壁面间存在温度差,导致流体各部分密度不同而形成对流运动,该运动属于对流换热的传热方式.电伴热加热方式通常分为恒热流与恒壁温两种,对于不同的加热方式,温差计算也存在差异.恒热流加热方式可实现热量的恒定输入,此过程流体温度与壁面温度持续升高,故其温差为流体温度与壁面温度之差;恒壁温加热方式是通过改变加热量,使壁面的温度保持恒定,此过程壁温不变,流体温度增加,因其局部温差是变化的,故温差数取其平均数.目前,极地海洋工程装备的防除冰普遍使用恒热流的电伴热加热方式[5 ] .
目前,极地环境下的海洋工程装备关于防除冰的设计大多参考船级社的相关规范,未充分考虑船舶航行时外部环境的变化对加热量的影响,导致建议的加热功率过大,造成一定的能耗浪费[6 -7 ] .低温环境下,各环境因素对构件的加热量影响较大[8 ] .为此,需确定已考虑极地环境因素的对流换热系数预测模型,为极地装备上部设施防寒设计提供依据.相较于平板构件,踏步板表面覆有凸出花纹,换热面积小,在极地环境下对流换热影响因素复杂且换热规律不明确[9 ] .
踏步板构件因其表面复杂,相关传热的研究尚有匮乏.Zontul等[10 ] 对具有矩形凹槽顶壁和底壁通道中的对流传热和流动特性进行了实验和数值研究,通过上下壁面施加恒定热量的恒热流加热方式进行实验,在雷诺数Re 为2×103 ~6.5×103 之间,得出壁面平均努塞尔数Nu 是直通道的1.9~2.4倍,且凹槽会导致额外的压降;Churchill[11 ] 得出完全层流与完全湍流状态下Nu 与普朗特数Pr 的精确公式;Danov等[12 ] 针对平板间完全湍流对流的状态,得出流体速度、温度分布及摩擦因数和Nu 的精确公式;郑卉等[13 ] 研究了不同构件截面、不同风向对构件对流换热系数的影响;李烨等[14 ] 通过实验对水流与模具钢之间的对流换热系数进行研究,分析了流量、热流密度和管道直径对对流换热系数的影响.因极地气候环境恶劣多变,与上述研究选取的气候条件有较大不同,且上述研究的环境影响因素也不全面,所以以极地主要环境因素为变量,进行对流换热系数研究.
结合Fluent数值模拟与室内模型实验,开展踏步板的电伴热加热方式下的对流换热影响研究.实验条件设置温度范围为-40~0 ℃、风速为0~13.9 m/s;仿真条件设置温度范围为-40~0 ℃,风速为 0~40 m/s.进一步研究对流换热系数随温度和风速的变化规律,建立对流换热系数的预测模型,并验证其合理性.
1 对流换热基本原理
受外界气流影响,电伴热加热过程中踏步板表面会形成对流换热流动.根据牛顿冷却公式可知,对流换热系数是热量交换的关键.对流换热系数又称表面传热系数,是反映对流换热快慢的物理量,其大小受限于流体流动起因、流体有无相变、流动状态、物理性质等因素.换热表面的几何形状也是影响对流换热系数的重要因素,踏步构件因其结构复杂,不属于光滑的平板构件,换热规律尚不明确.在踏步与平板对流换热过程中,流体流动皆属于施加外力做功而形成的强制对流.流动状态与Re 有关,当平板在Re <5×105 时,为层流层,流体微团轨迹没有明显的不规则脉动;当平板在Re ≥5×105 时,为湍流层,流体间相互掺杂,呈现无规则脉动.实际换热过程中,层流与湍流二者间存在过渡层.此外,踏步构件相较于平板构件,其换热面积因换热表面形状凸起花纹改变而有所增加,其理论值应大于平板构件.
在流体平行流过平板的流动问题中,对流换热系数与Pr 和Re 相关.局部努塞尔数为
(1) $N u_{x}=h_{x} \frac{l}{\lambda}$
式中:hx 为局部对流换热系数;l 为参数;λ 为流体的导热系数.
恒热流加热下,Nux 与流体流动状态有关,表达式如下:
(2) $N u_{x}=\left\{\begin{array}{ll}0.453 \operatorname{Re}_{x}^{1 / 2} \operatorname{Pr}^{1 / 3}, & R e<5 \times 10^{5} \\0.0308 \operatorname{Re}_{x}^{4 / 5} \mathrm{Pr}^{1 / 3}, & \operatorname{Re} \geqslant 5 \times 10^{5}\end{array}\right.$
式中:Rex 为局部雷诺数. 当Re <5×105 时,流体处于完全层流状态,0. 5<Pr <1 000;当Re ≥5×105 时,流体处于完全湍流状态,0. 6<Pr <60.
在平板构件长度尺寸大于临界雷诺数时,流动状态相对复杂,会随Re 的增长从层流过渡到湍流状态,局部对流换热系数h 会随平板前沿距离的变化而变化. 公式如下:
(3) $h=\frac{1}{L}\left(\int_{0}^{x} h_{x, l} \mathrm{~d} x+\int_{x}^{l} h_{x, t} \mathrm{~d} x\right)$
式中:L 为特征长度;hx , l hx , t
(4) $h=0.0385 \frac{\lambda}{l}\left(\operatorname{Re}^{4 / 5}-754.6\right) \operatorname{Pr}^{1 / 3}$
上述理论中,只考虑部分层流与部分湍流状态下的对流换热系数,由于过渡段的复杂性,所以忽略其影响.此外,踏步板对l 和Re 的影响需结合数值模拟及试验进行研究.
2 电加热踏步构件对流换热实验
为精准测量踏步构件各种工况下的对流换热系数,在大连理工大学低温实验室搭建了极地环境下踏步构件对流换热实验平台.实验室最低温度可达到-50 ℃,最大风速可达到15 m/s,可以模拟相对稳定且均匀的极地低温环境,基本满足实验要求.实验选用极地船上实际应用的踏步板试件,该试件为带有粗糙花纹的平板,试件长度为60 cm、宽度为30 cm.
2.1 实验原理
通常根据牛顿冷却公式来计算对流换热系数,适用于强制对流与稳定温差的自然对流运动.实验依托于牛顿冷却公式,测定不同环境下踏步构件的对流换热系数.
(5) $\Phi=h A\left(t_{\mathrm{w}}-t_{\mathrm{f}}\right)$
(6) $h=\frac{\Phi}{A\left(t_{\mathrm{w}}-t_{\mathrm{f}}\right)}$
式中: Φ 为电加热踏步构件的加热量;A 为踏步构件换热面积;t w 、t f 分别为踏步表面的平均温度和空气流体的平均温度.
电伴热加热属于恒热流加热,t w 与 t f 均稳定增长.当t w 稳定时,热对流带走热量与电伴热散失的加热量相同,此时便可计算得到踏步构件对流换热系数.
2.2 实验系统
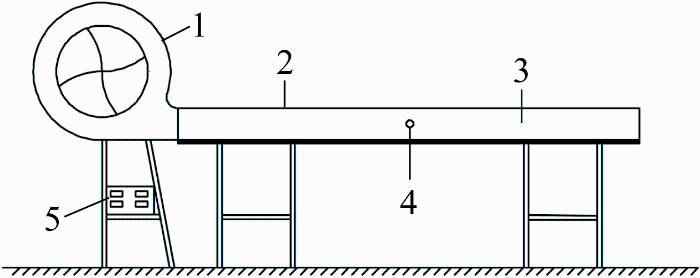
在低温实验室搭建的极地环境下踏步构件对流换热实验平台如图1 所示,主要由供风系统、风道系统、支撑台架和控制系统4部分组成.支撑架台高度为1.5 m,需满足出风口与风道轴线在同一高度的要求,从而避免在风道内产生折射扰动.
图1
图1
实验平台
1 —变频风机,2—风罩,3—风道,4—实验平板,5—控制箱
Fig.1
Experimental platform
电伴热丝布置于踏步板上表面,选取为200 W功率恒定的24 K硅胶碳纤维发热线,以保证加热效率与稳定性.为减少热量散失带来的误差,对踏步构件进行保温处理,选取厚度为3 cm的发泡丁晴橡胶保温隔热棉铺设于踏步板表面.踏步板加热及保温系统布置如图2 所示.
图2
图2
保温层布置示意图
Fig.2
Layout of insulation layer
踏步构件表面形状复杂,为精确测量,在试件表面均匀布置6个测温点,测点布置如图3 所示.风速、风温测点布置在踏步板试件温度测点的上方风道内,实验相关测量仪器如表1 所示.
图3
图3
测点位置布置图
Fig.3
Arrangement of measurement points
2.3 实验结果分析
共进行24组踏步板板对流换热实验,实验工况及实验结果如表2 所示,其中h 为实测值.
根据不同环境因素,对24组不同工况下得到的实验结果进行分析处理,结果如图4 和图5 所示.
图4
图4
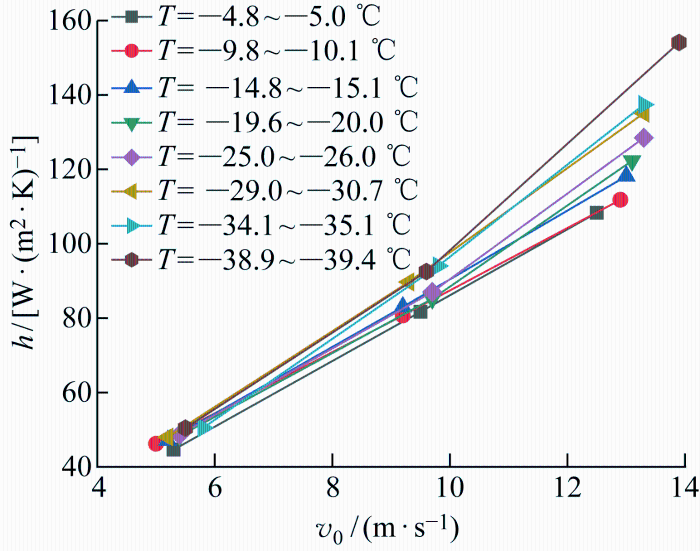
对流换热系数受风速影响分析
Fig.4
Analysis of influence of convection heat exchange coefficient on wind speed
图5
图5
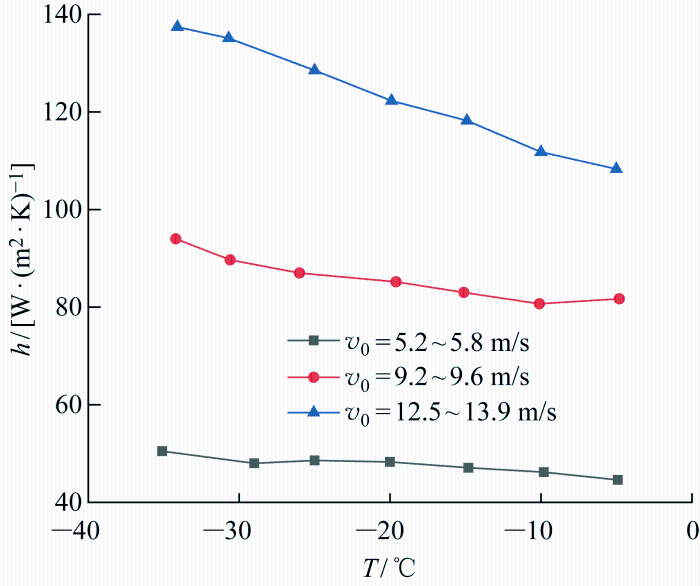
对流换热系数受温度影响分析
Fig.5
Analysis of influence of the convection heat exchange coefficient on temperature
由图4 可知,控制温度在一定范围内,风速增大,踏步构件对流换热系数随之增大.温度一定时,当风速在5.2~5.8 m/s之间时,对流换热系数平
均增长80.7%,折线平均斜率为9.57;当风速在9.2~13.9 m/s之间时,对流换热系数平均增大45.9%,折线平均斜率为10.9,因此高风速对踏步构件对流换热系数影响更显著.
由图5 可知,控制风速在一定范围内,踏步构件的对流换热系数随温度降低而增大.风速一定时,温度在-30~0 ℃内,踏步板对流换热系数平均增大2.6%,折线平均斜率为-0.52;温度在-40~-30 ℃ 内,踏步板对流换热系数平均增大3.7%,折线平均斜率为-0.9;温度在-40~-30 ℃ 内,对流换热系数变化更显著.
一定温度下,风速每增加约5 m/s,踏步构件对流换热系数也随之增大,平均增幅为63.3%;一定风速下,温度每降低约10 ℃,踏步构件对流换热系数随之增大,但平均增幅仅为2.9%.因此,风速为踏步构件对流换热系数的主要影响因素.
风速在5.2 ~5.8 m/s时,折线平均斜率为-0.15;风速在9.2~9.6 m/s时,折线平均斜率为 -0.36;风速在12.5~13.9 m/s时,折线平均斜率为-1.31.因此,风速越大,对流换热系数随温度变化的影响越明显.在实验过程中存在一定的误差,具体原因如下:
(1) 风道内的风速随距风口的距离变远而逐渐降低,并沿构件长度方向在0.1~0.5 m/s波动,测量取平均值.
(2) 实验室空间较大,导致实验室内温度场存在一定的不均匀性与延后性.
(3) 电伴热保温层虽具有良好的隔热性,但仍有少部分热量损失在空气中,引起计算误差.
(4) 随着使用时间的增加,电伴热的加热功率会少部分减小.
3 数值模拟分析
基于ANSYS Fluent有限体积分析软件,采用实验中踏步构件的实际尺寸来构建数值分析模型进行仿真计算.环境条件设置风速范围为0~40 m/s,温度范围为-40~0 ℃.
3.1 模型建立及求解方法
3.1.1 物理模型
踏步板所在的空气流动区域,即风道内区域,长为 2.4 m,宽为700 mm,高为200 mm.实验室测得踏步板实体面积为 300 mm×600 mm,高为10 mm;单个花纹长轴为30 mm,短轴为10 mm,厚度为0.5 mm;花纹间距为50 mm、纵间距为50 mm.花纹每行12个、每列7个.根据以上数据,利用ICEM CFD建立等比例的踏步模型,如图6 和图7 所示.
图6
图6
踏步板模型
Fig.6
Model of tread plate
图7
图7
踏步板对流换热物理模型
Fig.7
Physical model of convective heat transfer of tread plate
3.1.2 控制方程
空气横掠踏步板的对流换热过程是空气与接触的固体表面间的热量交换,其换热过程涉及空气的流动与热能的传递.因此,控制方程应包括3部分:质量守恒方程、动量守恒方程和能量守恒方程.
(7) ∂ ρ ∂ τ ∂ ( ρ u ) ∂ x ∂ ( ρ v ) ∂ y ∂ ( ρ w ) ∂ z
式中:ρ 为密度;τ 为时间;u 、v 、w 分别为x 、y 、z 方向的速度分量.
(8) $\begin{array}{l}\rho\left(\frac{\partial u}{\partial \tau}+u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}+w \frac{\partial u}{\partial z}\right)= \\F_{x}-\frac{\partial p}{\partial x}+\eta\left(\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}+\frac{\partial^{2} u}{\partial z^{2}}\right)\end{array}$
(9) $\begin{array}{l}\rho\left(\frac{\partial v}{\partial \tau}+u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}+w \frac{\partial v}{\partial z}\right)= \\F_{y}-\frac{\partial p}{\partial z}+\eta\left(\frac{\partial^{2} v}{\partial x^{2}}+\frac{\partial^{2} v}{\partial y^{2}}+\frac{\partial^{2} v}{\partial z^{2}}\right)\end{array}$
(10) $\begin{array}{l}\rho\left(\frac{\partial w}{\partial \tau}+u \frac{\partial w}{\partial x}+v \frac{\partial w}{\partial y}+w \frac{\partial w}{\partial z}\right)= \\F_{z}-\frac{\partial p}{\partial z}+\eta\left(\frac{\partial^{2} w}{\partial x^{2}}+\frac{\partial^{2} w}{\partial y^{2}}+\frac{\partial^{2} w}{\partial z^{2}}\right)\end{array}$
式中:Fx 、Fy 、Fz 分别为x 、y 、z 方向的体积力.
(11) $\begin{array}{c}\rho c_{p} \frac{\partial T}{\partial \tau}=\lambda\left(\frac{\partial^{2} T}{\partial x^{2}}+\frac{\partial^{2} T}{\partial y^{2}}+\frac{\partial^{2} T}{\partial z^{2}}\right)+ \\\alpha_{v} T \frac{\partial p}{\partial \tau}+\eta \phi\end{array}$
式中:cp 为定压比热容;αv 为体胀系数;p 为压力;ηϕ 为能量耗散函数.
3.1.3 湍流模型
踏步板的对流换热涉及到层流段和湍流段,考虑边界层过渡变化的影响,数值模拟选择k -ε 湍流模型.标准k -ε 模型是基于湍流动能和扩散率而提出的半经验公式,其中k 方程是一个准确的方程,ε 方程是一个由经验公式推导得到的方程,分别表示为
(12) $\begin{array}{c}\frac{\partial}{\partial t}(\rho k)+\frac{\partial}{\partial x_{i}}\left(\rho k u_{i}\right)=\frac{\partial}{\partial x_{j}}\left[\left(\mu+\frac{\mu_{t}}{\sigma_{k}}\right) \frac{\partial k}{\partial x_{j}}\right]+ \\G_{k}+G_{b}-\rho \varepsilon-Y_{M}+S_{k}\end{array}$
(13) $\begin{array}{c}\frac{\partial}{\partial t}(\rho \varepsilon)+\frac{\partial}{\partial x_{i}}\left(\rho \varepsilon u_{i}\right)=\frac{\partial}{\partial x_{j}}\left[\left(\mu+\frac{\mu_{t}}{\sigma_{\varepsilon}}\right) \frac{\partial \varepsilon}{\partial x_{j}}\right]+ \\C_{1 \varepsilon} \frac{\varepsilon}{K}\left(G_{k}+C_{3 \varepsilon} G_{b}\right)-C_{2 \varepsilon} \rho \frac{\varepsilon^{2}}{K}+S_{\varepsilon}\end{array}$
式中:μ 为动力黏度;μt 为湍流黏度;K 为湍流动能;Gk 表示由层流速度梯度而产生的湍流动能;Gb 表示由浮力产生的湍流动能;YM 是由于在可压缩湍流中过渡的扩散产生的波动;σk 、σε 是k 方程和ε 方程湍流普朗特数;Sk 和Sε 为定义项;C 1 ε ~C3 ε
3.1.4 边界条件
设置边界条件时,将入口inlet设置为速度入口,入口速度范围设置为5~40 m/s,取梯度为5 m/s;温度为233.15 ~263.15 K,取梯度为10 K;出口outlet设置为压力出口,出口温度设置为实验室室温;设置壁面为无滑移的静止壁面,热边界条件为固定热流密度,即为常值 1 111 W/m2 .
3.1.5 网格无关性验证
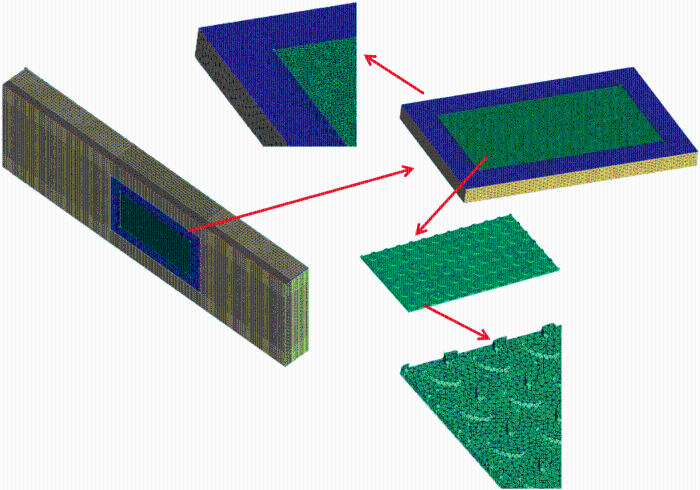
计算域网格的划分采用非结构化网格和结构化网格.计算域分为3部分:主矩形通道、踏步板构件放置矩形通道、踏步板实体.主矩形通道采用六面体结构网格进行划分,踏步板构件放置矩形通道和踏步板实体采用混合网格进行划分.全局最大尺寸为5 μm,最大网格尺寸为 15 μm,网格总数为 592 389,网格划分如图8 所示.
图8
图8
踏步板网格划分
Fig.8
Grid division of tread plate
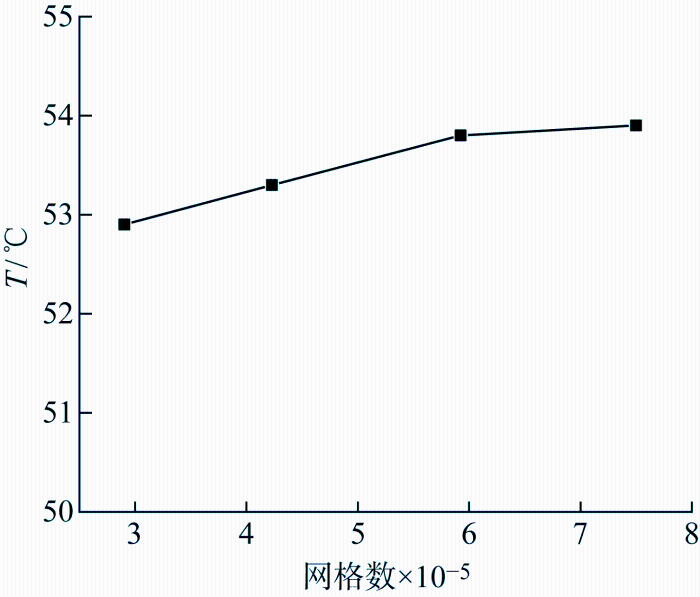
仿真模拟中共选取4套网格来验证网格无关性,网格总数分别为 290 375、422 892、592 389、749 827.工况条件设置温度为 -20 ℃,风速为5 m/s.4套网格的踏步板表面平均温度如图9 所示.由图可知,当网格总数高于 592 389 时,踏步板表面平均温度变化较小.为模拟准确性和节省计算时间,选择的网格数为 592 389,可看作该网格达到网格无关性要求.
图9
图9
网格无关性验证
Fig.9
Results of grid independency test
3.2 仿真结果分析
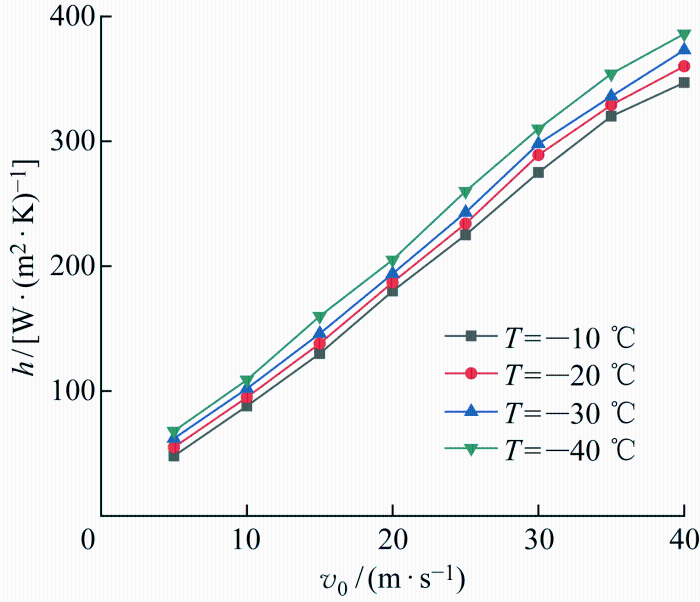
分析风速和温度变化对对流换热系数的影响,结果如图10 和图11 所示.由图10 可知,在-40~-10 ℃ 的温度环境下,控制温度不变,对流换热系数随风速增大而增大.在风速为30~40 m/s时,对流换热系数平均增长59.6%,折线平均斜率为7.9,变化趋势明显;在风速为5~30 m/s时,对流换热系数平均增幅17.7%,折线平均斜率为8.45.因此,风速为5~30 m/s时,对流换热系数受风速影响更大,风速每增大5 m/s,对流换热系数平均增长29.2%.
图10
图10
风速影响仿真结果
Fig.10
Simulation results of influence of wind speed
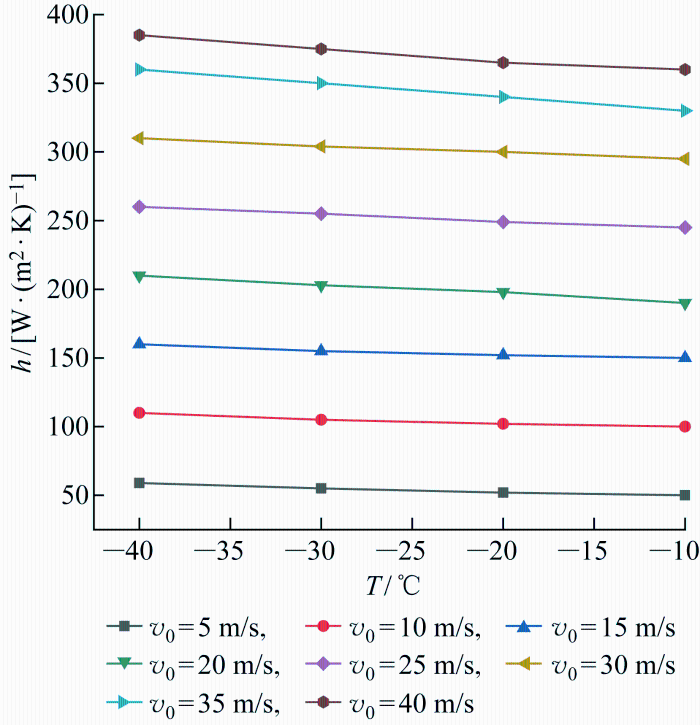
图11
图11
温度影响仿真结果
Fig.11
Simulation results of influence of temperature
由图11 可知,风速范围为5~40 m/s,保持风速不变,对流换热系数随温度增大而减小,但减幅较小;在风速大于25 m/s时,平均斜率为-3.5;而在5~20 m/s风速下,平均斜率为-1.7.因此风速越高,踏步板构件的对流换热系数受温度影响越大.温度每上升10 ℃,对流换热系数平均减幅为3.2%.
模拟结果表明,踏步构件的对流换热系数随风速变化的平均斜率为8.3,其受温度影响的平均斜率绝对值为2.6,因此,风速为踏步构件对流换热系数的主要影响因素.
3.3 踏步板与平板仿真分析对比
踏步板构件可看作表面带有复杂花纹的平板构件,因此两者的对流换热规律有相似之处.为进一步验证踏步板构件仿真结果准确性,对平板构件对流换热系数随温度和风速变化规律进行数值仿真分析.
3.3.1 平板的力学模型建立
使用ANSYS Fluent有限元数值模拟软件,利用Pro/E软件建立平板三维模型,平板模型面积为300 mm×600 mm,高为10 mm.设置边界条件时考虑到平板对流换热过程边界层中过渡层的影响不可忽视,模型选择κ -ε 湍流模型,平板壁面设置为非滑移边界条件,热边界条件设置为固定热流量.
3.3.2 仿真结果对比分析
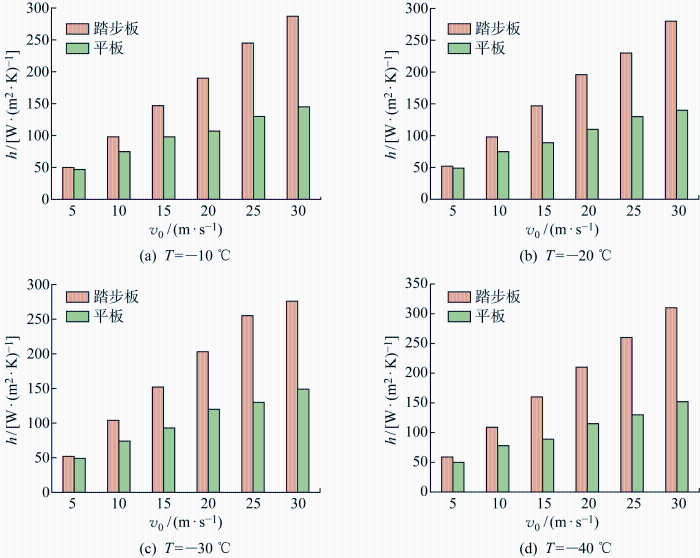
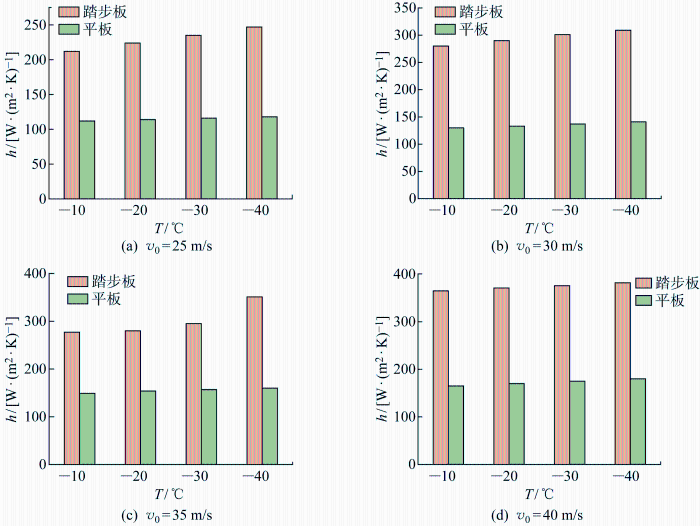
将踏步板构件仿真结果与平板构件仿真结果进行对比,如图12 和图13 所示.由图12 可知,保持温度一定时,踏步板构件与平板构件的对流换热系数均随风速增大而增大;由图13 可知,保持风速一定时,踏步板构件与平板构件的对流换热系数均随温度降低而增大.其中,踏步板构件变化幅度远高于平板构件.由仿真结果可知,两者对流换热系数都随风速增大和温度降低而增大,可验证踏步板构件仿真结果的合理性.
图12
图12
风速影响下仿真结果比较
Fig.12
Comparison of simulation results under the influence of wind speed
图13
图13
温度影响下仿真结果比较
Fig.13
Comparison of simulation results under the influence of temperature
3.4 踏步构件对流换热系数预测模型
由实验可知,在温度一定,风速在5.2~5.8 m/s 以内时,踏步板对流换热系数平均增长80.7%,折线平均斜率为9.57;风速在9.2~13.9 m/s以内时,对流换热系数平均增大45.9%,折线平均斜率为10.9.风速一定,温度在-30~0 ℃以内时,踏步板对流换热系数平均增大2.6%,折线平均斜率为-0.52;温度在-40~-30 ℃以内时,踏步板对流换热系数平均增大3.7%,折线平均斜率为-0.9.因此,风速对踏步构件对流换热系数影响效果更显著.
温度在-40~0 ℃以内时,Pr 为0.707~0.728,λ 为 0.021 2~0.024 0 W/(m·K),变化范围均很小,因此分别取其均值0.718以及 0.022 6 W/(m·K).
通过仿真已证实踏步构件对流换热系数受风速和温度影响规律与平板构件基本相同.理论分析表明,踏步构件的对流换热预测模型可参照于平板构件相关理论公式.踏步构件对流换热系数数学预测模型可表示为
(14) $h=a \frac{\lambda}{l}\left(\operatorname{Re}^{4 / 5}-b\right) \operatorname{Pr}^{1 / 3}, \quad 0.6<\operatorname{Pr}<60$
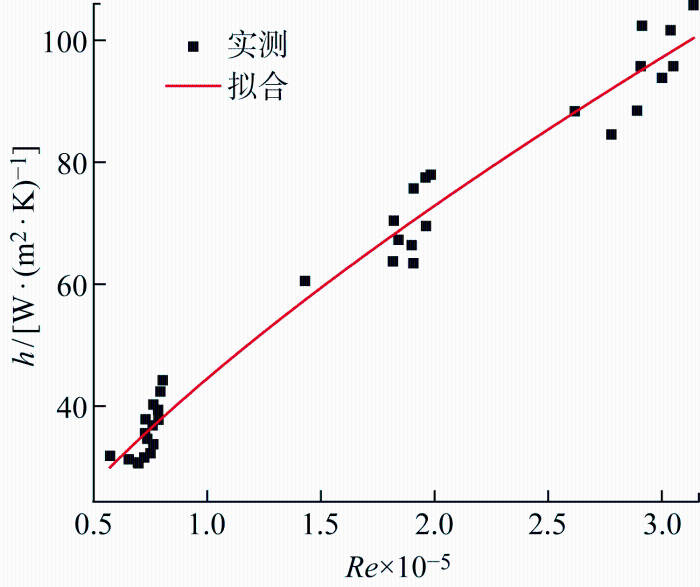
式中:a 为对流换热系数受风速和温度的影响;b 为对流换热系数受临界雷诺数和过渡段的影响.基于式(7),对实验实测数据进行拟合,结果如图14 所示,其中,a =0.082, b =4 594,决定系数R 2 为98%,说明拟合结果较好.
图14
图14
对流换热系数实测数据拟合
Fig.14
Fitting of measured data of convective heat transfer coefficients
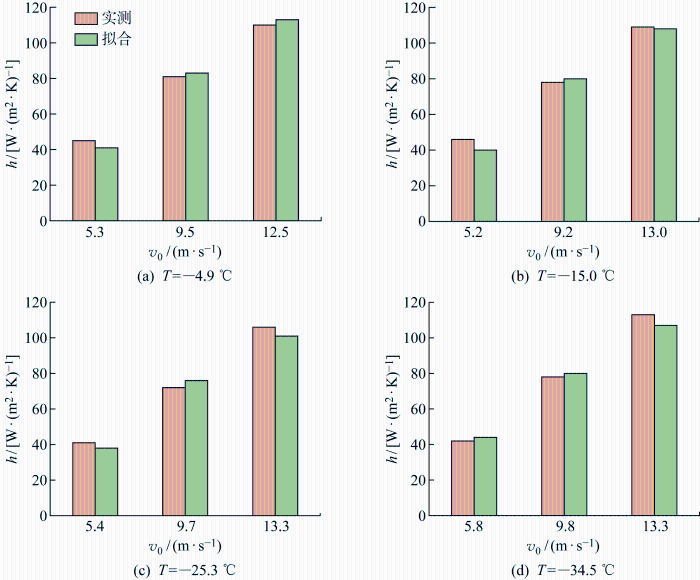
将对流换热预测模型计算结果与实验实测值进行比较,结果如图15 所示.由图可知,计算结果与实测值基本接近,最大误差为10.2%,平均误差为4.5%,验证了拟合结果的正确性.
图15
图15
拟合与实测结果对比
Fig.15
Comparison of fitting and measured results
3.5 对流换热系数预测模型的验证
踏步板对流换热系数预测模型与仿真结果对比如图16 所示.当风速小于25 m/s时,预测模型与仿真结果吻合度较好,其平均误差为4.4%,验证了数值仿真模型的准确性;当风速大于等于25 m/s时,拟合的预测模型结果小于仿真结果,两者间的偏差变大,平均误差为7.4%,满足工程要求.由风速影响分析可知,风速对对流换热系数的影响在 30~40 m/s 以内时减弱.踏步板的对流换热系数预测模型在拟合过程中未对不同风速区间的风速影响进行区分,在一定程度上解释了拟合结果在高风速时,预测模型结果与仿真结果偏差增大.由以上分析可知,在风速0~40 m/s以内时,踏步板对流换热系数预测模型可为海洋工程装备的踏步板构件热平衡计算提供参考.
图16
图16
数值仿真与拟合结果对比
Fig.16
Comparison of numerical simulation and fitting results
4 结论
为探究极地环境下海洋工程装备踏步板构件对流换热系数的影响因素,通过实验与数值仿真两种方式,明确了风速与温度对踏步构件对流换热系数的影响规律;通过在低温实验室搭建的实验平台,测试了温度在-40~0 ℃、风速在0~13.9 m/s内踏步构件对流换热的变化情况;通过Fluent数值模拟软件分析了温度在-40~0 ℃、风速在0~40 m/s 内踏步构件对流换热的变化情况.结果表明:
(1)温度一定时,对流换热系数随风速增大而增大,平均增长17.7%~80.7%.
(2)风速一定时,对流换热系数随温度减小而增大,平均增长2.6%~29.2%.
(3)温度低于-35 ℃ 时,温度对踏步板构件的对流换热系数影响开始增大,但依然小于风速的影响.
(4)风速越大,温度对踏步板构件的对流换热系数影响越大.
通过研究可得出以下结论:①提高风速与降低温度均可增大踏步板构件的对流换热系数;②风速对踏步板构件的对流换热系数影响较大,温度影响较小;③基于实验数据,拟合得到踏步构件对流换热系数预测模型,并通过数值模拟验证预测模型的适用性.本文仅考虑极地环境中的风速和温度对踏步构件对流换热系数的影响进行分析,对如湿度、盐雾等其他环境因素对踏步构件及极地海洋工程装备其他构件的换热规律的影响还需进一步研究分析.
参考文献
View Option
[1]
朱建钢 , 颜其德 , 凌晓良 . 南极资源及其开发利用前景分析
[J]. 中国软科学 2005 (8 ): 17 -22 .
[本文引用: 1]
ZHU Jiangang YAN Qide LING Xiaoliang The analysis of Antarctic resources, and their exploitation and potential utilization
[J]. China Soft Science 2005 (8 ): 17 -22 .
[本文引用: 1]
[2]
谢强 , 陈海龙 , 章继峰 . 极地航行船舶及海洋平台防冰和除冰技术研究进展
[J]. 中国舰船研究 2017 , 12 (1 ): 45 -53 .
[本文引用: 1]
XIE Qiang CHEN Hailong ZHANG Jifeng Research progress of anti-icing/deicing technologies for polar ships and offshore platforms
[J]. Chinese Journal of Ship Research 2017 , 12 (1 ): 45 -53 .
[本文引用: 1]
[3]
沈杰 , 白旭 . 基于Fluent和FENSAP-ICE的极区海洋平台甲板结构结冰数值模拟
[J]. 极地研究 2020 , 32 (2 ): 177 -183 .
DOI:10.13679/j.jdyj.20190033
[本文引用: 1]
极区自然资源丰富却气候恶劣, 海洋平台在此地区作业时甲板表面极易出现结冰现象。针对极区海洋平台甲板结构结冰问题, 采用Fluent与FENSAP-ICE软件相结合的方法, 分析在过冷雾和过冷雨条件下, 距海面高度和结构特征长度对甲板结构结冰的影响。结果表明: 当特征风速为5 m·s<sup>–1</sup>、6 m·s<sup>–1</sup>和7 m·s<sup>–1</sup>时, 在风速不变的条件下, 随着距海面高度由2 m增加到20 m, 结构表面的平均结冰厚度均逐渐增加且结构表面的结冰相对增长率逐渐减小; 在特征风速为5m·s<sup>–1</sup>条件下, 在距海面高度为20 m和80 m处, 随着结构特征长度由1 m增加到30 m时, 结构表面的平均结冰厚度均逐渐减小且减少程度逐渐减缓。
SHEN Jie BAI Xu Numerical simulations of deck structure icing on polar offshore platforms based on fluent and fensap-ice
[J]. Chinese Journal of Polar Research 2020 , 32 (2 ): 177 -183 .
DOI:10.13679/j.jdyj.20190033
[本文引用: 1]
<p>The polar region is rich in natural resources, but the climate is harsh. The deck surface of offshore platforms in this region is prone to icing, which is dangerous. To investigate factors affecting the icing of deck structures on polar marine platforms, a combination of the software programs Fluent and FENSAP-ICE was used to analyze the influence of sea surface height and structure length on deck icing under conditions of supercooled fog and rain. The results showed that when Characteristic wind speeds were 5 m·s<sup>–1</sup>, 6 m·s<sup>–1</sup> and 7 m·s<sup>–1</sup>, average ice thickness on the structure surface increased gradually with height from 2 m to 20 m and the relative growth rate of ice on the structure surface decreased gradually. Additionally, when Characteristic wind speed was 5 m·s<sup>–1</sup> at altitudes of 20 m and 80 m above sea level, the length of the structure increased from 1 m to 30 m, and average ice thickness on the structure surface and degree of reduction decreased.</p>
[4]
陆煊 , 崔玫 , 曹洪波 , 等 . 船舶防冻除冰技术现状与发展
[J]. 船海工程 2016 , 45 (2 ): 37 -39 .
[本文引用: 1]
LU Xuan CUI Mei CAO Hongbo et al Present situation and development of de-icing and prevent frostbite technology of ships
[J]. Ship & Ocean Engineering 2016 , 45 (2 ): 37 -39 .
[本文引用: 1]
[5]
操太春 , 吴刚 , 孔祥逸 , 等 . 极地海洋工程装备圆管结构的对流换热影响
[J]. 上海交通大学学报 2023 , 57 (1 ): 17 -23 .
DOI:10.16183/j.cnki.jsjtu.2021.205
[本文引用: 1]
电伴热是极地海洋工程装备防寒主要措施,而热平衡是对流换热的关键问题.以圆管构件为研究对象,采用有限元数值仿真软件Fluent数值仿真与模型实验相结合的方法,分析了圆管构件在风速为0~40 m/s、温度为-40~0 ℃的极地环境条件下对流换热系数变化情况;基于数值仿真数据建立了电加热圆管构件对流换热系数的预测模型.结果表明:增大风速和降低温度都会增加圆管构件的对流换热系数;温度低于-30 ℃ 或风速大于25 m/s且温度低于-20 ℃ 时,温度对圆管的对流换热系数影响增大;实测数据验证了该模型的合理性.
CAO Taichun WU Gang KONG Xiangyi et al Influence of convective heat transfer on circular tube structure of polar ocean engineering equipment
[J]. Journal of Shanghai Jiao Tong University 2023 , 57 (1 ): 17 -23 .
[本文引用: 1]
[6]
YANG M KHAN F I LYE L et al Risk-based winterization for vessels operations in Arctic environments
[J]. Journal of Ship Production and Design 2013 , 29 (4 ): 199 -210 .
[本文引用: 1]
[7]
ABS . Guide for building and classing vessels intended for navigation in polar waters:ABS 163-2008 [S]. Houston, USA : ABS , 2008 .
[本文引用: 1]
[8]
李金平 , 董玉慧 , 李彩军 , 等 . 寒冷地区空气源热泵辅助太阳能热水器供暖性能
[J]. 上海交通大学学报 2023 , 57 (7 ): 910 -920 .
DOI:10.16183/j.cnki.jsjtu.2022.005
[本文引用: 1]
为提高太阳能热水器供暖的稳定性并大幅降低空气源热泵供暖的成本,提出空气源热泵辅助太阳能真空管热水器供暖构想,在甘肃省兰州市七里河区魏岭乡绿化村搭建空气源热泵辅助太阳能热水器供暖试验系统,详细研究了晴天、阴天及多云3种典型工况下系统的集热效率、热泵性能系数、系统太阳能保证率和系统能效比等.研究结果表明,晴天、阴天及多云工况下太阳能集热器有效得热量分别为75.5、4.1和49. 2 kW·h,集热效率分别为61.3%、26.6%、55.2%,太阳能热泵平均性能系数(COP)分别为3.6、3.4、3.6,空气源热泵平均COP分别为0、2.9、3.1,系统实际供热量分别为113.4、125.9和124.8 kW·h,系统耗电量分别为33.4、50.5和42.7 kW·h,系统太阳能保证率分别为66.6%、3.3%、39.4%,系统能效比分别为3.4,2.5,2.9.研究证明了太阳能真空管集热器-空气源热泵系统用于寒冷地区供暖的可行性,为寒冷地区供暖提供了一种新途径.
LI Jinping DONG Yuhui LI Caijun et al Performance of solar vacuum tube water heater-air source heat pump system in cold area
[J]. Journal of Shanghai Jiao Tong University 2023 , 57 (7 ): 910 -920 .
[本文引用: 1]
[9]
INCROPERA F P DEWITT D P Fundamentals of heat and mass transfer [M]. 5th ed. New York, USA : John Wiley & sons , 2002 .
[本文引用: 1]
[10]
ZONTUL H HAMZAH H KURTULMUŞ N et al Investigation of convective heat transfer and flow hydrodynamics in rectangular grooved channels
[J]. International Communications in Heat and Mass Transfer 2021 , 126 : 105366 .
[本文引用: 1]
[11]
CHURCHILL S W A comprehensive correlating equation for forced convection from flat plates
[J]. AIChE Journal 1976 , 22 (2 ): 264 -268 .
[本文引用: 1]
[12]
DANOV S N ARAI N CHURCHILL S W Exact formulations and nearly exact numerical solutions for convection in turbulent flow between parallel plates
[J]. International Journal of Heat and Mass Transfer 2000 , 43 (15 ): 2767 -2777 .
[本文引用: 1]
[13]
郑卉 , 钱宏亮 , 金晓飞 , 等 . 钢构件对流换热系数计算方法综述
[C]//第十五届空间结构学术会议论文集. 上海 , 2014 : 409 -414 .
[本文引用: 1]
ZHENG Fen QIAN Hongliang JIN Xiaofei et al Summary of calculation methods for convective heat transfer coefficient of steel members
[C]//Proceedings of the 15th Spatial Structure Academic Conference . Shanghai, China , 2014 : 409 -414 .
[本文引用: 1]
[14]
李烨 , 盈亮 , 胡平 , 等 . 圆截面管对流换热系数的实验研究
[J]. 热加工工艺 2013 , 42 (19 ): 15 -18 .
[本文引用: 1]
LI Ye YING Liang HU Ping et al Experimental investigation of convectional heat transfer coefficient in circular cross-section tubes
[J]. Hot Working Technology 2013 , 42 (19 ): 15 -18 .
[本文引用: 1]
南极资源及其开发利用前景分析
1
2005
... 随着各国可开采海洋资源的不断减少,极地蕴藏的丰富资源被持续发现,各国逐步加大了对北极资源的勘探和开发力度[1 ] .极地海洋环境复杂,低温、强风及潮湿等恶劣气候极易导致海洋工程装备上部的设施结冰.极地船舶覆冰会影响船舶结构稳性与功能性,表现为增加船舶质量,改变整体结构应力[2 ] ,造成设备不同程度的损坏,影响其使用性能,甚至会危害到作业人员自身安全[3 ] .因此,开展极地装备的防寒研究具有重要意义.极地装备上部设施复杂,从结构外形特征上可分为平板类、圆管类等规则构件和不规则类型构件,如带有花纹的踏步板构件.目前,极地装备上部设施各类部件的防寒措施主要采用电伴热方式[4 ] . ...
The analysis of Antarctic resources, and their exploitation and potential utilization
1
2005
... 随着各国可开采海洋资源的不断减少,极地蕴藏的丰富资源被持续发现,各国逐步加大了对北极资源的勘探和开发力度[1 ] .极地海洋环境复杂,低温、强风及潮湿等恶劣气候极易导致海洋工程装备上部的设施结冰.极地船舶覆冰会影响船舶结构稳性与功能性,表现为增加船舶质量,改变整体结构应力[2 ] ,造成设备不同程度的损坏,影响其使用性能,甚至会危害到作业人员自身安全[3 ] .因此,开展极地装备的防寒研究具有重要意义.极地装备上部设施复杂,从结构外形特征上可分为平板类、圆管类等规则构件和不规则类型构件,如带有花纹的踏步板构件.目前,极地装备上部设施各类部件的防寒措施主要采用电伴热方式[4 ] . ...
极地航行船舶及海洋平台防冰和除冰技术研究进展
1
2017
... 随着各国可开采海洋资源的不断减少,极地蕴藏的丰富资源被持续发现,各国逐步加大了对北极资源的勘探和开发力度[1 ] .极地海洋环境复杂,低温、强风及潮湿等恶劣气候极易导致海洋工程装备上部的设施结冰.极地船舶覆冰会影响船舶结构稳性与功能性,表现为增加船舶质量,改变整体结构应力[2 ] ,造成设备不同程度的损坏,影响其使用性能,甚至会危害到作业人员自身安全[3 ] .因此,开展极地装备的防寒研究具有重要意义.极地装备上部设施复杂,从结构外形特征上可分为平板类、圆管类等规则构件和不规则类型构件,如带有花纹的踏步板构件.目前,极地装备上部设施各类部件的防寒措施主要采用电伴热方式[4 ] . ...
Research progress of anti-icing/deicing technologies for polar ships and offshore platforms
1
2017
... 随着各国可开采海洋资源的不断减少,极地蕴藏的丰富资源被持续发现,各国逐步加大了对北极资源的勘探和开发力度[1 ] .极地海洋环境复杂,低温、强风及潮湿等恶劣气候极易导致海洋工程装备上部的设施结冰.极地船舶覆冰会影响船舶结构稳性与功能性,表现为增加船舶质量,改变整体结构应力[2 ] ,造成设备不同程度的损坏,影响其使用性能,甚至会危害到作业人员自身安全[3 ] .因此,开展极地装备的防寒研究具有重要意义.极地装备上部设施复杂,从结构外形特征上可分为平板类、圆管类等规则构件和不规则类型构件,如带有花纹的踏步板构件.目前,极地装备上部设施各类部件的防寒措施主要采用电伴热方式[4 ] . ...
基于Fluent和FENSAP-ICE的极区海洋平台甲板结构结冰数值模拟
1
2020
... 随着各国可开采海洋资源的不断减少,极地蕴藏的丰富资源被持续发现,各国逐步加大了对北极资源的勘探和开发力度[1 ] .极地海洋环境复杂,低温、强风及潮湿等恶劣气候极易导致海洋工程装备上部的设施结冰.极地船舶覆冰会影响船舶结构稳性与功能性,表现为增加船舶质量,改变整体结构应力[2 ] ,造成设备不同程度的损坏,影响其使用性能,甚至会危害到作业人员自身安全[3 ] .因此,开展极地装备的防寒研究具有重要意义.极地装备上部设施复杂,从结构外形特征上可分为平板类、圆管类等规则构件和不规则类型构件,如带有花纹的踏步板构件.目前,极地装备上部设施各类部件的防寒措施主要采用电伴热方式[4 ] . ...
Numerical simulations of deck structure icing on polar offshore platforms based on fluent and fensap-ice
1
2020
... 随着各国可开采海洋资源的不断减少,极地蕴藏的丰富资源被持续发现,各国逐步加大了对北极资源的勘探和开发力度[1 ] .极地海洋环境复杂,低温、强风及潮湿等恶劣气候极易导致海洋工程装备上部的设施结冰.极地船舶覆冰会影响船舶结构稳性与功能性,表现为增加船舶质量,改变整体结构应力[2 ] ,造成设备不同程度的损坏,影响其使用性能,甚至会危害到作业人员自身安全[3 ] .因此,开展极地装备的防寒研究具有重要意义.极地装备上部设施复杂,从结构外形特征上可分为平板类、圆管类等规则构件和不规则类型构件,如带有花纹的踏步板构件.目前,极地装备上部设施各类部件的防寒措施主要采用电伴热方式[4 ] . ...
船舶防冻除冰技术现状与发展
1
2016
... 随着各国可开采海洋资源的不断减少,极地蕴藏的丰富资源被持续发现,各国逐步加大了对北极资源的勘探和开发力度[1 ] .极地海洋环境复杂,低温、强风及潮湿等恶劣气候极易导致海洋工程装备上部的设施结冰.极地船舶覆冰会影响船舶结构稳性与功能性,表现为增加船舶质量,改变整体结构应力[2 ] ,造成设备不同程度的损坏,影响其使用性能,甚至会危害到作业人员自身安全[3 ] .因此,开展极地装备的防寒研究具有重要意义.极地装备上部设施复杂,从结构外形特征上可分为平板类、圆管类等规则构件和不规则类型构件,如带有花纹的踏步板构件.目前,极地装备上部设施各类部件的防寒措施主要采用电伴热方式[4 ] . ...
Present situation and development of de-icing and prevent frostbite technology of ships
1
2016
... 随着各国可开采海洋资源的不断减少,极地蕴藏的丰富资源被持续发现,各国逐步加大了对北极资源的勘探和开发力度[1 ] .极地海洋环境复杂,低温、强风及潮湿等恶劣气候极易导致海洋工程装备上部的设施结冰.极地船舶覆冰会影响船舶结构稳性与功能性,表现为增加船舶质量,改变整体结构应力[2 ] ,造成设备不同程度的损坏,影响其使用性能,甚至会危害到作业人员自身安全[3 ] .因此,开展极地装备的防寒研究具有重要意义.极地装备上部设施复杂,从结构外形特征上可分为平板类、圆管类等规则构件和不规则类型构件,如带有花纹的踏步板构件.目前,极地装备上部设施各类部件的防寒措施主要采用电伴热方式[4 ] . ...
极地海洋工程装备圆管结构的对流换热影响
1
2023
... 在电伴热加热过程中,因热源与壁面间存在温度差,导致流体各部分密度不同而形成对流运动,该运动属于对流换热的传热方式.电伴热加热方式通常分为恒热流与恒壁温两种,对于不同的加热方式,温差计算也存在差异.恒热流加热方式可实现热量的恒定输入,此过程流体温度与壁面温度持续升高,故其温差为流体温度与壁面温度之差;恒壁温加热方式是通过改变加热量,使壁面的温度保持恒定,此过程壁温不变,流体温度增加,因其局部温差是变化的,故温差数取其平均数.目前,极地海洋工程装备的防除冰普遍使用恒热流的电伴热加热方式[5 ] . ...
Influence of convective heat transfer on circular tube structure of polar ocean engineering equipment
1
2023
... 在电伴热加热过程中,因热源与壁面间存在温度差,导致流体各部分密度不同而形成对流运动,该运动属于对流换热的传热方式.电伴热加热方式通常分为恒热流与恒壁温两种,对于不同的加热方式,温差计算也存在差异.恒热流加热方式可实现热量的恒定输入,此过程流体温度与壁面温度持续升高,故其温差为流体温度与壁面温度之差;恒壁温加热方式是通过改变加热量,使壁面的温度保持恒定,此过程壁温不变,流体温度增加,因其局部温差是变化的,故温差数取其平均数.目前,极地海洋工程装备的防除冰普遍使用恒热流的电伴热加热方式[5 ] . ...
Risk-based winterization for vessels operations in Arctic environments
1
2013
... 目前,极地环境下的海洋工程装备关于防除冰的设计大多参考船级社的相关规范,未充分考虑船舶航行时外部环境的变化对加热量的影响,导致建议的加热功率过大,造成一定的能耗浪费[6 -7 ] .低温环境下,各环境因素对构件的加热量影响较大[8 ] .为此,需确定已考虑极地环境因素的对流换热系数预测模型,为极地装备上部设施防寒设计提供依据.相较于平板构件,踏步板表面覆有凸出花纹,换热面积小,在极地环境下对流换热影响因素复杂且换热规律不明确[9 ] . ...
1
2008
... 目前,极地环境下的海洋工程装备关于防除冰的设计大多参考船级社的相关规范,未充分考虑船舶航行时外部环境的变化对加热量的影响,导致建议的加热功率过大,造成一定的能耗浪费[6 -7 ] .低温环境下,各环境因素对构件的加热量影响较大[8 ] .为此,需确定已考虑极地环境因素的对流换热系数预测模型,为极地装备上部设施防寒设计提供依据.相较于平板构件,踏步板表面覆有凸出花纹,换热面积小,在极地环境下对流换热影响因素复杂且换热规律不明确[9 ] . ...
寒冷地区空气源热泵辅助太阳能热水器供暖性能
1
2023
... 目前,极地环境下的海洋工程装备关于防除冰的设计大多参考船级社的相关规范,未充分考虑船舶航行时外部环境的变化对加热量的影响,导致建议的加热功率过大,造成一定的能耗浪费[6 -7 ] .低温环境下,各环境因素对构件的加热量影响较大[8 ] .为此,需确定已考虑极地环境因素的对流换热系数预测模型,为极地装备上部设施防寒设计提供依据.相较于平板构件,踏步板表面覆有凸出花纹,换热面积小,在极地环境下对流换热影响因素复杂且换热规律不明确[9 ] . ...
Performance of solar vacuum tube water heater-air source heat pump system in cold area
1
2023
... 目前,极地环境下的海洋工程装备关于防除冰的设计大多参考船级社的相关规范,未充分考虑船舶航行时外部环境的变化对加热量的影响,导致建议的加热功率过大,造成一定的能耗浪费[6 -7 ] .低温环境下,各环境因素对构件的加热量影响较大[8 ] .为此,需确定已考虑极地环境因素的对流换热系数预测模型,为极地装备上部设施防寒设计提供依据.相较于平板构件,踏步板表面覆有凸出花纹,换热面积小,在极地环境下对流换热影响因素复杂且换热规律不明确[9 ] . ...
1
2002
... 目前,极地环境下的海洋工程装备关于防除冰的设计大多参考船级社的相关规范,未充分考虑船舶航行时外部环境的变化对加热量的影响,导致建议的加热功率过大,造成一定的能耗浪费[6 -7 ] .低温环境下,各环境因素对构件的加热量影响较大[8 ] .为此,需确定已考虑极地环境因素的对流换热系数预测模型,为极地装备上部设施防寒设计提供依据.相较于平板构件,踏步板表面覆有凸出花纹,换热面积小,在极地环境下对流换热影响因素复杂且换热规律不明确[9 ] . ...
Investigation of convective heat transfer and flow hydrodynamics in rectangular grooved channels
1
2021
... 踏步板构件因其表面复杂,相关传热的研究尚有匮乏.Zontul等[10 ] 对具有矩形凹槽顶壁和底壁通道中的对流传热和流动特性进行了实验和数值研究,通过上下壁面施加恒定热量的恒热流加热方式进行实验,在雷诺数Re 为2×103 ~6.5×103 之间,得出壁面平均努塞尔数Nu 是直通道的1.9~2.4倍,且凹槽会导致额外的压降;Churchill[11 ] 得出完全层流与完全湍流状态下Nu 与普朗特数Pr 的精确公式;Danov等[12 ] 针对平板间完全湍流对流的状态,得出流体速度、温度分布及摩擦因数和Nu 的精确公式;郑卉等[13 ] 研究了不同构件截面、不同风向对构件对流换热系数的影响;李烨等[14 ] 通过实验对水流与模具钢之间的对流换热系数进行研究,分析了流量、热流密度和管道直径对对流换热系数的影响.因极地气候环境恶劣多变,与上述研究选取的气候条件有较大不同,且上述研究的环境影响因素也不全面,所以以极地主要环境因素为变量,进行对流换热系数研究. ...
A comprehensive correlating equation for forced convection from flat plates
1
1976
... 踏步板构件因其表面复杂,相关传热的研究尚有匮乏.Zontul等[10 ] 对具有矩形凹槽顶壁和底壁通道中的对流传热和流动特性进行了实验和数值研究,通过上下壁面施加恒定热量的恒热流加热方式进行实验,在雷诺数Re 为2×103 ~6.5×103 之间,得出壁面平均努塞尔数Nu 是直通道的1.9~2.4倍,且凹槽会导致额外的压降;Churchill[11 ] 得出完全层流与完全湍流状态下Nu 与普朗特数Pr 的精确公式;Danov等[12 ] 针对平板间完全湍流对流的状态,得出流体速度、温度分布及摩擦因数和Nu 的精确公式;郑卉等[13 ] 研究了不同构件截面、不同风向对构件对流换热系数的影响;李烨等[14 ] 通过实验对水流与模具钢之间的对流换热系数进行研究,分析了流量、热流密度和管道直径对对流换热系数的影响.因极地气候环境恶劣多变,与上述研究选取的气候条件有较大不同,且上述研究的环境影响因素也不全面,所以以极地主要环境因素为变量,进行对流换热系数研究. ...
Exact formulations and nearly exact numerical solutions for convection in turbulent flow between parallel plates
1
2000
... 踏步板构件因其表面复杂,相关传热的研究尚有匮乏.Zontul等[10 ] 对具有矩形凹槽顶壁和底壁通道中的对流传热和流动特性进行了实验和数值研究,通过上下壁面施加恒定热量的恒热流加热方式进行实验,在雷诺数Re 为2×103 ~6.5×103 之间,得出壁面平均努塞尔数Nu 是直通道的1.9~2.4倍,且凹槽会导致额外的压降;Churchill[11 ] 得出完全层流与完全湍流状态下Nu 与普朗特数Pr 的精确公式;Danov等[12 ] 针对平板间完全湍流对流的状态,得出流体速度、温度分布及摩擦因数和Nu 的精确公式;郑卉等[13 ] 研究了不同构件截面、不同风向对构件对流换热系数的影响;李烨等[14 ] 通过实验对水流与模具钢之间的对流换热系数进行研究,分析了流量、热流密度和管道直径对对流换热系数的影响.因极地气候环境恶劣多变,与上述研究选取的气候条件有较大不同,且上述研究的环境影响因素也不全面,所以以极地主要环境因素为变量,进行对流换热系数研究. ...
钢构件对流换热系数计算方法综述
1
2014
... 踏步板构件因其表面复杂,相关传热的研究尚有匮乏.Zontul等[10 ] 对具有矩形凹槽顶壁和底壁通道中的对流传热和流动特性进行了实验和数值研究,通过上下壁面施加恒定热量的恒热流加热方式进行实验,在雷诺数Re 为2×103 ~6.5×103 之间,得出壁面平均努塞尔数Nu 是直通道的1.9~2.4倍,且凹槽会导致额外的压降;Churchill[11 ] 得出完全层流与完全湍流状态下Nu 与普朗特数Pr 的精确公式;Danov等[12 ] 针对平板间完全湍流对流的状态,得出流体速度、温度分布及摩擦因数和Nu 的精确公式;郑卉等[13 ] 研究了不同构件截面、不同风向对构件对流换热系数的影响;李烨等[14 ] 通过实验对水流与模具钢之间的对流换热系数进行研究,分析了流量、热流密度和管道直径对对流换热系数的影响.因极地气候环境恶劣多变,与上述研究选取的气候条件有较大不同,且上述研究的环境影响因素也不全面,所以以极地主要环境因素为变量,进行对流换热系数研究. ...
Summary of calculation methods for convective heat transfer coefficient of steel members
1
2014
... 踏步板构件因其表面复杂,相关传热的研究尚有匮乏.Zontul等[10 ] 对具有矩形凹槽顶壁和底壁通道中的对流传热和流动特性进行了实验和数值研究,通过上下壁面施加恒定热量的恒热流加热方式进行实验,在雷诺数Re 为2×103 ~6.5×103 之间,得出壁面平均努塞尔数Nu 是直通道的1.9~2.4倍,且凹槽会导致额外的压降;Churchill[11 ] 得出完全层流与完全湍流状态下Nu 与普朗特数Pr 的精确公式;Danov等[12 ] 针对平板间完全湍流对流的状态,得出流体速度、温度分布及摩擦因数和Nu 的精确公式;郑卉等[13 ] 研究了不同构件截面、不同风向对构件对流换热系数的影响;李烨等[14 ] 通过实验对水流与模具钢之间的对流换热系数进行研究,分析了流量、热流密度和管道直径对对流换热系数的影响.因极地气候环境恶劣多变,与上述研究选取的气候条件有较大不同,且上述研究的环境影响因素也不全面,所以以极地主要环境因素为变量,进行对流换热系数研究. ...
圆截面管对流换热系数的实验研究
1
2013
... 踏步板构件因其表面复杂,相关传热的研究尚有匮乏.Zontul等[10 ] 对具有矩形凹槽顶壁和底壁通道中的对流传热和流动特性进行了实验和数值研究,通过上下壁面施加恒定热量的恒热流加热方式进行实验,在雷诺数Re 为2×103 ~6.5×103 之间,得出壁面平均努塞尔数Nu 是直通道的1.9~2.4倍,且凹槽会导致额外的压降;Churchill[11 ] 得出完全层流与完全湍流状态下Nu 与普朗特数Pr 的精确公式;Danov等[12 ] 针对平板间完全湍流对流的状态,得出流体速度、温度分布及摩擦因数和Nu 的精确公式;郑卉等[13 ] 研究了不同构件截面、不同风向对构件对流换热系数的影响;李烨等[14 ] 通过实验对水流与模具钢之间的对流换热系数进行研究,分析了流量、热流密度和管道直径对对流换热系数的影响.因极地气候环境恶劣多变,与上述研究选取的气候条件有较大不同,且上述研究的环境影响因素也不全面,所以以极地主要环境因素为变量,进行对流换热系数研究. ...
Experimental investigation of convectional heat transfer coefficient in circular cross-section tubes
1
2013
... 踏步板构件因其表面复杂,相关传热的研究尚有匮乏.Zontul等[10 ] 对具有矩形凹槽顶壁和底壁通道中的对流传热和流动特性进行了实验和数值研究,通过上下壁面施加恒定热量的恒热流加热方式进行实验,在雷诺数Re 为2×103 ~6.5×103 之间,得出壁面平均努塞尔数Nu 是直通道的1.9~2.4倍,且凹槽会导致额外的压降;Churchill[11 ] 得出完全层流与完全湍流状态下Nu 与普朗特数Pr 的精确公式;Danov等[12 ] 针对平板间完全湍流对流的状态,得出流体速度、温度分布及摩擦因数和Nu 的精确公式;郑卉等[13 ] 研究了不同构件截面、不同风向对构件对流换热系数的影响;李烨等[14 ] 通过实验对水流与模具钢之间的对流换热系数进行研究,分析了流量、热流密度和管道直径对对流换热系数的影响.因极地气候环境恶劣多变,与上述研究选取的气候条件有较大不同,且上述研究的环境影响因素也不全面,所以以极地主要环境因素为变量,进行对流换热系数研究. ...