走向深水是世界油气工业发展的必然趋势,浮式钻井生产储卸油装置(floating drilling production storage and offloading,FDPSO)和Spar钻井生产储卸油平台(spar drilling production storage and offloading,Spar FPSO)等新型多功能海洋平台应运而生.这些新型平台上安装着多种立式圆柱形储液容器,例如月池、中心井、油气分离器和储油舱等.当平台的运动频率接近圆柱形容器内液体的最低阶固有频率时,会产生大幅度的自由液面运动,并在壁面上产生冲击载荷,也就是“晃荡”现象.此外,由于此类平台的储油量通常非常大,例如,世界上第1个圆筒形FDPSO——Seven Driller[1]和第1个Spar FPSO——Aasta Hansteen[2]的储油量都为 25 000 m3.显然,储油舱内大量液体的剧烈晃动甚至会危及平台的动态稳定性和安全性.因此,掌握圆柱形容器内液体的晃荡特性对于新型浮式海洋平台的设计和操作至关重要.
国内外研究液舱晃荡问题采用的方法包括理论分析[3-4]、数值模拟[5-6]和模型试验[7⇓⇓⇓⇓-12].其中模型试验结果一般可信度高,不仅能发现新的物理现象,试验数据还可用于验证理论与数值方法的准确性,但成本高.刘戈等[7]利用有限元离散方式结合势流理论,计算了液化天然气运输船(LNG) 独立C型舱液体晃荡的理论固有频率,并通过模型试验对数值算法的结果进行了验证.薛米安等[8]开展了二维矩形液舱在不同频率激励下的水平晃荡试验,并分析了试验数据的可重复性、冲击压力的频率响应以及共振模态下的冲击压力特征.杨志勋等[9]通过开展大比尺晃荡模型试验得到晃荡荷载峰值的统计样本,利用广义极值分布、两参Weibull分布和三参 Weibull分布来拟合预测晃荡荷载峰值.Lee等[10]研究了密度比和相变对矩形液舱内晃动冲击的影响.Souto-Iglesias等[11]研究了规则受迫横摇运动中矩形液舱的宽度对冲击压力统计的影响.Kim等[12]研究了包含弹簧系统的水平挡板对晃荡抑制的影响.
在上述所有研究中,液舱都是受到单自由度运动激励,且舱内自由液面的运动都可近似为沿液舱运动方向的二维平面波运动.但对于圆柱液舱,当外部激励频率接近液体的最低阶固有频率时,即使液舱的运动方向是一维的,液舱内也会出现三维平移运动波和旋转运动波.目前,立式圆柱形液舱内共振三维旋转波的相关研究还较为少见.因此,本文搭建了一套液舱晃荡模型试验装置,对立式圆柱形液舱内一阶与二阶共振三维旋转波展开研究.
1 试验装置
在设计小尺度晃荡模型试验时,为了让模型试验观察到的晃荡现象能更好地反映真实液舱中出现的物理现象,选取一个合适的无量纲数至关重要.弗劳德数、雷诺数、欧拉数、韦伯数和马赫数是与液体晃荡相关的5个经典无量纲数[10].弗劳德数Fr表示流动的惯性力与重力之间的关系.由于自由液面晃荡由重力波主导,所以在大多数小尺度模型试验中,优先采用可以很好地反映整体晃荡特性的Fr.其他4个无量纲数,以雷诺数Re为例,主要适用于重点研究局部流场特性的晃荡模型试验.弗劳德数和雷诺数的定义分别为Fr=U/
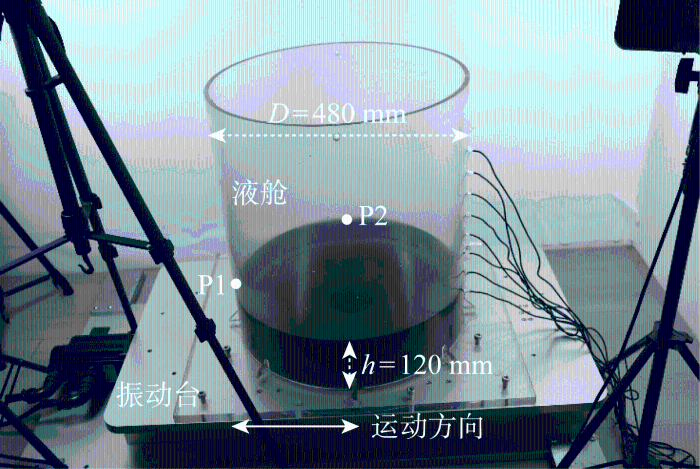
本文采用的试验装置如图1所示,包括半径R=240 mm的立式圆柱形液舱、振动台、电动缸、控制柜和LED灯.另外还包括计算机、摄相机和两个浪高仪.液舱模型由厚度为10 mm的透明有机玻璃制成,并安装在振动台上.振动台由电动缸驱动,因此能够在不同外部激励频率(0.01 Hz<fe<10 Hz)和振幅(1 mm<A<200 mm)下产生水平简谐激励.控制柜的两端分别连接电动缸和计算机,由计算机输入外部激励参数.摄像机用于记录拍摄自由液面的运动.此外,为监测自由液面沿平行液舱运动方向和垂直液舱运动方向的最大波幅,两个浪高仪分别安装在舱壁左侧(P1)和后方(P2)距离舱壁20 mm处,其中,P2处的波幅可用于指示是否出现旋转波.由于振动台安装在非常坚固的轨道上,所以可确保不会产生其他方向的振动.试验过程中,液舱内充装h=120 mm的染色水,即充液比h/D=0.25.由于液舱的厚度比较大,可以视舱壁为刚性,所以,本研究可忽略剧烈自由表面晃动冲击下的水弹性效应.
图1
2 试验工况
当液舱作振荡运动时,液舱提供能量以维持液体的运动.当液舱的振荡频率接近自由液面的固有频率时,液体的运动最为剧烈.圆柱液舱内自由液面运动固有频率的计算公式[13]如下:
式中:ξn表示Bessel函数的根,当n=1,2,3时,取值分别为ξ1 = 1.841,ξ2 = 5.331,ξ3 = 8.536.因此,图1所示圆柱液舱内自由表面的一阶、二阶和三阶固有频率分别为f1 = 1.177 Hz, f2 = 2.338 Hz, f3 = 2.972 Hz.
试验过程中,振动台带动液舱做水平正弦运动,公式如下:
考虑到共振工况下自由液面的运动最为剧烈,本文选择3个不同激励幅值下的一阶共振工况,1个一阶拍频工况以及1个二阶共振工况,5个试验工况的参数如表1所示.
表1 试验工况
Tab.1
| 工况 | A/mm | A/R | fe/Hz | fe/fn | 模态 |
|---|---|---|---|---|---|
| I | 0.48 | 0.002 | 1.177 | fe/f1=1.0 | 一阶共振 |
| II | 0.96 | 0.004 | 1.177 | fe/f1=1.0 | 一阶共振 |
| III | 1.44 | 0.006 | 1.177 | fe/f1=1.0 | 一阶共振 |
| IV | 1.44 | 0.006 | 1.118 | fe/f1=0.95 | 一阶拍频 |
| V | 1.44 | 0.006 | 2.338 | fe/f2=1.0 | 二阶共振 |
3 结果分析
图2
图2
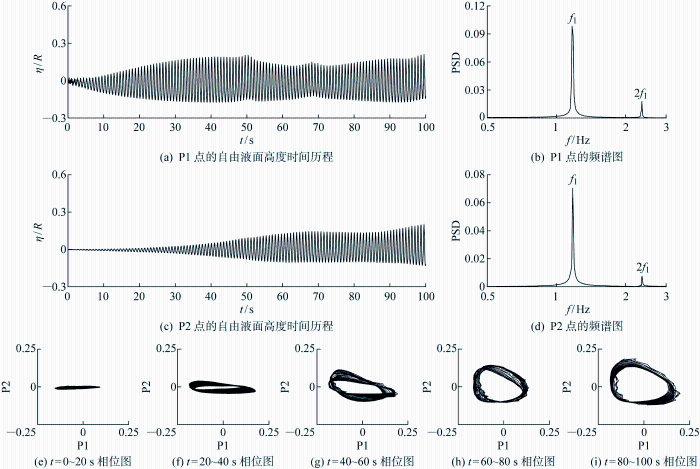
激励幅值A/R=0.002时自由液面的一阶共振运动情况
Fig.2
First-mode resonant motion of free surface at A/R=0.002
图3
图3
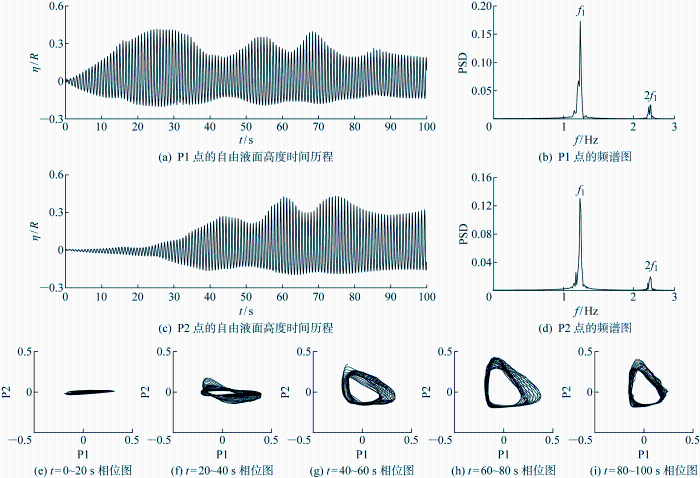
激励幅值A/R=0.004时自由液面的一阶共振运动情况
Fig.3
First-mode resonant motion of free surface at A/R=0.004
图4
图4
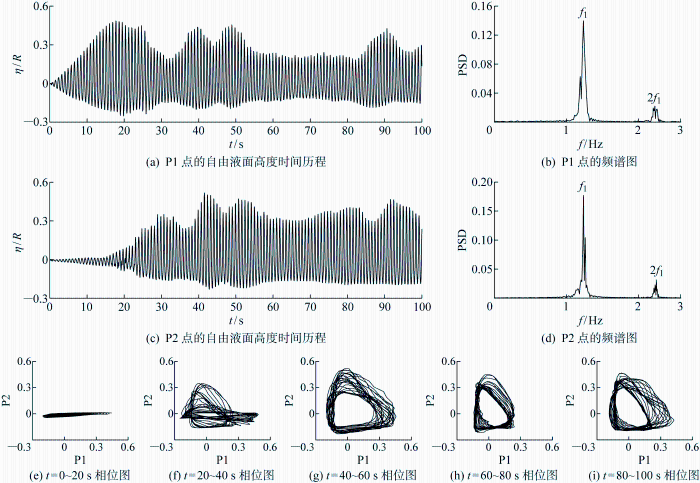
激励幅值A/R=0.006时自由液面的一阶共振运动情况
Fig.4
First-mode resonant motion of free surface at A/R=0.006
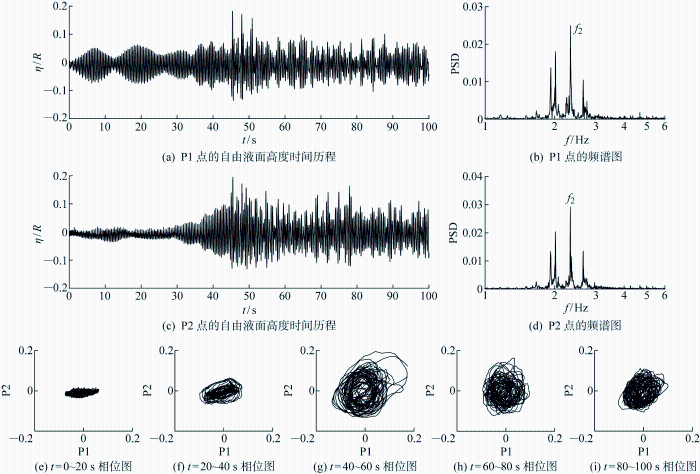
当激励幅值为A/R=0.002时,从图2(a)中可以看出,在共振效应的作用下,P1点自由液面高度逐渐增大.当增大到一定程度后,出现下降的趋势,然后再上升后下降.出现这种现象的原因有两个:一是自由液面旋转会消耗一部分能量,导致波幅下降;二是系统的强非线性效应会导致液体运动的实际固有频率偏离外部激励频率(即理论公式计算得到的固有频率).上述非线性效应可以从图2(b)给出的频率密度图上得到确认,图中存在两个峰值,主峰对应一阶固有频率f1,次峰对应2倍一阶固有频率2f1,次峰值越大,表示非线性效应越强.从图2(c)中可以看出,共振效应导致P2点自由液面高度逐渐增大,这表明液面旋转运动的幅度越来越大.图2(e)~2(i)给出的相位图可进一步确认旋转波的生成与发展.
除了共振工况之外,外部激励频率接近一阶固有频率时自由液面的运动特性也同样值得研究.Elahi等[14]在研究矩形液舱内液体的近共振运动时,发现当外部激励频率稍微偏离一阶固有频率时,自由液面会出现调制波,即所谓的“拍频现象”.
图5给出了激励幅值A/R=0.006,激励频率fe/f1=0.95时自由液面的一阶拍频运动情况.从图5(a)中可以看出,P1点处自由表面时间历程呈现出典型的调制波包络,幅值先增大后减小,如此循环交替.最大振幅出现在第1个包络周期内,在后面的包络后期逐渐衰减,直到系统最终达到具有恒定振幅的稳定状态.需要指出的是,为便于观察,这里没有给出100 s后的试验数据.图5(b)给出了自由表面时间历程的频谱图,从图中可以看出,最大的两个峰值对应的频率分别为外部激励频率fe和一阶固有频率f1.显然,在这两个频率的共同作用下,自由液面运动出现了独特的拍频现象.其中,外部激励频率fe对应的峰值高于一阶固有频率f1对应的峰值,表明自由液面运动主要由外部激励频率主导.从图5(c)中可以看出,P2点自由液面的运动幅度始终非常小,表明自由液面没有发生旋转运动.图5(e)~5(i)可以进一步表明自由液面始终保持平面波的形态,没有发生旋转.
图5
图5
激励幅值A/R=0.006时自由液面的一阶拍频运动情况
Fig.5
First-mode beating motion of free surface at A/R=0.006
除了一阶共振与拍频工况之外,本文还对圆柱液舱内自由液面的二阶共振运动特性进行了研究.图6给出了激励幅值A/R=0.006,激励频率fe/f2=1.0时自由液面的二阶共振运动情况.从图6(a)中可以看出,P1点自由液面的运动幅值先增大后减小,然后再增大后减小,自由液面位移时间历程与图5(a)所示的包络图类似.但不同的是,二阶共振工况下第一个瞬态周期的振幅在后续的瞬态后期并没有出现衰减,而是呈现增大趋势,而且,在 40 s 之后,运动变得极其不稳定.从图6(b)中可以看出,自由液面时间历程的频谱图呈现非常多的峰值,表明自由液面运动除了受到二阶固有频率主导之外,还受到众多其他频率的影响,最终导致系统的非线性效应非常强.从图6(c)中可以看出,最初P2 点的运动幅度并不是很大,但是30 s之后,运动幅值突然增大,当增大到一定程度后,运动也开始变得不稳定.同样地,在图6(d)所示频谱图中也可以观察到多个峰值,进一步表明自由液面的运动受到多个频率的作用.图6(e)~6(i)表明自由液面很快就出现旋转,而且旋转运动与一阶固有频率下的旋转运动差异非常大.
图6
图6
激励幅值A/R=0.006时自由液面的二阶共振运动情况
Fig.6
Second-mode resonant motion of free surface at A/R=0.006
图7给出了激励幅值A/R=0.006,激励频率fe/f1=1.0时自由液面的一阶共振运动图像.从图中可以看出,一阶共振激励下圆柱液舱内出现了3种典型的波形:平面波、破碎波与旋转波[15].顾名思义,平面波是指晃荡运动的初期(t=9.06,9.30,9.54,9.78,10.02 s),自由液面的形状可近似为平面.在共振效应下,波高会随着时间的推移而增大.当简谐共振激励下液面运动的能量积累到一定程度后,液面就会出现破碎,产生破碎波,详见t=28.22,28.46,28.70,28.94,29.18 s时的图像.当液面运动的能量进一步积累后,会激发垂直液舱运动方向的一阶固有频率,导致液体沿着逆时针方向旋转,详见t=44.23,44.39,44.55,44.71,44.87 s.液体的旋转方向主要取决于初始外部激励的方向.旋转晃荡会导致大量的液体沿着舱壁爬升,同时沿着舱壁四周做加速扫掠运动,这种运动对结构很危险,因为它会对圆柱形舱壁反复施加较大的水平力,进而有可能使结构失效,导致事故的发生[16].
图7
图7
激励幅值A/R=0.006时自由液面的一阶共振运动图像
Fig.7
Image of first-mode resonant motion of free surface at A/R=0.006
图8给出了当激励幅值A/R=0.006,激励频率fe/f2=1.0时自由液面的二阶共振运动图像.从图中可以看出,二阶共振激励下圆柱液舱内出现了3种典型的波形:二阶模态波、二阶模态旋转波与不规则波.二阶模态波的典型特征是在液舱中心位置存在一个完整的三维波峰和一个完整的三维波谷(t=10.00,10.24,10.48,10.72,10.84 s).在共振效应下,峰值和谷值也会随时间的推移而增大,当增大到一定程度后,垂直液舱运动方向的二阶固有模态被激发,导致波峰和波谷开始旋转,出现二阶模态旋转波(t=35.00,35.24,35.48,35.72,35.84 s).随着液面运动能量的进一步增加,其他高阶模态对应的频率被激发,液面运动开始变得不规则,舱壁处也出现多个波峰和波谷,并沿着舱壁做旋转运动,因此不规则波可视为舱壁旋转波与液舱中心旋转波的叠加(t=38.00,38.24,38.48,38.72,38.84 s).
图8
图8
激励幅值A/R=0.006时自由液面的二阶共振运动图像
Fig.8
Image of second-mode resonant motion of free surface at A/R=0.006
4 结论
本文搭建了一套液舱晃荡模型试验装置,包括立式圆柱形液舱、振动台、电动缸、控制柜、LED灯、计算机、摄相机和两个浪高仪.摄相机用于记录拍摄自由液面的运动,两个浪高仪用于监测自由液面沿平行液舱运动方向和垂直液舱运动方向的波高时间历程.考虑到共振工况下自由液面的运动最为剧烈,本文设计了5个试验工况,包括3个不同激励幅值下的一阶共振工况,1个一阶拍频工况以及1个二阶共振工况.通过对试验结果进行分析后发现:
(1) 当外部激励频率等于自由液面运动的一阶固有频率时,在共振效应下,舱壁处自由液面高度逐渐增大.当增大到一定程度后,出现下降的趋势,然后再上升后下降.此外,圆柱液舱内出现了3种典型的波形:平面波、破碎波与旋转波.
(2) 当外部激励频率接近自由液面运动的一阶固有频率时,舱壁处自由表面时间历程呈现出典型的调制波包络,幅值先增大后减小,如此循环交替.最大振幅出现在第一个包络周期内,在后面的包络后期逐渐衰减,直到系统最终达到具有恒定振幅的稳定状态.自由液面始终保持平面波的形态,没有发生旋转.
(3) 当外部激励频率等于自由液面运动的二阶固有频率时,舱壁处自由液面的运动幅值先增大后减小,然后再增大后减小,最后运动变得极其不稳定.此外,圆柱液舱内也可以观察到3种典型的波形:二阶模态波、二阶模态旋转波与不规则波.其中,不规则波可视为舱壁旋转波与液舱中心旋转波的叠加,它的出现是因为其他高阶模态对应的频率被激发,导致舱壁处也出现多个波峰和波谷,并沿着舱壁做旋转运动.
参考文献
基于非均质多相流模型的液舱晃荡数值模拟
[J].应用非均质多相流模型对不同装载率和激励频率下矩形液舱的横摇晃荡运动进行了数值模拟.分析了液体重心的横向和纵向运动情况,计算了不同工况下自由液面形状与速度场分布以及舱壁测点处压力的时间历程和相应的功率谱密度.模拟结果与均质模型计算结果和试验结果的对比分析验证了非均质模型在模拟液舱晃荡时的优越性.
Simulation of liquid tank sloshing by using inhomogeneous multiphase model
[J].
LNG独立C型舱晃荡的频域共振特性试验研究
[J].
Experimental study on frequency domain resonant characteristic of sloshing in LNG independent type C tank
[J].
低载液率液体晃荡冲击压力的试验研究
[J].
Experimental study on the impact pressure of sloshing liquid with low filling level
[J].
基于模型试验的晃荡荷载统计分析对比研究
[J].
Comparative study on statistical analysis of sloshing load based on model test
[J].
Experimental study on effect of density ratio and phase transition during sloshing impact in rectangular tank
[J].
A set of canonical problems in sloshing. Part 2: Influence of tank width on impact pressure statistics in regular forced angular motion
[J].
Experimental study on sloshing reduction effects of baffles linked to a spring system
[J].
Floating non-traditional manufacture of floating drilling storage and offloading units—Study on modeling and optimization method for the underwater rotating technology
[J].
Aasta hansteen Spar FPSO—A pioneer in Norwegian deepwater
[C]
Multidimensional model analysis of nonlinear sloshing in a rectangular tank with finite water depth
[J].
An adaptive multimodal approach to nonlinear sloshing in a rectangular tank
[J].
一种几何VOF方法在液舱晃荡流动模拟中的应用
[J].
Application of a geometric VOF method in the simulations of sloshing flow
[J].
Liquid sloshing dynamics: Theory and applications
[R].
Simulation of liquid sloshing in 2D containers using the volume of fluid method
[J].
Resonant three-dimensional nonlinear sloshing in a square-base basin
[J].
深水SDPSO平台油水置换储卸油系统排出水含油量研究
[J].
Study on oil content in discharged water from oil-water replacement storage offloading system of deepwater SDPSO platform
[J].