上海交通大学学报

上海交通大学学报, 2024, 58(11): 1654-1664 doi: 10.16183/j.cnki.jsjtu.2023.101

船舶海洋与建筑工程

基于物理信息神经网络的船舶螺旋桨尾流场重构

侯先瑞,a,b, 周星宇a, 黄骁骋a

a.上海海事大学 海洋科学与工程学院,上海 201306

b.上海海事大学 上海市“全渗透”深远海离岸能源动力前沿研究基地,上海 201306

Reconstruction of Ship Propeller Wake Field Based on Physics-Informed Neural Networks

HOU Xianrui,a,b, ZHOU Xingyua, HUANG Xiaochenga

a. College of Ocean Science and Engineering, Shanghai Maritime University, Shanghai 201306, China

b. Shanghai Frontiers Science Center of “Full Penetration” Far-Reaching Offshore Ocean Energy and Power, Shanghai Maritime University, Shanghai 201306, China

责任编辑: 王一凡

收稿日期: 2023-03-24   修回日期: 2023-06-3   接受日期: 2023-06-25  

基金资助: 国家青年自然科学基金项目(52001198)

Received: 2023-03-24   Revised: 2023-06-3   Accepted: 2023-06-25  

作者简介 About authors

侯先瑞(1986—),博士,讲师,从事船舶运动预报及控制、海洋波浪能开发应用研究.电话(Tel.):021-38284804;E-mail:xrhou@shmtu.edu.cn.

摘要

将物理信息神经网络(PINN)应用于船舶螺旋桨尾流场的重建.介绍了PINN的原理和基本框架;应用PINN求解Burgers方程,对PINN求解偏微分方程的可行性进行验证.利用计算流体力学(CFD)软件STAR CCM+对KVLCC2螺旋桨的敞水特性进行了数值模拟,得到了该桨在敞水中运动的流场信息.基于数值模拟得到的敞水桨流场特性信息,构造PINN训练样本集对PINN进行训练;训练后的PINN用于推断控制方程在任意时间和空间坐标的近似解.将PINN得到的速度和压力分布与STAR CCM+模拟的速度和压力分布进行了比较,对比结果验证了PINN在尾流场重建中的可靠性.研究结果表明,PINN可以应用于船舶螺旋桨尾流场的重建.

关键词： 物理信息神经网络; 偏微分方程; 流场信息; 流场重构; 螺旋桨

Abstract

Physics-informed neural networks (PINN) are applied to the reconstruction of the ship propeller wake field. First, the principle and basic framework of PINN were introduced. Then, the Burgers equation was selected to verify the feasibility of PINN in solving partial differential equations. After that, the propeller of KVLCC2 in open water is simulated using computational fluid dynamics (CFD) software STAR CCM+, and the flow field information of the KVLCC2 propeller is obtained. Based on the simulated flow field information data, the training sample set was constructed to train PINN. The trained PINN was used to infer the approximate solution of the governing equation at any time and space. Finally, the velocity and pressure distribution obtained by PINN were compared with the velocity and pressure distribution simulated by STAR CCM+. The results validate the reliability of PINN in propeller wake field reconstruction, which can be concluded that PINN can be applied to the reconstruction of the ship propeller wake field.

Keywords： physical-information neural network (PINN); partial differential equation; flow field information; flow field reconstruction; propeller

PDF (18611KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

侯先瑞, 周星宇, 黄骁骋. 基于物理信息神经网络的船舶螺旋桨尾流场重构[J]. 上海交通大学学报, 2024, 58(11): 1654-1664 doi:10.16183/j.cnki.jsjtu.2023.101

HOU Xianrui, ZHOU Xingyu, HUANG Xiaocheng. Reconstruction of Ship Propeller Wake Field Based on Physics-Informed Neural Networks[J]. Journal of Shanghai Jiaotong University, 2024, 58(11): 1654-1664 doi:10.16183/j.cnki.jsjtu.2023.101

鉴于Navier-Stokes方程的高度非线性和多尺度特性,目前在求解船舶流体力学问题时,主要采用基于计算流体力学(CFD)的数值模拟方法对该方程进行数值求解.在如船舶螺旋桨水动力性能的研究上[1],由多尺度特性带来的巨大计算量使得高精度的直接数值模拟技术难以实现,雷诺平均方法与大涡模拟技术仍是求解该类工程流动问题的主要手段,但是对雷诺应力或亚格子应力闭合模型建模的不确定性会影响数值模拟的计算精度[2].

近年来,随着深度学习技术的发展及其在各学科领域的广泛应用,利用深度学习技术求解CFD方面的相关问题吸引了众多学者的关注[3].应用传统深度学习网络求解偏微分方程问题时,其原理是通过从大量的样本数据中反复训练,学习得到数据中隐藏的内在规律,实现以任意精度逼近待求解函数[4].如Jin等[5]构造了一种基于卷积神经网络的数据驱动模型,基于CFD模拟得到的圆柱绕流场中的压力场数据,学习得到圆柱绕流的速度场.应用传统深度学习网络求解偏微分方程的方法本质上是将待求微分方程系统作为“黑箱”[6],没有考虑待求解系统的先验物理信息,仅是对偏微分方程系统的输入和输出数据的拟合,从而导致该方法在实际应用过程中的可解释性差,求解效果受限于学习样本的数量.

为提高深度学习网络求解偏微分方程系统的可解释性和适用性,Raissi等[7]在深度学习中引入偏微分方程,提出了一种基于物理信息的深度学习算法框架,并首次将其应用于求解偏微分方程的正问题和反问题.为了提高物理信息神经网络(PINN)在拟合偏微分方程上的求解效率和鲁棒性,Jagtap等[8]通过引入一个超参数,并将其作为神经网络参数进行优化,加速了PINN的训练收敛速度.为了提高PINN在稀缺数据和含噪声数据方面的学习能力,Chen等[9]提出了一种新的PINN学习框架,该深度学习网络集成了物理信息、自动微分和稀疏回归,并通过分别学习仿真数据和试验数据验证了其有效性和鲁棒性.在流体力学领域,PINN也有着诸多应用,Jin等[10]建立了速度-压力与速度-涡度两种形式的Navier-Stokes方程组的PINN网络模型,并命名为NSFnets,将之应用于求解二维Kovasznay流、二维圆柱绕流和三维Beltrami流3个层流问题,得到满意的结果后,进一步对湍流通道流问题进行了求解,体现了NSFnets的高适用性.Cheng等[11]将损失函数中嵌入了雷诺平均Navier-Stokes(RANS)方程和结构的动态运动方程,分别应用基于全连接神经网络(fully connected neural network,FCNN)和长短期记忆(long short-term memory,LSTM)神经网络的PINN求解了高雷诺数甚至湍流流动下圆柱的两自由度的涡激振动和尾流激振问题.为了提高PINN求解偏微分方程的求解精度,Sun等[12]以“硬方式”编码PINN网络结构,利用边界条件和距离函数强制使PINN满足相应的边界条件,并在血液动力学中得到了满意的结果.Wang等[13]从神经正切核(NTK)理论的角度,提出了根据分量核矩阵的特征值之和来自适应调整损失函数中不同组成成分之间权重的算法,解决了目标函数表现出高频或多尺度特征的情况下PINN训练缓慢甚至不收敛的情况.另外,将PINN与偏微分方程的经典数值算法相结合也吸引了一些研究者的兴趣.

Zhang等[14]将PINN与表示随机过程的动态正交法和双正交法相结合,去求解非线性随机偏微分方程;Wessels等[15]在PINN的基础上提出一种神经粒子方法,对于时间积分,采用高阶隐式龙格-库塔法,用更新的拉格朗日格式建立了无黏、不可压缩欧拉方程,该方法可以用来模拟自由表面处不可压缩流体的流动.为了PINN的推广,Lu等[16]开发了Python库“DeepXDE”用于实现PINN,并通过求解Poisson方程、Lorenz系统等验证了PINN求解偏微分方程的有效性.

本文应用PINN求解敞水桨流场中流体运动的连续性方程和N-S方程,从而对船舶敞水桨流场的压力场和速度场进行重构.对PINN的框架和基本原理进行简要介绍.为验证PINN应用于求解偏微分方程的可行性,应用PINN对一维Burgers方程进行求解.应用CFD数值模拟得到船舶螺旋桨在敞水条件下的流场信息,并据此构造训练样本集对PINN进行训练,实现对敞水桨流场的速度场和压力分布趋势的重构.将PINN得到的速度和压力分布与STAR CCM+模拟的速度和压力分布进行了比较.对比结果验证了PINN在尾流场重建中的可靠性.

1 PINN简介

基于深度学习模型求解船舶流体力学问题的本质在于利用深度神经网络去求解流体力学中的非线性偏微分方程.其基本原理是将深度神经网络作为非线性函数逼近器,借助在深度神经网络中被广泛使用的自动微分技术[17],将待求解的偏微分方程中的微分形式约束条件融入到神经网络的损失函数中进行优化,从而学习得到带物理模型约束的逼近偏微分方程解的深度神经网络模型.本文对PINN求解偏微分方程的基本结构进行简要介绍,有关PINN的详细内容见文献[7].

待求解的偏微分方程通常表示为

ut+D[u]=0, x∈Ω, t∈[0, T]

式中:u(t, x)为偏微分方程的待求解函数;D[·] 是非线性微分算子;x代表空间;t代表时间.

为对偏微分方程进行求解,常规的方法是给定待求解偏微分方程的初始条件和边界条件,从而借助数学手段求解得到偏微分方程的解u^(t, x).鉴于偏微分方程的非线性,通常是利用有限差分法、有限体积法等数值方法求解得到方程的数值解.而应用PINN对偏微分方程进行求解时,其原理是构建一个神经网络模型来逼近偏微分方程的解.PINN的结构主要由一个FCNN和一个残差网络(residual network,RN)构成,如图1所示.图中:xj(j=1,2,…,l)为神经网络的输入;f代表神经网络的输出.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   神经网络结构

Fig.1   Structure of neural networks


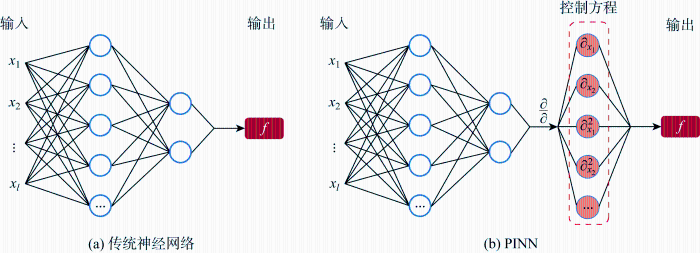
图1中,FCNN用来逼近偏微分方程的解;RN用于约束FCNN和控制方程之间的残差.在构建RN时,由自动微分算法计算FCNN的输出变量关于输入变量的偏导数.PINN的损失函数为

E=αEu+Er

式中:损失函数的第1项Eu表示标签数据约束的损失函数;系数α代表了该项在PINN损失函数中的权重.Eu表达式为

Eu= 1Nu∑i=1Nuupi(tui,xui)-usi2

Nu为样本的总数;tui,xuii=1Nu表示PINN的训练集;uip表示PINN神经网络的第i个预测值;uis为PINN学习的目标值,通常由数值模拟或物理试验得到.

式(2)中的第2项Er表示物理模型约束的损失函数,其表达式为

Er= 1Nr∑i=1Nrrp(tri,xri)2

式中:{tri, xri}i=lNu表示控制方程式(1)的训练配置点;rp(t,x)为偏微分方程的残差.

通过应用构造的训练样本集对PINN进行训练学习,使PINN能够逼近待求解偏微分方程的精确解,从而实现对偏微分方程的求解.

2 PINN 求解偏微分方程的可行性验证

Burgers方程可以用来模拟冲击波的传播和反射,虽然不包含压力梯度项,却包含非线性对流项和扩散项,可以看成Navier-Stokes方程的一个简化模型[18].为验证PINN在求解偏微分方程方面的可行性和所开发程序的正确性,应用PINN求解流体力学中的一维Burgers方程:

$\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+v \frac{\partial^{2} u}{\partial x^{2}}=0$

式中:u为流体的速度;υ为流体的运动黏性系数,本文中取为0.01/π.

定义该一维Burgers方程的初始条件和边界条件:

u(0, x)=-sin(πx),　　x∈[-1, 1]m,　t∈[0, 1]su(t, -1)=u(t, 1)=0

为了应用PINN对式(4)和式(5)构成的定解问题进行求解,需要构造PINN的训练样本集.应用 COMSOL 软件对定解方程进行数值求解,该软件有大量预定义的物理模式,可对一维Burgers方程快速建立模型,如图2所示.数值模拟结果与PINN预测结果对比如图3所示.求解时需对计算域进行离散,本文中将一维计算域离散成100个网格,网格划分结果如图2(a)所示,计算得到的一维Burgers方程的数值模拟结果如图3(a)所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

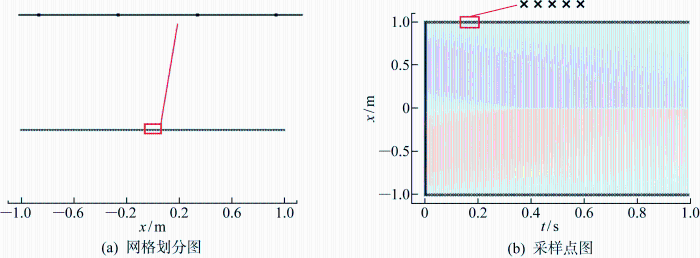
图2   一维Burgers方程网格和采样

Fig.2   Meshing and sampling of one-dimensional Burgers equation


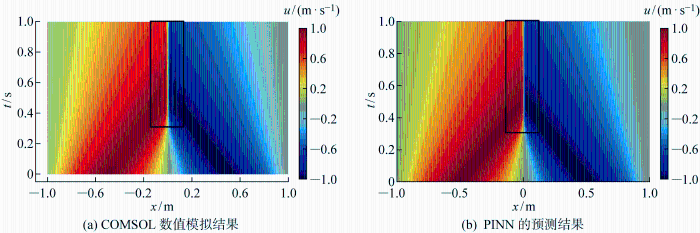
图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   数值模拟结果与PINN预测结果对比

Fig.3   Comparison of numerical simulation results and PINN prediction results


基于Burgers方程的数值模拟结果,构造PINN的训练样本集.如图2(b)中所示,“×”代表所取的样本点.在x∈[-1, 1] m, t∈[0,1] s内采样数据点,共取得初始条件与边界条件处456个点的数据构造PINN的训练集.应用Python语言对PINN进行编程实现,Python的编译环境为Python 3.9.13和TensorFlow 2.6.0,并基于Jupyter对程序进行编译.

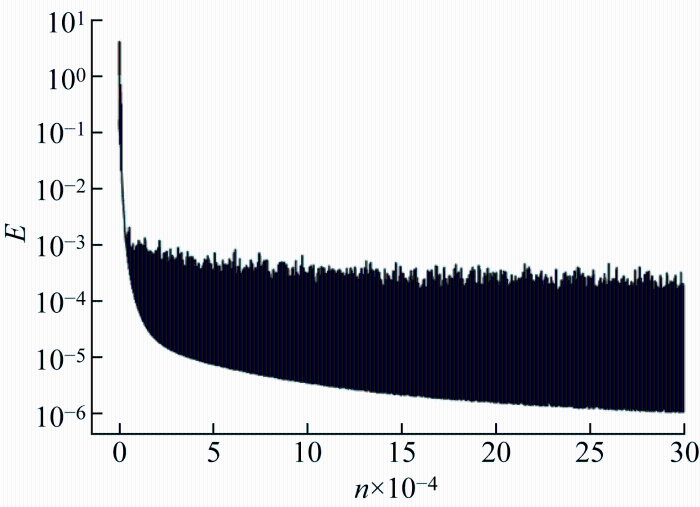
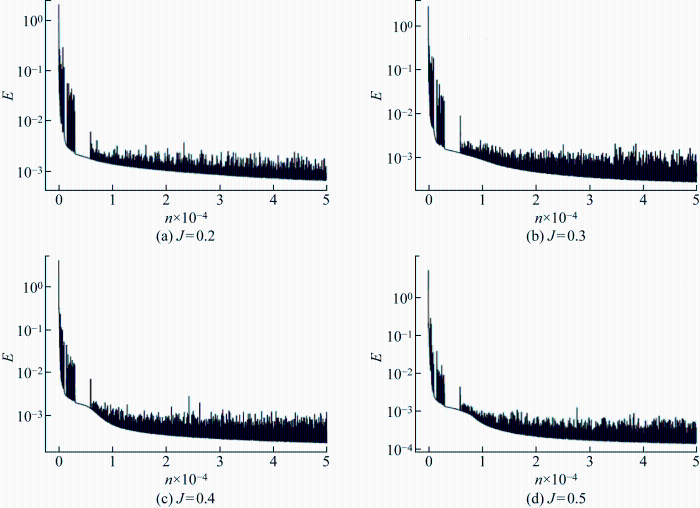
本研究在求解一维Burgers方程时所采用的PINN由FCNN和RN组成,其中FCNN由10层神经网络组成,分别为1个输入层、8个隐藏层和1个输出层.其中,输入层包含2个神经元,每层隐藏层中包含20个神经元,输出层包含1个神经元,层与层之间采用全连接网络.PINN的各层网络权重w和偏置b均采用Xavier方法进行初始化,各层神经元的激活函数选用双曲正切函数,优化函数为Adam函数.PINN的学习率设置为随迭代阶梯性变化.PINN总共训练 300 000 步,其中,前 1 000 步的学习率为1×10-2,1 000~3 000 步的学习率为1×10-3,3 000 步以后的学习率设置为5×10-4.PINN的损失函数E随训练迭代次数n的变化如图4所示,

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   PINN的损失函数变化

Fig.4   Variation in loss function of PINN


训练好后其损失函数的值约为1.68×10-6.应用训练好的PINN对一维Burgers方程进行求解,得到求解域各点处的速度随时间变化的分布,如图3(b)所示.

将图3(b)中PINN的预测结果与图3(a)中的数值模拟结果进行对比可以发现:PINN的预测结果和数值模拟得到的结果基本一致,验证了PINN在偏微分方程问题求解上的可行性.从图3(a)数值模拟结果中可以观察到在黑色方框标注区域内出现了振荡现象,而在图3(b)PINN的预测结果中在相同区域内却没有出现这一现象,其原因在于:在对Burgers方程进行数值求解时,需要在函数变化较为剧烈的地方进行非常细密的网格划分,若没有满足必要的网格密度就会难以避免地引起数值解的振荡;而PINN是在初始条件和边界条件处取得的样本集,仅依靠对Burgers方程构成的损失函数进行优化求解,同时PINN求解偏微分方程时具有无网格的特点,所以其预测结果中无法反映因网格划分所引起的解的振荡.

3 基于PINN的螺旋桨尾流场重构

应用构造的PINN对螺旋桨敞水条件下运转时的流场进行重构研究.为对构造的PINN进行训练,需要借助部分流场数据构造PINN的训练样本集.

3.1 数据集的获取

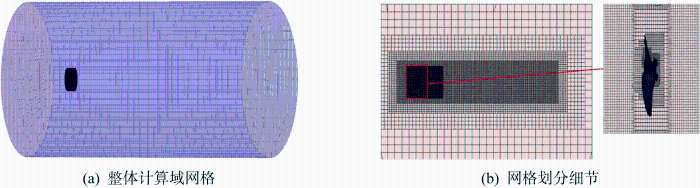
研究对象选择国际水动力学对比研究基本船型 KVLCC2 模型所适配的螺旋桨模型[19],螺旋桨模型的几何参数如表1所示,表中R为螺旋桨半径,采用半径为0.7R处的面螺旋距代表螺旋桨的螺距.COMSOL 软件网格划分功能欠佳,因此应用CFD软件STAR CCM+数值模拟该螺旋桨模型在不同进速条件下的敞水桨特性.数值模拟时建立的螺旋桨模型及其计算域如图5所示,对螺旋桨在敞水条件下进行模拟时,设置两个计算域,一个为远场的整体计算域,另一个为近场的螺旋桨旋转计算域.为减小计算域边界对螺旋桨性能数值模拟结果的影响,外部的远场计算域为圆柱体计算域,半径为0.4 m,计算域前后两端距离螺旋桨分别为0.2 m与1 m;在螺旋桨周围划分旋转计算域,半径为0.06 m,计算域前后两端距离螺旋桨的距离均为0.02 m,采用滑移网格法实现旋转计算域的运动.

表1   螺旋桨几何参数

Tab.1  Geometric parameter of propeller model

参数数值
直径/m0.089 6
叶片数量4
轮毂比0.155
螺距比(0.7R)0.721 2
盘面比0.431
侧斜角/(°)21.15
纵斜角/(°)0

新窗口打开| 下载CSV


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   螺旋桨的几何模型和计算域

Fig.5   Geometric model of propeller and computational domain


数值模拟时应用切割体网格对计算域进行离散,网格基础尺寸为 0.01 m,面网格增长率为1.3,采用了3层棱柱层,棱柱层延伸比为1.5,棱柱层的总厚度为网格基础尺寸的25%.为了能够精确捕捉到螺旋桨复杂的流场特性,在螺旋桨周围建立了两个圆柱形加密区域,内部的圆柱形网格加密区域半径为0.08 m,前后两端距螺旋桨的距离分别为0.05 m 与0.15 m,网格大小为网格基础尺寸的25%;外部的圆柱形网格加密区域半径为0.1 m,前后两端距螺旋桨的距离分别为0.1 m与0.8 m,网格大小为网格基础尺寸的50%.在旋转计算域和外部远场计算域的交界面,采用了2层棱柱层,棱柱层延伸比为1.0,棱柱层的总厚度为网格基础的尺寸的5%.网格划分结果如图6所示,划分的网格总数约为160万.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   螺旋桨计算域网格

Fig.6   Grid of propeller computational domain


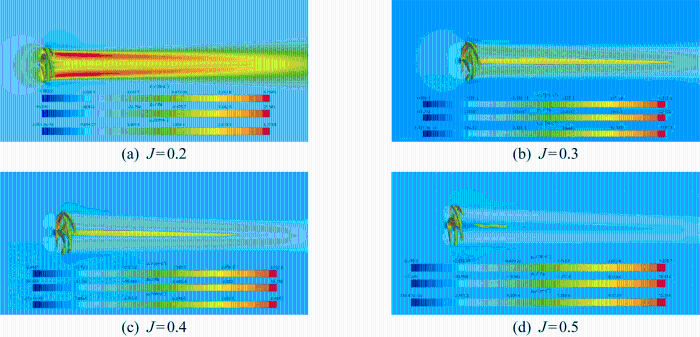
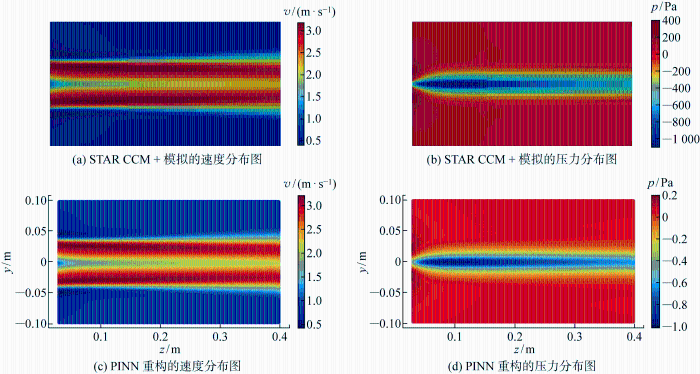
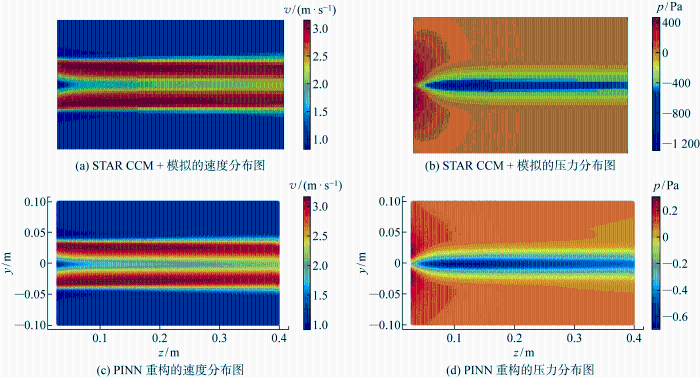
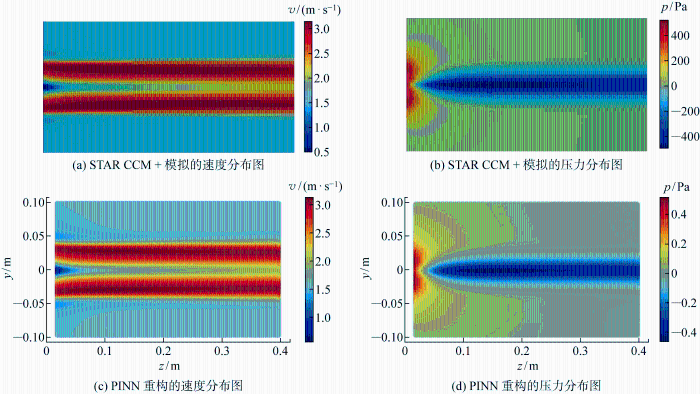
基于网格划分结果,选择RANS方程对螺旋桨的敞水流场进行模拟,湍流模式选择κ-ω模型,设定的计算域边界条件为:入口边界采用速度入口;出口边界采用压力出口边界条件;侧面边界采用对称边界条件;螺旋桨表面设置为无滑移边界,边界条件示意如图7所示.求解器中时间步长t=0.001 s,最大内步迭代为5步.设定螺旋桨转速为h=43.62 r/s,对进速系数J分别为0.2、0.3、0.4、0.5这4种工况下的敞水桨特性进行模拟计算,得到该螺旋桨模型在4种工况条件下的敞水桨z方向(垂直于螺旋桨旋转方向)速度分量vk的等值面、叶片表面的压力pb分布以及平面截面上的速度vM分布,如图8所示.同时计算得到4种工况条件下的螺旋桨推力系数KT和转矩系数10KQ,并将其与文献[19]中的NMRI模型试验结果进行对比,对比结果分别如表2和表3所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   边界条件示意图

Fig.7   Diagram of boundary condition


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   各工况的CFD仿真模拟结果

Fig.8   CFD simulation results of each working condition


表2   推力系数KT结果对比

Tab.2  Comparison of results of thrust coefficient KT

JKT相对误差/%
NMRI[19]CFD
0.20.234 70.218 27.03
0.30.199 40.185 76.87
0.40.161 20.159 60.99
0.50.117 30.111 45.02

新窗口打开| 下载CSV


表3   转矩系数10KQ结果对比

Tab.3  Comparison of results of torque coefficient 10KQ

J10KQ相对误差/%
NMRI[19]CFD
0.20.264 40.255 63.33
0.30.233 50.229 11.88
0.40.199 40.199 70.15
0.50.161 40.166 73.28

新窗口打开| 下载CSV


表2和表3中的对比结果表明:应用CFD模拟计算的螺旋桨敞水条件下的转矩系数的误差较小,而推力系数的误差较大,最大误差发生在螺旋桨进速系数J=0.2时.本研究的主要目的是验证应用PINN对螺旋桨流场进行重构的适用性和可行性,因此暂且忽略推力系数误差的影响,而直接应用CFD模拟计算的流场信息近似代替螺旋桨在敞水条件下运转的流场,去构造PINN的训练样本集.

基于STAR CCM+的数值模拟结果,选取螺旋桨求解域内的长方体区域{(x, y, z)|x∈[-1, 1] m, y∈[-0.1, 0.1] m, z∈[0.02, 0.4] m}作为采样空间,如图9中红色区域所示,以采样步长0.05 s在时间间隔1~6 s内通过简单随机抽样得到 30 300 个点的运动速度及其对应的时间和空间坐标,并据此构造PINN的训练集,其中输入是采样点的时间和空间坐标,输出为采样点处的流体速度.在构造训练集时,采样得到的训练集内的样本占采样空间内数据总量的约0.1%.另外,为验证PINN的泛化性能,将整个采样空间内的流场数据作为PINN的测试集.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   数据集的采集区域

Fig.9   Collection area of dataset


3.2 基于PINN的流场重构

在应用PINN对螺旋桨在敞水条件下转动时的尾流场进行重构时,将流体流动的控制方程即连续性方程和N-S方程作为PINN的先验物理信息.

$\left.\begin{array}{l}\boldsymbol{\nabla} \cdot \boldsymbol{u}=0 \\\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}+w \frac{\partial u}{\partial z}= \\- \\-\frac{1}{\rho} \frac{\partial p}{\partial x}+v\left(\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}+\frac{\partial^{2} u}{\partial z^{2}}\right) \\\frac{\partial v}{\partial t}+u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}+w \frac{\partial v}{\partial z}= \\\\-\frac{1}{\rho} \frac{\partial p}{\partial y}+v\left(\frac{\partial^{2} v}{\partial x^{2}}+\frac{\partial^{2} v}{\partial y^{2}}+\frac{\partial^{2} v}{\partial z^{2}}\right) \\\frac{\partial w}{\partial t}+u \frac{\partial w}{\partial x}+v \frac{\partial w}{\partial y}+w \frac{\partial w}{\partial z}= \\\\\quad-\frac{1}{\rho} \frac{\partial p}{\partial z}+v\left(\frac{\partial^{2} w}{\partial x^{2}}+\frac{\partial^{2} w}{\partial y^{2}}+\frac{\partial^{2} w}{\partial z^{2}}\right)\end{array}\right\}$

式中:$\boldsymbol{\nabla}$是哈密尔顿算子;$\boldsymbol{u}=(u, v, w)$为流体速度;p是压力;ρ是流体密度.

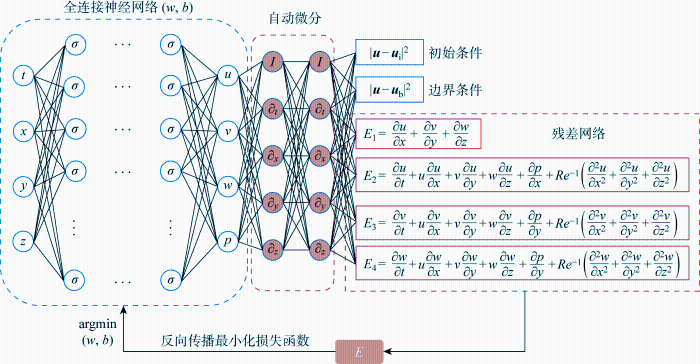
图10展示了所构建的PINN的网络结构.图中:Re为雷诺数.该PINN由FCNN和RN组成,其中FCNN由10层神经网络组成,分别为1个输入层、8个隐藏层和1个输出层.输入层与输出层均包含4个神经元,每层隐藏层中包含20个神经元,层与层之间采用全连接网络.ui=(ui, vi, wi)与ub=(ub, vb, wb)分别为初始时刻和边界上的数据点速度,E1为连续性方程的残差,E2~E4代表N-S方程的残差.PINN的各层网络权重w和偏置b均采用Xavier方式进行初始化,各层神经元的激活函数σ选用双曲正切函数,优化函数为Adam函数.PINN的学习率设置为随迭代阶梯性变化,前 1 000 步的学习率为1×10-2,1 000~3 000 步的学习率为1×10-3,3 000 步以后的学习率设置为5×10-4.在训练过程中,通过Adam优化算法对PINN的损失函数E进行优化,并更新权重w和偏置b.图11展示了4个不同工况下所构建的PINN在训练过程中损失函数的变化.PINN的损失函数值降低到设定的优化目标时得到的预测值,不仅与已知的训练数据间的误差足够小,并且已经最大程度满足了控制方程的约束条件,此时可以认为PINN实现了对流体控制方程的求解.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   PINN求解偏微分方程模型结构

Fig.10   Specific structure of PINN in solving PDE model


图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   各个工况下PINN的损失函数变化

Fig.11   Variation in loss function of PINN under each working condition


为验证PINN在流场重构方面的学习和泛化能力,应用训练好的PINN去分析构造的测试集数据,即输入测试集中各点的时间和空间坐标,重构采样空间内的流体速度和压力.限于篇幅,本文只展示了t=5 s,x=0 m时的y-z平面内y从 -0.1 m 到0.1 m,z从0.02 m到0.4 m的一个矩形区域的PINN的流场重构结果,并将PINN的流场重构结果与CFD模拟结果进行对比,分别如图12~15所示.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   J=0.2时的结果对比

Fig.12   Comparison of results at J=0.2


图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   J=0.3时的结果对比

Fig.13   Comparison of results at J=0.3


图14

新窗口打开| 下载原图ZIP| 生成PPT

图14   J=0.4时的结果对比

Fig.14   Comparison of results at J=0.4


图15

新窗口打开| 下载原图ZIP| 生成PPT

图15   J=0.5时的结果对比

Fig.15   Comparison of results at J=0.5


对比图12~15中的数值模拟结果与PINN的重构结果可以发现,STAR CCM+数值模拟得到的速度分布和PINN重构的速度分布基本一致,证明了PINN在流场重构问题上的有效性.而数值模拟得到的压力分布与PINN重构的压力分布在趋势上相同,但数值上有差异.出现该现象的原因是N-S方程中的压力项是压力关于空间坐标的偏导数,而PINN完全依靠对N-S方程构成的损失函数进行优化去重构压力场,由于训练集中没有加入压力数据,PINN只能预测流场的压力变化趋势,但无法对其中压力的具体数值进行精准预测.

4 结论

本文应用基于PINN对一维Burgers方程和船舶螺旋桨尾流场的重构问题进行求解,并将PINN的求解结果与CFD数值模拟的结果进行对比,得到以下结论:

(1) PINN在一维Burgers方程上的求解结果与数值模拟得到的结果基本一致,证明了PINN在求解偏微分方程问题上具有可行性.

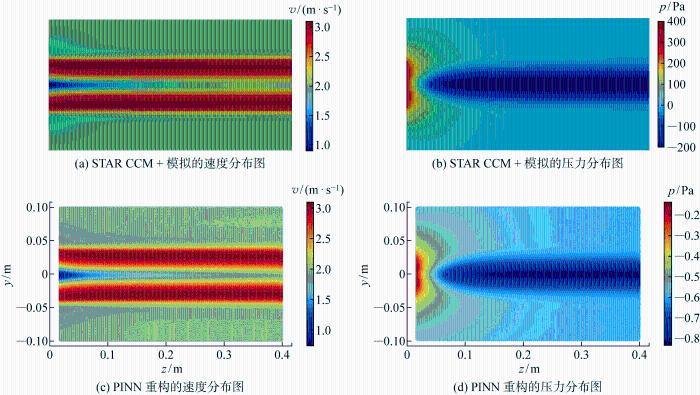
(2) 在流场重构问题上,仅需要少量数据构造训练集去训练PINN,就可以实现对敞水桨流场速度的准确重构.由于没有压力数据进行训练,PINN仅能对压力场的分布趋势进行准确预测.

本文构建的PINN对于偏微分方程具有良好的求解能力,但仍需要进一步的研究与改进.可将少量压力场数据和速度数据一起构造PINN的训练集,并对PINN的结构和损失函数进行改进,以实现对速度场和压力场的同步准确重构.将本文的PINN和流场的初值条件与边界条件相结合,在PINN的损失函数中融入流场的初值条件和边界条件,使PINN可以同时对多个工况下的流场进行重构.

参考文献

郭海鹏, 邹早建, 李广年.

基于OpenFOAM的螺旋桨紧急倒车工况数值模拟

[J]. 上海交通大学学报, 2023, 57(2): 168-176.

DOI:10.16183/j.cnki.jsjtu.2021.305      [本文引用: 1]

螺旋桨在紧急倒车工况下的水动力特性与船舶的紧急制动能力密切相关并直接影响船舶的航行安全性.基于开源计算流体动力学平台OpenFOAM中的雷诺平均求解器对螺旋桨在紧急倒车工况下的水动力特性及绕流场开展数值研究.以5叶螺旋桨DTMB4381模型为研究对象,对其正车前进以及紧急倒车工况进行数值模拟.通过与国际上公开的模型试验结果进行对比,验证了所采用的数值方法在预报螺旋桨不同工况下水动力性能方面的有效性.基于数值模拟获得的水动力载荷及流场信息,探讨了紧急倒车工况下局部绕流场特征随进速变化的规律及其与螺旋桨整体水动力特性之间的关系,为船舶紧急倒车制动能力评估提供了理论依据.

GUO Haipeng, ZOU Zaojian, LI Guangnian.

Numerical simulation of crashback ccondition of a propeller based on OpenFOAM

[J]. Journal of Shanghai Jiao Tong University, 2023, 57(2): 168-176.

[本文引用: 1]

ZHAO Y M, AKOLEKAR H D, WEATHERITT J, et al.

RANS turbulence model development using CFD-driven machine learning

[J]. Journal of Computational Physics, 2020, 411: 1-14.

[本文引用: 1]

崔永赫, 张文耀, 闫慧龙, 等.

“硬”边界低阶导数型物理信息神经网络: 一种流动求解器

[J]. 西安交通大学学报, 2022, 56(9): 123-133.

[本文引用: 1]

CUI Yonghe, ZHANG Wenyao, YAN Huilong, et al.

“Hard” boundary low-order derivative physics informed neural network: A fluid flow solver

[J]. Journal of Xi’an Jiaotong University, 2022, 56(9): 123-133.

[本文引用: 1]

郑素佩, 靳放, 封建湖, 等.

双曲型方程激波捕捉的物理信息神经网络(PINN)算法

[J]. 浙江大学学报(理学版), 2023, 50(1): 56-62.

[本文引用: 1]

ZHENG Supei, JIN Fang, FENG Jianhu, et al.

PINN-type algorithm for shock capturing of hyperbolic equations

[J]. Journal of Zhejiang University (Science Edition), 2023, 50(1): 56-62.

[本文引用: 1]

JIN X W, CHENG P, CHEN W L, et al.

Prediction model of velocity filed around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder

[J]. Physics of Fluids, 2018, 30(4): 1-16.

[本文引用: 1]

XU H, CHANG H B, ZHANG D X.

DL-PDE: Deep-learning based data-driven discovery of partial differential equations from discrete and noisy data

[J]. Communications in Computational Physics, 2021, 29(3): 698-728.

[本文引用: 1]

RAISSI M, PERDIKARIS P, KARNIADAKIS G E.

Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations

[J]. Journal of Computational Physics, 2019, 378: 686-707.

[本文引用: 2]

JAGTAP A D, KAWAGUCHI K, KARNIADAKIS G E.

Adaptive activation functions accelerate convergence in deep and physics-informed neural networks

[J]. Journal of Computational Physics, 2020, 404: 1-24.

[本文引用: 1]

CHEN Z, LIU Y, SUN H.

Physics-informed learning of governing equations from scarce data

[J]. Nature Communications, 2021, 12(1): 1-13.

[本文引用: 1]

JIN X W, CAI S Z, LI H, et al.

NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations

[J]. Journal of Computational Physics, 2021, 426: 1-26.

[本文引用: 1]

CHENG C, MENG H, LI Y Z, et al.

Deep learning based on PINN for solving 2 DOF vortex induced vibration of cylinder

[J]. Ocean Engineering, 2021, 240: 1-13.

[本文引用: 1]

SUN L N, GAO H, PAN S W, et al.

Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data

[J]. Computer methods in Applied Mechanics and Engineering, 2020, 361: 1-25.

[本文引用: 1]

WANG S, WANG H, PERDIKARIS P.

On the eigenvector bias of Fourier feature networks: From regression to solving multi-scale PDEs with physics-informed neural networks

[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 384: 1-27.

[本文引用: 1]

ZHANG D, GUO L, KARNIADAKIS G E.

Learning in modal space: Solving time-dependent stochastic PDEs using physics-informed neural networks

[J]. SIAM Journal on Scientific Computing, 2020, 42(2): A639-A665.

[本文引用: 1]

WESSELS H, WEIβENFELS C, WRIGGERS P.

The neural particle method—An updated Lagrangian physics informed neural network for computational fluid dynamics

[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 368: 1-15.

[本文引用: 1]

LU L, MENG X H, MAO Z P, et al.

DeepXDE: A deep learning library for solving differential equations

[J]. Siam Review, 2021, 63(1): 208-228.

[本文引用: 1]

曹艳华, 张姊同, 李楠.

时空多项式配点法求解三维Burgers方程

[J]. 应用数学和力学, 2022, 43(9): 1045-1052.

[本文引用: 1]

CAO Yanhua, ZHANG Zitong, LI Nan.

A space-time polynomial collocation method for solving 3D Burgers equations

[J]. Applied Mathematics and Mechanics, 2022, 43(9): 1045-1052.

[本文引用: 1]

任宏斌. 机器学习方法在第一性原理计算中的应用[D]. 北京: 中国科学院大学, 2021.

[本文引用: 1]

REN Hongbin. Machine learning method in first principle calculation[D]. Beijing: University of Chinese Academy of Sciences, 2021.

[本文引用: 1]

谭康力. 带桨舵的船舶操纵水动力数值研究[D]. 武汉: 武汉理工大学, 2019.

[本文引用: 4]

TAN Kangli. Numerical study of hydrodynamic forces on a hull with propeller and rudder in maneuvering motion[D]. Wuhan: Wuhan University of Technology, 2019.

[本文引用: 4]

/

〈 〉