在DAB变换器的控制方式中,最常用且最易实现的是移相控制,可以分为单移相(single phase shift, SPS)控制、双重移相(dual phase shift, DPS)控制、扩展移相(extended phase shift, EPS)控制和三重移相(triple phase shift, TPS)控制[7-8].文献[9]中通过SPS控制调节两侧全桥驱动电压的角度实现能量传输,控制原理简单但系统效率低、电流应力大.文献[10]中根据DPS控制原理提出关于电流应力控制的系统优化方法.该方法在电流应力优化方面有一定效果,但在轻载条件下并未达到理想优化效果.文献[11]中以TPS控制为基础,利用分段解析法详细分析12种工况下实现电流应力最优的相位控制,在电流应力优化方面效果最好,但存在系统建模及分析较为复杂、可移植性差等问题.EPS控制在SPS控制的基础上,仅在变换器一侧全桥增加移相角,相较于DPS控制提高了灵活性且扩展了功率选择范围,同时控制复杂度方面相较于TPS控制得到简化[12].
在未来电网中,光伏、风电等新能源系统将大规模接入.尤其在远距离大容量电缆输送系统中,交流电缆电容充电效应严重限制交流输电的发展,直流输送方式成为必然选择[13].DAB变换器作为直流变压器中核心电路,为了传输所需功率,必须具备具有不同系统性能(诸如电流应力、回流功率、软开关范围和效率)的无限多种开关驱动信号组合.因此,如何选择最佳驱动信号序列组合,在满足一定发射功率的前提下,使其他性能指标达到最优,是DAB变换器研究的主要目的.电流应力的最小化具有许多益处,并且对改善系统性能有很大帮助.电流峰值降低不仅有助于选择小容量设备从而降低系统成本,而且还有助于减小磁性元件的体积和损耗.此外,电流应力减小可以同时降低器件的导通损耗和开关损耗,有利于系统效率的提高.文献[14]中首次提出EPS控制,通过分析变换器的工作方式建立数学模型,相较于传统移相控制实现了电流应力和回流功率的优化.文献[15]中基于EPS控制针对不同传输功率及电压调节比实时优化电流应力,但系统的控制回路设计过于复杂.文献[14-15]中都只分析了EPS控制的一种工作模式,导致系统的优化并不全面.文献[16]中全面分析变压器两侧的回流功率特性,提出一种优化回流功率的调制策略,但在系统轻载下电流应力较大.文献[17]中基于移相量关系分出两种工作模式,通过拉格朗日优化得到优化电流应力的全局最优解,并引入虚拟电压分量提高系统的动态响应速度,但在系统轻载时电流应力优化并未达到最优.文献[18]中在考虑两种工作模式的基础上,分析了系统轻载时的电流应力特性,根据卡鲁什-库恩-塔克条件实现全功率范围内的电流应力优化.在文献[16⇓-18]的优化策略中,均存在系统传输功率表达式复杂导致传输功率和移相角关系复杂以及移相角之间强耦合的问题.针对这一问题,文献[19]中提出一种新扩展移相控制,通过重新定义移相角的含义简化DAB变换器传输功率的表达式,使传输功率与移相角的关系简洁明确,从而完成对系统控制回路的简化.上述文献基于EPS控制的内移相角均选择在变压器原边侧且均只考虑DAB变换器的降压模式,当变压器工作在升压模式下时,其电流应力特性发生变化导致文献[17⇓-19]中的控制策略优化效果降低;对于EPS控制中内移相角选择在变压器不同侧时电流应力的优化控制策略应如何调整,也并未给出具体分析.
综上所述,基于新扩展移相下内移相角的选择分析DAB变换器的降压-升压模式,提出降压-升压模式下的电流应力优化控制策略.首先,分析内移相角分别工作在变压器两侧时DAB变换器降压-升压模式下的工作特性,根据移相角划分3种工作模态,通过分析比较各模式下的电流应力表达式选择DAB变换器的工作模式并概括在四象限内.然后,根据拉格朗日乘数法(Lagrange multipler method, LMM)优化原理,推导出优化工作模式下的电流应力公式及其移相量组合D1和D2对应的计算公式.最后,搭建实验平台对所提的优化工作模式控制策略进行实验验证.
1 新扩展移相控制
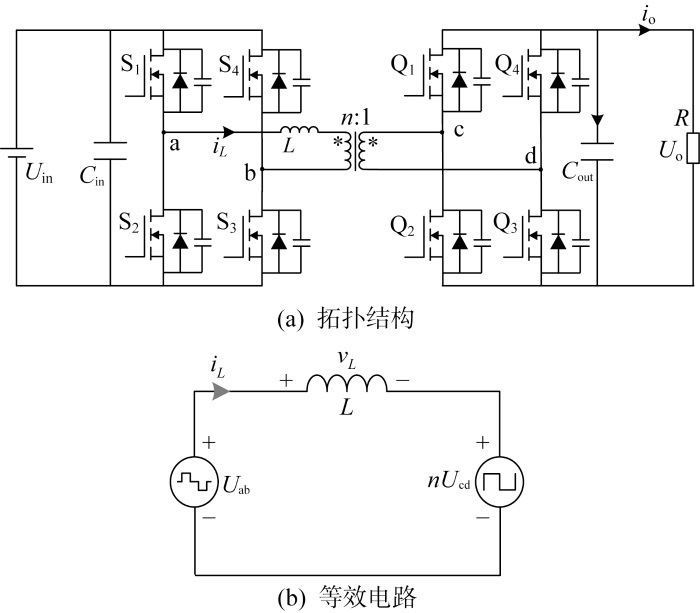
图1
扩展移相调制下DAB变换器的平均传输功率和最大电流应力公式分别为
式中:t为时间;Ts为系统开关周期的一半.
结合式(1)在扩展移相控制下,DAB变换器的最大传输功率和最大平均输入电流分别表示为
式中:f为系统开关频率.
文献[14]中扩展移相控制有两个控制自由度D1和D2,内移相角D1定义为变压器原边逆变桥对角开关管S1和S3的相移量,外移相角D2定义为两端H桥开关管S1和Q1的相移量,则在传统扩展移相控制下传输功率表达式为
图2
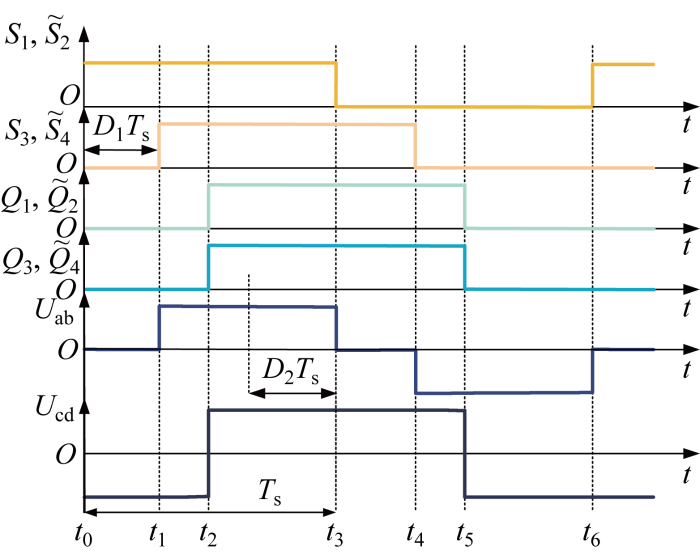
在新扩展移相控制下,内移相角D1定义不变,将外移相角D2更改为变压器两端电压Uab和Ucd高电平电压之间的移相角差,则高频变压器两端驱动信号波形和电压Uab和Ucd的波形如图3所示.图中:S1~S4、Q1~Q4分别为相应开关管驱动信号;~表示相反波形.
图3
图3
新扩展移相控制下DAB变换器单元波形
Fig.3
DAB converter unit waveforms under new EPS control
结合图3和式(1)~(2),新扩展移相下DAB变换器的平均传输功率的标幺值表达式为
分析式(3)~(4),功率表达式在传统扩展移相下,移相角之间存在较强的耦合关系,在新扩展移相下得到一定的简化.
绘制新扩展移相下系统的传输功率标幺值在三维空间的图形及在二维平面内的投影图,如图4所示.
图4
综上所述,新扩展移相控制通过重新定义外移相角简化传输功率表达式,将其划分为3种模态实现传输功率对移相量的全范围覆盖,降低了设计控制系统的难度,提高了移相组合取值的灵活性.因此,以新扩展移相调制为基础设计控制电路.
2 降压-升压模式变换器
2.1 原边侧移相控制
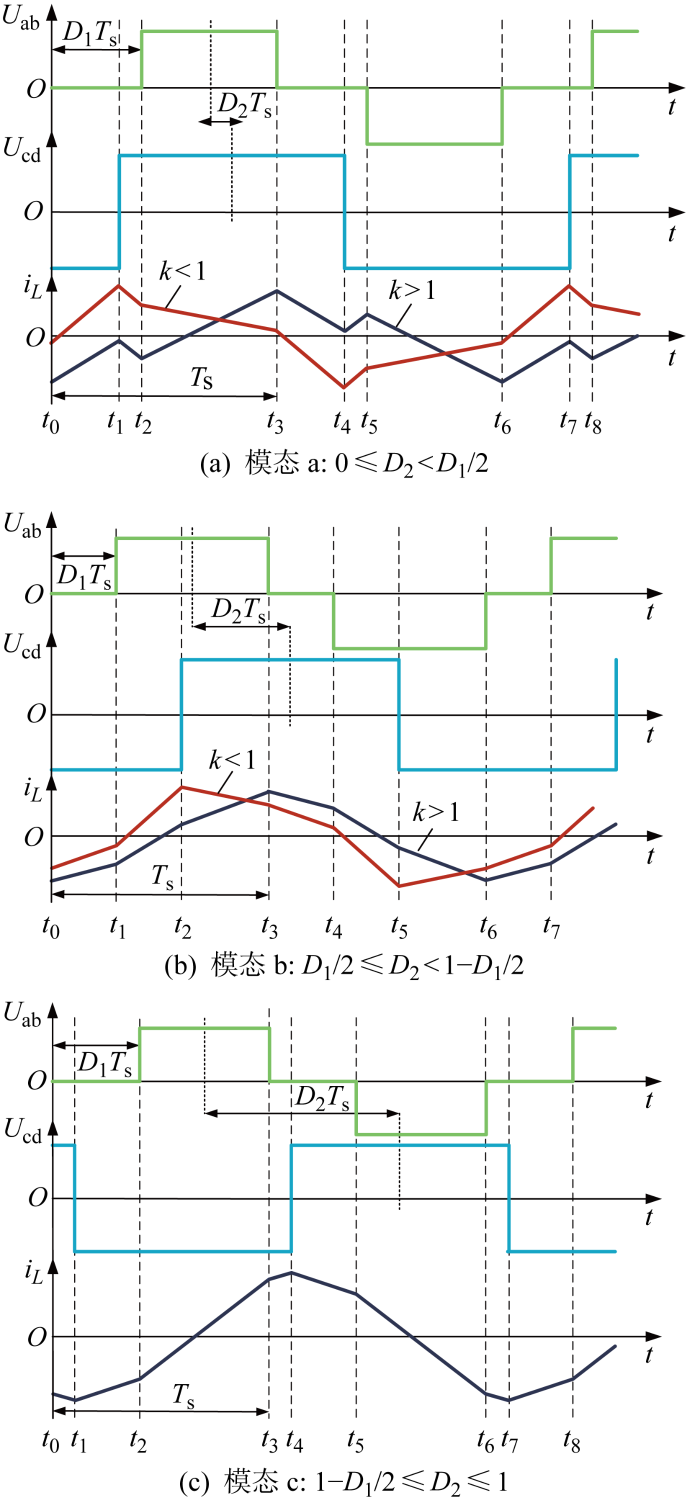
当内移相角D1选择在变压器原边侧时,DAB变换器工作在升压或降压模式下,即电压比k<1或k>1时,根据移相角D1和D2之间关系可划分为3种工作模态a、b、c,分别为0≤D2<D1/2、D1/2≤D2<1-D1/2和1-D1/2≤D2≤1,系统电压电流波形如图5所示.
图5
图5
内移相角在原边侧时DAB变换器的电压电流波形
Fig.5
Voltage and current waveforms of DAB converter with the inward phase shift angle on the primary side
式中:I为模态瞬时值,表示该时刻对应的电流值;i为模态的函数,表示这段时间内对应的电流值.
由式(5)可得模式a下t1~t3时刻电感电流标幺值分别为
同理求得工作模态b下电感电流标幺值
工作模态c下电感电流标幺值可表示为
尽管从传输功率的角度,模态a和c是等效的,但随着系统在升压和降压模式之间转变,工作模态a和c在传输相同功率时的电流应力不同.以系统工作在降压模式即电压比k>1为例分析内移相角选择在变压器原边侧时,结合式(6)和式(8)得到变换器传输相同功率分别工作在模态a和c下的电流应力差值为
式中:外移相角D2的取值由模式a的工作区间0≤D2<D1/2决定,代入式(9)可知Ia(t3)-Ic(t4)≤0恒成立,即在降压模式下内移相角D1选择在原边侧时,处于模态a下电流应力总是小于等于模态c下的电流应力.
当系统工作在升压模式k<1下,工作模态a的电流应力最大值发生变化由Ia(t3)变为Ia(t1),此时工作在模态a和c下的电流应力差值为
由式(10)可知,在升压模式下模态a和c的电流应力差值受内移相角D1的影响,在0<D1<0.5时模态a下的电流应力较小,在0.5<D1<1时模态c下的电流应力较小,且此时模态a和c下的最大电流应力都只有一个控制自由度,丧失了扩展移相多自由度优化的优势.结合式(9)和(10)可知,内移相角D1选择在变压器原边侧,在降压模式k>1下选择模态a作为系统的低功率模态.在升压模式k<1下,需考虑D1的取值来决定工作在模态a或c,增加了系统控制复杂度且无法达到最优电流应力.
2.2 副边侧移相控制
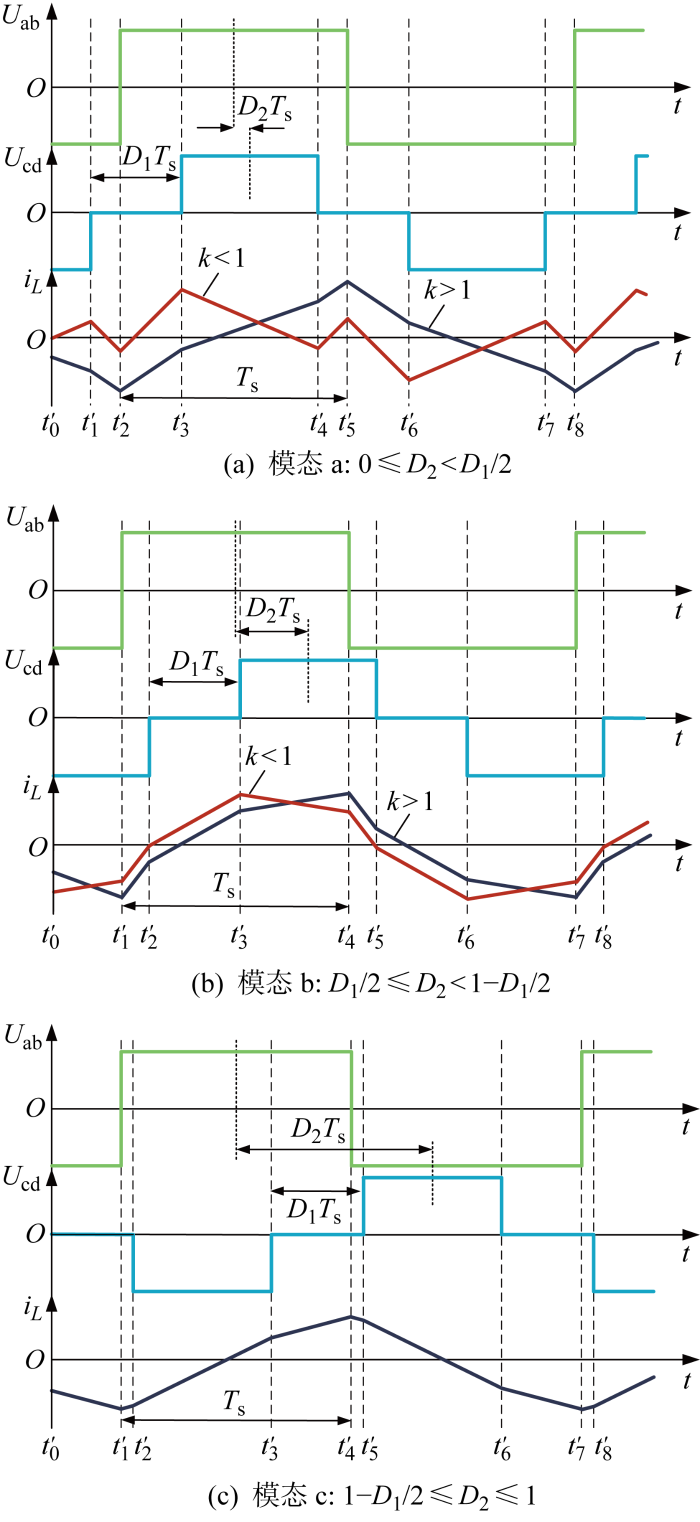
将内移相角D1选择在变压器副边侧,在DAB变换器降压-升压模式下,根据移相角D1和D2之间关系可分为3种模态,变压器两侧电压及降压-升压模式下的电感电流曲线如图6所示.
图6
图6
内移相角在副边侧时DAB变换器的电压电流波形
Fig.6
Voltage and current waveforms of DAB converter with the phase shift angle on the secondary side
由式(6)的推导得到模态a下t'1~t'3时刻电感电流标幺值分别为
同理模态b下t'1~t'4时刻电感电流标幺值为
模态c下t'1~t'4时刻电感电流标幺值为
联立式(1)和图6计算内移相角D1选择在变压器副边侧时的传输功率,则D1不论是在变压器原边侧还是副边侧,其功率表达式都相同,如式(4)所示.在模态a和c下电流应力的比较中,参考上述方法可得到类似结论:内移相角D1选择在变压器副边侧,在降压模式k>1下需考虑D1的取值来决定工作在模态a或c,且只受一个控制自由度影响.在升压模式k<1下,选择模态a作为系统的低功率模态.进一步得到,系统在电压比k>1时内移相角选择在原边侧,电压比k<1时内移相角选择在副边侧,以降低控制复杂度,实现电流应力最优化.
在升压模式k<1下,电流应力差值为
由式(14)和(15)可知,在k>1时Ib(t3)-Ib(t'4)<0恒成立,同理在k<1时Ib(t2)-Ib(t'3)>0恒成立.则在高功率模态b下,根据电压比k>1,内移相角选择在原边侧时电流应力更小;电压比k<1,内移相角选择在副边侧时电流应力更小.
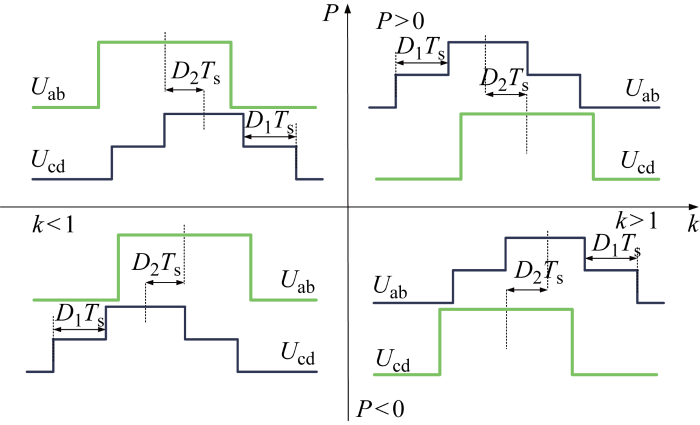
综上所述,根据变换器电压比k的值和系统传输功率的方向建立坐标轴,新扩展移相下内移相角的选择和外移相角的取值如图7所示.
图7
图7
DAB变换器在四象限的端口电压波形
Fig.7
Voltage waveform of DAB converter in four quadrants
3 电流应力优化控制策略
电流应力优化控制策略先根据采样系统的输入输出电压计算出系统电压比,根据电压比k判断内移相角D1工作在变压器原边侧或副边侧,然后使用LMM优化电流应力.LMM是一种寻找变量受一个或多个约束条件所限制的多元函数的极值的方法,将LMM应用到DAB变换器的电流应力优化中,定义拉格朗日函数为
式中:im为电感电流峰值,即电流应力;λ为拉格朗日乘子.将拉格朗日函数分别对移相角和λ求导,计算优化后的移相组合:
当系统工作在降压模式k>1时,内移相角选择在变压器原边侧,将式(6)~(7)代入上式进行LMM优化电流应力,得到在传输给定功率时的最优移相量组合为
式中:Pi为此刻瞬时功率.
同理,系统工作在升压模式k<1时,内移相角选择在变压器副边侧,最优移相量组合为
将式(18)~(19)优化移相量组合D1和D2分别代入相应的电流应力表达式中,求解相对应的最优电流应力值,则电流应力表达式如表1所示.
表1 LMM优化移相组合
Tab.1
| 降压-升压 | 功率范围 | 电流应力表达式 |
|---|---|---|
| k>1 | 0≤Pi≤ | 2 |
| 2k-2 | ||
| k<1 | 0≤Pi≤2k(1-k) | 2 |
| 2k(1-k)<Pi≤1 | 2-2 |
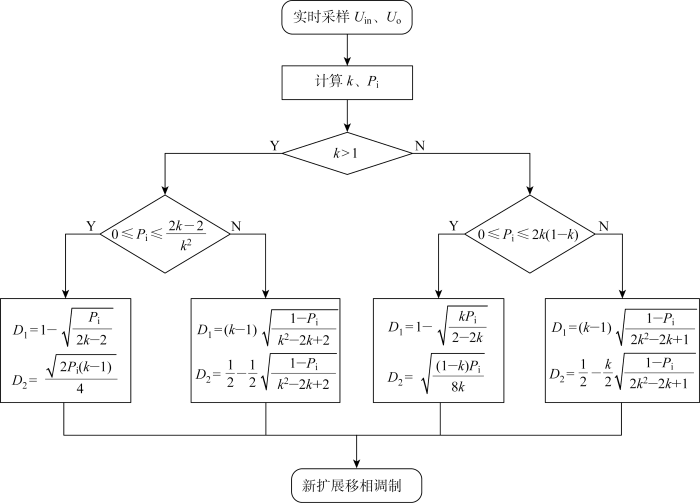
通过上述分析可知电压比k影响系统的工作模式,根据采样系统的输入输出电压计算电压比k的值,判断k>1决定最优移相量组合经过式(18)或式(19),再由输出电压参考值与采样输出电压作差经过比例积分(proportional integral, PI)计算系统传输功率来判断系统是处于高功率模态或低功率模态,优化工作模式控制流程图如图8所示.
图8
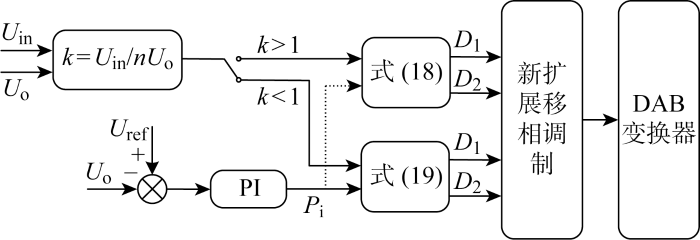
图9为优化工作模式闭环控制框图,利用PI调节输出系统传输功率和电压比k的实时计算,在系统发生功率突变或升降压时实现快速动态调节计算出最优移相组合.图中:Uref为系统输出参考电压.
图9
4 实验结果及分析
为验证对电流应力优化控制策略理论分析的正确性和有效性,搭建DAB变换器实验平台对上述控制策略进行验证,其主要参数如下:开关频率f=10 kHz;变压器变比n=1;等效电感L=200 μH;输入侧分压电容C=2.2 mF;输出侧滤波电容C=1.1 mF.
图10
图10
降压模式下DAB变换器的电压电流波形
Fig.10
Voltage and current waveforms of DAB converter in buck mode
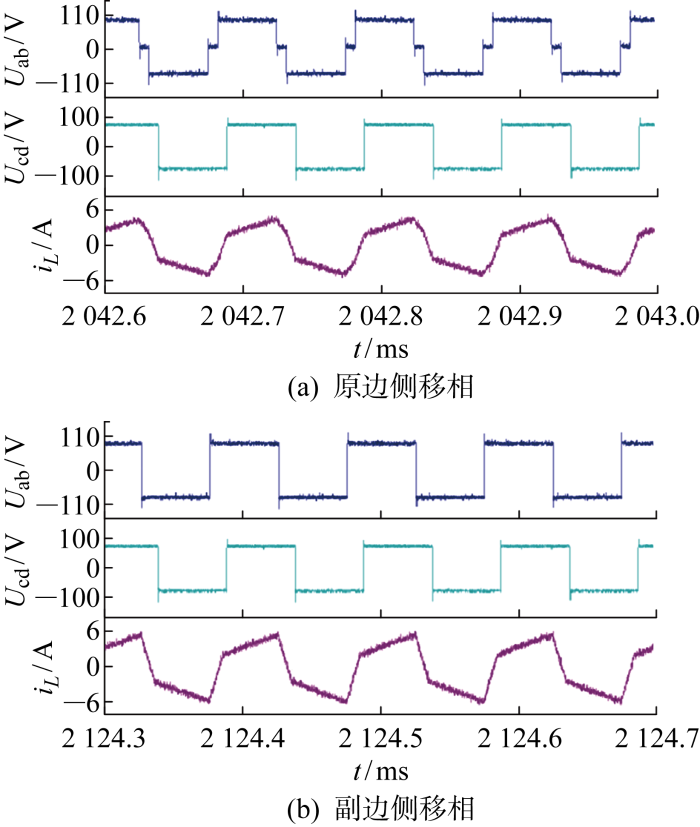
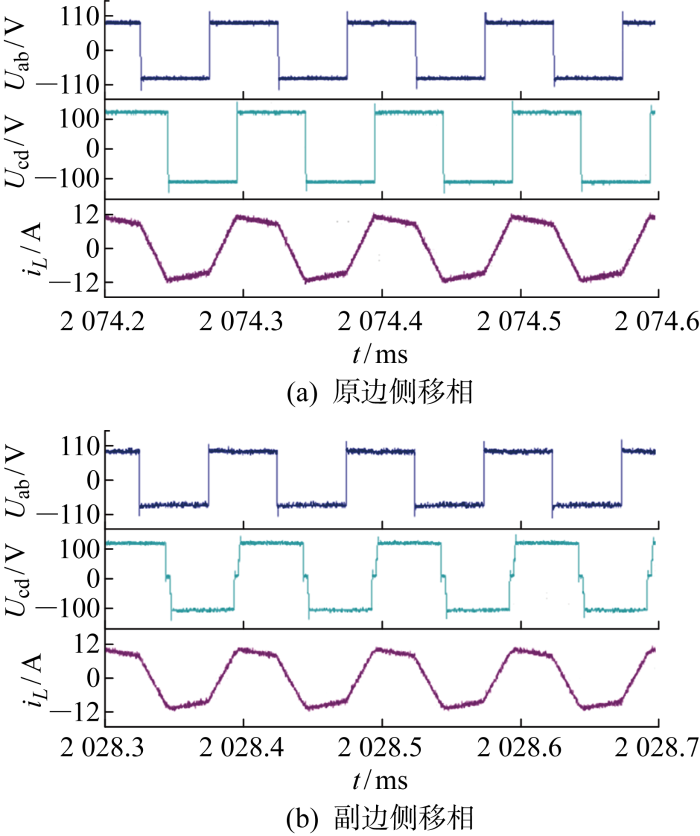
设置DAB变换器输入电压Uin=100 V,输出电压Uo=120 V,输出功率 1.44 kW,电压比k=0.83.图11为DAB变换器的变压器两侧电压波形及电感电流波形.其中,图11(a)为内移相角在原边侧工作时产生的电压电流波形,类似图10(b),此时电流应力受单一移相量控制导致内移相角经过优化为0变成单移相控制,电感电流应力优化为 12.1 A.图11(b)为内移相角在副边侧工作下的电压电流波形,经过LMM优化在电流应力优化方面达到最优,具有最优化的移相量组合,电流应力约为 11.6 A.分析图11可知,在升压模式k<1下,内移相角D1在副边侧工作时移相量经过LMM优化,电流应力达到最优.
图11
图11
升压模式下DAB变换器的电压电流波形
Fig.11
Voltage and current waveforms of DAB converter in boost mode
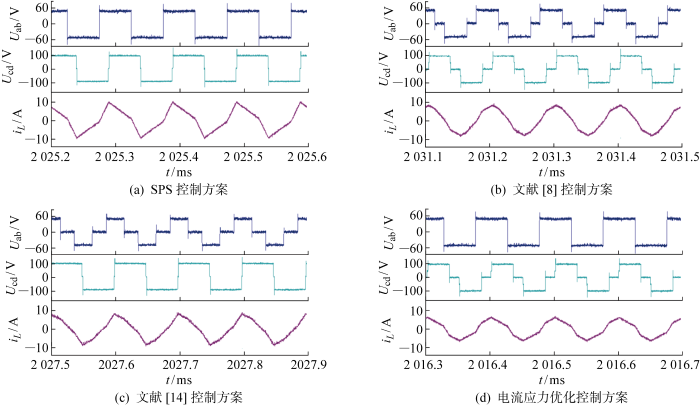
为了验证电流应力优化控制策略的电流应力优化效果,以SPS控制方案、文献[8]控制方案和文献[14]控制方案作为对比方案进行实验.设置DAB变换器输入电压Uin=50 V,输出电压Uo=20 V,电压转换比k=2.5,系统工作在降压模式下输出功率40 W.图12为变换器其变压器两侧的电压波形及电感电流波形.由图可见,在降压模式下,DAB变换器在不同控制策略下电流应力优化不同.在SPS移相控制、文献[8]控制方案、 文献[14]控制方案和所提优化工作模式控制方案下,电流应力分别为7.56、6.02、5.53和3.51 A.SPS移相控制的优化效果最差;EPS移相控制优化效果略优于DPS移相控制,但并未达到最优效果.电流应力优化控制方案利用LMM计算出最优电流应力组合,得到最优电流应力.
图12
图13
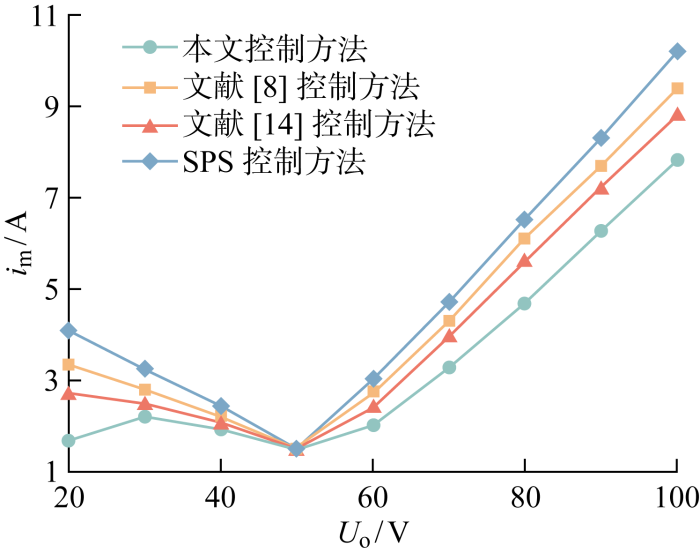
在实验中,采用TI公司的DSP(TMS320F28377D)控制芯片,时钟频率为200 MHz.控制算法在脉宽调制中断程序实现,进入中断时,对IO端口进行置位;中断返回前,对IO端口复位,用示波器测量IO端口输出波形,即可测试出控制算法的执行时间.所提算法的程序执行时间为8.5 μs.DAB变换器的电流应力是变换器高效运行重要的性能指标.为了直观体现不同工作模式在降压-升压模式之间电流应力优化效果的差异,图14展示了DAB变换器在输出电压Uo由20~100 V阶梯之间的电流应力曲线,设置系统的输入电压Uin=50 V,负载R=10 Ω.分析图14可知,不同工作模式随着电压比的变化电流应力优化效果不同,随着电压转换比偏离1的程度增大,这一现象更加明显.在所提电流应力优化控制方法下,DAB变换器的电流应力优化效果达到最优.
图14
5 结论
随着新能源发电系统的蓬勃发展,风能、光伏、潮汐能等新能源的发电量在电力系统中的占比不断提高,DAB变压器作为实现新能源高效、经济的大规模汇集和构建直流输配电一体化网络的关键设备受到广泛关注.电流应力定义为流过变换器的最大瞬时电流值,其对变换器的效率、开关器件的选型和安全操作具有重要影响.较小的电流应力可减小变换器的通态损耗,提高效率,延长器件的使用寿命.对于相同的功率水平还可通过选择较低应力水平的器件,降低开关器件的选型成本.本文在新扩展移相的基础上针对DAB变换器在降压-升压模式下的电流应力优化提出一种电流应力优化控制策略.分析新扩展移相的优势及DAB变换器在降压-升压模式下不同移相量关系下的电压电流波形图,并利用电流应力优化控制策略得到在全功率范围内的电流应力优化函数.通过理论分析,将降压-升压模式下内移相角分别工作在变压器两侧的情况作对比,结果表明:
(1) 在新移相调制下,重新定义移相角D2归化DAB变换器的功率表达式,使系统传输功率大小与移相角正相关;且随着系统工作模式的切换,新扩展移相下电流应力表达式和移相角的关系更简洁,为电流应力优化控制提供理论基础.
(2) 在降压-升压模式下,选择内移相角工作位置,由电流应力优化控制策略计算出最优移相组合,在全功率范围有效降低变换器电流应力.
参考文献
Modeling and advanced control of dual-active-bridge DC-DC converters: A review
[J].
Review on advanced control technologies for bidirectional DC/DC converters in DC microgrids
[J].
双向全桥DC-DC变换器高效能控制研究与实现
[J].
Research and implementation of bidirectional full bridge DC-DC converter with high-efficiency control
[J].
面向储能系统应用的隔离型双向DC-DC变换器分析方法与控制技术综述
[J].
DOI:10.12067/ATEEE1906021
[本文引用: 1]

对储能系统中的隔离型双向DC-DC变换器进行了较为全面的调研。首先介绍了储能系统的研究发展背景和其对高效率高功率密度隔离型双向DC-DC变换器的要求,然后对近年来隔离型双向DC-DC变换器的国内外研究现状进行了综述,并着重对CLLC谐振变换器和双有源桥(DAB)变换器的分析方法和控制技术进行了比较分析。CLLC谐振变换器和DAB变换器都适合于未来大规模储能系统的应用需要,其中DAB变换器技术已经趋于更加成熟,有望率先实现规模化应用,CLLC谐振变换器则在中小功率范围内更具效率、功率密度的优势,随着设计技术和制造工艺的不断进步,其应用前景也十分广阔。
A review of analysis method and control technology for isolated bidirectional DC-DC converter used in energy storage systems
[J].
SiC-MOSFET与Si-IGBT混合开关车载双向充电器中线桥臂设计及控制
[J].
Neutral leg design and control of electric vehicle on-board bidirectional charger based on SiC-MOSFET and Si-IGBT hybrid devices
[J].
电能路由器的发展及其关键技术
[J].
The development and key technologies of electric energy router
[J].
Current-stress-optimized switching strategy of isolated bidirectional DC-DC converter with dual-phase-shift control
[J].
Virtual direct power control scheme of dual active bridge DC-DC converters for fast dynamic response
[J].
双有源桥变换器电流应力优化
[J].
Optimization of current stress for dual active bridge converter
[J].
Current stress minimization of dual-active-bridge DC-DC converter within the whole operating range
[J].
基于开关组合规律的双有源桥DC-DC变换器传输功率特性
[J].
Transmission power characteristics of dual-active-bridge DC-DC converter based on the switching combination rules
[J].
双有源桥式直流变压器发展与应用
[J].
Development and application of DC transformer based on dual-active-bridge
[J].
Extended-phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid
[J].
双向全桥DC-DC变换器基于电感电流应力的双重移相优化控制
[J].
Optimized control based on current-stress of bi-directional full-bridge DC-DC converters with dual-phase-shifting control
[J].
Minimum-backflow-power scheme of DAB-based solid-state transformer with extended-phase-shift control
[J].
基于扩展相移的双有源全桥DC-DC变换器多目标优化控制方法
[J].
Multi-objective optimization control scheme based on extended phase-shift of dual-active-bridge DC-DC converters
[J].
扩展移相控制的双有源桥DC-DC变换器的优化控制策略
[J].
Optimal control strategy of dual active bridge DC-DC converters with extended-phase-shift control
[J].