适用于频率和电压动态分析的构网型新能源场站聚合建模

doi:10.16183/j.cnki.jsjtu.2023.061

适用于频率和电压动态分析的构网型新能源场站聚合建模

葛琛琛¹, 陈俊儒^,¹, 徐森², 常喜强², 毛善祥¹, 朱荣伍³

1.新疆大学电气工程学院,乌鲁木齐 830047

2.国网新疆电力有限公司,乌鲁木齐 830011

3.哈尔滨工业大学(深圳) 机电与自动化工程学院,广东深圳 518000

Aggregation Modelling of Grid-Forming Renewable Power Plant for Frequency and Voltage Dynamic Analysis

GE Chenchen¹, CHEN Junru^,¹, XU Sen², CHANG Xiqiang², MAO Shanxiang¹, ZHU Rongwu³

1. School of Electrical Engineering, Xinjiang University, Urumqi 830047, China

2. State Grid Xinjiang Electric Power Co., Ltd., Urumqi 830011, China

3. School of Mechanical Engineering and Automation, Harbin Institute of Technology (Shenzhen), Shenzhen 518000, Guangdong, China

通讯作者: 陈俊儒,副教授,博士生导师;E-mail:junru.chen@xju.edu.cn.

责任编辑: 王历历

收稿日期: 2023-02-22 修回日期: 2023-07-14 接受日期: 2023-07-18

基金资助:

新疆维吾尔自治区科技厅重大科技专项项目(2022A01004-1)

Received: 2023-02-22 Revised: 2023-07-14 Accepted: 2023-07-18

作者简介 About authors

葛琛琛(1997—),博士生,从事电力系统建模与仿真技术研究.

摘要

构网型新能源场站可模拟传统火力发电厂相关特性,具有主动支撑电网频率和电压的功能.提出一种适用于新型电力系统频率和电压稳定性分析的构网型新能源场站聚合模型,并分析场站整体运行特性,提出聚合模型参数识别与选取方法.所提聚合模型能够准确反映新能源场站与电网交互下的动态过程,并保障了较快的仿真速率.与MATLAB/Simulink中构网型新能源场站电磁暂态全拓扑模型进行比较,验证了所提聚合模型的有效性.基于IEEE 39母线系统的案例分析验证了所提聚合模型在电力系统频率和电压稳定性仿真分析中的准确性和快速性.

关键词： 构网型变流器; 新能源场站; 聚合模型; 系统稳定性

Abstract

Renewable power plant based on the grid-forming converter has a similar performance with the traditional thermal power plant on the function of active support for the frequency and voltage in the power system. An aggregation model is proposed for the frequency and voltage stability analysis of new power system, the overall operation characteristics of the plant are analyzed, and a method for identifying and selecting the parameters of the aggregation model is proposed. The proposed aggregation model can accurately reflect the dynamic process of the interaction between the renewable power plant and the grid, and ensure a quick simulation rate. In comparison with the electromagnetic transient model for grid-forming renewable power plant, the effectiveness of the proposed aggregation model is verified in MATLAB/Simulink. The accuracy and rapidity of the proposed aggregation model is verified in the frequency and voltage stability simulation analysis of power system based on the case study in the IEEE 39 bus system.

Keywords： grid-forming converter; renewable power plant; aggregation model; system stability

PDF (2974KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

葛琛琛, 陈俊儒, 徐森, 常喜强, 毛善祥, 朱荣伍. 适用于频率和电压动态分析的构网型新能源场站聚合建模[J]. 上海交通大学学报, 2024, 58(10): 1544-1553 doi:10.16183/j.cnki.jsjtu.2023.061

GE Chenchen, CHEN Junru, XU Sen, CHANG Xiqiang, MAO Shanxiang, ZHU Rongwu. Aggregation Modelling of Grid-Forming Renewable Power Plant for Frequency and Voltage Dynamic Analysis[J]. Journal of Shanghai Jiaotong University, 2024, 58(10): 1544-1553 doi:10.16183/j.cnki.jsjtu.2023.061

中央财经委员会第九次会议指出,“十四五”是碳达峰的关键期、窗口期,电力作为我国碳排放占比最大的单一行业,应当在保障电网安全稳定运行的前提下加快构建新型电力系统^[1].在新能源发电逐步替代同步电机成为电网主要电源的过程中,电网跟随型新能源不能像传统同步机一样作为电压源构建交流电力系统中的电压和频率,难以满足电网电压和频率支撑需求^[2].为使新能源自主形成电网的高电势,同时主动支撑电网频率,以虚拟同步机为主的电网构造型并网技术于2008年被提出后,受到学术界和工业界的广泛关注,并将于“十四五”期间大力推进技术落实.

构网型并网技术与当前新能源常用的跟网型并网技术具有显著区别.跟网型并网技术采用锁相环实时测量锁定公共耦合点(point of common coupling,PCC)电压的相位并控制电流输出,以电流源附加的形式被动接入电网;而构网型并网技术通过模拟同步机功角特性,根据有功发电量控制虚拟转角,并且在PCC处形成电压输出,以电压源的形式主动接入电网^[3].因此,在构网型新能源逐渐替代跟网型新能源的过程中,系统电压源数量逐渐增加,从而能够提升系统电压稳定性.此外,构网型新能源还具备主动提供惯性支持的能力,能够增强系统频率稳定性^[4].最基本的构网型控制是下垂控制和功率同步控制^[5-6].近年,为进一步支撑电网惯量和频率,同步变流器和虚拟同步机等控制技术相继被提出^[7⇓-9].构网型控制的核心参数可按照模拟同步机特性进行设置,其功率同步环动态响应速度明显慢于变换器内环控制的动态响应速度,因此在分析构网型输出特性时,内环控制暂态一般可忽略不计^[10⇓-12].关于单机系统稳定性的构网型阻抗参数选取已被广泛研究^[13],然而构网型控制技术在改善系统暂态过程的同时也引入同步机的振荡问题^[14].现实中,新能源场站由多个机组并列构成,当多个构网型新能源并联运行时,因新能源间阻尼缺乏,系统易发生功率振荡^[15⇓-17].该问题可以利用Bang-Bang控制、自适应惯性阻尼控制等方法解决^[18⇓-20].

对于电力系统而言,发电站需满足电网标准才能接入电网,仅需知道电站在接入点处表征的整体特性,而不必知道其内部具体参数.同时,模型的阶数和精度与模型的求解速度呈负相关,如何在不降低精度的同时加快仿真速度是电力系统建模的关键.因此,针对发电站构建动态聚合等值模型是电力系统控制与调度部门用于分析电力系统稳定性的常用方法.例如,文献[21]中提出同步机组的一般聚合模型;文献[22]中提出表征电力系统频率响应特性的传递函数模型.为了有效分析电力系统的频率稳定性,文献[23 ⇓-25]中提出跟网型风电场等值建模方法,并且给出其参数识别方法;文献[26]中将跟网型控制的多机系统等效为一个二阶电流源;而文献[27]中将虚拟电厂等效为电压源与电流源的并联.然而,对于构网型新能源场站的聚合动态模型少有研究.因此,在新能源由跟网型向构网型逐步转变的背景下,构建构网型新能源场站动态聚合模型是实现电力系统稳定性有效分析的重要前提.

本文提出构网型新能源场站的一般聚合模型,旨在确保准确反映新能源场站与电网动态交互过程的前提下,加快电网仿真速率.具体贡献如下:①提出一种适用于电力系统频率和电压稳定性分析的构网型新能源场站聚合模型;②根据构网型新能源场站整体运行特性提出聚合模型参数识别与选取方法;③利用单机无穷大系统和系统闭环仿真实验验证了场站聚合模型的准确性和快速性.

1 构网型新能源控制及建模

1.1 构网型新能源单元建模

构网型的典型控制方法包括下垂控制、功率同步控制、同步变流器和虚拟同步机控制,其控制核心为模拟同步机的功角暂态.因此,以上控制皆可转换为摇摆方程形式:

$\begin{aligned} M_{i} \frac{\mathrm{~d} \omega_{i}}{\mathrm{~d} t}= & P_{i}-P_{i}^{*}+K_{\mathrm{d}, i}\left(\omega^{*}-\omega_{\mathrm{g}}\right)- \\ & D_{i}\left(\omega_{i}-\omega_{\mathrm{g}}\right) \end{aligned}$

(1)

式中:M_i为新能源单元i的虚拟惯性常数;ω_i为构网型新能源输出频率;t为时间;P_i为新能源单元i的输出功率; $P_{i}^{*}$ 为新能源单元i参考功率输出;K_d_{, i}为下垂系数;D_i为阻尼常数;ω^*为参考电网频率;ω_g为电网频率.假设电网电压相位为0,则新能源在PCC处的电压相位(δ_i)为

$\frac{d δ_{i}}{d t}$ =ω_i-ω_g

(2)

另一方面,构网型控制可模拟同步机的电压调节器调节输出电压:

E_i=V^*-K_v_,_i(V^*-V_POC)

(3)

式中:V^*为额定电压;V_POC为公共连接点(point of connection,POC)电压;K_v,_i为电压调节系数.

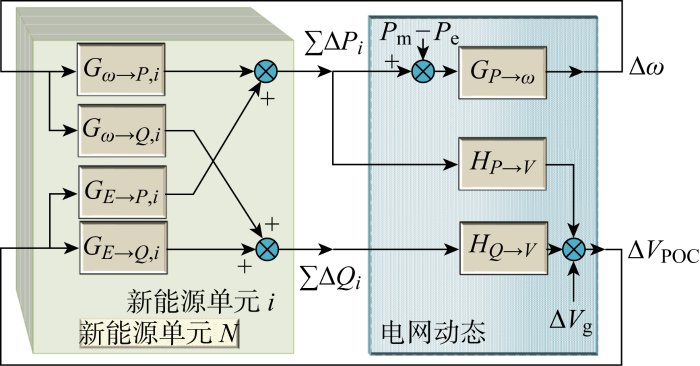
式(1)~(3)构成构网型控制外环,包括有功调节和电压调节以及并网同步环,其输入为电网频率与电压幅值,而输出E_i和δ_i作为内环控制的参考值.内环控制为电压源变换器的离网控制,即电压电流控制,其目的是控制变流器的输出电压追踪其参考值.文献[11]中已证明,当外环控制时间常数大于内环控制时间常数10倍及以上时,构网型变换器的内环控制暂态可忽略不计.由于本文重点为等值聚合模型,并非场站内部动态稳定性分析,所以假设变换器自身参数已择优选取,重点考虑构网型控制的外环特性.

假设线路阻抗仅为感性(l_i)时,则新能源单元在POC处的有功功率输出和无功功率输出分别为

$P_{i}=\frac{E_{i} V_{\mathrm{POC}} \sin \delta_{i}}{\omega_{i} l_{i}}$

(4)

$Q_{i}=\frac{E_{i} V_{\mathrm{POC}} \cos \delta_{i}-V_{\mathrm{POC}}^{2}}{\omega_{i} l_{i}}$

(5)

$\begin{array}{l} G_{ω \to P, i} = \frac{J K_{v} H_{d P / d E} s^{2} + K_{d} K_{v} H_{d P / d E} s}{J (1 + K_{v} H_{d Q / d E}) s^{2} + K_{d} (1 + K_{v} H_{d Q / d E}) s + H_{d P / d δ} + (H_{d P / d δ} - H_{d Q / d δ}) K_{v} H_{d P / d E}} \\ G_{ω \to Q, i} = \frac{J K_{v} H_{d P / d E} s^{2} + K_{d} K_{v} H_{d P / d E} s + H_{d P / d δ} K_{v} H_{d Q / d E} - H_{d Q / d δ} K_{v} H_{d P / d E}}{J (1 + K_{v} H_{d Q / d E}) s^{2} + K_{d} (1 + K_{v} H_{d Q / d E}) s + H_{d P / d δ} + H_{d P / d δ} K_{v} H_{d Q / d E} - H_{d Q / d δ} K_{v} H_{d P / d E}} \\ G_{E \to P, i} = \frac{(H_{d P / d δ} - H_{d Q / d δ} H_{d P / d E} \frac{K_{v}}{1 + K_{v} H_{d Q / d E}}) (J s + K_{d})}{J s^{2} + K_{d} s + H_{d P / d δ} - H_{d Q / d δ} H_{d P / d E} \frac{K_{v}}{1 + K_{v} H_{d Q / d E}}} \\ G_{E \to Q, i} = \frac{\frac{H_{d Q / d δ}}{1 + K_{v} H_{d Q / d E}} (J s + K_{d})}{J s^{2} + K_{d} s + H_{d P / d δ} - K_{v} H_{d P / d E} \frac{1 + K_{v} H_{d Q / d E}}{H_{d Q / d δ}}} \end{array}\}$

(6)

式中:H_d_P/_d_E、H_d_Q/_d_E、H_d_P/_d_δ和H_d_Q/_d_δ为有功和无功功率与电压幅值和相位之间的增益;J为惯性常数;s为拉普拉斯变换中的复变量.式(1)~(5)构成构网型变换器二阶模型.构网型变换器的优势为主动支撑电网频率与电压.本文致力于聚合构网型新能源场站模型以模拟其在电网频率与电压的动态特性.为此,对式(1)进行拉普拉斯变换,并对式(4)和(5)进行POC处电压与相位的小信号分析;由文献[13]可得构网型变换器输出功率与电网频率和电压变化的传递函数,如式(6)所示.式(6)可构成电网电压及频率变化对构网型新能源单元POC处有功与无功功率输出影响的动态模型.

1.2 系统动态等效建模

新能源场站中各单元在POC处汇集的总有功、无功功率分别为

$P_{\mathrm{a}}=\sum_{i=1}^{N} P_{i}=\sum_{i=1}^{N} \frac{E_{i} V_{\mathrm{POC}} \sin \delta_{i}}{\omega_{i} l_{i}}$

(7)

$Q_{\mathrm{a}}=\sum_{i=1}^{N} Q_{i}=\sum_{i=1}^{N} \frac{E_{i} V_{\mathrm{POC}} \cos \delta_{i}-V_{\mathrm{POC}}^{2}}{\omega_{i} l_{i}}$

(8)

二者经电网阻抗(l_g)注入电网,即

$P_{\mathrm{g}}=\frac{V_{\mathrm{POC}} V_{\mathrm{g}} \sin \delta_{\mathrm{g}}}{\omega_{\mathrm{g}} l_{\mathrm{g}}}$

(9)

$Q_{\mathrm{g}}=\frac{V_{\mathrm{POC}}^{2}-V_{\mathrm{POC}} V_{\mathrm{g}} \cos \delta_{\mathrm{g}}}{\omega_{\mathrm{g}} l_{\mathrm{g}}}$

(10)

式中:V_g为电网电压;δ_g为电网电压相位.

联立式(9)和(10)可求得V_POC电压为

V_POC=

$\sqrt{\frac{V_{g}^{2}}{2} + X_{g} Q_{g} + \sqrt{\frac{V_{g}^{4}}{4} - X_{g}^{2} P_{g} + X_{g} Q_{g} V_{g}^{2}}}$

(11)

式中:X_g=ω_gl_g.

在动态电网中,新能源场站在POC处注入有功和无功功率的变化将影响电网频率与电网电压,而变化的电网频率与电网电压又将反过来影响新能源场站的有功无功出力.定义电网发电机产生的有功功率为P_m,负载吸收的有功功率为P_e,电网综合惯量为M_syn,电网等值阻尼常数为D_syn,电网调速器的综合系数和其动态时间常数分别为K_{d, syn}和T_syn.以POC处为电网与新能源场站的交互点,则电网动态频率特性如下:

$\begin{array}{l} M_{\mathrm{syn}} \frac{\mathrm{~d} \Delta \omega_{\mathrm{g}}}{\mathrm{~d} t}+D_{\mathrm{syn}} \Delta \omega_{\mathrm{g}}= \\ \quad P_{\mathrm{m}}-P_{\mathrm{e}}+\sum_{i=1}^{N} \Delta P_{i}-K_{\mathrm{d}, \mathrm{syn}}\left(\omega^{*}-\omega_{\mathrm{g}}\right) \end{array}$

(12)

新能源场站的有功和无功功率扰动对POC处电压的影响作用可由式(11)求偏导表示,如下式所示:

$\begin{array}{l} H_{P \to V} = \frac{\partial V_{P O C}}{\partial P_{g}} = \frac{- P_{g} X_{g}^{2}}{{\{2 {[Q_{g} X_{g} + {(- P_{g}^{2} X_{g}^{2} + \frac{V_{g}^{4}}{4} + Q_{g} V_{g}^{2} X_{g})}^{0.5} + \frac{V_{g}^{2}}{2}]}^{0.5} (- P_{g}^{2} X_{g}^{2} + \frac{V_{g}^{4}}{4} + Q_{g} V_{g}^{2} X_{g})\}}^{0.5}} \\ H_{Q \to V} = \frac{\partial V_{P O C}}{\partial Q_{g}} = \frac{\frac{X_{g} + V_{g}^{2} X_{g}}{2 {(- P_{g}^{2} X_{g}^{2} + \frac{V_{g}^{4}}{4} + Q_{g} V_{g}^{2} X_{g})}^{0.5}}}{2 {[Q_{g} X_{g} + {(- P_{g} X_{g}^{2} + \frac{V_{g}^{4}}{4} + Q_{g} V_{g}^{2} X_{g})}^{0.5} + \frac{V_{g}^{2}}{2}]}^{0.5}} \end{array}\}$

(13)

对式(12)进行拉普拉斯变换,并根据文献[28]得到电网频率与功率的传递函数,如下式所示:

G_P_→_ω=

$\frac{Δ ω_{g}}{Δ (P_{m} - P_{e})}$ =

$\frac{T_{s y n} s + 1}{(M_{s y n} s + D_{s y n}) (T_{s y n} s + 1) + K_{d, s y n}}$

(14)

综上,以新能源电场接入点为观测点整个电力系统的动态特性可以由图1表示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 电力系统与新能源场站交互动态特性

Fig.1 Dynamic interaction of modern power system and renewable power plant

2 构网型新能源动态等值聚合建模

2.1 构网型新能源场站聚合建模

新能源场站可看作N个新能源单元并联,在动态下新能源场站中各单元输出电压接近,即整个场站可看成N个电压源并联,其整体等值阻抗(l_a)为

$\frac{1}{l_{a}}$ =

$\overset{N}{\sum_{i = 1}} \frac{1}{l_{i}}$

(15)

根据中心惯量的定义,新能源场站聚合惯量为各单元惯量之和,其等值输出频率为各输出频率对其惯量的权重,分别表示为

M_a=

$\overset{N}{\sum_{i = 1}}$ M_i

(16)

ω_a=

$\frac{\overset{N}{\sum_{i = 1}} M_{i} ω_{i}}{\overset{N}{\sum_{i = 1}} M_{i}}$

(17)

设锁相环控制器时间常数可忽略不计,则下垂输出为各单元下垂系数与电网频率的乘积,因此聚合下垂系数可以表示为

$K_{d}^{a}$ =

$\overset{N}{\sum_{i = 1}}$ K_d_{, i}

(18)

由于新能源场站在稳定运行时,各单元之间相角差值非常小,所以可以将场站的动态特性近似为二阶线性模型,而多个二阶线性模型之和仍然为二阶线性模型.因此,场站聚合模型与单元模型呈现相同形式,如下:

$\begin{aligned} M_{\mathrm{a}} \frac{\mathrm{~d} \omega_{\mathrm{a}}}{\mathrm{~d} t}= & P_{\mathrm{a}}-\sum_{i=1}^{N} P_{i}^{*}+K_{\mathrm{d}}^{\mathrm{a}}\left(\omega^{*}-\omega_{\mathrm{g}}\right)+ \\ & D_{\mathrm{a}}\left(\omega_{\mathrm{a}}-\omega_{\mathrm{g}}\right) \end{aligned}$

(19)

式中:D_a为聚合阻尼系数.

构网型新能源无功输出与有功输出耦合,输出相位与电网差值越大,则耦合程度越大.由于新能源输出的无功增量已由式(6)给出,而新能源单元在稳定运行时可近似为二阶模型,所以无功控制系数可为各单元输出相位权重的线性拟合:

$K_{v}^{a}$ =

$\frac{\overset{N}{\sum_{i = 1}} (K_{v, i} c o s δ_{i} / ω_{0} l_{i})}{\overset{N}{\sum_{i = 1}} c o s δ_{i} / ω_{0} l_{i}}$

(20)

为了简单起见,将构网型新能源的输出频率ω_i近似为其参考频率ω₀,即ω_i=ω₀.

由于各单元输出相位无法直接测得,而各单元输出电压近似,所以其cos δ_i/ω₀l_i项可由无功功率获得

ΔQ_a=ΔV

$\overset{N}{\sum_{i = 1}} \frac{K_{v, i} c o s δ_{i}}{ω_{0} l_{i}}$

(21)

式中:ΔV=V^*-V_POC.

因此,构网型新能源场站聚合无功控制系数可以被进一步表示为

$K_{v}^{a}$ ≈

$\frac{\overset{N}{\sum_{i = 1}} K_{v, i} Q_{i}}{\overset{N}{\sum_{i = 1}} Q_{i}}$

(22)

综上,构网型新能源单元并联可聚合为一个可控电压源.

2.2 构网型新能源场站聚合模型等值参数

对于电网而言,新能源电场表现为灰盒,其电压、电流、功率为可测量,而惯性、阻尼、阻抗为未知参数.为使聚合模型能准确反映新能源电场动态特性,需有效确定其等值参数.

整个新能源场站的阻尼由各发电单元阻尼和损耗组成,其本质为阻止系统频率改变时产生的摩擦功率,其值可由摇摆方程求得:

D_a=

$\frac{\overset{N}{\sum_{i = 1}} P_{i} - \overset{N}{\sum_{i = 1}} P_{i}^{*} - K_{d}^{a} (ω^{*} - ω_{a}) + {\overset{\cdot}{ω}}_{a} M_{a}}{ω_{a} - ω_{g}}$

(23)

而单元惯量可由文献[29]中的惯量评估方法求得:

$\begin{aligned} \dot{M}_{i}= & T_{n, i}\left[\Delta P_{i}-K_{\mathrm{d}, i}\left(\omega^{*}-\omega_{i}\right)-\right. \\ & \left.M_{i} \dot{\omega}_{i}\right] \operatorname{sign}\left(\dot{\omega}_{i}\right) \end{aligned}$

(24)

式中:T_n_,_i为用单元惯量估计的时间常数,其中n为场站内构网型新能源单元总个数.分段函数则表示为

sign(

${\overset{\cdot}{ω}}_{i}$ )=

$\{\begin{array}{l} - 1, & {\overset{\cdot}{ω}}_{i} \geq ε_{ω} \\ 0, & - ε_{ω} < {\overset{\cdot}{ω}}_{i} < ε_{ω} \\ 1, & {\overset{\cdot}{ω}}_{i} \leq - ε_{ω} \end{array}$

(25)

式中:ε_ω是一个接近于0的正阈值.

各单元阻抗可通过频率事件下有功潮流的变化量求得^[30]:

l_i=

$\frac{E_{i} V_{g} s i n δ_{i}}{Δ P_{i}}$ ≈

$\frac{E_{i} V_{g} \int (ω_{i} - ω_{g})}{Δ P_{i}}$

(26)

2.3 系统动态聚合建模

新型电力系统动态建模已由1.3节阐述,构网型新能源单元动态建模已由1.2节阐述,由此,以新能源电场接入点为观测点整个新型电力系统与新能源电站聚合动态特性与图1形式相同,而参数为聚合数值.

模型中关键参数为新能源单元的惯性和阻尼.将表2中参数代入全模型和聚合模型,并且令新能源场站总体的惯性与阻尼系数分别在0.7~1.3倍之间变化,可以得到全模型与聚合模型的根轨迹,如图2所示.由图可见,构网型新能源场站聚合模型与全模型最右特征值的根轨迹基本相同,然而最右特征根主导整个系统的动态,因此构网型新能源场站的聚合模型与原详细模型具有相同动态稳定性.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 详细模型与聚合模型的根轨迹对比

Fig.2 Comparison of root locus between detailed full model and aggregation model

3 单机无穷大系统仿真

所提新能源场站聚合模型主要应用于电网动态时域仿真与分析,即在电网频率和电压事件发生后模拟构网型新能源场站的快速频率和电压支撑效果,并准确反映其有功和无功功率输出特性.为验证所提聚合模型的合理性与准确性,基于 MATLAB/Simulink对比构网型新能源电场电磁暂态全模型与聚合数学模型在电网频率动态、电网电压动态和新能源电场发电激增动态下的输出特性.仿真所用新能源场站由3个构网型单元并联组成,并通过POC处接入无穷大系统中,其中无穷大系统被模拟为一个可以控制频率和电压的理想电压源.仿真系统额定频率与电压分别为50 Hz和10 kV,新能源容量的基准值为S_n=1 MW.设置所有构网型新能源单元并网变换器内环控制参数相同,各单元参数与聚合模型的主要参数如表1所示.表中:M为虚拟惯性常数;D为阻尼常数;p.u.表示标幺值.在以下案例分析中,仿真系统初始稳定状态下电网频率均为50 Hz、POC处电压p.u.均为1.

表1 构网型新能源单元和聚合模型参数(单机无穷大系统)

Tab.1 Parameters of grid-forming renewable unit and aggregation model (single-machine infinite system)

单元	M_p.u.	D_p.u.	$K_{d}^{p . u .}$	$K_{v}^{p . u .}$	$X_{g}^{p . u .}$
单元一	0.1571	15.7080	4.9951	0.5000	0.1280
单元二	0.0942	25.1327	4.9951	0.5000	0.1280
单元三	0.0628	25.1327	4.9951	0.5000	0.1280
聚合模型	0.3142	68.1726	14.9854	0.4984	0.0427

新窗口打开| 下载CSV

3.1 电网频率动态响应

基于电网频率事件验证构网型新能源场站聚合模型的准确性.仿真1.5 s时,电网频率分别以10、5和3 Hz/s的变化率从50 Hz下降到49.5 Hz.为了更好地说明动态响应,如图3所示,仅显示在POC处的惯量功率输出而未含线性下垂功率输出.由图可见,在事故发生阶段即频率变化期间,聚合模型可以完全反映原电场模型动态特性.然而在系统稳定时,聚合模型相比全模型表现出较大阻尼特性,致使在恢复阶段有功功率呈现一定暂态误差,且随频率变化率增大而误差增大,如仿真1.6~1.7 s的10 Hz/s对比曲线所示.这是因为在1.5~1.6 s的电网事故动态期间,由于频率变化率较大使惯性响应表现为主导,而聚合模型与全模型惯性相等,所以动态特性相同.然而,在1.6 s时,开环系统瞬时停止频率变换,即变化率从10 Hz/s瞬时变为0 Hz/s,且之后频率保持49.5 Hz恒定,此时电场响应为阻尼主导.因为聚合模型阻尼为故障前测量拟合值,所以无法完全精准反映全模型阻尼动态.当然,在电力系统中,事故恢复阶段频率变化连续,惯量和阻尼共同主导作用,聚合模型与全模型的误差将减小.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 惯量功率输出动态对比

Fig.3 Comparison of dynamics of inertia power outputs

3.2 电网电压动态响应

根据电网电压事件验证聚合模型的准确性.仿真1.5 s时,电网电压p.u.从1阶跃至0.9,在此情景下分别讨论当各单元电压控制相等和不等时的情形.

如图4所示,当新能源场站中各单元无功控制系数相同时,全模型和聚合模型无功功率动态基本相同;而无功控制系数不等时,聚合模型无功动态略有差异.这种差异是由于无功控制聚合系数(见式(20))与各单元输出实时相位相关,而计算时仅采取初始相位.然而,一方面,如果电网阻抗相对较小,动态时相位偏移也较小;另一方面,现实应用中同一机组控制参数设计一般相同,因此该误差可一定程度上忽略不计.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 无功功率动态对比

Fig.4 Comparison of dynamics of reactive power

3.3 新能源电场发电激增动态响应

在构网型控制中,除了电网频率和电压事件驱动构网型控制动作外,当发电量激增时,其功率动态亦经历构网控制暂态过程,并通过并网变换器输送给电网.为验证在新能源场站出力增加时聚合模型的准确性,考虑两种情形:①仿真1.5 s时,所有单元发电增加10%;②仿真1.5 s时,仅单元2发电增加10%.

如图5所示,全部单元发电等比例增加时,全模型和聚合模型暂态表现基本相同.仅无功功率输出在暂态时出现较小偏差,聚合模型相比全模型表现出较大阻尼,这是因为构网型控制有功与无功功率动态耦合,如3.1节所叙,聚合模型在无功输出表现出较大阻尼效应.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 新能源发电激增时全模型和聚合模型功率对比

Fig.5 Power comparison between full model and aggregation model at generation surge

仅单元2发电增加时,聚合模型无法捕捉到全模型的暂态过程,这是因为在此情况下聚合模型受到全场站的惯性与阻尼作用,而单个发电单元出力改变仅受其自身惯性与阻尼影响.如图5所示,单元2阻尼系数较大,运行在过阻尼状态;而聚合模型动态过程呈现出欠阻尼效应.在电力系统中,即使考虑风力的尾流效应,一个风电场中的风机增发量也基本接近,因此聚合模型可以应用于发电动态分析.

4 系统闭环仿真

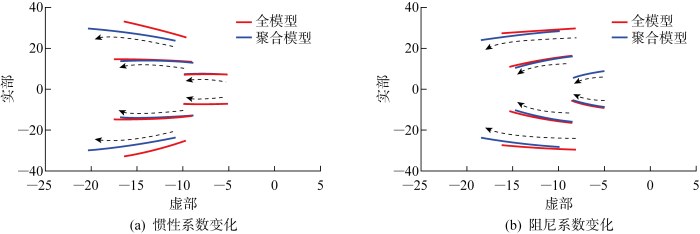
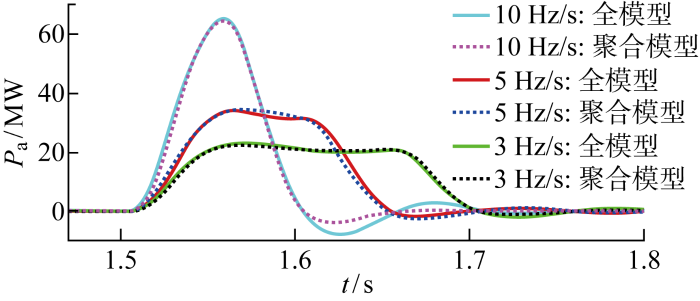
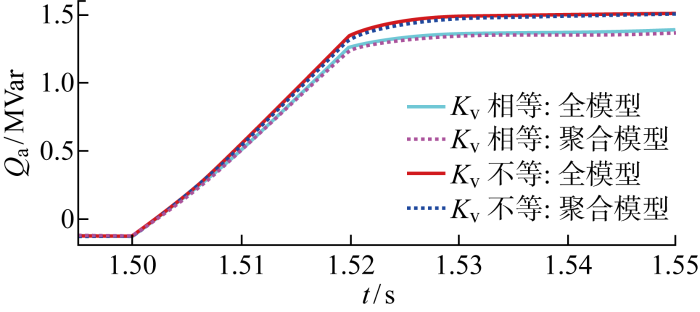
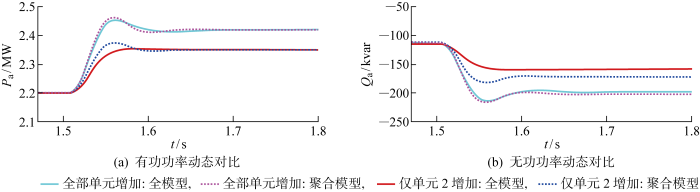
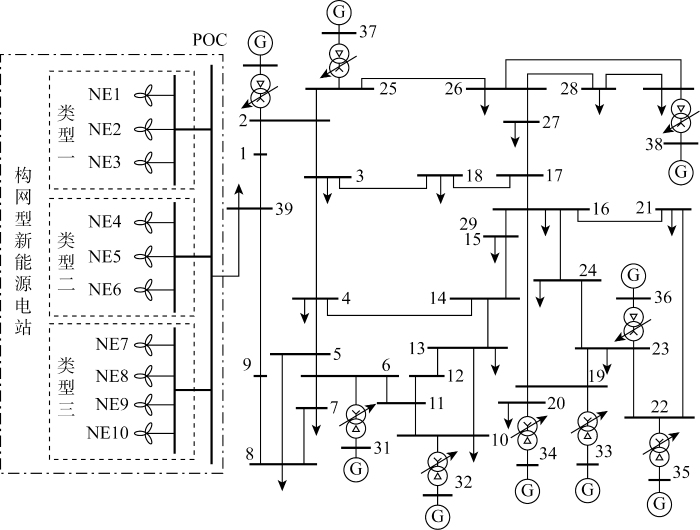
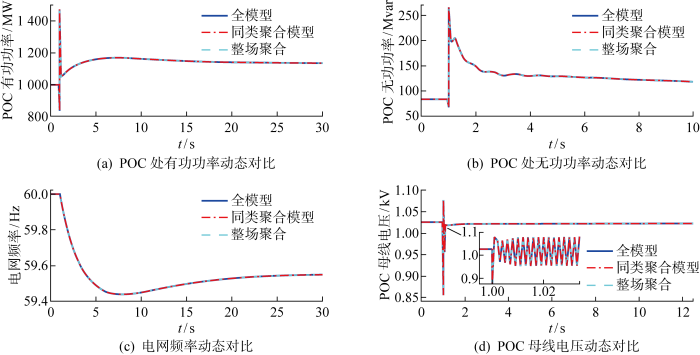
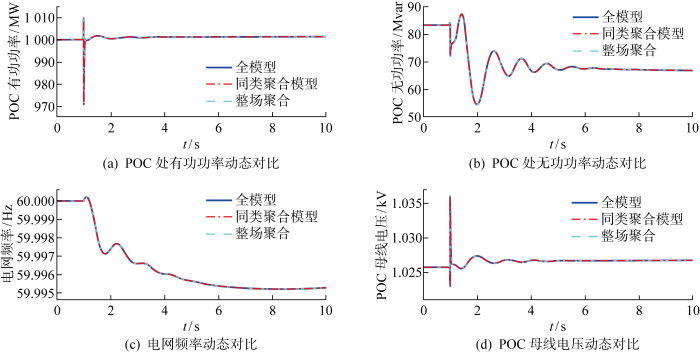
从系统层面验证所提聚合模型的准确性与快速性.仿真电网是一个改进的IEEE 39母线系统,其中包含1个构网型新能源场站,此场站由3类共10个构网型新能源单元组成.构网型新能源场站和整个电网的拓扑如图6所示.图中:G为发电机.假定同类新能源单元的容量和参数相同,主要参数如表2所示,由于此处忽略了虚拟阻抗,所以聚合模型的阻尼为各单元之和.表中:P^*为参考功率输出.本案例研究旨在验证所提聚合模型在电网发生频率和电压事件的准确性.最后,使用基于Python的新型电力系统仿真软件DOME^[31]进行闭环仿真,对模型正确性与新型电力系统适用性进行验证.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 改进的IEEE 39母线系统拓扑

Fig.6 Topology of modified IEEE 39 bus system

表2 构网型新能源单元和聚合模型参数(系统闭环)

Tab.2 Parameters of grid-forming renewable unit and aggregation model parameters (closed-loop system)

单元	$P_{p . u .}^{*}$	M_p.u.	D_p.u.	$K_{d}^{p . u .}$	$K_{v}^{p . u .}$	$L_{g}^{p . u .}$
NE1~NE3	80	10.00	200	30.0	0.9	0.0600
NE4~NE6	100	9.00	100	20.0	0.9	0.0900
NE7~NE10	125	8.25	225	7.5	0.9	0.0400
类型一聚合	240	30.00	600	90.0	0.9	0.0200
类型二聚合	300	27.00	300	60.0	0.9	0.0300
类型三聚合	460	33.00	900	30.0	0.9	0.0100
全部聚合	1 000	90.00	1800	180.0	0.9	0.0055

新窗口打开| 下载CSV

该仿真由联想Y700计算机执行,其配置为4 Core Intel i5-6300HQ 2.3GHz CPU.在下列电网频率事件和电网电压事件中,全模型、同类聚合模型和整场聚合模型仿真时间如表3所示.由表可见,在电网频率事件下,与全模型相比,同类聚合仿真时间减少17.066%,整场聚合仿真时间减少36.022%.在电网电压事件下,同类聚合模型仿真时间减少12.702%,整场聚合仿真时间减少30.870%.因此,在电网动态时域仿真与分析中使用所提构网型新能源场站聚合模型可以有效提升仿真速率.可以预见,在新型电力系统建设的进程中,随着构网型新能源发电渗透率的增加,所提聚合模型对计算力的节约效果将更加显著.

表3 不同的构网型新能源场站模型仿真时间对比

Tab.3 Comparison of simulation time of different grid-forming renewable plant models

模型	电网频率事件仿真时间/s	电网电压事件仿真时间/s
全模型	24.335	24.8850
同类聚合模型	20.182	21.7243
整场聚合模型	15.569	17.2028

新窗口打开| 下载CSV

4.1 电网频率事件

考虑t=1 s时30号母线发电机脱网的故障事件.图7展示了频率事件发生后电网频率动态、构网型新能源场站在POC处的有功功率和无功功率,以及附近电网母线的电压的动态演化过程.由图可见,构网型新能源场站的有功功率和无功功率动态均可由聚合模型精准捕获,因此电网频率响应和附近母线的电压与使用全模型获得的响应相同.与3.1节中的分析相同,在电力系统仿真分析中,事故恢复阶段频率变化连续,场站的动态由惯性和阻尼共同参与,聚合模型与全模型的误差将得以减小,甚至可以忽略不计.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 电网频率事件仿真结果对比

Fig.7 Simulation results of frequency dynamics

4.2 电网电压事件

考虑连接母线2和25的线路在t=1 s时断开的故障事件.图8展示了使用新能源场站全模型和聚合模型的系统响应.由图可见,构网型新能源场站的有功功率和无功功率响应均可利用聚合模型来精确描述,因此电网频率动态和附近母线的动态与使用全模型获得的响应相同.该仿真结果与3.1节中的分析相符,当构网型新能源场站各单元无功控制系数相同时,全模型和聚合模型的功率动态基本相同.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 电网电压事件仿真结果对比

Fig.8 Simulation results of voltage dynamics

5 结语

提出一种适用于电力系统频率和电压稳定性分析的构网型新能源场站聚合模型,并根据场站整体运行特性提出聚合模型的参数识别与选取方法.通过理论分析论证了聚合方法的可行性.系统仿真结果表明,本聚合模型能够准确描述构网型新能源场站对系统突发事件的动态响应,在电网频率和电压事件下单个新能源场站整场聚合模型仿真速率分别提升36.022%、30.870%.

所提构网型新能源场站聚合模型可准确捕获电力系统大扰动故障后频率和电压的动态演化过程,但不能反映新能源电站内部故障动态特性.故该模型的主要适用场景为电力系统动态稳定性分析.当新能源内部出力出现差异以及当新能源场站运行到新的工作点时,应该重新辨识聚合模型参数.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

张硕, 李薇, 李英姿, 等.

面向新型电力系统的可再生能源绿色电力证书差异化配置模型

[J]. 上海交通大学学报, 2022, 56(12): 1561-1571.

DOI:10.16183/j.cnki.jsjtu.2022.150 [本文引用: 1]

实现我国“30·60”双碳目标,能源绿色低碳转型是基础支撑,构建以新能源为主体的新型电力系统是关键举措,绿色电力证书(简称绿证)则是体现可再生能源绿色价值的重要凭证.当前我国绿证分配机制单一,无法有效衡量不同可再生能源发电类型可获得绿色价值的差异性,并发挥其平衡可再生能源协调发展的杠杆作用.为此,从可再生能源发电类型电量兑换绿证的差异化入手,建立考虑可再生能源综合价值的绿证差异化评价指标体系,应用CRITIC法、熵权法和TOPSIS法构建可再生能源电力绿证差异化评价模型.以2030年碳达峰目标为发展场景,分析模型对集中式光伏发电、分布式光伏发电、陆上风力发电和海上风力发电绿色收益的影响,进而修正其发展规划,并提出绿证相关政策建议.所构建的绿证差异化分配模型可为我国绿证市场机制的建设和完善提供相应的辅助决策支持.

ZHANG

Shuo

, LI

Wei

, LI

Yingzi

, et al.

Differentiated allocation model of renewable energy green certificates for new-type power system

[J]. Journal of Shanghai Jiao Tong University, 2022, 56(12): 1561-1571.