Processing math: 0%
上海交通大学学报

上海交通大学学报, 2024, 58(10): 1524-1533 doi: 10.16183/j.cnki.jsjtu.2023.131

新型电力系统与综合能源

基于低秩逼近代理模型的N-1安全约束经济调度快速计算方法

陈熠1, 王晗,1, 曾丹2, 严正1, 薛必克2, 赵乐3, 熊雪君3, 冯煜尧3

1.上海交通大学 电力传输与功率变换控制教育部重点实验室,上海 200240

2.中国电力科学研究院(南京分院),南京 210003

3.国网上海市电力公司, 上海 200122

A Fast Calculation Method for N-1 Security-Constrained Economic Dispatch via Low-Rank Approximation Surrogate Model

CHEN Yi1, WANG Han,1, ZENG Dan2, YAN Zheng1, XUE Bike2, ZHAO Le3, XIONG Xuejun3, FENG Yuyao3

1. Key Laboratory of Control of Power Transmission and Conversion of the Ministry of Education, Shanghai Jiao Tong University, Shanghai 200240, China

2. China Electric Power Research Institute (Nanjing Branch), Nanjing 210003, China

3. State Grid Shanghai Municipal Electric Power Company, Shanghai 200122, China

通讯作者: 王 晗,助理研究员;E-mail:wanghan9894@sjtu.edu.cn.

责任编辑: 孙伟

收稿日期: 2023-04-13   修回日期: 2023-06-16   接受日期: 2023-07-24  

基金资助: 国家电网公司总部科技项目(5100-202055494A-0-0-00)

Received: 2023-04-13   Revised: 2023-06-16   Accepted: 2023-07-24  

作者简介 About authors

陈熠(1999—),硕士生,从事电力市场优化调度研究.

摘要

随着新能源并网比例不断提高,为保障电力系统可靠运行,安全约束经济调度(SCED)需要考虑海量的N-1安全约束,对模型求解造成极大的计算负担. N-1安全约束中只有少量约束在计算过程中起作用,剔除大量冗余约束有助于提高SCED模型的求解效率.提出基于低秩逼近(LRA)代理模型的SCED模型快速计算方法,首先构建考虑风力发电、光伏的SCED模型,并根据SCED模型的历史运行信息建立LRA代理模型;其次基于LRA代理模型的估计结果辨识关键约束和构建积极约束集,并提出基于LRA的SCED模型迭代求解流程;最后在IEEE 39节点系统下进行算例仿真.仿真结果表明,LRA代理模型与SCED模型的求解结果误差小于10%,约束辨识准确率高,所提求解流程的平均迭代求解时间降低了50%以上,显著提高了SCED模型的求解效率.

关键词： 安全约束经济调度; 低秩逼近; 约束辨识; 积极约束集

Abstract

With the increase in the proportion of renewable energy connected to the grid, a large number of N-1 security constraints should be considered in the security-constrained economic dispatch (SCED) to ensure the reliable operation of the power system, which causes a great computational burden. However, only a small number of constraints in the N-1 security constraints are contributing factors. Therefore, the elimination of redundant constraints can significantly improve the solution efficiency of the SCED model. First, a new SCED model considering wind power and photovoltaic is established, and a low-rank approximation (LRA) surrogate model is constructed based on the historical operation information of the SCED model. Then, the active constraints are identified based on the estimation results of the LRA surrogate model and the active constraint set is constructed. Next, an iterative solution process of the SCED model based on LRA surrogate model is proposed. Finally, the simulations are conducted on an IEEE 39-bus system. The simulation results show that the error between the solution results of the LRA surrogate and the SCED models is less than 10%, the active constraint identification accuracy is raised, and the average iterative solution time of the proposed solution process is reduced by more than 50%, which indicates the improvement of the solution efficiency of the SCED model.

Keywords： security-constrained economic dispatch (SCED); low-rank approximation (LRA); constraints identification; active constraint set

PDF (2240KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

陈熠, 王晗, 曾丹, 严正, 薛必克, 赵乐, 熊雪君, 冯煜尧. 基于低秩逼近代理模型的N-1安全约束经济调度快速计算方法[J]. 上海交通大学学报, 2024, 58(10): 1524-1533 doi:10.16183/j.cnki.jsjtu.2023.131

CHEN Yi, WANG Han, ZENG Dan, YAN Zheng, XUE Bike, ZHAO Le, XIONG Xuejun, FENG Yuyao. A Fast Calculation Method for N-1 Security-Constrained Economic Dispatch via Low-Rank Approximation Surrogate Model[J]. Journal of Shanghai Jiaotong University, 2024, 58(10): 1524-1533 doi:10.16183/j.cnki.jsjtu.2023.131

自工业革命以来,高速的工业发展所产生的大量温室气体对全球气候造成了巨大影响,清洁低碳的可持续发展已成为世界各国的共同目标[1⇓-3].随着我国“双碳”目标的提出,以风力发电(简称风电)、光伏为主的新能源将逐步取代传统的化石能源,我国电力系统中发电占比将逐渐提高[4⇓-6].但新能源出力具有随机性与波动性的特点,给电力系统的安全约束经济调度(security-constrained economic dispatch,SCED)带来了挑战[7].

近年来,兼顾清洁能源的消纳与电网的可靠运行是SCED问题研究的重点,国内外学者对此展开了大量研究.文献[8]中基于实际省级电网搭建了考虑新能源参与的SCED模型,仿真结果表明新能源报量报价参与现货市场会导致电价剧烈波动.文献[9]中构建了计及风电出力不确定性的多时间尺度下电力系统随机优化模型,提高了电力系统运行的可靠性.文献[10]中建立了考虑新能源发电的近实时随机前瞻经济调度模型,评估了与净负荷不确定性相关的电力系统经济风险.文献[11]中建立了考虑光热电站深度调峰补偿的日前SCED模型,提高了风光消纳水平并降低了系统运行成本.文献[12]中提出了考虑风电消纳的区域综合能源系统源-荷协调优化调度方法,促进了冷热电联供与可再生能源的协同互补.上述文献在常规的SCED模型中进一步考虑了清洁能源发电,在保障电网可靠运行的前提下尽可能地消纳清洁能源,对电力系统清洁低碳运行提供了重要的模型支撑.

为了保障电力系统运行安全性,SCED模型中需要考虑N-1安全约束,但海量约束条件使得SCED问题规模变得极为庞大,给模型的高效求解带来了严峻挑战[13-14].为提高SCED问题的求解效率,目前常用的方法主要包括决策变量降维和约束条件降维.决策变量降维包括合并具有相似特性的决策变量[15]和剔除不起作用的决策变量[16];约束条件降维指辨识并剔除冗余约束,具体包括解辅助优化问题法[17]、迭代法[18]、代理模型法[19]等.决策变量降维和约束条件降维能减少SCED模型中决策变量和约束条件的数量,直接提高模型求解效率.然而,在实际计算中,决策变量降维会对关键决策变量的取值产生影响,可能会影响计算结果的精度;而约束条件降维可以在求解结束后对被削减的约束进行校验,若违反约束,则将相应约束重新加入到SCED模型中再次进行求解,直至满足所有约束条件,因此约束条件降维可通过后验方法保证计算结果的准确性.

为提升复杂电力系统问题的计算效率,基于代理模型的方法近年来被广泛应用于电力系统分析计算,如概率潮流计算[20]、不确定性分析[21]等,其将原始模型替换为代理模型,在保证精度的同时显著提高了计算效率.传统代理模型构建方法包括随机响应面法[22]、克里金法[23]、径向基法[24]等,但随着输入变量维度增加,上述方法会遇到“维数灾”问题.目前,稀疏多项式混沌展开、高斯过程回归和低秩逼近(low-rank approximation,LRA)代理模型构建方法能有效克服该问题[25⇓-27],为输入变量维度高、约束条件复杂的SCED问题快速求解研究提供了技术方法支撑.

针对考虑新能源发电的含N-1安全约束的SCED模型,采用LRA代理模型对约束条件进行降维,以实现模型的快速求解.首先,构建包含风电、光伏的SCED模型,并阐述常规的SCED模型求解方法.其次,介绍基于LRA算法的代理模型构建方法,并提出结合LRA的SCED高效求解算法.最后,在IEEE 39节点系统下进行算例仿真,相比传统迭代求解算法,所提算法的迭代次数显著减少,并大幅提高了求解效率.

1 SCED模型及求解

1.1 SCED模型

考虑高比例新能源接入,电力系统SCED模型以最小化发电成本、旋转备用成本、弃风弃光成本之和为目标函数:

min
(1)

式中:T为时段数集合;G、W、V分别为发电机、风电、光伏集合;Pg,t为发电机g在时段t的出力;Rg,t为发电机g在时段t的旋转备用;ag、bg、cg为发电机g的二次项、一次项、常数项发电成本系数;dg为发电机g的旋转备用成本系数;Pw,tloss、Pv,tloss分别为弃风、弃光电量;ηw、ηv分别为弃风、弃光惩罚成本.

SCED模型的约束条件包括:

(1) 电力平衡约束.

\begin{array}{l} \sum_{g \in G} P_{g, t}+\sum_{w \in W}\left(P_{w, t}-P_{w, t}^{\text {loss }}\right)+ \\ \sum_{v \in V}\left(P_{v, t}-P_{v, l}^{\text {loss }}\right)=\sum_{l \in L} P_{l, t}, \quad \forall t \in T \end{array}
(2)

式中:L为负荷集合;Pl,t为负荷l在时段t的需求;Pw,t、Pv,t分别为风电和光伏的预测出力.

(2) 旋转备用约束.

∑g∈GRg,t≥α ∑l∈LPl,t, ∀t∈T
(3)

式中:α为电网旋转备用系数.

(3) 发电机出力约束.

Pg, t+Rg, t≤Pgmax,　∀g∈G, ∀t∈TPg, t-Rg, t≥Pgmin,　∀g∈G, ∀t∈T
(4)

式中:Pgmax、Pgmin为发电机g的最大、最小出力.

(4) 发电机爬坡约束.

Pg,t+1-Pg,t≤Pgup,∀g∈G,∀t∈TPg,t+1-Pg,t≥-Pgdown,∀g∈G,∀t∈T
(5)

式中:Pgup、Pgdown为发电机g的上、下爬坡速率限值.

(5) 弃风、弃光功率约束.

0≤Pv,tloss≤Pv,t,　∀v∈V, ∀t∈T0≤Pw,tloss≤Pw,t,　∀w∈W, ∀t∈T
(6)

(6) 线路潮流约束.

\begin{aligned} F_{s, t}= & \sum_{s \in G} \pi_{s, g} P_{g, t}+\sum_{w \in W} \pi_{s, w}\left(P_{w, t}-P_{w, t}^{\text {loss }}\right)+ \\ & \sum_{v \in V} \pi_{s, v}\left(P_{v, t}-P_{v, t}^{\text {loss }}\right)-\sum_{l \in L} \pi_{s, l} P_{l, t}, \\ & \forall s \in S, \forall t \in T \end{aligned}
(7)
Fsmin≤Fs,t≤ Fsmax, ∀s∈S, ∀t∈T
(8)

式中:S为线路集合;Fs, t为线路s在时段t的传输功率;πs,g、πs,w、πs,v、πs,l分别为发电机g、风电机组w、光伏v、负荷l对线路s的潮流转移因子;Fsmax、Fsmin分别为线路s的潮流上、下限.

(7) N-1线路潮流安全约束.

\begin{array}{c} F_{s, \theta, t}=\sum_{g \in G} \pi_{s, g, \theta} P_{g, t}+\sum_{w \in W} \pi_{s, w, \theta}\left(P_{w, t}-P_{w, t}^{\text {loss }}\right)+ \\ \sum_{v \in V} \pi_{s, v, \theta}\left(P_{v, t}-P_{v, t}^{\text {loss }}\right)-\sum_{l \in L} \pi_{s, l, \theta} P_{l, t}, \\ \forall s \in S, \forall \theta \in \Theta, \forall t \in T \end{array}
(9)
\begin{aligned} F_{s, \theta}^{\min } \leqslant F_{s, \theta, t} & \leqslant F_{s, \theta}^{\max }, \\ \forall s & \in S, \forall \theta \in \Theta, \forall t \in T \end{aligned}
(10)

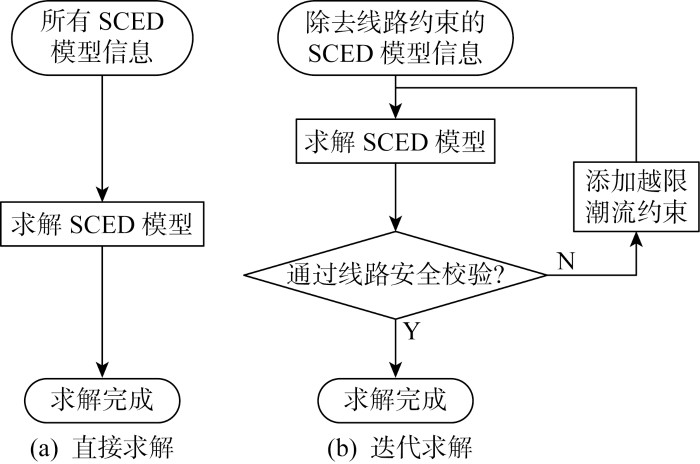
式中:Θ为N-1线路故障集合;Fs, θ, t为N-1线路故障情况θ下线路s在时段t的潮流;πs,g,θ、πs,w,θ、πs,v,θ、πs,l,θ分别为发电机g、风电w、光伏v、负荷l在N-1线路故障情况θ下对线路s的潮流转移因子;Fs,θmax、Fs,θmin分别为在N-1线路故障情况θ下线路s的短期潮流上、下限.需要注意的是,当N-1线路故障导致某台发电机脱离电网时,将该台发电机对于主网所有线路的潮流转移因子均设为0.

1.2 SCED模型常规求解流程

根据文献[19]中所述,SCED模型的常规求解方法主要为直接法和迭代法,分别如图1(a)和图1(b)所示.直接法的求解流程简单,易于实现,但在考虑N-1线路安全约束后,海量约束会导致模型求解困难,甚至无法求解;迭代法求解SCED模型时,事先不考虑线路约束,当线路安全校验不通过即求解结果出现越限线路时,将越限线路对应的潮流约束重新加入到原SCED模型中,再次进行求解,不断迭代直至线路安全校验通过,从而得到最优求解结果.与直接法相比,迭代法虽然每次求解的模型约束较少,但是迭代次数可能较多,从而导致最终求解时间较长.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   SCED模型求解流程图

Fig.1   Flow chart of SCED model solution


为实现考虑N-1线路安全约束的SCED模型快速求解,可在迭代法的基础上,将关键线路约束在第一次迭代前加入到除去线路约束的SCED模型中,以减少迭代次数,提升求解效率.因此,如何辨识关键线路约束至关重要.目前电力系统运营商主要根据人工经验来判断线路约束是否为关键约束,缺乏一定的理论依据.相比于人工识别,根据历史数据辨识关键线路约束更为可靠,文献[19]中提出了基于数据驱动的关键线路约束辨识方法,一定程度上提升了迭代法求解SCED模型的效率.相较于现有研究,本文引入代理模型计算,从数据与模型相结合的角度实现关键线路约束的辨识,从而提升了考虑N-1线路安全约束下SCED模型的求解效率.

2 LRA代理模型

2.1 基于LRA方法的代理模型构建

LRA使用正则分解将期望的响应分解为秩1函数的和,并利用多元多项式基的张量积结构,提供高度压缩格式的多项式表示[28].LRA代理模型的优点在于其所需求解的系数随着输入变量维度的增加呈线性增长,而不是指数增长,因此LRA方法在处理高维问题时的优势明显[29-30].

假设存在一个复杂的函数Y=f(X),其中X =[x1x2 … xK], 为K维输入变量.为解决函数f(·)计算时间长的问题,可将函数f(·)近似等效为一个可快速计算的代理模型f'(·),从而提高计算效率.采用LRA方法构建代理模型,所构建的代理模型表达如下:

Y≈Y'=f'(X)= ∑r=1Rbrwr(X)
(11)

式中:R为秩1函数的个数;wr(·)为第r个秩1函数;br为第r个秩1函数wr(·)的权重系数.其中,秩1函数是单变量函数乘积的函数,wr(·)可表示为

\begin{aligned} w_{r}(\boldsymbol{X})= & \prod_{k=1}^{K} v_{r}^{(k)}\left(x_{k}\right)= \\ & \prod_{k=1}^{K}\left(\sum_{p=0}^{P} z_{p, r}^{(k)} \psi_{p}^{(k)}\left(x_{k}\right)\right) \end{aligned}
(12)

式中:vr(k)(xk)为第r个秩1函数中对应xk的单变量函数,并可将其分解为正交多项式基的组合,包括勒让德多项式、埃尔米特多项式、拉盖尔多项式等;P为正交多项式总阶数;ψp(k)(xk)为对应xk的p阶单变量正交多项式;zp,r(k)为ψp(k)(xk)的权重系数.

2.2 代理模型系数计算

LRA代理模型系数计算是通过不断增加代理模型的秩,并通过修正步骤和更新步骤中分别确定zp,r(k)和br两个权重系数实现,具体计算过程如下.

2.2.1 修正步骤 为叙述方便,定义如下表达式:

aΩ= ∑m=1Ma(Xm)2M
(13)

式中:a(·)为任意函数;Ω为样本空间,Ω={X1, X2, …, XM};M为输入样本集的样本规模;Xm=[xm, 1xm, 2 … xm, K]为第m个输入样本.

对于每一维输入变量xk,其在第r个秩1函数下的单变量正交多项式的权重系数zr(k)(zr(k)=[z1,r(k)z2,r(k) … zP,r(k)])可以通过求解如下最小化问题的方式获得:

\begin{aligned} \boldsymbol{z}_{r}^{(k)}= & \underset{\boldsymbol{\alpha}}{\arg \min } \| f-\sum_{i=1}^{r-1} b_{i} w_{i}- \\ & \left(\prod_{j=1, j \neq k}^{K} v_{r}^{(j)}\right)\left(\sum_{p=0}^{P} \alpha_{p} \psi_{p}^{(k)}\right) \|_{\Omega} \end{aligned}
(14)

式中:α=[α1α2 … αp],为待求解变量.式(14)可解释为通过增加新的秩1函数来减小代理模型与原函数之间的平方和误差,从而起到修正代理模型的作用.其可以采用交替最小二乘法(ALS)进行迭代求解,即每次优化求解权重系数zr(k)时,固定其他权重系数zr(j)(j≠k)的值,不断重复迭代直至两次连续迭代中相对经验误差的减小量小于设定值,具体步骤可参见文献[31].

2.2.2 更新步骤 修正步骤结束后,优化求解并更新各个秩1函数的权重系数:

b= arg minβf-∑i=1rβiwiΩ
(15)

式中:b=[b1b2 … br];β=[β1β2 … βr],为待求解变量.最小化问题可以采用普通最小二乘法(OLS)进行求解[32].

2.3 最佳秩的选取

在上节的修正步骤和更新步骤中,代理模型的秩不断增加.当代理模型的秩增加并不能提升代理模型的精度时,秩为代理模型最佳秩Ropt.代理模型最佳秩Ropt的选取可采用N-折交叉验证(N-fold cross validation)的方法:将M个输入样本等分成N份,取其中一份作为测试集ΩTS,其余N-1份作为训练集ΩTR,测试集ΩTS用于评估采用训练集ΩTR构建的LRA代理模型的误差:

ε= f-fTRΩTSV(YTS)
(16)

式中:fTR为采用训练集ΩTR构建的LRA代理模型;YTS为以测试集ΩTS输入到代理模型fTR后的输出结果;V(YTS)为代理模型输出的经验方差,具体为

V(YTS)= 1MTS-1∑m=1MTSYmTS-1MTS∑j=1MTSYjTS2
(17)

式中:MTS为测试集中的输入样本集个数;YmTS为测试集ΩTS中第m个输入样本下代理模型的输出结果.

通过更换测试集,可以得到N个代理模型,其平均误差可以视为代理模型的泛化误差,当该泛化误差随着代理模型秩的增加而不再减小时,代理模型的秩为最佳秩Ropt.确定最佳秩Ropt后,采用完整的样本空间Ω来构建LRA代理模型.同理,最佳阶数Popt的选取也采用N-折交叉验证方法,不再赘述.

3 基于LRA的SCED快速求解算法

基于历史数据信息,构建LRA代理模型,其中负荷需求、风电出力和光伏出力作为LRA代理模型的输入,线路潮流作为代理模型的输出.进而,在给定新的输入数据(负荷需求、风电出力和光伏出力)后,即可通过LRA代理模型迅速得出线路潮流的估计值,从而判断对应的线路潮流约束是否为关键约束,判断依据如下:

F_{s}^{\max }-\hat{F}_{s, t} \leqslant \tau
(18)
\hat{F}_{s, t}-F_{s}^{\min } \leqslant \tau
(19)
F_{s, \theta}^{\max }-\hat{F}_{s, \theta, t} \leqslant \tau
(20)
\hat{F}_{s, \theta, t}-F_{s, \theta}^{\min } \leqslant \tau
(21)

式中:F^s, t为线路s在时段t的潮流估计值;F^s, θ, t为N-1线路故障情况θ下线路s在时段t的潮流估计值;τ为一个较小的正值.

当F^s,t满足式(18)或式(19)时,对应的约束为关键约束;当F^s,θ,t满足式(20)或式(21)时,对应的约束为关键约束.利用LRA代理模型识别出关键线路约束,构建积极约束集,从而减少模型中约束数量.基于LRA的SCED模型快速求解流程如图2所示,与图1(b)的迭代求解流程相比,所提方法将通过LRA代理模型构建的积极约束集提前加入到SCED模型中,从而减少线路安全校验迭代次数,提高求解效率.值得注意的是,尽管LRA代理模型的计算存在误差,识别出的关键线路约束也存在误差,但由于迭代计算流程中包含线路安全校验环节,基于LRA的SCED模型求解得到的结果将和图1的直接法和迭代法的求解结果一致.为便于区分,下文将图1(b)中的迭代法称为普通迭代法,将图2中采用LRA代理模型的迭代法称为基于LRA的迭代法.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   基于LRA的SCED模型求解流程图

Fig.2   Flow chart of LRA-based SCED model solution


4 算例分析

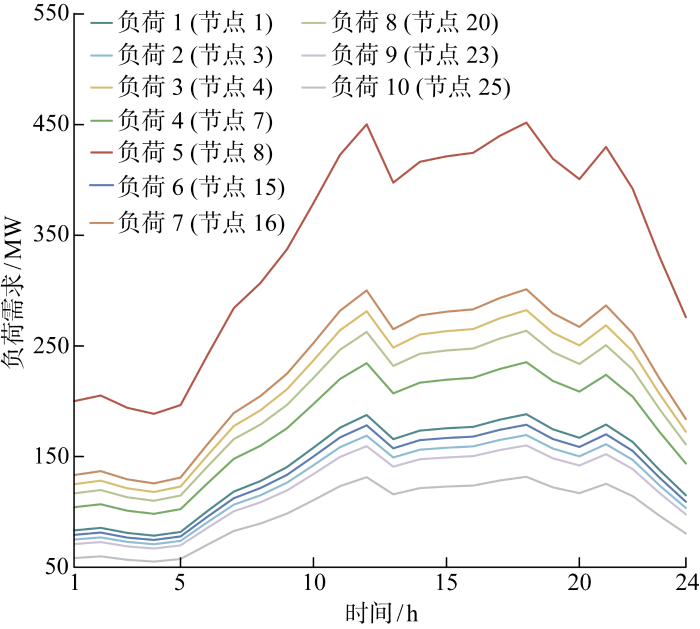
4.1 算例数据

在IEEE 39节点系统下进行仿真验证,目前调度阶段发电机数据如表1所示,并在节点36、37接入风电,在节点38、39接入光伏,风电、光伏出力分别如图3(a)和3(b)所示,弃风、弃光成本均为40元/(MW·h).负荷采用标准负荷需求曲线,其中不同节点的日负荷最大值不同,具体如图4所示.

表1   日前调度阶段成本发电机数据

Tab.1  Data of generators in day-ahead dispatch stage

发电机所在节点二次项发电成本系数/
[元·(MW2·h)-1]		一次项发电成本系数/
[元·(MW·h)-1]		常数项发电成本系数/
(元·h-1)		备用成本系数/
[元·(MW·h)-1]
G1节点300.22630.42786.8020
G2节点310.58865.12451.3215
G3节点320.66560.401049.5010
G4节点330.46863.12251.3212
G5节点340.68754.24670.1116
G6节点350.69855.48469.3113

新窗口打开| 下载CSV


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   风电、光伏出力曲线

Fig.3   Wind and photovoltaic power output


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   不同节点的负荷需求

Fig.4   Load demand of different nodes


假设风电、光伏在 ±20% 范围内波动,负荷在±10% 范围内波动,并满足均匀分布,随机生成 2 000 个样本作为电力市场的历史运行信息,通过UQLab构建LRA代理模型[33].算例在Intel Core i7-8550U CPU@1.80 GHz、16 GB RAM的硬件环境下进行仿真,SCED模型通过MATLAB R2020b调用Gurobi求解器进行求解.

4.2 SCED求解结果分析

采用图1(b)所示的普通迭代法求解所构建的SCED模型,求解时间为119.8 s,总成本为 1 644 370 元,其中发电成本为 1 613 940 元,备用成本为 25 739 元,弃风成本为 2 669 元,弃光成本为 2 022 元.可以看出,为了满足电网安全经济运行,存在弃风、弃光现象.

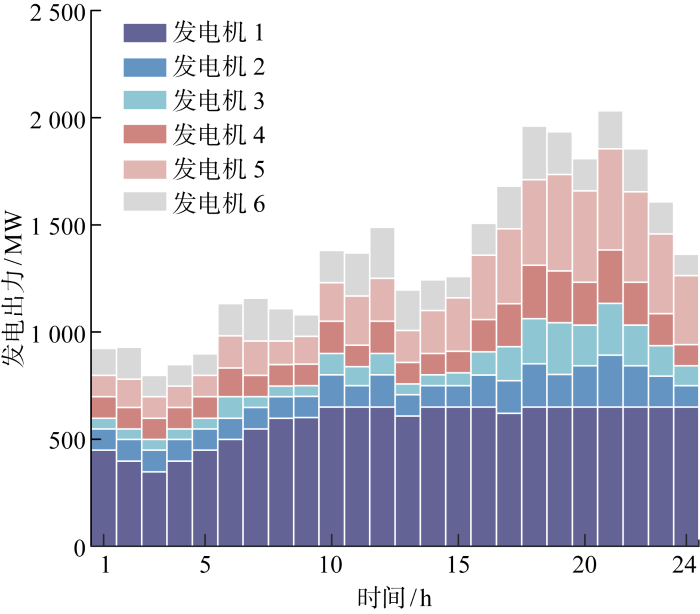
具体的发电机出力曲线如图5所示,从图中可以看出,发电机1在时段10~24 h几乎处于最大出力状态,因为其发电成本低,而在时段1~5 h由于其他发电机处于最小出力,发电机1并不能达到其最大出力.在时段17~22 h,负荷需求较高而风光电出力较少,发电成本相对较高的发电机2~4出力增加以满足负荷需求.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   发电机出力曲线

Fig.5   Generator power output


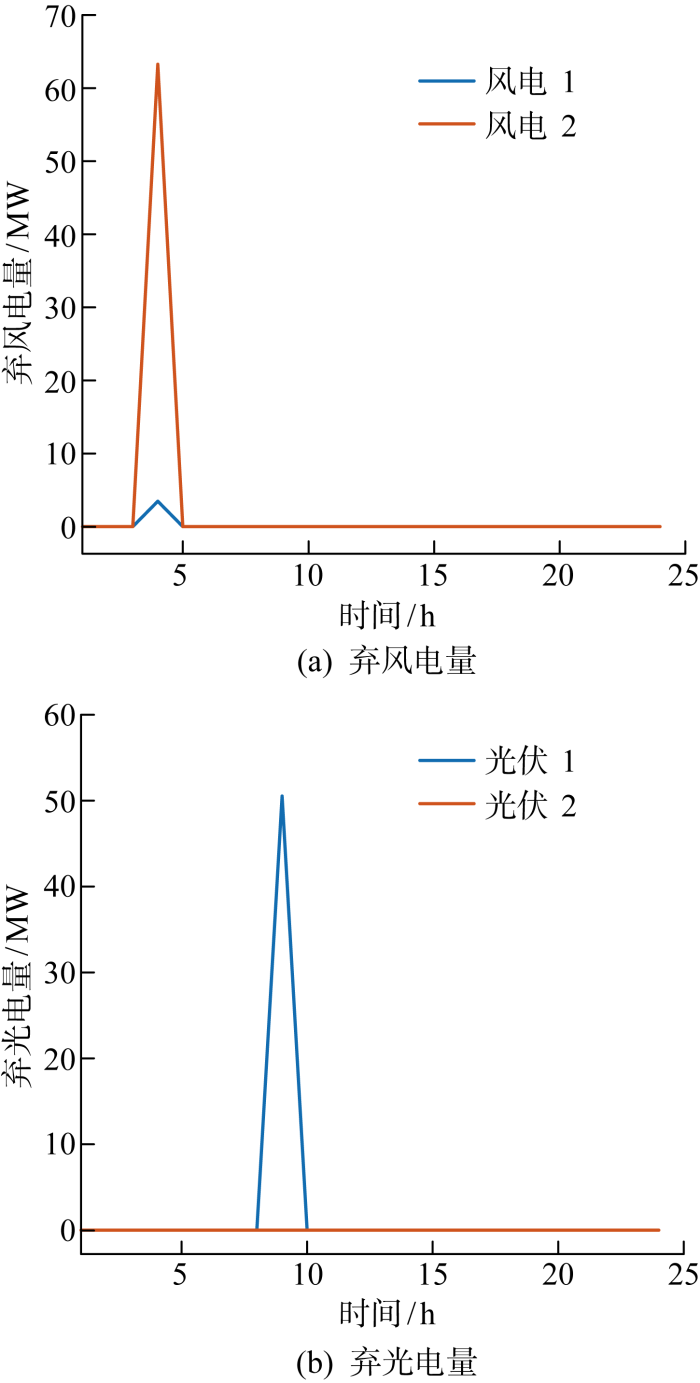
弃风、弃光电量如图6所示,其中在第4 h和第9 h分别产生弃风、弃光现象,但产生弃风、弃光现象的原因不同.第4 h弃风是为了提高电网运行的经济性,因为第5 h与第4 h的净负荷之差大于发电机1的最大爬坡速率,如果不弃风则其他机组在第5 h的出力增加成本大于第4 h弃风成本;第9 h弃光是为了保障电网运行的安全性,因为第9 h的净负荷大幅低于第10 h的净负荷,所有发电机的总最大爬坡速率小于第10 h与第9 h的净负荷之差,所以受到爬坡约束限制而弃光.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   弃风、弃光电量

Fig.6   Electricity of wind power loss and photovoltaic power loss


4.3 LRA代理模型求解结果

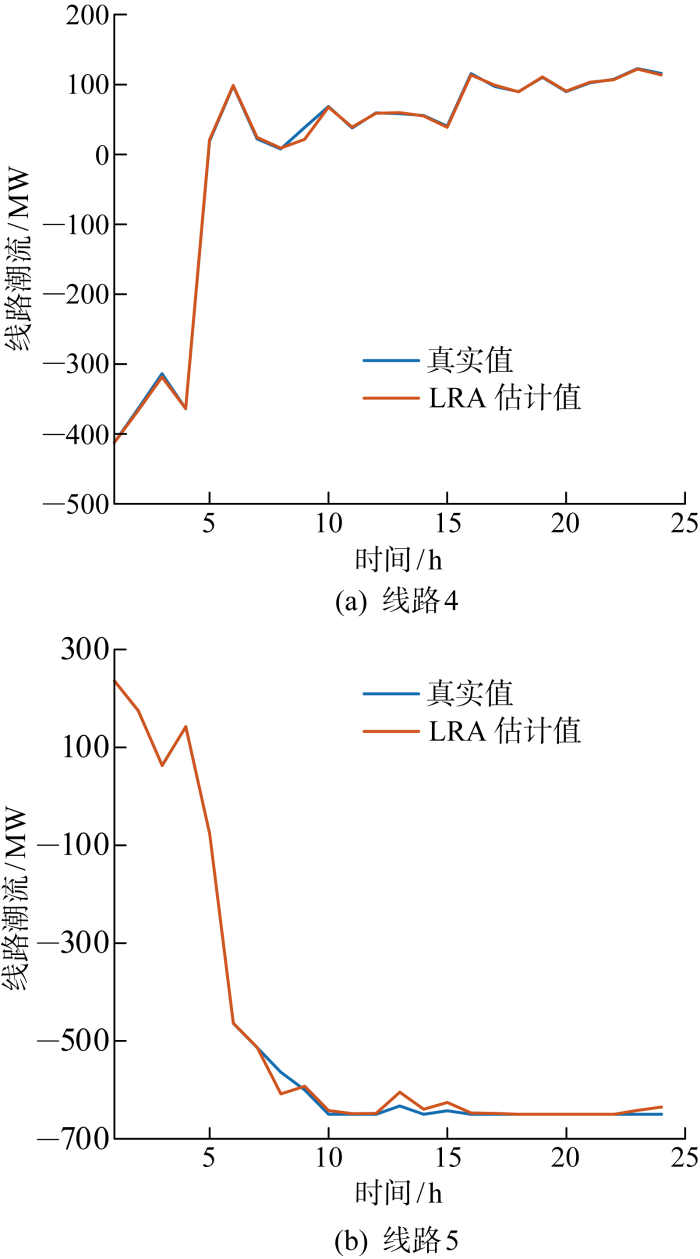
基于电力市场的历史运行信息构建立LRA代理模型后,输入本次市场运行信息,得出LRA代理模型对线路潮流的估计结果.以N-1场景中的线路13开断为例,观察并比较LRA代理模型计算结果与真实计算结果,如图7所示.图中选取各时段均未达到潮流限值的线路4与部分时段达到潮流限值的线路5进行分析,可以发现:当潮流未达到限值时,LRA代理模型计算结果与真实计算结果十分接近;当潮流达到限值时,LRA代理模型计算结果的误差相对大一些,但是误差仍在可接受范围内.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   LRA估计值与真实值对比

Fig.7   Comparison of LRA estimated results with true values


为评估LRA代理模型的准确性,定义时段t下LRA估计值的平均误差为

δt= 1NS+NΘ,S× ∑s∈SF^s,t-Fs,tFs,t+∑θ∈Θ∑s∈SF^s,θ,t-Fs,θ,tFs,θ,t,∀t∈T
(22)

式中:NS为正常运行下的线路总和;NΘ, S为所有 N-1 故障场景下的线路总和.

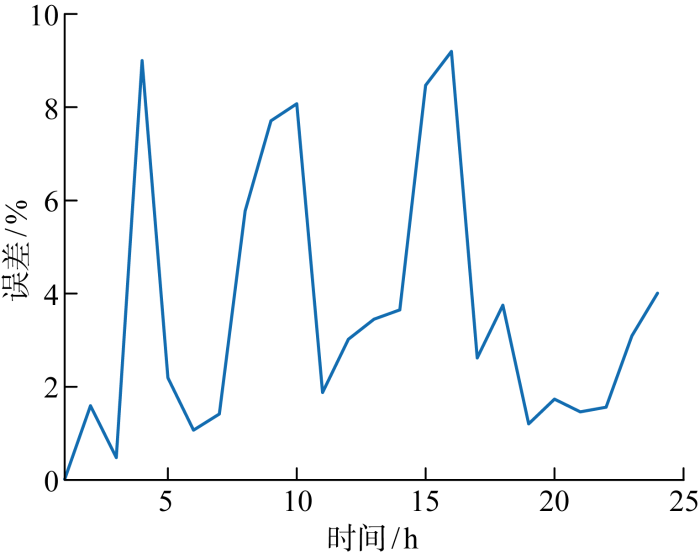
各时段LRA估计值的平均误差如图8所示,可以发现所有时段的误差都小于10%,说明LRA代理模型的计算准确性,能够有效识别关键约束.而第4、9~10、15~16 h的误差相对较大,其原因在于在该时段下,多条线路潮流处于临界状态.在不同的负荷需求、风电、光伏出力条件下,线路潮流约束可能起作用,也可能不起作用,这对LRA代理模型的精度造成了影响.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   各时段LRA估计值的平均误差

Fig.8   Mean errors of LRA estimated results


根据LRA代理模型的计算结果,能够识别出线路约束中存在关键约束 2 163 条,占总线路约束的2.3%,剔除冗余约束能大幅提高SCED模型的求解效率.

4.4 基于LRA的SCED模型求解效率分析

虽然算例分析说明了LRA代理模型精度高,但对实际SCED模型中的线路约束辨识仍会存在误差,即辨识出的关键线路约束中可能存在冗余约束,或者冗余约束中可能存在关键线路约束.由于本文SCED模型的求解采取如图2所示的迭代法,包含了线路安全校验环节,通过迭代能保证所有关键线路约束都能被考虑到SCED模型中,所以确保了方法的求解结果与普通SCED求解方法结果一致.

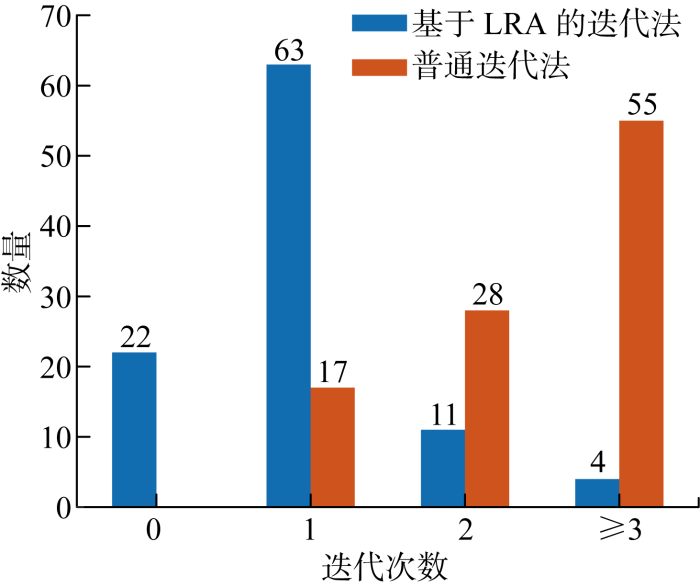
为检验所提基于LRA的迭代法求解SCED模型的高效性,随机生成100个LRA代理模型训练样本外的新样本,与普通迭代法进行对比,两种求解方法的迭代次数如图9所示.整体来看,基于LRA的迭代法比普通迭代法的迭代次数少,说明LRA代理模型辨识的关键约束较为准确,能够有效减少求解SCED模型的迭代次数.此外,有22个样本外模型采用基于LRA的迭代法, 无需迭代便能求解,说明LRA代理模型辨识出了这22个样本外模型中的所有关键线路约束.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   普通迭代法与基于LRA的迭代法迭代次数对比

Fig.9   Comparison of number of iterations between the ordinary iterative method and the LRA-based iterative method


进一步对比两种求解方法的计算时间,结果如表2所示,其中“空白”表示无此项,eItr为迭代次数.从表中可以看出,随着迭代次数的增加,两种迭代求解方法的求解时间增加.并且,相比于普通迭代法,基于LRA的迭代法因迭代次数较少而总平均求解时间较短.此外,采用图1(a)中的直接求解法所需要的平均求解时间为 117.64 s,远大于普通迭代法和基于LRA的迭代法,原因为一次性处理海量的N-1线路安全约束需要耗费大量时间.

表2   两种迭代法的计算时间对比

Tab.2  Comparison of computation time of two iterative methods

求解方法平均求解时间/s总平均求解时间/s
eItr=0eItr=1eItr=2eItr≥3
普通迭代法5.487.9215.2711.54
基于LRA的迭代法2.945.177.3310.045.11

新窗口打开| 下载CSV


5 结论

为高效求解包含海量N-1安全约束的SCED模型,提出基于LRA代理模型的迭代求解方法,并通过算例仿真验证了所提方法的有效性,主要结论如下:

(1) 对于含高比例新能源发电的SCED问题,当净负荷波动较大时,存在弃风、弃光现象以保障电网安全经济运行.

(2) 通过大量历史数据样本训练所得的LRA代理模型精度较高,对线路潮流的估计值较为准确,能够准确地辨识出关键线路约束.

(3) 相较于常规SCED迭代求解方法所得结果,基于LRA代理模型的SCED问题计算结果具有较高的准确性,迭代次数相对较少,求解时间大幅减小.

随着全国统一电力市场的开展,可进一步考虑省间市场的因素,在SCED模型中加入跨省联络线输电的影响.

参考文献

黄强, 郭怿, 江建华, 等.

“双碳”目标下中国清洁电力发展路径

[J]. 上海交通大学学报, 2021, 55(12): 1499-1509.

DOI:10.16183/j.cnki.jsjtu.2021.272      [本文引用: 1]

目前,第三次能源革命已经开始,为了减少碳排放,发达国家先后制定了清洁能源发展战略,并公布了放弃火电、核电的时间表.与此同时,中国也向世界作出承诺:2030年前碳排放达峰,2060年实现碳中和.因此,在&#x0201c;双碳&#x0201d;目标下,研究清洁电力发展路径具有重要意义.分析了中国水、风、光等清洁能源储量及其特征,预测了中长期电力需求,依据电力电量平衡原理,估算了2030和2050规划水平年电力系统结构组成,并分析了未来CO<sub>2</sub>排放趋势,提出了未来中国清洁电力的发展对策与建议.结果表明:预计2027年中国电力系统将实现&#x0201c;碳达峰&#x0201d;;2030年中国清洁电力发电量将超过总发电量的50%;2050年火电、核电将被水、风、光等清洁电力全部取代,电力行业将实现CO<sub>2</sub>的&#x0201c;零排放&#x0201d;,基本全面实现电力系统的绿色转型,以响应国家的&#x0201c;双碳&#x0201d;目标.

HUANG Qiang, GUO Yi, JIANG Jianhua, et al.

Development pathway of China’s clean electricity under carbon peaking and carbon neutrality goals

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(12): 1499-1509.

[本文引用: 1]

姜海洋, 杜尔顺, 金晨, 等.

高比例清洁能源并网的跨国互联电力系统多时间尺度储能容量优化规划

[J]. 中国电机工程学报, 2021, 41(6): 2101-2114.

[本文引用: 1]

JIANG Haiyang, DU Ershun, JIN Chen, et al.

Optimal planning of multi-time scale energy storage capacity of cross-national interconnected power system with high proportion of clean energy

[J]. Proceedings of the CSEE, 2021, 41(6): 2101-2114.

[本文引用: 1]

CHENG J H, YI J H, DAI S, et al.

Can low-carbon city construction facilitate green growth? Evidence from China’s pilot low-carbon city initiative

[J]. Journal of Cleaner Production, 2019, 231: 1158-1170.

[本文引用: 1]

WANG Y, ZHANG D Y, JI Q, et al.

Regional renewable energy development in China: A multidimensional assessment

[J]. Renewable and Sustainable Energy Reviews, 2020, 124: 109797.

[本文引用: 1]

陈文溆乐, 向月, 彭光博, 等.

“双碳”目标下电力系统供给侧形态发展系统动力学建模与分析

[J]. 上海交通大学学报, 2021, 55(12): 1567-1576.

DOI:10.16183/j.cnki.jsjtu.2021.294      [本文引用: 1]

为了模拟双碳目标对电力系统供给侧形态发展的影响,通过分析电源结构转型过程中碳排放的主要影响因素及其相关关系,构建4种不同发展情景的系统动力学模型.仿真分析了4种发展路径下发电结构、电力碳排放的演化趋势.结果表明:电力系统能源供给侧形态发展受多种因素的共同影响,在政策大力支持的前提下,市场消纳机制和消纳技术的发展促进电力系统发电结构的转型,对双碳目标的实现具有重要意义.

CHEN Wenxule, XIANG Yue, PENG Guangbo, et al.

System dynamic modeling and analysis of power system supply side morphological development with dual carbon targets

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(12): 1567-1576.

[本文引用: 1]

张智刚, 康重庆.

碳中和目标下构建新型电力系统的挑战与展望

[J]. 中国电机工程学报, 2022, 42(8): 2806-2818.

[本文引用: 1]

ZHANG Zhigang, KANG Chongqing.

Challenges and prospects of building a new power system under the goal of carbon neutrality

[J]. Proceedings of the CSEE, 2022, 42(8): 2806-2818.

[本文引用: 1]

DU E S, ZHANG N, HODGE B M, et al.

The role of concentrating solar power toward high renewable energy penetrated power systems

[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6630-6641.

[本文引用: 1]

魏利屾, 冯宇昂, 方家琨, 等.

现货市场环境下新能源并网接入对市场出清的影响

[J]. 上海交通大学学报, 2021, 55(12): 1631-1639.

DOI:10.16183/j.cnki.jsjtu.2021.329      [本文引用: 1]

为实现&#x0201c;碳达峰、碳中和&#x0201d;目标,发展新能源迫在眉睫.而与传统火电机组不同,新能源机组边际成本为0,随着电力现货市场改革的不断推进,其大规模并网接入势必会对市场交易结果与系统运行情况造成巨大影响.基于实际现货市场运行规则,采用安全约束机组组合与安全约束经济调度模型搭建电力现货市场仿真分析框架,实现电力现货市场的运行模拟.并以某实际省级电网为例,对现货市场环境下新能源对于市场出清结果的影响进行定量分析.仿真结果表明,在现货市场环境下,新能源参与市场会降低全省平均电价与系统运行成本,使得新能源消纳率降低,同时还会压缩市场化机组的利润空间.

WEI Lishen, FENG Yuang, FANG Jiakun, et al.

Impact of renewable energy integration on market-clearing results in spot market environment

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(12): 1631-1639.

[本文引用: 1]

WU H Y, KRAD I, FLORITA A, et al.

Stochastic multi-timescale power system operations with variable wind generation

[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3325-3337.

[本文引用: 1]

GU Y Z, XIE L.

Stochastic look-ahead economic dispatch with variable generation resources

[J]. IEEE Transactions on Power Systems, 2017, 32(1): 17-29.

[本文引用: 1]

崔杨, 于世鹏, 张节潭, 等.

考虑光热电站调峰补偿的高比例新能源电力系统经济调度

[J]. 中国电机工程学报, 2023, 43(13): 4922-4934.

[本文引用: 1]

CUI Yang, YU Shipeng, ZHANG Jietan, et al.

Economic dispatch of high-proportion renewable energy power system considering peak-shaving compensation of concentrating solar power plant

[J]. Proceedings of the CSEE, 2023, 43(13): 4922-4934.

[本文引用: 1]

崔杨, 姜涛, 仲悟之, 等.

考虑风电消纳的区域综合能源系统源荷协调经济调度

[J]. 电网技术, 2020, 44(7): 2474-2482.

[本文引用: 1]

CUI Yang, JIANG Tao, ZHONG Wuzhi, et al.

Coordinated economic dispatch of source and load of regional comprehensive energy system considering wind power consumption

[J]. Power System Technology, 2020, 44(7): 2474-2482.

[本文引用: 1]

张衡, 程浩忠, 张建平, 等.

高比例风电背景下计及N-1安全网络约束的发输电优化规划

[J]. 中国电机工程学报, 2018, 38(20): 5929-5936.

[本文引用: 1]

ZHANG Heng, CHENG Haozheng, ZHANG Jianping, et al.

Generation and transmission expansion planning considering N-1 security constraints with high penetration of wind power

[J]. Proceedings of the CSEE, 2018, 38(20): 5929-5936.

[本文引用: 1]

赵博石, 胡泽春, 宋永华.

考虑N-1安全约束的含可再生能源输电网结构鲁棒优化

[J]. 电力系统自动化, 2019, 43(4): 16-24.

[本文引用: 1]

ZHAO Boshi, HU Zechun, SONG Yonghua.

Robust optimization of transmission topology with renewable energy sources considering N-1 security constraint

[J]. Automation of Electric Power Systems, 2019, 43(4): 16-24.

[本文引用: 1]

宋嗣博, 郭红霞, 杨苹, 等.

基于节点边际电价的电力市场分区策略研究

[J]. 电力建设, 2017, 38(9): 132-138.

DOI:10.3969/j.issn.1000-7229.2017.09.019      [本文引用: 1]

&nbsp;摘 要：随着中国新一轮电力体制改革的加速推进，区域中长期交易市场逐渐成熟，现货市场成为深化电力改革推进的突破点。针对现货市场下的节点边际电价展开研究，基于各省电改政策分析了最优潮流下的节点边际电价计算方式，采用预测-校正原偶内点法进行优化，并通过Psat搭建仿真模型进行验证。基于阻塞对节点边际电价的区域影响特性，考虑空间分布、发电企业报价和节点边际电价，提出一种电力市场分区策略。经仿真验证，所提策略可以较好地应用于现货市场分区，能够明确反映电力市场价格信号，为发电企业和电力用户的投资提供方向，促进电力现货市场的有序发展。&nbsp;

SONG Sibo, GUO Hongxia, YANG Ping, et al.

Electricity market partitioning strategy based on locational marginal price

[J]. Electric Power Construction, 2017, 38(9): 132-138.

DOI:10.3969/j.issn.1000-7229.2017.09.019      [本文引用: 1]

<div><div>ABSTRACT： &nbsp; &nbsp;With the acceleration of electricity market reform in China, the regional long-term electricity market gradually matures, and the spot market is becoming the breaking point of the deepen reform of electric power. This paper researches the locational marginal price （LMP） in spot market. Based on the electric reform policies of each province, we analyze the calculation method of LMP under the optimal power flow, use the prediction-correction original-interior-point method to optimize it and build a simulation model in Psat to verify it. Based on the regional influence of blockage on LMP, this paper proposes a partitioning strategy for spot market &nbsp; &nbsp;by considering the regional distance, the bidding of power generation enterprises and the LMP. Simulation results show that the proposed strategy can be applied to spot market partition, which can clearly reflect the price signal of electricity market, provide investment direction for power generation enterprises and power consumers, and promote the orderly development of power spot market.</div></div><div>&nbsp;</div>

TAN Z F, ZHONG H W, XIA Q, et al.

Non-iterative multi-area coordinated dispatch via condensed system representation

[J]. IEEE Transactions on Power Systems, 2021, 36(2): 1594-1604.

[本文引用: 1]

王砚平. 安全约束机组组合问题的冗余约束削减方法研究[D]. 杭州: 浙江大学, 2021.

[本文引用: 1]

WANG Yanping. Research on redundancy constraint reduction method for unit commitment problem with safety constraints[D]. Hangzhou: Zhejiang University, 2021.

[本文引用: 1]

SANTOS XAVIER A, QIU F, WANG F Y, et al.

Transmission constraint filtering in large-scale security-constrained unit commitment

[J]. IEEE Transactions on Power Systems, 2019, 34(3): 2457-2460.

[本文引用: 1]

朱正春, 杨知方, 余娟, 等.

面向小样本场景的数据驱动安全约束经济调度快速计算方法

[J]. 中国电机工程学报, 2022, 42(12): 4430-4439.

[本文引用: 3]

ZHU Zhengchun, YANG Zhifang, YU Juan, et al.

Fast calculation method of data-driven security constrained economic scheduling for small sample scenarios

[J]. Proceedings of the CSEE, 2022, 42(12): 4430-4439.

[本文引用: 3]

NI F, NGUYEN P H, COBBEN J F G.

Basis-adaptive sparse polynomial chaos expansion for probabilistic power flow

[J]. IEEE Transactions on Power Systems, 2017, 32(1): 694-704.

[本文引用: 1]

WANG X T, LIU R P, WANG X Z, et al.

A data-driven uncertainty quantification method for stochastic economic dispatch

[J]. IEEE Transactions on Power Systems, 2022, 37(1): 812-815.

[本文引用: 1]

孙鑫, 陈金富, 段献忠, 等.

计及高维随机变量的随机响应面法概率潮流计算

[J]. 中国电机工程学报, 2018, 38(9): 2551-2560.

[本文引用: 1]

SUN Xin, CHEN Jinfu, DUAN Xianzhong, et al.

Probabilistic power flow calculation by random response surface method considering high-dimensional random variables

[J]. Proceedings of the CSEE, 2018, 38(9): 2551-2560.

[本文引用: 1]

XIA B, REN Z Y, KOH C S.

Utilizing kriging surrogate models for multi-objective robust optimization of electromagnetic devices

[J]. IEEE Transactions on Magnetics, 2014, 50(2): 693-696.

[本文引用: 1]

陈乾, 张沈习, 程浩忠, 等.

基于径向基函数随机响应面法的综合能源系统概率能流计算

[J]. 中国电机工程学报, 2022, 42(22): 8075-8088.

[本文引用: 1]

CHEN Qian, ZHANG Shenxi, CHENG Haozhong, et al.

Probabilistic energy flow calculation for integrated energy systems based on radial basis function-stochastic response surface method

[J]. Proceedings of the CSEE, 2022, 42(22): 8075-8088.

[本文引用: 1]

何琨, 徐潇源, 严正, 等.

基于稀疏多项式混沌展开的孤岛微电网概率潮流计算

[J]. 电力系统自动化, 2019, 43(2): 67-75.

[本文引用: 1]

HE Kun, XU Xiaoyuan, YAN Zheng, et al.

Probabilistic power flow calculation of islanded microgrid based on sparse polynomial chaos expansion

[J]. Automation of Electric Power Systems, 2019, 43(2): 67-75.

[本文引用: 1]

方晓涛, 严正, 王晗, 等.

考虑源-荷随机-模糊特征的配电网潮流不确定性量化方法

[J]. 中国电机工程学报, 2022, 42(20): 7509-7523.

[本文引用: 1]

FANG Xiaotao, YAN Zheng, WANG Han, et al.

Uncertainty quantification method of distribution network power flow considering the random and fuzzy characteristics of source-load

[J]. Proceedings of the CSEE, 2022, 42(20): 7509-7523.

[本文引用: 1]

潘忠美, 刘健, 吴建中, 等.

基于低秩逼近法的下垂控制孤岛微电网三相概率潮流计算

[J]. 中国电机工程学报, 2020, 40(20): 6506-6515.

[本文引用: 1]

PAN Zhongmei, LIU Jian, WU Jianzhong, et al.

Three-phase probabilistic power flow calculation of sag control islet microgrid based on low rank approximation method

[J]. Proceedings of the CSEE, 2020, 40(20): 6506-6515.

[本文引用: 1]

KONAKLI K, SUDRET B.

Polynomial meta-models with canonical low-rank approximations: Numerical insights and comparison to sparse polynomial chaos expansions

[J]. Journal of Computational Physics, 2016, 321: 1144-1169.

[本文引用: 1]

DOOSTAN A, VALIDI A, IACCARINO G.

Non-intrusive low-rank separated approximation of high-dimensional stochastic models

[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 263: 42-55.

[本文引用: 1]

SHENG H, WANG X Z.

Probabilistic power flow calculation using non-intrusive low-rank approximation method

[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3014-3025.

[本文引用: 1]

CHEVREUIL M, LEBRUN R, NOUY A, et al.

A least-squares method for sparse low rank approximation of multivariate functions

[J]. ASA Journal on Uncertainty Quantification, 2015, 3(1): 897-921.

[本文引用: 1]

RAMOS C J, MARTINS A P, CARVALHO A S.

Frequency and phase-angle estimation using ordinary least squares

[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5677-5688.

[本文引用: 1]

MARELLI S, SUDRET B.

UQLab: A framework for uncertainty quantification in Matlab

[C]// Proc. 2nd Int. Conf. on Vulnerability, Risk Analysis and Management (ICVRAM2014). Liverpool, United Kingdom: American Society of Civil Engineers, 2014: 2554-2563.

[本文引用: 1]

/

〈 〉