基于增强型Benders分解的区域综合能源系统联合规划

doi:10.16183/j.cnki.jsjtu.2023.059

基于增强型Benders分解的区域综合能源系统联合规划

刘炳文, 吴雄^,, 曹滨睿, 麻淞, 何雯雯

西安交通大学电气工程学院,西安 710054

Joint Planning of Regional Integrated Energy System Based on Enhanced Benders Decomposition

LIU Bingwen, WU Xiong^,, CAO Binrui, MA Song, HE Wenwen

School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710054, China

通讯作者: 吴雄,副教授,博士生导师;E-mail:wuxiong@mail.xjtu.edu.cn.

责任编辑: 王历历

收稿日期: 2023-02-20 修回日期: 2023-07-26 接受日期: 2023-07-31

基金资助:

国家重点研发计划(2022YFB2403100)
国家电网有限公司科技项目(5108-202218280A-2-236-XG)

Received: 2023-02-20 Revised: 2023-07-26 Accepted: 2023-07-31

作者简介 About authors

刘炳文(1998—),硕士生,从事综合能源系统规划与调度研究.

摘要

随着能源交易的逐步市场化,区域综合能源系统(RIES)内部将形成综合能源服务商(IESP)和用户聚合商(UA)等多类经济实体,如何在保护隐私的情况下协调各方参与联合规划,制定全局最优的规划方案成为RIES规划面临的新挑战.首先,明确电-气-热耦合RIES的结构,并从IESP、UA和电-气-热网络3个方面构建数学模型.其次,以经济性最优为目标提出考虑IESP和多个UA的RIES联合规划模型.再次,出于对各实体隐私保护的考虑,采用基于增强型Benders算法的分布式求解方法,以适应含非凸子问题的联合规划问题.最后,通过对比4组算例分析联合规划方案在经济性和能源利用效率方面的优势,同时验证了所提分布式算法良好的收敛性.

关键词： 区域综合能源系统; 联合规划; 增强型Benders分解; 分布式求解; 隐私保护

Abstract

With the gradual marketization of energy trading, different economic entities such as the integrated energy service provider (IESP) and user aggregators (UAs) will form within the regional integrated energy system (RIES). The coordination of all entities to participate in joint planning for a globally optimal planning scheme while protecting privacy has posed a new challenge for RIES planning. First, the structure of the coupled electrical-gas-thermal RIES is clarified in this paper, and a mathematical model is constructed from IESP, UA, and electrical-gas-thermal network. Then, a RIES joint planning model considering IESP and multiple UAs is proposed with the objective of economical optimization. Afterwards, in order to adapt to the non-convexity of the sub-problem of the joint planning problem, the enhanced Benders algorithm is proposed to realize the distributed solution of the model, which protects the privacy of all entities to the greatest extent. Finally, the advantages of the joint planning scheme in terms of economy and energy efficiency are analyzed by comparing four sets of cases, and the good convergence of the proposed distributed algorithm is verified.

Keywords： regional integrated energy system (RIES); joint planning; enhanced Benders decomposition; distributed solution; privacy protection

PDF (3310KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘炳文, 吴雄, 曹滨睿, 麻淞, 何雯雯. 基于增强型Benders分解的区域综合能源系统联合规划[J]. 上海交通大学学报, 2024, 58(10): 1513-1523 doi:10.16183/j.cnki.jsjtu.2023.059

LIU Bingwen, WU Xiong, CAO Binrui, MA Song, HE Wenwen. Joint Planning of Regional Integrated Energy System Based on Enhanced Benders Decomposition[J]. Journal of Shanghai Jiaotong University, 2024, 58(10): 1513-1523 doi:10.16183/j.cnki.jsjtu.2023.059

综合能源系统能对多类能源的产、供、储、销等环节进行有机协调,实现能源结构转型,提升能源利用效率,是我国实现低碳绿色发展的必由之路^[1].近年来,随着能源互联网等概念的提出,区域综合能源系统(regional integrated energy system, RIES)发展迅速,国内外也进行了大量工程实践^[2].目前对RIES的理论研究十分丰富,但在规划、运行、运营等问题上仍面临诸多挑战^[3].

对于RIES的规划问题,现有文献已开展了深入研究.文献[4]中提出针对单一RIES的随机规划模型,重点考虑多阶段规划的多重不确定性;文献[5]中重点研究包含冷热电联产机组(combined cooling heating and power, CCHP)的电-气耦合枢纽与管网规划,建立了多阶段多场景规划模型;文献[6]中提出考虑经济性和熵效率的RIES多目标规划方法.上述研究大都针对单个或整体RIES,没有考虑多系统互联时的合作规划方法.另有部分研究考虑了多区域或多个RIES的互联,例如文献[7]中对RIES进行分区优化设计,得到各分区最优的系统配置方案;文献[8]中提出一种考虑多微电网合作的规划框架;文献[9]中研究了面向多个RIES的联合规划方法;文献[10]中针对RIES供能侧提出基于碳排放的能源站和管道网络的协同规划方法,但没有考虑负荷侧的优化.此类研究均侧重多系统或多区域间的合作,不适用于RIES内部不同实体的联合规划.

事实上,随着能源市场逐步开放,RIES内部也存在综合能源服务商(integrated energy service provider, IESP)和用户聚合商(user aggregator, UA)等多类市场主体.IESP与UA共属同一RIES但又受不同经济实体管理:IESP负责区域内能源的生产和销售并从中获利,UA可负责整合用户需求并统一管理.IESP与UA不同的规划方法直接影响RIES的经济性和能源效率.因此,有必要研究考虑IESP和UA的RIES联合规划方法.

出于保护隐私的考虑,IESP和各UA倾向于独立制定规划方案, RIES联合规划问题难以集中求解.现有研究提出诸多面向RIES的分布式求解方法,例如文献[11 ⇓-13]中针对RIES运行问题提出一系列分布式优化方法;文献[14]中利用Benders分解很好地保护了子系统隐私;文献[15-16]中均基于广义Benders分解实现综合能源系统的分布式优化.尽管能实现混合整数线性规划问题的分布式求解,但上述算法都要求布尔变量、整数变量只存在于主问题,且分解后的子问题必须是凸优化问题.而在本研究中,要实现RIES联合规划问题的分布式求解,IESP和各UA需独立求解含0-1变量的子问题,上述算法并不适用.为此,文献[17]中借助辅助变量和极大极小不等式,提出并证明了一种增强型Benders分解算法,以适应Benders子问题非凸的情况;文献[18-19]中进一步验证了增强型Benders分解算法的准确性和良好的收敛性,但都针对系统的运行问题.为此,拟基于增强型Benders分解算法实现RIES联合规划问题的分布式求解.

基于上述分析,建立RIES的数学模型,提出一种包含IESP和多个UA主体的RIES联合规划模型.为保护各方隐私,利用基于增强型Benders分解的分布式求解方法,得到经济性最优的联合规划方案.算例结果证明了联合规划的优势,验证了分布式求解方法的有效性.

1 区域综合能源系统

1.1 区域综合能源系统结构

拟建立的RIES结构如图1所示.系统涉及电能、天然气及热能的耦合,其内部包括1个IESP和N个UA,分别代表不同实体的利益.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 区域综合能源系统的结构

Fig.1 Structure of RIES

IESP负责购买和生产各类能源,并向各UA出售和输送以赚取利润.其从特定节点接入电网、气源以购入电能、天然气;在区域内投建风电(wind turbine, WT)、光伏(photovoltaic, PV)用于发电,投建热电联产(combined heat and power, CHP)机组用于集中制热,投建电池储能系统(battery energy storage system, BESS)用于调节富余电能,投建电、气、热管网用于向各UA输送能源.

UA负责聚合一定范围内用户的能源需求并管理综合需求响应.其就近投建小型电热锅炉(electric boiler, EB)、燃气锅炉(gas boiler, GB)用于分布式制热,以减少供热损耗,提升能源效率.

1.2 区域综合能源系统模型

1.2.1 IESP模型具体如下.

(1) 风电、光伏.风电、光伏机组的输出功率不应超过其发电功率:

(1)

\begin{array}{l} 0 \leq P_{d, t, s}^{W T} \leq η_{d, t, s}^{W T} {\bar{P}}_{d}^{W T} \\ 0 \leq P_{v, t, s}^{P V} \leq η_{v, t, s}^{P V} {\bar{P}}_{v}^{P V} \end{array}\}

式中:d∈D,为风电候选节点;v∈V,为光伏候选节点;t∈T, s∈S分别为时段数和场景数; $P_{d, t, s}^{W T}$ 、 $P_{v, t, s}^{P V}$ 分别为风电、光伏机组输出功率; ${\bar{P}}_{d}^{W T}$ 、 ${\bar{P}}_{v}^{P V}$ 分别为风电、光伏额定容量; $η_{d, t, s}^{W T}$ 、 $η_{v, t, s}^{P V}$ 分别为风电、光伏机组发电功率的标幺值.

弃风、光功率等于发电功率与输出功率之差:

(2)

\begin{array}{l} P_{d, t, s}^{L o s s, d} = η_{d, t, s}^{W T} {\bar{P}}_{d}^{W T} - P_{d, t, s}^{W T} \\ P_{v, t, s}^{L o s s, v} = η_{v, t, s}^{P V} {\bar{P}}_{v}^{P V} - P_{v, t, s}^{P V} \end{array}\}

式中: $P_{d, t, s}^{L o s s, d}$ 、 $P_{v, t, s}^{L o s s, v}$ 分别为弃风、光功率.

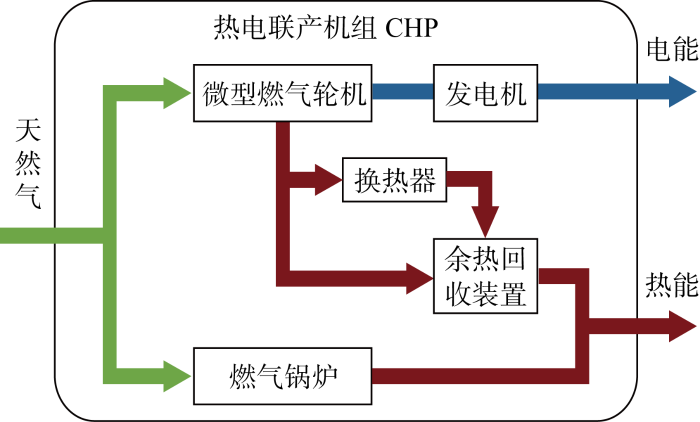
(2) 热电联产机组.CHP结构如图2所示,由微型燃气轮机、燃气锅炉、余热回收装置和换热器等组成.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 热电联产机组结构

Fig.2 Structure of CHP

微型燃气轮机的输出电功率受其额定容量和爬坡速率的限制:

(3)0≤

P_{h, t, s}^{C H P, e}

≤

{\bar{P}}_{h}^{C H P, e}

(4)

\begin{array}{l} - P_{h, r a t e}^{C H P, e} \leq P_{h, t, s}^{C H P, e} - P_{h, t - 1, s}^{C H P, e} \leq P_{h, r a t e}^{C H P, e}, \\ t \in [2, T] \\ - P_{h, r a t e}^{C H P, e} \leq P_{h, T, s}^{C H P, e} - P_{h, 1, s}^{C H P, e} \leq P_{h, r a t e}^{C H P, e} \end{array}\}

式中:h∈H,为候选CHP; $P_{h, t, s}^{C H P, e}$ 为微型燃气轮机输出电功率; ${\bar{P}}_{h}^{C H P, e}$ 为微型燃气轮机的额定容量; $P_{h, r a t e}^{C H P, e}$ 为最大爬坡速率.

微型燃气轮机输出热功率与输出电功率的关系如下:

(5)

P_{h, t, s}^{C H P, h - a}

=(1-

{η^{e}}_{h}

η_{h}^{L o s s}

{η^{e}}_{h} P_{h, t, s}^{C H P, e}

式中: $P_{h, t, s}^{C H P, h - a}$ 为输出热功率; ${η^{e}}_{h}$ 为微型燃气轮机发电效率; $η_{h}^{L o s s}$ 为余热回收装置和换热器的热损耗系数.

燃气锅炉输出热功率表示如下:

(6)

P_{h, t, s}^{C H P, h - b}

{η^{h}}_{h}

k_h

P_{h}^{C H P, e}

式中: ${η^{h}}_{h}$ 为燃气锅炉制热效率;k_h为燃气锅炉与微型燃气轮机输出功率之比; $P_{h}^{C H P, e}$ 为燃气锅炉的额定容量.

CHP的天然气消耗总量表示为

(7)

V_{h, s}^{C H P}

\sum_{t \in T} (\frac{P_{h, t, s}^{C H P, e}}{{η^{e}}_{h} L_{g}} + \frac{P_{h, t, s}^{C H P, h - b}}{{η^{h}}_{h} L_{g}})

式中:L_g为天然气的低位热值.

(3) 电化学储能.BESS的运行需考虑功率平衡约束、充放电功率约束、储电量约束,具体表示为

(8)$ \begin{aligned} E_{e, t, s}^{\text {es }}= & \left(1-\mu_{e}^{\text {Loss }}\right) E_{e, t-1, s}^{\text {es }}+\eta_{e}^{\text {cha }} P_{e, t, s}^{\text {es, chas }} \Delta t- \\ & \eta_{e}^{\text {disc }} P_{e, t, s}^{\text {es, disc }} \Delta t \end{aligned}$

(9)

\begin{array}{l} 0 \leq P_{e, t, s}^{e s, c h a} \leq {\bar{P}}_{e}^{e s, c h a} \\ 0 \leq P_{e, t, s}^{e s, d i s c} \leq {\bar{P}}_{e}^{e s, d i s c} \end{array}\}

(10)$ S_{e}^{\min } \bar{E}_{e}^{\text {es }} \leqslant E_{e, t, s}^{\mathrm{es}} \leqslant S_{e}^{\max } \bar{E}_{e}^{\mathrm{es}}$

式中:e∈E,为候选BESS; $E_{e, t, s}^{e s}$ 为储电量; $μ_{e}^{L o s s}$ 为能量损耗率; $η_{e}^{c h a}$ 、 $η_{e}^{d i s c}$ 分别为充、放电效率; $P_{e, t, s}^{e s, c h a}$ 、 $P_{e, t, s}^{e s, d i s c}$ 分别为充、放电功率; ${\bar{P}}_{e}^{e s, c h a}$ 、 ${\bar{P}}_{e}^{e s, d i s c}$ 分别为最大充、放电功率; $S_{e}^{m i n}$ 、 $S_{e}^{m a x}$ 分别为最小、最大荷电系数; ${\bar{E}}_{e}^{e s}$ 为BESS额定容量.

设定BESS的循环周期为总时段数T:

(11)

E_{e, 0, s}^{e s}

E_{e, T, s}^{e s}

式中: $E_{e, 0, s}^{e s}$ 为BESS的初始储电量.

1.2.2 UA模型具体如下.

(1) 电锅炉、燃气锅炉.利用电热锅炉与燃气锅炉就近供热,可避免供热管道带来的损耗,以提升能源效率和系统经济性.电热锅炉、燃气锅炉的运行需考虑功率约束和爬坡速率限制:

(12)

\begin{array}{l} 0 \leq P_{i, t, s}^{E B} \leq {\bar{P}}_{i}^{E B} \\ 0 \leq P_{i, t, s}^{G B} \leq {\bar{P}}_{i}^{G B} \end{array}\}

(13)

\begin{array}{l} - P_{i, r a t e}^{E B} \leq P_{i, t, s}^{E B} - P_{i, t - 1, s}^{E B} \leq P_{i, r a t e}^{E B} \\ - P_{i, r a t e}^{G B} \leq P_{i, t, s}^{G B} - P_{i, t - 1, s}^{G B} \leq P_{i, r a t e}^{G B} \end{array}\}

式中:i∈N,为UA所在节点; $P_{i, t, s}^{E B}$ 、 $P_{i, t, s}^{G B}$ 分别为电热锅炉、燃气锅炉输出热功率; ${\bar{P}}_{i}^{E B}$ 、 ${\bar{P}}_{i}^{G B}$ 分别为电热锅炉、燃气锅炉额定容量; $P_{i, r a t e}^{E B}$ 、 $P_{i, r a t e}^{G B}$ 分别为电热锅炉、燃气锅炉最大爬坡速率.

电热锅炉、燃气锅炉消耗的能源可表示如下:

(14)

P_{i, t, s}^{E B, e}

P_{i, t, s}^{E B}

η_{i}^{E B}

(15)$ V_{i, t, s}^{\mathrm{GB}}=\frac{P_{i, t, s}^{\mathrm{GB}}}{\eta_{i}^{\mathrm{GB}} L_{\mathrm{g}}}$

式中: $P_{i, t, s}^{E B, e}$ 为电热锅炉消耗的电功率; $η_{i}^{E B}$ 为电热锅炉的制热效率; $V_{i, t, s}^{G B}$ 为燃气锅炉消耗的天然气量; $η_{i}^{G B}$ 为燃气锅炉的制热效率.

(2) 电、气、热负荷.UA中聚合的电、气、热负荷可划分为固定负荷和弹性负荷,弹性负荷具有一定需求响应能力.单位时段弹性负荷的削减量或平移量满足下式:

(16)

\begin{array}{l} Δ {D^{e}}_{i, t, m i n} \leq Δ {D^{e}}_{i, t, s} \leq Δ {D^{e}}_{i, t, m a x} \\ Δ {D^{g}}_{i, t, m i n} \leq Δ {D^{g}}_{i, t, s} \leq Δ {D^{g}}_{i, t, m a x} \\ Δ {D^{h}}_{i, t, m i n} \leq Δ {D^{h}}_{i, t, s} \leq Δ {D^{h}}_{i, t, m a x} \end{array}\}

式中: Δ ${D^{e}}_{i, t, s}$ 、Δ ${D^{g}}_{i, t, s}$ 、Δ ${D^{h}}_{i, t, s}$ 分别为电、气、热弹性负荷的需求响应量;ΔD_{i, t,}_min、ΔD_{i, t,}_max分别为需求响应下、上限.

所有时段弹性负荷的削减总量满足下式:

(17)

\begin{array}{l} \overset{T}{\sum_{t = 1}} Δ {D^{e}}_{i, t, s} \leq {D^{e}}_{i, s u m} \\ \overset{T}{\sum_{t = 1}} Δ {D^{g}}_{i, t, s} \leq {D^{g}}_{i, s u m} \\ \overset{T}{\sum_{t = 1}} Δ {D^{h}}_{i, t, s} \leq {D^{h}}_{i, s u m} \end{array}\}

式中: ${D^{e}}_{i, s u m}$ 、 ${D^{g}}_{i, s u m}$ 、 ${D^{h}}_{i, s u m}$ 分别为电、气、热弹性负荷的最大需求响应量.

进一步得到UA的实际能源需求:

(18)

\begin{array}{l} {D^{e}}_{i, t, s} = D_{i, t, s}^{e, 0} - Δ {D^{e}}_{i, t, s} + P_{i, t, s}^{E B, e} \\ {D^{g}}_{i, t, s} = D_{i, t, s}^{g, 0} - Δ {D^{g}}_{i, t, s} + V_{i, t, s}^{G B} \\ {D^{h}}_{i, t, s} = D_{i, t, s}^{h, 0} - Δ {D^{h}}_{i, t, s} - P_{i, t, s}^{E B} - P_{i, t, s}^{G B} \end{array}\}

式中: ${D^{e}}_{i, t, s}$ 、 ${D^{g}}_{i, t, s}$ 、 ${D^{h}}_{i, t, s}$ 分别为UA实际电、气、热能需求; $D_{i, t, s}^{e, 0}$ 、 $D_{i, t, s}^{g, 0}$ 、 $D_{i, t, s}^{h, 0}$ 分别为UA原始负荷需求.

1.2.3 电-气-热网络模型

具体如下.

(1) 电力网络.考虑到网络规模较小,以直流潮流方程描述电力网络约束,即

(19)-

{\bar{P}}_{l}^{l i n e}

≤

P_{l, t, s}^{l i n e}

≤

{\bar{P}}_{l}^{l i n e}

(20)$ P_{l, t, s}^{\text {line }}=\frac{\theta_{l, s, t}}{x_{l}}$

(21)$ -\theta_{l}^{\max } \leqslant \theta_{l, s, t} \leqslant \theta_{l}^{\max }$

式中:l∈L,为RIES内候选电力线路; $P_{l, t, s}^{l i n e}$ 为线路传输功率; ${\bar{P}}_{l}^{l i n e}$ 为线路额定容量;θ_l_,_s_,_t为线路两端相角差;x_l为线路电抗; $θ_{l}^{m a x}$ 为线路允许的最大相角差.

RIES通过联络线从特定节点接入电网,联络线的容量限制可表示为各节点的电能购入限制:

(22)

{\underline{E}}^{e}_{b}

≤

{E^{e}}_{b, t, s}

≤

{\bar{E}}^{e}_{b}

式中:b∈B,为RIES内所有节点的集合,即D, V, H, E, N⊆B; ${E^{e}}_{b, t, s}$ 为节点b从电网购入的电能; ${\bar{E}}^{e}_{b}$ 、 ${\underline{E}}^{e}_{b}$ 分别为电能购入上、下限.

RIES内各节点购电量、设备输出功率、UA电负荷和线路送出功率的总和为0,其内部电力平衡方程如下式所示:

(23)$ \begin{aligned} E_{b, t, s}^{\mathrm{e}}+ & \sum_{d \in D} K_{b, d} P_{d, t, s}^{\mathrm{WT}}+\sum_{v \in V} K_{b, v} P_{v, t, s}^{\mathrm{PV}}+ \\ & \sum_{h \in H} K_{b, h} P_{h, t, s}^{\mathrm{CHP}, \mathrm{e}}+\sum_{e \in E} K_{b, e}\left(P_{e, t, s}^{\mathrm{es}, \text { disc }}-P_{e, t, s}^{\mathrm{es}, \text { cha }}\right)- \\ & \sum_{i \in N} K_{b, i} D_{i, t, s}^{\mathrm{e},}-\sum_{l \in L} K_{b, l} P_{l, t, s}^{\mathrm{line}}=0 \end{aligned}$

式中:关联矩阵元素K_b_,_d、K_b_,_v、K_b_,_h、K_b_,_e、K_b_,_i、K_b_,_l分别表示节点b与各类设备候选节点、各UA节点或线路两端节点的连接关系.

(2) 天然气网络.考虑到输送距离较短,采用静态燃气网络模型.表示为

(24)-

{\bar{V}}_{p}^{p i p}

≤

V_{p, t, s}^{p i p}

≤

{\bar{V}}_{p}^{p i p}

(25)$ V_{p, t, s}^{\mathrm{pip}^{2}}=k_{p}\left(f_{\mathrm{pi}, t, s}^{2}-f_{\mathrm{po}, t, s}^{2}\right)$

(26)$ f^{\min } \leqslant f_{\mathrm{pi}, t, s}, f_{\mathrm{p} 0, t, s} \leqslant f^{\max }$

式中:p∈P,为RIES内候选天然气管道; $V_{p, t, s}^{p i p}$ 为管道流量; ${\bar{V}}_{p}^{p i p}$ 为管道额定容量;f_pi_{, t, s}、f_po_{, t, s}分别为管道两端气压;f^min、f^max分别为最小、最大气压.

RIES通过特定节点接入气源,气源本身具有流量限制:

(27)

{\underline{E}}^{g}_{b}

≤

{E^{g}}_{b, t, s}

≤

{\bar{E}}^{g}_{b}

式中: ${E^{g}}_{b, t, s}$ 为节点b从气源购入的天然气量; ${\underline{E}}^{g}_{b}$ 、 ${\bar{E}}^{g}_{b}$ 分别为对应气源的流量下、上限.

RIES内各节点购气量、CHP消耗量、UA气负荷和管道送出量的总和为0,其内部天然气平衡方程表示如下式所示:

(28)$ \begin{array}{l} E_{b, t, s}^{\mathrm{g}}-\sum_{h \in H} K_{b, h}\left(V_{h, t, s}^{\mathrm{CHP}-\mathrm{a}}+V_{h, t, s}^{\mathrm{CHP}-\mathrm{b}}\right)- \\ \quad \sum_{p \in P} K_{b, p} V_{p, t, s}^{\mathrm{pip}}-\sum_{i \in N} K_{b, i} D_{i, t, s}^{\mathrm{g}}=0 \end{array}$

式中:关联矩阵元素K_b_,_p表示节点b与天然气管道两端节点的连接关系; $V_{h, t, s}^{C H P - a}$ 为CHP中微型燃气轮机的天然气消耗总量; $V_{h, t, s}^{C H P - b}$ 为CHP中燃气锅炉的天然气消耗总量.

(3) 供热网络.区域集中供热管网多采用质调节的控制方式,即保持管道内流量、压强等物理量不变,仅调整导热介质温度^[20].管道传递热功率的限制为

(29)

{\underline{P}}_{m}^{p i p}

≤

P_{m, t, s}^{p i p}

≤

{\bar{P}}_{m}^{p i p}

式中:m∈M,为RIES内候选供热管道; $P_{m, t, s}^{p i p}$ 为管道传递的热功率; ${\underline{P}}_{m}^{p i p}$ 、 ${\bar{P}}_{m}^{p i p}$ 分别为传递热功率的下、上限.

热力惯性带来的热能损耗为

(30)

P_{m, t, s}^{L o s s}

=(1-

e^{- λ^{p i p} L_{m}^{p i p, h} / C^{p i p}}

)

P_{m, t, s}^{p i p}

式中: $P_{m, t, s}^{L o s s}$ 为热功率损耗;λ^pip为传热系数; $L_{m}^{p i p, h}$ 为管道长度;C^pip为供热介质的比热容.

RIES内各节点CHP、管道供热量、管道热损耗和UA热负荷的总和为0,其内部热能平衡方程表示如下式所示:

(31)

\sum_{h \in H}

K_b_,_h(

P_{h, t, s}^{C H P - a}

P_{h, t, s}^{C H P - b}

\sum_{m \in M} {K^{p}}_{b, m} P_{m, t, s}^{p i p}

\sum_{m \in M} K_{b, m}^{L o s s} P_{m, t, s}^{L o s s}

\sum_{i \in N}

K_b_,_i

{D^{h}}_{i, t, s}

式中:关联矩阵元素 ${K^{p}}_{b, m}$ 、 $K_{b, m}^{L o s s}$ 分别表示节点b与供热管道两端节点的连接关系、损耗关系; $P_{h, t, s}^{C H P - a}$ 为CHP中微型燃气轮机输出热功率; $P_{h, t, s}^{C H P - b}$ 为CHP中燃气锅炉输出热功率.

2 RIES联合规划模型

2.1 目标函数

RIES联合规划模型以全系统年度总成本最低为目标,包括等值年投资成本和年运行成本两部分.

(32)min

(C_{i n v}^{I E S P} + \sum_{i \in N} C_{i n v, i}^{U A} + D \sum_{s \in S} κ_{s} C_{s}^{o p r})

式中: $C_{i n v}^{I E S P}$ 为IESP等值年投资成本; $C_{i n v, i}^{U A}$ 为UAi等值年投资成本; $C_{s}^{o p r}$ 为场景s的运行成本;κ_s为场景s出现概率;D为全年总天数.

IESP的投资费用包括风电、光伏、CHP、BESS、电-气-热网络的费用,UA的投资费用包括电热锅炉、燃气锅炉两部分. $C_{i n v}^{I E S P}$ 、 $C_{i n v, i}^{U A}$ 可分别表示如下:

(33)$ \begin{array}{l} C_{\mathrm{inv}}^{\mathrm{IESP}}=\left(\mu^{\mathrm{WT}} \sum_{d \in D} \bar{P}_{d}^{\mathrm{WT}}+\mu^{\mathrm{PV}} \sum_{v \in V} \bar{P}_{v}^{\mathrm{PV}}+\right. \\ \mu^{\mathrm{CHP}} \sum_{h \in H} \bar{P}_{h}^{\mathrm{cHP}, \mathrm{e}}+\mu^{\mathrm{es}} \sum_{e \in E} \bar{E}_{e}^{\mathrm{es}}+ \\ \mu^{\mathrm{line}} \sum_{l \in L} \bar{P}_{l}^{\text {line }} L_{l}^{\text {line }}+\mu^{\mathrm{pip}, \mathrm{~g}} \sum_{p \in P} \bar{V}_{p}^{\mathrm{pip}} L_{p}^{\mathrm{pip}, \mathrm{~g}}+ \\ \left.\mu^{\mathrm{pip}, \mathrm{~h}} \sum_{m \in M} \bar{P}_{m}^{\mathrm{pip}} L_{m}^{\mathrm{pip}, \mathrm{~h}}\right) \end{array}$

(34)

C_{i n v, i}^{U A}

=μ^EB

{\bar{P}}_{i}^{E B}

+μ^GB

{\bar{P}}_{i}^{G B}

式中:μ为相应设备折算至年的单位投资成本; $L_{l}^{l i n e}$ 、 $L_{p}^{p i p, g}$ 、 $L_{m}^{p i p, h}$ 为电力线路、天然气管道、供热管道的长度; ${\bar{P}}_{d}^{W T}$ 、 ${\bar{P}}_{v}^{P V}$ 、 ${\bar{P}}_{h}^{C H P, e}$ 、 ${\bar{E}}_{e}^{e s}$ 、 ${\bar{P}}_{l}^{l i n e}$ 、 ${\bar{V}}_{p}^{p i p}$ 、 ${\bar{P}}_{m}^{p i p}$ 为反映IESP投资容量的连续决策变量; ${\bar{P}}_{i}^{E B}$ 、 ${\bar{P}}_{i}^{G B}$ 反映各UA投资容量的连续决策变量.

RIES的运行费用包括IESP的购能费用、各类设备的运行维护费、弃风弃光惩罚以及UA中用户满意度惩罚. $C_{s}^{o p r}$ 可表示为

(35)$ \begin{array}{l} C_{s}^{\mathrm{opr}}=\sum_{t \in T}\left[\rho_{t, s}^{\mathrm{e}} \sum_{b \in B} E_{b, t, s}^{\mathrm{e}}+\rho_{t, s}^{\mathrm{g}} \sum_{b \in B} E_{b, t, s}^{\mathrm{g}}+\right. \\ \rho^{\mathrm{cHP}} \sum_{h \in H} K_{b, h} V_{h, t, s}^{\mathrm{CHP}}+\rho^{\mathrm{es}} \sum_{e \in E}\left(P_{e, t, s}^{\mathrm{es}, \mathrm{cha}}+P_{e, t, s}^{\mathrm{es}, \mathrm{disc}}\right)+ \\ \left.\rho^{\text {Loss }}\left(\sum_{d \in D} P_{d, t, s}^{\mathrm{Loss}, d}+\sum_{v \in V} P_{v, t, s}^{\mathrm{Loss}, v}\right)\right]+ \\ \sum_{i \in N} \sum_{t \in T}\left(\rho^{\mathrm{EB}} P_{i, t, s}^{\mathrm{EB}, \mathrm{e}}+\rho^{\mathrm{GB}} V_{i, t, s}^{\mathrm{GB}}+f_{i}\right) \end{array}$

式中: ${ρ^{e}}_{t, s}$ 、 ${ρ^{g}}_{t, s}$ 分别为电网和气源的能源单价;ρ^CHP为CHP的单位运行成本;ρ^es为BESS的损耗及运行维护费用;ρ^Loss为单位弃风光惩罚;ρ^EB为电热锅炉的单位运行成本;ρ^GB为燃气锅炉的单位运行成本; $V_{h, t, s}^{C H P}$ 为CHP的天然气消耗总量;f_i为UAi的用户满意度惩罚函数,用以量化电、气、热需求响应对用户满意度的影响,如下:

(36)f_i=

\sum_{* \in {e, g, h}}

[

α_{i}^{*}

(Δ

D_{i, t, s}^{*}

)²+

β_{i}^{*} |Δ D_{i, t, s}^{*}|

]

式中: $α_{i}^{*}$ 、 $β_{i}^{*}$ 分别为相应的成本系数;Δ $D_{i, t, s}^{*}$ 为实际的电、热、气需求响应总量.

2.2 投资约束

受区域内资源、环境等现实因素的制约,由IESP和各UA投资决策的机组、线路、管道等设备均需满足投资容量约束.反映IESP投资容量的决策变量主要为 ${\bar{P}}_{d}^{W T}$ 、 ${\bar{P}}_{v}^{P V}$ 、 ${\bar{P}}_{h}^{C H P, e}$ 、 ${\bar{E}}_{e}^{e s}$ 、 ${\bar{P}}_{l}^{l i n e}$ 、 ${\bar{V}}_{p}^{p i p}$ 、 ${\bar{P}}_{m}^{p i p}$ ;反映各UA投资容量的决策变量主要为 ${\bar{P}}_{i}^{E B}$ 、 ${\bar{P}}_{i}^{G B}$ . 为简化表示,将上述各类设备的决策变量记为C,则各类设备的投资容量约束可统一表示为

(37)

C_{k, m i n}^{x} I_{k}^{x}

≤

C_{k}^{x}

≤

C_{k, m a x}^{x} I_{k}^{x}

I_{k}^{x}

∈{0, 1}

式中: $C_{k}^{x}$ 为第k个x类设备的额定容量; $I_{k}^{x}$ 为投资第k个x类设备的布尔决策变量; $C_{k, m i n}^{x}$ 、 $C_{k, m a x}^{x}$ 分别为第k个x类设备投资容量下、上限.

对于BESS,还需考虑充放电功率及时长约束:

(38)

\begin{array}{l} {\bar{P}}_{e}^{e s, c h a}, {\bar{P}}_{e}^{e s, d i s c} = {\bar{E}}_{e}^{e s} / T_{e} \\ T_{e, m a x} \leq T_{e} \leq T_{e, m i n}, T_{e} \in Z \end{array}\}

式中:∀e∈E; T_e为满功率充放电时段数;T_e_,max、T_e_,min分别为最大、最小功率充放电时段数.

2.3 运行约束

RIES联合规划模型需满足式(1)~(31)全部运行约束.

3 分布式求解方法

联合规划问题中,IESP与各UA追求整体经济最优的同时也有隐私保护的需求.用户需求特性、规划结果等信息往往难以共享,为此采用基于增强型Benders分解的分布式求解方法.

3.1 增强型Benders分解

增强型Benders分解是对传统Benders分解的改进,其适用于含0-1变量的非凸子问题.文献[17]中详细推导并证明了该方法的有效性.针对RIES联合规划问题,增强型Benders分解过程如下.

RIES联合规划问题的矩阵表示如下,记为原问题.

(39)

\begin{array}{l} \underset{x, y, x'_{i}, y'_{i}, m}{m i n} (g y + \sum_{i \in N} h_{i} y'_{i}) \\ s . t . A x + B y + C m \geq e \\ D_{i} m + E_{i} x'_{i} + F_{i} y'_{i} \geq f_{i}, \forall i \in N \\ x, x'_{i} \in {0, 1}, \forall i \in N \end{array}\}

式中:x为IESP相关0-1变量构成的向量,包括其投资各类设备的0-1决策变量;x'_i为 UAi 相关0-1变量构成的向量,包括投资电热锅炉、燃气锅炉的0-1决策变量;y为IESP相关连续变量构成的向量,包括设备额定容量和相关运行变量;y'_i为 UAi 相关连续变量构成的向量,包括设备额定容量和相关运行变量;m为IESP与各UA之间耦合变量构成的向量,具体为UAi从IESP购入的电、气、热负荷 ${D^{e}}_{i, t, s}$ 、 ${D^{g}}_{i, t, s}$ 、 ${D^{h}}_{i, t, s}$ (∀i, ∀s, ∀t);式(39)中目标函数对应式(32),其中gy为IESP投资和运行成本的总和,h_iy'_i为 UAi 投资和运行成本的总和;Ax+By+Cm≥e表示IESP相关约束,对应式(1)~(11)、式(19)~(31)、式(37)~(38);D_im+E_ix'_i+F_iy'_i≥f表示 UAi 相关约束,对应式(12)~(18)和式(37);A、B、C、D_i、E_i、F_i分别为常系数矩阵;e、f_i、g、h_i分别为常系数向量.

原问题可被分解为1个主问题和N个统一原始子问题.主问题表示为

(40)

\begin{array}{l} \underset{x, y, m, θ_{i}}{m i n} (g y + \sum_{i \in N} θ_{i}) \\ s . t . A x + B y + C m \geq e \\ θ_{i} \geq 0, \forall i \in N \\ x \in {0, 1} \\ 添 加 B e n d e r s 割 (如 果 存 在) \end{array}\}

式中:θ_i为主问题确定的UAi相关成本的下限,并随着迭代时Benders割的添加而增加.

统一原始子问题可同时验证主问题当前解的可行性和最优性,简化表示为

(41)

\begin{array}{l} \underset{x'_{i}, y'_{i}, v'_{i}}{m i n} 1^{T} v'_{i} \\ s . t . E'_{i} x'_{i} + F'_{i} y'_{i} + v'_{i} \geq f'_{i} - D'_{i} \bar{m}' \\ x'_{i} \in {0, 1} \\ v'_{i} \geq 0 \end{array}\}

式中:v'_i为松弛变量构成的向量;D'_i、E'_i、F'_i、f'_i分别为对应系数矩阵或系数向量; $\bar{m}$ '为主问题当前解中 ${\bar{θ}}_{i}$ 和 $\bar{m}$ 构成的向量;1、0分别表示1向量和零向量.具体推导过程见附录A.

由于存在0-1变量,式(41)无法直接通过对偶化生成Benders割,增强型Benders分解通过引入辅助0-1变量 $\tilde{x}$ '_i和极大极小不等式对统一原始子问题进行近似对偶化处理,得到统一对偶子问题,具体过程见附录A.当其最优解 $F_{D, i}^{*}$ =0时,认为主问题的当前解满足可行性和最优性要求;否则,为排除当前解,应向主问题添加Benders割如下

(42)(f'_i-D'_i

\bar{m}

')^T

{\bar{J}}_{i}

+1^T

{\bar{L}}_{i}

≤0

式中: ${\bar{J}}_{i}$ 、 ${\bar{L}}_{i}$ 为统一对偶子问题中对偶变量的最优解.

不同于传统Benders分解,近似对偶化方法使统一对偶子问题与统一原始子问题最小化目标值之间存在对偶间隙,式(41)所示Benders割无法排除全部不可行解或非最优解.为消除对偶间隙,有必要在 $F_{D, i}^{*}$ =0时进一步求解可行性恢复子问题,具体形式见附录A.当其最优解 $F_{F, i}^{*}$ >0时,以消除对偶间隙,应向主问题添加Benders割如下

(43)

\begin{array}{l} Δ_{i} (m', \bar{m}') \geq F_{F, i}^{*} \\ Δ (m', \bar{m}') = \sum_{n} o_{n} / w_{n} \\ o_{n} = |m'_{n} - \bar{m}'_{n}| \\ w_{n} = \{\begin{array}{l} |\bar{m}'_{n}|, & 如 果 |\bar{m}'_{n}| > 0 \\ τ, & 如 果 |\bar{m}'_{n}| = 0 \end{array} \end{array}\}

式中:Δ_i(m', $\bar{m}$ ')用于度量 $\bar{m}$ '与任何可行性解m'之间的偏差;o_n为绝对偏差量;w_n为归一化因子;m'_n、 $\bar{m}$ '_n分别为m'、 $\bar{m}$ '中的具体元素;τ是一个足够小的正数.

3.2 分布式求解流程

所用基于增强型Benders分解的分布式求解流程如图3所示.IESP独立求解主问题,并向各UA传递关键信息;各个UA独立求解子问题,并生成Benders割;当且仅当各UA均无Benders割生成,主问题当前解不变时,计算过程收敛.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 分布式求解流程图

Fig.3 Flow chart of distributed solution

4 算例分析

4.1 算例设置

对含有14个电力节点、8个天然气节点和8个供热节点的某区域进行RIES联合规划,拓扑结构如图4所示.选取4种典型场景,包含各风光机组的出力、各UA的能源需求、能源价格等信息,每个场景的总时段数T=24.各类设备的年投资费用、单位运行费用如表1所示,其中空白表示不适用.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 RIES拓扑结构

Fig.4 Topology of RIES

表1 设备投资与运行费用

Tab.1 Equipment investment and operating costs

类型	使用年限	年投资成本	单位运行成本/ (元·kW^-1)
CHP	30	390元/kW	0.03
PV	30	228元/kW
WT	20	522元/kW
BESS	15	125元/(kW·h)	0.04
电力线路	70	2.10元/(kW·km^-1)
天然气管道	20	23.83元/(m³·kW^-1)
供热管道	15	2.95元/(kW·km^-1)
EB	20	361元/kW	0.08
GB	20	281元/kW	0.07

新窗口打开| 下载CSV

为验证所提规划方法,设置以下4组情景.

情景1 利用所提规划方法实现IESP与UA的联合规划.

情景2 IESP与UA独立规划.各UA首先根据能源需求制定规划方案,随后IESP根据UA规划结果制定自身规划方案.

情景3 电、气、热系统解耦规划.首先规划供热系统以满足热能需求,随后根据供热系统规划结果分别规划电力系统和供气系统.

情景4 采取集中制热供热的方式,由IESP统一规划CHP、电热锅炉、燃气锅炉等设备.

4.2 规划结果分析

情景1的规划结果如图5所示,IESP和各UA设备的容量如表2所示.表中:空白表示未规划该类设备.各线路、管道的容量见附录B,全系统年度总成本为2.99×10⁷元.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 RIES联合规划结果

Fig.5 Joint planning results of RIES

表2 RIES联合规划设备容量

Tab.2 Equipment capacity of RIES joint planning

序号	CHP/ kW	PV/kW	WT/ kW	BESS/ (kW·h)	EB/ kW	GB/ kW
1	4143	0	1500	1019	811	477
2	3205	1301	1100	438	316	70
3	353	1882	1700	1600	60	0
4		191	1200	1800	889	7
5		1818	1500		266	0
6			1600

注:EB、GB序号为其所在UA的编号.

新窗口打开| 下载CSV

据此规划方案,系统电能需求的83.62%由可再生能源满足,8.96%由CHP满足,仅7.42%电能需从电网购入;系统供热需求32.03%由CHP提供,57.36%由电热锅炉提供,10.60%由燃气锅炉提供.

表3中比较了情景1~4的规划结果.情景2的总成本为3.15×10⁷元,比情景1高出5.45%.对比情景1,由于无法准确计算各类能源成本,所以各UA投建了更少的电热锅炉、燃气锅炉,而IESP需投建更多CHP.CHP在制热时产生的大量电能既限制了光伏和风电的投资,又需要更多BESS消纳.从运行角度看,该方案增加了40.64%的购气量,CHP提供超过20%的电能,可再生能源发电量占比下降13.15个百分点.

表3 各情景结果比较

Tab.3 Comparison of the results of each case

项目	年度总成本/元	CHP总容量/kW	PV和WT 总容量/kW	BESS总容量/ (MW·h)	电力线路总容量/kW	天然气管道总容量/m³	供热管道总容量/kW	各UA中EB、 GB总容量/kW
情景1	2.99×10⁷	1423	1.27×10⁴	3366	1.60×10⁴	672	3718	2896
情景2	3.15×10⁷	2151	7831	3551	1.10×10⁴	986	4099	1799
情景3	3.41×10⁷	3066	6083	4736	1.27×10⁴	1244	5376	0
情景4	3.00×10⁷	1427	1.27×10⁴	3195	1.44×10⁴	666	5783	2909

新窗口打开| 下载CSV

情景3的总成本为3.41×10⁷元,比情景1高出14.13%.对比情景1,由于在供热系统规划阶段无法考虑电价、气价等成本因素,系统优先选择投建成本更低的CHP,各UA不再投建电热锅炉、燃气锅炉.因此,CHP和BESS的容量进一步增加,天然气及供热管道容量有所增加,光伏和风电容量进一步减少.从运行角度看,该方案增加了63.78%的购气量,CHP提供了超过28%的电能,可再生能源发电占比下降28.71个百分点.

情景4的总成本比情景1高出0.33%.对比情景1,集中制热供热使得供热管道总容量增加,为平衡供热损耗,CHP、电热锅炉、燃气锅炉的容量均有所增加;电力线路、供热管道总容量则有所降低,光伏和风电容量略有增加.该方案增加0.66%的购气量,减少0.81%的购电量.

根据不同规划方案求得的RIES能源利用效率分别为88.47%、86.35%、82.44%和88.19%.对比各实体独立规划方案或各系统解耦规划方案,所提联合规划方案有更高的能源利用效率.对比集中制热供热的规划方案,UA投建分布式电热锅炉、燃气锅炉可减少一定供热损耗,进一步提升能源利用效率.

综上所述,所提RIES联合规划方案在系统经济性、能源利用率等方面都更具优势,更好地激励区域内可再生能源的开发,避免过度的容量配置或能源购入,同时减少能源损耗.

4.3 算法收敛性分析

图6展示了基于增强型Benders分解的分布式求解方法的收敛过程,将每次迭代中各UA得到的 $F_{D, i}^{*}$ 或 $F_{F, i}^{*}$ 的总和记为偏差.由图可见,随着迭代进行系统总成本单调递增,而偏差振荡衰减至0,符合增强型Benders分解的收敛特性.迭代过程中UA1、UA4和UA5分别向主问题添加27、11和54次同式(43)所示的Benders割,以消除对偶间隙.算法经过 2 091 次迭代后收敛,总用时967 s, 偏差为6.52×10^-10.与传统Benders分解类似,本算法也存在迭代次数较多、计算速度稍慢的问题, 但对RIES联合规划问题而言,这样的求解时间完全可接受.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 所提方法迭代求解过程

Fig.6 Iterative solution process of method proposed

5 结语

提出一种RIES内部IESP与多个UA联合规划的方法,制定了全系统经济性最优的规划方案.为保护各实体的隐私,RIES联合规划问题由各实体独立求解,为适应子问题的非凸性采用了一种基于增强型Benders分解的分布式求解方法.算例结果表明,RIES联合规划方法较一般方法有更好的经济性和更高的能源利用率,且促进了可再生资源的开发,借助电热锅炉、燃气锅炉的分布式供热模式有更低的供热损耗.基于增强型Benders分解的方法具有良好的收敛性,能准确地实现分布式求解.该方法可进一步适用于其他互联型多能流电力系统优化配置,例如电-热RIES系统、电-气-热RIES系统以及电-氢RIES系统等.另外,减少迭代次数、提升计算速度是未来研究增强型Benders分解的重点.

附录见本刊网络版(xuebao.sjtu.edu.cn/article/2024/1006-2467/1006-2467-58-10-1513.shtml)

附录A

增强型Benders分解的详细推导过程如下:

首先,推导统一原始子问题.根据Benders分解,原问题式(39)可被分解为主问题式(40)和多个子问题.各子问题需根据主问题的当前解分别进行可行性检验和最优性检验,即先后求解可行性子问题和最优性子问题.

可行性子问题用于验证主问题当前解 $\bar{m}$ '的可行性,当且仅当目标函数值等于0时, 满足可行性要求;否则,应向主问题添加可行性割,以消除不可行结果,具体表示如下:

(A1)

\begin{matrix} \begin{array}{l} \underset{x'_{i}, y'_{i}, v_{i}}{m i n} 1^{T} v_{i} \\ s . t . E_{i} x'_{i} + F_{i} y'_{i} + v_{i} \geq f_{i} - D_{i} \bar{m} \\ x'_{i} \in {0, 1} \\ v_{i} \geq 0 \end{array}\} \end{matrix}

式中: $v_{i}$ 为一组非负松弛变量构成的向量.

当满足可行性要求时,进一步求解最优性子问题.比较目标函数值与主问题确定的 UAi 相关成本的下限 ${\bar{θ}}_{i},$ 当且仅当两者相等时,主问题的当前解满足子问题i最优性的要求;否则,应向主问题添加最优性割,具体表示如下:

(A2)

\begin{matrix} \begin{array}{l} \underset{x'_{i}, y'_{i}}{m i n} h_{i} y'_{i} \\ s . t . E_{i} x'_{i} + F_{i} y'_{i} \geq f_{i} - D_{i} \bar{m} \\ x'_{i} \in {0, 1} \end{array}\} \end{matrix}

当主问题的解满足所有子问题的可行性和最优性要求时,子问题不再向主问题添加Benders割,主问题最优解不再变化,迭代过程收敛.

为简化后续推导及实现过程,本研究将 ${\bar{θ}}_{i}$ 视为特殊的耦合变量,最优性子问题松弛为一组可行性约束,得到可行性子问题与最优性子问题的统一表示:

(A3)

\begin{matrix} \begin{array}{l} \underset{x'_{i}, y'_{i}, v_{i}, ξ_{i}, η_{i}}{m i n} (1^{T} v_{i} + ξ_{i} + η_{i}) \\ s . t . h_{i} y'_{i} + ξ_{i} \geq {\bar{θ}}_{i} \\ - h_{i} y'_{i} + η_{i} \geq - {\bar{θ}}_{i} \\ E_{i} x'_{i} + F_{i} y'_{i} + v_{i} \geq f_{i} - D_{i} \bar{m} \\ x'_{i} \in {0, 1} \\ v_{i} \geq 0, ξ_{i} \geq 0, η_{i} \geq 0 \end{array}\} \end{matrix}

式中: $ξ_{i} 、 η_{i}$ 均为非负松弛变量.

根据式(A3),当 $v_{i} 中各元素为 0 时, 主问题的当前解满足可行性要求; 当 ξ_{i} 、 η_{i}$ 均为0时,主问题的当前解满足最优性要求;当且仅当式(A3)最优解为0时,迭代过程收敛.文中式(41)即为式(A3)的简化表示,记为统一原始子问题.

进一步,推导式(42)所示Benders割.统一原始子问题为混合整数线性规划问题,无法对其对偶化生成Benders割.为此,本方法首先引入辅助布尔变量构成的向量 $\tilde{x}'_{i}, x'_{i} 并令等于 \tilde{x}'_{i} . 此时, x'_{i}$ 可视为连续变量,统一原始子问题可表示如下:

(A4)

\begin{array}{l} \underset{x'_{i}, y'_{i}, v'_{i}, \tilde{x}'_{i}}{m i n} 1^{T} v'_{i} \\ s . t . E'_{i} x'_{i} + F'_{i} y'_{i} + v'_{i} \geq f'_{i} - D'_{i} \bar{m}' J_{i} \\ x'_{i} = \tilde{x}'_{i} K_{i} \\ v'_{i} \geq 0 \\ \tilde{x}'_{i} \in {0, 1} \end{array}\}

式中: $J_{i} 、 K_{i}$ 分别为两类约束相应的对偶变量组成的向量.

可将式(A4)表示如下:

(A5)

\begin{matrix} \underset{\tilde{x}'_{i} \in {0, 1}}{m i n} \underset{x'_{i}, y'_{i}, v'_{i} \in O_{i}}{m i n} 1^{T} v'_{i} \end{matrix}

式中: $O_{i} = {E'_{i} x'_{i} + F'_{i} y'_{i} + v'_{i} \geq f'_{i} - D'_{i} \bar{m}', x'_{i} = \tilde{x}'_{i}, v'_{i} \geq 0} .$

对式(A5)内部线性规划问题求对偶,得到如下形式:

(A6)

\underset{\tilde{x}'_{i} \in {0, 1}}{m i n} \underset{(J_{i}, K_{i}) \in N_{i}}{m a x} [{(f'_{i} - D'_{i} \bar{m}')}^{T} J_{i} + {\tilde{x}}_{i}^{' T} K_{i}]

式中: $N_{i} = {E_{i}^{' T} J_{i} + K_{i} = 0, F_{i}^{' T} J_{i} = 0,0 \leq J_{i} \leq 1} .$

根据极大极小不等式,存在如下不等关系:

(A7)

\begin{array}{l} \underset{\tilde{x}'_{i} \in {0, 1}}{m i n} \underset{(J_{i}, K_{i}) \in N_{i}}{m a x} [{(f'_{i} - D'_{i} \bar{m}')}^{T} J_{i} + {\tilde{x}}_{i}^{' T} K_{i}] \geq \\ \underset{(J_{i}, K_{i}) \in N_{i}}{m a x} \underset{\tilde{x}'_{i} \in {0, 1}}{m i n} [{(f'_{i} - D'_{i} \bar{m}')}^{T} J_{i} + {\tilde{x}}_{i}^{' T} K_{i}] \end{array}

考虑到式(A7)中 $\tilde{x}'_{i}$ 中元素均为0-1变量,采用枚举法列举所有可能的0、1组合,可表示为如下形式:

(A8)

\begin{matrix} \underset{\tilde{x}'_{i} \in {0, 1}}{m i n} {\tilde{x}}_{i}^{' T} K_{i} = \underset{L_{i} \in M_{i}}{m a x} 1^{T} L_{i} \end{matrix}

式中: $M_{i} = \{L_{i} \leq 0, L_{i} \leq K_{i}\} .$

因此,式(A6)中右端项可表示为

(A9)

\begin{array}{l} \underset{(J_{i}, K_{i}) \in N_{i}}{m a x} [{(f'_{i} - D'_{i} \bar{m}')}^{T} J_{i} + \underset{\tilde{x}'_{i} \in {0, 1}}{m i n} {\tilde{x}}_{i}^{' T} K_{i}] = \\ \underset{(J_{i}, K_{i}) \in N_{i}}{m a x} [{(f'_{i} - D'_{i} \bar{m}')}^{T} J_{i} + \underset{L_{i} \in M_{i}}{m a x} 1^{T} L_{i}] \end{array}

对式(A9)进一步整理可得到下式,记为统一对偶子问题:

(A10)

\begin{array}{l} F_{D, i}^{*} = \\ \underset{(J_{i}, K_{i}, L_{i}) \in N_{i} ⋃ M_{i}}{m a x} [{(f'_{i} - D'_{i} \bar{m}')}^{T} J_{i} + 1^{T} L_{i}] \end{array}

式中: $F_{D, i}^{*} 为当 J_{i} 和 L_{i} 有最优解 {\bar{J}}_{i} 和 {\bar{L}}_{i} 时 \bar{m}'$ 对应的目标函数值.

由式(A10)容易得到式(42)所示Benders割.

最后,推导式(43)所示Benders割.由于式(A6)中极大极小不等式的引入,统一对偶子问题与统一原始子问题之间存在对偶间隙.式(41)无法排除全部非最优解,为消除对偶间隙需在统一对偶子问题之后求解如下可行性恢复子问题:

(A11)

\begin{array}{l} \begin{matrix} \begin{array}{l} F_{F, i}^{*} = \underset{m', x'_{i}, y'_{i}}{m i n} Δ_{i} (m', \bar{m}') \\ s . t . D'_{i} m' + E_{i} x'_{i} + F_{i} y'_{i} \geq f'_{i} \\ x'_{i} \in {0, 1} \end{array}\} \end{matrix} \end{array}

式中: $F_{F, i}^{*} 为目标函数值; Δ_{i} (m', \bar{m}') 表示 \bar{m}' 与可行域内任意 m'$ 的可行性偏差,计算方式与式(43)一致.

求解式(A11)可行性恢复子问题,当 $F_{F, i}^{*}$ 大于0时,可将式(43)所示Benders割加入主问题以排除非最优解.

附录B

表B1~B3中空白表示未对相应编号线路或管道进行规划.

表B1 情景1供热管道规划容量

Tab.B1 Heating pipeline planning capacity in Case 1

编号	容量/kW	编号	容量/kW
1	345	6	464
2	621	7	464
3	1324	8
4	44	9	173
5	282

新窗口打开| 下载CSV

表B2 情景1天然气管道规划容量

Tab.B2 Natural gas pipeline planning capacity in Case 1

编号	容量/m³	编号	容量/m³
1		7	52
2	37	8
3	5	9	85
4	17	10
5	200	11	43
6	230	12	2

新窗口打开| 下载CSV

表B3 情景1电力线路规划容量

Tab.B3 Power Line planning capacity in Case 1

编号	容量/kW	编号	容量/kW
1	1293	12	1166
2		13	353
3	423	14	442
4	875	15	2166
5	80	16	428
6	1538	17	258
7	2526	18	1609
8	163	19	578
9		20
10	594	21
11	1425

新窗口打开| 下载CSV

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘子旭, 米阳, 卢长坤, 等.

计及需求响应和风力发电消纳的电-热系统低碳优化调度

[J]. 上海交通大学学报, 2023, 57(7): 835-844.

DOI:10.16183/j.cnki.jsjtu.2022.056 [本文引用: 1]

针对热电联产机组存在热电耦合性大、火电机组碳排放量高和负荷侧资源灵活性未充分挖掘等问题,建立计及负荷需求响应和风力发电消纳的电-热系统低碳调度模型.首先,在源侧考虑增加储热和碳捕集设备,同时在负荷侧考虑电价型需求响应和供暖建筑热负荷惯性.然后,以机组运行成本、碳交易成本和弃风惩罚成本总和为目标函数,考虑相关约束,并调用Gurobi求解器进行求解.最后,针对不同案例下系统的经济成本、风力发电消纳量和碳排放速率等方面进行算例对比分析,证明该调度策略在提高系统风力发电消纳能力的同时兼顾经济性和低碳性.

LIU

Zixu

, MI

Yang

, LU

Changkun

, et al.

Low-carbon optimal dispatch of electric-thermal system considering demand response and wind power consumption

[J]. Journal of Shanghai Jiao Tong University, 2023, 57(7): 835-844.