考虑新能源爬坡的风光火耦合系统源荷匹配性分析及容量优化配置

doi:10.16183/j.cnki.jsjtu.2022.260

考虑新能源爬坡的风光火耦合系统源荷匹配性分析及容量优化配置

夏芹芹¹, 罗永捷¹, 王荣茂², 邹尧^,¹, 罗桓桓², 李金灿³, 周念成¹, 王强钢¹

1.重庆大学输配电装备及系统安全与新技术国家重点实验室,重庆 400044

2.国网辽宁省电力有限公司,沈阳 110002

3.广西电网有限责任公司,南宁 530012

Source-Load Matching Analysis and Optimal Planning of Wind-Solar-Thermal Coupled System Considering Renewable Energy Ramps

XIA Qinqin¹, LUO Yongjie¹, WANG Rongmao², ZOU Yao^,¹, LUO Huanhuan², LI Jincan³, ZHOU Niancheng¹, WANG Qianggang¹

1. State Key Laboratory of Power Transmission Equipment and System Security and New Technology, Chongqing University, Chongqing 400044, China

2. State Grid Liaoning Electric Power Supply Co., Ltd., Shenyang 110002, China

3. Guangxi Power Grid Co., Ltd., Nanning 530012, China

通讯作者: 邹尧,博士生;E-mail:zoyire@foxmail.com.

责任编辑: 王历历

收稿日期: 2022-07-5 修回日期: 2022-09-9 接受日期: 2022-12-13

基金资助:

国家重点研发计划项目(2019YFB1505400)

Received: 2022-07-5 Revised: 2022-09-9 Accepted: 2022-12-13

作者简介 About authors

夏芹芹(1992-),博士生,从事电力系统优化相关研究.

摘要

风力发电、光伏发电与火力发电经同一点并网形成耦合系统,是我国北方地区发电侧灵活性调节电源与新能源间高效、低碳协同的一种形式.考虑区域新能源爬坡特性,结合源荷匹配分析,发掘和利用其规律,研究风光火耦合系统的容量优化配置方法,为耦合系统规划提供参考.首先,简述耦合系统运行模式和不确定性处理方法;其次,考虑耦合系统风光互补、爬坡事件和关键负荷特性,选取并提出相关指标用于源荷匹配评价;再次,考虑源荷特性、匹配、成本和收益等约束,建立耦合系统容量优化配置模型;最后,基于辽宁地区实际数据进行算例仿真,得到该地区耦合系统风、光的最优安装容量,并分析上述源荷相关因素与容量优化配置结果之间的相互影响,为新能源最优容量配置提供了参考与建议.

关键词： 风光火耦合系统; 容量优化配置; 源荷匹配; 爬坡事件

Abstract

Wind, photovoltaic, and thermal power generation can form a coupled system through the same grid-connected point, which is a high coordination and low-carbon approach of renewable energy and flexible regulating power source at generation side in northern China. By considering renewable energy ramps and source-load matching analysis, this paper studies the optimal capacity planning of a wind-solar-thermal coupled system to provide reference for coupled system planning. First, the operation model and the uncertainty method of coupled system are briefly described. Then, considering the wind-solar complementary, ramp events, and critical load characteristics, relevant indices are selected and proposed for source-load matching evaluation. After that, considering the constraints of source-load characteristics, matching, and cost, an optimal capacity planning model of wind-solar-thermal coupled system is established. Finally, based on the actual data in Liaoning Province, a case study is conducted to acquire the optimal capacity of the wind and solar generation in the area, and the interaction between the source-load relevant indices and the planning results is analyzed, which provides reference and suggestion for the optimal capacity planning of renewable energy generation.

Keywords： wind-solar-thermal coupled system; optimal capacity planning; source-load matching; ramp event

PDF (3526KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

夏芹芹, 罗永捷, 王荣茂, 邹尧, 罗桓桓, 李金灿, 周念成, 王强钢. 考虑新能源爬坡的风光火耦合系统源荷匹配性分析及容量优化配置[J]. 上海交通大学学报, 2024, 58(1): 69-81 doi:10.16183/j.cnki.jsjtu.2022.260

XIA Qinqin, LUO Yongjie, WANG Rongmao, ZOU Yao, LUO Huanhuan, LI Jincan, ZHOU Niancheng, WANG Qianggang. Source-Load Matching Analysis and Optimal Planning of Wind-Solar-Thermal Coupled System Considering Renewable Energy Ramps[J]. Journal of Shanghai Jiaotong University, 2024, 58(1): 69-81 doi:10.16183/j.cnki.jsjtu.2022.260

当前,国务院出台关于碳达峰、碳中和的重大战略决策^[1-2],全面推进风力发电(风电)、光伏发电(光伏)大规模开发和高质量发展,推动建立风、光互补调节的新能源发电基地.国家发展改革委员会和国家能源局指导相关企事业单位积极探索“风光水火储一体化”实施,以提升各类能源互补协调能力^[3].因此,研究风电、光伏的高效利用对推动新能源高质量发展、能源互补协调、降低火电机组碳排放具有现实意义.

然而,风光出力波动性和不确定性给电力系统带来挑战.一方面,风光出力波动性表现在预测与实际出力的误差,这些误差需要电力系统的可控灵活资源进行调控,如果调控能力不足可能引发弃风弃光或供电不足的问题^[4];另一方面,风光出力波动性也表现在短时间内输出功率发生大幅度单方向变化,即爬坡事件^[5].风光爬坡事件主要与区域气象资源有关^[6-7].爬坡事件可能导致电力系统难以消纳新能源,并可能威胁系统安全运行.因此,研究风电、光伏爬坡事件,减少其影响是新能源发电研究的重要课题之一.

风光不确定性首先可通过同地区的风光互补和源荷匹配解决.文献[8]中提出描述风光出力与负荷贴近程度的负荷匹配和互补指标,对新能源互补进行评价;文献[9]中考虑风光2种新能源之间的相关性,提出大规模风光互补的多目标电网扩展规划方法;文献[10]中针对风光互补发电系统,提出一种改进的优化规模确定方法,以实现注入电网的功率波动更小的目标.

除风光互补和源荷匹配外,风电、光伏不确定性主要由电力系统的可控灵活性发电资源进行消纳.在我国北方地区,火力发电(火电)是发电侧主要灵活性资源^[11].当前,通过机组改造和政策支持,火电已具备更强的调控能力以更好地消纳新能源^[12].与仅具备常规调峰(RPR)能力的机组相比,具备深度调峰(DPR)能力的火电机组能够低于正常最小出力运行^[13],以提供更多调峰能力.此外,我国东北地区已有调峰辅助服务政策,使火电可通过该服务获得额外利益^[14].

火电与新能源的配合可采用耦合系统的形式.耦合系统是一种将物理距离较近的新能源和火电机组整合组成的集成系统.因其通过同一并网点连接到主电网,对外可视作单个电源由调度部门进行调控,系统运行者根据总出力对其内部电源出力进行分配,以提高各电源的协同性,并通过辅助服务获得更多经济效益.文献[15]中考虑新能源与火电耦合系统的耦合机制,建立多维协同性能评价体系,并提出耦合潜力辨识方法,验证耦合系统在电源协同互补方面的优势.文献[16]中提出一种通过阶梯式爬坡率进行表征的火电机组深度调峰运行模型,应用于含风电和火电耦合系统的优化调度模型中,并通过仿真验证含风电和火电的耦合系统中,通过充分挖掘火电的深度调峰特性可提高可再生能源的利用率.

在新能源与常规电源耦合的规划方面,相关研究主要考虑综合能源系统或电源打捆的形式.文献[17]中针对基于冷热电联供系统耦合的电力、天然气区域综合能源系统,采用多阶段规划和多场景分析,获得线路、管网规划及冷热电联供系统的定容选址方案.文献[18]中构建了一个考虑可靠性与成本的多目标协调电-气耦合系统容量规划模型,以实现发电机组与储能装置的选址定容.文献[19]中提出一种基于时序运行模拟的风火打捆容量最优配比整定方法,对比大范围区域中不同风火配比下的风电消纳能力及运行经济性数据,给出兼顾环保性、安全性与经济性的风火配比.文献[20]中以保证输电工程的安全运行为目标,构建了一个考虑大区域新能源穿透功率极限、新能源出力反调峰及大波动风险的区域风光火打捆多目标优化配置模型.

总结上述文献可知,目前已有的相关研究主要集中在多能源耦合系统容量规划或发电侧大范围新能源与传统电源打捆外送的宏观层面容量规划,缺少针对发电侧含风、光、火且距离较近的多电源耦合系统的精细化源荷协同配合分析,缺少考虑风电、光伏爬坡特性和源荷匹配特性与耦合系统的相互影响,无法精确反映风光火资源在耦合系统内部电源间、耦合系统和外部负荷需求间的协同作用效果.此外,未有研究针对给定火电机组如何充分挖掘火电调峰能力及利用源荷特性,合理配置风电、光伏容量,组成高效协同风光火耦合系统作定量分析.

针对上述不足,以含风电、光伏、火电机组的耦合系统为基础,考虑新能源爬坡特性和负荷关键指标,结合相关文件中控制新增火电、加快现役机组灵活性改造、推动火电向基础保障性和调节性电源转型的政策导向^[1],研究在已有火电机组的情况下,风电、光伏的容量优化配置方法.首先,分析风光火耦合系统的运行模式,对相关不确定性变量进行表征;其次,提取风电、光伏及其耦合后的年爬坡事件总发生时间,结合关键负荷特性指标进行源荷匹配性评价;再次,以综合收益最优为目标,建立考虑源荷特性、源荷匹配和多种成本、收益的不确定性风光火耦合系统容量优化配置模型;最后,通过我国辽宁地区的实际算例,验证所提容量优化配置模型的有效性,并分析容量优化配置结果、爬坡事件及源荷匹配性的影响因素,为耦合系统规划人员提供不同情形中风、光装机容量配置的参考.本文的创新性主要在于:针对发电侧风光火耦合系统,充分考虑源荷关键特性,确定已有火电机组如何配置风电、光伏的最优装机容量,解决发电基地工程实际中电源协调配置问题;针对区域特点,从源、荷两个方面挖掘和利用风光火耦合系统的规律,为新能源最优容量配置提供参考与提升建议.

1 风光火耦合系统的不确定性建模及其关键特征分析

1.1 风光火耦合系统的运行模式

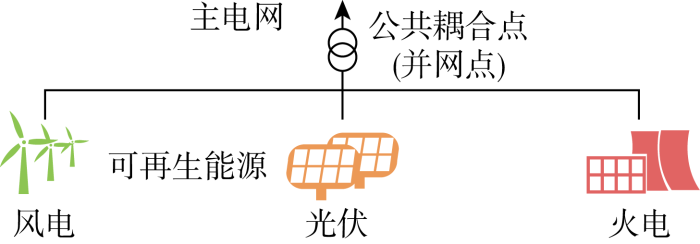
风光火耦合系统由物理距离相近的火电、风电和光伏电源组成,并通过同一点接入主电网,其主要结构如图1所示.风光火耦合系统运行模式为:①电力系统调度部门综合考虑风、光、负荷预测数据和火电特性,制订负荷需求计划曲线;②耦合系统以自身经济性最优原则,对外根据负荷需求计划曲线发电,对内协调各电源出力;③耦合系统可从外部电力系统购买一定电量,也可进行一定的弃风、弃光;④耦合系统可参与调峰辅助服务获得收益.在容量配置阶段,调度部门可与耦合系统进行配合,针对性调整负荷需求曲线以实现源侧和负荷侧的匹配及双向高效利用.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 风光火耦合系统示意图

Fig.1 Diagram of wind-solar-thermal coupled system

1.2 不确定性的表征

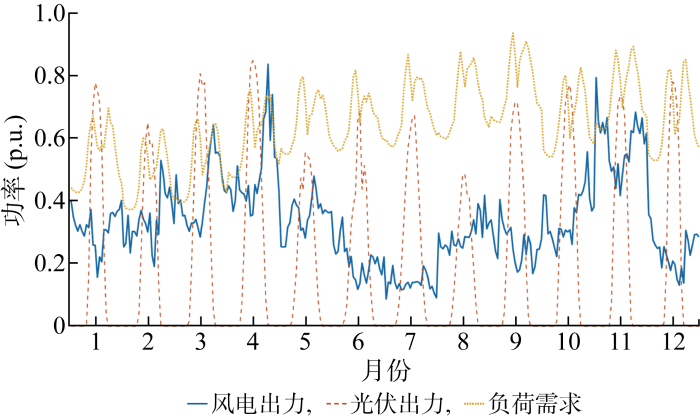
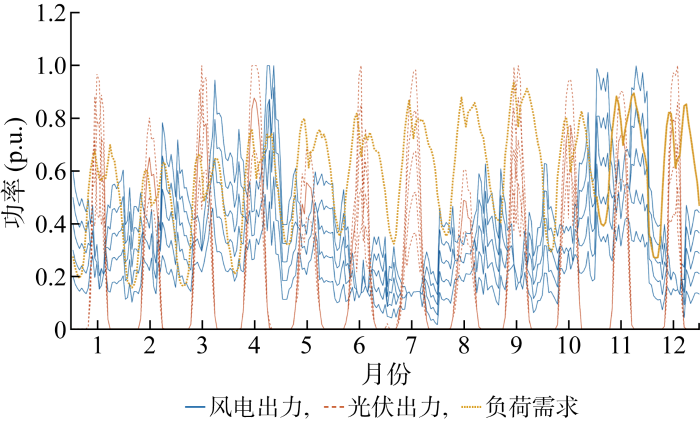
本文考虑的不确定性变量包括风电、光伏发电功率和负荷需求,采用场景法表征不确定性.场景法的主要思想如下:①对每种类型的相互独立不确定性变量或具有相关性的不确定性变量,根据其相应概率密度函数或联合概率密度函数,获得代表性场景及场景的相应概率^[21-22];②根据不同类型的相互独立不确定性变量概率密度函数及具有相关性的不确定性变量联合概率密度函数,通过场景生成、聚合和削减,得到多个包含所有类型不确定性变量的场景及其相应概率,以此将不确定性问题转换为多个确定性问题;由于得到的不确定性变量场景概率之和为1,最终可通过期望值体现在待求问题中^[21].为表征风、光出力和负荷的不确定性,采用场景法的步骤如下:通过风、光发电功率和负荷1年12个月的月度数据,采用削减方法,每月生成一条具有代表性的典型日每小时期望风、光出力和负荷需求曲线,如图2所示.考虑风、光出力、负荷需求之间相互独立,采用正态分布表征每小时实际风、光出力、负荷需求与期望值的误差,其中风、光出力、负荷需求对应正态分布的均值为其每小时期望值,即图2中的值,方差与期望值和最大出力有关^[16].使用上文所述场景法获得同时考虑风、光出力和负荷整体曲线的代表性场景及其相应概率,用于耦合系统容量优化配置仿真,每小时最终场景数为5个,如图3所示.使用MATLAB 进行场景生成和聚合,GAMS软件提供的Scenred^[23]模块用于场景削减.结合12个典型日场景的风、光出力、负荷曲线及每个典型日中每个时刻的5个场景计算,每种不确定性变量的总场景数量为1440个,根据文献[21]中的研究,场景削减后的精度已经过验证,故综合考虑计算量与容量优化配置的目的,经削减后的场景数量能够满足精度需求.场景法的更多详情可参考文献[21 ⇓-23].

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 每月典型日的期望风电、光伏出力和负荷需求曲线

Fig.2 Typical daily expected profiles of wind output, photovoltaic output, and load demand in each month

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 场景法得到的每月典型日的风电、光伏出力和负荷需求具体场景

Fig.3 Typical daily specific scenarios of wind output, photovoltaic output, and load demand in each month obtained by scenario method

1.3 风电/光伏的爬坡事件分析

爬坡事件可表征风光出力的大尺度波动,是分析耦合系统所在地区风光资源,研究其出力互补性的重要手段.根据最优爬坡时段,同时考虑不确定性,对每个具体场景的风电、光伏及其耦合后的爬坡事件进行辨识分析.

目前对于爬坡事件主要有4种定义形式^[6],其核心内容均为表征给定观测时间段内功率变化是否超过阈值.在给定火电装机容量配置风电、光伏装机容量的耦合系统中,因灵活性调节资源固定,所关心的爬坡事件为观测时间内新能源发电功率在单位时间内是否超过给定的实际数值.因此,风电、光伏爬坡事件的表征如下:给定时间和功率的序列{(t₁,P₁), (t₂,P₂), …, (t_n,P_n)},如果在时间段[t_s,t_e]内,存在

(1)(P_e-P_s)/(t_e-t_s)>|R_a|

则认为在起始时刻t_s至结束时刻t_e时间段内发生爬坡事件.式中:P_e、P_s分别为t_e、t_s时刻的功率;|R_a| 为爬坡率阈值,当(P_e-P_s)/(t_e-t_s)>R_a时,发生上爬坡;当(P_e-P_s)/(t_e-t_s)<-R_a时,发生下爬坡.

利用式(1)可判别爬坡事件,但无法确定爬坡事件的起始和持续时间,可能造成重复统计.因此,还需确定最优爬坡时段,即若对于时间段[t_s,t_e],满足式(1),而对任意时刻t'_s、t'_e,且t'_s<t_s<t_e<t'_e,[t'_s,t_e]和[t_s, t'_e]均不满足式(1),则称时间段[t_s, t_e]为最优爬坡时段.最优爬坡时段可通过求解如下动态规划问题对时间段评分确定^[24]:

(2)J(t_i, t_j)=

\underset{t_{i} \leq t_{k} \leq t_{j}}{m a x}

W(t_i,t_k)+J(t_k₊₁,t_j)

式中:J(t_i,t_j)是在时间间隔[t_i,t_j]内获得的最大分数,其值可通过t_j-t_i个子问题的最大值计算;W(t_i,t_k)是时间间隔[t_i,t_k]的权重,其值与发生爬坡事件的时间段长度有关,时间段长度越长,其值越大.更多关于最优爬坡时段的计算可参考文献[24].

1.4 负荷的关键特征选取

风光火耦合系统的供电能力需要与耦合点外部的负荷需求相匹配才能够更好地发挥耦合系统中发电资源的作用.因耦合系统同时为本地负荷和上级电力系统供电,针对其负荷需求曲线的制订虽具有一定灵活调整空间,但负荷需求曲线的部分特性仍主要与耦合系统所在地区有关,难以改变.针对上述问题,从我国常用负荷特性指标^[25]中,选择年最大负荷、年峰谷差率及其对风光火耦合系统容量优化配置的结果影响进行研究.这些指标可随负荷需求曲线的制订直接改变,且在耦合系统容量优化配置研究中具有代表性.其中,年最大负荷涉及耦合系统最大供电能力,年峰谷差率与耦合系统调节能力相关.

1.5 源荷匹配性评价

为分析耦合系统所在区域的源荷耦合程度及影响因素,选取已有研究中的2个典型源荷评价指标,再针对其局限性提出额外2个源荷评价指标,共同对风光火耦合系统源荷匹配性进行评价.其中,选取的指标及其计算方法如下:

(1) 源荷追踪系数^[26].表征风、光出力曲线与负荷需求曲线的贴合程度,其值越大表示贴合程度越高.其公式表示为

(3)I₁=

\frac{\overset{T_{m a x}}{\sum_{t = 1}} (P_{L} (t) - {\bar{P}}_{L}) [P_{W T} (t) + P_{P V} (t) - ({\bar{P}}_{W T} + {\bar{P}}_{P V})]}{\sqrt{\overset{T_{m a x}}{\sum_{t = 1}} (P_{L} (t) - {\bar{P}}_{L})^{2}} \sqrt{\overset{T_{m a x}}{\sum_{t = 1}} [P_{W T} (t) + P_{P V} (t) - ({\bar{P}}_{W T} + {\bar{P}}_{P V} {)]}^{2}}}

式中:P_L(t)、P_WT(t)和P_PV(t)分别为负荷需求、风电出力和光伏出力在t时刻的值; ${\bar{P}}_{L}$ 、 ${\bar{P}}_{W T}$ 和 ${\bar{P}}_{P V}$ 分别为负荷需求、风电出力和光伏出力平均值;T_max为总计算时刻.

(2) 源荷变化系数^[26].表征风、光出力曲线与负荷需求曲线差值相对于其平均值的波动水平,其值越大表示曲线整体较平均值的波动水平越大.其公式表示为

(4)$\begin{aligned} I_{2}= & \left\{\frac { 1 } { T _ { \operatorname { m a x } } } \sum _ { t = 1 } ^ { T _ { \operatorname { m a x } } } \left[P_{\mathrm{L}}(t)-\left(P_{\mathrm{WT}}(t)+P_{\mathrm{PV}}(t)\right)-\right.\right. \\ & \left.\left.\left(\bar{P}_{\mathrm{L}}-\left(\bar{P}_{\mathrm{wT}}+\bar{P}_{\mathrm{PV}}\right)\right)\right]^{2}\right\}^{1 / 2} \end{aligned}$

上述指标主要表征源荷匹配后曲线的整体趋势,无法反映源荷匹配后曲线在相邻时刻的波动水平以分析火电机组爬坡压力和调节能力.因此,提出源荷平均绝对值变化率和源荷动态时间弯曲距离指标,作为上述指标的补充,具体如下:

(1) 源荷平均绝对值变化率.表征风、光出力曲线与负荷需求曲线差值在相邻时刻的波动率,其值越大表示曲线相邻时刻波动越大.其公式为

(5)I₃=

\frac{1}{T_{m a x}} \overset{T_{m a x} - 1}{\sum_{t = 1}}

|P_L(t+1)-(P_WT(t+1)+P_PV(t+1))-P_L(t)-(P_WT(t)+P_PV(t))|

(2) 源荷动态时间弯曲距离.表征风、光出力曲线与负荷需求曲线形态的相似程度,其值越小表示两条曲线越相似^[27],即相邻时刻曲线差值变化越小.该指标通过迭代计算为

(6)

\begin{array}{l} L_{i, j} = m i n {L_{i, j - 1}, L_{i - 1, j}, L_{i - 1, j - 1}} + d_{i, j} \\ d_{i, j} = \sqrt{(P_{W T} (i) + P_{P V} (i) - P_{L} {(j))}^{2}} \\ I_{4} = L_{T_{m a x}, T_{m a x}} \\ i, j = 1,2, \dots, T_{m a x} \end{array}\}

式中:L_i_,_j为i时刻和j时刻的动态时间弯曲距离,L_0,0=0,L_0,_j=L_i_,0=+∞;d_i_,_j为i时刻和j时刻风光出力与负荷需求的欧氏距离;I₄为源荷动态时间弯曲距离.

所选取的源荷匹配评价指标具有显著针对性,从源荷曲线数值差异、整体波动、相邻时间波动和曲线时序相似度4个具体方面直观反映源荷匹配中的不同关键特征.这些评价指标均可独立使用,不依赖其指标之间的协助判断,不受指标之间相关性的影响.

2 风光火耦合发电系统容量优化配置模型

从耦合系统运营者角度,风光火耦合系统容量规划目标是最大化经济效益,结合上文所述提倡减少新增火电机组的原则,风光火耦合系统容量配置主要考虑我国东北缺少水电地区中已投产的火电机组配置风光机组容量的场景,并以最大化经济效益为目标.

2.1 目标函数

考虑风光出力和负荷需求的不确定性,建立一个两阶段不确定性风光火耦合系统容量规划模型,在考虑耦合系统发电收益、调峰辅助服务收益、投资成本、运行维护成本和污染排放成本的条件下,实现年化总收入(F_A)最大,目标函数如下:

(7)max F_A=F_GI-(F_OP_,_d+F_OP_,_u)-(F_TE_,_d+F_TE_,_u)+F_WTI_,_u+F_PVI_,_u-F_WTC_,_u-F_PVC_,_u-F_gs_,_u

目标函数含有两个决策阶段,第1阶段使用下标d表示,第2阶段使用下标u表示.其中第1阶段是确定性的,该阶段的决策变量在不确定性被考虑前就已被确定;第2阶段是不确定性的,该阶段的决策变量是实时可变动资源对不确定因素在第1阶段中产生影响后进行的修正.使用不同场景法表征模型中的不确定性因素,并在最终通过计算期望值将第2阶段中的场景由不确定性转化为确定性.式(7)中各部分计算的均为年化收益期望值.

式(7)中F_GI为火电机组售电收益,与耦合系统参与调峰辅助服务的情况有关.根据东北电力市场辅助服务相关规定^[14],当运行的火电机组发电功率小于补偿基准时,可获调峰辅助服务补偿.风光火耦合系统可充分利用风光资源获得调峰辅助服务补偿,取得竞争优势.火电机组的发电收益由下式计算:

(8)μ_TH(t_M)=

\overset{N_{T H}}{\sum_{g = 1}}

C_TH(t_M)(P_TH(g,t_M)+

\overset{S}{\sum_{s = 1}}

p(t_M,s)P_THR(g,t_M,s))/

\overset{N_{T H}}{\sum_{g = 1}} P_{T H}^{m a x}

(g)

(9)F_GI=

\overset{12}{\sum_{M = 1}}

N_d(M)

\overset{T}{\sum_{t_{M} = 1}} \overset{N_{T H}}{\sum_{g = 1}}

F_GI(g,t_M)

p_{TH_EXP}(g,t_M)=P_TH(g,t_M)+ $\overset{S}{\sum_{s = 1}}$ p(t_M,s)P_THR(g,t_M,s)

(10)F_GI(g,t_M)=

\{\begin{array}{l} C_{0} P_{T H_E X P} (g, t_{M}), μ_{1} < μ_{T H} (t_{M}) \leq 1 \\ C_{0} P_{T H_E X P} (g, t_{M}) + \\ C_{1} (μ_{1} P_{T H}^{m a x} (g) - P_{T H_E X P} (g, t_{M})), \\ μ_{2} < μ_{T H} (t_{M}) \leq μ_{1} \\ C_{0} P_{T H_E X P} (g, t_{M}) + \\ C_{2} (μ_{1} P_{T H}^{m a x} (g) - P_{T H_E X P} (g, t_{M})), \\ 0 \leq μ_{T H} (t_{M}) \leq μ_{2} \end{array}

式中:μ_TH(t_M)为所有火电机组当前发电功率与最大发电功率的比值;N_TH为耦合系统中火电机组总台数;P_TH(g,t_M)为第一决策阶段第M个月典型日t时刻火电g的发电功率,该部分根据风光发电功率和负荷需求的预测值事先制定;P_THR(g,t_M,s)为第二决策阶段火电g在场景s的发电功率,该部分为火电的实时灵活性调节资源针对风光和负荷波动的平衡;p(t_M,s)为场景s的概率; $P_{T H}^{m a x}$ (g)为火电g的最大发电功率;T为每日最大时刻;S为最大场景数;N_d(M)为第M个月的时间;F_GI(g,t_M)为t时刻火电g根据所处辅助服务补偿基准确定的售电收益;C₀、C₁、C₂分别为不同补偿基准下的售电价格;μ₁、μ₂为不同补偿基准对应的比值;P_{TH_EXP}(g,t_M)为临时变量,可定义t为时刻火电g的期望发电功率.

式(7)中F_OP,d+F_OP,u为火电机组运行成本,考虑了火电机组常规调峰和深度调峰两种状态.常规调峰状态运行费用考虑了机组单位发电量的煤耗和维护费用;深度调峰状态由于火电机组工况较差,运行费用还需考虑此状态的额外损耗费用,运行成本通过下式计算:

(11)$\begin{array}{l} F_{\mathrm{OP}, \mathrm{d}}+F_{\mathrm{OP}, \mathrm{u}}=\sum_{M=1}^{12} N_{\mathrm{d}}(M) \sum_{t_{M}=1}^{T} \sum_{g=1}^{N_{\mathrm{TH}}}\left[f_{\mathrm{OP} \_\mathrm{RPR}}^{g} \times\right. \\ \left(P_{\mathrm{TH}}\left(g, t_{M}\right)+\sum_{s=1}^{S} p\left(t_{M}, s\right) P_{\mathrm{THR}}\left(g, t_{M}, s\right)\right) \times \\ \beta_{\mathrm{RPR}}\left(g, t_{M}, s\right)+f_{\mathrm{OP}_{-} \mathrm{DPR}}^{g}\left(P_{\mathrm{TH}}\left(g, t_{M}\right)+\right. \\ \left.\left.\sum_{s=1}^{S} p\left(t_{M}, s\right) P_{\mathrm{THR}}\left(g, t_{M}, s\right)\right) \beta_{\mathrm{DPR}}\left(g, t_{M}, s\right)\right] \end{array}$

式中:β_RPR(g,t_M,s)和β_DPR(g,t_M,s)分别表示火电g是否处于常规调峰和深度调峰状态的0或1变量; $f_{O P_R P R}^{g}$ (·)和 $f_{O P_D P R}^{g}$ (·)分别为火电机组在常规调峰和深度调峰状态运行费用与发电功率关系的函数,通过曲线拟合获得^[28],即

(12)

\begin{array}{l} f_{O P_R P R}^{g} (p_{T H_E X P} (g)) = \\ a_{O P} P_{T H_E X P}^{2} (g) + b_{O P} P_{T H_E X P} (g) + c_{O P} \\ f_{O P_D P R}^{g} (P_{T H_E X P} (g)) = \\ a_{O P} P_{T H_E X P}^{2} (g) + b_{O P} P_{T H_E X P} (g) + \\ c_{O P} + a_{D P R} P_{T H_E X P} (g) + b_{D P R} \end{array}\}

式中:a_OP、b_OP、c_OP、a_DPR、b_DPR为拟合函数中的计算系数.

式(7)中F_TE,d+F_TE,u为火电机组污染排放处理费用:

(13)$\begin{aligned} F_{\mathrm{TE}, \mathrm{d}}+F_{\mathrm{TE}, \mathrm{u}}= & \sum_{M=1}^{12} N_{\mathrm{d}}(M) \sum_{t_{M}=1}^{T} \sum_{g=1}^{N_{\mathrm{TH}}} \sum_{n=1}^{N} C_{\mathrm{TE}}(n) \times \\ & \frac{\rho_{\mathrm{TE}}(n)}{\tau_{\mathrm{TE}}(n)}\left(P_{\mathrm{TH}}\left(g, t_{M}\right)+\right. \\ & \left.\sum_{s=1}^{S} p\left(t_{M}, s\right) P_{\mathrm{THR}}\left(g, t_{M}, s\right)\right) \end{aligned}$

式中:C_TE(n)、ρ_TE(n)、τ_TE(n)分别为火电机组第n种污染物的单位当量处理费用、单位发电量排放系数和污染当量值;N为污染物总数,考虑的污染物为烟尘、SO₂和NO_x.

式(7)中F_WTI,u、F_PVI,u分别为风电、光伏的售电收益:

(14)F_WTI,u=

\overset{12}{\sum_{M = 1}}

N_d(M)

\overset{T}{\sum_{t_{M} = 1}}

C_WT×

\overset{S}{\sum_{s = 1}}

p(t_M,s)P_WT(t_M,s)

(15)F_PVI,u=

\overset{12}{\sum_{M = 1}}

N_d(M)

\overset{T}{\sum_{t_{M} = 1}}

C_PV×

\overset{S}{\sum_{s = 1}}

p(t_M,s)P_PV(t_M,s)

式中:P_WT(t_M,s)、P_PV(t_M,s)分别为考虑不同场景不确定性波动的风、光发电功率;C_WT、C_PV分别为风、光单位发电量售电收益.

式(7)中F_WTC,u、F_PVC,u分别为风、光的投资和维护成本.风电、光伏在寿命周期内维护成本相对固定且费用较低,同投资成本类似,可折算至单位装机容量进行表征^[29]:

(16)F_WTC,u=

\frac{r {(1 + r)}^{y_{W T}}}{r {(1 + r)}^{y_{W T}} - 1}

S_WTI_WT

(17)F_PVC,u=

\frac{r {(1 + r)}^{y_{P V}}}{r {(1 + r)}^{y_{P V}} - 1}

S_PVI_PV

式中:S_WT、S_PV分别为风电、光伏的规划装机容量;I_WT、I_PV分别为风电、光伏单位装机容量的投资和维护成本;y_WT、y_PV分别为风电、光伏的使用年限;r为年利率.

式(7)中F_gs,u为耦合系统无法满足负荷需求时从外部电力系统的购电费用:

(18)F_gs,u=

\overset{12}{\sum_{M = 1}}

N_d(M)

\overset{T}{\sum_{t_{M} = 1}}

C_gs

\overset{S}{\sum_{s = 1}}

p(t_M,s)P_gs(t_M,s)

式中:C_gs为从外部电力系统购买单位电量的费用;P_gs(t_M,s)为不同场景下耦合系统从外部电力系统购买的发电功率,即耦合系统发电功率缺额.

2.2 约束条件

风光火耦合系统容量优化配置的约束条件包括功率平衡约束,电源相关发电约束,以及源荷匹配限制爬坡事件约束.约束条件针对每个典型日独立列写,不同月份典型日之间的约束无关联.

2.2.1 功率平衡约束

功率平衡约束反映耦合系统内部的发电功率应满足耦合点的负荷需求:

(19)

\overset{N_{T H}}{\sum_{g = 1}}

(P_TH(g,t)+P_THR(g,t,s))+P_PV(t,s)+P_WT(t,s)=P_L(t,s)-P_gs(t,s)

P_gs(t,s)应小于该时刻负荷需求预测值P_{L_pre}(t)的一定比例,即P_gs(t,s)≤φ_LP_{L_pre}(t),其中φ_L为比例系数.

2.2.2 火电机组发电约束

火电机组发电约束主要包括运行状态约束和爬坡约束:

(20)

\begin{array}{l} β_{R P R} (g, t, s) + β_{D P R} (g, t, s) = 1 \\ β_{R P R} (g, t, s) P_{T H_R P R}^{m i n} (g) \leq \\ P_{T H} (g, t) + P_{T H R} (g, t, s) \leq \\ β_{R P R} (g, t, s) P_{T H}^{m a x} (g) \\ β_{D P R} (g, t, s) P_{T H_D P R}^{m i n} (g) \leq \\ P_{T H} (g, t) + P_{T H R} (g, t, s) \leq \\ β_{D P R} (g, t, s) P_{T H_R P R}^{m i n} (g) \\ t P_{r a m p}^{d o w n} (g) \leq (P_{T H} (g, t + 1) + \\ P_{T H R} (g, t + 1, s)) - \\ (P_{T H} (g, t) + P_{T H R} (g, t, s)) \leq \\ t P_{r a m p}^{u p} (g) \end{array}\}

式中:第1个公式表示火电机组在t时刻仅可处于常规调峰或深度调峰状态;第2、3个公式表示火电机组在2种状态时的出力范围,其中 $P_{T H_R P R}^{m i n}$ (g)和 $P_{T H_D P R}^{m i n}$ (g)分别为火电机组g在2种状态的最小出力;第4个公式为爬坡率约束,其中 $P_{r a m p}^{u p}$ (g)和 $P_{r a m p}^{d o w n}$ (g)分别为火电机组g的上爬坡率和下爬坡率.

火电机组的实时灵活性调节资源P_THR(g,t,s)会受到火电机组的爬坡率,当前出力状态、出力范围限制:

(21)

\begin{array}{l} P_{T H}^{s u p} (g, t) \leq P_{T H}^{m a x} (g) - P_{T H} (g, t) \\ P_{T H}^{s u p} (g, t) \leq t P_{r a m p}^{u p} (g) \\ P_{T H}^{s d n} (g, t) \leq P_{T H} (g, t) - P_{T H_D P R}^{m i n} (g) \\ P_{T H}^{s d n} (g, t) \leq t P_{r a m p}^{d o w n} (g) \\ P_{T H}^{s d n} (g, t) \leq P^{T H R} (g, t, s) \leq P_{T H}^{s u p} (g, t) \\ P_{T H}^{s u p} (g, t), P_{T H}^{s d n} (g, t) \geq 0 \end{array}\}

式中: $P_{T H}^{s u p}$ (g,t)和 $P_{T H}^{s d n}$ (g,t)分别为火电机组g的灵活性调节资源上下限.

2.2.3 风电/光伏发电约束

耦合系统中的风电和光伏在发电时可通过降低利用率以满足功率平衡:

(22)

\begin{array}{l} u_{W T} P_{W T_r e} (t, s) S_{W T} \leq P_{W T} (t, s) \leq \\ P_{W T_r e} (t, s) S_{W T} \\ u_{P V} P_{P V_r e} (t, s) S_{P V} \leq P_{P V} (t, s) \leq \\ P_{P V_r e} (t, s) S_{P V} \\ 0 \leq P_{W T_r e} (t, s) \leq 1, 0 \leq P_{P V_r e} (t, s) \leq 1 \\ 0 \leq S_{W T} \leq S_{W T}^{m a x}, 0 \leq S_{P V} \leq S_{P V}^{m a x} \end{array}\}

式中:P_{WT_re}(t,s)、P_{PV_re}(t,s)分别为风电和光伏在t时刻场景s的实时出力标幺值;u_WT、u_PV分别为风电和光伏的利用率限值;S_WT、S_PV分别为风电、光伏装机容量; $S_{W T}^{m a x}$ 、 $S_{P V}^{m a x}$ 分别为相应最大值.

2.2.4 风光爬坡事件限制约束

为限制耦合系统中的风电和光伏安装容量过大引起爬坡事件增加,利用源荷耦合对相邻时刻的净功率差进行限制:

(23)$\begin{array}{l} \mid\left(P_{\mathrm{WT}}\left(t^{\prime \prime}, s\right)+P_{\mathrm{PV}}\left(t^{\prime \prime}, s\right)-P_{\mathrm{L}}\left(t^{\prime \prime}, s\right)\right)- \\ \quad\left(P_{\mathrm{WT}}\left(t^{\prime \prime}, s\right)+P_{\mathrm{PV}}\left(t^{\prime}, s\right)-P_{\mathrm{L}}\left(t^{\prime}, s\right)\right) \mid / \\ \quad\left(t^{\prime \prime}-t^{\prime}\right) \geqslant \sigma_{\mathrm{R}} \end{array}$

式中:1≤t'<t″≤T;σ_R为相邻时刻净功率差限值.

2.3 决策变量

建立的风光火耦合系统容量优化配置模型中包括第1阶段和第2阶段决策变量.第1阶段决策变量包括火电确定性发电功率P_TH(g,t),风电、光伏的装机容量S_PV、S_WT.第2阶段决策变量包括火电灵活性发电功率P_THR(g,t,s),风电、光伏的实时出力P_WT(t,s)、P_PV(t,s),耦合系统供电缺额P_gs(t,s).

3 算例分析

3.1 算例基础数据

以我国辽宁某区域具备形成图1所示耦合系统条件的2台600 MW火电机组为算例进行风光火耦合系统容量优化配置仿真.风、光出力及负荷需求曲线使用图3所示的12个典型日场景及其相应概率,作为容量优化配置模型的输入之一.本算例的调峰辅助服务相关政策参考文献[14],火电机组的污染排放相关参数参考文献[16],火电机组常规运行状态和深度调峰状态的最小出力为机组容量的50%和30%,爬坡率分别为9 MW/min和6 MW/min;源荷耦合后相邻时刻的净功率差限值σ_R为 100 MW;风电、光伏的装机与运维综合成本分别为 1.6158×10⁷ 元/MW和4.001×10⁶ 元/MW,售电价格分别为850元/(MW·h)和740元/(MW·h),寿命分别为30 a和25 a;年利率为5%.为避免耦合系统中电源因各类情况无法供电可能导致的较大负荷缺额,最大负荷值仅考虑略大于或等于火电机组总装机容量的情形.

建立的风光火耦合系统容量优化配置模型为混合整数非线性规划模型.为方便求解,通过分段线性化和大M法将优化模型中整数变量松弛后^[30]使用商业求解器Gurobi^[31]进行求解,展示的结果均为期望值.

3.2 容量优化配置结果的影响因素分析

为研究负荷需求曲线最大值对容量优化配置结果的影响,基于区域原始负荷需求曲线,结合1.4节中选取的两个负荷特性指标,考虑该区域的源荷特性,调整负荷需求曲线,研究上述因素对耦合系统容量优化配置结果的影响,结果如表1所示.需要注意的是,负荷曲线基于源荷特性仅作略微调整,保证容量优化配置有解且符合实际情况.

表1 不同情形风光火耦合系统容量优化配置结果

Tab.1 Optimal planning results of wind-solar-thermal coupled system in different cases

输入				输出
情形	最大负荷/MW	峰谷差率	新能源最小利用率/%	风电安装容量/MW	光伏安装容量/MW	新能源渗透率/%	总综合收益/元
1	1400	0.6	99	357.01	263.58	34.09	1.8987×10⁹
2	1400	0.6	95	372.05	274.68	35.02	1.9343×10⁹
3	1400	0.6	90	392.71	289.94	36.26	1.9824×10⁹
4	1400	0.6	85	415.82	306.99	37.59	2.0320×10⁹
5	1400	0.55	99	473.6	293.32	38.99	2.1385×10⁹
6	1400	0.55	90	520.96	322.65	41.28	2.2383×10⁹
7	1300	0.6	99	295.27	230.08	30.44	1.7672×10⁹
8	1300	0.6	90	324.8	253.09	32.50	1.8290×10⁹
9	1300	0.55	99	403.57	260.17	35.61	1.9960×10⁹
10	1300	0.55	90	443.93	286.19	37.83	2.0780×10⁹
11	1200	0.6	99	226.71	199.02	26.19	1.6047×10⁹

新窗口打开| 下载CSV

在峰谷差率和新能源利用率相等时,最大负荷减小会导致风光装机容量和总综合收益减小,且每减小100 MW最大负荷可导致新能源渗透率减少4%左右,如情形1、7、11和5、9,这是因为负荷整体减小后,更少的风光装机容量即可满足负荷需求.

在最大负荷和新能源利用率相等时,峰谷差率减小可导致风光装机容量增大,总综合收益增大,如情形1、5、7、9和3、6、8、10.这是由于负荷需求曲线的峰谷差率减小,使火电可投入更多的调节资源给风光,而风光在获得更多调节资源后,能增加装机容量使总收益变大.虽然负荷峰谷差率受区域负荷特性影响无法大幅调整,但可略微减小以提升耦合系统综合收益.

在最大负荷和峰谷差率相等时,新能源利用率减小可导致风光总装机容量和总收益变大,如情形1~4和情形7~8.这是由于新能源最小利用率的降低表示耦合系统可弃更多风光发电负荷.由此,在一些风光出力较极端且耦合系统的新能源最小利用率较低的场景下,通过弃风弃光即可满足功率平衡需求;此外,更多的弃风弃光意味着火电投入的调节资源更少.上述因素综合作用导致风光装机容量及综合收益增大,仍需指出,新能源最小利用率减小虽利于提升综合收益,但弃风弃光过多与保证新能源最小利用率的政策不符.因此耦合系统容量优化配置中,应考虑新能源最小利用率达一定标准.

计算不同情形下风电、光伏的装机容量比可知,风电装机容量大于光伏装机容量,新能源最小利用率对风光装机容量比影响较小,如情形1~4,这是由于新能源中风电在全时间段中具有更好的发电能力,且爬坡事件发生较少,新能源最小利用率主要与运行情况有关;最大负荷相同时,负荷峰谷差率减小可导致风光装机容量比增大,如情形1和5,这是由于负荷峰谷差率减小可使火电具有更多的灵活性资源平抑新能源波动,而新能源中风电在全时间段中具有更好的发电能力;负荷峰谷差率相同时,最大负荷减小可导致风光装机容量比减小,如情形1、7、11,这是由于最大负荷减小后,新能源装机容量需求减小,而风电装机成本较光伏高.

综合上述情形,本文研究区域的耦合系统中,考虑最大负荷略大于火电机组总装机容量的情况,新能源的最佳渗透率主要在30%~40%左右,其中风电装机容量大于光伏装机容量,且随着新能源渗透率增大,风光装机容量比增加;当最大负荷较大、峰谷差率和新能源最小利用率均较小时,耦合系统的新能源渗透率可达到40%以上,如情形6所示.

3.3 爬坡事件的影响因素分析

采用1.3节中最优爬坡区间计算方法,分析耦合系统中风、光年爬坡事件,风光耦合后爬坡事件的影响因素.

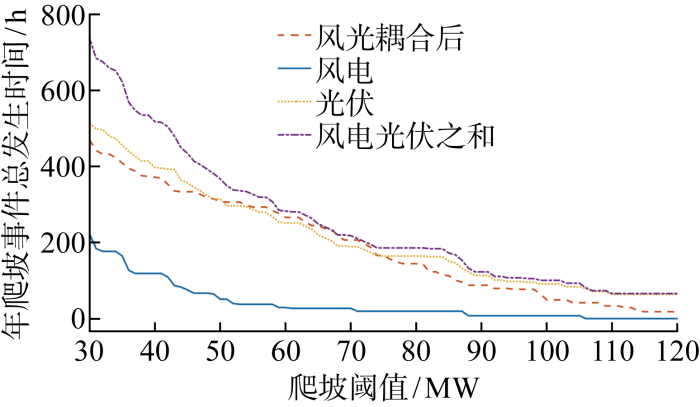
首先分析不同爬坡阈值对上述爬坡事件发生时间的影响,设置最大负荷为 1400 MW,峰谷差率为0.55,新能源最小利用率为0.9,爬坡阈值设置为30~120 MW,间隔1 MW,分别计算风、光和风光耦合后年爬坡事件总发生时间,结果如图4所示.由图可知,在相同爬坡阈值下,光伏比风电的年爬坡事件总发生时间高出很多,结合图2中风光期望出力曲线可知,该地区风电整体波动较小,而光伏在每天日出和日落时功率变化很大,容易发生爬坡事件.爬坡阈值较小和较大,即30~50 MW和75~120 MW时,风光耦合后的年爬坡事件总发生时间小于光伏的年爬坡事件总发生时间;爬坡阈值处于中等值,即50~75 MW时,风光耦合后的年爬坡事件总发生时间大于光伏的年爬坡事件总发生时间;在本节研究的爬坡阈值下,风光耦合后的年爬坡事件总发生时间几乎均小于风电、光伏的年爬坡事件总发生时间直接相加.上述现象说明该地区的风光互补性较好,风电可以减少光伏爬坡事件,尤其在抑制较大或者较小的爬坡事件时效果较好.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 风电、光伏及其耦合后年爬坡事件总发生时间与爬坡阈值的关系

Fig.4 Relationship between annual total ramp time and ramp threshold of wind power, photovoltaic, and after their coupling

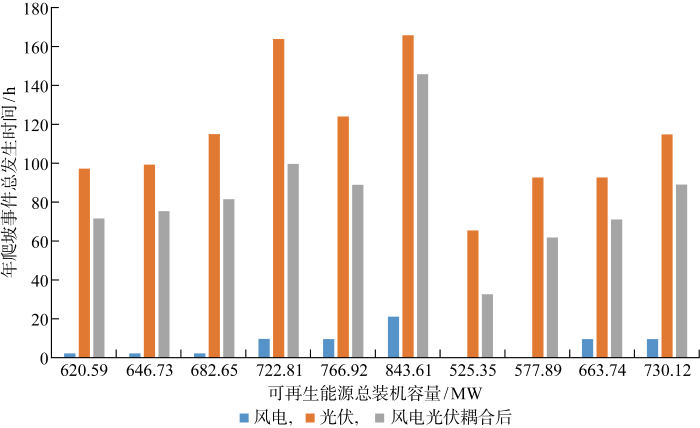
其次分析给定爬坡阈值下,不同容量优化配置结果对风、光年爬坡事件总发生时间和风光耦合后年爬坡事件总发生时间的影响,爬坡阈值设为80 MW,结果如图5所示,图中10组数据从左至右分别对应情形1~10.分析可得,虽然新能源装机容量大会引起其波动变大,更易达到给定爬坡阈值,但年爬坡事件总发生时间与风光装机容量并非完全正相关,如情形4和5.这是因为最大负荷、峰谷差率较大,新能源利用率较小时,风电、光伏会为了追求更多收益进行更多弃风、弃光,从而引起更大波动,导致爬坡事件增加.综上,耦合系统的新能源最小利用率不应过小,否则会导致出现更多爬坡事件,增加火电机组的调峰压力,并可能进一步引起其他问题.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 80 MW爬坡阈值下不同情形风电、光伏及其耦合后爬坡事件影响分析

Fig.5 Relationship between annual total ramp time and cases of wind power, photovoltaic, and after their coupling at a ramp threshold of 80 MW

综上所述,该地区风电是较为优质的新能源,其爬坡事件发生概率较小,同时与光伏相比全天均具备发电能力,因此风电可较光伏配置更多装机容量.

3.4 源荷匹配性的影响因素分析

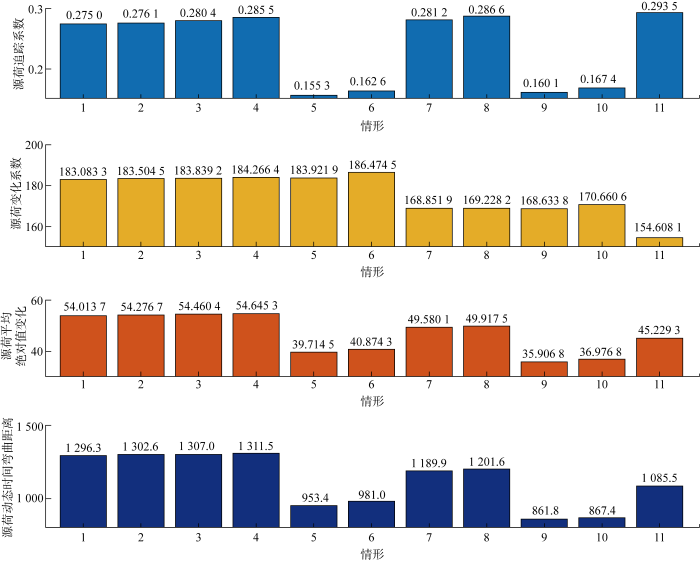
根据容量优化配置结果计算源荷匹配评价指标并分析其影响因素,结果如图6所示.由图可见,最大负荷减小,源荷追踪系数增大,而源荷变化系数、源荷平均绝对值变化和源荷动态时间弯曲距离均减小,如情形1、7、11,这是因为最大负荷减小导致负荷需求曲线整体波动和变化变小,同时风光出力可更好地追踪负荷需求,并更好地与负荷需求曲线保持一致;峰谷差率减小可导致源荷追踪系数、源荷平均绝对值变化和源荷动态时间弯曲距离减小,源荷变化系数增大,如情形3、6,这是由于峰谷差率减小时的负荷需求曲线更平缓,但负荷需求曲线的平缓会导致新能源出力曲线与其更难贴合和近似;新能源最小利用率减小会导致4个源荷匹配指标增大,如情形1~4,这是由于新能源最小利用率减小后,风光可灵活弃风、弃光以更好地贴近负荷曲线并保持形状相似.这有利于源荷匹配且可减小其匹配后的波动,但因新能源最小利用率减小导致风光装机容量增大,在装机容量增大的同时为保证耦合系统利益最大化,会在风光充足时优先出力,上述原因共同作用使源荷变化系数、源荷平均绝对值变化和源荷动态时间弯曲距离略微提升.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 源荷匹配评价指标分析

Fig.6 Analysis of source-load matching indices

从源荷匹配评价可以看出,在源荷匹配较好时,适当降低可再生能源最小利用率可进一步增加风、光装机容量,即尽可能合适的负荷需求曲线制定对耦合系统的收益及新能源的充分利用具有较大作用.

4 结语

研究风光火耦合系统的容量优化配置,针对已有火电机组,考虑多种源荷特性、成本和收益,配置风电、光伏的装机容量,并分析多种源荷因素与容量优化配置结果之间的相互影响.以辽宁地区含两台600 MW 火电机组的风光火耦合系统容量优化配置为算例进行仿真,结果表明:减小新能源最小利用率、峰谷差率和发电缺额率可增大装机容量;该地区风电发生爬坡事件的概率较光伏小,风、光互补后,可较好地平抑较大和较小的爬坡事件;新能源最小利用率小会导致更多爬坡事件发生,增加火电的调峰压力;最大负荷和峰谷差率对源荷匹配性有相反的影响,减小新能源最小利用率有利于更好的源荷匹配.综上所述,本文研究区域的耦合系统中,考虑最大负荷略大于火电机组总装机容量的情况,新能源的最佳渗透率在30%~40%左右;其中风电可较光伏配置更多装机容量,以实现更好的爬坡事件平抑及源荷匹配;若源荷匹配较好,适当减小新能源最小利用率可进一步增加新能源的装机容量.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

国务院.

国务院关于印发2030年前碳达峰行动方案的通知

[EB/OL]. (2021-10-24)[2022-06-10]. http://www.gov.cn/zhengce/content/2021-10/26/content_5644984.htm.

URL [本文引用: 2]

State Council.

State Council about printed and distributed notice of action plan for carbon peak before 2030

[EB/OL]. (2021-10-24)[2022-06-10]. http://www.gov.cn/zhengce/content/2021-10/26/content_5644984.htm.

URL [本文引用: 2]

[2]

中共中央, 国务院.

中共中央国务院关于完整准确全面贯彻新发展理念做好碳达峰碳中和工作的意见

[EB/OL]. (2021-09-22)[2022-06-10]. http://www.gov.cn/zhengce/2021-10/24/content_5644613.htm.

URL [本文引用: 1]

CPC Central Committee, State Council.

CPC Central Committee, State Council about opinion of fully and accurately implementing the new development philosophy, and ensuring the success of the carbon peak and carbon neutrality goals

[EB/OL]. (2021-09-22)[2022-06-10]. http://www.gov.cn/zhengce/2021-10/24/content_5644613.htm.

URL [本文引用: 1]

[3]

国家能源局.

关于公开征求对《国家发展改革委国家能源局关于开展“风光水火储一体化”“源网荷储一体化”的指导意见(征求意见稿)》意见的公告

[EB/OL].(2020-08-27)[2022-06-10]. http://www.nea.gov.cn/2020-08/27/c_139321964.htm.

URL [本文引用: 1]

National Energy Administration.

Announcement on soliciting public comments on the guiding opinions (draft for comments) of the National Development and Reform Commission and the National Energy Administration on the integrated development of wind, solar, hydro, and energy storage, and the integrated development of generation, grid, load, and energy storage

[EB/OL].(2020-08-27)[2022-06-10]. http://www.nea.gov.cn/2020-08/27/c_139321964.htm.

URL [本文引用: 1]

[4]

谢鹏, 蔡泽祥, 刘平, 等.

考虑多时间尺度不确定性耦合影响的风光储微电网系统储能容量协同优化

[J]. 中国电机工程学报, 2019, 39(24): 7126-7136.