考虑个体自私的热电联产系统完全分布式经济调度

doi:10.16183/j.cnki.jsjtu.2022.495

考虑个体自私的热电联产系统完全分布式经济调度

米阳^,, 吴继伟, 田书欣, 马思源, 王育飞

上海电力大学电气工程学院,上海 200090

Fully Distributed Economic Dispatch of Combined Heat and Power System Considering Individual Selfishness

MI Yang^,, WU Jiwei, TIAN Shuxin, MA Siyuan, WANG Yufei

College of Electrical Engineering, Shanghai University of Electric Power, Shanghai 200090, China

责任编辑: 王一凡

收稿日期: 2022-12-6 修回日期: 2023-01-18 接受日期: 2023-02-15

基金资助:

国家自然科学基金(61873159)
上海市自然科学基金(22ZR1425500)

Received: 2022-12-6 Revised: 2023-01-18 Accepted: 2023-02-15

作者简介 About authors

米阳(1976-),教授,从事微网控制、电力系统稳定运行与控制等研究;E-mail:miyangmi@163.com.

摘要

针对传统集中式经济调度策略需要获取全局信息以及无法适应系统灵活拓扑的缺陷,同时考虑能量以电能和热量形式并存出现的情况,基于一致性算法提出了一种完全分布式热电联产经济调度策略.将热电联产系统中各机组电价和热价的增量成本作为一致性变量进行迭代计算,直至增量成本达到收敛,实现系统经济最优.此外,还分析了个别机组为了提升自身利益,向相邻机组传输带有偏差增量成本值的情况,设计了一个增量成本补偿项来消除该自私行为的影响.在3个仿真算例中得到的结果表明,所提策略在解决热电联产系统经济调度问题中具有有效性和可行性.

关键词： 一致性算法; 热电联产系统; 完全分布式; 经济调度; 个体自私

Abstract

In response to the defects of the traditional centralized economic dispatching strategy which needs to obtain global information and cannot adapt to the flexible topology of the system, and considering the coexistence of energy in the form of electricity and heat, a completely distributed cogeneration economic dispatching strategy based on the consistency algorithm is proposed. The incremental cost of electricity price and heat price of each unit in the cogeneration system is taken as the consistent variable to conduct the iterative calculation until the incremental cost converges to achieve the economic optimum of the system. In addition, the case of individual unit transmitting to neighboring units with deviating incremental cost values in order to enhance their own interests is also analyzed, and an incremental cost compensation term is designed to eliminate the impact of this selfish behavior. The simulation results indicate that the proposed strategy is effective and viable in the solution of the cogeneration economic dispatching problems.

Keywords： consensus algorithms; combined heat and power; fully distributed; economic dispatch; individual selfishness

PDF (1726KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

米阳, 吴继伟, 田书欣, 马思源, 王育飞. 考虑个体自私的热电联产系统完全分布式经济调度[J]. 上海交通大学学报, 2024, 58(1): 50-58 doi:10.16183/j.cnki.jsjtu.2022.495

MI Yang, WU Jiwei, TIAN Shuxin, MA Siyuan, WANG Yufei. Fully Distributed Economic Dispatch of Combined Heat and Power System Considering Individual Selfishness[J]. Journal of Shanghai Jiaotong University, 2024, 58(1): 50-58 doi:10.16183/j.cnki.jsjtu.2022.495

在全球范围内,能源不足危机以及能源产出过程中造成的环境问题日趋严重,为了充分利用已经开发的能源,提出了综合能源的概念^[1-2].而热电联产系统是综合能源系统中非常重要的一个环节,可以同时向用户提供电能和热量.但是热电联产系统中发电量和产热量相互依存,不仅要满足电力需求,还要满足热需求,增加了传统经济调度问题的复杂性^[3].

经济调度问题是满足各种约束的情况下,实现电力系统发电成本最小,其本质是等耗量微增率准则,这也是电力系统最基础的问题之一.在分布式方法出现之前,经济调度问题一般采用lambda迭代法^[4]等数值方法或者优化算法求解,采用lamdba迭代法求解经济调度问题时,所设计的成本目标必须是凸函数,否则lamdba迭代法将无法求解.为此,文献[5-6]中分别提出了改进蚂蚱优化算法和改进粒子群优化算法去求解非凸成本目标函数.虽然上述求解方法为解决经济调度问题提供了一些可靠的方案,但是所提方法都是集中式的,所有的机组需要通过通信中心进行状态信息的交流与处理,然后由通信中心向机组发出调度指令^[7],在面对日益复杂的电力系统拓扑结构以及大量接入的分布式电源时,缺乏鲁棒性和灵活性^[8].

为了消除电力系统集中式求解方法的缺陷,分布式求解方法受到了越来越多的研究.分布式求解方法的计算量更小、可靠性更高,还可以满足机组“即插即用”的需求^[9].文献[10]中基于一致性理论提出一种多能源局域网双层实时动态功率分配策略,来解决能源互联网中实时功率分配问题.但是仍然需要设置1个“领导者”来承担功率偏差,并不属于完全分布式求解方法.文献[11]中利用基于一致性原理的经济调度算法估计负荷量和发电量的功率不平衡量,并反馈到各个发电机组,以调节每个发电机的当前发电量,这种算法无需设置领导者.但是需要设置机组总发电量初值与负荷功率相等,难以应对系统负荷变动的情况.文献[8]中为了实现完全分布式经济调度,选择增量成本作为一致性变量进行迭代计算,利用调整项来调节功率偏差,使其满足约束条件.但是上述文献都没有考虑分布式环境下个体会经常出现自私行为.为了应对个体的自私行为,文献[12]中在增量成本中加入了修正向量,消除了个体自私行为的不利影响,使系统的发电成本重新达到最小.

基于上述研究,本文考虑了热量和电能同时出现的热电联产情况,将一致性原理应用到热电联产系统中,以电价和热价的增量成本作为一致性变量,设计了完全分布式经济调度策略.还考虑了个体出现自私行为的情况,为电价和热价的增量成本设置了补偿量,以抵消自私个体的自私行为.

1 图论知识和一致性算法

1.1 图论知识

利用图论知识对系统中分布式机组的通信拓扑信息进行描述,将每一台机组当作一个智能体,故热电联产经济调度系统中各智能体间通信关系可以由图G=(V, E)表示.V={1,2,…,N}为图G的智能体有限非空节点集合(N为系统中机组数量),其元素为节点,代表实际的发电、产热机组^[13].边集E是节点的所有无序连接,其元素称为边,代表机组间的通信信道,用E[k]表示,其中,边(i,j)∈E[k]表示在时刻k智能体i接受到了智能体j发送的信息^[14].

对于每一条边赋一个实数的加权图,定义A为n阶邻接矩阵.若节点i与j之间有交流,则邻接矩阵A的第i行第j列元素a_ij=1,节点自身无交流,即 a_ii=0.

拉普拉斯矩阵可以量化机组在通信网络中的连通程度,拉普拉斯矩阵的特征值包含了该通信拓扑的大量信息^[15-16].图G的拉普拉斯矩阵L=[l_ij],其中:

(1)

\begin{array}{l} l_{i i} = \sum_{i \neq j} a_{i j}, & 对 角 元 素 \\ l_{i j} = - a_{i j}, & 非 对 角 元 素 \end{array}\}

1.2 一阶一致性算法

一致性算法的本质是在分布式系统中本地节点与邻接节点进行信息交流,更新本地节点的一致性变量,使得通信网络中各节点的一致性变量收敛于稳定的共同值^[17].

定义x_i∈R表示节点i的一致性变量,令机组的增量成本为节点的一致性变量,通过一致性算法的迭代计算后一致性变量收敛于一个共同值,机组的增量成本达到一致,即满足等耗量微增率准则,电力系统总的发电成本最小.对于所有的节点i和j,网络中节点的一致性变量达到一致时,所有机组的一阶动态特性表示如下:

(2)

{\overset{\cdot}{x}}_{i}

=x_i

用一阶连续一致性算法表示如下:

(3)

{\overset{\cdot}{x}}_{i}

\overset{n}{\sum_{j = 1}}

a_ij(x_i-x_j)

用矩阵的形式表示如下:

(4)

{\overset{\cdot}{x}}_{i}

=-L_nx

式中:L_n为n阶的拉普拉斯矩阵.

考虑智能体之间的通信延时,利用离散一致性算法来描述热电联产系统内各机组的动态特性,一阶离散一致性算法表示如下:

(5)x_i(k+1)=

\overset{n}{\sum_{j = 1}}

d_ijx_j(k)

式中:k为迭代次数;d_ij为状态转移矩阵D第i行第j列的元素,

(6)d_ij=

\frac{| l_{i j} (k) |}{\overset{n}{\sum_{j = 1}} | l_{i j} (k) |}

2 热电联产系统经济调度模型

2.1 热电联产系统机组建模

热电联产系统主要由传统发电机组、传统产热机组和热电联产机组组成.发电机组的成本函数^[18]和传统发电机组的发电极限功率约束分别表示为

(7)C_i(P_i)=α_i+β_iP_i+γ_i

P_{i}^{2}

(8)

P_{i}^{m i n}

≤P_i≤

P_{i}^{m a x}

式中:P_i为传统发电机组i发电功率; $P_{i}^{m i n}$ 和 $P_{i}^{m a x}$ 分别为传统发电机组i发电功率的下限与上限;α_i、β_i、γ_i分别为传统发电机组i的发电成本系数.

热电联产机组的成本函数:

(9)C_j(P_j,Q_j)=α_j+β_jP_j+γ_j

P_{j}^{2}

+δ_jQ_j+ ε _j

Q_{j}^{2}

+ζ_jP_jQ_j

式中:P_j、Q_j分别为热电联产机组j的输出的有功功率与热量;α_j、β_j、γ_j、δ_j、ε_j、ζ_j分别为热电联产机组j的成本系数.

传统产热机组的成本函数和产热极限功率约束分别表示为

(10)C_k(Q_k)=α_k+β_kQ_k+γ_k

Q_{k}^{2}

(11)

Q_{k}^{m i n}

≤Q_k≤

Q_{k}^{m a x}

式中:α_k、β_k、γ_k分别为传统产热机组k的产热成本系数;Q_k为传统产热机组k的产热量; $Q_{k}^{m i n}$ 和 $Q_{k}^{m a x}$ 分别为传统产热机组k产热量的下限与上限.

热电联产系统经济调度总的成本函数由式(7)、式(9)和式(10)叠加而得,因此系统发电成本总的目标函数表示如下:

(12)F=min(

\overset{n_{p}}{\sum_{i = 1}}

C_i(P_i)+

\overset{n_{c}}{\sum_{j = 1}}

C_j(P_j,Q_j)+

\overset{n_{h}}{\sum_{k = 1}}

C_k(Q_k))

将热电联产系统中发电量与电负荷以及产热量和热负荷的功率平衡约束:

(13)

\overset{n_{p}}{\sum_{i = 1}}

P_i+

\overset{n_{c}}{\sum_{j = 1}}

P_j-P_d≤δ_P

(14)

\overset{n_{c}}{\sum_{j = 1}}

Q_j+

\overset{n_{h}}{\sum_{k = 1}}

Q_k-Q_d≤δ_Q

式中:n_p、n_c、n_h分别为传统发电机组、热电联产机组、传统产热机组的数量;P_d、Q_d分别为热电联产系统的电负荷和热负荷;δ_P和δ_Q分别为电能和热量偏差允许值.

2.2 等耗量微增量准则

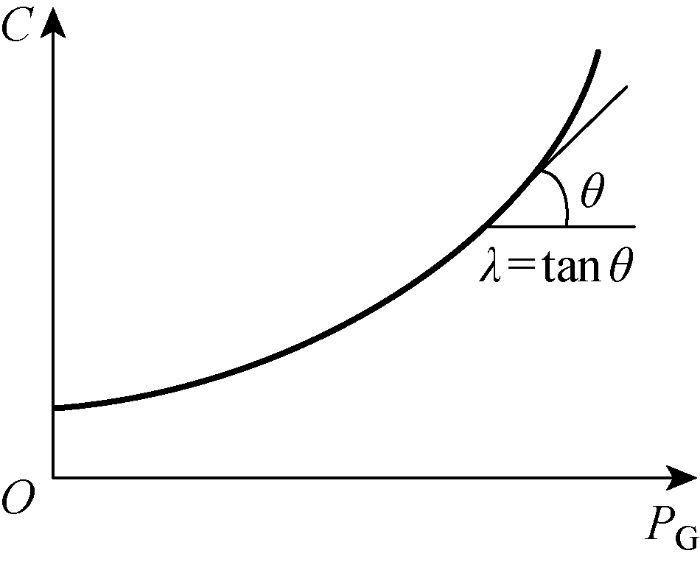
电力系统经济调度目标是在满足系统各种约束条件的情况下,使各机组满足等耗量微增率准则,即机组发电成本最小.为此需要先了解机组的耗量特性,以传统发电机组为例,其耗量特性如图1所示.图中:C为发电成本;P_G为机组的发电量;λ为耗量微增率;θ为斜率倾斜角.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 机组耗量特性

Fig.1 Characteristics of unit consumption

耗量特性曲线上某一点切线的斜率为发电机组的耗量微增率,由下式表示:

(15)λ=

\frac{d C}{d P}

=tan θ

等耗量微增率准则具有明显的物理意义,假设两台发电机运行在耗量微增率不等的情况下,并且两台发电机组满足 $\frac{d C_{1}}{d P_{1}}$ < $\frac{d C_{2}}{d P_{2}}$ .在两台发电机组的发电功率之和不变的情况下进行负荷分配,让机组1增加ΔP的发电功率,机组2减少ΔP的发电功率,即 $\frac{d C_{1}}{d P_{1}}$ 增加, $\frac{d C_{2}}{d P_{2}}$ 减小.因此,机组1消耗的燃料增加 $\frac{d C_{1}}{d P_{1}}$ ΔP,机组2消耗的燃料减少 $\frac{d C_{2}}{d P_{2}}$ ΔP.而总的燃料减少量为

(16)ΔC=

\frac{d C_{2}}{d P_{2}}

ΔP-

\frac{d C_{1}}{d P_{1}}

ΔP=

(\frac{d C_{2}}{d P_{2}} - \frac{d C_{1}}{d P_{1}})

ΔP>0

当两台发电机的耗量微增率相等时,即 $\frac{d C_{2}}{d P_{2}}$ - $\frac{d C_{1}}{d P_{1}}$ =0,燃料节约量为0,不再需要进行发电功率调整,发电成本最小.显然,等耗量微增率准则也适用于热电联产系统内多台设备的负荷分配.

3 热电联产系统分布式经济调度策略

3.1 分布式经济调度策略

在分布式优化调度方法中,将电能和热量的增量成本(λ_P和λ_Q)选为热电联产系统各机组的一致性变量.为了保证系统的出现单点故障,不再设置控制中心采集热电联产系统各机组的信息,分布式的通信网络如图2所示.图中:G1和G5分别为传统发电机组和传统产热机组,G2、G3和G4为热电联产机组.在分布式经济调度中,机组仅与相邻机组的信息交换,采用一致性算法进行迭代计算,使得各机组的增量成本达到一致,实现热电联产系统的发电和产热成本最小.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 分布式通信拓扑

Fig.2 Topology of distributed communication

应用目标函数的可分解性求解热电联产系统的经济调度问题.首先,通过初始化系统中各机组的λ_P和λ_Q;其次,λ_P和λ_Q将根据提出的一致性算法进行逐步迭代更新.这两个步骤将重复进行,直到满足系统中电能和热量的需求.目标函数的分解如下:

传统发电机组经济调度的目标函数

(17)min

\overset{n_{p}}{\sum_{i = 1}}

(C_i(P_i)-λ_PP_i)

热电联产机组经济调度的目标函数

(18)min

\overset{n_{c}}{\sum_{j = 1}}

(C_j(P_j,Q_j)-λ_PP_j-λ_QQ_j)

传统产热机组经济调度的目标函数

(19)min

\overset{n_{h}}{\sum_{k = 1}}

(C_k(Q_k)-λ_QQ_k)

通过一致性算法求解热电联产系统经济调度问题,电能和热量增量成本由下式进行更新:

(20)λ_P_,_m(k+1)=

\overset{N}{\sum_{n = 1}}

d_mnλ_P_,_n(k), m∈N

(21)λ_Q_,_m(k+1)=

\overset{N}{\sum_{n = 1}}

d_mnλ_Q_,_n(k), m∈N

选择增量成本λ_P和λ_Q作为一致性算法的状态变量,在迭代的过程中,λ_P和λ_Q会分别向其“固定值”逐渐逼近.在不满足功率平衡的情况下,需要指定一个“领导者”,对发电量与电负荷以及产热量和热负荷的偏差量进行修正,以满足热电联产系统的有功功率和热量的平衡.但是领导者的存在导致系统仍需要集中处理器来计算功率偏差量,为此设计了一个修正项,不再需要领导者来承担功率偏差,实现完全分布式经济调度.为了保证热电联产系统内有电能和热量的平衡,一致性增量成本更新规则由下式表示:

(22)λ_P_,_m(k+1)=

\overset{N}{\sum_{n = 1}}

d_mnλ_P_,_n(k)+ξϕ_P_,_m(k)

(23)λ_Q_,_m(k+1)=

\overset{N}{\sum_{n = 1}}

d_mnλ_Q_,_n(k)+ξϕ_Q_,_m(k)

(24)ϕ_P_,_m(k+1)=

\sum_{n \in N}

v_mnϕ_P_,_n(k)-(P_i(k+1)-P_i(k))

(25)ϕ_Q_,_m(k+1)=

\sum_{n \in N}

v_mnϕ_Q_,_n(k)-(Q_i(k+1)-Q_i(k))

式中:ξ为收敛系数,当ξ取值过大时,一致性算法收敛速度快,但是容易引起系统振荡,当ξ取值过小时,一致性算法的收敛精度高,但是收敛速度很慢;ϕ_P_,_m(k)和ϕ_Q_,_m(k)分别为电能和热量增量成本的修正项;v_mn为状态转移矩阵的转置矩阵D^T的元素;P(k)和Q(k)为热电联产机组、发电机组和产热机组经过第k次迭代后出力值.

3.2 个体自私行为影响及消除策略

在多智能体分布式通信环境下,个体会经常出现自私行为实现自己利益最大化.个体自私行为可以分为本地自私行为和社会自私行为.本地自私行为是个体的自私行为对其他个体的影响相同,即其他节点仍然能达到一致;社会自私行为是由于个体间的关联程度不一致,自私行为会对关联强的个体产生更强的影响,导致其余个体无法全部达到一致^[19].本文不考虑节点间的关联强度,故仅对本地自私行为进行研究.在基于一致性原理的分布式经济调度模式中,一个机组恶意减小自身的电能或者热量增量成本,来降低自身的发电量或者产热量,即在节点间的状态交互过程中,向其相邻节点传输经过修改的一致性变量.

以b_i表示个体i是加入个体真实一致性变量的自私量,为了便于计算用B=[b₁b₂ … b_N]表示个体的自私量.则考虑个体自私行为时,一致性增量成本更新规则变为

(26)λ_P_,_m(k+1)=

\overset{N}{\sum_{n = 1}}

d_mn(λ_P_,_n(k)+B_P)+ξϕ_P_,_m(k)

(27)λ_Q_,_m(k+1)=

\overset{N}{\sum_{n = 1}}

d_mn(λ_Q_,_n(k)+B_Q)+ξϕ_Q_,_m(k)

式中:B_P和B_Q分别为加入个体真实电能和热量一致性变量的自私量.

以发电机组为例其耗量微增率即增量成本为

(28)λ_P_,_i=

\frac{d C}{d P}

=β_i+2γ_iP_i

因此机组出力为

(29)P_i=

\frac{λ_{P, i} - β_{i}}{2 γ_{i}}

考虑机组的自私行为时,第i个机组的出力变为

(30)P'_i=P_i-

\overset{N}{\sum_{j = 1}}

f_ijb_P_,_j

(31)f_ij=

\{\begin{array}{l} - \frac{\frac{1}{2} \frac{1}{γ_{i} γ_{j}}}{\sum \frac{1}{γ_{n}}}, & i \neq j \\ - \sum_{i \neq j} f_{i j}, & i = j \end{array}

式中:b_P_,_j为第j个机组的电出力偏差.

由式(30)和(31)可知,自私个体给相邻个体传输带偏差的增量成本值,使其减小了自身的出力,提高了自私个体经济效益,然而其他无自私行为的个体为满足系统发电量与电负荷以及产热量和热负荷的平衡将自身提高出力,导致系统无法达到经济最优.

设式(30)中,第j个机组有自私行为,则自私个体与不自私个体的出力偏差为

(32)ΔP_b=b_P_,_j(E+F)

式中:ΔP_b为自私个体与不自私个体的出力偏差;E和F分别为式(31)中i≠j和i=j的两项.由此可以知道自私个体与不自私个体一致性变量的偏差为Δλ_i=2γ_iΔP_b,为了能消除自私行为的影响设置补偿量Y=[Δλ₁ Δλ₂ … Δλ_N].一致性增量成本更新规则变为

(33)λ_P_,_m(k+1)=

\overset{N}{\sum_{n = 1}}

d_mn(λ_P_,_n(k)+B_P-Y_P)+ξϕ_P_,_m(k)

(34)λ_Q_,_m(k+1)=

\overset{N}{\sum_{n = 1}}

d_mn(λ_Q_,_n(k)+B_Q-Y_Q)+ξϕ_Q_,_m(k)

由式(33)和(34)知,补偿项Y的设置消除了个体自私行为的不利影响,使热电联产系统的增量成本重新达到收敛,达到发电和产热经济最优的状态.

3.3 经济调度策略的实现步骤

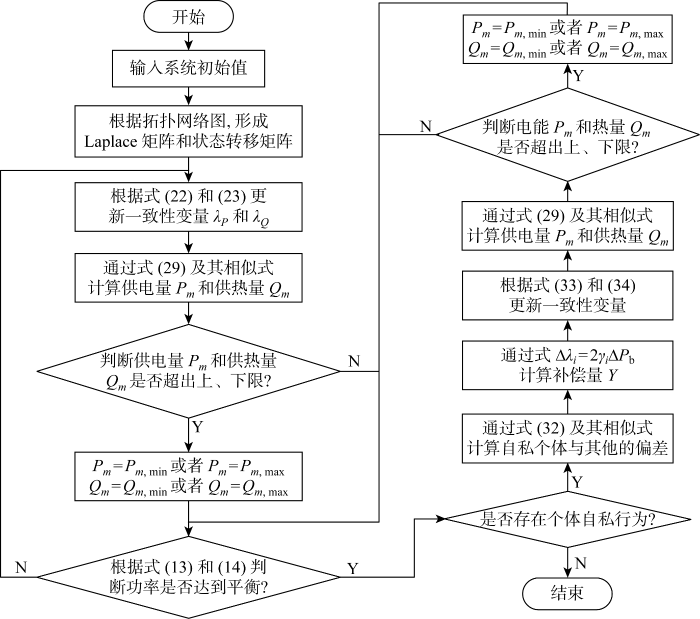
基于一致性算法的完全分布式热电联产经济调度策略具体实现步骤如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 热电联产分布式经济调度流程图

Fig.3 Flow chart of cogeneration of heat and power distributed economy dispatch

4 仿真算例分析

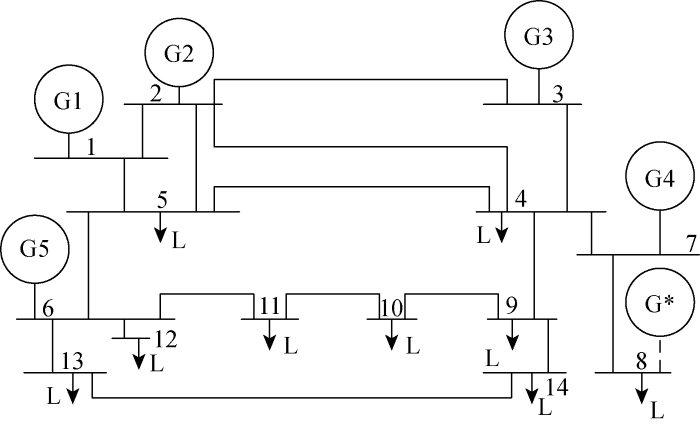
为了验证所提基于一致性算法的热电联产分布式经济调度策略的有效性,利用MATLAB 2016b软件搭建了调整后的IEEE-14节点配电网模型,如图4所示.图中:G^*为3.2节中即插即用的机组;L为负荷.通过此5机系统模拟热电联产系统有电能和热量的分配,其通信网络如图2所示.上述机组的基本参数如表1所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 调整的IEEE-14节点系统

Fig.4 Adjusted IEEE-14 node system

表1 热电联产机组的基本参数

Tab.1 Basic parameters of cogeneration unit

机组	α	β	γ	δ	ε	ζ
G1	500	13.55	0.081 2	0	0	0
G2	840	12.93	0.049 6	4.6	0.027	0.016
G3	810	12.22	0.043 5	3.7	0.037	0.023
G4	830	12.76	0.088 3	3.9	0.025	0.022
G5	360	0	0	4.3	0.035	0
G*	860	13.89	0.068 6	4.2	0.033	0.031

新窗口打开| 下载CSV

4.1 正常情况增量成本一致性仿真

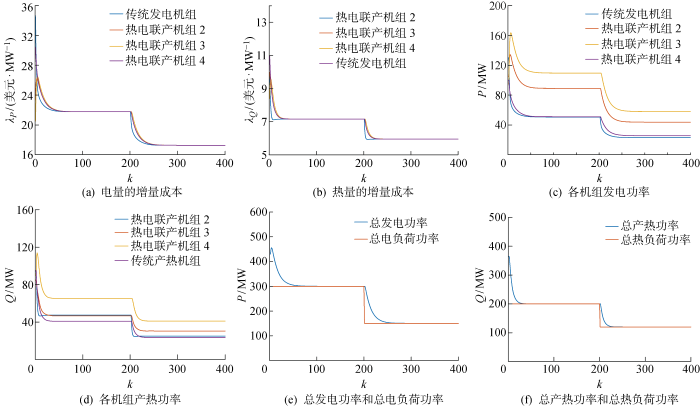
本算例验证增量成本一致性算法在热电联产系统中电能和热量分配的有效性.设各机组初始发电功率为P₀=130, 105, 95, 100 MW,初始电负荷设为P_L=300 MW;初始产热功率为Q₀=95, 85, 90, 95 MW,初始热负荷设为Q_L=200 MW.在k=200时,令电负荷大小减少到100 MW,电负荷大小减少到120 MW.收敛系数ξ设为0.008.热电联产系统中各机组的增量成本一致性收敛过程及出力大小如图5所示.图中:P为机组的电出力;Q为机组的热出力.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 各机组的增量成本一致性收敛过程及出力大小

Fig.5 Incremental cost convergence process and output of each unit

由图5(a)、5(b)可知,算法经过90次迭代后第一次达到收敛,在负荷发生变化后,又经过200次迭代后达到收敛,热电联产系统中机组的电能的增量成本和热量的增量成本均收敛于一个共同值,满足等耗量微增率准则,系统在经济上达到最优.由图5(c)、5(d)可知,所提一致性算法达到收敛时各机组的发电功率分别为P=22.86, 43.68, 57.97, 25.5 MW;各机组产热功率分别为Q=25.01, 30.41, 41.01, 23.58 MW.由图5(e)、5(f)可知,各机组输出的电能和热量与电负荷和热负荷达到平衡.综上可知,所提的增量成本一致性算法能够降低热电联产系统的运行成本.

4.2 即插即用时的增量成本一致性仿真

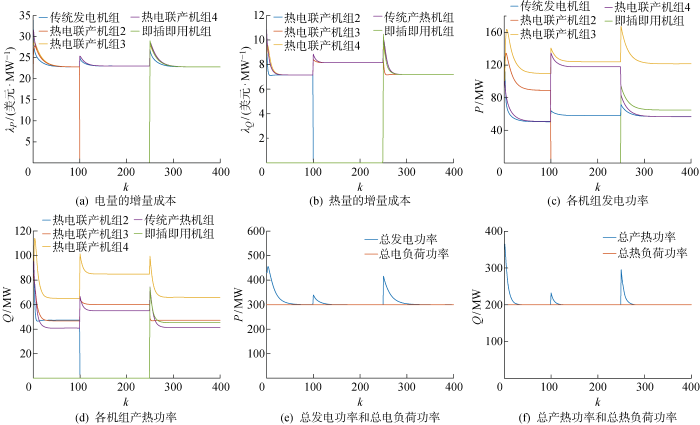
为了验证所提分布式经济调度策略在机组发生故障退出后,以及其他机组加入系统时的有效性,设计了即插即用时增量成本一致性仿真.设各机组的初始出力与4.1节一致,电负荷和热负荷分别保持300 MW和200 MW不变.在算法迭代至100次时,热电联产机组2因故障退出运行,在算法迭代至250次加入热电联产系统,接入的位置如图4中G^*所示.各机组增量成本的收敛过程和出力情况如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 即插即用时各机组增量成本一致性收敛过程及出力大小

Fig.6 Consistency convergence process and output size of incremental cost of each unit during plug and play

由图6可以看出,迭代到100次时热电联产2因故障退出运行后,其承担的一部分电负荷和热负荷由其余的机组承担,其余机组的发电功率和产热功率有所增加,系统的电能增量成本和热量增量成本也有所增加,但是算法仍能收敛于同一个值.迭代到250次时即插即用机组加入系统,其承担了一部分电负荷和热负荷,其余机组的发电功率和产热功率有所减少,系统的电能增量成本和热量增量成本也有所减少,且算法仍能收敛于同一个值.因此,所提一致性算法能够满足热电联产系统中机组的即插即用,系统具有良好的鲁棒性.

4.3 考虑个体自私行为时增量成本一致性仿真

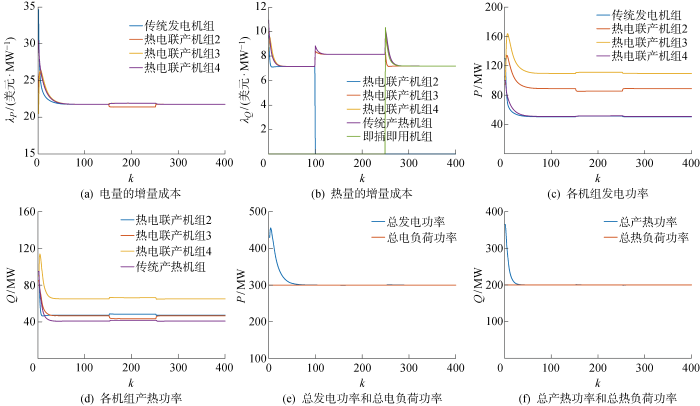
为了验证所提分布式经济调度策略在热电联产系统中有机组做出自私行为时的有效性,设计了考虑个体自私行为时增量成本一致性仿真.设各机组的初始出力与4.1节一致,电负荷和热负荷分别保持300 MW和200 MW不变.在算法迭代至150次时,热电联产机组2做出自私行为,分别减小了0.5 美元/MW的电能增量成本以及0.3 美元/MW的热量增量成本.在算法迭代至250次时,加入消除自私行为的策略,热电联产系统又收敛于同一个值.考虑个体自私行为时的各机组增量成本一致性收敛过程以及出力情况如图7所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 考虑个体自私行为时各机组增量成本一致性收敛过程及出力大小

Fig.7 Uniform convergence process and output of incremental cost of each unit considering individual selfish behavior

由图7可以看出,当热电联产机组2做出自私行为后,其承担的电负荷和热负荷都有所减少,减少的部分由其他机组进行承担,导致各机组的电功率输出和热量输出均有所上升,系统中电能增量成本和热量增量成本较正常运行时有所提高,经济效益无法达到最优.加入补偿量后,热电联产机组2的自私行为被消除,其增量成本和出力增加,热电联产系统所有机组的增量成本又达到收敛,恢复了经济效益最优状态.综上,所提热电联产系统分布式经济调度策略可以较好地应对个体的自私行为.

5 结论

本文从分布式优化的角度出发,设计了一种基于一致性算法的完全分布式热电联产系统经济调度策略,以完全分布式的形式克服传统集中式经济调度中的缺陷.在所构建的热电联产系统模型中,将各机组电能和热量的增量成本作为一致性变量,在经过一致性算法的迭代计算后可以达到收敛,即增量成本达到一致,保持实现发电成本经济最优.通过理论分析和MATLAB仿真分析可以得出如下结论:

(1) 所提基于一致性算法的完全分布式经济调度策略在负荷变化和机组的投切时,仍可以使机组的增量成本达到收敛,即系统具有良好的鲁棒性,满足“即插即用”的要求.

(2) 当某个机组为了提升自身利益在与相邻机组通信中传输带有偏差的一致性变量值时,各机组的增量成本将不能收敛,无法满足系统经济最优.在自私行为发生后给机组加入了补偿量,各机组的增量成本又达到收敛,即个别机组的自私行为能够被消除,以恢复系统发电成本最小.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

江婷, 邓晖, 陆承宇, 等.

电能量和旋转备用市场下电-热综合能源系统低碳优化运行

[J]. 上海交通大学学报, 2021, 55(12): 1650-1662.