基于PMU梯度动态偏差的新型电力系统快速稳定性

doi:10.16183/j.cnki.jsjtu.2022.370

基于PMU梯度动态偏差的新型电力系统快速稳定性

于淼¹^,²^,³, 胡敬轩^,¹^,², 张寿志¹^,², 魏静静¹^,², 孙建群¹^,², 吴屹潇¹^,²

1.北京建筑大学机电与车辆工程学院,北京 100044

2.北京市建筑安全检测工程技术研究中心, 北京100044

3.清华大学电力系统及发电设备安全控制和仿真国家重点实验室,北京 100084

Fast Stability of New Power System Based on a PMU Gradient Dynamic Deviation Method

YU Miao¹^,²^,³, HU Jingxuan^,¹^,², ZHANG Shouzhi¹^,², WEI Jingjing¹^,², SUN Jianqun¹^,², WU Yixiao¹^,²

1. School of Mechanical-Electronic and Vehicle Engineering, Beijing University of Civil Engineering and Architecture, Beijing 100044, China

2. Beijing Engineering Research Center of Monitoring for Construction Safety, Beijing 100044, China

3. State Key Laboratory of Control and Simulation of Power System and Generation Equipment, Tsinghua University, Beijing 100084, China

通讯作者: 胡敬轩,硕士生,电话(Tel.): 010-61209603;E-mail:olivermiaoer@163.com.

责任编辑: 孙伟

收稿日期: 2022-09-23 修回日期: 2022-12-8 接受日期: 2022-12-30

基金资助:

清华大学电力系统及大型发电设备安全控制与仿真国家重点实验室基金资助项目(SKLD20M17)
北京市高等教育学会项目(YB2021131)
北京建筑大学金字塔人才培养工程项目(JDYC20200324)
北京建筑大学研究生创新项目(PG2022132)
国家级大学生创新创业训练计划项目(202110016052)
国家自然科学基金委青年科学基金资助项目(51407201)

Received: 2022-09-23 Revised: 2022-12-8 Accepted: 2022-12-30

作者简介 About authors

于淼(1982-),博士,副教授,现主要从事电力系统辨识与控制研究.

摘要

在能源转型和科技进步双重推动下,高比例可再生能源和高比例电力电子设备正成为电力系统发展重要趋势和关键特征.新型电力系统动态行为随之发生重大变化,传统小干扰稳定性分析方法满足使用需要,在应对运行工况快速变化场合时尚存在亟需解决问题.提出基于同步相量测量装置(PMU)数据梯度动态偏差李雅普诺夫直接分析法对新型电力系统小干扰稳定性进行分析,利用PMU数据矩阵降维得到低维矩阵,代入含双馈异步风力发电机组的电力系统矩阵模型,求解李雅普诺夫方程式得到对角矩阵,通过判定矩阵正定性对系统稳定性作出判断.利用求解后得到的对角矩阵计算相应状态变量动态偏差值,对相应状态变量曲线使用梯度下降法迭代计算该曲线极值点数值,时间加权计算整个振荡过程时间加权动态偏差量,为阻尼稳定控制器配置位置提供指导.利用含风力发电新英格兰10机39节点系统仿真验证方法可以达到改善系统小干扰稳定性以及对新型电力系统快速稳定性分析的有效性.

关键词： 同步相量测量装置数据; 新型电力系统; 稳定性分析; 李雅普诺夫直接法; 梯度动态偏差

Abstract

The high proportion of renewable energy and power electronic equipment is emerging as a significant trend and key characteristic of the power system development driven by the dual promotion of the energy transformation and scientific technological advancement. Major modifications have been made to the dynamic behavior of the new power system. The traditional small signal stability analysis approach is difficult to apply, and there are still urgent issues to be resolved for the quick change of operating conditions. In this paper, a Lyapunov direct analysis method of gradient dynamic deviation based on phasor measurement unit (PMU) data is proposed to analyze the small signal stability of the new power system. First, the PMU data matrix is used to reduce the dimension to obtain the low dimension matrix, which is substituted into the power system matrix model with a doubly-fed induction generator (DFIG). The diagonal matrix is obtained by solving the Lyapunov equation, and the positive definiteness of the matrix is determined to judge the system stability. Then, the dynamic deviation of corresponding state variable is calculated by solving the obtained diagonal matrix. The gradient descent method is applied to the corresponding state variable curve to iterate the extreme point value of curve. The time-weighted dynamic deviation of the whole oscillation process is calculated by time weighting, which provides guidance for the subsequent configuration position of damping stability controller, i.e., power system stabilizer (PSS). The method can improve the small interference stability of the system. The effectiveness of the fast stability analysis of the new power system is verified by simulations of the new England 10-machine 39-bus system with DFIG.

Keywords： phasor measurement unit (PMU) data; new power system; stability analysis; Lyapunov direct method; gradient dynamic deviation

PDF (2171KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

于淼, 胡敬轩, 张寿志, 魏静静, 孙建群, 吴屹潇. 基于PMU梯度动态偏差的新型电力系统快速稳定性[J]. 上海交通大学学报, 2024, 58(1): 40-49 doi:10.16183/j.cnki.jsjtu.2022.370

YU Miao, HU Jingxuan, ZHANG Shouzhi, WEI Jingjing, SUN Jianqun, WU Yixiao. Fast Stability of New Power System Based on a PMU Gradient Dynamic Deviation Method[J]. Journal of Shanghai Jiaotong University, 2024, 58(1): 40-49 doi:10.16183/j.cnki.jsjtu.2022.370

随着电力系统核心设备电力电子化发展以及新能源发电快速变革,当前电力系统呈现出向高比例可再生能源以及电力电子设备“双高”发展态势.同时输电网中高压大容量变流设备持续推广以及配用电侧电力电子技术广泛应用,将逐步成为新一代电力系统重要技术特征.在新型电力系统中,大型同步发电机组被小型电源替代,海量分布式电源、电动汽车、分布式储能等以电力电子为接口的新型设备从中低压侧接入系统,使得稳定性分析中需要考虑动态元件数目可能达到十万到百万量级^[1],并且各类设备动态特性差异相对较大,呈现出高度异构性.对新型电力系统小干扰稳定性分析需要解决由于维数爆炸引发的计算负担、通信负担等严峻挑战^[2].此外,电力系统变化时间尺度在稳定性分析模型中可以视为恒定时间,现有稳定性分析理论与工具多是针对给定平衡点进行,当平衡点变化时,稳定性分析需要重新进行.新能源供能所引起的波动以及来自大量电力电子设备频繁投切和系统拓扑结构高速变化,使得新型电力系统运行位置变化更加快速^[3].因此,深入研究新型电力系统小干扰稳定性机理迫在眉睫.

从我国未来新型电力系统“双碳”目标方面出发,肖先勇等^[4]阐述未来新型电力系统对“双碳”贡献.在此基础上,论述构建新型电力系统关键技术,总结建设新型电力系统将要面对的主要挑战.文献[5]中针对我国“30·60双碳”目标和新型电力系统建设背景,阐述我国燃气发电发展前景,提出我国新型电力系统安全低碳发展若干建议.文献[6]中阐述在“双碳”目标下研究清洁电力发展路径具有重要意义,分析我国水、风、光等清洁能源储量及其特征,预测中长期电力需求,提出我国未来清洁电力发展的对策与建议.

在新型电力系统稳定性分析研究方面,文献[7]中从分析“双高”电力系统特点出发,对经典稳定性进行概述以及简要归纳,探讨经典稳定性分类适用性,最后尝试提出一种新的稳定性分类方法,以求在经典分类逻辑上兼容“双高”电力系统稳定性分析.文献[8]中对电力系统由于小干扰产生失稳现象进行总结与归纳,再结合“双高”系统特性与需求,探讨现有研究理论方法不足.文献[9]中基于电力系统提出宽频振荡广域监测与预警系统分析方法,并通过模拟振荡场景验证该系统有效性.文献[10 ⇓-12]中主要对非线性系统以及新型并网电力系统稳定平衡点、稳定域及建模进行分析和研究,对直接法研究结果具有一定参考价值.文献[13 ⇓⇓-16]中以新型电力系统为研究对象,基于李雅普诺夫直接法理论对系统不同扰动形式稳定性进行分析,并对所提方法进行仿真验证.文献[17]中基于系统稳定性分析方法,提出适用于新型电力系统稳定判据以及稳定性分类思路.文献[18]中基于等系统模型分析策略,依据所提方法进行阻尼稳定控制器参数设计,提出优化函数进行参数计算新思路,在特定工况下进行阻尼稳定控制器参数配置.文献[19]中综述目前大型风力发电(简称风电)机组实现惯量控制,从稳定性分析、控制系统优化、性能分析与评估等方面,介绍惯量控制在双馈风电机组以及全功率风电机组的研究与工程现状.文献[20]中研究随机扰动下电力系统强迫振荡特点,基于同步机机械功率上随机扰动功率谱密度模型,为多机系统建立模态叠加形式频率响应模型,由功率谱密度分析方法得到同步机功角的功率谱密度表达式,进而分析随机扰动下系统强迫振荡的4个影响因素.

综上文献研究发现,当前新型电力系统小干扰稳定性研究普遍使用基于增广状态矩阵描述线性化模型.此种模型实现较为复杂,且编程繁琐,为后续计算分析带来极大不便.现有新型电力系统稳定性分析方法对应对运行工作点快速变化尚存在亟需解决问题,对小扰动稳定分析提出更高要求.传统小干扰稳定性分析特征值法会产生由于维数过高而引起的计算负担,对电力系统运行工作点快速变化情况无法做到快速稳定性分析,并且单纯求解特征值无法为之后控制提供理论指导依据.为解决上述问题,提出一种基于李雅普诺夫函数直接分析法的新型电力系统快速稳定性研究方法,利用同步相量测量装置(PMU)广域监测系统数据,在理论上考虑运行工况不确定稳定性,为实现小干扰稳定性增强控制策略提供基础,可实现对新型电力系统小干扰稳定性快速分析,并可在实际应用中改善系统稳定性.

1 基本理论

1.1 梯度下降法

梯度下降法^[21]是经典优化方法之一,通常用于无约束问题.梯度下降法的依据是对某个具体函数而言,沿梯度正方向函数值增加速度最快,与之相反,函数值减少最快.

假设希望求解目标函数f(x)=(x₁,x₂,…,x_n)的最小值可以从一个初始点 $x_{n}^{(0)}$ =( $x_{1}^{(0)}$ , $x_{2}^{(0)}$ ,…, $x_{n}^{(0)}$ )开始,基于学习率η>0开始构建一个迭代过程;当迭代次数i≥0时,

(1)

\begin{array}{l} x_{1}^{(i + 1)} = x_{1}^{(i)} - η \frac{\partial f}{\partial x_{1}} x^{(i)} \\ \dots \\ x_{n}^{(i + 1)} = x_{n}^{(i)} - η \frac{\partial f}{\partial x_{n}} x^{(i)} \end{array}\}

式中:

(2)

x_{n}^{(i)}

x_{1}^{(i)}

x_{2}^{(i)}

,…,

x_{n}^{(i)}

)

在达到收敛条件时,迭代结束.由梯度下降法迭代公式可知,下一个点选择与当前点位置和梯度相关;反之,如果要计算函数的最大值,沿着梯度反方向前进即可.从整体看,无论是计算函数的最大值或最小值,都需要构建一个迭代关系λ':

(3)$x^{(0)} \stackrel{\lambda^{\prime}}{\longrightarrow} x^{(1)} \stackrel{\lambda^{\prime}}{\longrightarrow} x^{(2)} \stackrel{\lambda^{\prime}}{\longrightarrow} \cdots$

即对所有的i,都满足迭代关系.从而可以得到梯度下降法函数表达式:

(4)λ(x)=x-ηf(x)

1.2 新型电力系统稳定性直接法分析模型

对于实际大型电力系统性能分析而言,要建立整个新型电力系统高阶数学模型难度较大,即便建立出模型,在实际应用过程中也会产生诸如维数爆炸、模型过于复杂、计算过于繁琐等问题.为规避电力系统模型建立过于复杂,文献[22]中提出将大型电力系统中每个发电机模型假定为一个子系统,各子系统通过传输网络互相连接,在考虑子系统模型及其相互作用条件的情况下,通常采用子系统模型代替整个系统模型进行稳定性分析.对于整个系统统一的惯性中心,在某一区域发生振荡时,总存在表现为两组发电机之间相对摇摆的减速与加速机组,上述机组可以简化为一个由两台等值发电机构成互联的电力系统等效研究^[23],等值系统机间振荡对应原系统的区间振荡.当发生低频振荡时,两台发电机转速增量和功角增量具有同频反向正弦振荡的特点.

首先对于PMU所持续采集到的原始大数据,采用文献[24]中的方法进行筛选与降维预处理,建立数据矩阵,利用数据降维方法将高维矩阵降阶到低维矩阵,代入电力系统状态方程中,从而可以利用PMU所采集到的数据代入数据矩阵中对新型电力系统稳定性进行分析.基于同步发电机模型进行推导,利用接入双馈异步风力发电机组(DFIG)的电力系统状态矩阵代替新型电力系统模型进行分析,并依据其已被证明有效性的降阶模型进行进一步稳定性分析.

在对新型电力系统小扰动稳定性分析时,为降低整个系统状态方程组阶数,避免维数过高等计算问题,在实际应用中,转子阻尼绕组时间常数较小,在满足实际应用情况下可以适当忽略.当忽略阻尼绕组等效d、q轴以及阻尼g的作用,只在计算中考虑励磁绕组暂态以及转子动态的三阶模型时,励磁系统采用一阶线性环节表示,发电机模型可降为如下所示三阶模型,其中状态量分别为q轴暂态电动势E'_q、电角速度ω、功角δ,以下为模型推导过程.

发电机励磁绕组方程:

(5)T'_d₀pE'_q=E_f-E'_q-(X_d-X'_d)i_d

式中:T'_d₀为定子开路时间常数;p为微分算子;E_f为励磁系统电动势;X_d为d轴同步电抗;X'_d为d轴暂态电抗;i_d为d轴电流.

定子电压方程:

(6)u_d=X_qi_q-r_ai_d

(7)u_q=E'-X'_di_d-r_ai_q

式中:u_d为d轴电压;u_q为q轴电压;X_q为q轴同步电抗;i_q为q轴电流;r_a为电枢电阻.

转子运动方程:

(8)T_J

\frac{d ω}{d t}

+D(ω-1)=T_m-E'_qi_q+(X'_d-X_q)i_qi_d

(9)

\frac{d δ}{d t}

=ω-1

式中:T_J为发电机组的惯性时间常数;D为转轴定阻尼常数;T_m为原动机输出机械力矩.

进一步忽略f绕组的暂态过程,上述模型可以降阶为发电机经典二阶实用模型即负荷采用恒阻抗模型:

(10)

\begin{array}{l} u_{d} = X_{q} i_{q} - r_{a} i_{d} \\ u_{q} = E'_{q} - X'_{d} i_{d} - r_{a} i_{q} \\ T_{J} \frac{d ω}{d t} = T_{m} - E'_{q} i_{q} + (X_{d} - X_{q}) i_{q} i_{d} - \\ D (ω - 1) \\ \frac{d δ}{d t} = ω - 1 \end{array}\}

当发电机组采用二阶经典模型时,前文所述等效两台等值发电机系统转子运动方程组为

(11)

\begin{array}{l} Δ {\overset{\cdot}{δ}}_{1} = Δ ω_{1} \\ Δ {\overset{\cdot}{δ}}_{2} = Δ ω_{2} \\ Δ {\overset{\cdot}{ω}}_{1} = \frac{- Δ P_{1 e} - D_{1} Δ ω_{1}}{M_{1}} \\ Δ {\overset{\cdot}{ω}}_{2} = \frac{- Δ P_{2 e} - D_{2} Δ ω_{2}}{M_{2}} \end{array}\}

式中:Δδ₁和Δδ₂分别为两台发电机的功角增量;Δω₁和Δω₂分别为两台发电机的转速增量;M₁和M₂、D₁和D₂分别为两台发电机惯性时间常数和阻尼力矩系数;ΔP₁_e和ΔP₂_e为电磁功率增量.

考虑新型电力系统中电力系统核心设备的变化以及新能源发电大规模的应用,风电已经成为现今主流的分布式发电形式之一,本文应用接入DFIG电力系统矩阵进行分析,给出新型电力系统状态矩阵:

(12)x=[Δδ₁ Δδ₂ Δω₁ Δω₂]^T

(13)A=

[\begin{array}{l} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ - \frac{K_{12}}{M_{1}} & \frac{K_{12}}{M_{1}} & - \frac{D_{1}}{M_{1}} + \frac{K_{13}}{M_{1}} & 0 \\ - \frac{K_{12}}{M_{2}} & \frac{K_{12}}{M_{2}} & \frac{K_{13}}{M_{2}} & - \frac{D_{2}}{M_{2}} \end{array}]

式中:x为状态偏差列向量;A为状态空间矩阵.

(14)K₁₂=

\frac{k_{1} k_{2}}{k_{1} + k_{2}}

, K₁₃=

\frac{k_{1} k_{3}}{k_{1} + k_{3}}

电磁功率方程可表示为

(15)

\begin{array}{l} Δ P_{1 e} = k_{1} (Δ δ_{1} - Δ δ_{w}) \\ Δ P_{2 e} = k_{2} (Δ δ_{w} - Δ δ_{2}) \end{array}\}

风电场的动态有功表示为

(16)

\begin{array}{l} Δ P_{w 1} = k_{3} Δ ω_{1} \\ Δ P_{w 2} = k_{4} Δ ω_{2} \end{array}\}

式中:k₁=(E₁V_w₀/X₁₃)cos(δ₁₀-δ_w₀)∝1/X₁₃; k₂=(-E₂V_w₀/X₂₃)cos(δ_w₀-δ₂₀)∝1/X₂₃;k₃=g₁g₂∝ΔP_w; k₄=g₁g₃∝ΔP_w. 其中:E₁和E₂分别为区域1和区域2的电动势;V_w₀为风电场接入点电压初始值,δ_w₀为风电场接入点相位增量Δδ_w的初始值;X₁₃和X₂₃分别为两台发电机到风电场接入点的电抗;g₁, g₂, g₃为风电场动态频率特性模值,各变量下标中的0表示初始值.

2 基于梯度动态偏差李雅普诺夫直接法稳定性分析

2.1 李雅普诺夫直接法

李雅普诺夫直接法借助一个李雅普诺夫能量函数V(x(t))及根据微分方程所计算得到的V沿着轨迹导数符号性质直接推断稳定性问题^[25].考虑以下一般非线性自治动力系统:

(17)

\overset{\cdot}{x}

(t)=f(x(t))

系统存在以下状态方程式:

(18)

\overset{\cdot}{x}

=Ax

对于线性定常系统而言,找到一个使得状态在原点平衡渐近稳定充分必要条件为:对于任意给定的一个对称正定矩阵Q,一定存在唯一一个正定对称矩阵P,使得原线性定常系统状态方程成立.对于其平衡状态达到大范围渐近稳定充分必要条件以代数方程表示为

(19)A^TP+PA=-Q

并且有

(20)V(x)=x^TPx

V(x)称作该系统的李雅普诺夫能量函数,被用作系统稳定性分析.由于正定实对称矩阵Q任意给定,为计算简便,下文计算取Q为单位矩阵.将矩阵A代入系统状态式(18),建立李雅普诺夫方程式(19),求解方程式可得对称矩阵P,通过对称矩阵P正定性判定可以对系统稳定性进行判断.

2.2 新型电力系统小干扰状态变量偏差值

利用以下对角矩阵代入求解计算系统某个状态变量偏差:

(21)Q_J=diag[…,0]

若求解某个状态变量的偏差量,取相对应的对角矩阵元素为1,其余为0即可.当式(21)中描述系统已被判定为稳定后,借助李雅普诺夫方程所得矩阵求取状态变量积分值^[16]如下:

(22)J=

\int_{0}^{\infty}

x^TQ_Jxdt

(23)Q_J=diag(q₁,q₂,…,q_n)

在计算中,用单位矩阵I代入Q_J矩阵,可得下式:

(24)J=-

\int_{0}^{\infty}

(x^TA^TP_Jx+x^TP_JAx)dt

(25)J=x^TP_Jx

式中:P_J为对称矩阵,将Q_J和A代入式(19)可求得.J值能够反映系统状态偏差量的动态稳定性,J值越小,表明状态偏差量衰减速度快且振荡幅度小,动态过程短,系统小干扰稳定性好^[16].

2.3 基于梯度下降法的状态响应曲线时间加权动态偏差值

当分别分析每个发电机组时,为计算简便,且起到与上述积分状态偏差量近似效果,提出一种基于状态量曲线梯度下降偏差的时间加权值,用于描述单个状态量的低频振荡过程,对状态量的动态过程进行分析评价,且可以对稳定过程进行分析.首先以振荡曲线为梯度下降的目标函数:

(26)x(t)=(t₁,t₂,…,t_n)

对该函数进行如下梯度下降迭代过程,当i>0时有:

(27)

t_{1}^{(i + 1)}

t_{1}^{(i)}

-η

\frac{d f}{d t_{1}}

t⁽ⁱ⁾

…

(28)

t_{n}^{(i + 1)}

t_{n}^{(i)}

-η

\frac{d f}{d t_{n}}

t⁽ⁱ⁾

一旦达到收敛条件,在梯度为零点时求得该点极值,梯度下降迭代结束.由梯度下降法迭代公式可知,下一个点选择和当前点位置与其梯度相关.反之,如果计算函数最大值,沿着梯度反方向前进即可.如此反复,即可计算出整条曲线每次振荡波峰以及波谷极值点数值.从整体来看,无论是计算函数最大值或最小值,都需要构建如下迭代关系h:

(29)h(t)=t-ηf(t)

在经过本文直接法判定系统稳定性步骤后,如果系统已经可被判定为稳定,则记录整个振荡过程时间,对该状态变量曲线使用梯度下降法,迭代计算出该曲线每次振荡波峰以及波谷极值点数值,依据每次振荡过程时间在整个振荡过程占比加权计算出整个振荡过程极值偏差量,并以该值来具体评估单个机组单一状态量振荡剧烈程度.设t_i为波峰到波谷之间的时间间隔,α_i为波峰/波谷,具体加权偏差值计算式如下:

(30)

\overset{m}{\sum_{i = 1}}

(α_i-α_i₊₁)²t_i

2.4 基于PMU数据的梯度动态偏差李雅普诺夫直接法实现

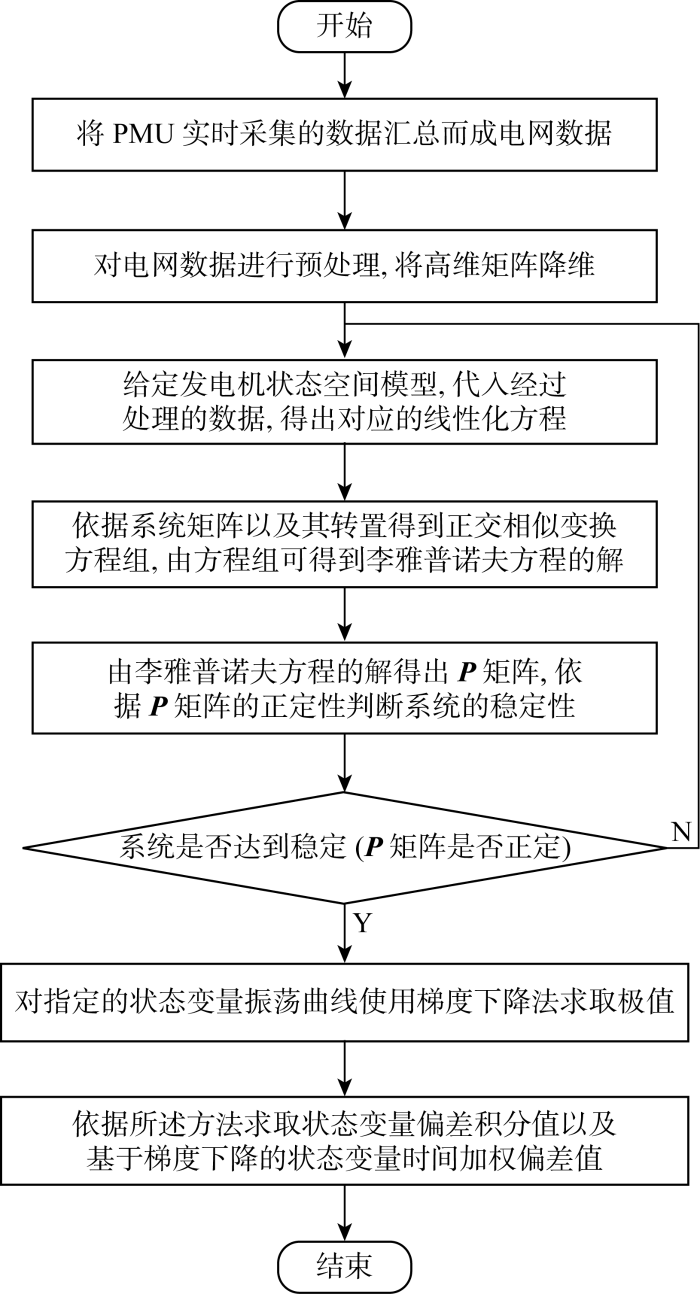
提出基于梯度动态偏差李雅普诺夫直接法对新型电力系统稳定性分析,具体实现流程图如图1所示.算法步骤如下:

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 基于梯度动态偏差李雅普诺夫直接法流程图

Fig.1 Flow chart of gradient dynamic deviation Lyapunov direct method

步骤1 将PMU数据进行汇总形成电网数据,对PMU所实时采集到的数据进行降维预处理,生成小干扰稳定性分析模型需要的数据矩阵.

步骤2 采用二阶同步发电机模型代替整个电力系统模型进行小干扰稳定性分析,并给出前文已推导接入风电机组新型电力系统小干扰稳定性分析所需要的状态空间矩阵A.

步骤3 将经过处理的PMU数据带入状态空间矩阵A,利用MATLAB中命令求解李亚普诺夫方程,并利用其求解式(19).在求解方程式时,由于正定实对称矩阵Q任意给定,为计算简便,故可以取Q为单位矩阵I,可以快速解出正定对称矩阵P.通过矩阵P的正定性来判定电力系统稳定性,借助李雅普诺夫方程分析系统稳定性比较简捷快速.基于已推导出接入DFIG电力系统状态空间矩阵A,采用直接法已求取P矩阵对新型电力系统进行小干扰稳定性分析.

步骤4 借助李雅普诺夫方程求出的矩阵P获取所求状态偏差量平方积分值,实际上是系统各状态偏差量平方在正无穷时间轴上的积分之和;在系统被判定稳定之后,根据矩阵对角元素取值不同求得各状态偏差量平方积分值加权和,可以对已被判定稳定系统进行动态过程描述.如果仅关心部分状态变量动态过程,可以利用求取偏差变量平方积分值方法分析该系统达到稳定的动态过程,且某个单独动态偏差量可以通过对角矩阵代入求解.

步骤5 为了单个状态量偏差计算方便,且起到与积分状态偏差量近似作用,在经过直接法判定系统小干扰稳定性步骤后,如果系统已被判定为稳定,此时记录下整个振荡过程时间,对该状态变量曲线使用梯度下降法,迭代计算出该曲线每次振荡波峰以及波谷极值点数值.依据式(30),每次振荡过程时间在整个振荡过程的占比加权计算出整个振荡过程极值偏差量.

3 算例仿真

3.1 小干扰稳定性直接法算例分析

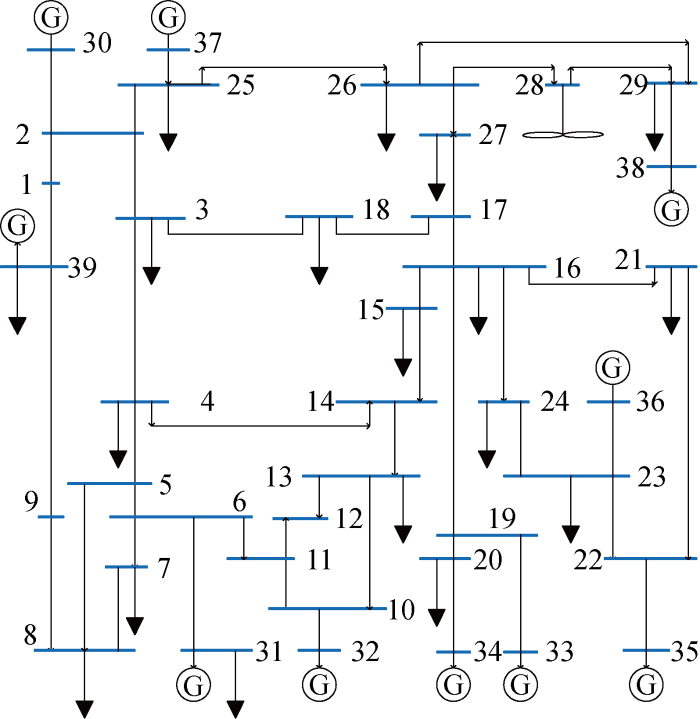
将IEEE 10机39节点新英格兰系统^[26]接入风电场,如图2所示.图2中每个节点处均安装 PMU,系统电压等级为 345 kV,频率为 60 Hz,采样频率为 3 kHz,系统中各母线负荷设置为恒功率模型.首先,在节点28和节点29处加入PMU数据,并分出一条支路,由多台DFIG风力机等效为一个风电场.然后,借助文献[22]中实测PMU数据,选择其中 0~179.9 s时间段所采集到的电流电压幅值、相角,采用文献[24]中方法对数据进行预处理,将高维矩阵降维生成稳定性分析需要的参数矩阵,将PMU数据代入状态空间A矩阵中,运用前文所提李雅普诺夫直接法对算例系统进行小扰动稳定性分析计算.使用MATLAB设计稳定性判定以及计算指标函数值的算法程序.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 风电场接入新英格兰10机39节点系统结构

Fig.2 System structure of new England 10-machine 39-bus system with wind farm

利用2.4节所述算法步骤分别对WSCC 3机系统、中国电科院6机系统以及新英格兰10机系统应用特征值法和直接法进行稳定性判定,分析结果如表1所示.可知,两种方法呈现判定结果一致,表明采用李雅普诺夫直接法可以准确可靠地判定电力系统稳定性,且不会因为某些参数省略导致判定错误结果.

表1 特征值法与直接法稳定性判定结果

Tab.1 Stability determination results of eigenvalue method and direct method

算例系统	特征值,λ<0	矩阵P正定
WSCC 3机系统	是	是
中国电科院6机系统	是	是
新英格兰10机系统	否	否

新窗口打开| 下载CSV

3.2 不同风电场出力下新型电力系统低频特性影响

参照文献[27],设置区域1向区域2送电,风电机组在送电侧,输送距离为25 km,在增大风电场输出功率同时调整同步发电机的输出功率,保持联络线传输功率为400 MW不变,其中风电场输出功率占区域1总输出功率比例用风力场出力表示,新型电力系统区域间振荡模式变化情况如表2所示.可知,随着风电场出力的增加,区域间振荡模式1的振荡频率和阻尼比在总体上均表现为增大趋势;区域间振荡模式2的振荡频率逐渐增大,但是阻尼比却逐渐减小.

表2 新型电力系统区域间振荡模式随风电场出力变化

Tab.2 Variation of inter-area oscillation mode of new power system with output of wind farm

模式	风电场出力/%	特征根	阻尼比	振荡频率/Hz
区域间振荡模式1	0	-0.8405±j3.6049	0.2271	0.5737
	3	-0.8458±j3.6222	0.2274	0.5765
	6	-0.8499±j3.6268	0.2281	0.5772
区域间振荡模式2	0	-0.5692±j0.5288	0.7326	0.0842
	3	-0.5729±j0.7247	0.6202	0.1153
	6	-0.5569±j0.7863	0.5779	0.1251

新窗口打开| 下载CSV

3.3 状态偏差平方积分值的低频振荡算例分析

在电力系统发生小干扰时,机电模式最小阻尼比常作为低频振荡评价指标,文献[16]中按照动态最小阻尼比配置准则对电力系统进行阻尼稳定控制器(PSS)配置,并给出特征值法所得最小阻尼比.本文采用的系统动态偏差平方积分值法利用系统状态矩阵A建立李雅普诺夫方程组,调用 MATLAB 中李雅普诺夫方程函数解出矩阵P,判定矩阵P正定性,从而利用直接法判断系统稳定性.根据前文所述动态偏差值方法,借助李亚普诺夫方程求得指标函数值即各状态偏差量加权平方积分值,动态偏差方积分值能够反映系统状态偏差量动态性能.

表3列出文献[16]中最小阻尼比以及动态偏差量平方积分值计算结果,最小阻尼比是广为应用的低频振荡评价指标,而动态平方积分值也可以对系统性能进行分析.如表3所示,随着PSS在系统中配置数量越来越多,最小阻尼比也越来越大,表明系统稳定性越来越好.

表3 算例系统稳定性分析过程

Tab.3 Stability analysis process of example system

已配置PSS机组	最小阻尼比	动态偏差量平方积分值
1,2	0.0243	0.6765
1,2,9	0.0245	0.6486
1,2,9,7	0.0272	0.6375
1,2,9,7,4	0.0288	0.6055
1,2,9,7,4,5	0.0654	0.5994
1,2,9,7,4,5,3	0.0916	0.5732
1,2,9,7,4,5,3,8	0.0963	0.5629
1,2,9,7,4,5,3,8,10	0.1057	0.4968

新窗口打开| 下载CSV

3.4 依据状态变量曲线时间加权梯度动态偏差值PSS配置

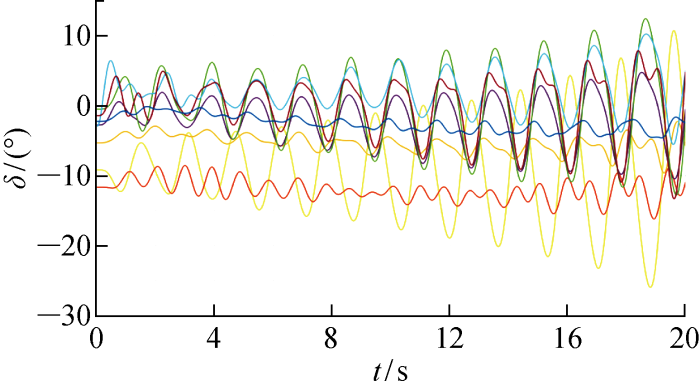
利用所得指标函数值对算例系统小扰动稳定性进行分析,以验证方法的可行性及正确性.由文献[27]可知,在新英格兰10机39节点系统中6#机组为等值机,故不需要设计PSS.动态阻尼比配置方法可用于配置PSS位置确定,从而达到优化及电力系统小干扰稳定性目的.在MATLAB软件Simulink中搭建含风电新英格兰10机39节点系统,在该系统中6#机组构建小干扰信号模块,模拟系统受到小干扰低频振荡,从而达到对系统进行小干扰稳定性分析目的.利用所求取状态变量曲线时间加权梯度动态偏差值描述系统受到小干扰后发电机组低频振荡动态过程,通过对系统中不同机组低频振荡动态偏差值比较,对系统中振荡幅度大且振荡时间长机组进行PSS配置,发电机未配置PSS功角振荡情况如图3所示,各发电机组状态曲线时间加权梯度偏差和阻尼比如表4所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 发电机未配置PSS功角振荡

Fig.3 Power angle oscillation of generator without PSS configuration

表4 各发电机组状态曲线时间加权梯度偏差和阻尼比

Tab.4 State curve time-weighted gradient deviation and damping ratio of each generator unit

发电机机组编号	状态曲线时间加权梯度偏差值	该工况下机组阻尼比
1	0.03569	0.0339
2	0.02602	0.0403
3	0.03271	0.0392
4	0.07179	-0.0017
5	0.08368	0.0331
7	0.05546	-0.0175
8	0.06102	0.0187
9	0.04219	-0.0070
10	0.04847	-0.0078

新窗口打开| 下载CSV

3.5 依据状态变量曲线时间加权梯度动态偏差值与动态最小阻尼比配置方法PSS配置

为进一步验证所提状态变量曲线时间加权梯度动态偏差值对PSS配置可行性和有效性,针对算例仿真系统,按照表4数据采用本文方法所得功角动态偏差平方积分值对系统PSS进行配置,配置PSS机组结果分别为4#、5#、7#、8#、10#机组.同时根据文献[16],利用动态最小阻尼比法对发电机组配置PSS用于应用效果对比,配置PSS机组结果分别为1#、2#、4#、7#、9#机组.因此,在新型电力系统中配置PSS改善系统小干扰稳定性,对同一系统采用不同PSS配置方案,可通过振荡曲线直观反映振荡动态过程以及电力系统小干扰稳定性改善性能,已配置PSS发电机功角振荡如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

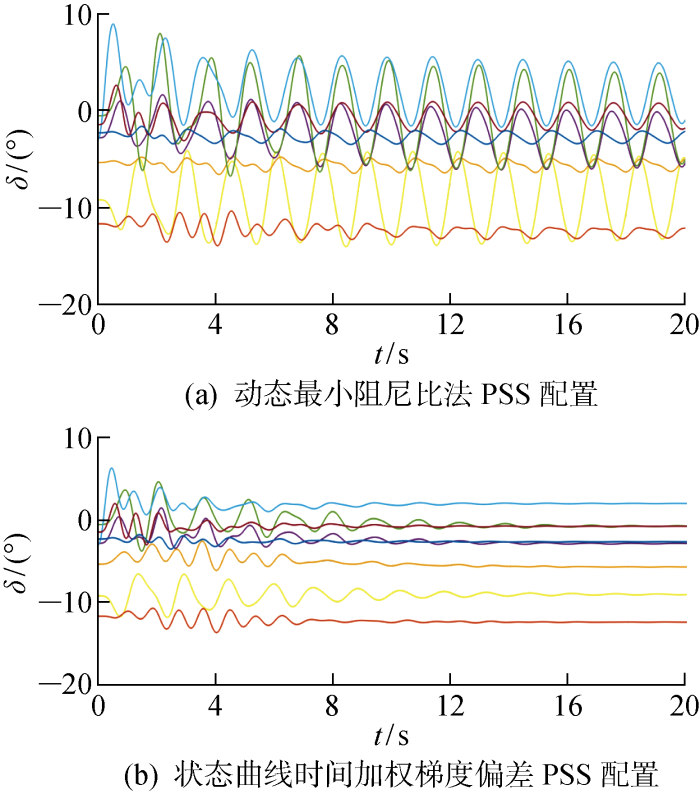
图4 已配置PSS发电机功角振荡

Fig.4 Power angle oscillation of generator with PSS configuration

由图3与图4对比可知,与配置前相比,算例系统机组配置PSS后稳定性有所提升,功角波动程度明显减小,说明依据动态阻尼比配置方法以及依据状态曲线时间加权偏差值配置方法的有效性,但本文提出的功角偏差时间加权值可反映出所有机组在时间区间上振荡幅度,因此可更准确全面地反映系统动态过程.进一步对比图4(a)和图4(b)可知,状态曲线时间加权梯度偏差PSS配置系统低频振荡过程时间显著缩短,并且振荡幅度也得到降低,故本文所提依据状态曲线时间加权梯度偏差PSS配置法在特定情况下具有显著有效性和可行性.

4 结语

在“30·60”碳达峰碳中和背景下,未来电力系统将会发生结构性变化,研究新型电力系统小干扰稳定性机理意义重大.针对目前新型电力系统中存在影响稳定性问题,提出基于PMU数据的梯度动态偏差李雅普诺夫直接分析机制,在建立新型电力系统稳定性直接法分析所需二阶模型基础上,将李雅普诺夫直接法、新型电力系统小干扰状态变量偏差值以及基于梯度下降法的状态响应曲线时间加权动态偏差值有机结合,完成基于PMU数据的梯度动态偏差李雅普诺夫直接法的实现.根据含风电新英格兰10机39节点系统,从小干扰稳定性直接法算例分析、不同风电场出力下新型电力系统低频特性影响、状态偏差平方积分值的低频振荡算例分析、依据状态变量曲线时间加权梯度动态偏差值PSS配置以及依据状态变量曲线时间加权梯度动态偏差值与动态最小阻尼比配置方法PSS配置5个方面验证方法的正确性和有效性.结果表明,本文方法可缩短系统振荡过程,在PSS配置数量相对有限情况下能够提升新型电力系统小干扰稳定性.此外,新能源引起发电波动性以及来自大量电力电子设备频繁投切和系统拓扑结构改变,导致新型电力系统的运行点变化更快速,本文方法对系统动态过程评估还没有统一评价指标,后续将进一步研究新型电力系统小干扰稳定方法适应性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

QUINT

, DANGELMAIER

, GREEN

, et al.

Transformation of the grid: The impact of distributed energy resources on bulk power systems

[J]. IEEE Power and Energy Magazine, 2019, 17(6): 35-45.