双馈风电场抑制电网低频振荡的自适应附加控制策略

doi:10.16183/j.cnki.jsjtu.2022.135

双馈风电场抑制电网低频振荡的自适应附加控制策略

刘新宇^,¹, 王森¹, 曾龙², 原绍恒¹, 郝正航³, 逯芯妍¹

1.华北水利水电大学电力学院,郑州 450011

2.广东工业大学自动化学院,广州 510006

3.贵州大学电气工程学院,贵阳 550025

An Adaptive Additional Control Strategy for Suppressing Low-Frequency Grid Oscillations in Doubly-Fed Wind Farms

LIU Xinyu^,¹, WANG Sen¹, ZENG Long², YUAN Shaoheng¹, HAO Zhenghang³, LU Xinyan¹

1. School of Electric Power, North China University of Water Resources and Electric Power, Zhengzhou 450011, China

2. School of Automation, Guangdong University of Technology, Guangzhou 510006, China

3. The Electrical Engineering College, Guizhou University, Guiyang 550025, China

责任编辑: 王历历

收稿日期: 2022-05-3 修回日期: 2022-06-28 接受日期: 2022-11-28

基金资助:

河南省高等学校重点科研项目(21A120006)

Received: 2022-05-3 Revised: 2022-06-28 Accepted: 2022-11-28

作者简介 About authors

刘新宇(1976-),副教授,从事控制理论与控制工程、新能源发电与智能电网、模式识别与智能系统研究.E-mail:lxy@ncwu.edu.cn.

摘要

针对大型风电场跨区输送电能时引起的弱或负阻尼低频振荡问题,提出一种基于李雅普诺夫稳定性理论的快速终端滑模附加阻尼控制策略.研究双馈风力发电机(DFIG)灵活的功率调控特性和快速响应阻尼调节能力,根据DFIG转子外加电压与磁链之间的关系和滑模变结构控制方法设计转子磁链控制器.在系统发生低频振荡时,期望磁链值与实际磁链值产生偏差,附加阻尼控制器输出一个自适应控制信号到转子侧功率控制环节,提高风电场有功出力,抑制系统的低频振荡.在MATLAB/Simulink中建立风电并网系统仿真模型进行离线仿真实验,并搭建基于实时数字仿真系统的大型风电场跨区输电模型进行实时仿真验证.离线仿真和实时仿真结果均表明:当系统发生低频振荡时,应用所提控制方法能够快速调节DFIG发出有功功率,增强系统的阻尼水平,有效抑制系统低频振荡抑制.

关键词： 双馈风力发电机; 频率稳定性; 低频振荡; 李雅普诺夫稳定性; 滑模控制

Abstract

Aiming at the problem of weakly or negatively damped low-frequency oscillations caused by cross-zone transmission of electricity from large wind farms, this paper proposes a fast terminal sliding-mode additional damping controller based on the Lyapunov stability theory. By investigating the flexible power regulation characteristics and the capability of dynamic frequency response to damping regulation of doubly-fed wind turbines (DFIG), a rotor magnetic chain controller is designed according to the relationship between the applied voltage and magnetic chain of DFIG rotor and the sliding mode variable structure control method. When low-frequency oscillations occur in the system, the desired magnetic chain value will deviate from the actual magnetic chain value. The additional damping controller outputs an adaptive control signal for the rotor-side power control link to increase the active output of the wind farm and suppress low-frequency oscillations in the system. A simulation model of the wind power grid-connected system is established in MATLAB/Simulink for off-line simulations, and a real-time simulation experiment of a large wind farm cross-zone transmission model based on real time digital simulation system is conducted. The results of both off-line and real-time simulations show that when low-frequency oscillations occur in the system, the proposed control method can quickly regulate the active power emitted by the DFIG and enhance the damping level of the system, which is effective in suppressing low-frequency oscillations in the system.

Keywords： doubly-fed wind turbines (DFIG); frequency stability; low-frequency oscillation; Lyapunov stability; sliding mode control

PDF (4403KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘新宇, 王森, 曾龙, 原绍恒, 郝正航, 逯芯妍. 双馈风电场抑制电网低频振荡的自适应附加控制策略[J]. 上海交通大学学报, 2023, 57(9): 1156-1164 doi:10.16183/j.cnki.jsjtu.2022.135

LIU Xinyu, WANG Sen, ZENG Long, YUAN Shaoheng, HAO Zhenghang, LU Xinyan. An Adaptive Additional Control Strategy for Suppressing Low-Frequency Grid Oscillations in Doubly-Fed Wind Farms[J]. Journal of Shanghai Jiaotong University, 2023, 57(9): 1156-1164 doi:10.16183/j.cnki.jsjtu.2022.135

现代工业的迅猛发展已经造成对煤和石油等化石能源的过度依赖和严重的环境污染等一系列问题.由于风力发电(简称风电)不会污染环境且风能属于可再生能源,风能的充分利用对能源结构的调整和实现“双碳”目标具有重要意义.近些年,伴随着大规模风电并网的快速发展,建设更大规模的风电场以及远距离输电问题应运而生^[1].由于风能具有随机、不稳定的特点,而我国的用电负荷中心往往距离风电场比较远,输电线路负荷较重,加之风电场又处于相对薄弱的电网末端,所以给风电并网系统的稳定性造成较大影响^[2].

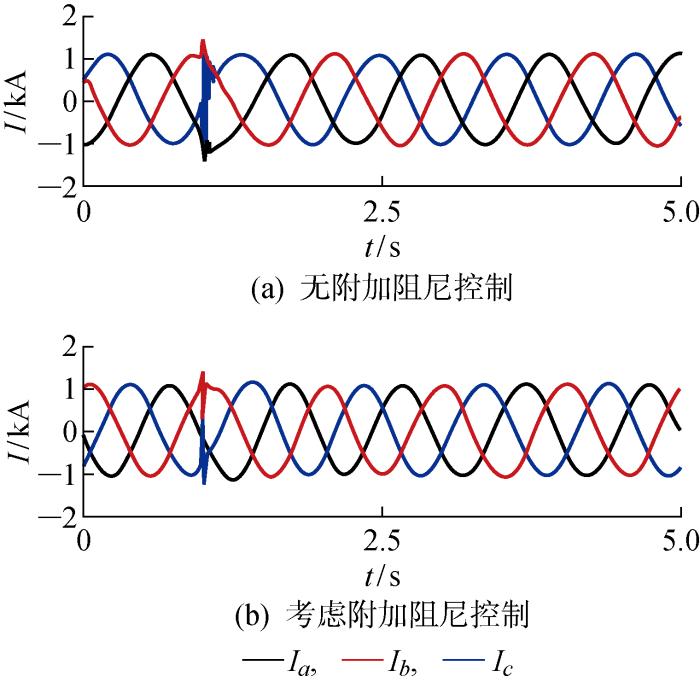
大规模的风电并网、长距离的输送线路、风能不稳定这些问题大大降低了系统的阻尼,因此当系统发生跳闸、三相接地短路或是小扰动干扰时,易引起传输线路的功率低频振荡.迄今为止,已经发现多次电力系统低频振荡现象,给电力系统带来很大影响.在国内,随着中国新疆维吾尔自治区北部地区风电装机容量的迅速增加,自2014年6月以来,广域测量系统已反复捕获次同步频率下的持续功率振荡^[3].在国外,德克萨斯电力可靠性委员会电网中已经发现多次4 Hz的低频振荡^[4].在此类严重事故中,低频振荡甚至会激起附近涡轮发电机的强烈扭转振动,从而导致发电厂的所有发电机跳闸.因此,有必要增强包含风电的混合电力系统的阻尼,以提高系统频率稳定性.

为保证风电并网系统稳定安全运行,很多国家已经出台相关的政策规定在风电机组中必须带有可以增强系统阻尼的附加环节.文献[5]中提出基于区域极点配置的风电系统弱阻尼低频振荡抑制控制策略,采用线性矩阵不等式的区域极点配置方法设计反馈控制器,将系统中的弱阻尼振荡模式配置到所控制区域,提高系统的阻尼比.文献[6]中以系统的频率偏差值作为输入,根据不同的风速设置桨距角,设计基于变系数的下垂控制调节风力发电机的有功出力,为系统注入正阻尼.文献[7]中根据两区域电力系统模型,选择合适的输入输出变量,对输入函数和状态函数求导得到反馈控制律,提出基于非线性控制算法的附加阻尼控制策略,可以有效地处理阻尼控制器中的非线性环节.文献[8]中将双馈风力发电机(DFIG)和电力系统静态稳定器(PSS)放在一起,建立系统的状态方程,定义系统振荡模式对传递函数的灵敏度,然后运用定义的灵敏度优化控制参数,该控制策略能有效抑制系统低频振荡.文献[9]中分析含DFIG的风电系统可能会引起低频振荡的原因,对比基于复转矩系数法的4种控制策略,为开发最优控制策略以抑制DFIG系统在不同条件下的轴系振动提供了参考.文献[10]中提出一种有源-无源协调双通道功率调制阻尼控制器,该控制器可以较好地发挥DFIG转子侧控制器的阻尼控制能力.文献[11]中提出基于电力系统稳定器和功率振荡阻尼器的鲁棒协调控制策略改善低频振荡阻尼,该方法使用改进的基于特征值的目标函数实现,并用灰狼优化器进行优化.文献[12]中提出基于阻耗系数的附加阻尼模糊控制策略,通过控制转子侧换流器调节DFIG无功功率来增强系统阻尼,进而抑制系统低频振荡.文献[13]中提出一种基于主动抗扰控制的有功无功附加阻尼控制器,能起到很好的抑制负阻尼的作用.文献[14]中提出一种基于自抗扰控制器的广域阻尼控制器协调优化策略,采用人工蜂群算法对自抗扰控制器和广域阻尼控制器进行协调优化,提高系统阻尼水平.文献[15]中设计基于频率反馈的大规模柔性负荷控制策略和统一潮流控制器串联侧功率反馈附加控制策略,最后运用遗传算法优化协同控制参数,得到最优控制策略.文献[16]中分析有功功率环节和无功功率环节附加阻尼控制的差异,提出一种基于bang-bang调制的混合快速阻尼控制策略和基于二阶滑模的双馈风电机组鲁棒阻尼控制策略,对电力系统区间振荡有很好的抑制效果.文献[17]中利用状态反馈的方法将系统输入、输出作线性化处理,将非线性系统线性化,最后提出基于超螺旋算法的阻尼控制器,该控制方法不依赖于系统的详细建模参数,具有良好的工程应用价值.

综上所述,国内外学者针对电力系统区域间功率低频振荡已经进行了深入的研究,也提出大量的附加阻尼控制器设计方法.然而,大多数设计方案将系统中联络线功率或发电机功角偏差等参数作为输入,忽略系统平衡点变化后的动态特性对低频振荡的影响,在系统平衡点附近线性化的基础上设计类似于PSS结构的附加阻尼控制器,而很少有研究将DFIG自身转子电压和磁链的关系应用到阻尼控制器设计上.本文对DFIG的动态频率响应和转子励磁电压与磁链之间的关系进行研究,结合终端滑模变结构控制的思想,设计基于转子磁链偏差的快速终端滑模附加阻尼控制器,并证明该系统的收敛性和稳定性.该控制器将磁链的偏差作为输入,输出一个附加信号到转子侧功率控制环节,进而控制转子侧换流器,调节DFIG出力,抑制系统低频振荡现象.最后,通过仿真验证本文所提控制方法对系统低频功率振荡的影响.

1 DFIG响应阻尼调节能力分析

DFIG系统在三相静止坐标系中的模型阶是一个多变量、高阶次、强耦合、非线性的复杂时变系统.为了便于计算和控制,运用坐标变换将其转换到两相同步旋转d-q坐标系下进行分析^[18].忽略定子绕组压降和电磁暂态变化过程,将定子电压定向于d轴上,DFIG定子输出有功功率(P_s)、无功功率(Q_s)和转子磁链方程可表示为

(1)

\begin{array}{l} P_{s} = \frac{L_{m} ω_{1} ψ_{q s}}{L_{m}^{2} - L_{s} L_{r}} ψ_{d r} \\ Q_{s} = \frac{ω_{1} L_{m} ψ_{q s}}{L_{m}^{2} - L_{s} L_{r}} ψ_{q r} - \frac{ω_{1} L_{r} ψ_{q s}^{2}}{L_{m}^{2} - L_{s} L_{r}} \end{array}\}

式中:L_s、L_r、L_m分别代表定子自感、转子自感和定转子互感;ω₁为同步转速;ψ_q_s为d-q坐标系下定子q轴磁链分量;ψ_d_r、ψ_q_r分别为d-q坐标系下转子磁链分量.

(2)

\begin{array}{l} {\overset{\cdot}{ψ}}_{d r} = - \frac{L_{s} R_{r}}{L_{s} L_{r} - L_{m}^{2}} ψ_{d r} + ω_{s} ψ_{q r} + u_{d r} \\ {\overset{\cdot}{ψ}}_{q r} = - \frac{L_{s} R_{r}}{L_{s} L_{r} - L_{m}^{2}} ψ_{q r} - ω_{s} ψ_{d r} - \\ \frac{R_{r} L_{m} U_{g}}{ω_{1} (L_{s} L_{r} - L_{m}^{2})} + u_{q r} \end{array}\}

式中:R_r为转子电阻;ω_s=ω₁-ω_r为发电机转差角速度,其中ω_r为发电机转子转速;u_d_r、u_q_r分别为转子d-q轴电压分量;U_g为电网侧电压.

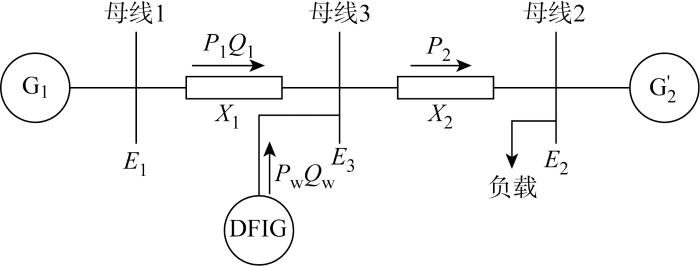
可以看出,DFIG转子磁通的大小取决于控制电压u_d_r和u_q_r.另外,双馈风电场暂态功率的控制时间常数为τ= $\frac{L_{s} L_{r} - L_{m}^{2}}{L_{s} R_{r}}$ ,该参数值一般为8~15 ms.因此,双馈风电场的暂态功率调节速度可以满足毫秒级快速调节的要求.

风电并入电网的两区域电力系统模型如图1所示.模型中包括同步发电机G₁,电力系统G'₂,母线2为参考母线.E₁∠δ为G₁的暂态电势,E₂∠0°为母线2电压,E₃∠δ-θ为母线3电压, 其中θ、δ分别为E₁和E₃、E₂的相角差;X₁、X₂分别为线路1和线路2的电抗;P₁、Q₁分别为G₁有功功率和无功功率;P_w、Q_w分别为DFIG有功功率和无功功率;P₂为线路2传输功率.当风电场并入电网时,系统的等价阻尼系数^[19-20]为K'_D= $\frac{k_{1} k}{k_{1} + k_{2}}$ -K_D,其中k为DFIG动态有功功率与转子角速度的比例关系,K_D为推导出的系统接入风电场后的等价阻尼系数,k₁= $\frac{E_{1} E_{3}}{X_{1}}$ cos θ₀,k₂= $\frac{E_{2} E_{3}}{X_{2}}$ cos (δ₀-θ₀),θ₀、δ₀为θ、δ初始条件下的取值;动态有功注入增强系统阻尼的条件为k>K_D(k₁+k₂)/k₁.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 两区域电力系统模型

Fig.1 Two-region power system model

2 终端滑模附加控制器设计

由上述分析可知,调节DFIG输出有功功率可以提高系统的阻尼水平,因此可以通过调节DFIG的有功功率改善系统阻尼水平,进而抑制系统区域间的低频振荡.

2.1 系统滑模面与控制律设计

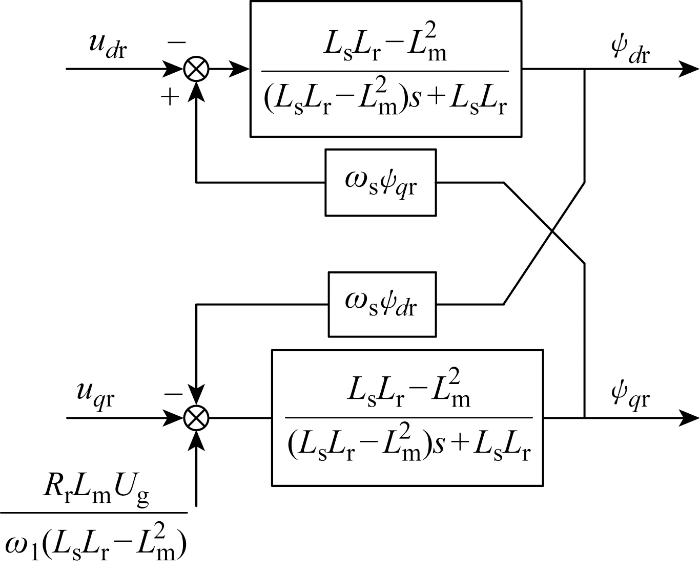
由式(2)可得,DFIG运行过程中,转子外加电压和转子磁链之间的关系如图2所示.图中:s为DFIG转差率.DFIG在发电状态时,将转子磁链分量ψ_d_r、ψ_q_r作为系统的受控输出,则转子励磁电压u_d_r、u_q_r为系统的控制输入.为达到系统快速控制的目的,将终端滑模变结构控制方法运用到DFIG转子磁链控制方案之中,设计转子磁链控制器,使系统磁链跟踪期望磁链,确保系统在指定时间内迅速达到稳定状态.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 DFIG转子外加电压与磁链之间的关系图

Fig.2 Relationship between applied voltage and flux linkage of DFIG rotor

假设转子d轴磁链期望值为 $ψ_{d r}^{*}$ ,则转子d轴磁链误差e_d_r= $ψ_{d r}^{*}$ -ψ_d_r,根据式(2)可得如下转子d轴磁链误差状态方程:

(3)

{\overset{\cdot}{e}}_{d r}

{\overset{\cdot}{ψ}}_{d r}^{*}

{\overset{\cdot}{ψ}}_{d r}

{\overset{\cdot}{ψ}}_{d r}^{*}

\frac{1}{τ}

ψ_d_r-ω_sψ_q_r-u_d_r

基于以上分析,设计如下滑模面:

(4)S_d=

{\overset{\cdot}{e}}_{d r}

+ρ₁

e_{d r}^{p_{1} / q_{1}}

式中:参数ρ₁>0;p₁、q₁为正奇数,且0<q₁/p₁<1.

式(4)对时间求导得:

(5)

{\overset{\cdot}{S}}_{d}

{\ddot{e}}_{d r}

+ρ₁

\frac{q_{1}}{p_{1}} e_{d r}^{p_{1} / q_{1} - 1} {\overset{\cdot}{e}}_{d r}

将式(3)代入式(5)得:

(6)

{\overset{\cdot}{S}}_{d}

{\ddot{ψ}}_{d r}^{*}

\frac{1}{τ} {\overset{\cdot}{ψ}}_{d r}

-ω_s

{\overset{\cdot}{ψ}}_{q r}

{\overset{\cdot}{u}}_{d r}

+ρ₁

\frac{q_{1}}{p_{1}} e_{d r}^{p_{1} / q_{1} - 1} {\overset{\cdot}{e}}_{d r}

则转子d轴磁链采用的控制律可设计为

(7)u_d_r=u_d_req+u_d_rn

式中:u_d_rep、u_d_rn分别为等效控制律和切换控制律,且满足

(8)

\begin{array}{l} u_{d r e q} = {\overset{\cdot}{ψ}}_{d r}^{*} + \frac{1}{τ} ψ_{d r} - ω_{s} ψ_{q r} \\ u_{d r n} = \int_{0}^{t} (ρ_{1} \frac{q_{1}}{p_{1}} e_{d r}^{q_{1} / p_{1} - 1} {\overset{\cdot}{e}}_{d r} + η'_{d} s g n (S_{d})) d t \end{array}\}

式中:η'_d=(1+μ(S_d) $e_{d r}^{λ_{d} μ (S_{d}) t}$ )η_dsgn(S_d),0<λ_d<1,μ(S_d)=sgn(S_d)sgn(S'_d), S'_d(t)=S_d(t+τ), η_d为大于零的切换常数;t为时间.

综上所述,η'_d可以迅速增大使控制器输出增大,从而使远离滑模面的系统状态快速向滑模面运动;当系统状态在做穿越滑模面运动时,η'_d迅速减小,从而使系统状态快速稳定在指定的滑模面上.

2.2 系统收敛性与稳定性分析

(1) 系统收敛性证明.

证明当S_d=0时,系统位于滑模面上,此时有

(9)

{\overset{\cdot}{e}}_{d r} \frac{1}{ρ_{1} e_{d r}^{p_{1} / q_{1}}}

=-1

求解可得:

(10)Δt_d=

\frac{q_{1}}{ρ_{1} (q_{1} - p_{1})} e_{d r}^{1 - p_{1} / q_{1}}

则DFIG的d轴磁链状态可在有限时间Δt_d内快速收敛到0,证毕.

(2) 系统稳定性证明.

证明取李雅普诺夫函数:

(11)V(t)=S_d(t)/2

求导可得:

(12)

\overset{\cdot}{V}

(t)=S_d

{\overset{\cdot}{S}}_{d}

将式(6)代入式(12)可得:

(13)

\overset{\cdot}{V}

(t)=S_d

{\overset{\cdot}{S}}_{d}

=S_d

({\ddot{e}}_{d r} + ρ_{1} \frac{p_{1}}{q_{1}} e_{d r}^{p_{1} / q_{1} - 1} {\overset{\cdot}{e}}_{d r})

=S_d (

{\ddot{ψ}}_{d r}^{*}

\frac{1}{τ} {\overset{\cdot}{ψ}}_{d r}

-ω_s

{\overset{\cdot}{ψ}}_{q r}

{\overset{\cdot}{u}}_{d r}

+ρ₁

\frac{p_{1}}{q_{1}} e_{d r}^{p_{1} / q_{1} - 1} {\overset{\cdot}{e}}_{d r}

)=S_d(-η'_dsgn(S_d))=-η'_d|S_d|≤0

所以V(t)≤0,系统在李雅普诺夫稳定性理论上全局渐进稳定,证毕.

同理可得转子q轴磁链控制律为

(14)u_q_r=u_q_req+u_q_rn

(15)

\begin{array}{l} u_{q r e q} = {\overset{\cdot}{ψ}}_{q r}^{*} + \frac{1}{τ} ψ_{q r} + ω_{s} ψ_{d r} + \frac{L_{m} U_{g}}{ω_{1} L_{s} τ} \\ u_{q r n} = \int_{0}^{t} (ρ_{2} \frac{q_{2}}{p_{2}} e_{q r}^{q_{2} / p_{2} - 1} e_{q r} + η'_{q} s g n (S_{q})) d t \end{array}\}

式中:参数ρ₂>0;p₂、q₂为正奇数,且0<q₂/p₂<1.

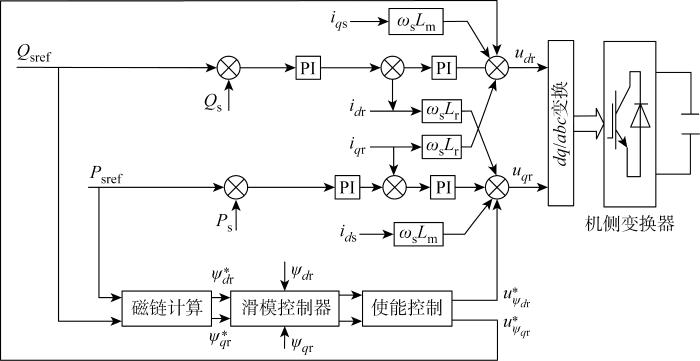
根据上述控制算法即可搭建如图3所示的机侧附加控制模型.图中:P_sref、Q_sref分别为有功功率和无功功率参考值,i_q_s、i_q_r、i_d_s、i_d_r分别为定转子q轴电流分量和d轴电流分量.根据功率参考值计算得到期望的转子磁链值,使之与实际转子磁链比较得到磁链误差值作为输入信号,通过滑模控制器输出控制信号 $u_{ψ_{d r}}^{*}$ 和 $u_{ψ_{q r}}^{*}$ .当系统发生低频振荡时,转子磁链产生偏差,使能环节工作,将该附加控制信号附加到转子侧换流器功率控制环节,调节风电场出力以增强系统阻尼.本文所设计的快速终端滑模附加阻尼控制器对外界干扰有很强的鲁棒性,对于系统低频振荡响应速度快,结合传统比例-积分(PI)控制, 能使DFIG能更好地抑制系统低频振荡.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 机侧控制器模型

Fig.3 Control model of machine side

系统中使能环节表达式如下:

(16)

\begin{array}{l} u_{ψ_{d r}}^{*} = u_{ψ_{d r}} s g n (| ψ_{d r}^{*} - ψ_{d r} |) \\ u_{ψ_{q r}}^{*} = u_{ψ_{q r}} s g n (| ψ_{q r}^{*} - ψ_{q r} |) \end{array}\}

3 系统离线仿真与分析

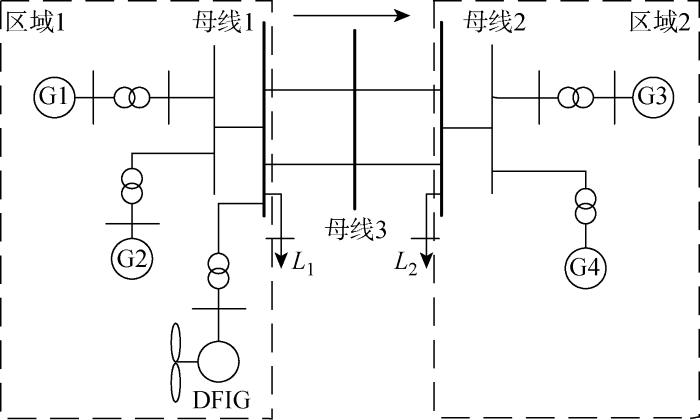
根据前文推导的快速终端滑模附加控制的原理设计附加阻尼控制器,在MATLAB/Simulink中建立如图4所示的四机两区域模型并进行仿真分析.图中:G2、G3和G4为同步发电机,L₁、L₂分别代表区域1和区域2负荷.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 含风电接入的四机两区域电力系统模型

Fig.4 A four-machine two-region power system model with wind power integration

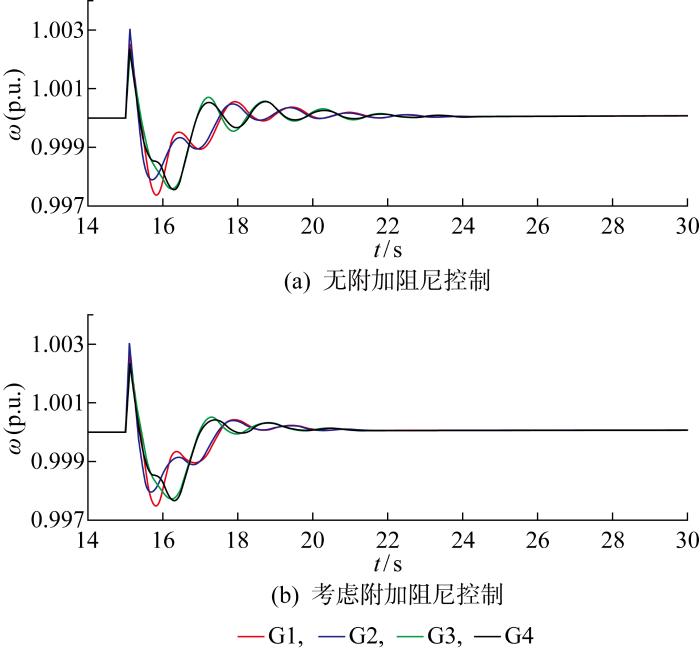
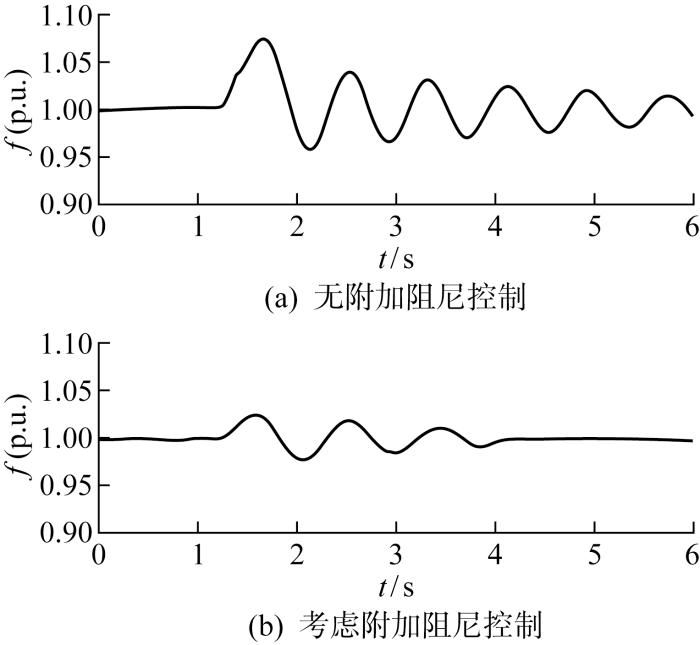
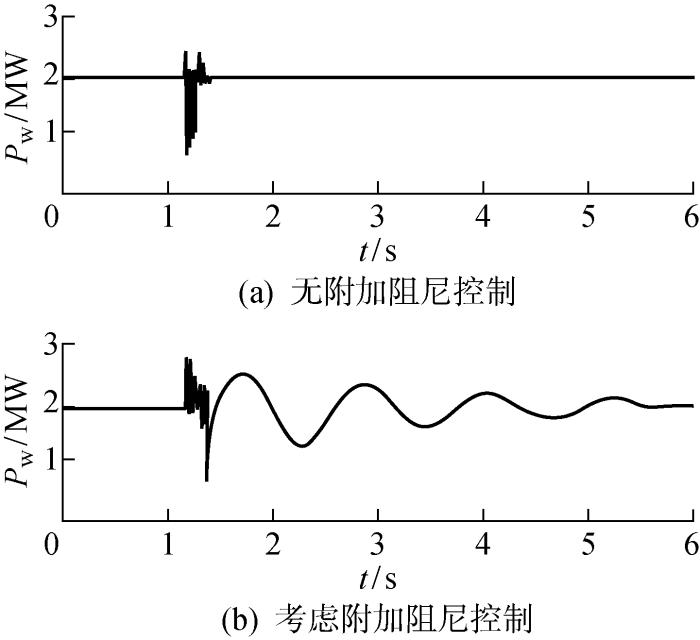
假设系统中风力发电机的运行状态相同,采用单机等值模型,即采用100台1.5 MW的风力发电机代替,风电场通过10 km长的输电线接入四机两区域系统的母线1处,因此DFIG接入容量为150 MW.仿真系统中,用5台DFIG等值机模拟风电场群.其中,等值风力发电机定子电阻为 $R_{s}^{p . u .}$ =0.004 6,定子漏抗为 $X_{s}^{p . u .}$ =0.102,转子电阻为 $R_{r}^{p . u .}$ =0.006 0,转子漏抗为 $X_{r}^{p . u .}$ =0.085 9,上标p.u.为标幺值,下同.4台同步发电机组采用同步发电机模型、励磁系统和调速系统模型模拟.其中,同步发电机定子电阻为 $R_{s}^{p . u .}$ =0.002 0,定子漏抗为 $X_{s}^{p . u .}$ =0.233 0,d轴不饱和电抗为 $X_{d}^{p . u .}$ =1.713 0,q轴不饱和电抗为 $X_{q}^{p . u .}$ =1.642 0.高压直流系统为定功率控制,线路等效为 II 型有损耗线路.调节同步机组的输出功率将区域1至区域2的传输线输电有功功率控制在400 MW.在整个仿真过程中,设置平均风速为12 m/s.

仿真环境设置:设t=15 s时,两区域联络线发生0.1 s的三相短路,此时系统由于阻尼不足,在联络线上发生功率振荡;t=15.1 s时故障消除,系统恢复正常运行状态.观察无附加阻尼控制下和本文提出的附加阻尼控制策略下系统中各项参数的响应曲线.

图5为同步发电机转速振荡曲线.图中:ω为转速.对比有、无附加控制的响应曲线可知,在考虑附加阻尼控制情况下的同步发电机转子转速响应曲线的振幅更小,更快趋于稳定,具有更好的阻尼特性.由图6所示的同步机G1和G3转子角速度的差值(Δω₁₃)振荡曲线可知,在考虑附加阻尼的情况下,G1和G3转子角速度偏差振荡的振幅和时间均减小.说明所提出的附加控制策略对系统同步发电机的振荡有一定抑制作用.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 同步发电机转速变化曲线

Fig.5 Speed curves of synchronous generator

图6

新窗口打开| 下载原图ZIP| 生成PPT

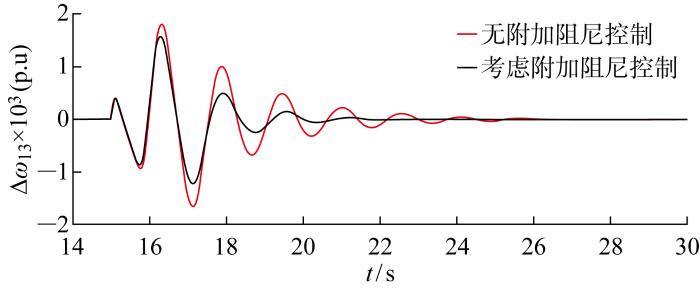
图6 同步发电机G1和G3转子角速度偏差振荡曲线

Fig.6 Angular velocity deviation oscillation mode of synchronous generator G1 and G3

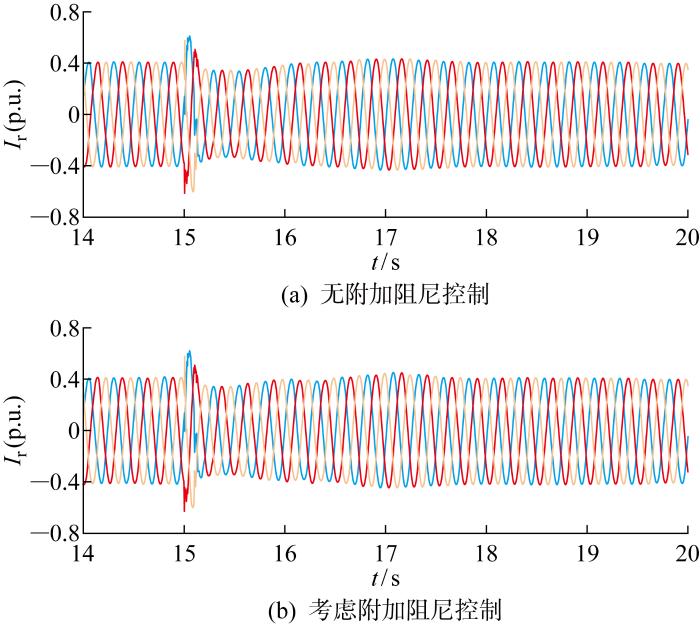
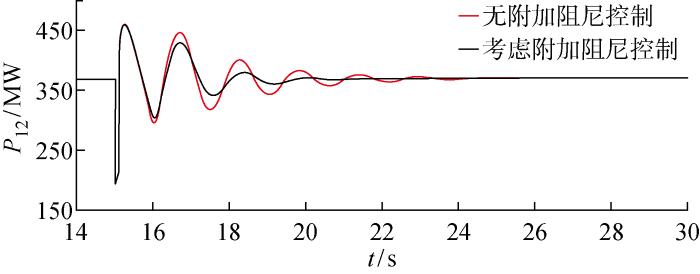
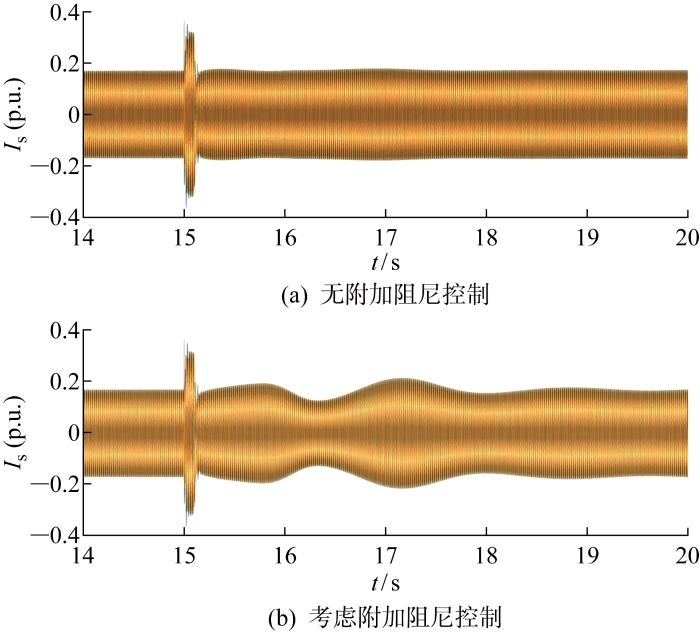
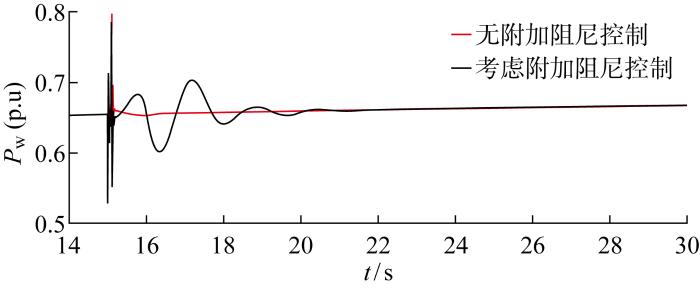
图7为DFIG转子励磁电流(I_r)的变化曲线.对比图7(a)和7(b)可以看出,当系统发生低频振荡时,在有附加阻尼控制情况下,故障期间DFIG转子电流增大并有一段时间的振荡响应,使DFIG及时发出有功功率支撑电网;在没有附加阻尼控制情况下,故障期间DFIG转子电流变化较小,不能很好地响应系统振荡.图8为两区域联络线功率(P₁₂)变化曲线,从图中可以看出在考虑了附加控制的情况下,联络线功率振荡的振幅明显减小,并且更快地趋于稳定.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 双馈发电机转子电流变化曲线

Fig.7 Rotor current curves of DFIG

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 联络线功率振荡曲线

Fig.8 Power oscillation curves of transmission line

图9为DFIG定子电流(I_s)变化曲线.由图可知,在无附加控制下,故障期间DFIG定子电流几乎没有变化.而在采用附加控制时,故障期间定子会短时振荡现象,但其电流值仍在安全范围之内,说明所提的附加阻尼控制策略在及时调节有功功率输出的同时,并不会对双馈风电系统带来负面影响.图10为DFIG有功功率(P_w)响应曲线.从图中可以看出,在没有考虑附加控制情况下,系统发生低频振荡之后,DFIG有功功率并没有响应系统振荡,而在考虑本文所设计的附加阻尼控制情况下,DFIG有功功率输出能快速做出动态响应以提高系统的阻尼水平来抑制低频振荡.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 双馈发电机定子电流响应变化

Fig.9 Stator current curve of DFIG

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 DFIG有功输出振荡曲线

Fig.10 Response curves of DFIG active power

4 系统实时仿真实验验证与分析

为了充分验证所提附加控制策略在工程应用上的可行性,开发基于RTDS的风电并网四机两区域实时仿真系统,主要仿真参数和离线仿真参数相同.

在RTDS平台实验中,系统运行至t=1.2 s时,在两区域联络线上设置三相瞬时短路故障,传输线路出现功率低频振荡现象;t=1.4 s时,去除故障;监测DFIG定子电流、转子电流和有功输出响应情况以及系统振荡频率在是否考虑附加阻尼两种情况下变化曲线,结果如图11, 图12 ~14所示.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 系统频率变化曲线

Fig.11 Frequency change curves of system

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 DFIG有功出力变化曲线

Fig.12 Active output oscillation curves of DFIG

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 DFIG转子电流变化曲线

Fig.13 Rotor current curves of DFIG

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 DFIG定子电流变化曲线

Fig.14 Stator current variation curves of DFIG

图11为系统频率(f)响应曲线.从图中可以看出,在系统发生低频振荡故障期间,无附加阻尼控制情况下的系统频率衰减较慢,振荡持续时间相对较长.而采用所提附加控制之后,系统频率振荡曲线衰减较快,且振荡的幅值更低,系统整体表现出更好的阻尼特性.图12为DFIG有功出力响应曲线.由图可见,当联络线发生功率振荡时,如果考虑附加控制,DFIG就可以及时输出更多有功功率响应其振荡,为系统提供更多阻尼.

图13为转子励磁电流实时仿真曲线.图中:I为电流;I_a、I_b、I_c分别为abc三相电流.对比实验结果可知:在采用附加阻尼控制策略的情况下,在故障期间,转子励磁电流增大,以便使双馈发电机及时发出更多有功功率;而无附加阻尼控制下,转子励磁电流在故障期间几乎没有变化.而且从图14可以看出,定子电流实时仿真结果与离线仿真时的动态响应曲线一致,均能够保证DFIG的安全运行.

5 结语

研究风电功率调节对系统低频振荡抑制问题,在DFIG的机侧电流控制环上引入以增加电力系统阻尼为目标、基于李雅普诺夫稳定性理论的快速终端滑模附加阻尼控制器.利用MATLAB仿真测试与实验验证,在电力系统出现低频振荡故障时,所提出的快速终端滑模控制不仅可以快速调节DFIG有功功率,提高系统的阻尼水平,有效抑制低频振荡;而且在系统响应过程中,风力发电机的有功功率响应速度快、变化平滑,定子电流振荡持续时间很短且振荡幅值在安全范围内,不会影响风电场安全运行,具有一定的应用参考价值.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

郝正航, 余贻鑫, 曾沅.

改善电力系统阻尼特性的双馈风电机组控制策略

[J]. 电力系统自动化, 2011, 35(15): 25-29.