我国70%以上的煤炭和水力资源集中在西部地区,而电力负荷中心在中东部地区,电力供应资源与电力负荷需求逆向分布的特点决定了我国需要在全国范围内开展跨省电力输送与电力交易,打破资源配置壁垒,实现更大范围内资源的优化配置[1-2].为此,我国不断深化电力市场改革,并逐步形成“统一市场,两级运作”的电力市场框架.其中,“统一市场”强调实现电力资源在全国范围内优化配置,“两级运作”强调省间电力市场与省内电力市场协调运行、联合出清.与此同时,为实现“碳达峰、碳中和”的目标,未来可再生能源接入电网的比例将不断升高[3],可再生能源发电的间歇性将给电力系统的安全经济运行带来严峻挑战.在上述背景下,计及不确定性因素的影响,实现省间-省内两级市场运作下电力系统的安全经济调度具有重要意义.
目前,不少学者已开展考虑“跨区跨省”电力传输与交易的电力系统经济调度模型研究.文献[4]中提出考虑省间交易商的省间-省内两级电力市场最优购电模型,有效降低市场运行成本.文献[5]中建立跨省区大电网安全约束经济调度模型,并采用优化目标和约束条件的灵活配置实现求解效率的提高.文献[6]中提出跨省互联电网双级调度策略——日前调度制定机组启停和跨省联络线输电计划;日内调度根据实际光伏和负荷来调整机组出力和联络线输电,提升系统运行的经济性.文献[7]中建立直流联络线功率阶梯化运行的模型,协调互补多个送端电网和受端电网,促进新能源的消纳.文献[8]中考虑送端储能及功率跨区流动状态,平抑送、受端交换功率的波动,充分发挥不同区域间的互济效益.文献[9]中提出转供电力交易补偿模型,能够有效控制跨省电力交易的高运行风险的线路.上述模型的构建与求解为研究省间-省内协调的电力系统经济调度问题奠定了基础.
上述文献侧重于跨区跨省电力系统经济调度模型构建、跨区域输电计划制定的研究.随着全国统一电力市场逐步建设,省间市场和省内市场协调运作需求凸显,省间-省内两级市场的协调运作机制与模型受到广泛关注,而如何在省间-省内两级市场协调运作下实现日前-日内两阶段的经济调度,目前研究尚不深入,需要进一步探索可行的调度框架与建模方法.与此同时,由于可再生能源发电比例不断提高、电动汽车等新兴负荷大量接入,源-荷不确定性因素也将对省间-省内两级运作的经济调度决策过程产生影响.2020年7月1日实施的《电力系统技术导则》明确指出电力系统应充分考虑跨省跨区支援能力及新能源利用,以应对新能源发电随机性、间歇性的特征.针对源-荷不确定性因素,传统电力系统优化方法包括随机优化(Stochastic Optimization,SO)[10-11]和鲁棒优化(Robust Optimization,RO)[12⇓-14],然而随机优化需要准确获取随机变量的概率分布,且计算结果的样本外表现不佳;鲁棒优化结果过于保守,影响系统运行的经济性.近年来,不少学者提出分布鲁棒优化(Distributionally Robust Optimization, DRO)方法以弥补SO和RO的不足[15⇓-17],为两级市场协调运作下研究含源-荷不确定性因素的日前-日内两阶段经济调度问题提供了可行手段.
在省间-省内两级电力市场运作框架下,计及源-荷不确定性因素的影响,提出一种不确定性环境下考虑省间-省内两级市场运作的经济调度模型,包括日前调度和日内调度两个阶段.在日前调度阶段,以最小化省内日前调度成本和省间购电成本为目标,构建省间-省内双层日前经济调度模型;在日内调度阶段,以最小化省内再调度成本为目标,建立考虑源-荷预测偏差的日内备用调度模型.同时,构建范数距离模糊集用以刻画源-荷预测偏差的不确定性,并提出双层两阶段分布鲁棒优化方法,以实现上述模型的求解.最后,利用IEEE 39节点和118节点系统构建多送端-多受端多省互联的测试系统,并利用算例仿真验证了所提模型及方法的有效性.
1 省间-省内两级电力市场下经济调度框架
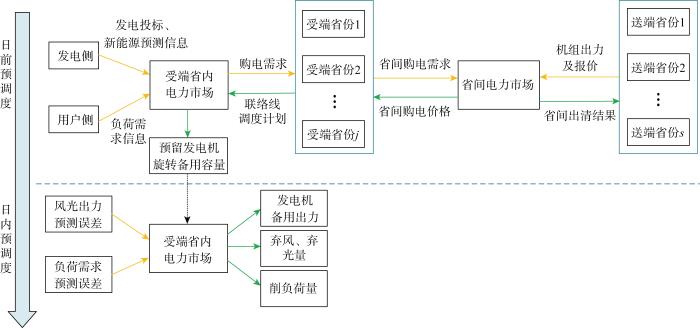
我国各地的资源分布特点和电力供需差异造成不同区域间的电能输送,也促进了跨省电力交易的实施.然而,各区域输电体系不同、各省市电价相差较大、各地域资源禀赋不同,因此在保障省内电力供需平衡下如何实现电力资源在更大范围内的优化配置是全国统一电力市场建设中需要解决的问题.为此,在全国统一电力市场体系顶层设计中提出符合我国实际情况的“统一市场,两级运作”市场运行方式.其中,两级市场包括省间市场和省内市场,省间市场用于促进跨省跨区间清洁能源的消纳和大规模电力资源的配置;省内市场用于保障省内电力用户需求,实现电力供需平衡[18].在此背景下,提出省间-省内两级电力市场运作下日前-日内两阶段经济调度框架(见图1),旨在实现省间-省内市场协调下的安全经济调度,保障区域资源的合理利用与省内电力的供需平衡.
图1
图1
考虑省间-省内两级电力市场的日前-日内两阶段经济调度框架
Fig.1
Framework of inter-provincial and intra-provincial bi-level electricity market
1.1 日前调度
如图1所示,在日前调度阶段,首先,受端省份申报省间购电需求量,送端省份申报发电机组出力及报价.根据受端和送端的申报信息,以最小化省间购电成本为目标,完成省间电力市场出清并得到省间联络线日前调度计划.然后,各受端省份以省间联络线日前调度计划为边界条件,运行省内电力市场,并根据省内发电机组投标、负荷需求和新能源预测出力信息,以最小化省内市场运作成本为目标,完成省内市场出清.图中黄色箭头代表电力市场出清的输入参数,绿色箭头代表市场出清结果,黑色虚线箭头代表日前调度阶段的出清结果作为输入参数传递到日内调度阶段.
在省间-省内两级市场协调运行中,省间市场出清后所得省间购电价格会影响受端省内电力市场的出清结果,从而使得受端省份调整省间购电需求量并重新申报.因此,需要省间-省内多次迭代以获得最优省间购电需求和省间购电价格.在构建模型时,将省内市场和省间市场分别作为模型的上、下层,上层模型传递省间购电需求给下层模型,下层模型传递省间购电价格给上层模型.在实际市场运作过程中,可设置省间购电商以完成上述信息的传递[4].
1.2 日内调度
如图1所示,在日内调度阶段,市场主体为各受端省份,不涉及送端省份及省间市场,送-受端联络线功率为日内调度边界条件.为了弥补风光可再生能源出力和负荷需求的实际值与预测值之间的偏差,各受端省份采取发电机备用出力、弃风弃光和削负荷措施,以保障电力供需平衡,应对不确定性的影响.针对日内调度阶段可再生能源出力和负荷需求不确定性的影响,在后续模型的构建中,采用基于1-范数和∞-范数的距离模糊集刻画各典型随机源-荷场景发生概率的不确定性,并在表征随机源-荷预测偏差的不确定性后,利用分布鲁棒优化方法实现经济调度过程的建模.
所提出的日前-日内两阶段经济调度框架能够适应省间-省内两级市场运作流程,并通过发电机备用容量设置充分应对新能源发电和负荷的不确定性,避免大量弃风弃光和削负荷.
2 省间-省内两级市场协调运行下经济调度模型
2.1 日前调度阶段
2.1.1 上层省内模型
在日前调度阶段,上层省内模型的目标是最小化省内市场运作成本,目标函数为
式中:J为受端省份集合;T为优化调度时间的集合;Nj为第j个受端省份的发电机集合;
日前调度阶段上层模型的约束条件如下.
(1) 省内电力平衡约束:
式中:
(2) 发电机出力约束:
式中:
(3) 发电机爬坡约束:
式中:
(4) 发电机备用容量约束:
(5) 线路潮流约束:
式中:
2.1.2 下层省间模型
获取省间购电需求量后,运行省间电力市场,并以最小化省间购电成本作为下层省间模型优化的目标:
式中:S为送端省份集合;Ns为第s个送端省份参与省间市场的发电机集合;
日前调度阶段下层模型的约束条件如下.
(1) 省间联络线电力平衡约束:
式中:ωs, j为第s个送端省份与第j个受端省份之间联络线的电力传输损耗系数.
(2) 联络线传输容量约束:
式中:Cs,j,max、Cs,j,min分别为第s个送端省份与第j个受端省份之间联络线的传输容量上、下限.
(3) 送端省份发电机组容量约束:
式中:
需要说明的是,省间市场在时刻t的购电价格
2.2 日内调度阶段
日内调度阶段需要根据新能源、负荷预测偏差进行电力供需调整,包括省内发电机组出力上调、下调和弃风、弃光以及负荷削减.基于省内市场,日内调度阶段以省内再调度成本最小为目标函数:
式中:F1为日内调度发电机上调和下调出力的成本;F2为弃风、弃光和负荷削减的惩罚成本.F1和F2的表达式为
式中:
日内调度阶段的约束条件如下.
(1) 日内调度电力平衡约束:
式中:
(2) 省内机组出力调整和负荷削减约束:
式中:
(3) 备用容量约束:
其中,日内调度的可用容量受到日前调度预留备用容量的约束.
(4) 弃风量、弃光量、负荷削减量约束:
式中:ηw、ηpv、ηload分别为最大弃风量、弃光量和负荷削减量占比.
(5) 线路潮流约束:
与日前调度阶段相比,日内调度阶段只在受端省份的省内市场之间进行,并且受端省份之间设计了备用共享机制,即各受端省份共同享用所有的备用容量,各省间的备用电力可以相互传递.若出现一个受端省份新能源和负荷预测偏差波动较大的情况,其余受端省份可以将省内富余的备用电力输送到该预测偏差波动较大的省份.因此在备用共享机制下,单个省份的备用容量可以相对较少,各省可以共同面对新能源出力和负荷需求预测偏差不确定性的影响,从而有效减少备用容量总量.对于预测偏差带来的不确定性因素,采用分布鲁棒优化方法进行处理.
3 两阶段分布鲁棒优化调度模型构建与求解
3.1 日前调度阶段双层模型的转换
3.2 日前-日内两阶段分布鲁棒优化模型的构建
相比于日前调度阶段,日内调度阶段考虑了风电、光伏和负荷的预测偏差,但实际运行中新能源发电和负荷的预测偏差值存在不确定性,如何应对上述不确定性因素的影响是需要解决的问题.目前,常用于处理不确定性因素的方法包括随机优化和鲁棒优化,但随机优化需要准确获取不确定性因素的概率分布信息,鲁棒优化所得优化结果过于保守.近年来,分布鲁棒优化方法逐渐被采用,其结合了随机优化和鲁棒优化的特点,既无需获得准确的概率分布信息,又克服鲁棒优化过于保守的缺点,能够实现不确定性环境下的最优决策.因此,引入分布鲁棒优化方法应对日内调度阶段不确定性因素的影响.
分布鲁棒优化的核心在于构建不确定性因素的概率分布模糊集,然后基于模糊集的表征方式计算最劣概率分布情况下的最优决策结果.针对新能源发电和负荷预测偏差的不确定性,采用基于1-范数和∞-范数的距离信息模糊集实现不确定性表征.首先,对源-荷的历史数据样本进行聚类处理[22],得到K个源-荷预测偏差典型场景以及各场景发生的概率pk(k = 1, 2, …, K);然后,构建基于1-范数和∞-范数的模糊集来刻画上述K个典型场景可能出现概率的不确定性;最后,完成随机源-荷预测偏差的表征.上述过程中,基于1-范数距离和∞-范数距离所构建的模糊集如下:
式中:
根据文献[16]可知,{pk}中所有的元素满足如下置信度约束:
式中:Pr{·}为满足条件“·”的概率;M为样本规模.
当式(21)不等式右边的置信度分别设置为α1和α∞时,可得到:
利用式(22),在实际优化计算中便可通过设置置信度参数α1和α∞来确定模糊集中的允许偏差上限值θ1和θ∞.
在形成表征源-荷预测偏差不确定性的模糊集后,将源-荷预测偏差作为随机变量,在日前阶段模型所转化的单层模型基础上,构建如下紧凑形式的日前-日内两阶段分布鲁棒经济调度模型:
式中:pk为第k个源-荷预测偏差不确定性场景发生的概率;x和y分别为日前调度阶段和日内调度阶段的决策变量,其中日前调度阶段模型已转换为单层模型;yk为第k个源-荷预测偏差场景下的日内调度阶段的决策变量;ξk为表征第k个源-荷预测偏差场景下风电、光伏和负荷预测偏差值的随机变量;Ω为源-荷预测偏差场景概率取值的可行域;X为x的可行域;Y(x, ξk)为第k个源-荷预测偏差场景下yk的可行域;a~e、A~F分别在紧凑形式中代表向量和矩阵.
式(23)为日前-日内两阶段分布鲁棒优化目标函数的紧凑形式,对应式(A10)和式(11);约束式(24)对应约束式(2)~(6)、(A2)~(A3)和(A5)~(A6);约束式(25)对应约束式(14)、(15)和(18);约束式(26)对应约束式(16)和(17).
3.3 日前-日内两阶段分布鲁棒优化模型的求解
图2
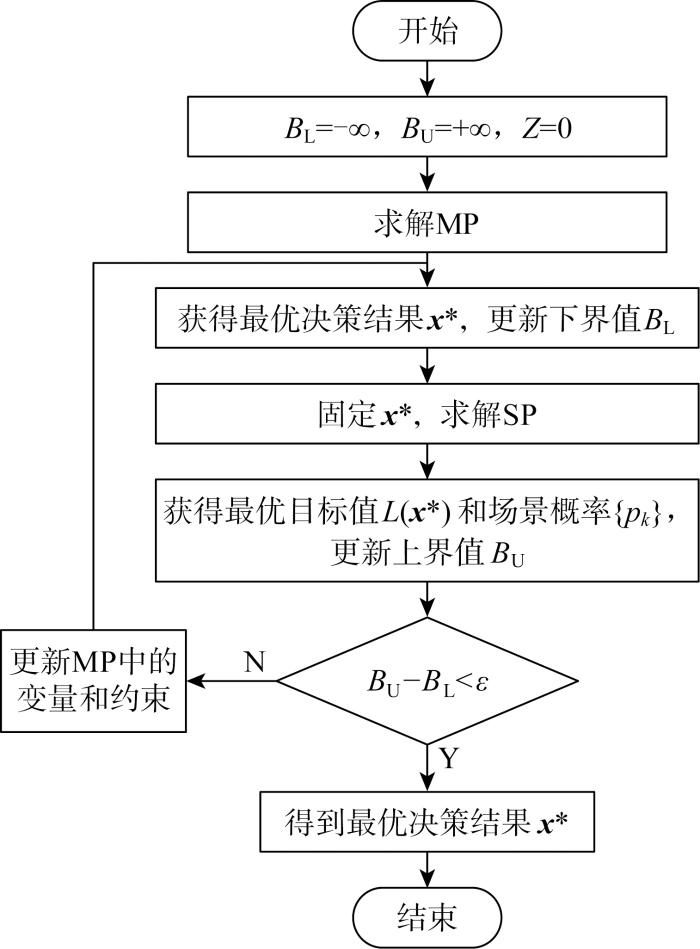
(1) 主问题(MP):
式中:G为最大值;Z为迭代次数.
求解主问题得到日前调度阶段最优决策结果x*,并更新下界值BL,即
(2) 子问题(SP):
在给定的第一阶段决策结果x*的条件下,求解上述子问题.由于各典型场景下内层优化问题
式(32)求解完成后更新上界值,即
当BU-BL<ε,ε为一个很小值时,迭代结束并返回最优解x*;否则,在主问题中更新变量
4 算例仿真
4.1 算例设置
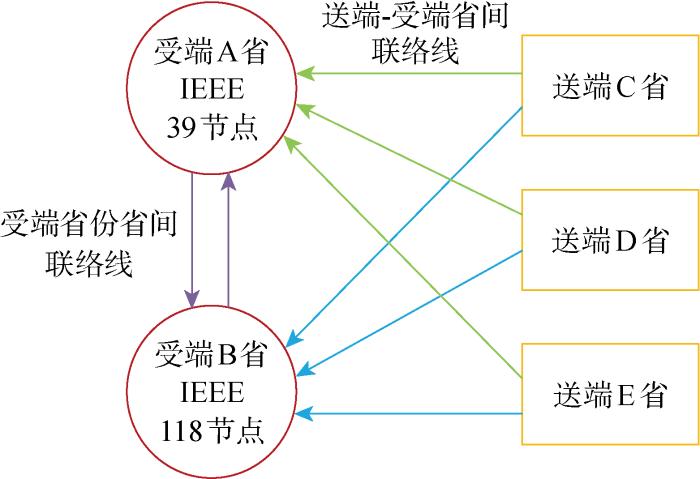
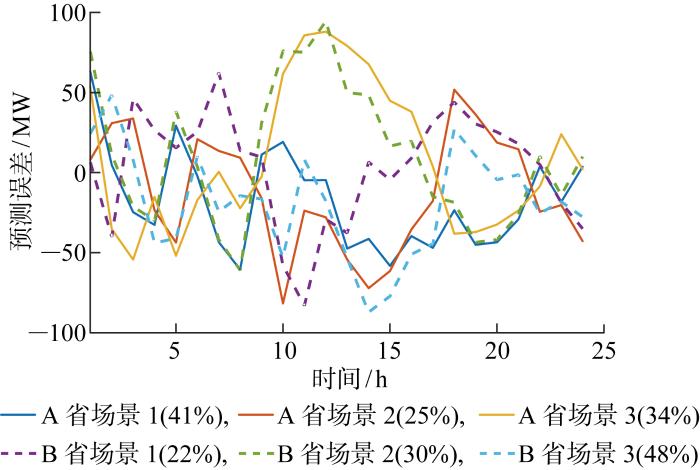
采用IEEE 39节点和118节点系统进行算法仿真,系统数据参见文献[24].其中,39节点和118节点系统分别作为受端省份A省、B省,并分别接入1个新能源风光电厂,风力和光伏发电均接入同一个节点;分别设置3个送端省份C省、D省和E省参与省间市场.送端和受端省份的划分考虑水电、新能源等电力富足省份向负荷中心省份的电力输送行为,并且以省间联络线作为划分边界.送端-受端的电网传输结构图如图3所示,新能源电站和送端-受端联络线的接入位置如表1所示;受端省份省间联络线分别接于A省节点30和B省节点58;参与省间市场的机组容量、报价以及跨省联络线线损率如附录B所示;电力传输损耗系数参见文献[4].根据受端A省和B省的新能源出力及负荷的历史预测数据和实际数据,利用K-means算法聚类处理,分别得到受端A、B两省的3个预测误差典型场景,如图4所示.此外,测试环境为Intel Core i7-8550四核CPU,16 GB内存,使用MATLAB R2020b编译和测试.
表1 新能源电厂和省间联络线接入点位置
Tab.1
| 受端 省份 | 新能源 风光电厂 接入点 | 送端C省 联络线 接入点 | 送端D省 联络线 接入点 | 送端E省 联络线 接入点 |
|---|---|---|---|---|
| A省 | 节点20 | 节点10 | 节点18 | 节点16 |
| B省 | 节点70 | 节点37 | 节点79 | 节点107 |
图3
图4
图4
受端A省、B省源-荷预测偏差场景及概率
Fig.4
Scenarios and probability of source-load with forecast errors in receiving provinces A and B
4.2 日前调度结果
4.2.1 日前调度阶段成本分析
表2 日前调度阶段成本
Tab.2
| 受端 省份 | 省内发电 成本/元 | 省间购电 成本/元 | 备用 成本/元 | 总成本/元 |
|---|---|---|---|---|
| A省 | 492310 | 35136 | 265020 | 792466 |
| B省 | 880837 | 115523 | 193154 | 1189514 |
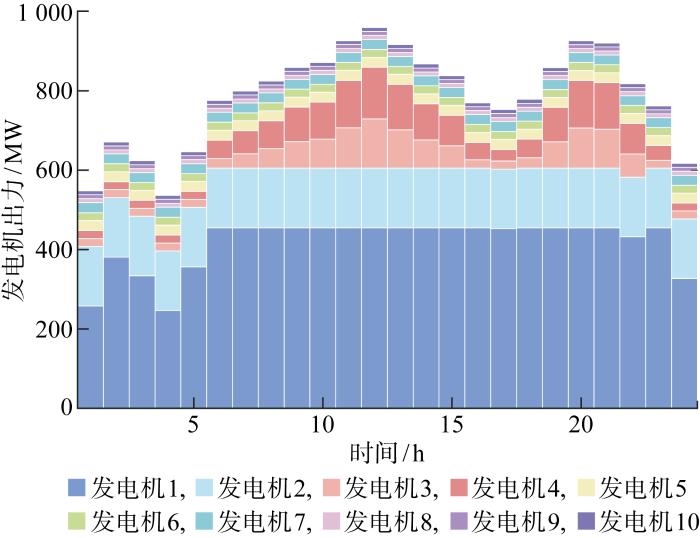
图5
图5
受端A省日前调度阶段发电机出力
Fig.5
Generator outputs of receiving end A in day-ahead dispatch stage
4.2.2 省间市场购电行为分析
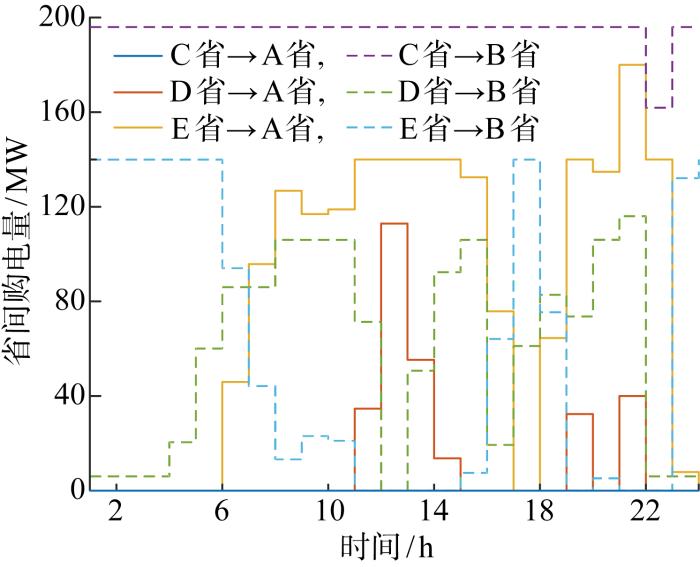
图6为受端省份A、B在省间市场的购电情况,根据电力市场出清准则,即满足最大化社会福利的目标,只有当省间购电价格低于省内发电机组边际电价时,省间购电交易才会发生,整体社会福利才会增加.结合附录B中图B1所示的净负荷曲线可知,中午12时A、B省的净负荷,即负荷与新能源出力的差值均增加,而A省边际发电机组的边际价格17.3 美元/MW高于B省边际发电机组的边际价格16.9 美元/MW,且均高于省间购电价格16.2 美元/MW,这使得D、E省至A省的省间购电量显著增加、至B省的省间购电量显著减少(12时为0).晚上21时,由于新能源出力减少、负荷增加导致系统净负荷增大,此时省间购电量也达到峰值,A、B省大部分机组的边际价格均大于省间购电价格16.9 美元/MW.值得注意的是,C省的外送电量均传输到B省,这是由于C省本身存在发电成本较低的机组,同时在不考虑省间购电时B省的边际电价高于A省,所以在净负荷较低时(如0—6时)B省均存在省间购电,C省外送电量也优先支持B省用电,以降低系统运行总成本.
图6
图6
受端A省、B省的省间购电量
Fig.6
Inter-provincial power purchase of receiving provinces A and B
4.2.3 省内线路阻塞分析
调整受端省份A、B省内线路容量上限值,A省内线路容量由500 MW降低为400 MW,B省内线路容量由500 MW降低为450 MW.降低线路容量上限值后,A省、B省会发生线路阻塞,阻塞情况下目标函数与未阻塞情况下的目标函数相同,只是线路潮流约束更为严格,参照式(1)分别计算线路阻塞与未阻塞情况下系统的发电成本和购电成本,如表3所示.总体而言,发生阻塞之后A、B两省的发电成本与购电成本之和略有增加.其中,线路阻塞导致A省的边际电价增加并高于B省的边际电价,从而使得B省的省间购电量降低,A省的省间购电量增加,并表现为A省阻塞情况下的省内发电成本略低于未阻塞情况下的成本,B省阻塞情况下的省间购电成本略低于未阻塞情况下的成本.
表3 阻塞与未阻塞时A、B省的发电、购电成本
Tab.3
| 发/购电 | A省成本/元 | B省成本/元 | 总成本/元 |
|---|---|---|---|
| 非阻塞-省内发电 | 492310 | 880837 | 1373147 |
| 阻塞-省内发电 | 482420 | 890610 | 1373030 |
| 非阻塞-省间购电 | 35136 | 115523 | 150659 |
| 阻塞-省间购电 | 45007 | 106033 | 151040 |
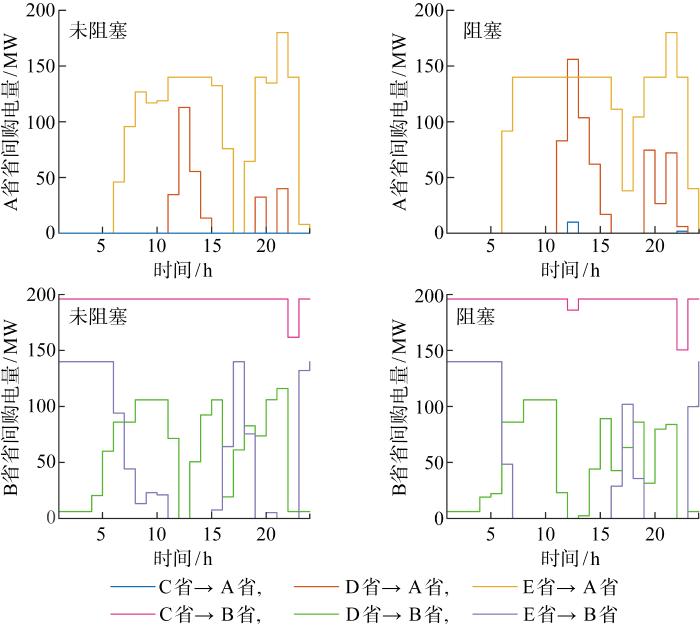
图7具体给出A、B省在阻塞与非阻塞情况下的省间购电量.在线路阻塞情况下,11—15时和19—22时D省向A省的输电量大于非阻塞时向A省的输电量,6—10、15—18、20和23时E省向A省的输电量大于非阻塞时向A省的输电量,且在12、22时C省也向A省外送输电.
图7
图7
阻塞与未阻塞时省间购电量对比
Fig.7
Comparison of inter-provincial power purchase in congestion and non-congestion scenarios
4.3 日内调度结果
4.3.1 DRO方法分析
表4 SO、RO与DRO方法结果对比
Tab.4
| 优化算法 | 备用 成本/元 | 弃风弃光 成本/元 | 削负荷 成本/元 | 总成本/元 |
|---|---|---|---|---|
| SO | 187672 | 110132 | 307028 | 604832 |
| RO | 210744 | 250533 | 480136 | 941413 |
| DRO(1-范数) | 187548 | 109684 | 312424 | 609656 |
| DRO(∞-范数) | 187343 | 112650 | 312331 | 612324 |
为对比DRO和SO的样本外表现,先根据给定典型场景样本计算出第一阶段日前调度决策变量,然后重新随机生成新的场景,并进行第二阶段日内调度优化计算,总成本如表5所示.可以发现,SO计算结果的平均值低于DRO计算结果的平均值,但是SO计算结果的标准差大于DRO计算结果的标准差,波动幅度较大.SO最大值的情况出现在新能源波动性较大导致机组备用不能平衡新能源波动,此时被迫需要削负荷或弃风弃光,使得运行成本大大增加.相比于SO,DRO在日前调度阶段保留更为充足的机组备用,能够在日内调度阶段更有效地面对新能源不确定性的波动,削负荷和弃风弃光的量较少,总成本波动较小,样本外表现结果具有鲁棒性较好的特征.
表5 SO与DRO方法样本外结果对比
Tab.5
| 优化算法 | 总成本 平均值/元 | 总成本 最大值/元 | 总成本 最小值/元 | 标准差/ 元 |
|---|---|---|---|---|
| SO | 2465734 | 2676148 | 2233658 | 84397 |
| DRO(1-范数) | 2493761 | 2578582 | 2388515 | 71523 |
| DRO(∞-范数) | 2532489 | 2592486 | 2407077 | 73295 |
由式(22)可知,置信度α1、α∞不同,则DRO方法中允许偏差上限值θ1、θ∞不同,选取不同的α1、α∞,对比分析其对双层两阶段经济调度结果的影响.如表6所示,对于1-范数和∞-范数,置信度越高,两阶段经济调度的总成本越高.此外,可设置不同的置信度来调整计算结果的鲁棒性,置信度越高,所得结果鲁棒性越强.当置信度α1、α∞相同时,采用∞-范数所得总成本高于采用1-范数的结果,说明∞-范数下调度结果较1-范数更为保守.
表6 1-范数与∞-范数结果对比
Tab.6
| α1=α∞ | 1-范数成本/元 | ∞-范数成本/元 |
|---|---|---|
| 0.2 | 2590724 | 2592887 |
| 0.4 | 2591283 | 2593754 |
| 0.6 | 2592070 | 2594977 |
| 0.8 | 2593415 | 2597066 |
| 0.99 | 2599231 | 2606097 |
4.3.2 受端省份日内备用共享情况
图8
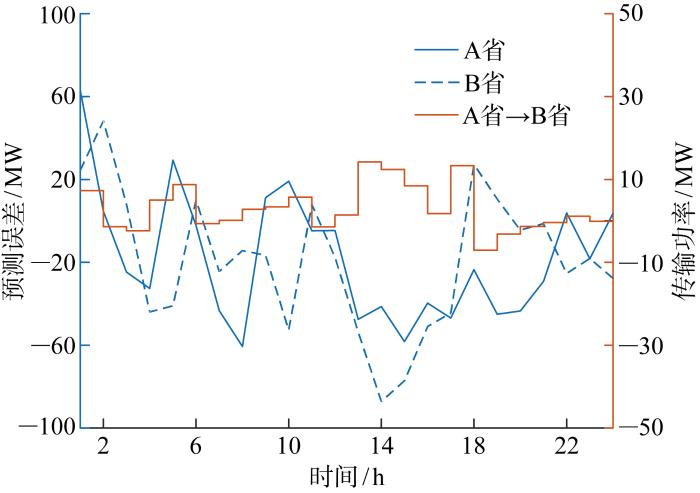
图8
受端A省、B省源-荷预测偏差及传输功率
Fig.8
Forecast errors of source-load and transmission power between receiving provinces A and B
5 结论
基于我国省间-省内两级电力市场运作现状,充分考虑新能源和负荷不确定性的影响,提出一种不确定性环境下考虑省间-省内两级市场运作的两阶段经济调度模型,并得到以下结论.
(1) 利用范数距离(1-范数和∞-范数)模糊集有效刻画不确定性源-荷预测偏差,建立双层两阶段分布鲁棒优化模型,利用KKT条件转换和CCG算法迭代求解,有效实现不确定性环境下考虑省间-省内两级市场运作的电力系统经济调度,验证了DRO方法相对于SO和RO方法的优点.
(2) 省间-省内两级电力市场运作下的两阶段经济调度模型具有如下特点:在日前调度阶段,省间市场的存在有效降低省内市场的运行成本,且能够有效缓解省内线路阻塞所引起的运行成本增加的问题;在日内调度阶段,受端省份间的备用共享机制提升受端省份共同应对新能源和负荷预测偏差的能力,有助于降低日内再调度成本.
未来将研究虚拟电厂对两级电力市场的影响,并研究储能在两级市场环境下对平抑新能源波动性的作用.
附录见本刊网络版(
参考文献
Analysis of the distribution and evolution of energy supply and demand centers of gravity in China
[J].DOI:10.1016/j.enpol.2012.07.012 URL [本文引用: 1]
Inter-regional power grid planning up to 2030 in China considering renewable energy development and regional pollutant control: A multi-region bottom-up optimization model
[J].DOI:10.1016/j.apenergy.2016.11.021 URL [本文引用: 1]
清洁低碳, 能源结构这样转型
[EB/OL]. (
Clean and low-carbon, energy structure transformation
[EB/OL]. (
两级电力市场环境下计及风险的省间交易商最优购电模型
[J].
An optimal power purchase model of inter-provincial traders in two-level electricity market considering risk management
[J].
考虑多级调度的跨省区大电网安全约束经济调度模型
[J].
Security constrained economic dispatch model of inter-provincial power grid considering multi-level dispatch
[J].
计及光伏-负荷预测不确定性的直流跨省互联电网双级调度策略
[J].
Two level scheduling strategy for inter-provincial DC power grid considering the uncertainty of PV-load prediction
[J].
促进跨区新能源消纳的直流联络线功率优化模型及分析
[J].
Power optimization model and analysis of HVDC tie-line for promoting integration of inter-regional renewable energy accommodation
[J].
基于源荷状态的跨区互联系统协调优化调度
[J].
Coordinated and optimal scheduling of inter-regional interconnection system based on source and load status
[J].
考虑电网运行风险的省间转供电力交易补偿模型
[J].
Compensation model of inter-provincial transfer electricity transaction considering grid operation risk
[J].
A decomposition approach to the two-stage stochastic unit commitment problem
[J].DOI:10.1007/s10479-012-1092-7 URL [本文引用: 1]
Risk-constrained bidding strategy with stochastic unit commitment
[J].DOI:10.1109/TPWRS.2006.887894 URL [本文引用: 1]
含风电电力系统的多场景鲁棒调度方法
[J].
A multi-scenario robust dispatch method for power grid integrated with wind farms
[J].
A robust approach to chance constrained optimal power flow with renewable generation
[J].DOI:10.1109/TPWRS.2015.2499753 URL [本文引用: 1]
Contingency-constrained unit commitment with n-K security criterion: A robust optimization approach
[J].DOI:10.1109/TPWRS.2010.2087367 URL [本文引用: 1]
Distributionally robust optimization for planning and scheduling under uncertainty
[J].DOI:10.1016/j.compchemeng.2017.12.002 URL [本文引用: 1]
Data-driven stochastic unit commitment for integrating wind generation
[J].DOI:10.1109/TPWRS.2015.2477311 URL [本文引用: 2]
考虑风电不确定性的电热综合系统分布鲁棒协调优化调度模型
[J].
A distributionally robust coordinated dispatch model for integrated electricity and heating systems considering uncertainty of wind power
[J].
中国特色、全国统一的电力市场关键问题研究(3): 省间省内电力市场协调运行的交易出清模型
[J].
Key issues of national unified electricity market with Chinese characteristics (3): Transaction clearing models and algorithms adapting to the coordinated operation of provincial electricity markets
[J].
Profit-oriented BESS siting and sizing in deregulated distribution systems
[J].DOI:10.1109/TSG.2022.3150768 URL [本文引用: 1]
基于云模型和k-means聚类的风电场储能容量优化配置方法
[J].
Capacity configuration method of energy storage system for wind farm based on cloud model and k-means clustering
[J].
Solving two-stage robust optimization problems using a column-and-constraint generation method
[J].DOI:10.1016/j.orl.2013.05.003 URL [本文引用: 1]
MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education
[J].DOI:10.1109/TPWRS.2010.2051168 URL [本文引用: 1]