工作辊是轧机上发挥轧制功能的主要部件之一,在精轧工序中使金属产生连续塑性变形,其工作损耗约占精轧工序总成本的25%.精轧机持续轧制一段时间后,工作辊辊身温度上升,需定时下机冷却;为避免产品质量缺陷,连续上机轧制后轧辊工作层磨损量达到一定厚度,需适时对工作辊进行磨削.通常出于生产需求,各辊需同时下机,而各轧机上轧辊规格及轧制条件不同导致磨削周期也不同,因此给组合磨削带来机会进而降低维护成本.在精轧场景中,轧辊的下机和磨削安排相互交错,下机点和磨削点变动会影响轧辊故障率、轧件质量及轧辊耗材.目前,钢铁企业常采用定周期下机和磨削的策略,各轧辊依据厂商建议值进行单独磨削,在辊组系统层面缺乏对故障、质量等的统一考虑,产线协同水平低.因此,如何依据具体轧制场景优化各工作辊的磨削周期和组合维护方案,对企业降低工作辊磨削损耗、提升轧线产品质量具有重要意义.
工作辊维护策略需考虑单辊磨削周期,即维护周期的优化及系统中各辊的组合优化两方面问题.在单辊维护建模方面,目前针对轧辊维护的研究大多侧重于磨损量静态预测模型.张炯等[1]构建轧辊典型磨损量预测模型及轧辊可靠度模型,以可靠度阈值作为轧辊更换标准;尹一岚[2]考虑轧辊性能退化随机特性,提出混合蚁群算法以优化多品种小批量轧制任务下工作辊换辊次数;张晓红[3]将轧辊系统抽象为可修多部件系统,结合联合劣化状态空间划分模型进行系统视情机会维修决策建模;邱红雷等[4]针对中厚板轧机轧辊的磨损,将轧辊磨损量视为沿辊身横向分布的函数并借助回归分析方法建立轧辊磨损模型;Song等[5]使用有限元分析方法总结工作辊磨损规律,利用粒子群优化算法和差分进化算法优化工作辊磨损模型参数;John等[6]建立具有适用性的轧辊磨损预测模型,适用于轧制力、轧件品类、轧辊性能、轧制工序等不同工况变化下的一般性场景;高坤等[7]结合轧辊本身运维特点,提出成批更换及离线视情磨削相结合的轧辊更换磨削策略.综上所述,现有的轧辊维护策略研究仅考虑磨损量或工艺可靠度等性能因素,且在研究性能退化建模时未建立轧辊磨损、轧辊故障及轧件质量的相关性机制,未涉及轧辊系统整体维护成本的建模研究,无法反映轧辊维护方案变动对精轧生产的综合影响.
在多辊的组合维护方面,机会维护是解决多部件系统组合维护的有效策略[8⇓-10],但目前,机会维护策略尚未应用于轧辊系统,在其他生产领域则有较多研究.例如,Sheu等[11]结合部件故障和性能退化等短期信息,提出动态调整原有维护计划的两阶段机会维护模型;Najafi等[12]基于矩阵算法推导具有连续状态劣化过程的两单元串联系统的条件可靠度,并针对具有经济依赖性的串联机械系统提出新的机会维修策略;Oakley等[13]针对具有经济和随机依赖性的连续监测多组分系统,提出一种基于条件效用函数的维修策略以获得最优更换决策;Xiao等[14]提出以最小化总成本为目标的机组群生产调度和预防维护联合优化模型,量化解析组合维护对生产调度与维护策略的影响;Song等[15]基于风电场系统内多部件设备的衰退差异进行组合维护,在减少系统停机次数的同时节约成本;Colledani等[16]以系统的特征行为为基础制定设备生产的机会维护策略,利用机会维护时间窗执行预防性维护任务;Do等[17]考虑性能退化相关性和经济相关性的两部件系统,提出基于设备状态的机会维修模型.以上研究对降低多部件系统的整体维护成本具有重要意义,但现有的机会维护研究没有涉及类似精轧机组的生产场景,缺少对下机和磨削两种维护动作及两者的约束关系和协调机制及相应的维护成本建模方法的综合考虑,无法有效识别精轧特殊生产场景下的辊组维护需求.
提出一种新的机会维护模型,将轧辊随机磨损作为关键因素,综合考虑轧辊磨削、机组两类故障、轧件质量损失的影响,以维护成本为中心构建单辊维护模型,从而实现单辊维护周期的动态决策.在此基础上,结合各轧辊磨削周期不同、下机周期相同、下机计划允许小幅调整等特殊场景,建立工作辊动态机会维护模型,以实现精轧机组工作辊机会维护决策方案的动态优化.
1 问题描述
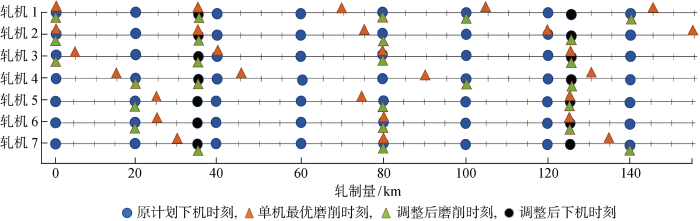
以某钢厂热轧生产线精轧机组为研究对象,该机组配置有7台常规半连续式热轧带钢轧机,每台轧机上安装有上下工作辊,如图1所示.
图1
轧线在轧制带钢产品时采用连续生产方式.工作辊在轧制一段时间后需下机冷却,为保证生产的连续性,该精轧机组配备多套工作辊轮换使用.一套工作辊同时上下机,各套辊之间不会同时进行磨削,可针对单套辊进行维护策略研究.各轧机上下辊配对固定,工作条件和磨损量几乎相同,更换、磨削等维护动作需同时进行,因此在考虑磨损和故障等问题时将一对辊视为整体.为满足精轧工序中变化的轧制力需求,各轧机使用不同规格型号轧辊,因此各轧辊的磨损速度、故障率等各不相同.其他相关假设如下:
(1) 各轧机工作辊由于热特性约束必须同时下机,但由于规格及轧制力不同其磨削周期不尽相同.
(2) 出于减少停机次数、保障连续生产的考虑,磨削安排在下机后进行.同一时刻任意数量的轧辊需要磨削,产生同样的磨削固定成本.
(3) 精轧机组使用轧制长度而非轧制时间来制定维护周期,每轧制20 km钢材后各工作辊需要下机.出于轧件批量最小规格约束,下机点只能前后调整5 km或不变,调整时产生下机时间调整成本,磨削点则可以选择调整5 km的倍数,如图2所示.
图2
图2
工作辊下机与磨削计划示意图
Fig.2
Schematic diagram of dismounting and grinding plan of work roll
2 单辊维护建模
磨削能够修复轧辊表面,恢复轧制性能.生产维护中若轧辊磨削频率提高,则轧辊磨削耗材增加,同时故障率、轧件质量不合格概率降低.因此在建立维护模型时,需考虑对应磨削成本、故障损失成本与质量损失的变化.其中,磨削成本受轧辊自身磨损量和磨削工艺的影响;故障成本与轧辊磨损等性能退化直接相关;轧件质量损失受轧辊磨损量和辊缝控制系统自动调节阈值影响.由于各类成本多与磨损相关,维护建模需首先建立轧辊磨损模型.
磨削会改变轧辊直径等参数,影响下一周期轧辊耗材和故障等成本,因此维护建模过程中需对每个磨削周期分别考虑.假设轧辊磨削后投入使用时已累计轧制长度为
式中:Cm为磨削成本;Cq为轧件质量成本;Ca为轧辊故障成本.通过建立轧辊单磨削周期维护成本模型,动态解析轧辊单磨削周期内总维护成本随周期长度的变化机制,进而确定轧辊的最优磨削周期.
2.1 随机磨损建模
轧制过程中工作辊和轧件表面之间存在相对滑动产生磨损,剧烈磨损会使轧辊运行功能受损,带来经济损失.轧辊磨损机理属于机械工程领域中的结构退化问题,建模方法较成熟,如企业常用轧辊磨损计算模型(RWEAR)[1]以估算工作辊磨损情况,该模型中单辊轧制单位长度磨损量可表示为
式中: G为给定工况下轧辊属性系数;A为轧制产品系数;α为轧制速率影响指数.G、A分别可定义为
式中:a为磨损换算系数;
实际生产中,随着轧辊性能退化,轧辊参数无法准确计算且轧制速度存在波动,因此需对轧辊属性系数与轧制速率系数进行随机化处理.参考文献[1]中对轧辊随机磨损模型进行研究,近似认为轧辊属性系数服从对数正态分布,轧制速率影响指数服从正态分布,即
式中:μ为期望值;
分布参数获取方法与参考文献[1]中相同.单辊单位轧制长度内磨损量满足:
累计求和可得单辊在磨削周期内轧制长度T的总磨损量满足:
式(6)表明,磨削周期内轧制长度T内的总磨损量服从对数正态分布.据此,可得到当前直径为D的轧辊在轧制长度T内的磨损量期望值为
2.2 磨削成本建模
轧辊工作层磨损达到给定的极限时,需进行磨削来恢复工作性能.磨削时除辊磨损部分外,还需额外磨去给定的安全余量,以保证辊身随机磨损不均处均被修复.基于以上考虑,轧辊单次磨削量为
式中:
W1可视为正常工作耗材,实际磨削量中超出W1的部分则视为维护耗材,可表示为
磨削时产生固定成本C1和轧辊耗材成本CM,其中CM可通过轧辊磨削额外损失部分占总工作层比例以及该轧辊价格为
式中:
2.3 质量成本建模
轧制生产中轧辊直径发生不均匀变化,为降低磨损不均对生产稳定性的影响,轧机上配有辊缝自动控制系统,使轧制中轧件与工作辊保持贴合.该系统存在调整范围,如轧辊磨损量超出调整阈值将无法获得稳定的轧制力,导致轧制品出现生产质量问题.将辊缝自动控制系统调整阈值为Wmax,则当工作辊在T内的磨损量W>Wmax时,辊缝自动控制系统失效.根据式(8)中W随机分布形式,令
式中:
式中:T'为最优磨削周期.
当前直径为D的轧辊在单次磨削周期T内由于生产质量问题导致的维护成本为
式中:C2为单位长度轧件质量问题成本.
2.4 故障成本建模
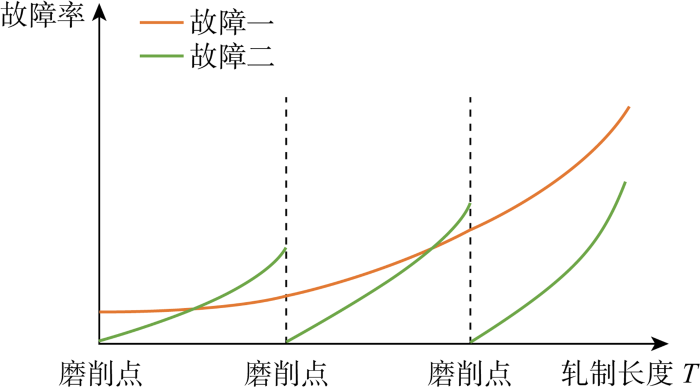
精轧工作辊常见故障类型主要包括甩尾、轧破、粘铁、打滑、卡钢、断面不良、表面细孔、表面凹陷坑等.前4类故障(简称故障一)与轧辊老化程度相关,故障率随累计轧制里程增加而上升;后4类故障(简称故障二)与轧辊表面状态和老化程度均相关,由于轧辊磨削后表面状态修复,故障率在轧辊全生命周期内呈周期性上升趋势,如图3所示.
图3
威布尔分布可较好地拟合机械类设备故障率曲线[18].采用标准二参数威布尔分布进行建模,当前直径为D的轧辊从初始投入使用时的[0,T]工作周期内故障一对应故障率为
式中:
故障二的故障率受轧辊老化程度和磨削状态影响,磨削会引起轧辊直径的变化,因此在标准威布尔分布的基础上引入直径变化对故障概率的影响,当前直径为D的轧辊在
式中:α_2和β_2分别为故障二时威布尔分布的形状参数和尺寸参数; k_1为比例系数.给出周期初始已轧制长度T_0和当前直径D,则T内故障发生概率为
取产线统计均值作为单次故障损失成本C3,则单次磨削周期内总故障成本为
3 系统层动态机会维护建模
实际生产中,多对轧辊若同时磨削能降低包括运输和磨削机床开动等在内的整体维护组成本.通过调整各轧辊下机和磨削周期,能平衡各类维护成本,从而满足系统层维护经济性.基于单辊最优维护策略,提出基于成组成本变化率的动态机会维护策略,进一步优化精轧辊组机会维护方案,具体决策步骤及相应建模方案如下.
3.1 确定备选磨削点
式(1)建立了单辊单磨削周期维护成本
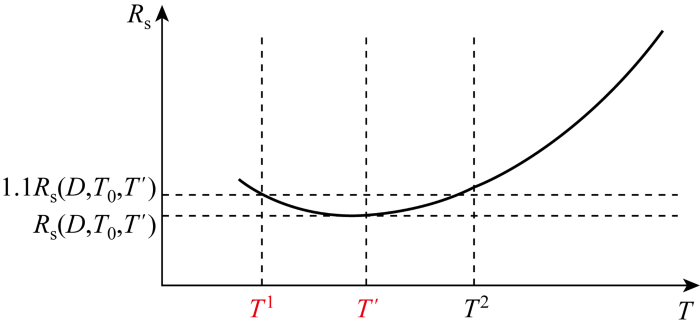
在
共有i个备选磨削点进行选择且该辊必须在其中进行磨削,备选磨削点确定方法如图4所示.T'处单辊维护成本率为
图4
3.2 获取最优成组方案
对各备选磨削点,按式(22)中成本率变动规则确定其余各辊是否可移动至该备选磨削点进行组合,列举所有成组方案并根据成组后总成本率降低的规则,确定各备选磨削点的最优成组方案.成组后,该组轧辊周期长度T内组合磨削成本为
式中:n为成组后辊对数量;
成组成本变化率表示成组维护相比该组合中各辊单独维护成本之和的比例.考虑磨削固定成本降低及可能增加的辊组下机点移动成本后,能确定该备选磨削点下Kg最小的最优成组方案.
对i个备选磨削点分别进行以上步骤并得到对应成组方案.然后,比较各备选磨削点的最优成组方案的
3.3 系统维护计划的动态生成
执行
迭代轧辊参数和磨削组合信息后,可累计得到系统全生命周期总维护成本及总维护成本率,分别表示为
式中:m为系统全生命周期磨削次数;
4 实例分析
4.1 算例概览
基于钢厂热轧生产线2017—2020年生产维护实绩进行分析.维护模型中涉及大量待定参数,依据获取方法可划分为如下两类.
第一类为设备与生产参数,可由企业轧制设备的基本参数表、生产数据表等得到.其中,轧制产品系数根据该轧线轧制量最高的某硅钢板型号进行计算;轧辊属性系数、轧辊初始直径、报废直径、耗材成本、磨削工艺固定值、辊缝自动控制系统调整阈值等参数随轧辊规格和工艺要求相应发生改变;单次故障损失成本根据产线统计的平均故障停机时间、平均额外磨削量及轧辊耗材成本等进行计算;单次质量问题成本考虑单次轧制批量带钢返修价格及相应停机时间成本;单次磨削固定成本包含装卸运输人力成本、磨削机启动耗材成本以及生产管理成本.以上成本取值由企业直接反馈得到.第j台轧机的上述参数取值如表1所示.
表1 设备与生产参数
Tab.1
| j | WG/mm | Wmax/mm | Proll/元 | pM | C1/元 | C2/元 | C3/元 | C4/元 | D0/mm | D2/mm |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.8 | 2.0 | 20 500 | 0.99 | 11 800 | 15 300 | 35 100 | 9 700 | 655 | 535 |
| 2 | 1.8 | 2.0 | 20 500 | 0.99 | 11 800 | 15 300 | 35 100 | 9 700 | 655 | 535 |
| 3 | 1.8 | 2.0 | 20 500 | 0.99 | 11 800 | 15 300 | 35 100 | 9 700 | 655 | 535 |
| 4 | 1.6 | 1.5 | 26 000 | 0.99 | 11 800 | 15 300 | 35 100 | 9 700 | 650 | 530 |
| 5 | 1.4 | 1.2 | 32 000 | 0.99 | 11 800 | 15 300 | 35 100 | 9 700 | 630 | 510 |
| 6 | 1.4 | 1.2 | 32 000 | 0.99 | 11 800 | 15 300 | 35 100 | 9 700 | 630 | 510 |
| 7 | 1.4 | 1.2 | 32 000 | 0.99 | 11 800 | 15 300 | 35 100 | 9 700 | 630 | 510 |
第二类为统计拟合参数,根据实际轧制生产现场数据在给定的模型中拟合得到.其中,轧辊故障威布尔参数根据企业给出的故障类型、发生时间及对应的轧辊已工作长度使用最大似然法拟合得到;轧辊故障二直径比例系数通过将轧辊按发生故障二时的直径分组,代入轧辊故障二威布尔参数后分别求得比例系数值,并将各组比例系数与平均直径进行线性拟合得到;轧制速率随机指数则根据各轧机历史生产耗时和产量数据计算出的轧制速率进行正态分布拟合得到.第j台轧机的上述参数取值如表2所示.
表2 统计拟合参数
Tab.2
| j | A | ln G | α | (α1,β1) | (α2,β2) | k1 |
|---|---|---|---|---|---|---|
| 1 | 2.83 | N(-9.83, 0.912) | N(0.83, 0.112) | (81.7, 1.3) | (193.7, 1.9) | 1.15 |
| 2 | 2.83 | N(-9.59, 0.932) | N(0.85, 0.132) | (92.6, 1.4) | (184.2, 1.5) | 1.17 |
| 3 | 2.83 | N(-9.67, 0.852) | N(0.87, 0.152) | (79.6, 1.3) | (203.2, 2.3) | 1.31 |
| 4 | 2.83 | N(-9.92, 0.872) | N(0.92, 0.172) | (65.1, 1.5) | (164.3, 1.3) | 1.19 |
| 5 | 2.83 | N(-9.92, 0.992) | N(0.96, 0.192) | (113.2, 1.3) | (228.1, 1.4) | 1.26 |
| 6 | 2.83 | N(-9.94, 0.962) | N(0.94, 0.162) | (94.2, 1.4) | (195.7, 1.1) | 1.21 |
| 7 | 2.83 | N(-9.66, 0.872) | N(0.96, 0.172) | (85.3, 1.5) | (206.6, 1.8) | 1.33 |
表4 机会维护策略下磨削排程
Tab.4
| j | T/km | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 40 | 75 | 100 | 120 | 155 | 180 | 200 | 240 | 265 | 300 | |
| 1 | o | o | o | o | o | o | o | ||||
| 2 | o | o | o | o | o | o | o | ||||
| 3 | o | o | o | o | o | o | o | ||||
| 4 | o | o | o | o | o | ||||||
| 5 | o | o | o | o | |||||||
| 6 | o | o | o | o | |||||||
| 7 | o | o | o | o | |||||||
4.2 参数分析
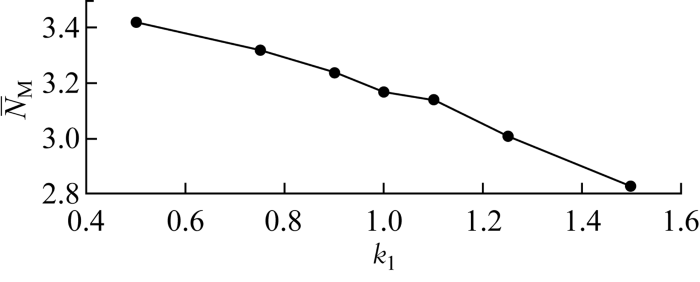
在轧制不同产品时,轧制工艺要求和允许误差相应发生变化,通过缩小辊缝自动控制阈值Wmax,能实现对轧辊随机磨损量的限制,从而保证轧制力更稳定.保持设备其他参数不变,使Wmax变为原值的k1倍后,系统的
图5
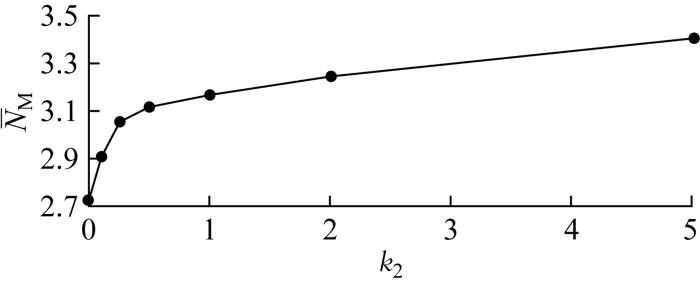
制定维护计划时,磨削固定成本数值会对成组结果有直接影响,系统磨削次数和磨削成本相应改变.保持设备其他参数不变,使磨削固定成本
图6
对于理论最优磨削点提前或延后于原下机点的磨削组合,可通过移动下机点来满足成组需求,其涉及下机点移动成本和磨削固定成本间的平衡,因此下机点移动成本同样影响成组效果.保持设备其他参数不变,使下机点移动成本
图7
图7
不同下机点移动成本下的成组规模
Fig.7
Group size of different deplaning point movement cost
4.3 策略对比
为验证动态机会维护策略(策略一)在工作辊系统维护决策中的有效性,设置基于单机最优磨削周期(策略二)和基于时间窗(策略三)的两种对照维护策略进行结果比较,对照策略具体如下.
策略二为严格按照标准下机周期和3.1节中单辊最优磨削周期执行维护计划,即不进行成组维护,各轧辊均按照单辊的最优磨削点进行定周期维护.
策略三为机会维护领域的传统时间窗策略.基本思路是:轧制过程中,当某一工作辊首先到达理论最优磨削点时,将其他辊中最优磨削点距此辊最优磨削点小于等于某一固定轧制长度的辊成组,这一固定轧制长度可通过最小化规划期内总维护成本率得到.
相比策略一,策略二没有进行磨削组合调整;策略三同样使用机会维护的思想,但组合维护方法较为简单,磨削点相近则进行组合.在计算系统全生命周期总维护成本时,同样可以按照策略一中累积各次组合磨削成本的方法计算得到相应策略下系统的Rt(Tt)值.
各策略下的整体结果对比如表5所示.策略一相比策略二、三,通过成组优化提高每次磨削的辊数量,减少总体磨削次数.虽然策略一中,各轧辊不能在最优磨削时刻进行磨削,但组合后总维护成本率得到了显著降低.由于精轧场景中下机和磨削的特殊规则约束,传统时间窗策略不能有效判断条件限制下组合维护对成本率的影响,而策略一针对单个磨削组合优化的方式更适用于精轧场景.
表5 不同策略下的结果对比
Tab.5
| 策略 | Tt/km | NM | Rt(Tt)/(元·km-1) | |
|---|---|---|---|---|
| 1 | 2 780 | 104 | 3.17 | 7 509 |
| 2 | 2 920 | 137 | 2.53 | 7 915 |
| 3 | 2 840 | 112 | 2.96 | 7 768 |
系统总维护成本由磨削成本、质量成本、故障成本和下机移动成本组成,不同策略下各子成本项对比如表6所示.可知,相比其他策略,策略一优势在于通过成组维护降低了磨削成本,同时也实现了系统故障损失的降低.
表6 不同策略下的子成本项率对比
Tab.6
| 策略 | Rt(Tt)/(元·km-1) | |||
|---|---|---|---|---|
| Cm | Cq | Ca | C4 | |
| 1 | 3 797 | 1 407 | 2 305 | 57 |
| 2 | 4 189 | 1 385 | 2 341 | 0 |
| 3 | 3 966 | 1 421 | 2 381 | 0 |
表7 不同策略和质量成本下的总成本率
Tab.7
| k'C2 | Rt(Tt)/(元·km-1) | ||
|---|---|---|---|
| 策略1 | 策略2 | 策略3 | |
| 0.1 | 7 018 | 7 395 | 7 258 |
| 0.25 | 7 321 | 7 715 | 7 572 |
| 0.5 | 7 473 | 7 875 | 7 729 |
| 1 | 7 509 | 7 915 | 7 768 |
| 2 | 7 617 | 8 031 | 7 881 |
| 5 | 8 138 | 8 580 | 8 421 |
表8 不同策略和故障成本下的总成本率
Tab.8
| k'C3 | Rt(Tt)/(元·km-1) | ||
|---|---|---|---|
| 策略1 | 策略2 | 策略3 | |
| 0.1 | 6 998 | 7 383 | 7 244 |
| 0.25 | 7 308 | 7 709 | 7 564 |
| 0.5 | 7 462 | 7 872 | 7 724 |
| 1 | 7 509 | 7 915 | 7 768 |
| 2 | 7 610 | 8 032 | 7 879 |
| 5 | 8 140 | 8 591 | 8 428 |
5 结语
以钢铁企业精轧机组工作辊为对象,综合考虑轧辊磨损、机组两类故障、辊缝质量控制对故障损失、轧件质量损失与维护成本的影响,构建单辊动态维护模型,在此基础上考虑精轧机组生产场景特殊性,提出工作辊动态机会维护策略和基于成组成本变化率的系统决策模型.实例分析表明,动态机会维护策略可以减少工作辊系统磨削次数,在不同的磨削固定成本和下机时间调整成本下均能有效降低工作辊系统维护总成本率.同时,相对于单辊维护模型和传统时间窗模型等常用维护策略,动态机会维护策略可以获得更低的工作辊系统维护总成本率,对于不同轧制生产场景具有适应性与稳定性,能够满足企业实际应用需求.
参考文献
轧辊随机磨损模型及其最优更换策略研究
[J].
Research on stochastic wear model of roller and its optimal replacement policy
[J].
中厚板轧机轧辊磨损预测
[J].
Roll wear prediction for plate mill
[J].
Study on mathematical model of work roll wear in skin-pass rolling of hot steel strip
[J].DOI:10.1007/s00170-018-2076-9 [本文引用: 1]
Roll wear prediction model for finishing stands of hot strip mill
[J].
轧辊维修策略与备件库存联合优化研究
[J].
The joint optimization strategies of rollers maintenance policy and spare parts provisioning policy
[J].
基于约束理论的串联型港口装卸系统多机机会维护方法
[J].
Opportunistic maintenance policy for series port handling systems based on theory of constraints
[J].
批量生产模式下考虑设备运行负荷的预防维护策略
[J].
Preventive maintenance of a single machine system with batch production pattern under time-varying workload
[J].
非计划停机下考虑结构相关性的串并联系统机会维修决策研究
[J].
Research on opportunistic maintenance decision method of series-parallel system at unscheduled shutdown considering structural dependency
[J].
A generalized group maintenance policy
[J].DOI:10.1016/S0377-2217(96)00073-2 URL [本文引用: 1]
An optimal opportunistic maintenance policy for a two-unit series system with general repair using proportional hazards models
[J].DOI:10.1016/j.ress.2021.107830 URL [本文引用: 1]
A condition-based maintenance policy for continuously monitored multi-component systems with economic and stochastic dependence
[J].DOI:10.1016/j.ress.2022.108321 URL [本文引用: 1]
Joint optimization of production scheduling and machine group preventive maintenance
[J].DOI:10.1016/j.ress.2015.10.013 URL [本文引用: 1]
Integrated optimization of offshore wind farm layout design and turbine opportunistic condition-based maintenance
[J].DOI:10.1016/j.cie.2018.04.051 URL [本文引用: 1]
Impact of opportunistic maintenance on manufacturing system performance
[J].DOI:10.1016/j.cirp.2018.04.078 URL [本文引用: 1]
Modelling and application of condition-based maintenance for a two-component system with stochastic and economic dependencies
[J].DOI:10.1016/j.ress.2018.10.007 URL [本文引用: 1]