基于BESO算法的高桩承台式水平轴风力机支撑结构优化

doi:10.16183/j.cnki.jsjtu.2022.182

基于BESO算法的高桩承台式水平轴风力机支撑结构优化

占玲玉¹, 何文君¹, 周岱^,¹^,², 韩兆龙¹^,², 朱宏博¹, 张凯¹, 涂佳黄³

1.上海交通大学船舶海洋与建筑工程学院,上海 200240

2.上海交通大学海洋工程国家重点实验室,上海 200240

3.湘潭大学土木工程与力学学院,湖南湘潭 411105

Support Structure Optimization of High-Pile Cap Supported Horizontal Axis Wind Turbine System Based on BESO Algorithm

ZHAN Lingyu¹, HE Wenjun¹, ZHOU Dai^,¹^,², HAN Zhaolong¹^,², ZHU Hongbo¹, ZHANG Kai¹, TU Jiahuang³

1. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

3. College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, Hunan, China

通讯作者: 周岱,教授,博士生导师;E-mail:zhoudai@sjtu.edu.cn.

责任编辑: 李博文

收稿日期: 2022-05-24 修回日期: 2022-10-18 接受日期: 2022-11-10

基金资助:

上海市教育委员会科研创新计划自然科学重大项目(2019-01-07-00-02-E00066)
国家自然科学基金(52122110)
国家自然科学基金(42076210)
上海市曙光计划(19SG10)
上海交通大学深蓝计划(SL2020PT201)
湖南省自然科学基金(2021JJ50027)

Received: 2022-05-24 Revised: 2022-10-18 Accepted: 2022-11-10

作者简介 About authors

占玲玉(1998-),硕士生,从事海上风机结构优化、减振研究.

摘要

研究大型水平轴风力机塔筒的合理支撑结构形式对风力发电结构系统安全至关重要.针对高桩承台式水平轴风力机,基于反比例型删除率的双向渐进结构优化(BESO)算法,拓扑优化风力机塔筒结构,根据计算流体动力学方法和桩土相互作用原理,建立考虑桩土作用的风力机结构风致动力响应数值模型,比较分析优化前后风力机结构动力响应特性,验证结构优化方法的可靠性.经拓扑优化得到新的高桩承台水平轴风力机支撑结构,相较于初始结构,优化后的支撑结构风致动力响应显著降低,成果可为高桩承台式水平轴风力机支撑结构设计优化提供技术参考.

关键词： 水平轴风力机; 高桩承台式风力机基础; 双向渐进结构优化算法; 风致动力响应

Abstract

The study of reliable support structure is of great significance to the safety of large-scaled horizontal axis wind turbine (HAWT) system. In this paper, for cap-supported HAWT with high pile, the bidirectional evolutional structure optimization (BESO) algorithm based on inversely proportional deletion rate was used to optimize its support structure. Using computational fluid dynamics (CFD) and the principle of pile-soil interaction, the finite element model of HAWT was established, where the wind load and pile-soil interaction were taken into consideration. The reliability of the structural optimization method was verified through the comparison of the dynamic response characteristics between the initial and the optimized model. The results show that the current BESO algorithm can effectively generate a novel support structure form for high-pile HAWT, whose dynamic response is significantly reduced. The results can provide useful references for HAWTs designs.

Keywords： horizontal axis wind turbine (HAWT); high-pile cap foundation; bidirectional progressive structural optimization algorithm (BESO); wind-induced dynamic response

PDF (9027KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

占玲玉, 何文君, 周岱, 韩兆龙, 朱宏博, 张凯, 涂佳黄. 基于BESO算法的高桩承台式水平轴风力机支撑结构优化[J]. 上海交通大学学报, 2023, 57(8): 939-947 doi:10.16183/j.cnki.jsjtu.2022.182

ZHAN Lingyu, HE Wenjun, ZHOU Dai, HAN Zhaolong, ZHU Hongbo, ZHANG Kai, TU Jiahuang. Support Structure Optimization of High-Pile Cap Supported Horizontal Axis Wind Turbine System Based on BESO Algorithm[J]. Journal of Shanghai Jiaotong University, 2023, 57(8): 939-947 doi:10.16183/j.cnki.jsjtu.2022.182

风力机大型化可有效提高风力发电量和风能利用率,是海上风力发电的世界发展趋势^[1].研发建造包括10、15和20 MW在内的大型风力机是我国海洋绿色能源开发利用的战略重点.然而随着风力机转子、塔筒尺寸的不断增加^[2],大型风力机结构系统柔性增加,抗风能力明显降低^[3],风力机风致动力响应更加复杂,系统风致动力灾变风险更加凸显.

研究并优化大型水平轴风力机支撑结构对保证系统运行安全十分重要.风力机大型化导致塔筒顶部大型转子和发电机质量增加、支撑塔筒高度增大.常用的圆锥塔筒无法满足风力机结构的强度和刚度要求.迄今,学者们对大型水平轴风力机支撑结构优化已有一定研究.Gentils等^[4]基于遗传算法,考虑多准则约束,对美国国家可再生能源实验室(NREL)提出的5 MW单桩式风力机(NREL 5 MW)塔架和基础进行优化分析并计算风力机支撑结构优化尺寸参数;Oest等^[5]基于疲劳损伤荷载、准静态分析和动态分析,对海上风力机支撑结构进行梯度优化设计;葛旭等^[6]结合有限元分析与进化策略,对海上三桩单立柱风力机支撑结构主尺度参数进行多参数同步优化设计;Tian等^[7]对导管架式海上风力机的导管架基础进行拓扑优化,结合尺寸和形状优化实现结构重分布,得到质量更轻的导管架结构.上述研究仅为针对特定风力机结构形式的参数优化,未改变其支撑结构形式,虽对风力机结构稳定性有一定提高,但设计方法具有局限性.相较于参数优化,拓扑优化方法具有更多的设计自由度,是优化大型水平轴支撑结构的新途径.

拓扑优化方法应用于包括结构优化在内的广泛领域,其双向渐进结构优化(BESO)算法优化效果较好.王章骏等^[8]采用BESO算法对吸能管进行拓扑优化,提高了带隔板薄壁方管的耐撞性能, 实现了吸能管轻量化的设计目标;刘昆等^[9]基于BESO算法对船体梁腹板开孔进行设计优化,提出适用于船体结构孔型的BESO算法;BESO还在罗马小体育宫^[10]、卡塔尔国家会议中心^[11]等建筑工程设计中得到应用.目前,大型水平轴风力机塔筒支撑结构拓扑优化还鲜有研究.

基础是风力机系统的关键结构之一,高桩承台基础的结构安全性能高,适合我国海床地质条件,施工工艺成熟,在我国近海风电场建设中多有应用^[12].但不考虑桩-土相互作用会导致风力机位移响应被严重低估^[13⇓-15],是结构安全设计的重要隐患.

考虑桩土相互作用的风力机支撑结构性能,开展支撑结构优化分析.基于反比例型删除率的BESO算法,提出大型高桩承台式水平轴风力机支撑结构拓扑的优化算法,运用有限元软件ANSYS开展大型水平轴风力机支撑结构寻优分析,获得一种风力机优化支撑结构,显著降低了风力机风致动力响应.

1 风力机结构建模与分析

1.1 风力机支撑结构建模

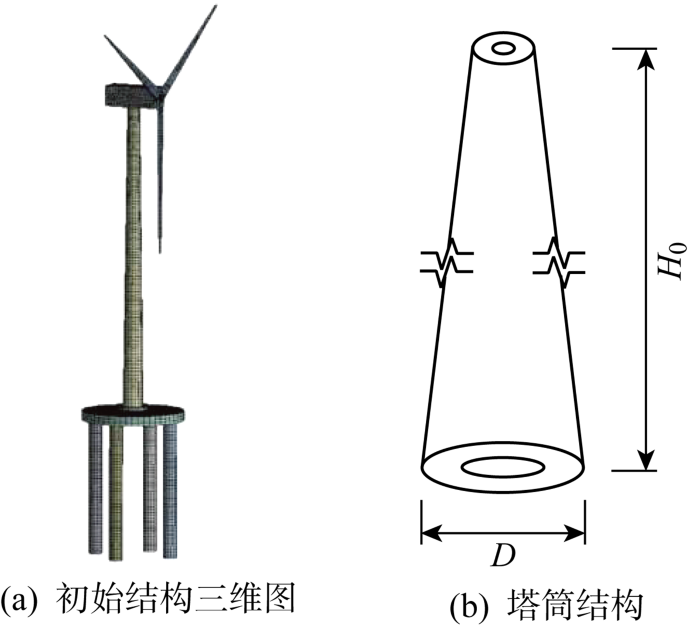
以应用较广的NREL 5 MW^[16]风力机为背景,进行考虑桩土作用的近海坐底式高桩承台大型水平轴风力机塔筒结构优化研究.高桩承台式水平轴风力机初始模型如图1(a)所示,其支撑系统包括上部塔筒结构、承台和群桩.水平轴风力机塔筒为圆筒式支撑结构,如图1(b)所示,塔筒底部外径D=6 m,塔筒高度H₀=90 m^[16].塔筒选用Q345钢材^[17],密度ρ₀=7.85 g/m³,弹性模量E₀=211 N/m²,泊松比ν₀=0.3,风力机额定风速为11.4 m/s,具体参数如表1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 水平轴风力机塔筒结构初始模型

Fig.1 Horizontal axis wind turbine initial model

表1 5 MW水平轴风力机塔架参数

Tab.1 5 MW horizontal axis wind turbine parameters

参数	数值	参数	数值
塔筒底部外径,D/m	6	额定输出功率/MW	5
塔筒顶部外径/m	3.87	叶片长度,L/m	61.5
塔架高度,H₀/m	90	额定风速/(m·s^-1)	11.4
转子质量/kg	110000	额定叶尖速度/(m·s^-1)	80
机舱质量/kg	240000	塔架质量/kg	591942

新窗口打开| 下载CSV

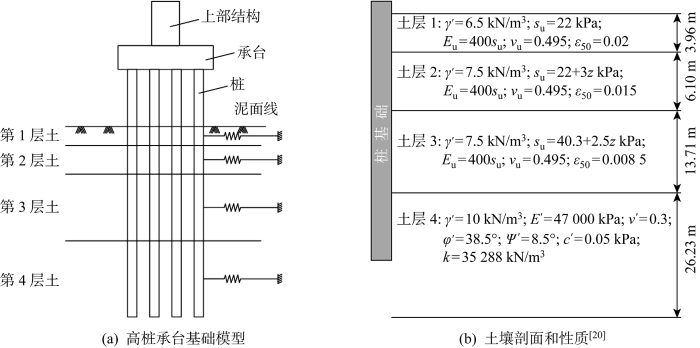
参照上海东海大桥海上大型风力发电工程项目采用高桩承台式基础^[18],混凝土承台直径D₁=20 m,承台厚度S=5 m,设置4根直径d₁=3 m、壁厚 t=20 mm的全直钢管基桩,桩基长度 H₁=52 m,入土深度h=40 m.承台材料选用C45标号混凝土,弹性模量E=33.5 GPa,密度为2500 kg/m³,泊松比ν=0.2^[19],基础模型如图2(a)所示.基于Jung等^[20]和Chen等^[21]确定土体模型和力学参数:土体浮重度 $γ'$ 、弹性模量 $E'$ 、泊松比 $ν'$ 、内摩擦角 $φ'$ 和不排水抗剪强度s_u、黏土泊松比ν_u、50%的最大有效应力下的轴向应变 $ε_{50}$ 、土层深度 $z$ 、膨胀角 $ψ'$ 、黏聚力 $c'$ 、地基反力模量 $k$ ,如图2(b)所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 基础与土体模型

Fig.2 Foundation geometric model and soil profiles

1.2 风力机支撑结构风荷载

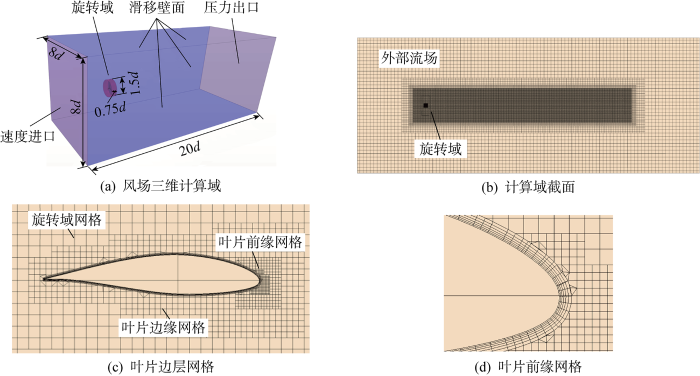
对高桩承台大型水平轴风力机结构系统,基于计算流体动力学(CFD)方法并运用Star-CCM+计算软件^[22]数值模拟获得风力机叶片气动荷载,风力机风轮直径为d,选取长方体风场计算域,计算域长度、宽度和高度分别为20d、8d和8d,如图3(a)和3(b)所示.计算域划分共 1700 万个网格.计算域中,风力机叶片圆柱体旋转域在竖平面的直径为1.5d,旋转域高度即顺风向尺度为0.75d;旋转域之外的计算域等其他部分为静止域.对旋转域和静止域设置交界面,采用滑移网格处理风轮运行旋转问题,如图3(c)和3(d)所示.叶片表面采用棱柱层网格,延伸因子为1.3,总厚度为0.08 m,无量纲化壁面距离为y⁺<1.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 风场计算域和边界条件

Fig.3 Wind field computation domain and boundary condition

对大型风力机支撑结构采用锥筒结构^[23],塔筒高度为90 m.将塔筒简化为受弯曲变形、轴向压缩和扭转变形的悬臂梁.风力机运行时,需考虑塔筒沿高度的风压变化.沿塔筒高度l处的风荷载^[24]为

(1)

\begin{matrix} f (l) = \frac{1}{2} C_{d} ρ D_{l} V^{2} (l) \end{matrix}

式中:C_d为风阻力系数,取值1.2; $ρ$ 为空气密度; $D_{l}$ 为塔筒高度 $l$ 处的塔筒截面直径; $V (l)$ 为沿塔架高度 $l$ 处的瞬时风速.

1.3 桩土相互作用

美国石油协会(API)规范推荐的土体p-y曲线,即非线性弹簧模型广泛应用于海洋工程桩基设计.引入用于分析风力机支撑结构的桩土相互作用^[25],该模型考虑了土体非线性、土层变化和土体种类等因素的影响,软土中各层p-y曲线为

(2)

p = \{\begin{array}{l} \frac{p_{u}}{2} {(\frac{y}{y_{c}})}^{1 / 3}, y \leq 3 y_{c} \\ 0.72 p_{u} [1 - (1 - \frac{X}{X_{R}}) \frac{y - y_{c}}{12 y_{c}}], \\ 3 y_{c} < y \leq 15 y_{c} \\ 0.72 p_{u} \frac{X}{X_{R}}, y > 15 y_{c} \end{array}

式中:p为深度X处单位桩长的极限水平土抗力标准值;y_c为实验室中对未扰动工试样做不排水压缩试验时,其应力达到最大应力一半时的变形;y为泥面以下深度X处桩的侧向水平变形;X_R为泥面以下到土抗力减少区域底部的深度;p_u为深度X处单位桩长的极限水平土抗力标准值.

对于砂土情况,p-y曲线为

(3)

\begin{matrix} p = A p_{u} t a n h (\frac{K X}{A p_{u}} y) \end{matrix}

式中:K为地基反力初始模量;A为计入静力荷载和循环荷载条件的参数.

基于API规范的p-y曲线法,计算循环荷载作用情况下的桩侧土抗力,使用ANSYS软件的Combine39单元模拟p-y曲线,该单元是具有非线性功能的单向拉压单元,常用于桩土相互作用模拟.在搭建有限元模型时,根据计算得到的土体p-y曲线参数,每间隔1 m设置一个Combine39土弹簧单元.在桩土相互作用模拟过程中,为简化计算未考虑桩土循环弱化作用及桩端设置竖向简支约束.

1.4 风力机支撑结构系统振动响应

采用 Newmark-β法^[26]中的平均常加速度法对风力机支撑结构系统风致振动进行瞬态分析,其中控制Newmark-β法精度和稳定性的参数取值为 γ=0.5,β=0.25.采用瑞利阻尼模拟风力机结构阻尼,刚度阻尼系数取值为0.03^[27].风力机结构系统动力激励下的振动方程^[28]为

(4)

\begin{matrix} M \ddot{u} (t) + C \overset{\cdot}{u} (t) + K u (t) = F_{I} (t) + F_{C} (t) + F_{K} (t) \end{matrix}

式中: $\ddot{u}$ (t)、 $\overset{\cdot}{u}$ (t)、u(t)分别为水平轴风力机的加速度、速度和位移矩阵;M、C、K分别为大型水平轴风力机结构的质量、阻尼和刚度矩阵;F_I(t)、F_C(t)和F_K(t)分别为风力机的惯性力、阻尼力和恢复力矩阵.

2 大型水平轴风力机支撑拓扑优化

2.1 BESO算法的数学模型

针对大型水平轴风力机支撑结构优化问题,建立以结构静刚度最大为目标、以结构体积为约束条件的数学力学模型^[29],表示为

(5)

m i n C_{T} = C_{T} (x) = \frac{1}{2} u^{T} K u

(6)

s . t . \overset{n}{\sum_{i = 1}} - V^{*} = 0, x_{i} \in {x_{m i n}, 1}

式中: $C_{T}$ 为结构平均柔顺度; $V^{*}$ 为目标体积比; $v_{i}$ 为第 $i$ 个单元的体积; $n$ 为迭代次数; $x_{i}$ 为设计变量; $x_{m i n}$ 和1分别代表某一单元在设计域内缺失或存在.

2.2 单元灵敏度过滤及更新

为避免产生奇异单元刚度矩阵,算法以x_min代替0表示空单元,在该软删单元的BESO算法^[30]中所有单元的材料弹性模量可根据材料插值模型设置为

(7)

\begin{matrix} E (x_{i}) = E_{0} x_{i}^{q} \end{matrix}

式中: $q$ 为惩罚因子.

单元灵敏度表示增删单元对结构平均柔顺度的影响程度,单元灵敏度大小为单元灵敏度的相对排序,表示为

(8)

α_{i} = - \frac{1}{q} \frac{\partial C_{T}}{\partial x_{i}} = \{\begin{array}{l} \frac{1}{2} {u^{T}}_{i} K_{i} u_{i}, & x_{i} = 1 \\ \frac{x_{m i n}^{q - 1}}{2} {u^{T}}_{i} K_{i} u_{i}, & x_{i} = x_{m i n} \end{array}

式中: $K_{i} 和 u_{i}$ 分别为单元刚度矩阵和单元位移向量.

为抑制优化过程中出现实体单元与空洞单元交替出现的棋盘格等数值不稳定现象^[31],通过权重系数引入节点灵敏度节点概念:

(9)

\begin{matrix} β_{j} = \overset{M}{\sum_{i = 1}} w_{i} {α^{e}}_{i} \end{matrix}

式中: $β_{j}$ 为节点 $j$ 的灵敏度; $M$ 为对节点 $j$ 有影响的单元总数; $w_{i}$ 为权重系数; ${α^{e}}_{i}$ 为单元 $i$ 的灵敏度.

在迭代过程中,根据节点灵敏度对单元灵敏度进行过滤并更新单元灵敏度,更新过程为

(10)

α_{i}^{n} = \frac{\overset{J}{\sum_{j = 1}} (r_{m i n} - r_{i j}) β_{i}^{n}}{\overset{J}{\sum_{j = 1}} (r_{m i n} - r_{i j})}

(11)

α_{i} = \frac{α_{i}^{n} + α_{i}^{n - 1}}{2}

式中: $r_{i j}$ 为 $j$ 节点到 $i$ 单元的中心的距离; $r_{m i n}$ 为以 $i$ 单元中心为原点的过滤圆半径; $α_{i}^{n}$ 为第 $n$ 次迭代的单元灵敏度,将式(11)计算得到的 $α_{i}$ 赋予 $α_{i}^{n}$ ,进行下一次迭代.

2.3 基于BESO算法的结构拓扑优化

鉴于水平轴风力机结构系统对称性,将支撑结构三维优化问题转化为二维平面优化,以风力机塔筒支撑形式和支撑点位置为优化对象.将风力机塔筒主轴高度方向和塔筒半径方向围成的平面作为初始设计域,采用ANSYS软件中的4节点Plane182单元对计算模型进行网格划分.设置底部为固定端约束,选取最不利气动荷载作为外部风荷载.采用反比例型删除率优化模型^[32]对风力机支撑结构进行拓扑优化:

(12)

ω = ω_{m a x} (\frac{1}{1 - V^{*}}) (1 - \frac{V^{*}}{V_{i}}) (1 - \frac{ω_{m i n}}{ω_{m a x}}) + ω_{m i n}

式中: $ω$ 为结构材料的删除率; $ω_{m a x}$ 为给定的最大删除率,取0.057; $ω_{m i n}$ 为给定的最小删除率,取0.012; $V_{i}$ 为优化过程中每一步迭代过程的体积比; $V^{*}$ 值取0.4.

在迭代过程中,根据删除率对体积比进行更新

(13)

\begin{matrix} V_{k + 1} = V_{k} (1 \pm ω), k = 1, 2, 3, \dots \end{matrix}

式中: $V_{k}$ 为第 $k$ 次迭代的体积比: $V_{k + 1}$ 为第k+1次迭代的体积比.

当迭代结果满足根据体积约束和收敛准则^[31]时,终止迭代.为提高迭代效率,设置收敛准则,表示当前迭代步之前10次迭代中平均柔顺度的相对变化量,当目标函数变化随着迭代变化足够小时,则判定迭代结束:

(14)

τ_{c h} = \frac{|\overset{5}{\sum_{i = 1}} (C_{k - i + 1} - C_{k - 5 - i + 1})|}{\overset{5}{\sum_{i = 1}} C_{k - i + 1}} \leq τ

式中: $C_{k}$ 为第 $k$ 次迭代的平均柔顺度; $τ$ 为收敛因子,取值为0.001.

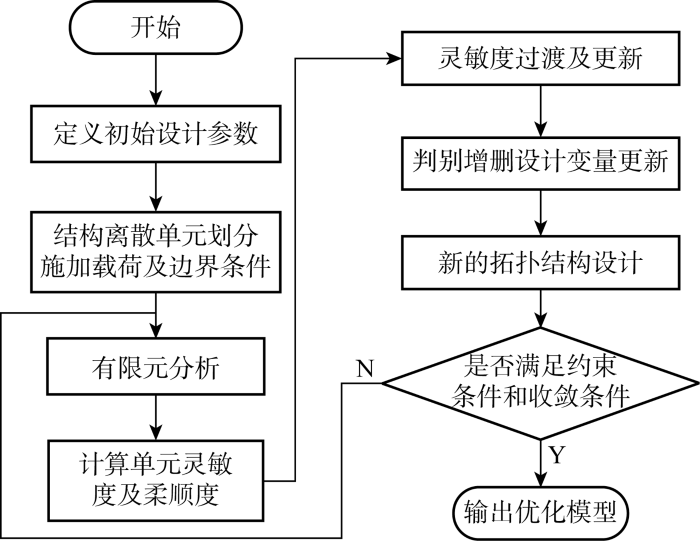
根据上述计算过程实现基于BESO算法的水平轴风力机支撑结构优化,流程如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 拓扑优化流程图

Fig.4 Flow chart of topology optimization

3 优化前后模型受力特性

3.1 基于BESO算法的支撑结构优化

运用BESO双向渐进结构优化算法,对5 MW大型水平轴风力机塔筒结构(高度为90 m)进行拓扑优化,如图5所示.为防止风力机塔筒顶部发生过大位移,通常对风力机塔筒受弯矩作用较大的底部区域进行加固,所选取的底部拓扑区域为宽度a=10 m、长度b=50 m所围成的平面,以此作为初始设计域Ω,采用4节点Plane182单元进行网格划分.在设计域区域施加外部荷载,包括风力机机舱、转子质量等纵向荷载 $F_{z}$ ,风力机叶片运动产生的推力、沿塔筒高度分布的梯度风荷载等在设计域顶部产生的荷载 $F_{x y}$ 和弯矩 $M_{x y}$ .底部边界条件为固定端约束,拓扑优化的结构目标体积分数为40%.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 塔架结构底部受力及拓扑设计区域

Fig.5 Tower structure force diagram and topology design area

分析拓扑过程中体积比即单元删除量变化和平均柔顺度相对迭代次数的变化历程,如图6所示.拓扑迭代初期,拓扑单元较多,单元删除量较大,拓扑迭代速率较快.随着迭代进行,单元体积比逐渐减小,迭代20次后,结构单元体积比开始趋近于目标体积约束条件,拓扑形态开始稳定,最终得到反比例型删除率的优化模型柔顺度量值为1 557.1 N·m.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 迭代过程结构平均柔顺度和体积分数变化

Fig.6 Average flexibility and volume fraction of optimized structure

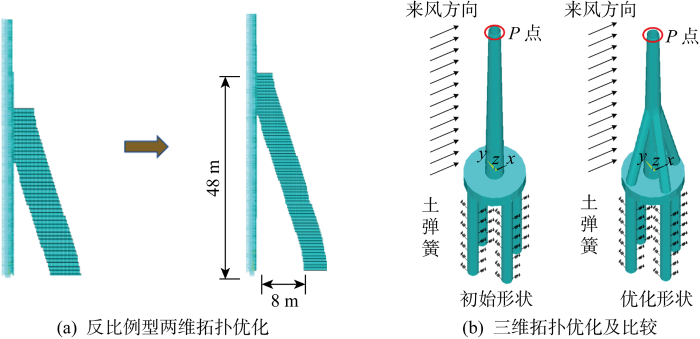
对初始设计域,通过上述二维拓扑找形得到带有侧向支撑的塔筒形状如图7(a)所示,其侧向支撑高度为48 m、宽度为8 m.基于支撑结构的对称性,考虑基础为四桩布局,将二维拓扑结果扩展到三维空间,获得的四支撑结构优化形式如图7(b)所示.根据拓扑优化结果,构建高桩承台式水平轴风力机支撑结构模型.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 塔筒支撑结构拓扑优化

Fig.7 Topology optimization of tower support structures

3.2 优化后风力机支撑结构特性

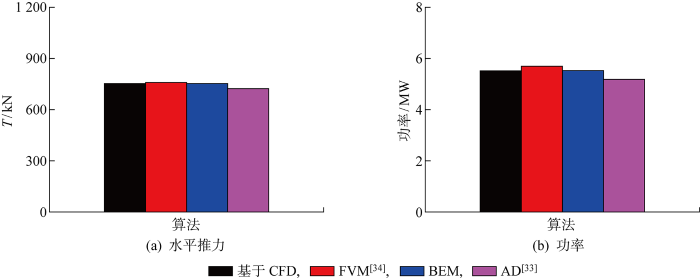
基于CFD数值方法计算优化后风力机支撑结构的风致水平推力和风力机功率.为考虑最不利荷载工况,在进行CFD数值计算时,设速度入口风速等于切出风速为25 m/s,与边界元法(BEM)、致动盘(AD)^[33]及有限体积法(FVM)^[34]中的结果进行对比分析,如图8所示.可知,本文风力机功率、风力机旋转时叶片对塔筒的水平推力(T=750 kN)均与相关文献结果接近.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 本文结果及其分析对比

Fig.8 Power comparison between CFD model and reference

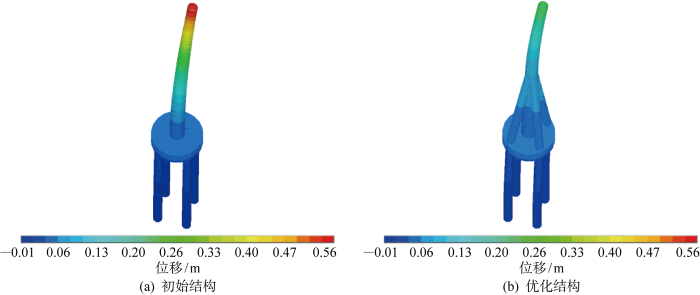
分别计算优化后支撑结构和原塔筒结构的静力特性,注意到风力机塔筒经受周期性脉动风荷载作用,可将风力机旋转多圈并稳定后叶片对塔筒的水平推力用于计算最不利工况下的塔筒位移, 运用式(1)计算沿风机塔筒高度的风荷载.风力机支撑结构顺风向 $(x 向) 、横风向 (y 向) 和竖向 (z 向)$ 最大动位移均发生于塔筒顶部,其中顺风向位移明显大于横风向位移.针对5 MW大型水平轴风力机,分别计算初始支撑结构和优化后支撑结构在额定风速下的塔顶位移.初始结构塔顶顺风向位移为550 mm,竖向位移为-2.5 mm,而优化后结构塔顶的顺风向位移为250 mm,竖向位移为-1.7 mm.优化后支撑结构的位移明显减少,顺风向和竖向位移相对初始支撑结构减少了54.5%和32%,如图9所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 初始结构与优化结构位移响应云图

Fig.9 Comparison of displacement of initial structure and optimized structure

3.3 桩土作用优化后支撑结构风致动力响应分析

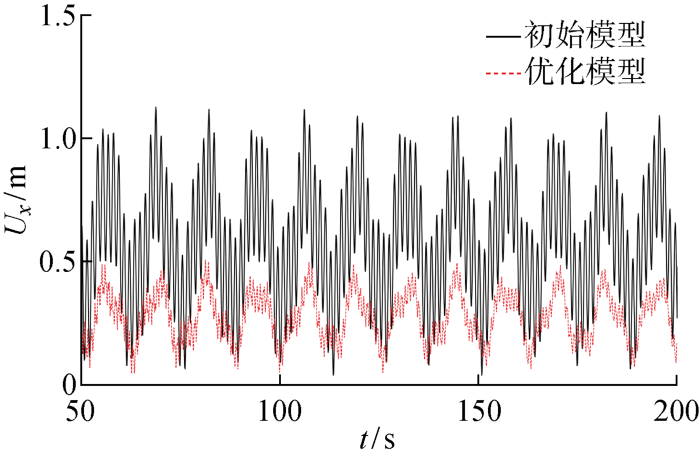
考虑桩土作用,分析5 MW风力机初始和优化后结构在顺风向和竖向的动力响应.设来流风速为25 m/s,风力机叶片转速为0.664 rad/s,风力机运动周期为9.463 s.风力机旋转6~10圈后气动性能基本稳定,相应的风力机旋转时长为50~200 s.初始和优化后结构的塔筒顶端顺风向位移(U_x)时程曲线如图10所示.计算发现在t=68 s时刻,风力机结构振幅较大.因此分析该时刻优化前后支撑结构的顺风向和竖向位移,得到初始和优化后塔顶顺风向最大位移分别为 1 130 和300 mm,减少73.45%;竖向位移分别为 -49~-26 mm和-18~-8 mm,最大竖向位移减少了63.27%.由此可见,在保持与初始结构体积相同情况下,优化后风力机支撑结构位移明显减少,结构刚度大于初始结构.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 初始结构和优化结构的塔顶顺风向位移时程曲线

Fig.10 Comparison of displacement time history curve of two models at the top of tower

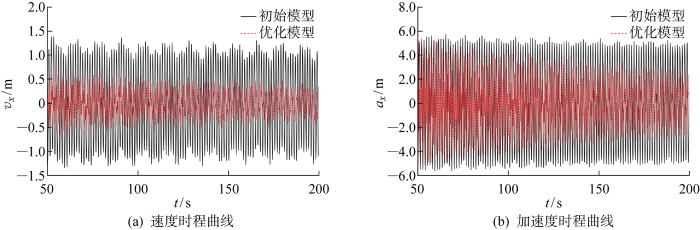
考虑桩土作用的初始和优化后结构在50~200 s时段顺风向的速度(v_x)响应时程和加速度(a_x)响应时程如图11所示.可见优化后结构的速度和加速度响应小于初始结构,风振特性得到显著改善,在风力机旋转多圈如100 s进入稳态后改善效果更明显,如塔顶加速度由初始结构的5.02 m/s²减小为优化后结构的3.8 m/s²,减幅达24%.考虑桩土作用的支撑结构振动效应明显减小,具有较好的减振效果.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 初始和优化结构的塔顶顺风向速度时程和加速度时程

Fig.11 Comparison of velocity and acceleration time history curve at the top of tower

4 结论

针对大型高桩承台式水平轴风力机支撑结构系统,运用CFD方法计算风致效应,考虑桩土作用效应,运用基于反比例函数的双向渐进结构优化算法对风力机塔筒支撑结构进行拓扑优化,开展风力机结构系统的静动力响应特性分析,得到结论如下:

(1) 运用基于反比例型删除率的BESO算法并考虑桩土作用影响,开展水平轴风力机塔筒支撑结构拓扑优化,得到风力机支撑结构的新形式.

(2) 优化后支撑结构风致效应明显减小,在保持结构体积不变情况下,优化后支撑结构整体刚度明显提高,塔顶顺风向和竖向静力位移分别减小54.5%和32%,动力分析下塔顶在顺风向和竖向最大位移分别减少73.45%和63.27%.

运用BESO算法进行水平轴风力机支撑结构的二维平面优化,后续将对风力机支撑结构开展三维优化研究.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

AGUILAR

VARGAS S

, TELLES

ESTEVES G R

, MAÇAIRA

P M

, et al.

Wind power generation: A review and a research agenda

[J]. Journal of Cleaner Production, 2019, 218: 850-870.

DOI:10.1016/j.jclepro.2019.02.015 [本文引用: 1]

The use of renewable energy resources, especially wind power, is receiving strong attention from governments and private institutions, since it is considered one of the best and most competitive alternative energy sources in the current energy transition that many countries around the world are adopting. Wind power also plays an important role by reducing greenhouse gas emissions and thus attenuating global warming. Another contribution of wind power generation is that it allows countries to diversify their energy mix, which is especially important in countries where hydropower is a large component. The expansion of wind power generation requires a robust understanding of its variability and thus how to reduce uncertainties associated with wind power output. Technical approaches such as simulation and forecasting provide better information to support the decision-making process. This paper provides an overview of how the analysis of wind speed/energy has evolved over the last 30 years for decision-making processes. For this, we employed an innovative and reproducible literature review approach called Systematic Literature Network Analysis (SLNA). The SLNA was performed considering 145 selected articles from peer-reviewed journals and through them it was possible to identify the most representative approaches and future trends. Through this analysis, we identified that in the past 10 years, studies have focused on the use of Measure-Correlate-Predict (MCP) models, first using linear models and then improving them by applying density or kernel functions, as well as studies with alternative techniques, like neural networks or other hybrid models. An important finding is that most of the methods aim to assess wind power generation potential of target sites, and, in recent years the most used approaches are MCP and artificial neural network methods. (C) 2019 Elsevier Ltd.

[2]

KAEWNIAM

, CAO

M S

, ALKAYEM

N F

, et al.

Recent advances in damage detection of wind turbine blades: A state-of-the-art review

[J]. Renewable and Sustainable Energy Reviews, 2022, 167: 112723.

DOI:10.1016/j.rser.2022.112723 URL [本文引用: 1]

[3]

孟珣.

基于动力特性的海上风力发电支撑结构优化技术研究[D]. 青岛: 中国海洋大学, 2010.

[本文引用: 1]

MENG

Xun

Optimum technology on support structures of offshore wind turbine based on dynamic properties[D]. Qingdao: Ocean University of China, 2010.

[本文引用: 1]

[4]

GENTILS

, WANG

, KOLIOS

Integrated structural optimisation of offshore wind turbine support structures based on finite element analysis and genetic algorithm

[J]. Applied Energy, 2017, 199: 187-204.

DOI:10.1016/j.apenergy.2017.05.009 URL [本文引用: 1]

[5]

OEST

, SANDAL

, SCHAFHIRT

, et al.

On gradient-based optimization of jacket structures for offshore wind turbines

[J]. Wind Energy, 2018, 21(11): 953-967.

DOI:10.1002/we.v21.11 URL [本文引用: 1]

[6]

葛旭, 徐业鹏, 黄丹.

基于进化策略的海上风电支撑结构多参数同步优化设计

[J]. 可再生能源, 2020, 38(7): 900-904.

[本文引用: 1]

, XU

Yepeng

, HUANG

Dan

Multi-parameter simultaneously optimal design of support structure for offshore wind turbine based on evolutionary strategy

[J]. Renewable Energy Resources, 2020, 38(7): 900-904.

[本文引用: 1]

[7]

TIAN

X J

, SUN

X Y

, LIU

G J

, et al.

Optimization design of the jacket support structure for offshore wind turbine using topology optimization method

[J]. Ocean Engineering, 2022, 243: 110084.

DOI:10.1016/j.oceaneng.2021.110084 URL [本文引用: 1]

[8]

王章骏, 许平, 邢杰, 等.

基于改进BESO算法的带隔板薄壁方管耐撞性拓扑优化

[J]. 铁道科学与工程学报, 2021, 18(6): 1573-1581.

[本文引用: 1]

WANG

Zhangjun

, XU

Ping

, XING

Jie

, et al.

Crashworthiness topology optimization of the thin-walled square tube with diaphragms based on improved BESO algorithm

[J]. Journal of Railway Science and Engineering, 2021, 18(6): 1573-1581.

[本文引用: 1]

[9]

刘昆, 郭德松, 王仁华, 等.

基于改进BESO方法的多工况船体开孔孔形优化

[J]. 中国海洋平台, 2021, 36(4): 1-8.

[本文引用: 1]

LIU

Kun

, GUO

Desong

, WANG

Renhua

, et al.

Shape optimization of hull structure hole opening under multiple conditions based on improved BESO method

[J]. China Offshore Platform, 2021, 36(4): 1-8.

[本文引用: 1]

[10]

YAN

, BAO

D W

, ZHOU

Y F

, et al.

Detail control strategies for topology optimization in architectural design and development

[J]. Frontiers of Architectural Research, 2022, 11(2): 340-356.

DOI:10.1016/j.foar.2021.11.001 [本文引用: 1]

With the ability to generate forms with high efficiency and elegant geometry, topology optimization has been increasingly used in architectural and structural designs. However, the conventional topology optimization techniques aim at achieving the structurally most efficient solution without any potential for architects or designers to control the design details. This paper introduces three strategies based on Bi-directional Evolutionary Structural Optimization (BESO) method to artificially pre-design the topological optimized structures. These strategies have been successfully applied in the computational morphogenesis of various structures for solving practical design problems. The results demonstrate that the developed methodology can provide the designer with structurally efficient and topologically different solutions according to their proposed designs with multi-filter radii, multi-volume fractions, and multi-weighting coefficients. This work establishes a general approach to integrating objective topology optimization methods with subjective human design preferences, which has great potential for practical applications in architecture and engineering industry.

[11]

周豪, 江滨.

矶崎新引领世界建筑创新潮流的先锋

[J]. 中国勘察设计, 2019(4): 68-75.

[本文引用: 1]

ZHOU

Hao

, JIANG

Bin

Arata Isozaki is a pioneer in the world of architectural innovation

[J]. China Engineering & Consulting, 2019(4): 68-75.

[本文引用: 1]

[12]

孙明明, 李昕, 李炜.

海上风力机高桩承台基础反应特性研究

[J]. 太阳能学报, 2020, 41(7): 265-273.

[本文引用: 1]

SUN

Mingming

, LI

Xin

, LI

Wei

Study on response of offshore wind turbine with high-pile cap foundation

[J]. Acta Energiae Solaris Sinica, 2020, 41(7): 265-273.

[本文引用: 1]

[13]

FUTAI

M M

, HAIGH

S K

, MADABHUSHI

G S P

Comparison of the dynamic responses of monopiles and gravity base foundations for offshore wind turbines in sand using centrifuge modelling

[J]. Soils and Foundations, 2021, 61(1): 50-63.

DOI:10.1016/j.sandf.2020.10.009 URL [本文引用: 1]

[14]

ABHINAV

K A

, SAHA

Nonlinear dynamical behaviour of jacket supported offshore wind turbines in loose sand

[J]. Marine Structures, 2018, 57: 133-151.

DOI:10.1016/j.marstruc.2017.10.002 URL [本文引用: 1]

[15]

刘晨晨, 张琪, 李明广, 等.

波浪与地震荷载共同作用下桩的动力响应

[J]. 上海交通大学学报, 2021, 55(6): 638-644.

[本文引用: 1]

LIU

Chenchen

, ZHANG

, LI

Mingguang

, et al.

Dynamic response of pile at waterwave load and seismic load

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(6): 638-644.

[本文引用: 1]

[16]

JONKMAN

, BUTTERFIELD

, MUSIAL

, et al.

Definition of a 5-MW reference wind turbine for offshore system development

[J]. Contract, 2009: 1-75.

[本文引用: 2]

[17]

Det Norske Veritas.

Support structures for wind turbines: DNVGL-ST-0126[S/OL]. (2021-12-01) [2022-10-18]. https//www.dnv.com/energy/standards-guidelines/dnv-st-0126-support-structures-for-wind-turbines.html.

URL [本文引用: 1]

[18]

张佳丽, 李少彦.

海上风电产业现状及未来发展趋势展望

[J]. 风能, 2018(10): 48-52.

[本文引用: 1]

ZHANG

Jiali

, LI

Shaoyan

Present situation and future development trend of offshore wind power industry

[J]. Wind Energy, 2018(10): 48-52.

[本文引用: 1]

[19]

中华人民共和国交通运输部.

水运工程大体积混凝土温度裂缝控制技术规程: JTS 202-1—2022[S]. 北京: 人民交通出版社, 2022.

[本文引用: 1]

Ministry of Transport of the People’s Republic of China.

Technical specification for thermal cracking control of mass concrete of port and waterway engineering: JTS 202-1—2022[S]. Beijing: China Communications Press, 2022.

[本文引用: 1]

[20]

JUNG

, KIM

S R

, PATIL

, et al.

Effect of monopile foundation modeling on the structural response of a 5-MW offshore wind turbine tower

[J]. Ocean Engineering, 2015, 109: 479-488.

DOI:10.1016/j.oceaneng.2015.09.033 URL [本文引用: 1]

[21]

CHEN

J Y

, MATEREK

B A

, CARPENTER

J F

, et al.

Analysis of potential conservatism in foundation design for offshore platform assessment

[R]. Texas: Offshore Technology Research Center, 2009.

[本文引用: 1]

[22]

张建, 杨庆山.

基于标准k-ε模型的平衡大气边界层模拟

[J]. 空气动力学学报, 2009, 27(6): 729-735.

[本文引用: 1]

ZHANG

Jian

, YANG

Qinshan

Application of standard k-ε model to simulate the equilibrium ABL

[J]. Acta Aerodynamica Sinica, 2009, 27(6): 729-735.

[本文引用: 1]

[23]

ALI

H M

, AL-ESBE

, ALWAN

H M

A review of offshore wind turbines: Global added capacity, monopile structure foundations stresses and deflection

[J]. Periodicals of Engineering and Natural Sciences, 2021, 9(2): 712.

[本文引用: 1]

[24]

BURTON

, JENKINS

, BOSSANYI

, et al.

Aerodynamics of horizontal axis wind turbines[M]. Chichester: John Wiley & Sons, 2021: 15-20.

[本文引用: 1]

[25]

国家能源局.

海上风电场工程风电机组基础设计规范: NB/T 10105—2018[S]. 北京: 中国水利水电出版社, 2019.

[本文引用: 1]

National Energy Administration.

Code for design of wind turbine foundations for offshore wind power projects: NB/T 10105—2018[S]. Beijing: China Water & Power Press, 2019.

[本文引用: 1]

[26]

KATONA

M C

, ZIENKIEWICZ

O C

A unified set of single step algorithms part 3: The beta-m method, a generalization of the Newmark scheme

[J]. International Journal for Numerical Methods in Engineering, 1985, 21(7): 1345-1359.

DOI:10.1002/(ISSN)1097-0207 URL [本文引用: 1]

[27]

WANG

, MOAN

, HANSEN

M O L

Stochastic dynamic response analysis of a floating vertical-axis wind turbine with a semi-submersible floater

[J]. Wind Energy, 2016, 19(10): 1853-1870.

DOI:10.1002/we.v19.10 URL [本文引用: 1]

[28]

张森文, 曹开彬.

计算结构动力响应的状态方程直接积分法

[J]. 计算力学学报, 2000, 17(1): 94-97.

[本文引用: 1]

ZHANG

Senwen

, CAO

Kaibin

Direct integration of state equation method for dynamic response of structure

[J]. Chinese Journal of Computational Mechanics, 2000, 17(1): 94-97.

[本文引用: 1]

[29]

TIAN

X J

, WANG

, LIU

, et al.

Jack-up platform leg optimization by topology optimization algorithm-BESO

[J]. Ocean Engineering, 2022, 257: 2-15.

[本文引用: 1]

[30]

ZUO

W J

, SAITOU

Multi-material topology optimization using ordered SIMP interpolation

[J]. Structural and Multidisciplinary Optimization, 2017, 55(2): 477-491.

DOI:10.1007/s00158-016-1513-3 URL [本文引用: 1]

[31]

MOVAHEDI

RAD M

, HABASHNEH

, LÓGÓ

Elasto-Plastic limit analysis of reliability based geometrically nonlinear bi-directional evolutionary topology optimization

[J]. Structures, 2021, 34: 1720-1733.

DOI:10.1016/j.istruc.2021.08.105 URL [本文引用: 2]

[32]

罗静, 张大可, 李海军, 等.

基于一种动态删除率的ESO方法

[J]. 计算力学学报, 2015, 32(2): 274-279.

[本文引用: 1]

LUO

Jing

, ZHANG

Dake

, LI

Haijun

, et al.

ESO method based on a kind of dynamic deletion rate

[J]. Chinese Journal of Computational Mechanics, 2015, 32(2): 274-279.

[本文引用: 1]

[33]

TRAN

T T

, KIM

D H

A CFD study into the influence of unsteady aerodynamic interference on wind turbine surge motion

[J]. Renewable Energy, 2016, 90: 204-228.

DOI:10.1016/j.renene.2015.12.013 URL [本文引用: 1]

[34]

WEN

B R

, TIAN

X L

, DONG

X J

, et al.

Influences of surge motion on the power and thrust characteristics of an offshore floating wind turbine

[J]. Energy, 2017, 141: 2054-2068.

DOI:10.1016/j.energy.2017.11.090 URL [本文引用: 1]

Wind power generation: A review and a research agenda

2019

... 风力机大型化可有效提高风力发电量和风能利用率,是海上风力发电的世界发展趋势^[1].研发建造包括10、15和20 MW在内的大型风力机是我国海洋绿色能源开发利用的战略重点.然而随着风力机转子、塔筒尺寸的不断增加^[2],大型风力机结构系统柔性增加,抗风能力明显降低^[3],风力机风致动力响应更加复杂,系统风致动力灾变风险更加凸显. ...

Recent advances in damage detection of wind turbine blades: A state-of-the-art review

2022

2010

Integrated structural optimisation of offshore wind turbine support structures based on finite element analysis and genetic algorithm

2017

... 研究并优化大型水平轴风力机支撑结构对保证系统运行安全十分重要.风力机大型化导致塔筒顶部大型转子和发电机质量增加、支撑塔筒高度增大.常用的圆锥塔筒无法满足风力机结构的强度和刚度要求.迄今,学者们对大型水平轴风力机支撑结构优化已有一定研究.Gentils等^[4]基于遗传算法,考虑多准则约束,对美国国家可再生能源实验室(NREL)提出的5 MW单桩式风力机(NREL 5 MW)塔架和基础进行优化分析并计算风力机支撑结构优化尺寸参数;Oest等^[5]基于疲劳损伤荷载、准静态分析和动态分析,对海上风力机支撑结构进行梯度优化设计;葛旭等^[6]结合有限元分析与进化策略,对海上三桩单立柱风力机支撑结构主尺度参数进行多参数同步优化设计;Tian等^[7]对导管架式海上风力机的导管架基础进行拓扑优化,结合尺寸和形状优化实现结构重分布,得到质量更轻的导管架结构.上述研究仅为针对特定风力机结构形式的参数优化,未改变其支撑结构形式,虽对风力机结构稳定性有一定提高,但设计方法具有局限性.相较于参数优化,拓扑优化方法具有更多的设计自由度,是优化大型水平轴支撑结构的新途径. ...

On gradient-based optimization of jacket structures for offshore wind turbines

2018

基于进化策略的海上风电支撑结构多参数同步优化设计

2020

基于进化策略的海上风电支撑结构多参数同步优化设计

2020

Optimization design of the jacket support structure for offshore wind turbine using topology optimization method

2022

基于改进BESO算法的带隔板薄壁方管耐撞性拓扑优化

2021

... 拓扑优化方法应用于包括结构优化在内的广泛领域,其双向渐进结构优化(BESO)算法优化效果较好.王章骏等^[8]采用BESO算法对吸能管进行拓扑优化,提高了带隔板薄壁方管的耐撞性能, 实现了吸能管轻量化的设计目标;刘昆等^[9]基于BESO算法对船体梁腹板开孔进行设计优化,提出适用于船体结构孔型的BESO算法;BESO还在罗马小体育宫^[10]、卡塔尔国家会议中心^[11]等建筑工程设计中得到应用.目前,大型水平轴风力机塔筒支撑结构拓扑优化还鲜有研究. ...

基于改进BESO算法的带隔板薄壁方管耐撞性拓扑优化

2021

基于改进BESO方法的多工况船体开孔孔形优化

2021

基于改进BESO方法的多工况船体开孔孔形优化

2021

Detail control strategies for topology optimization in architectural design and development

2022

矶崎新引领世界建筑创新潮流的先锋

2019

矶崎新引领世界建筑创新潮流的先锋

2019

海上风力机高桩承台基础反应特性研究

2020

... 基础是风力机系统的关键结构之一,高桩承台基础的结构安全性能高,适合我国海床地质条件,施工工艺成熟,在我国近海风电场建设中多有应用^[12].但不考虑桩-土相互作用会导致风力机位移响应被严重低估^[13⇓-15],是结构安全设计的重要隐患. ...

海上风力机高桩承台基础反应特性研究

2020

Comparison of the dynamic responses of monopiles and gravity base foundations for offshore wind turbines in sand using centrifuge modelling

2021

Nonlinear dynamical behaviour of jacket supported offshore wind turbines in loose sand

2018

波浪与地震荷载共同作用下桩的动力响应

2021

波浪与地震荷载共同作用下桩的动力响应

2021

Definition of a 5-MW reference wind turbine for offshore system development

2009

... 以应用较广的NREL 5 MW^[16]风力机为背景,进行考虑桩土作用的近海坐底式高桩承台大型水平轴风力机塔筒结构优化研究.高桩承台式水平轴风力机初始模型如图1(a)所示,其支撑系统包括上部塔筒结构、承台和群桩.水平轴风力机塔筒为圆筒式支撑结构,如图1(b)所示,塔筒底部外径D=6 m,塔筒高度H₀=90 m^[16].塔筒选用Q345钢材^[17],密度ρ₀=7.85 g/m³,弹性模量E₀=211 N/m²,泊松比ν₀=0.3,风力机额定风速为11.4 m/s,具体参数如表1所示. ...

... [16].塔筒选用Q345钢材^[17],密度ρ₀=7.85 g/m³,弹性模量E₀=211 N/m²,泊松比ν₀=0.3,风力机额定风速为11.4 m/s,具体参数如表1所示. ...

海上风电产业现状及未来发展趋势展望

2018

... 参照上海东海大桥海上大型风力发电工程项目采用高桩承台式基础^[18],混凝土承台直径D₁=20 m,承台厚度S=5 m,设置4根直径d₁=3 m、壁厚 t=20 mm的全直钢管基桩,桩基长度 H₁=52 m,入土深度h=40 m.承台材料选用C45标号混凝土,弹性模量E=33.5 GPa,密度为2500 kg/m³,泊松比ν=0.2^[19],基础模型如图2(a)所示.基于Jung等^[20]和Chen等^[21]确定土体模型和力学参数:土体浮重度

γ'

、弹性模量

E'

、泊松比

ν'

、内摩擦角

φ'

和不排水抗剪强度s_u、黏土泊松比ν_u、50%的最大有效应力下的轴向应变

ε_{50}

、土层深度

z

、膨胀角

ψ'

、黏聚力

c'

、地基反力模量

k

,如图2(b)所示. ...

海上风电产业现状及未来发展趋势展望

2018

γ'

、弹性模量

E'

、泊松比

ν'

、内摩擦角

φ'

和不排水抗剪强度s_u、黏土泊松比ν_u、50%的最大有效应力下的轴向应变

ε_{50}

、土层深度

z

、膨胀角

ψ'

、黏聚力

c'

、地基反力模量

k

,如图2(b)所示. ...

2022

γ'

、弹性模量

E'

、泊松比

ν'

、内摩擦角

φ'

和不排水抗剪强度s_u、黏土泊松比ν_u、50%的最大有效应力下的轴向应变

ε_{50}

、土层深度

z

、膨胀角

ψ'

、黏聚力

c'

、地基反力模量

k

,如图2(b)所示. ...

2022

γ'

、弹性模量

E'

、泊松比

ν'

、内摩擦角

φ'

和不排水抗剪强度s_u、黏土泊松比ν_u、50%的最大有效应力下的轴向应变

ε_{50}

、土层深度

z

、膨胀角

ψ'

、黏聚力

c'

、地基反力模量

k

,如图2(b)所示. ...

Effect of monopile foundation modeling on the structural response of a 5-MW offshore wind turbine tower

2015

γ'

、弹性模量

E'

、泊松比

ν'

、内摩擦角

φ'

和不排水抗剪强度s_u、黏土泊松比ν_u、50%的最大有效应力下的轴向应变

ε_{50}

、土层深度

z

、膨胀角

ψ'

、黏聚力

c'

、地基反力模量

k

,如图2(b)所示. ...

Analysis of potential conservatism in foundation design for offshore platform assessment

2009

γ'

、弹性模量

E'

、泊松比

ν'

、内摩擦角

φ'

和不排水抗剪强度s_u、黏土泊松比ν_u、50%的最大有效应力下的轴向应变

ε_{50}

、土层深度

z

、膨胀角

ψ'

、黏聚力

c'

、地基反力模量

k

,如图2(b)所示. ...

基于标准k-ε模型的平衡大气边界层模拟

2009

... 对高桩承台大型水平轴风力机结构系统,基于计算流体动力学(CFD)方法并运用Star-CCM+计算软件^[22]数值模拟获得风力机叶片气动荷载,风力机风轮直径为d,选取长方体风场计算域,计算域长度、宽度和高度分别为20d、8d和8d,如图3(a)和3(b)所示.计算域划分共 1700 万个网格.计算域中,风力机叶片圆柱体旋转域在竖平面的直径为1.5d,旋转域高度即顺风向尺度为0.75d;旋转域之外的计算域等其他部分为静止域.对旋转域和静止域设置交界面,采用滑移网格处理风轮运行旋转问题,如图3(c)和3(d)所示.叶片表面采用棱柱层网格,延伸因子为1.3,总厚度为0.08 m,无量纲化壁面距离为y⁺<1. ...

基于标准k-ε模型的平衡大气边界层模拟

2009

A review of offshore wind turbines: Global added capacity, monopile structure foundations stresses and deflection

2021

... 对大型风力机支撑结构采用锥筒结构^[23],塔筒高度为90 m.将塔筒简化为受弯曲变形、轴向压缩和扭转变形的悬臂梁.风力机运行时,需考虑塔筒沿高度的风压变化.沿塔筒高度l处的风荷载^[24]为 ...

2021

2019

... 美国石油协会(API)规范推荐的土体p-y曲线,即非线性弹簧模型广泛应用于海洋工程桩基设计.引入用于分析风力机支撑结构的桩土相互作用^[25],该模型考虑了土体非线性、土层变化和土体种类等因素的影响,软土中各层p-y曲线为 ...

2019

A unified set of single step algorithms part 3: The beta-m method, a generalization of the Newmark scheme

1985

... 采用 Newmark-β法^[26]中的平均常加速度法对风力机支撑结构系统风致振动进行瞬态分析,其中控制Newmark-β法精度和稳定性的参数取值为 γ=0.5,β=0.25.采用瑞利阻尼模拟风力机结构阻尼,刚度阻尼系数取值为0.03^[27].风力机结构系统动力激励下的振动方程^[28]为 ...

Stochastic dynamic response analysis of a floating vertical-axis wind turbine with a semi-submersible floater

2016

计算结构动力响应的状态方程直接积分法

2000

计算结构动力响应的状态方程直接积分法

2000

Jack-up platform leg optimization by topology optimization algorithm-BESO

2022

... 针对大型水平轴风力机支撑结构优化问题,建立以结构静刚度最大为目标、以结构体积为约束条件的数学力学模型^[29],表示为 ...

Multi-material topology optimization using ordered SIMP interpolation

2017

... 为避免产生奇异单元刚度矩阵,算法以x_min代替0表示空单元,在该软删单元的BESO算法^[30]中所有单元的材料弹性模量可根据材料插值模型设置为 ...

Elasto-Plastic limit analysis of reliability based geometrically nonlinear bi-directional evolutionary topology optimization

2021

... 为抑制优化过程中出现实体单元与空洞单元交替出现的棋盘格等数值不稳定现象^[31],通过权重系数引入节点灵敏度节点概念: ...

... 当迭代结果满足根据体积约束和收敛准则^[31]时,终止迭代.为提高迭代效率,设置收敛准则,表示当前迭代步之前10次迭代中平均柔顺度的相对变化量,当目标函数变化随着迭代变化足够小时,则判定迭代结束: ...

基于一种动态删除率的ESO方法

2015

... 鉴于水平轴风力机结构系统对称性,将支撑结构三维优化问题转化为二维平面优化,以风力机塔筒支撑形式和支撑点位置为优化对象.将风力机塔筒主轴高度方向和塔筒半径方向围成的平面作为初始设计域,采用ANSYS软件中的4节点Plane182单元对计算模型进行网格划分.设置底部为固定端约束,选取最不利气动荷载作为外部风荷载.采用反比例型删除率优化模型^[32]对风力机支撑结构进行拓扑优化: ...

基于一种动态删除率的ESO方法

2015

A CFD study into the influence of unsteady aerodynamic interference on wind turbine surge motion

2016

... 基于CFD数值方法计算优化后风力机支撑结构的风致水平推力和风力机功率.为考虑最不利荷载工况,在进行CFD数值计算时,设速度入口风速等于切出风速为25 m/s,与边界元法(BEM)、致动盘(AD)^[33]及有限体积法(FVM)^[34]中的结果进行对比分析,如图8所示.可知,本文风力机功率、风力机旋转时叶片对塔筒的水平推力(T=750 kN)均与相关文献结果接近. ...

Influences of surge motion on the power and thrust characteristics of an offshore floating wind turbine

2017

〈

〉