为应对气候变化,我国提出“二氧化碳排放力争于2030年前达到峰值,努力争取2060年前实现碳中和”等庄严的目标和承诺.“十四五”规划也将加快推动绿色低碳发展列入其中,大规模风电场并网已成为一种不可避免的趋势.然而,风力发电(简称风电)接入配电网会改变配电网的拓扑结构,将导致更复杂的功率和潮流分布[1 ] .因此,研究风电并网时接入配电网的短路电流具有重要意义.
小规模风电以分布式电源的方式接入配电网,这种接入方法能避免大容量风电集中接入对电压稳定性的影响,但对配电网短路电流的分布和大小影响较大[2 ] .风电机组类型主要有鼠笼异步风力机、直驱式风力机和双馈异步风力机.文献[3 ]中分析了同步发电机、鼠笼异步风电机组、双馈异步风电机组和直驱同步风电机组等各种风力发电机接入配电网对系统短路电流的影响.在现今的风电系统中,双馈异步风力发电机(Doubly Fed Induction Generator, DFIG)因其小容量的变换器和相应的成本优势得到广泛应用.文献[4 ]中分析在三相短路故障时双馈风力发电机的暂态特性,并研究该特性对输电线路的影响.文献[5 ]中分析双馈风力发电机的短路特性,并结合理论计算配电网在保证安全运行的情况下接入双馈风力发电机的最大容量.文献[6 ]中研究风电接入对配电网的保护影响,虽然只重点研究风力机接入的下游部分,但实际上风力机接入对其上游、下游的短路电流及保护都会产生影响.文献[7 ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构.
风电接入会对配电网上游、下游及相邻馈线的电流保护产生影响,并且不同容量的风电接入电网会导致电压等级也发生改变;不同的电压等级保护方式也不同,故有必要对风电接入配电网时的短路电流特性进行深入研究.本文将双馈风力发电系统作为分布式电源接入10 kV配电网仿真模型中,设置不同的三相短路故障点,仿真分析风力机的控制策略、容量大小及接入位置对配电网短路电流的影响,并得出结论.
1 双馈风力发电系统数学模型
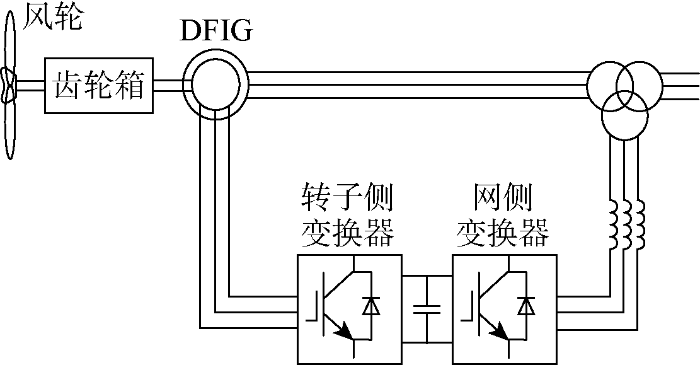
双馈风力发电系统结构如图1 所示.同步旋转dq 坐标系下DFIG定转子电压方程为
图1
图1
DFIG风电系统结构图
Fig.1
Diagram of structure of DFIG wind power system
(1) u s d q = R s i s d q + d ψ s d q d t + j ω 1 ψ s d q u r d q = R r i r d q + d ψ r d q d t + j ( ω 1 - ω r ) ψ r d q
式中:u s dq u r dq i s dq i r dq R s 、R r 分别为定子、转子电阻;ψ s dq ψ r dq ω 1 、ω r 分别为同步角速度、转子旋转角速度.
(2) ψ s d q = L s i s d q + L m i r d q ψ r d q = L m i s d q + L r i r d q
式中:L s 为转子绕组全自感;L m 为定转子互感;L r 为定子绕组全自感.
由式(1)和式(2)得d 、q 分量形式的转子电压方程:
(3) u r d = R r i r d + σ L r d i r d d t - ( ω 1 - ω r ) ψ r q u r q = R r i r q + σ L r d i r q d t + ( ω 1 - ω r ) ψ r d
式中:u r d u r q d 、q 轴电压;i r d i r q d 、q 轴电流;ψ r d ψ r q d 、q 轴磁链;σ =1-L m 2 / (L s L r ).
(4) ψ r d = L m L s u s q - R s i s q ω 1 + σ L r i r d ψ r q = L m L s u s d - R s i s d - ω 1 + σ L r i r q
式中:u s q u s d q 、d 轴电压;i s q i s d q 、d 轴电流.
(5) u r d = R r i r d + σ L r d i r d d t - ( ω l - ω r ) × L m L s u s d - R s i s d - ω l + σ L r i r q u r q = R r i r q + σ L r d i r q d t + ( ω l - ω r ) × L m L s u s q - R s i s q - ω l + σ L r i r d
2 模型预测控制策略
在双馈风力发电系统的控制策略中,矢量控制一直都占据着主流地位.但传统矢量控制也存在一些问题,例如比例积分(Proportional Integral,PI)控制器中的积分环节存在滞后效应、动态性能不尽如人意等[8 ] .
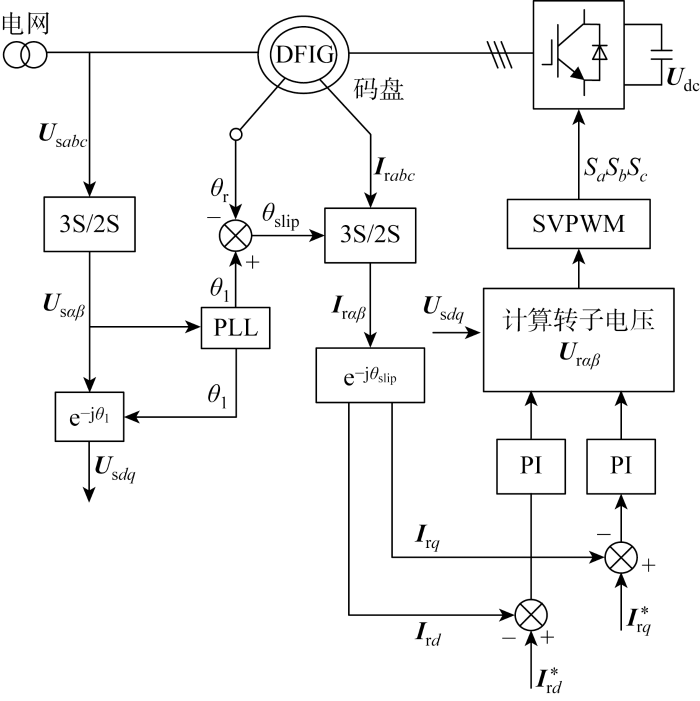
图2 为附加PI控制器的矢量控制策略框图.图中:U s abc U dc 为直流母线电压;I r abc αβ 坐标系的变换;θ r 、θ slip 、θ l 分别为转子位置角、转差角、d 轴与α 轴之间的夹角;SVPWM为空间矢量脉宽调制;U s αβ I r αβ U s dq dq 坐标系下的定子电压;U r αβ I r d * I r q * d 、q 轴转子电流参考值;I r d I r q d 、q 轴转子电流;Sa 、Sb 、Sc 分别为静止坐标系下a 、b 、c 三相.为改进对风电系统的控制,提出模型预测控制.MPC是依据系统当前状态和数学模型,进而预测出系统未来状态,再根据期望值实现在线寻优的控制算法[9 ] .相比于附加PI控制器的矢量控制,模型预测控制策略能有效减小电流和电磁转矩波动,同时拥有良好的动态性能.
图2
图2
矢量控制策略控制框图
Fig.2
Diagram of control block of vector control strategy
2.1 模型预测电流控制原理
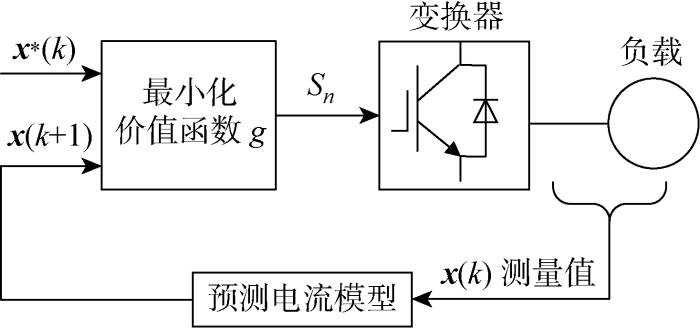
运用有限集模型预测控制思想,根据k 时刻测量值构建预测电流模型,将其预测结果代入价值函数g ,使g 最小化的开关函数Sn 在k +1时刻作用于变换器. 其有限集模型预测控制原理图如图3 所示. 图中:x (·)、x* (·)分别为模型使用的被测变量和被测变量参考值.
图3
图3
有限集模型预测控制原理图
Fig.3
Schematic diagram of predictive control of finite set model
2.2 控制延时补偿
采用前向欧拉逼近代替式(5)中转子电流i r d i r q i r ,将式(5)离散化为
(6) i r d ( k + 1 ) = i r d ( k ) + T s σ L r { u r d ( k ) - R r i r d ( k ) + ( ω l - ω r ) × L m ( u s d ( k ) - R s i s d ( k ) ) - L s ω l + σ L r i r q ( k ) } i r q ( k + 1 ) = i r q ( k ) + T s σ L r { u r q ( k ) - R r i r q ( k ) - ( ω l - ω r ) × L m ( u s q ( k ) - R s i s q ( k ) ) - L s ω l + σ L r i r d ( k ) }
式中:i r d k +1)、i r q k +1)为k +1时刻的预测值;i r d k )、i r q k )、i s d k )、i s q k )、u s d k )、u s q k )为k 时刻的采样值;T s 为控制周期;u r d k )、u r q k )由k 时刻开关函数作用得出.
由式(6)可见,转子电流i r 的预测值是基于当前时刻(k 时刻)的电流i r (k ). 然而数字控制系统有一拍延迟的问题[10 ] ,选择的最优矢量输出要延迟到下一时刻(k +1时刻),从而导致逆变器应用上一时刻开关状态,增加电流脉动. 因此,需要以k +1时刻的变量作为初始值对k +2时刻的变量进行预测,从而消除一拍延迟影响.
2.3 价值函数确定
考虑延迟补偿后,需使用k +2时刻电流参考值.由于传统MPC控制采样频率较高,可认为短时间电流变化不大,近似认为电流参考值i r d * ( k )=i r d * ( k +2),i r q * ( k )=i r q * ( k +2).
将经过延迟补偿之后得到的k +1时刻电流初值代入预测方程求出k +2时刻变量,然后代入如下所示价值函数,从而得到最优矢量,即为最小价值函数与之对应的电压矢量.
(7) g(n)=| i r d * r d (k+2)|+ | i r q * r q (k+2)|
2.4 风力机控制策略的短路特性
对比如图2 和图3 所示机侧变流器的矢量控制策略和模型预测控制原理图,矢量控制策略采用双控制回路,外环为功率,内环为转子电流.机侧变流器只保留速度环,用模型预测控制器取代矢量控制的电流环,无需参数调试,简化了控制结构.当三相对称短路故障导致端电压下降时,出现功率偏差,矢量控制采用双回路结构,调节速度慢,波形畸变大;而模型预测控制策略动态响应迅速且波形平滑.因此,模型预测控制提供的短路电流瞬时值比矢量控制更平稳,变化幅度小.
3 风电对配电网短路电流的影响
风电场接入配电网后,配电网传统的单电源辐射型供电方式变为双电源供电结构,系统结构及潮流分布将发生变化[11 ] .若配电网线路发生故障,风电场提供的不确定的短路电流会给配电网运行造成不利影响[12 -13 ] .
3.1 配电网及其继电保护装置
在单侧电源电网中发生短路时,通过保护装置的短路电流只能指向被保护设备的方向,因而不需要考虑保护装置反方向,不需要配置方向原件,其构成最为简单.采用三段式结合的电流保护,当风电场接入配电网后,配电网传统的单电源辐射型供电方式变为双电源供电结构,系统结构及潮流分布会发生变化.
3.2 风电接入配电网的短路电流特性
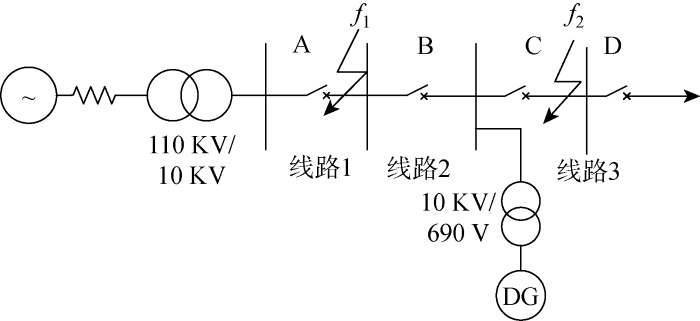
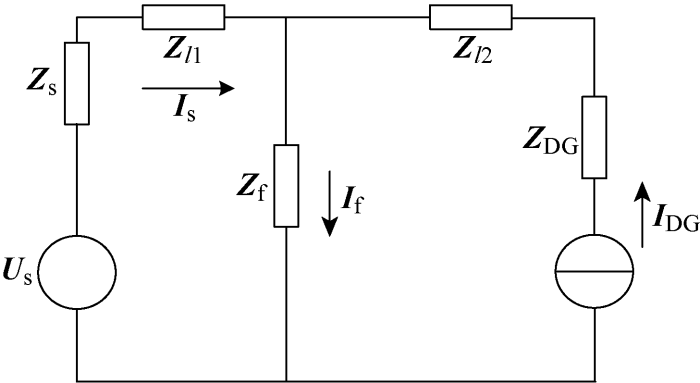
图4 为双馈风力发电机组接入10 kV配电网简化等效模型,母线设置为A、B、C、D.分析风力机接入点上游f 1 点及下游f 2 点发生三相短路时流过各线路的短路电流. 当f 1 点发生短路时,处于故障点上游的电源侧与处于下游的风电机组均会向故障点提供短路电流,系统的等效电路如图5 所示. 设系统电源U s 侧阻抗为Z s ;风电机组端口电压为U DG ;阻抗为Z DG ,Zl 1 、Zl 2 分别为故障点f 1 上游侧、下游侧线路阻抗;Z f 为故障点的接地阻抗;I s 、I f 、I DG 分别为系统提供的f1 短路电流、故障点电流和风力机提供的电流.
图4
图4
含风电的10 kV配电网
Fig.4
10 kV distribution network with wind power
图5
图5
f 1 短路时的系统等效电路
Fig.5
Equivalent circuit of the system when f 1 is short-circuited
(8) Is = U s - Z f I D G Z s + Z l 1 + Z f
(9) If = U s + ( Z s + Z l 1 + Z f ) I D G Z s + Z l 1 + Z f
上游f1 点发生三相短路,风力机接入后,故障点下游产生反向的短路电流. 由式(8)可知,风力机的接入降低了电源提供的故障电流;从式(9)可看出,系统和风力机都对故障点提供短路电流,故故障处f1 的短路电流增大;且电源侧提供的短路电流和短路点的故障电流都与接地阻抗有关.
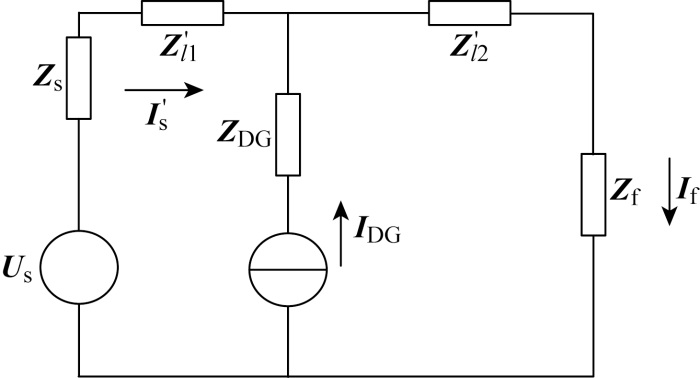
当f2 点发生短路时,系统的等效电路如图6 所示.图中:Z'l 1 、Z'l 2 分别为故障点f 2 上游侧、下游侧线路阻抗;I 's 、I 'f 为系统提供的f2 短路电流和故障点电流.
图6
图6
f 2 短路时的系统等效电路
Fig.6
Equivalent circuit of the system when f 2 is short-circuited
(10) I's = U s - ( Z ' l 2 + Z f ) I D G Z s + Z ' 1 l + Z ' l 2 + Z f
(11) I'f = U s + ( Z s + Z ' l 1 ) I D G Z s + Z ' l 1 + Z f + Z ' l 2
下游f 2 点发生三相短路时,由式(10)可知,风力机接入使电源提供的故障电流降低;从式(9)可看出,系统和风力机都对故障点提供短路电流,故故障处f 2 的短路电流增大;且电源侧提供的短路电流和短路点的故障电流都与接地阻抗有关.
比较式(8)~(11)可知,风力机接入配电网后,上游的短路电流将比风力机未接入时减小,下游的短路电流将比风力机未连接时增加.
4 仿真结果与分析
运用MATLAB/Simulink仿真平台分别搭建附加PI控制器的矢量控制和模型预测电流控制的变速恒频双馈风力机的仿真模型,仿真并网后DFIG的输出特性.经验证,两种控制方法的双馈风力机模型均能有效运行.然后,在此基础上搭建如图4 所示的风电机组接入配电网的仿真模型.当接入点上游和下游分别发生三相短路故障时,分析风力机控制策略、接入位置和容量对配电网线路1、2、3的短路电流I 1 、I 2 、I 3 的影响.
4.1 DFIG控制策略对配电网短路电流的影响
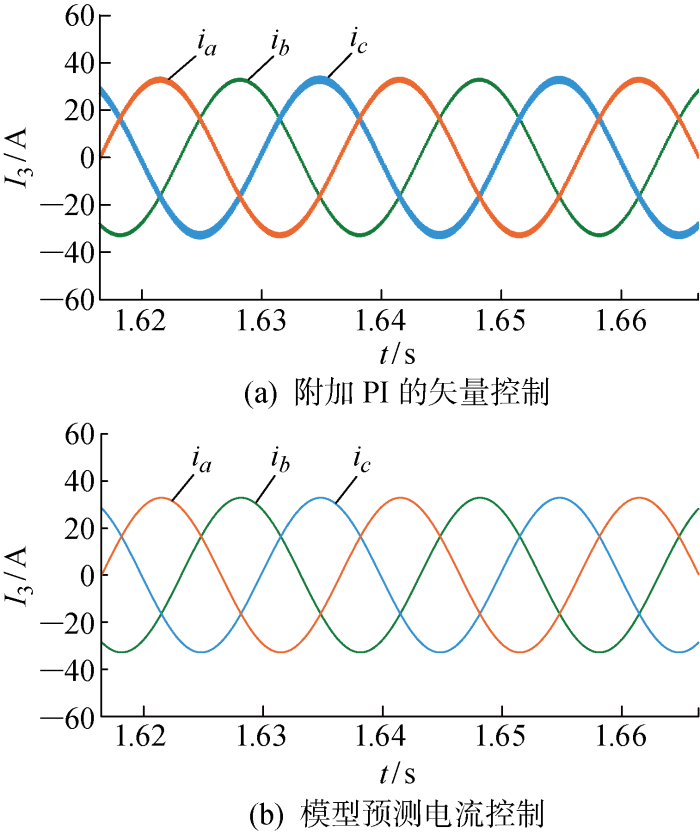
图7 为三相短路故障点设置为风力机接入点上游f 1 处,在不同控制策略下配电网线路3的短路电流I 3 的变化情况.图中:ia 、ib 、ic 分别为三相电流的a 相、b 相、c 相.图7(a) 和图7(b) 为DFIG分别采用附加PI控制和模型预测控制所对应的配电网线路3的短路电流.
图7
图7
DFIG控制方式对配电网短路电流的影响
Fig.7
Impact of DFIG control mode on short-circuit current of distribution network
矢量控制对参数的依赖性较强,需相对繁琐的控制器调试工作.MPC无需参数整定,直接通过模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的控制性能和更加灵活的控制结构.由图7 可见,模型预测控制与矢量控制的DFIG分别接入配电网,配电网短路电流暂态过程基本一致,但采取模型预测控制的短路电流有更好的正弦度,电流脉动和谐波含量更小.
4.2 短路电流随风机接入位置的变化
因为使用模型预测控制会减小短路电流脉动,提高电能质量,但不会改变配电网中的短路电流值,所以采用模型预测控制下的DFIG接入配电网进行分析.首先,图4 中线路1末端f 1 点发生三相短路故障,风力机容量固定为2 MW,然后逐渐将其并网位置由母线A向线路3末端的母线D移动,以获得配电网各线路中流过的短路电流I 1 、I 2 、I 3 和风力机提供给配电网的电流I DG ,如表1 所示.
由表1 可知,当风力机并网位置越靠近故障点,风力机出口处的电流I DG 就会逐渐增大.因此,并网点离故障点越近,双馈风电机组提供的短路电流越大.
同样,如果图4 中线路3末端的f 2 点发生三相短路故障,则馈线上各线路中流过的短路电流I 1 、I 2 、I 3 和风力机提供给配电网的电流I DG 的值如表2 所示.
由表2 可知,并网位置与故障点的距离越小,短路电流I DG 就会越大,这与表1 得出的结论相同.并且随着并网点逐渐后移,系统电源给予的电流就越来越小.而且,当风力机接入位置处于故障点上游时,由表2 可知,越靠近故障点,越呈现I 3 > I 2 > I 1 的趋势.因此,风力机接入位置相对故障点位置越近,对故障点短路电流的贡献就越大.
4.3 短路电流随风力机接入容量的变化
将风力机接入点固定在母线C处,三相短路故障点为线路1上的f 1 处.在持续最高运行工况下,逐渐将双馈风电机组容量增大,由此得到各线路上的短路电流I 1 、I 2 、I 3 ,如表3 所示.
由表3 可知,当并网点上游发生故障,风电并网容量逐步增加时,线路2、3的短路电流I 2 、I 3 也会增大,即双馈风电系统并网容量越大时,提供给上游短路点的反向短路电流与下游线路的负荷电流也会增大.表3 中的电流I 1 无变化,因此可知尽管风力机容量发生变化,但系统侧注入短路点的短路电流不会随之改变.
将风力机接入点固定在母线C处,三相短路故障点为线路3上的f 2 处.在持续最高运行工况下,逐渐将并网的双馈风电机组容量增大,由此得到各线路上的短路电流I 1 、I 2 、I 3 ,如表4 所示.
由表4 可知,当并网点下游发生故障,并网容量逐渐增大,线路1、2中的短路电流I 1 、I 2 会越来越小.说明风电并网容量的增大,反而会使得系统电源侧注入的短路电流变小.而由表4 可以看出,风电并网容量增大,线路3中短路电流I 3 却随之增加.因此,风力机对其并网点上游存在汲流作用,对其下游线路存在助增作用.
综上所述,双馈风电系统在母线C处并网,对其配电网短路电流进行分析和仿真,可以得到以下几点结论:
(1) 配电网发生三相短路时,运用模型预测电流控制策略,配电网短路电流有更好的正弦度,电流脉动和谐波含量更小,电能质量更好.
(2) 故障点与并网位置相距越近,在风力机出口处的短路电流就会越大.而且在并网点逐步向后移动时,系统提供的电流会逐步减弱.可以推断当风力机并网容量增大,风力机对上游线路短路电流存在汲流作用,对下游线路短路电流存在助增作用.
(3) 短路点位于双馈风力机上游时,风力机会向短路点提供反向短路电流.AB段的保护装置不受风力机影响,BC段的保护装置中会流过反向电流,并随着风力机容量增大而增大;若超过BC段的整定电流,则会发生误跳闸的情况.因此,当风力机接入配电网时,应该在风力机上游部分装设保护装置,并限制风力机接入的容量,使其风力机提供的反向电流不能超过上游线段的保护整定值.
(4) 短路点位于双馈风力机下游时,风力机和系统一起向故障点提供短路电流.但如果风电接入容量过大,可能会导致CD段失去选择性,发生误跳闸.且风力机下游出现故障时,风力机上游的短路电流会比无风力机时的短路电流减少,上游BC段的保护装置范围缩短.故应限制风力机接入的容量,保证发生故障时各级保护能正确配合.
5 结语
首先提出一种控制双馈风电系统的模型预测电流控制策略.相比较于附加PI的矢量控制,运用模型预测电流控制方法更加简便,无需参数整定,省去调制环节,而且具有更好的控制性能.对含有双馈风电系统的配电网进行仿真,在此基础上分析风力机的控制策略、容量大小及接入位置对配电网短路电流的影响,并结合其特性对配电网的保护提出建议.
参考文献
View Option
[1]
徐覃萍 . 风电接入对配电网继电保护的影响及其保护配置研究 [D]. 南宁 : 广西大学 , 2014 .
[本文引用: 1]
XU Qinping . Research on the influence of wind power access to distribution network of relay protection and protection configuration [D]. Nanning : Guangxi University , 2014 .
[本文引用: 1]
[2]
沈鑫 , 曹敏 . 分布式电源并网对于配电网的影响研究
[J]. 电工技术学报 2015 , 30 (Sup.1 ): 346 -351 .
[本文引用: 1]
SHEN Xin CAO Min . Research on the influence of distributed power grid for distribution network
[J]. Transactions of China Electrotechnical Society 2015 , 30 (Sup.1 ): 346 -351 .
[本文引用: 1]
[3]
傅旭 , 李想 , 王笑飞 . 新能源发电接入对电网短路电流的影响研究
[J]. 分布式能源 2018 , 3 (1 ): 58 -63 .
[本文引用: 2]
FU Xu LI Xiang WANG Xiaofei . Short circuit current of electric power system with new energy power generation
[J]. Distributed Energy 2018 , 3 (1 ): 58 -63 .
[本文引用: 2]
[4]
靳方超 . 双馈风电场接入对其送出线路保护的影响 [D]. 天津 : 天津大学 , 2014 .
[本文引用: 2]
JIN Fangchao . Influence of DFIG wind farms integration on transmission line protection [D]. Tianjin : Tianjin University , 2014 .
[本文引用: 2]
[5]
贾耕涛 , 翟学 , 杨雪瑞 . 考虑故障特性和保护约束条件的分布式电源准入容量研究
[J]. 电力科学与技术学报 2016 , 31 (4 ): 89 -95 .
[本文引用: 2]
JIA Gengtao ZHAI Xue YANG Xuerui . Research on penetration level of DG considering fault characteristics and relay protection constraint
[J]. Journal of Electric Power Science and Technology 2016 , 31 (4 ): 89 -95 .
[本文引用: 2]
[6]
杨国生 , 李欣 , 周泽昕 . 风电场接入对配电网继电保护的影响与对策
[J]. 电网技术 2009 , 33 (11 ): 87 -91 .
[本文引用: 2]
YANG Guosheng LI Xin ZHOU Zexin . Impacts of wind farm on relay protection for distribution network and its countermeasures
[J]. Power System Technology 2009 , 33 (11 ): 87 -91 .
[本文引用: 2]
[7]
程金牛 , 童晓阳 . 风电DG布置、容量等多因素对配电网电流保护的影响
[J]. 电气应用 2013 , 32 (16 ): 112 -117 .
[本文引用: 2]
CHENG Jinniu TONG Xiaoyang . Influence of DG arrangement, capacity and other factors on current protection of distribution network
[J]. Electrotechnical Application 2013 , 32 (16 ): 112 -117 .
[本文引用: 2]
[8]
王霄鹤 . 双馈风力发电系统友好并网运行控制策略研究 [D]. 杭州 : 浙江大学 , 2019 .
[本文引用: 1]
WANG Xiaohe . Investigation on grid-friendly control strategy of DFIG wind power system [D]. Hangzhou : Zhejiang University , 2019 .
[本文引用: 1]
[9]
RODRIGUEZ J KENNEL R M ESPINOZA J R , et al High-performance control strategies for electrical drives: An experimental assessment
[J]. IEEE Transactions on Industrial Electronics 2012 , 59 (2 ): 812 -820 .
DOI:10.1109/TIE.2011.2158778
URL
[本文引用: 1]
[10]
ZHANG Y C ZHU J G XU W . Analysis of one step delay in direct torque control of permanent magnet synchronous motor and its remedies
[C]// 2010 International Conference on Electrical Machines and Systems Incheon, Korea : IEEE , 2010 : 792 -797 .
[本文引用: 1]
[11]
郑淑文 , 靳鹏飞 , 丁婧 . 风电场接入配电网对电流保护的影响
[J]. 通信电源技术 2016 , 33 (2 ): 147 -148 .
[本文引用: 1]
ZHENG Shuwen JIN Pengfei DING Jing . Wind farm access distribution network impact on current protection
[J]. Telecom Power Technology 2016 , 33 (2 ): 147 -148 .
[本文引用: 1]
[12]
DE CARVALHO R V R NIELSON R LIMA C R , et al Operational conditions analyses of distributed generation (DG) connected on power distribution grid based on ieee Std. 1547
[C]// 2013 IEEE PES Conference on Innovative Smart Grid Technologies (ISGT Latin America) Sao Paulo, Brazil : IEEE , 2013 : 1 -8 .
[本文引用: 1]
[13]
李凤婷 , 李智才 . 含异步机风电场的配电网故障特性及其保护分析
[J]. 电网技术 2013 , 37 (4 ): 981 -986 .
[本文引用: 1]
LI Fengting LI Zhicai . Analysis on impacts of asynchronous wind farm on fault current characteristics and protective relaying of distribution network
[J]. Power System Technology 2013 , 37 (4 ): 981 -986 .
[本文引用: 1]
1
2014
... 为应对气候变化,我国提出“二氧化碳排放力争于2030年前达到峰值,努力争取2060年前实现碳中和”等庄严的目标和承诺.“十四五”规划也将加快推动绿色低碳发展列入其中,大规模风电场并网已成为一种不可避免的趋势.然而,风力发电(简称风电)接入配电网会改变配电网的拓扑结构,将导致更复杂的功率和潮流分布[1 ] .因此,研究风电并网时接入配电网的短路电流具有重要意义. ...
1
2014
... 为应对气候变化,我国提出“二氧化碳排放力争于2030年前达到峰值,努力争取2060年前实现碳中和”等庄严的目标和承诺.“十四五”规划也将加快推动绿色低碳发展列入其中,大规模风电场并网已成为一种不可避免的趋势.然而,风力发电(简称风电)接入配电网会改变配电网的拓扑结构,将导致更复杂的功率和潮流分布[1 ] .因此,研究风电并网时接入配电网的短路电流具有重要意义. ...
分布式电源并网对于配电网的影响研究
1
2015
... 小规模风电以分布式电源的方式接入配电网,这种接入方法能避免大容量风电集中接入对电压稳定性的影响,但对配电网短路电流的分布和大小影响较大[2 ] .风电机组类型主要有鼠笼异步风力机、直驱式风力机和双馈异步风力机.文献[3 ]中分析了同步发电机、鼠笼异步风电机组、双馈异步风电机组和直驱同步风电机组等各种风力发电机接入配电网对系统短路电流的影响.在现今的风电系统中,双馈异步风力发电机(Doubly Fed Induction Generator, DFIG)因其小容量的变换器和相应的成本优势得到广泛应用.文献[4 ]中分析在三相短路故障时双馈风力发电机的暂态特性,并研究该特性对输电线路的影响.文献[5 ]中分析双馈风力发电机的短路特性,并结合理论计算配电网在保证安全运行的情况下接入双馈风力发电机的最大容量.文献[6 ]中研究风电接入对配电网的保护影响,虽然只重点研究风力机接入的下游部分,但实际上风力机接入对其上游、下游的短路电流及保护都会产生影响.文献[7 ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
分布式电源并网对于配电网的影响研究
1
2015
... 小规模风电以分布式电源的方式接入配电网,这种接入方法能避免大容量风电集中接入对电压稳定性的影响,但对配电网短路电流的分布和大小影响较大[2 ] .风电机组类型主要有鼠笼异步风力机、直驱式风力机和双馈异步风力机.文献[3 ]中分析了同步发电机、鼠笼异步风电机组、双馈异步风电机组和直驱同步风电机组等各种风力发电机接入配电网对系统短路电流的影响.在现今的风电系统中,双馈异步风力发电机(Doubly Fed Induction Generator, DFIG)因其小容量的变换器和相应的成本优势得到广泛应用.文献[4 ]中分析在三相短路故障时双馈风力发电机的暂态特性,并研究该特性对输电线路的影响.文献[5 ]中分析双馈风力发电机的短路特性,并结合理论计算配电网在保证安全运行的情况下接入双馈风力发电机的最大容量.文献[6 ]中研究风电接入对配电网的保护影响,虽然只重点研究风力机接入的下游部分,但实际上风力机接入对其上游、下游的短路电流及保护都会产生影响.文献[7 ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
新能源发电接入对电网短路电流的影响研究
2
2018
... 小规模风电以分布式电源的方式接入配电网,这种接入方法能避免大容量风电集中接入对电压稳定性的影响,但对配电网短路电流的分布和大小影响较大[2 ] .风电机组类型主要有鼠笼异步风力机、直驱式风力机和双馈异步风力机.文献[3 ]中分析了同步发电机、鼠笼异步风电机组、双馈异步风电机组和直驱同步风电机组等各种风力发电机接入配电网对系统短路电流的影响.在现今的风电系统中,双馈异步风力发电机(Doubly Fed Induction Generator, DFIG)因其小容量的变换器和相应的成本优势得到广泛应用.文献[4 ]中分析在三相短路故障时双馈风力发电机的暂态特性,并研究该特性对输电线路的影响.文献[5 ]中分析双馈风力发电机的短路特性,并结合理论计算配电网在保证安全运行的情况下接入双馈风力发电机的最大容量.文献[6 ]中研究风电接入对配电网的保护影响,虽然只重点研究风力机接入的下游部分,但实际上风力机接入对其上游、下游的短路电流及保护都会产生影响.文献[7 ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
... ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
新能源发电接入对电网短路电流的影响研究
2
2018
... 小规模风电以分布式电源的方式接入配电网,这种接入方法能避免大容量风电集中接入对电压稳定性的影响,但对配电网短路电流的分布和大小影响较大[2 ] .风电机组类型主要有鼠笼异步风力机、直驱式风力机和双馈异步风力机.文献[3 ]中分析了同步发电机、鼠笼异步风电机组、双馈异步风电机组和直驱同步风电机组等各种风力发电机接入配电网对系统短路电流的影响.在现今的风电系统中,双馈异步风力发电机(Doubly Fed Induction Generator, DFIG)因其小容量的变换器和相应的成本优势得到广泛应用.文献[4 ]中分析在三相短路故障时双馈风力发电机的暂态特性,并研究该特性对输电线路的影响.文献[5 ]中分析双馈风力发电机的短路特性,并结合理论计算配电网在保证安全运行的情况下接入双馈风力发电机的最大容量.文献[6 ]中研究风电接入对配电网的保护影响,虽然只重点研究风力机接入的下游部分,但实际上风力机接入对其上游、下游的短路电流及保护都会产生影响.文献[7 ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
... ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
2
2014
... 小规模风电以分布式电源的方式接入配电网,这种接入方法能避免大容量风电集中接入对电压稳定性的影响,但对配电网短路电流的分布和大小影响较大[2 ] .风电机组类型主要有鼠笼异步风力机、直驱式风力机和双馈异步风力机.文献[3 ]中分析了同步发电机、鼠笼异步风电机组、双馈异步风电机组和直驱同步风电机组等各种风力发电机接入配电网对系统短路电流的影响.在现今的风电系统中,双馈异步风力发电机(Doubly Fed Induction Generator, DFIG)因其小容量的变换器和相应的成本优势得到广泛应用.文献[4 ]中分析在三相短路故障时双馈风力发电机的暂态特性,并研究该特性对输电线路的影响.文献[5 ]中分析双馈风力发电机的短路特性,并结合理论计算配电网在保证安全运行的情况下接入双馈风力发电机的最大容量.文献[6 ]中研究风电接入对配电网的保护影响,虽然只重点研究风力机接入的下游部分,但实际上风力机接入对其上游、下游的短路电流及保护都会产生影响.文献[7 ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
... ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
2
2014
... 小规模风电以分布式电源的方式接入配电网,这种接入方法能避免大容量风电集中接入对电压稳定性的影响,但对配电网短路电流的分布和大小影响较大[2 ] .风电机组类型主要有鼠笼异步风力机、直驱式风力机和双馈异步风力机.文献[3 ]中分析了同步发电机、鼠笼异步风电机组、双馈异步风电机组和直驱同步风电机组等各种风力发电机接入配电网对系统短路电流的影响.在现今的风电系统中,双馈异步风力发电机(Doubly Fed Induction Generator, DFIG)因其小容量的变换器和相应的成本优势得到广泛应用.文献[4 ]中分析在三相短路故障时双馈风力发电机的暂态特性,并研究该特性对输电线路的影响.文献[5 ]中分析双馈风力发电机的短路特性,并结合理论计算配电网在保证安全运行的情况下接入双馈风力发电机的最大容量.文献[6 ]中研究风电接入对配电网的保护影响,虽然只重点研究风力机接入的下游部分,但实际上风力机接入对其上游、下游的短路电流及保护都会产生影响.文献[7 ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
... ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
考虑故障特性和保护约束条件的分布式电源准入容量研究
2
2016
... 小规模风电以分布式电源的方式接入配电网,这种接入方法能避免大容量风电集中接入对电压稳定性的影响,但对配电网短路电流的分布和大小影响较大[2 ] .风电机组类型主要有鼠笼异步风力机、直驱式风力机和双馈异步风力机.文献[3 ]中分析了同步发电机、鼠笼异步风电机组、双馈异步风电机组和直驱同步风电机组等各种风力发电机接入配电网对系统短路电流的影响.在现今的风电系统中,双馈异步风力发电机(Doubly Fed Induction Generator, DFIG)因其小容量的变换器和相应的成本优势得到广泛应用.文献[4 ]中分析在三相短路故障时双馈风力发电机的暂态特性,并研究该特性对输电线路的影响.文献[5 ]中分析双馈风力发电机的短路特性,并结合理论计算配电网在保证安全运行的情况下接入双馈风力发电机的最大容量.文献[6 ]中研究风电接入对配电网的保护影响,虽然只重点研究风力机接入的下游部分,但实际上风力机接入对其上游、下游的短路电流及保护都会产生影响.文献[7 ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
... ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
考虑故障特性和保护约束条件的分布式电源准入容量研究
2
2016
... 小规模风电以分布式电源的方式接入配电网,这种接入方法能避免大容量风电集中接入对电压稳定性的影响,但对配电网短路电流的分布和大小影响较大[2 ] .风电机组类型主要有鼠笼异步风力机、直驱式风力机和双馈异步风力机.文献[3 ]中分析了同步发电机、鼠笼异步风电机组、双馈异步风电机组和直驱同步风电机组等各种风力发电机接入配电网对系统短路电流的影响.在现今的风电系统中,双馈异步风力发电机(Doubly Fed Induction Generator, DFIG)因其小容量的变换器和相应的成本优势得到广泛应用.文献[4 ]中分析在三相短路故障时双馈风力发电机的暂态特性,并研究该特性对输电线路的影响.文献[5 ]中分析双馈风力发电机的短路特性,并结合理论计算配电网在保证安全运行的情况下接入双馈风力发电机的最大容量.文献[6 ]中研究风电接入对配电网的保护影响,虽然只重点研究风力机接入的下游部分,但实际上风力机接入对其上游、下游的短路电流及保护都会产生影响.文献[7 ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
... ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
风电场接入对配电网继电保护的影响与对策
2
2009
... 小规模风电以分布式电源的方式接入配电网,这种接入方法能避免大容量风电集中接入对电压稳定性的影响,但对配电网短路电流的分布和大小影响较大[2 ] .风电机组类型主要有鼠笼异步风力机、直驱式风力机和双馈异步风力机.文献[3 ]中分析了同步发电机、鼠笼异步风电机组、双馈异步风电机组和直驱同步风电机组等各种风力发电机接入配电网对系统短路电流的影响.在现今的风电系统中,双馈异步风力发电机(Doubly Fed Induction Generator, DFIG)因其小容量的变换器和相应的成本优势得到广泛应用.文献[4 ]中分析在三相短路故障时双馈风力发电机的暂态特性,并研究该特性对输电线路的影响.文献[5 ]中分析双馈风力发电机的短路特性,并结合理论计算配电网在保证安全运行的情况下接入双馈风力发电机的最大容量.文献[6 ]中研究风电接入对配电网的保护影响,虽然只重点研究风力机接入的下游部分,但实际上风力机接入对其上游、下游的短路电流及保护都会产生影响.文献[7 ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
... ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
风电场接入对配电网继电保护的影响与对策
2
2009
... 小规模风电以分布式电源的方式接入配电网,这种接入方法能避免大容量风电集中接入对电压稳定性的影响,但对配电网短路电流的分布和大小影响较大[2 ] .风电机组类型主要有鼠笼异步风力机、直驱式风力机和双馈异步风力机.文献[3 ]中分析了同步发电机、鼠笼异步风电机组、双馈异步风电机组和直驱同步风电机组等各种风力发电机接入配电网对系统短路电流的影响.在现今的风电系统中,双馈异步风力发电机(Doubly Fed Induction Generator, DFIG)因其小容量的变换器和相应的成本优势得到广泛应用.文献[4 ]中分析在三相短路故障时双馈风力发电机的暂态特性,并研究该特性对输电线路的影响.文献[5 ]中分析双馈风力发电机的短路特性,并结合理论计算配电网在保证安全运行的情况下接入双馈风力发电机的最大容量.文献[6 ]中研究风电接入对配电网的保护影响,虽然只重点研究风力机接入的下游部分,但实际上风力机接入对其上游、下游的短路电流及保护都会产生影响.文献[7 ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
... ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
风电DG布置、容量等多因素对配电网电流保护的影响
2
2013
... 小规模风电以分布式电源的方式接入配电网,这种接入方法能避免大容量风电集中接入对电压稳定性的影响,但对配电网短路电流的分布和大小影响较大[2 ] .风电机组类型主要有鼠笼异步风力机、直驱式风力机和双馈异步风力机.文献[3 ]中分析了同步发电机、鼠笼异步风电机组、双馈异步风电机组和直驱同步风电机组等各种风力发电机接入配电网对系统短路电流的影响.在现今的风电系统中,双馈异步风力发电机(Doubly Fed Induction Generator, DFIG)因其小容量的变换器和相应的成本优势得到广泛应用.文献[4 ]中分析在三相短路故障时双馈风力发电机的暂态特性,并研究该特性对输电线路的影响.文献[5 ]中分析双馈风力发电机的短路特性,并结合理论计算配电网在保证安全运行的情况下接入双馈风力发电机的最大容量.文献[6 ]中研究风电接入对配电网的保护影响,虽然只重点研究风力机接入的下游部分,但实际上风力机接入对其上游、下游的短路电流及保护都会产生影响.文献[7 ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
... -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
风电DG布置、容量等多因素对配电网电流保护的影响
2
2013
... 小规模风电以分布式电源的方式接入配电网,这种接入方法能避免大容量风电集中接入对电压稳定性的影响,但对配电网短路电流的分布和大小影响较大[2 ] .风电机组类型主要有鼠笼异步风力机、直驱式风力机和双馈异步风力机.文献[3 ]中分析了同步发电机、鼠笼异步风电机组、双馈异步风电机组和直驱同步风电机组等各种风力发电机接入配电网对系统短路电流的影响.在现今的风电系统中,双馈异步风力发电机(Doubly Fed Induction Generator, DFIG)因其小容量的变换器和相应的成本优势得到广泛应用.文献[4 ]中分析在三相短路故障时双馈风力发电机的暂态特性,并研究该特性对输电线路的影响.文献[5 ]中分析双馈风力发电机的短路特性,并结合理论计算配电网在保证安全运行的情况下接入双馈风力发电机的最大容量.文献[6 ]中研究风电接入对配电网的保护影响,虽然只重点研究风力机接入的下游部分,但实际上风力机接入对其上游、下游的短路电流及保护都会产生影响.文献[7 ]中研究风电分布式发电(Distributed Generation,DG)的布置方式、接入容量对配电网电流保护的影响.文献[3 ⇓ ⇓ ⇓ -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
... -7 ]中DFIG变流器的控制方法为矢量控制,对参数的依赖性较强,需相对繁琐的控制器调试.矢量控制具有局限性,因此提出基于模型预测控制(Model Predictive Control, MPC)的双馈风力发电系统运行控制方法,MPC无需参数整定,直接利用模型预测控制算法产生变换器驱动信号,省去调制环节,而且具有更好的稳态性能和更加灵活的控制结构. ...
1
2019
... 在双馈风力发电系统的控制策略中,矢量控制一直都占据着主流地位.但传统矢量控制也存在一些问题,例如比例积分(Proportional Integral,PI)控制器中的积分环节存在滞后效应、动态性能不尽如人意等[8 ] . ...
1
2019
... 在双馈风力发电系统的控制策略中,矢量控制一直都占据着主流地位.但传统矢量控制也存在一些问题,例如比例积分(Proportional Integral,PI)控制器中的积分环节存在滞后效应、动态性能不尽如人意等[8 ] . ...
High-performance control strategies for electrical drives: An experimental assessment
1
2012
... 图2 为附加PI控制器的矢量控制策略框图.图中:U s abc U dc 为直流母线电压;I r abc αβ 坐标系的变换;θ r 、θ slip 、θ l 分别为转子位置角、转差角、d 轴与α 轴之间的夹角;SVPWM为空间矢量脉宽调制;U s αβ I r αβ U s dq dq 坐标系下的定子电压;U r αβ I r d * I r q * d 、q 轴转子电流参考值;I r d I r q d 、q 轴转子电流;Sa 、Sb 、Sc 分别为静止坐标系下a 、b 、c 三相.为改进对风电系统的控制,提出模型预测控制.MPC是依据系统当前状态和数学模型,进而预测出系统未来状态,再根据期望值实现在线寻优的控制算法[9 ] .相比于附加PI控制器的矢量控制,模型预测控制策略能有效减小电流和电磁转矩波动,同时拥有良好的动态性能. ...
Analysis of one step delay in direct torque control of permanent magnet synchronous motor and its remedies
1
2010
... 由式(6)可见,转子电流i r 的预测值是基于当前时刻(k 时刻)的电流i r (k ). 然而数字控制系统有一拍延迟的问题[10 ] ,选择的最优矢量输出要延迟到下一时刻(k +1时刻),从而导致逆变器应用上一时刻开关状态,增加电流脉动. 因此,需要以k +1时刻的变量作为初始值对k +2时刻的变量进行预测,从而消除一拍延迟影响. ...
风电场接入配电网对电流保护的影响
1
2016
... 风电场接入配电网后,配电网传统的单电源辐射型供电方式变为双电源供电结构,系统结构及潮流分布将发生变化[11 ] .若配电网线路发生故障,风电场提供的不确定的短路电流会给配电网运行造成不利影响[12 -13 ] . ...
风电场接入配电网对电流保护的影响
1
2016
... 风电场接入配电网后,配电网传统的单电源辐射型供电方式变为双电源供电结构,系统结构及潮流分布将发生变化[11 ] .若配电网线路发生故障,风电场提供的不确定的短路电流会给配电网运行造成不利影响[12 -13 ] . ...
Operational conditions analyses of distributed generation (DG) connected on power distribution grid based on ieee Std. 1547
1
2013
... 风电场接入配电网后,配电网传统的单电源辐射型供电方式变为双电源供电结构,系统结构及潮流分布将发生变化[11 ] .若配电网线路发生故障,风电场提供的不确定的短路电流会给配电网运行造成不利影响[12 -13 ] . ...
含异步机风电场的配电网故障特性及其保护分析
1
2013
... 风电场接入配电网后,配电网传统的单电源辐射型供电方式变为双电源供电结构,系统结构及潮流分布将发生变化[11 ] .若配电网线路发生故障,风电场提供的不确定的短路电流会给配电网运行造成不利影响[12 -13 ] . ...
含异步机风电场的配电网故障特性及其保护分析
1
2013
... 风电场接入配电网后,配电网传统的单电源辐射型供电方式变为双电源供电结构,系统结构及潮流分布将发生变化[11 ] .若配电网线路发生故障,风电场提供的不确定的短路电流会给配电网运行造成不利影响[12 -13 ] . ...