近年来,装配小规模分布式发电(Distributed Generation,DG)的新型主体,即“产消者”在电力系统中扮演愈来愈重要的角色[1].一方面,在深化电力体制改革背景下,国家发展改革委员会和国家能源局于2017年11月发布《关于开展分布式发电市场化交易试点的通知》(简称《通知》),拉开分布式发电市场化交易帷幕[2].另一方面,在构建以新能源为主体的新型电力系统部署方案下,配网中大量产消者将改变系统电源结构,导致配网的运行机理和平衡模式发生变化.此外,由于产消者的自利性交易特征,其交易行为将加重配电网络的运维负担,倒逼电网公司加大网络投资建设力度,扩充网络线路容量.而过网费(Network Usage Charge,NUC)作为电网公司向使用网架的用户收取的网络使用费,能够以有效的价格机制保障电力供需平衡,维持系统稳定运行并协助电网公司回收网架运维成本.
《通知》中虽明确了过网费的核算标准,即过网费为电力用户接入电压等级对应的输配电价(含政策性交叉补贴)扣减分布式发电市场化交易所涉最高电压等级的输配电价,但该核算标准依然存在缺陷,较大程度上制约分布式发电市场化交易的推进.一方面,按照该标准,对电力用户在自发自用以及在10 kV电压等级且同一变电台区内消纳的情况下免收过网费,损害了电网公司利益.另一方面,由于不同电压等级交叉补贴情况不同,配电价格级差低,无法体现实际的配电网消纳成本;而一些分布式发电交易试点所在地方政府核定的过网费较高,也无法发挥“隔墙售电”的优势.因此,为了推动分布式发电市场化交易的可持续发展,亟需建立合理的过网费定价机制.目前国际上确定过网费的方法主要有:依据传输电能数量计费的邮票法[3]、主观限定潮流流向的合同路径法[4]、根据电网潮流分布计费的兆瓦-千米法[5]等,应用这些方法计算的过网费难以有效反映用户对电网资产使用程度.针对该问题,文献[6]中提出一种有功潮流追踪方法,能够准确分析出用户的潮流分布情况.但该核算方法一般只适用于单向潮流、运行模式单一的输电网络,对于接入配电网运行的分布式发电过网费计算仍存在局限性.文献[7]中提出按照用户接入电压等级、输电及电力消纳范围分级确定过网费.文献[8-9]中面向分布式交易双方,提出计及电气距离和占用电网资产的过网费核算方法.文献[10]中考虑光伏发电成本,建立适应光伏成本学习曲线的过网费机制.但文献[7⇓⇓-10]中的过网费核算方法多为静态统一定价形式,难以实现分布式发电、电网企业、电力用户等多方主体之间的利益均衡.为弥补上述研究不足之处,文献[11⇓⇓⇓-15]中提出动态过网费的相关核算方法.文献[11]中提出一种按用户边际贡献分摊过网费的方法.文献[12]中考虑配网分布式交易中电能传输的过网费成本,在不计及配网潮流约束的条件下,构建基于纳什谈判理论的多微电网交易合作博弈模型.文献[13]中构建基于零和博弈的动态过网费计算模型,提出实时滚动的配网安全校核方法,有效解决线路潮流越限和电压治理问题.文献[14]中构建配网运营商和多投资主体之间的协同规划决策模型,提出基于交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)的动态过网费更新方法.文献[15]中构建考虑过网费的混合整数规划模型,并采用改进的ADMM分布式算法进行求解,采取基于电能供需比的分摊策略实现利润的合理分配.
然而,在分布式能源市场中,少量且高频的电能交易容易造成线路阻塞和节点电压波动异常,威胁配网安全稳定运行,上述研究中的过网费核算方法大多未考虑线路阻塞和电压不稳定对网络安全的影响.此外,应结合分布式发电市场不同交易模式的特征具体分析过网费,提出与之相对应的过网费核算准则.因此,本文基于上述过网费计算方法研究和《通知》中过网费核算标准的不足,对分布式发电市场化交易的过网费计算方法进行补充和完善.立足于产消者时代下分布式发电市场交易模式的多样性特征,围绕产消者与网络拓扑深度融合路径,以最优潮流模型的对偶乘子为信息域、配网网络架构为物理域、产消者为社会域,分别构建不同交易模式的信息-物理-社会相耦合的过网费计算模型,利用夏普利值法公平合理分摊过网费.首先,面向分布式发电市场中的产消者,分别建立点对点(Peer-to-Peer, P2P)交易模式和社区(Community-Based,CB)交易模式的电能交易模型,实现产消者之间电能交易匹配.其中,CB交易模型基于分解协调思想,按产消者交易偏好划分社区,并引入第三方代理协调社区电能交易,既满足产消者利益最大化诉求又能使系统整体内部稳定、高效运行.然后,建立配网最优潮流模型描述网络潮流分布情况,同时将配网节点电价(Distribution Locational Marginal Price, DLMP)表达为模型对偶乘子的一般函数形式.利用DLMP的传递性特征,耦合最优潮流模型和P2P、CB电能交易模型分别建立不同交易模式过网费计算模型,并采用夏普利值法将过网费公平分摊至用户节点.最后,在改进的IEEE15和IEEE123节点系统上验证提出的适应分布式发电市场化交易的过网费计算方法的合理性和可行性.
1 分布式发电市场电能交易模式
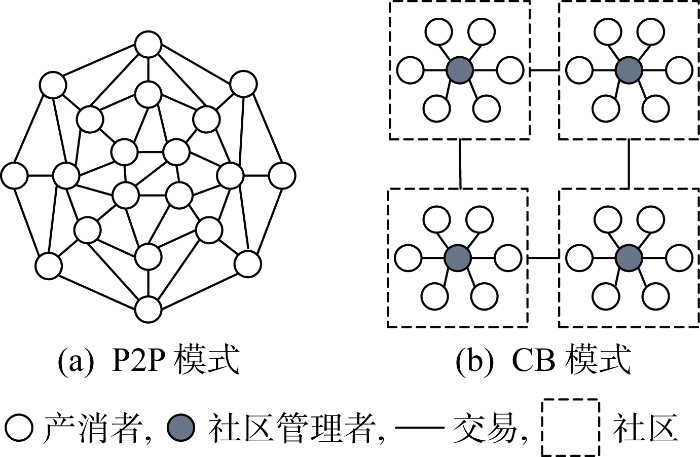
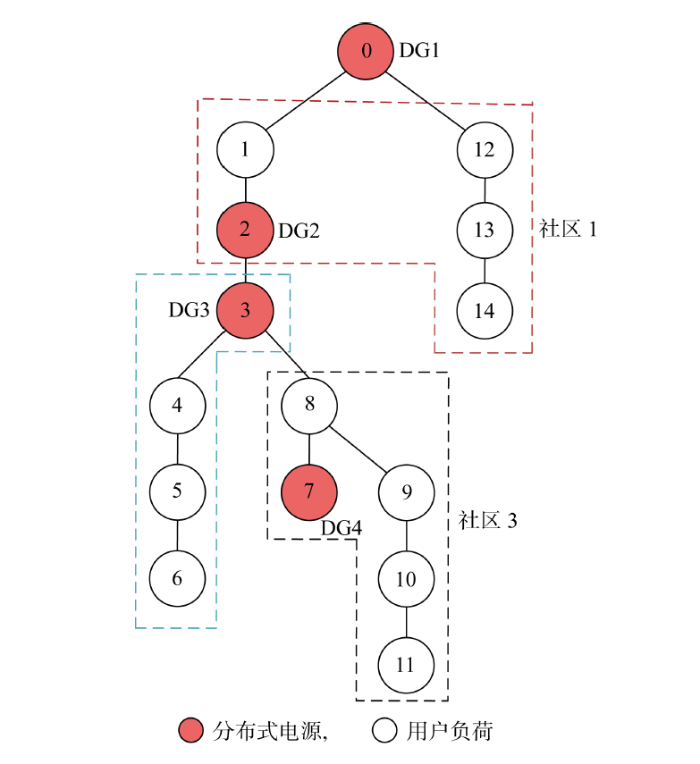
随着配电网中出现大量产消者,传统的电力市场结构正在经历巨大转变,呈现逐步从集中化到弱中心化再到去中心化的演变.Parag等[16]从技术经济角度阐述了一种产消者时代电力网络演化路径,明确了未来潜在的电力市场交易模式,以满足社会利益最大化、福利损失最小化的市场诉求.基于该路径下的电力市场交易模式,以拥有分布式发/用电设备的产消者与公共电网为研究对象,以P2P模式和CB模式为典型交易模式,阐述分布式发电市场去中心化和弱中心化两种电能交易模式.
图1
2 过网费计算模型
2.1 分布式发电市场电能交易模型
2.1.1 P2P模式电能交易模型
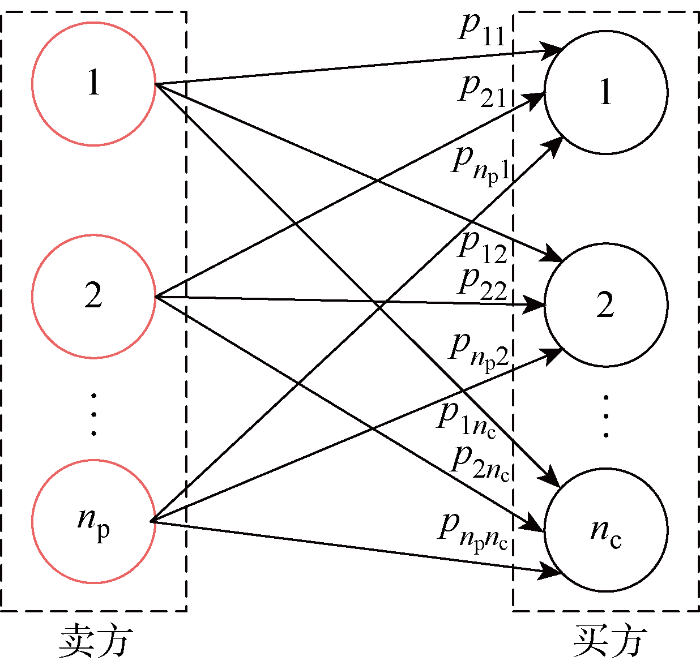
P2P模式电能交易如图2所示.为了简化建模,将分布式发电市场中的产消者根据自身电能的供需情况分别描述为卖方与买方,并用i、 j表示,其中i∈Ωp={1, 2, …, np},j∈Ωc={1, 2, …, nc},Ωp、Ωc分别为卖方集合和买方集合.产消者以集合Ω表示,其中 Ω=Ωp∪Ωc,Ωp∩Ωc =⌀.由于P2P电能交易模型包含np个卖方和nc个买方,所以可用供需矩阵
式中:pij为买方j从卖方i购买的电能数量.买方j购买的电能总量可表示为
卖方i出售的电能总量可表示为
图2
将P2P模式电能交易模型描述为社会福利最大化的优化问题:
式中:ΞP2P={gi,dj,pij}为决策变量集合,且该集合中的任一元素不小于0;Uj和Ci分别为买方j效用函数和卖方i成本函数;
其中,买方j效用函数和卖方i成本函数均用线性函数描述,分别表示为
式中:aj为买方j购买电能的满意度参数;bi为卖方i的单位发电成本.
2.1.2 CB模式电能交易模型
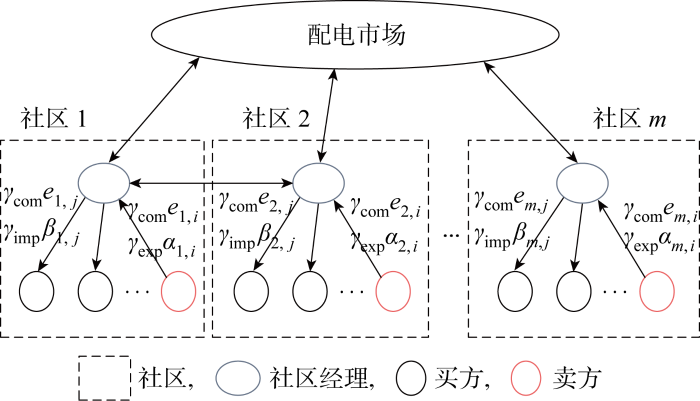
CB模式电能交易如图3所示.图中:γcom为买卖双方参与社区内电能交易的单位成本;γimp和γexp分别为买方和卖方参与社区外电能交易的惩罚系数;em, i、αm, i分别为社区m卖方i向社区内部、外部出售的电能数量;em, j、βm, j分别为社区m买方j向社区内部、外部购买的电能数量.基于分解协调思想,在CB模式中,买卖双方可以根据自身偏好选择参与本社区内或者本社区外的电能交易,即通过调整γcom、γimp和γexp反映其交易偏好,进而划分社区组织范围.此外,该交易模式的电能匹配方式基于买卖双方反馈给CM的交易偏好,由CM负责匹配电能交易,发挥社区自治优势,实现个人理性与集体理性相统一.随后CM将匹配信息传送至上级电网,由上级电网完成调度,实现本地能源市场电能交易出清.其中,CM可被视为一个非盈利的本地数据共享中心[17]或者小型聚合商[18].
图3
同样,将CB模式电能交易模型描述为社会福利最大化的优化问题:
式中:ΞCB={gm, i,dm, j,em, i,em, j,αm, i,βm, j}为决策变量集合,且该集合中的任一元素不小于0;Um, j和Cm, i分别为社区m买方j效用函数和卖方i成本函数;Hm为社区管理者的交易函数;M为社区集合;gm, i为社区m卖方i出售的总电能数量;dm, j为社区m买方j购买的总电能数量;
式(10)为该模型目标函数,即最大化社会福利;式(11)、(12)分别为社区m卖方i出售、买方j购买的电能数量;式(13)、(14)分别为社区管理者统一匹配社区m卖方i、买方j与本社区外部主体的电能交易;式(15)为社区管理者统一匹配社区m卖方i、买方j与本社区内部主体的电能交易;式(16)为CB模式的电能平衡约束.
其中,买方j效用函数为
卖方i成本函数为
社区管理者的交易函数[19]为
式中:κm, j为买方j满意度参数;πm, i为卖方i的单位发电成本.
2.2 两种交易模式下过网费模型
2.2.1 网络模型
考虑辐射型配电网络(N,L)的节点集合和支路集合分别为N和L,其中节点集合N由平衡节点{0}和其余节点集合N+={1, 2, …, |N|}构成,每个节点均包含一个父节点和一组子节点,分别用An和集合Cn表示.由于配电网络是辐射型网络,支路集合L可用N+进行索引.通过建立配电网络模型即最优潮流模型,一方面可以获得各支路上的潮流分布,分析电网资产的利用情况;另一方面从经济学角度而言,配网最优潮流模型的对偶乘子反映对应稀缺资源的内在价值,可以作为有效的价格信号引导资源合理分配.基于此,利用模型中价格信号的传递性,耦合最优潮流模型和电能交易模型获得对偶乘子,用于过网费计算及分摊.首先,将文献[20]中基于二阶锥规划的配网交流最优潮流模型作为网络模型,表示如下:
式中:ΞDist={
根据配网最优潮流模型式(22)~(33),利用卡罗需-库恩-塔克条件推导出DLMP的计算公式如下[20]:
式中:A1~A5为非线性函数,其详细计算方法见附录A.
2.2.2 P2P模式过网费模型
为充分体现P2P模式电能交易对DLMP的影响,对式(23)做出相应修改,实现P2P模式电能交易模型式(4)~(9)和网络模型式(22)~(33)相互耦合,确保DLMP能够准确反映电能交易的价格信号,修改后的约束条件如下:
P2P模式过网费计算模型如下:
求解模型式(36)~(38),将优化结果代入式(34),可得各节点DLMP,利用式(39)计算P2P模式的过网费:
式中:
依据经济学“谁受益谁承担”原则核算P2P模式电能交易产生的过网费,则过网费用由买方承担[11].
买方消费者剩余函数为
卖方生产者剩余函数为
2.2.3 CB模式过网费模型
与P2P模式相比,CB模式引入CM角色,在充分考虑社区自组织性的基础上,不仅简化电能交易过程的复杂度,同时还降低过网费的计算量.为了体现CB模式电能交易对DLMP的影响,对约束式(23)做出调整,使CB模式电能交易模型式(10)~(18)和网络模型式(22)~(33)相互耦合,修改后的约束条件如下:
CB模式过网费计算模型如下:
求解模型式(43)~(45),将得到的优化结果代入式(39),可得各节点DLMP.由于社区属于弱中心化交易的自组织形态,电能交易均由CM进行代理匹配,所以可将社区组织等效为相对较大的节点,进而简化过网费的计算流程,体现分解协调方法的高效.以平均售、购电价确定社区卖方、买方主体的DLMP,其中买方主体DLMP表示为
式中:
卖方主体DLMP表示为
式中:
根据下式计算社区m交易所产生的总过网费,即
式中:(ωm,b-ωm,s)
3 过网费分摊方法
目前我国分布式发电市场过网费分摊一般按用户接入电压等级和输电及电力消纳范围分级确定[2],但这种分摊方式忽略了分布式发电接入位置等要素对电网资产的影响,难以有效激励分布式发电和负荷有序接入电网,造成资源不合理配置.因此,如何公平合理地分摊过网费需要进一步研究.在上述两种交易模式的过网费计算模型中,P2P模式的过网费模型基于供需双方DLMP差值计算各个买方所支付的过网费,实现了过网费的直接分摊.而由于建模机理不同,CB模式过网费计算模型按照卖方、买方的平均售、购电价格,计算社区之间及社区自身的总过网费.但CB模式的总过网费无法精确分摊至社区内部的用户节点,导致过网费的激励效应丧失,不能实现资源合理配置.因此,需要进一步优化社区过网费的分摊机制,以激励产消者合理配置资源来实现自身利益最大化.
因此,采用夏普利值法将社区过网费分摊至社区内买方,社区中第t个买方应承担的过网费计算如下:
式中:对于由Nt个买方构成的社区,t为第t个买方;Qt为社区中买方构成的子联盟;Nt\{t}为社区中不包含买方t的所有子联盟;|Qt|为联盟Qt中买方数量;c(Qt∪{t})-c(Qt)表示买方t并入子联盟Qt所产生的过网费,c(Qt)表示子联盟Qt进行电能交易产生的过网费.
4 算例分析
基于改进的IEEE15、IEEE123节点测试系统,利用MATLAB软件进行模拟仿真,调用基于Yamip工具箱的IPOPT求解器求解建立的优化模型,验证所提出分布式发电市场化交易过网费计算方法的有效性.计算机环境配置为因特尔双核i5-6300HQ CPU 2.30 GHz、8 GB内存,操作系统为Windows 1 064 bit.
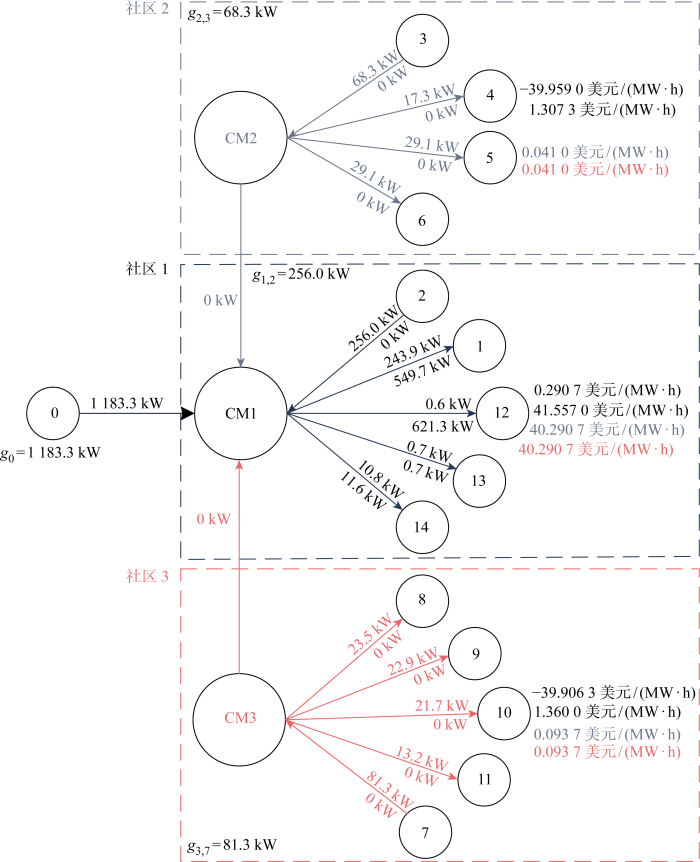
4.1 算例1:改进的IEEE15节点测试算例
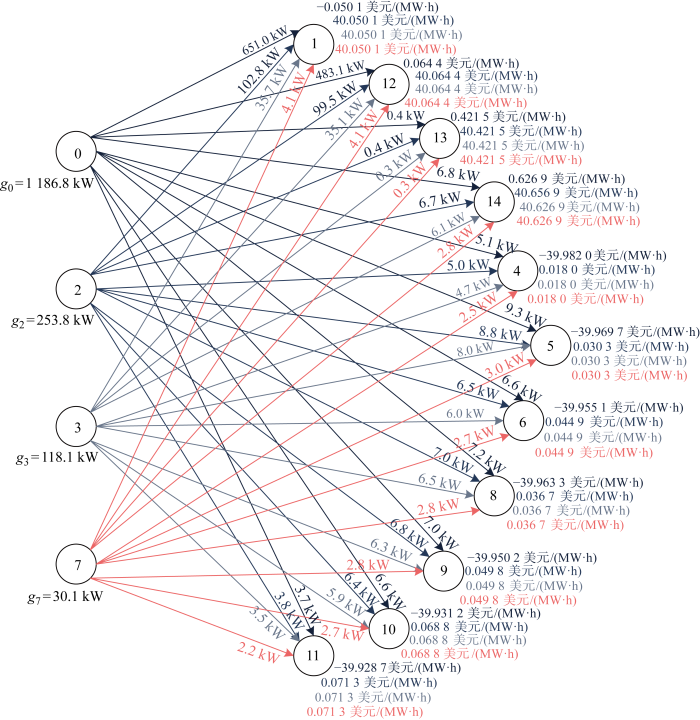
0.651 0 MW×0.050 1 美元/(MW·h)+0.102 8 MW×40.0501 美元/(MW·h)+0.0357 MW×40.0501 美元/(MW·h)+0.0041 MW×40.0501 美元/(MW·h)=5.743 8 美元.
图4
值得注意的是,有些买方支付的过网费为负值,如买方4支付的过网费为 -0.203 6 美元.这是由于在配网中存在双向潮流现象,买方通过向卖方购买电能,在一定程度上缓解了线路阻塞,电网公司对该买方给予相应补贴,则过网费为负值.
图5
表1 基于Shapley值的CB模式过网费分摊结果
Tab.1
| 社区编号 | 买方编号 | ϕt/美元 |
|---|---|---|
| 1 | 1 | 4.6746 |
| 1 | 12 | 0.1029 |
| 1 | 13 | 0.0240 |
| 1 | 14 | 0.1766 |
| 2 | 4 | 0.0004 |
| 2 | 5 | 0.0013 |
| 2 | 6 | 0.0014 |
| 3 | 8 | 0.0020 |
| 3 | 9 | 0.0023 |
| 3 | 10 | 0.0026 |
| 3 | 11 | 0.0015 |
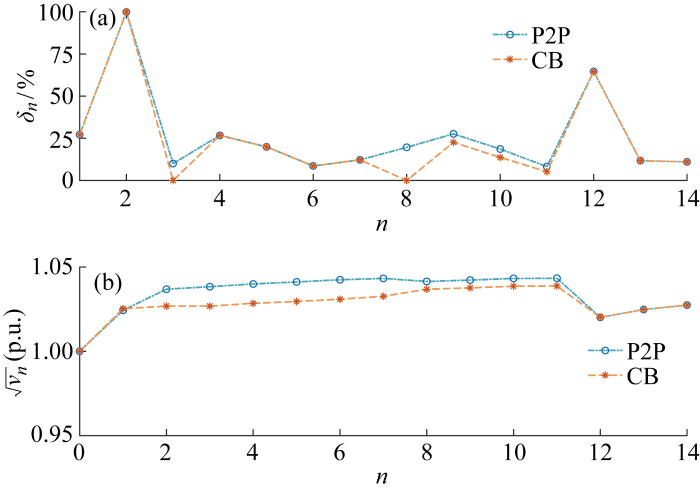
图6比较了P2P和CB模式电能交易中的线路负载率(δn)和节点电压幅值(
图6
图6
不同交易模式下线路负载率和节点电压幅值对比
Fig.6
Comparison of line loading ratio and nodal voltage magnitude of different trading models
由上述分析可得,CB模式下用户对电网资产的使用程度低于P2P模式,同时CB模式能够更好地缓解电各节点电压幅值分布情况,维持电网安全稳定运行.表2展示了两种交易模式下的产消者福利.首先,从生产者收益及消费者支付两个角度可以看出,CB模式产消者的电能交易福利要优于P2P模式.其次,从过网费计算结果看,P2P模式、CB模式下电能交易产生的过网费分别为 10.199 7 美元、4.989 6 美元,准确地反映出用户对电网资产的利用情况.
表2 不同交易模式下的产消者福利
Tab.2
| 交易模式 | 生产者收益/美元 | 消费者支付/美元 | 过网费/美元 |
|---|---|---|---|
| P2P | 73.5621 | 83.7618 | 10.1997 |
| CB | 76.1426 | 81.1322 | 4.9896 |
4.2 算例2:改进的IEEE123节点测试算例
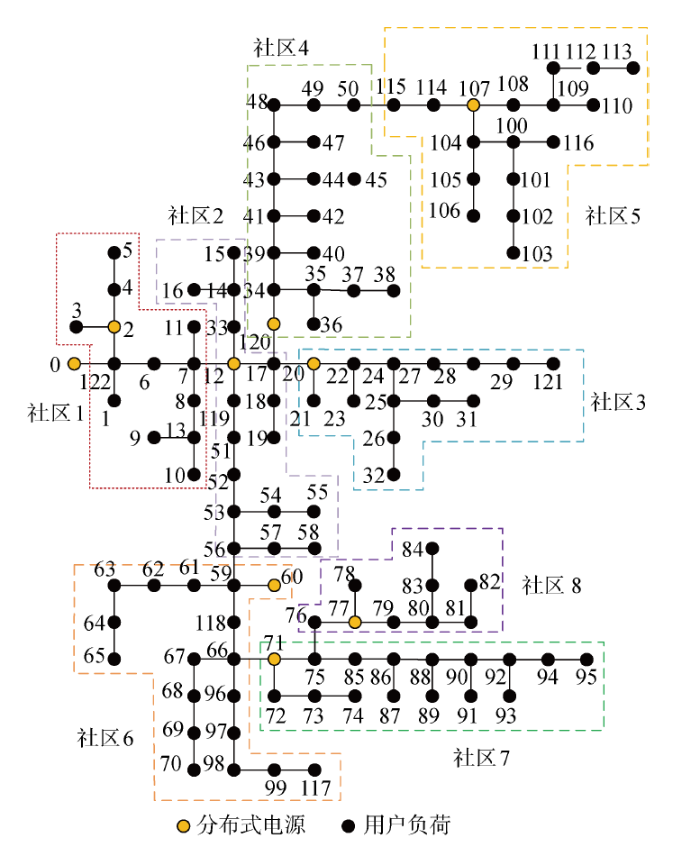
为进一步验证本文提出的适应分布式发电市场化的过网费计算方法在大系统中的适用性及有效性,采用与实际复杂配电网应用场景相接近的IEEE123节点测试系统进行仿真分析,改进后的IEEE123节点测试系统的拓扑图如附录图C1所示,相关的参数设置如附录表C1所示.
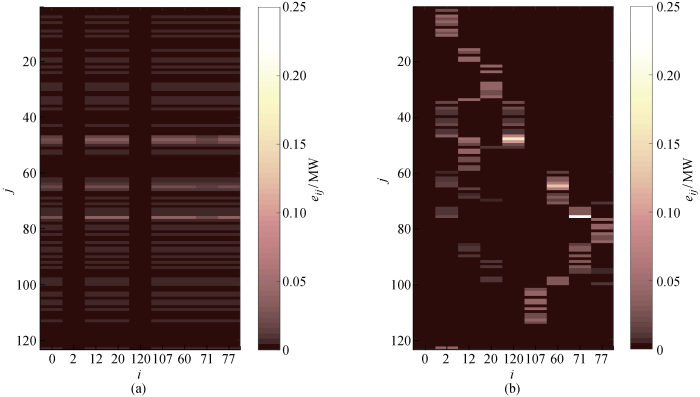
图7
图7
分布式发电市场中不同模式的电能交易结果
Fig.7
Results of power trading in different modes in DG market
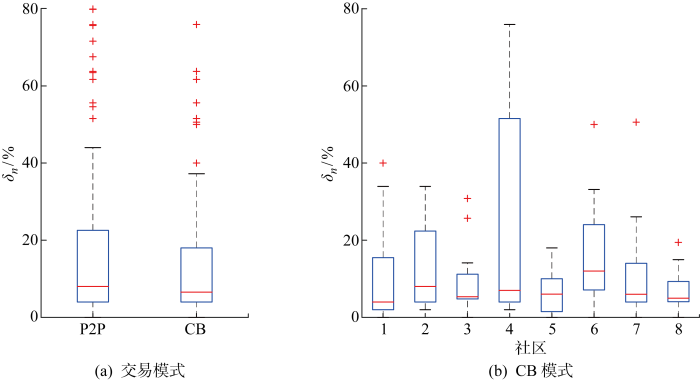
图8
图8
分布式发电市场不同交易模式线路负载率对比
Fig.8
Comparison of line loading ratio between different trading models in DG market
图9
图9
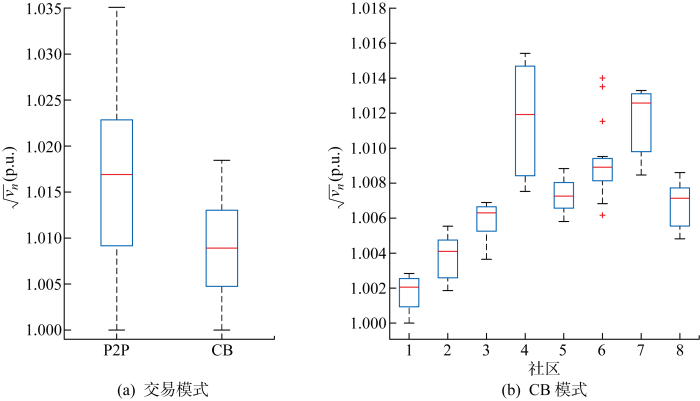
分布式发电市场不同交易模式节点电压幅值对比
Fig.9
Comparison of nodal voltage magnitudes between different trading models in DG market
综上所述,基于电能交易情况、线路负载率和电压幅值三要素,比较P2P模式与CB模式电能交易在电网资产利用度和维护电网稳定运行两方面的差异,验证过网费计算结果的合理性.从过网费计算结果看,P2P模式、CB模式的过网费分别为81.597 6、34.927 2 美元,符合上述对不同模式电网资产使用度的分析,即P2P模式线路负载率高于CB模式线路负载率;其中CB模式下,社区1~8的过网费分别为 4.701 4、4.618 5、3.162 5、5.382 4、3.485 3、5.082 1、5.607 9、2.887 1 美元.由于社区4、社区6、社区7电能交易数量及线路负载率都处于较高水平,所以支付的过网费较高.
5 结论
面向配电网环境下的分布式发电市场,构建去中心和弱中心化两种电能交易模式的数学模型.考虑各交易模式的特性及建模机理,提出基于DLMP的过网费计算方法;同时针对CB模式,应用夏普利值法对其过网费进行合理分摊.采用改进的IEEE15节点和IEEE123节点测试系统验证本文所提过网费计算方法的适用性和可行性,主要结论如下:
(1) 从电能交易的分布看,与具有分散性电能交易特征的P2P模式相比,CB模式下的电能交易具有相对集中性,即基本在社区内完成交易匹配,不需向上级电网或其他社区购电,一定程度上实现电能就近交易,提高系统整体运行效率.
(2) 从电网架构的利用率看,CB模式的线路负载率和电压幅值波动水平均低于P2P模式,从而反映出CB模式下产消者的电网资产使用度以及进行电能交易产生的网损相对较低.
(3) 从过网费计算结果看,P2P模式过网费一般高于CB模式.其中P2P模式部分产消者过网费可能为负值,这是由于买方通过从价格较高的卖方购电缓解了线路阻塞,电网公司对其进行相应的补贴.相反,若买方从价格较低的卖方购电造成线路阻塞则需向电网公司支付较高过网费.
附录见本刊网络版(
附录
附录A
附录B
图B1
表B1 IEEE15 节点测试系统参数设置
Tab.B1
| 节点 | R | X | S | B | pc/kW | qc/kvar | π /[美元· (MW·h)-1] | γcom /[美元· (MW·h)-1] | γimp /[美元· (MW·h)-1] | γexp /[美元· (MW·h)-1] |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 50 | |||||||||
| 1 | 0.0010 | 0.1200 | 2.000 | 0.0011 | 793.6 | 185.5 | 0.2000 | 1.0 | ||
| 2 | 0.0833 | 0.1262 | 0.256 | 0.0028 | 0.0000 | 0.0000 | 10 | 0.1809 | 0.90 | |
| 3 | 0.1384 | 0.1978 | 0.256 | 0.0024 | 0.0000 | 0.0000 | 10 | 0.9045 | 0.90 | |
| 4 | 0.0191 | 0.0273 | 0.256 | 0.0004 | 17.3 | 4.3 | 0.2000 | 1.0 | ||
| 5 | 0.0175 | 0.0251 | 0.256 | 0.0008 | 29.1 | 7.3 | 0.2000 | 1.0 | ||
| 6 | 0.0482 | 0.0689 | 0.256 | 0.0006 | 21.9 | 5.5 | 0.2000 | 1.0 | ||
| 7 | 0.0523 | 0.0747 | 0.256 | 0.0006 | 0.0000 | 0.0000 | 10 | 0.9045 | 0.95 | |
| 8 | 0.0407 | 0.0582 | 0.256 | 0.0012 | 23.5 | 5.9 | 0.2000 | 1.1 | ||
| 9 | 0.0100 | 0.0143 | 0.256 | 0.0004 | 22.9 | 14.2 | 0.2000 | 1.1 | ||
| 10 | 0.0241 | 0.0345 | 0.256 | 0.0004 | 21.7 | 6.5 | 0.2000 | 1.1 | ||
| 11 | 0.0103 | 0.0148 | 0.256 | 0.0001 | 13.2 | 3.3 | 0.2000 | 1.1 | ||
| 12 | 0.0010 | 0.1200 | 1.000 | 0.0001 | 621.9 | 129.1 | 0.2000 | 1.0 | ||
| 13 | 0.1559 | 0.1119 | 0.204 | 0.0002 | 1.4 | 0.8 | 0.2000 | 1.0 | ||
| 14 | 0.0953 | 0.0684 | 0.204 | 0.0001 | 22.4 | 8.3 | 0.2000 | 1.0 |
注:R为线路的电阻;X为线路的电抗;S为线路的视在功率;B为线路的电纳;pc为消费者的有功负荷;qc为消费者的无功负荷;π为生产者的单位发电成本;空白项表示不适用.
附录C
图C1
表C1 IEEE123 节点测试系统参数设置
Tab.C1
| 卖方编号 | 边际成本/ [美元·(MW·h)-1] | 设备容量/MW |
|---|---|---|
| 0 | 20 | 0.8 |
| 2 | 10 | 0.5 |
| 12 | 10 | 0.5 |
| 20 | 9 | 0.5 |
| 60 | 11 | 0.5 |
| 71 | 10 | 0.5 |
| 77 | 9 | 0.5 |
| 107 | 10 | 0.5 |
| 120 | 11 | 0.5 |
参考文献
面向高比例可再生能源的电力市场研究综述
[J].
Review on electricity market towards high proportion of renewable energy
[J].
关于开展分布式发电市场化交易试点的通知
[EB/OL]. (
Notice on piloting market-based distributed generation trading
[EB/OL]. (
Toward regional transmission provision and its pricing in New England
[J].DOI:10.1016/S0957-1787(97)00020-9 URL [本文引用: 1]
Review of usage-based transmission cost allocation methods under open access
[J].
Cost of wheeling methodologies
[J].DOI:10.1109/59.317547 URL [本文引用: 1]
Contributions of individual generators to loads and flows
[J].DOI:10.1109/59.574923 URL [本文引用: 1]
基于区块链的分布式电力交易机制
[J].
DOI:10.3969/j.issn.1000-7229.2019.12.001
[本文引用: 2]

随着光伏(photovoltaic,PV)发电的大力发展和上网补贴的逐步下调,就近消纳的优势得以显现,这促进了分布式发电的市场化交易 (market trading for distributed generation, MTDG)。MTDG的发、用电双方都在电网末端,具有参与主体数量大、单笔交易规模小、点对点等特点。传统的中心化交易模式存在透明度低、成本高、效率低下、数据不可信等问题,不适合MTDG。区块链技术具有去中心化、不可篡改、匿名等特点,满足MTDG的需要,能够提升这种交易的安全性、自主性、透明性等。在此背景下,文章将区块链技术引入MTDG,针对MTDG的特点,构建了相应的交易机制、结算机制和奖惩机制。最后,采用算例对所发展的MTDG机制进行了说明。
A blockchain based distributed power trading mechanism
[J].
DOI:10.3969/j.issn.1000-7229.2019.12.001
[本文引用: 2]

With the rapid development of photovoltaic (PV) power generation and the gradual downward subsidies, the advantages of satisfying load demand by local generation supply are becoming more and more significant, and market trading for distributed generation (MTDG) is then promoted. In MTDG, both power generation and load demand are located at the end of the utility grid, with some features exhibited including numerous participating entities, small transaction sizes, and point-to-point transactions. The traditional centralized transaction model suffers some problems such as low transparency, high cost, low efficiency, and untrustworthy data, and is not suitable for MTDG. Blockchain technology has the characteristics of decentralization, non-tampering, and anonymity, and can well meet the needs of MTDG for improved security, autonomy and transparency of electricity transactions. Given this background, the blockchain technology is applied in MTDG, and the corresponding trading mechanism, settlement mechanism and reward and punishment mechanism are developed considering the characteristics of MTDG. Finally, an example is employed to demonstrate the developed MTDG mechanism.
Peer-to-peer energy trading in transactive markets considering physical network constraints
[J].DOI:10.1109/TSG.2021.3063960 URL [本文引用: 2]
Peer-to-peer energy trading in smart grid considering power losses and network fees
[J].DOI:10.1109/TSG.5165411 URL [本文引用: 2]
适应光伏学习曲线的分布式交易过网费机制
[J].
Probe into mechanism of use of system charge in distributed trading adapted to photovoltaic learning curve
[J].
Designing efficient distribution network charges in the context of active customers
[J].DOI:10.1016/j.apenergy.2017.08.103 URL [本文引用: 3]
配电侧多微电网日前电能交易纳什议价方法
[J].
Nash bargaining method for multi-microgrid energy trading in distribution network
[J].
多售电主体点对点交易模式及其动态过网费机制
[J].
Peer-to-peer transaction model of multiple power sellers and its dynamic network fee mechanism
[J].
基于过网费动态更新的分布式电源多主体协同规划方法
[J].
Multi-agent collaborative planning method for distributed generators based on dynamic updating of network tariffs
[J].
Multi-level trading community formation and hybrid trading network construction in local energy market
[J].DOI:10.1016/j.apenergy.2020.116399 URL [本文引用: 2]
Electricity market design for the prosumer era
[J].DOI:10.1038/nenergy.2016.32 [本文引用: 1]
Distributed market clearing approach for local energy trading in transactive market
[C]//
Designing decentralized markets for distribution system flexibility
[J].DOI:10.1109/TPWRS.59 URL [本文引用: 1]
Energy collectives: A community and fairness based approach to future electricity markets
[J].DOI:10.1109/TPWRS.59 URL [本文引用: 1]
Analysis of distribution locational marginal prices
[J].DOI:10.1109/TSG.5165411 URL [本文引用: 2]
基于夏普利值的中压配电网扩建费用分摊方法
[J].
Distribution system expansion cost allocation based on shapley value
[J].
An aumann-shapley approach to allocate transmission service cost among network users in electricity markets
[J].DOI:10.1109/TPWRS.2007.907133 URL [本文引用: 1]
Transmission network cost allocation based on circuit theory and the aumann-shapley method
[J].DOI:10.1109/TPWRS.2013.2278296 URL [本文引用: 1]
Complex losses allocation to generators and loads based on circuit theory and aumann-shapley method
[J].DOI:10.1109/TPWRS.2010.2044425 URL [本文引用: 1]
Shapley game for expansion planning of generating companies at many non-coincident criteria
[J].DOI:10.1109/TPWRS.2006.873053 URL [本文引用: 1]