基于改进TOPSIS的楼宇多指标综合评价

doi:10.16183/j.cnki.jsjtu.2022.117

基于改进TOPSIS的楼宇多指标综合评价

蒋毅¹, 傅俊诚², 李泽文², 张雨青³, 尹骏刚^,⁴, 姚建刚⁴

1.国网湖南省电力有限公司,长沙 410004

2.长沙理工大学电气与信息工程学院,长沙 410114

3.三峡大学电气与新能源学院,湖北宜昌 443002

4.湖南大学电气与信息工程学院,长沙 410082

A Comprehensive Evaluation Model of Buildings Based on Improved TOPSIS

JIANG Yi¹, FU Juncheng², LI Zewen², ZHANG Yuqing³, YIN Jungang^,⁴, YAO Jiangang⁴

1. State Grid Hunan Electric Power Co., Ltd., Changsha 410004, China

2. School of Electrical and Information Engineering, Changsha University of Science and Technology, Changsha 410114, China

3. College of Electrical Engineering and New Energy,China Three Gorges University, Yichang 443002, Hubei, China

4. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China

通讯作者: 尹骏刚,研究员;E-mail:yinjungang126@126.com.

责任编辑: 王历历

收稿日期: 2022-04-18 修回日期: 2023-01-18 接受日期: 2023-02-24

基金资助:

国家自然科学基金(51877012)

Received: 2022-04-18 Revised: 2023-01-18 Accepted: 2023-02-24

作者简介 About authors

蒋毅(1971-),硕士,从事综合能源系统能效优化与治理研究.

摘要

为综合评价大型办公楼宇在能耗、环保、经济性等方面的运行情况,提出基于改进灰色关联逼近理想解排序法(TOPSIS)的多指标综合评价模型.在对楼宇运行实际情况分析的基础上,构建包含楼宇运行能耗、环境因素、经济性的多指标评价体系;引入改进TOPSIS评价方法,利用灰色关联度算法和层次分析法-熵权法确定TOPSIS评估模型距离测度;建立楼宇多属性加权评价模型,全面分析楼宇运行状况.分析8栋电力办公楼宇单元的多指标评价可知:楼宇综合评价结果随时间变化,能耗指标评分起主要作用;与采用其他评价方法的评价结果进行对比,验证了所提楼宇多指标评价模型的有效性.

关键词： 改进灰色关联逼近理想解排序法; 层次分析法; 熵权法; 灰色关联度算法; 办公楼宇

Abstract

In order to evaluate the operation of energy consumption, environmental protection, and economy, a multi-index comprehensive evaluation model based on an improved technique for order preference by similarity to ideal solution (TOPSIS) is proposed. Based on the analysis of building operation, a multi-index evaluation system is constructed. Then, an improved TOPSIS evaluation method is introduced and a distance measure of the TOPSIS evaluation model by the gray correlation algorithm and analytic hierarchy process (AHP)-entropy weight method is determined. Next, a multi-attribute weighted evaluation model is established to analyze the building operation comprehensively. The multi-index evaluation of eight power office buildings indicates that the building comprehensive evaluation results vary with time and the energy consumption index score plays the main role in all indexes. A comparison of the evaluation results with those obtained by other evaluation methods verifies the effectiveness of the proposed building multi-index evaluation model.

Keywords： improved technique for order preference by similarity to ideal solution (TOPSIS); analytic hierarchy process (AHP); entropy weight method; gray correlation algorithm; office buildings

PDF (1198KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

蒋毅, 傅俊诚, 李泽文, 张雨青, 尹骏刚, 姚建刚. 基于改进TOPSIS的楼宇多指标综合评价[J]. 上海交通大学学报, 2023, 57(7): 868-877 doi:10.16183/j.cnki.jsjtu.2022.117

JIANG Yi, FU Juncheng, LI Zewen, ZHANG Yuqing, YIN Jungang, YAO Jiangang. A Comprehensive Evaluation Model of Buildings Based on Improved TOPSIS[J]. Journal of Shanghai Jiaotong University, 2023, 57(7): 868-877 doi:10.16183/j.cnki.jsjtu.2022.117

随着经济快速发展,能耗环保问题越来越受到重视,中国为此制定了一系列节能降耗与环境治理措施^[1].大型办公楼宇作为城市主要能源消耗单元,在能耗、环境和经济方面的影响不可忽视.综合考虑楼宇在能耗、环保、经济性等指标表现情况,对楼宇进行多指标量化评价^[2],全面掌握楼宇运行情况具有重要意义,可根据评价结果有目的地优化指标,如采用需求响应等手段实现楼宇绿色用能.

办公楼宇包含中央空调等大型能耗设备、运维设备和屋顶光伏设备等,为掌握楼宇运行情况,需对楼宇进行能耗、环保、经济等方面的多指标评价,进行横纵向对比分析.目前常用的多指标评价方法有超效率CCR模型法、层次分析法(Analytic Hierarchy Process, AHP)、灰色关联逼近理想解排序法(Technique for Order Preference by Similarity to Ideal Solution, TOPSIS)等^[3⇓-5].针对评价方法的应用,国内外学者进行了大量探索实践,文献[6]中采用交叉超效率CCR模型,构造包含经济、可靠、环保、能耗4方面的综合能源系统评价体系,分析夏冬季的综合效率,指导配置能源装机容量.文献[7]中采用熵权法对AHP进行修正,应用于分布式能源系统的综合评价研究,对6个指标进行评价,数据信息利用率较高.文献[8]中采用AHP并基于专家打分方式确定权值,建立包含设备和用户的指标体系,实现对综合能源系统的评价.文献[9]中采用改进灰色TOPSIS方法对园区进行能效评估,采用熵权法确定能效指标权值,从压力、状态、响应3个维度分析园区能效.文献[10]中采用AHP法,综合考虑投资、运维、环保、能耗4方面指标,提出一种多准则决策模型,对综合能源系统进行综合评价.分析上述方法发现,AHP和TOPSIS法主观性较强^[11⇓-13],未能充分利用指标数据信息;超效率CCR模型法计算权值时能够使有效单元效率进行大小比较,但存在各决策评价标准不一致的缺陷.

上述评价方法多用于电力系统评价,而针对大型办公楼宇进行综合评价的方法较少,缺少完整的评价流程.随着智能楼宇概念的提出,楼宇评估研究成为一大热点.文献[14]中基于K-均值聚类和频繁模式增长算法关联规则,建立了电力能耗分析模型,但未考虑投资、环境等指标.文献[15]中基于楼宇中央空调电能消耗数据, 提出一种基于信息熵分段聚合近似和谱聚类的楼宇负荷分类评估方法.文献[16]中采用灰色关联和AHP,以多个目标构建工厂评估模型,但存在主观性强的缺陷.

本文全面分析大型办公楼宇运行特点,考虑实际生产需求,建立包含能耗、环保、经济3方面的楼宇综合评价体系以及一套完整的评价流程.基于TOPSIS法,使用AHP-熵权法确定评价指标权值,主客观相结合弥补单一方法赋权的不足,使用灰色加权的关联度代替欧氏距离测度,弥补传统欧氏距离评价不足,建立基于改进TOPSIS的办公楼宇多指标综合评价模型.以该模型对某省8栋电力办公大楼进行多指标评价,并与其他评价方法对比,验证所提评价模型有效性.

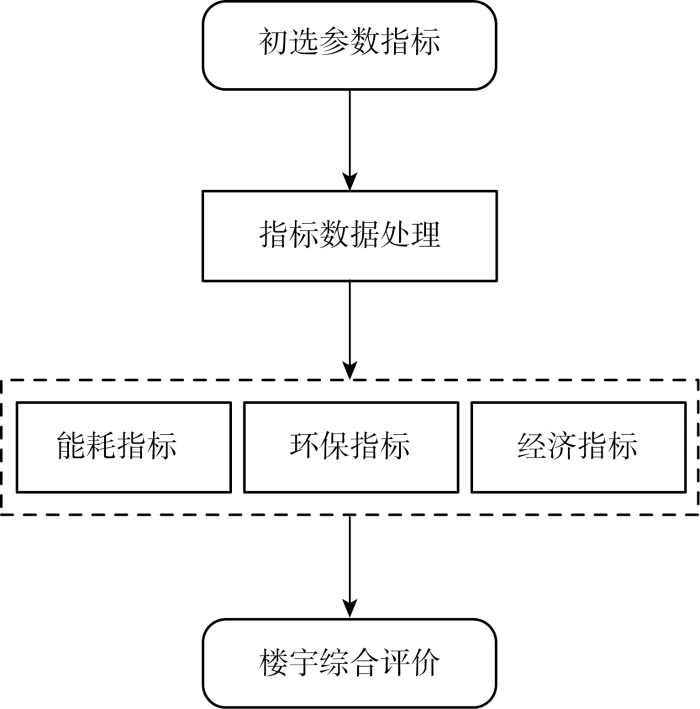
1 办公楼宇多指标评价流程

新建大型电力办公楼宇多采取“电网供电+可再生能源”的供电方式.利用楼宇屋顶、空余场地安装光伏、储能等新能源及相关设备,将可再生能源转化为电能供给楼宇^[17],能有效降低电网负荷、减少环境污染.因此,为综合评价楼宇运行状态,制定如图1所示评价路线.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 楼宇系统综合评价流程

Fig.1 Flow chart of building system evaluation

初选指标尽可能考虑楼宇多维度参数指标^[18-19];对初步指标数据进行数据预处理,包括指标数据归一化、无量纲化处理;再通过主成分分析法(Principal Component Analysis, PCA)和相关系数矩阵筛选得到最终的评价指标,并基于改进TOPSIS的评价模型进行评价.

2 办公楼宇多评价指标选取

2.1 多评价指标选取

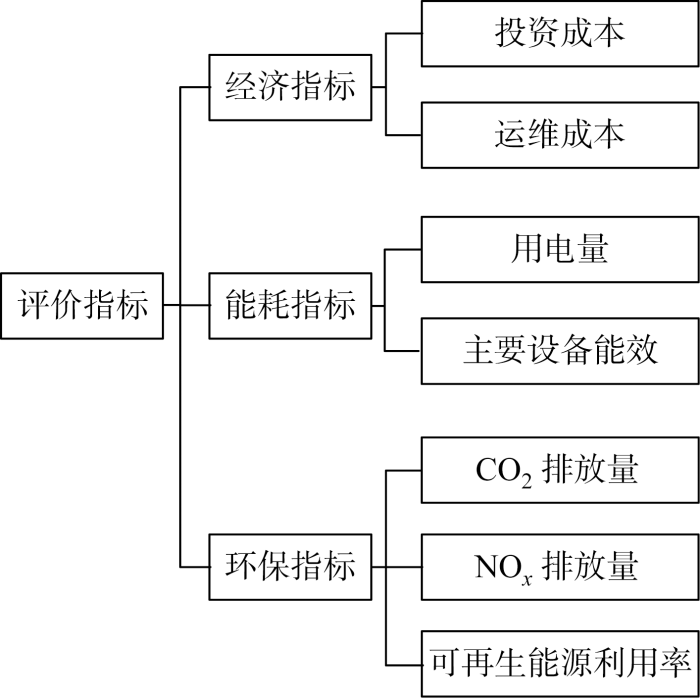
对电力办公大楼进行实地调研,查找主要关心问题,并结合相关文献内容,按照实用性和可操作性以及科学性与系统性要求初取评价指标,构建得到如表1所示的楼宇多评价指标体系.

表1 楼宇多指标评价体系

Tab.1 Multi-index evaluation system of buildings

指标		编号	指标类型
一级	二级	编号	指标类型
E₁	投资成本	E₁₁	成本型
E₁	运维成本	E₁₂	成本型
E₁	购能成本	E₁₃	成本型
E₂	用电量	E₂₁	成本型
E₂	主要设备能效	E₂₂	效益型
E₃	CO₂年排放量	E₃₁	成本型
E₃	NO_x年排放量	E₃₂	成本型
E₃	可再生能源利用率	E₃₃	效益型

新窗口打开| 下载CSV

表1中办公楼宇多指标评价体系包含经济、能耗、环保3个一级指标.经济一级指标E₁包含办公楼宇的投资成本、运维成本和购能成本;能耗一级指标E₂包含办公楼宇年用电量、月用电量和主要设备能效;环保一级指标E₃包含CO₂年排放量、NO_x年排放量和可再生能源利用率.二级指标中包含6个成本型指标,2个效益型指标.楼宇投资成本包括楼宇系统设备的投资费用、新加设备费用;运维成本包含楼宇设备维护、折旧费用;购能成本包括电能费用、化石能源购买费用;用电量指楼宇所有耗电设备评价周期内总电能使用量;主要设备能效指楼宇大型耗电设备中央空调等能效比值,即设备输出能量与所消耗能量的比值;CO₂年排放量指一年内等效计算下从楼宇排向大气的CO₂总量,包括电能使用折合的CO₂量、天然气燃烧、汽车尾气等;NO_x年排放量指一年内等效计算下从楼宇排向大气的NO_x总量,包括制冷剂排放等;可再生能源利用率指楼宇利用可再生能源转化为的电能与楼宇总耗电能的比值.

2.2 多评价指标筛选

初选能效指标必须包括楼宇评价的主要方面,且具有较强的代表性.为避免指标间存在较多的信息冗余和重复,需要对初选指标进行筛选.PCA和相关性分析是统计分析常用方法,主成分系数能够反映指标参数数据间的原始变量信息,相关性分析可判断指标间线性相关程度大小.

采用PCA计算得到的第一、第二主成分含有原始信息中大部分信息,据此计算第一、第二主成分系数并仅保留对应的重要变量,就能达到筛选初选指标的目的.进行相关性分析时计算各指标间相关系数,系数大小表明指标间的线性相关性大小,线性相关性较大说明两指标存在信息重复,结合PCA计算结果对其中一个指标进行删除.当相关性分析结果和PCA计算结果矛盾时,取PCA计算结果.当某个指标主成分系数较大,但同时和其他主成分的相关性也较大时,应保留该指标.PCA重构指标参数步骤如下所示.

(1) 求取标准化指标参数矩阵:

E'=

$[\begin{array}{l} E'_{11} & E'_{12} & \dots & E'_{1 m} \\ E'_{21} & E'_{22} & \dots & E'_{2 m} \\ \dots & \dots & \dots & \dots \\ E'_{i 1} & E'_{i 2} & \dots & E'_{i m} \end{array}]$

(1)

式中:E'_im为指标参数数据标准化处理后指标值;i为评价楼宇单元数;m为评价指标数.

(2) 计算指标参数矩阵协方差矩阵:

M_C=

$[\begin{array}{l} C'_{11} & C'_{12} & \dots & C'_{1 m} \\ C'_{21} & C'_{22} & \dots & C'_{2 m} \\ \dots & \dots & \dots & \dots \\ C'_{m 1} & C'_{m 2} & \dots & C'_{m m} \end{array}]$

(2)

C'_xy=cov(E'(:; x), E'(:; y)), x,y=1,2,…,m

(3)

式(2)中每个矩阵元素数值为式(1)中对应两指标数据集合的协方差值,据此可知矩阵M_C为对称阵.

(3) 计算主成分分析矩阵A.

|M_C-λI|=0

(4)

式中:λ为M_C的特征根;I为单位矩阵.

由式(4)求得i个特征根,将特征根数值由大到小依次排列,取前v个主成分进行分析.求取v个特征根对应的特征向量a_m=[a₁_m a₂_m … a_im]^T,构成主成分分析矩阵:

$[\begin{array}{l} a_{11} & a_{12} & \dots & a_{1 m} \\ a_{21} & a_{22} & \dots & a_{2 m} \\ \dots & \dots & \dots & \dots \\ a_{i 1} & a_{i 2} & \dots & a_{i m} \end{array}]$

(5)

(4) 计算楼宇多指标评估矩阵E.

对式(5)中矩阵元素数值大小进行分析比较,设定阈值,删除绝对值较小的指标,并结合相关性分析,剔除指标间相关性较大的指标,最终筛选得到楼宇多指标评估矩阵:

$[\begin{array}{l} E_{11} & E_{12} & \dots & E_{1 j} \\ E_{21} & E_{22} & \dots & E_{2 j} \\ \dots & \dots & \dots & \dots \\ E_{i 1} & E_{i 2} & \dots & E_{i j} \end{array}]$

(6)

式中:j为筛选后剩余的指标数.

3 基于改进TOPSIS楼宇多指标评价模型

3.1 多评价指标标准化

表1中选取的办公楼宇指标包含两种类型:成本型和效益型.成本型表示该指标数值越小,成本投入或环保表现越优秀,楼宇综合评分越高;效益型表示该指标数值越大,效率或资源利用率越高,楼宇评分越高.

为统一评价标准,均采用效益型指标.将成本型指标处理如下:

E'_ij=maxe'_j-e'_ij

(7)

式中:E'_ij为标准化后数据;e'_j为原指标数据集合;e'_ij为原指标数据.

效益型指标处理如下:

E'_ij=e'_ij

(8)

为消除量纲对数据计算的影响,将各指标数据进行无量纲化处理:

E'_ij=

$\frac{e'_{i j} - μ}{σ}$

(9)

式中:μ为e'的期望值;σ为e'的标准差.对各指标数据进行标准化处理即得到式(1)中各标准化指标参数矩阵E'.

3.2 多评价指标赋权

AHP采用专家打分的方式确定指标权值,有较强的主观性.熵权法根据熵值判断指标的变化程度,并确定其权值.对于指标参数而言,其提供的信息量对应该指标参数的“熵值”.若某项指标对应的熵值越小,则表明该指标变化程度越大,在进行能效评估时则需对应提高其权重.利用AHP-熵权法确定权值,能够避免单一主观或客观评分存在的弊端.

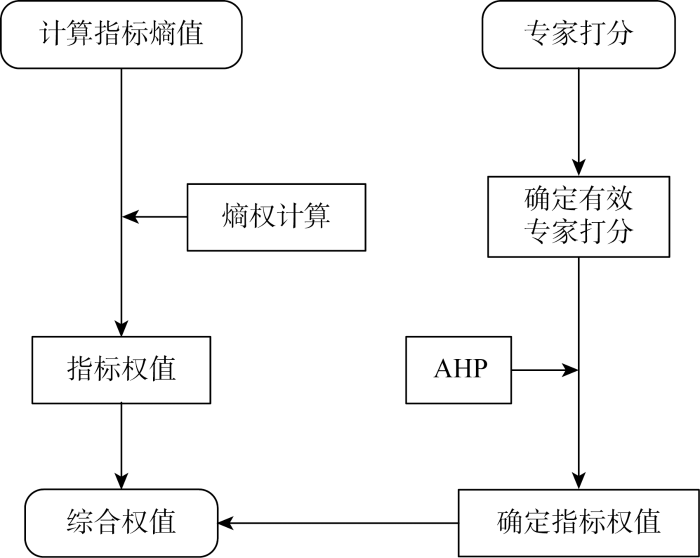
3.2.1 AHP赋权

AHP在确定各指标权值时采用一致性矩阵^[20],将各指标两两比较,对两两比较后的相对重要性进行量化,并将比较结果的量化值作为相对重要性矩阵中的各个元素.AHP-熵权法赋权流程如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 AHP-熵权法赋权流程

Fig.2 Procedure of AHP-entropy weight method

(1) 根据相对重要性确定各指标权值.

首先聘请专家打分,得到与该专家对应的相对重要性矩阵;求取重要性矩阵最大特征值及特征向量后,再进行一致性判断;满足一致性检验后,计算专家打分对应各指标权值,得到专家权值矩阵:

$[\begin{array}{l} z_{1} \\ z_{2} \\ ︙ \\ z_{n} \end{array}]$ =

$[\begin{array}{l} r_{11} & r_{12} & \dots & r_{1 j} \\ r_{21} & r_{22} & \dots & r_{2 j} \\ \dots & \dots & \dots & \dots \\ r_{n 1} & r_{n 2} & \dots & r_{n j} \end{array}]$

(10)

式中:z_n表示n位专家权重向量;r_nj表示第n位专家对j指标的权值.

(2) 淘汰权值偏离程度较大的专家打分.

首先计算相关系数矩阵各元素取值:

d_pq=1-

$\sqrt{\frac{1}{j} \overset{j}{\sum_{k = 1}} (r_{p k} - r_{q k})^{2}}$ , p,q=1,2,…,n

(11)

由式(11)可知,当p=q时满足d_pq=1,且d_ij=d_ji.d_pq构成相关系数矩阵:

$[\begin{array}{l} 1 & d_{12} & \dots & d_{1 n} \\ d_{21} & 1 & \dots & d_{2 n} \\ \dots & \dots & \dots & \dots \\ d_{n 1} & d_{n 2} & \dots & 1 \end{array}]$

(12)

根据矩阵D结合下式计算出每行元素之和,d_n即该专家打分与其他专家打分相似度之和:

d_n=

$\overset{j}{\sum_{q = 1}}$ d_nq

(13)

式中:d_n越小,表示专家n评价结果与其他专家偏离程度越大.依据d_n值的大小并根据表2所示的专家保留人数及淘汰人数,淘汰掉权值偏离程度较大的专家打分.

表2 专家保留人数及淘汰人数

Tab.2 Number of retained experts and eliminated experts

专家数量	淘汰人数	保留人数
5	1	4
6	1	5
7	2	5
8	2	6
9	3	6

新窗口打开| 下载CSV

(3) 求取AHP赋权结果.

分析保留意见专家打分情况,计算对应专家权值矩阵R的列向量均值,求取指标j的权值r_p,即

r_p=

$\frac{1}{n} \overset{n}{\sum_{i = 1}}$ r_ip, p=1,2,…,j

(14)

式中:0≤r_p≤1, $\overset{j}{\sum_{p = 1}}$ r_p=1.

对于楼宇多指标评估矩阵E中j个评估指标,AHP赋权结果为r=[r₁r₂ … r_j].

3.2.2 熵权法赋权

为避免AHP赋权存在的主观性缺陷,引入熵权法,当指标参数变化范围较大时,数据包含的信息量较大,则此时熵值越小,该指标权值越大,反之亦然^[21].基于楼宇多指标评估矩阵E,第p个指标熵值定义式为

$\begin{array}{l} H_{p} = - l \overset{i}{\sum_{q = 1}} f_{q p} l n f_{q p}, p = 1,2, \dots, j \\ f_{q p} = \frac{E_{q p}}{\overset{i}{\sum_{q = 1}} E_{q p}} \\ l = \frac{1}{l n i} \end{array}\}$

(15)

式中:E_qp对应式(6)中矩阵元素.

第p个指标熵权值定义为

w_p=

$\frac{1 - H_{p}}{j - \overset{j}{\sum_{p = 1}} H_{p}}$ , p=1,2,…,j

(16)

式中:0≤w_p≤1, $\overset{j}{\sum_{p = 1}}$ w_p=1.

对于楼宇多指标评估矩阵E中j个评估指标,熵权法赋权结果为w=[w₁w₂ … w_j].

3.2.3 AHP-熵权法综合赋权

参考其他赋权方法,引入AHP-熵权法综合赋权法,结合各评价指标熵值和两种方法确定的权值,确定AHP-熵权法综合赋权权值,最终权值如下:

w'_p=r_pH_p+w_p(1-H_p), p=1,2,…,j

(17)

式中: $\overset{j}{\sum_{p = 1}}$ w'_p=1.

对于楼宇多指标评估矩阵E中的j个评估指标,AHP-熵权法综合赋权的结果为w'=[w'₁w'₂ … w'_j].

3.3 基于改进TOPSIS楼宇单元评价策略

TOPSIS是一种基于逼近理想解思想的多目标决策分析方法.理想解分为正理想解和负理想解,将各评价单元指标参数与正负理想解进行比较,得出该评价单元的评分,越接近正理想解综合评分越高,越接近负理想解综合评分越低.

传统TOPSIS方法采用欧氏距离计算到理想解的距离,存在一定的缺陷:在未考虑指标间的线性关系时,欧氏距离计算值无效,此时评价结果的准确性受到严重影响;当两个评价单元的评价结果接近时,无法区分各个评价单元的空间位置,不能客观反映各评价单元的状态.

为弥补上述缺陷,采用改进TOPSIS对楼宇评价单元进行综合评价.采用加权灰色关联度替代欧氏距离求解,以单元各指标参数与正负理想解之间整体趋势的相似度作为评价结果,能够反映评估单元内部的变化规律.基于改进TOPSIS楼宇单元评价步骤如下.

(1) 计算正负理想解:

E⁺={

$\underset{q}{m a x}$ E_qp}= {

$E_{1}^{+}$ ,

$E_{2}^{+}$ , …,

$E_{j}^{+}$ }

(18)

E^-={

$\underset{q}{m i n}$ E_qp}= {

$E_{1}^{-}$ ,

$E_{2}^{-}$ , …,

$E_{j}^{-}$ }

(19)

式中: $E_{j}^{+}$ 、 $E_{j}^{-}$ 分别为各指标参数的正负理想解.

(2) 计算改进TOPSIS法距离测度.

改进TOPSIS法采用加权灰色关联度替代传统的距离测度,首先计算该楼宇评价单元i各指标参数与正负理想解之间的灰色关联度系数 $δ_{i}^{+}$ 和 $δ_{i}^{-}$ ,然后根据灰色关联度系数计算出加权灰色关联度 $L_{i}^{+}$ 和 $L_{i}^{-}$ ,即改进TOPSIS法的距离测度.

$δ_{i}^{+}$ ={

$δ_{i 1}^{+}$ ,

$δ_{i 2}^{+}$ , …,

$δ_{i j}^{+}$ }

(20)

$δ_{i}^{-}$ ={

$δ_{i 1}^{-}$ ,

$δ_{i 2}^{-}$ , …,

$δ_{i j}^{-}$ }

(21)

$δ_{i j}^{\pm}$

$\frac{\underset{i}{m i n} \underset{j}{m i n} | E_{i j} - E_{j}^{\pm} | + ρ \underset{i}{m a x} \underset{j}{m a x} | E_{i j} - E_{j}^{\pm} |}{| E_{i j} - E_{j}^{\pm} | + ρ \underset{i}{m a x} \underset{j}{m a x} | E_{i j} - E_{j}^{\pm} |}$

(22)

$L_{i}^{\pm}$ =

$\overset{j}{\sum_{i = 1}}$ w'_p

$δ_{i p}^{\pm}$

(23)

式中:ρ为分辨系数,取0.5.

(3) 评估结果比较与分析.

求取各楼宇单元评估指标贴近度,将贴近度作为量化的评估结果,并对楼宇进行多指标评价对比分析.贴近度为

T_i=

$\frac{L_{i}^{+}}{L_{i}^{-} + L_{i}^{+}}$

(24)

求取各楼宇综合贴近度及各指标贴近度,可对楼宇进行系统和多指标评价,并对相同楼宇不同时间和不同楼宇相同时间两种情况进行纵向分析和横向分析.

4 算例分析

对某省所属市级电力公司办公楼宇的能效数据进行多指标评价,选取8栋办公楼宇单元2019年第一季度的数据进行综合评价.分别对楼宇评价指标进行筛选,构建多指标评估矩阵,利用改进TOPSIS对楼宇进行综合评价,并对该评价方法进行适应性分析.

4.1 楼宇多指标评价流程分析

首先从楼宇后勤数据台中读取2.1节初选的楼宇各个评价指标的历史数据,并对数据进行无量纲化处理,得到各楼栋评价单元指标数据,处理后的数据如表3所示.

表3 各楼宇评价单元指标数据

Tab.3 Index data of evaluation unit of each building

楼宇单元	投资成本	运维成本	购能成本	用电量	主要设备能效	CO₂年排放量	NO_x年排放量	可再生能源利用率
#1	0.213	0.101	0.217	0.347	0.233	0.154	0.121	0.324
#2	0.221	0.097	0.174	0.275	0.192	0.132	0.089	0.267
#3	0.304	0.114	0.193	0.288	0.214	0.201	0.096	0.421
#4	0.187	0.103	0.181	0.323	0.228	0.167	0.126	0.305
#5	0.247	0.125	0.244	0.315	0.216	0.145	0.097	0.299
#6	0.226	0.133	0.248	0.324	0.225	0.218	0.101	0.314
#7	0.277	0.159	0.251	0.297	0.195	0.199	0.124	0.322
#8	0.241	0.121	0.212	0.284	0.197	0.177	0.132	0.412

新窗口打开| 下载CSV

采用PCA法对表3中楼宇评价单元指标数据进行分析,结合相关性分析法对初选评价指标进行筛选,得到最终评价指标.并采用2.2节中PCA重构指标参数方法,计算各评价指标第一和第二主成分,构成主成分分析矩阵A,各评价指标第一和第二主成分系数如表4所示.

表4 评价指标主成分系数

Tab.4 Main component coefficients of indexes

参数	第一主成分系数	第二主成分系数
投资成本	0.5112	0.2014
运维成本	-0.0025	0.0171
购能成本	0.3521	0.4428
用电量	0.2037	0.3212
主要设备能效	0.4057	-0.1546
CO₂年排放量	0.1282	0.5143
NO_x年排放量	0.2143	0.3012
可再生能源利用率	0.1733	-0.2938

新窗口打开| 下载CSV

利用相关性分析各指标间相关性,计算得到表4中各指标间的相关系数矩阵如下:

$[\begin{array}{l} 1.000 & - 0.213 & 0.102 & 0.311 & - 0.347 & 0.068 & 0.077 & 0.262 \\ - 0.213 & 1.000 & 0.803 & 0.421 & 0.355 & 0.107 & 0.058 & 0.143 \\ 0.102 & 0.803 & 1.000 & 0.524 & 0.346 & 0.016 & 0.145 & 0.010 \\ 0.311 & 0.421 & 0.524 & 1.000 & 0.792 & 0.221 & 0.423 & - 0.374 \\ - 0.347 & 0.355 & 0.346 & 0.792 & 1.000 & 0.434 & 0.012 & 0.002 \\ 0.068 & 0.107 & 0.016 & 0.221 & 0.434 & 1.000 & 0.467 & - 0.174 \\ 0.077 & 0.058 & 0.145 & 0.423 & 0.012 & 0.467 & 1.000 & - 0.203 \\ 0.262 & 0.143 & 0.010 & - 0.374 & 0.002 & - 0.174 & - 0.203 & 1.000 \end{array}]$

(25)

矩阵D中各数据分别对应表3中各参数间的相关系数.其中“运维成本”和“购能成本”的相关系数为0.803;“用电量”和“主要设备能效”的相关系数为0.792,均高于0.750,表明对应两评价指标间相关性较高,应各删去其中一个指标.从表4中各评价指标的第一和第二主成分构成系数,可以看出“运维成本”构成系数较小,分别为-0.002 5和 0.017 1,因此在“运维成本”和“购能成本”两指标中删去“运维成本”;因为“用电量”和“主要设备能效”的第一和第二主成分构成系数较大,所以将二者保留.

经过筛选,得到楼宇综合评价指标体系,如图3所示.按照图3中各指标次序,构造标准化指标参数矩阵如下:

E'=

$[\begin{array}{l} 0.213 & 0.101 & 0.347 & 0.233 & 0.154 & 0.121 & 0.324 \\ 0.221 & 0.097 & 0.275 & 0.192 & 0.132 & 0.089 & 0.267 \\ 0.304 & 0.114 & 0.288 & 0.214 & 0.201 & 0.096 & 0.421 \\ 0.187 & 0.103 & 0.323 & 0.228 & 0.167 & 0.126 & 0.305 \\ 0.247 & 0.125 & 0.315 & 0.216 & 0.145 & 0.097 & 0.299 \\ 0.226 & 0.133 & 0.324 & 0.225 & 0.218 & 0.101 & 0.314 \\ 0.277 & 0.159 & 0.297 & 0.195 & 0.199 & 0.124 & 0.322 \\ 0.241 & 0.121 & 0.284 & 0.197 & 0.177 & 0.132 & 0.412 \end{array}]$

(26)

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 楼宇综合评价指标体系

Fig.3 Evaluation index system of buildings

AHP赋权结果为r=[0.112 0.183 0.217 0.264 0.101 0.017 0.106],熵权法求取各结果为w=[0.204 0.124 0.157 0.301 0.098 0.012 0.104],采用AHP-熵权法综合赋权结果为w'=[0.131 0.124 0.196 0.267 0.094 0.085 0.103].对上述3种方法的结果分析可得,AHP-熵权法综合赋权法得出的权重值介于AHP赋权法和熵权法之间,改善了AHP赋权法主观性过强的问题,同时也避免熵权法不反映主观意见的问题,对于评价结果具有较好的主客观性.

AHP-熵权法综合赋权结果表明“主要设备能效”权值最大,在楼宇综合评价中重要性最大;“NO_x排放量”权值最小,在楼宇综合评价中重要性最小.优化楼宇的主要设备能效是加强楼宇建设的有效手段.

采用改进TOPSIS方法,在式(26)数据基础上,分别计算各评价指标正负理想解、改进TOPSIS法的距离测度;以及贴近度,得到楼宇单元#1~#8的评价结果,如表5所示.根据表5横向比较8栋楼宇单元综合评分,排序依次为:P₆>P₃>P₅>P₁>P₄>P₂>P₈>P₇,楼宇单元6综合评分最高为0.632,楼宇单元7评分最低为0.439.

表5 改进TOPSIS评估结果

Tab.5 Evaluation results by using improved TOPSIS

楼宇单元	$L_{i}^{+}$	$L_{i}^{-}$	T_i	评分排序
#1	0.707	0.492	0.590	4
#2	0.617	0.529	0.538	6
#3	0.825	0.516	0.615	2
#4	0.668	0.564	0.542	5
#5	0.859	0.583	0.596	3
#6	0.776	0.451	0.632	1
#7	0.529	0.677	0.439	8
#8	0.553	0.624	0.470	7

新窗口打开| 下载CSV

由AHP-熵权法综合赋权结果w'=[0.131 0.124 0.196 0.267 0.094 0.085 0.103]可知,“主要设备能效”指标的权值最大,“用电量”指标的权值次之,说明“主要设备能效”和“用电量”指标重要性最大,对评估结果影响也最大,即楼宇单元的能耗指标越好其评估结果也越优.表3各楼宇评价单元指标数据均为“效益型”数据,数值越大代表指标越好.从表3可看出8栋楼宇单元的经济、能耗和环保指标各不相同,楼宇单元#3、#6、#5的能耗指标优于其他楼宇单元,其评分也将高于其他楼宇单元.改进TOPSIS方法解得的结果符合分析,证明了所提方法的正确性.

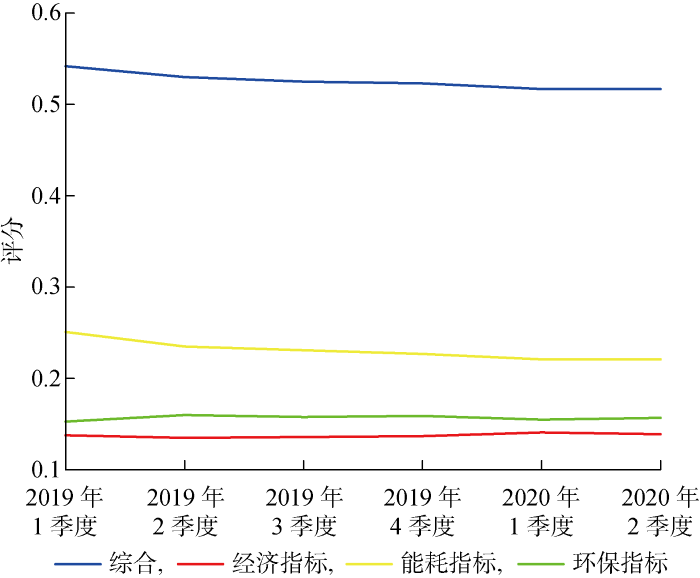
为纵向研究单一楼宇时间维度上评分变化,对比分析综合评分及经济、能耗、环保指标评分随时间的变化规律,选择楼宇单元#1作为分析对象,选取2019年全年和2020年上半年共6个季度的数据进行计算分析,得到综合评分及经济、能耗、环保指标评分如图4所示.观察可得楼宇综合评分随时间变化趋势和楼宇能耗指标变化趋势一致,且均呈减小趋势.当楼宇综合评分较低时,优先对能效指标进行优化处理,提高楼宇综合评分.需求响应机制是一种较为有效的提高评分的方法,有助于电力系统削峰填谷,保证系统经济可靠运行.针对楼宇需求响应机制可以优化各项指标,文献[22]中提出一种基于楼宇空调需求响应的实时控制方法,可有效减少负荷,降低楼宇能耗.实验仿真也证明采用需求响应等手段的楼宇具有更高的评价结果.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 楼宇评分季度变化

Fig.4 Quarterly change of scores of buildings

4.2 评价方法适应性分析

利用改进TOPSIS方法对楼宇综合评价进行适应性分析,选择基于交叉超效率CCR模型法、AHP法和传统TOPSIS法对式(26)标准化数据进行评分计算,将评分结果排序得到表6所示结果.

表6 与其他方法评价结果对比

Tab.6 Comparison of evaluation results by different methods

楼宇单元	评分排序
楼宇单元	CCR	TOPSIS	AHP	改进TOPSIS
#1	4	4	4	4
#2	6	6	6	6
#3	3	2	2	2
#4	5	5	5	5
#5	2	3	3	3
#6	1	1	1	1
#7	8	7	7	8
#8	7	8	8	7

新窗口打开| 下载CSV

观察表6中4种评价方法评分排序,各楼宇单元排序基本相同,说明所提方法对楼宇综合评价具有有效性;由楼宇单元#3各评价结果及表5计算结果可知,当楼宇评价指标正负理想解接近时,传统TOPSIS法利用欧氏距离求解不能准确地区分计算出楼宇单元评分结果,而所提方法能有效改善这一问题;由楼宇单元#3和#5评价结果可知,所提方法优于CCR模型评价结果;由楼宇单元#7和#8评价结果可知,AHP与传统TOPSIS法存在共性,即主观性较强;改进TOPSIS法基于主观经验,充分利用数据蕴含的客观信息,在楼宇综合评价中具有较好的效果.

5 结语

为实现对大型办公楼宇进行综合评价,建立基于改进TOPSIS的楼宇综合评价模型.该模型考虑楼宇经济、能耗、环境因素,基于TOPSIS方法,采用AHP-熵权法确定各指标权值,避免单一主客观问题;采用加权灰色关联度替代欧氏距离,即使评价结果接近时,仍能较好地区分计算;分别对楼宇单元进行横向和纵向对比分析,为查找楼宇评分变化原因提供解决路径,表明优化楼宇的能耗指标是提高楼宇评分的重要技术手段.经适应性分析,该模型在楼宇综合评价时兼具全面、高效、准确等特点,适合大型办公楼宇的综合评价.在未来研究中,将更细分各级指标,优化评价模型,进一步分析各指标与大型办公楼宇综合评分之间的定量关系,并结合需求响应等手段,提升楼宇绿色用能的效果.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

赵景茜, 米翰宁, 程昊文, 等.

考虑岸电负荷弹性的港区综合能源系统规划模型与方法

[J]. 上海交通大学学报, 2021, 55(12): 1577-1585.