改进型自激谐振无线电能传输系统

doi:10.16183/j.cnki.jsjtu.2022.427

改进型自激谐振无线电能传输系统

赵志斌^,¹, 骆彬¹, 唐婷¹, 王春芳², 孙中华¹

1.海军航空大学青岛校区,山东青岛 266041

2.青岛大学电气工程学院,山东青岛 266071

Improved Self-Excited Resonant Wireless Power Transmission System

ZHAO Zhibin^,¹, LUO Bin¹, TANG Ting¹, WANG Chunfang², SUN Zhonghua¹

1. Qingdao Campus of Naval Aeronautical University, Qingdao 266041, Shandong, China

2. College of Electrical Engineering, Qingdao University, Qingdao 266071, Shandong, China

责任编辑: 王历历

收稿日期: 2022-10-28 修回日期: 2022-12-15 接受日期: 2023-01-19

基金资助:

国家自然科学基金(51877113)

Received: 2022-10-28 Revised: 2022-12-15 Accepted: 2023-01-19

作者简介 About authors

赵志斌(1983-),副教授,从事电力电子技术、运动控制技术研究,电话(Tel.):0446-58832446;E-mail:278139331@qq.com.

摘要

针对一种自激式谐振无线电能传输(WPT)系统的主功率管驱动能力弱、软开关性能差、开关损耗大等问题,通过分析谐振主电路工作原理,发现问题的根源是两个不可控二极管限制了主功率管驱动电阻值.采用全控型小功率开关管代替二极管提出一种改进型自激谐振电路,通过对电路4种工作模态的理论分析,证实改进型电路主功率管具有较强的驱动能力.为了进一步得到改进型系统的最优参数,综合考虑各参数容限值建立系统非线性规划模型,设计一种混合优化算法,得到系统全局最优解.利用系统仿真及实验样机进行对比验证,结果表明:改进型WPT系统软开关性能优良,开关管温度降低约7 ℃,效率提升约4%.

关键词： 无线电能传输系统; 自激谐振; 参数优化; 非线性规划; 遗传算法

Abstract

Aimed at the main power tube with problems of weak driving ability, poor soft switching performance, and large switching loss in a self-excited resonant wireless power transmission (WPT) system, an analysis of the working principle of resonant main circuit is conducted, which indicates that the root cause of the problem is that two uncontrollable diodes limit the driving resistance of main power tube. Thereofre, an improved self-excited resonant circuit is proposed by using a fully controlled low power switch instead of the diode. The circuit theoretical analysis of four working modes suggests that the main power tube of the improved circuit has a stronger driving ability. To further obtain the optimal parameters of the improved system, a nonlinear programming model of the system is established by considering the tolerance limit of each parameter, and a hybrid optimization algorithm is designed to obtain the system global optimal solution. A comparison of the results of system simulation and experimental prototype shows that the improved WPT system has an excellent soft switching performance. The temperature of the switch tube is reduced by about 7 ℃, and the efficiency is increased by about 4%.

Keywords： wireless power transmission (WPT) system; self-excited resonance; parameter optimization; non-linear programming; genetic algorithm (GA)

PDF (3593KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

赵志斌, 骆彬, 唐婷, 王春芳, 孙中华. 改进型自激谐振无线电能传输系统[J]. 上海交通大学学报, 2023, 57(7): 859-867 doi:10.16183/j.cnki.jsjtu.2022.427

ZHAO Zhibin, LUO Bin, TANG Ting, WANG Chunfang, SUN Zhonghua. Improved Self-Excited Resonant Wireless Power Transmission System[J]. Journal of Shanghai Jiaotong University, 2023, 57(7): 859-867 doi:10.16183/j.cnki.jsjtu.2022.427

无线电能传输(Wireless Power Transfer, WPT)系统通过磁场或电场完成原、副边设备的非接触能量传递,克服传统有线输电的磨损、漏电、火花放电等各种问题,增强设备对复杂环境的适应能力,具有广阔的应用前景^[1-2].磁耦合WPT技术在手机、家用电器、穿戴式医疗设备等中小功率产品方面的研究和应用已经成为热点^[3-4].中小功率产品对体积、质量、效率、可靠性、稳定性及性价比等方面都有较高要求,很多学者从电路拓扑结构、耦合变压器优化设计等方面进行了深入研究.文献[5-6]中采用单个开关管实现软开关,降低开关损耗,缺点是复杂的控制电路、辅助电源及检测电路等增大了系统体积质量.文献[7]中采用两个开关管的自激推挽拓扑结构来实现WPT,但为了实现频率跟踪设计了较为复杂的控制激励电路.文献[8 ⇓-10]中设计的自激推挽谐振式逆变电路的驱动控制电路较为简单,实现了零电压开关(Zero Voltage Switching, ZVS)^[11],具有良好的频率自动跟踪性能,但不足之处有两点:一是功率开关管的驱动电阻过大,参数一般在hΩ级别,而根据金属-氧化物半导体场效应晶体管(Metal Oxide Semiconductor Field Effect Transistor,MOSFET)技术手册及使用经验,要使开关管减小驱动冲击的条件下迅速开通,该驱动电阻选为10 Ω左右即可,过大的驱动电阻会使开关管驱动脉冲上升过缓,造成开关损耗增大;二是该电路虽然实现了软开关ZVS,但由于驱动电阻及谐振互锁二极管导通压降的影响,无论是零电压开通还是零电压关断,开关管漏源电压与栅源驱动电压的交叠区面积还可以进一步减小,以降低开关损耗.

重点针对这种自激推挽谐振式WPT技术进行改进优化,以提高其在中小功率设备中的应用能力.采用小功率开关管代替谐振互锁二极管构建一种改进型自激谐振电路,主功率开关管的驱动电阻只需要考虑驱动要求进行合理设置,不再受限于谐振电路的影响;另外,中间驱动开关管的导通电压及通态阻抗均比二极管低,主功率管具有更好的驱动波形,且ZVS特性得到进一步优化.WPT系统设计需要重复迭代以得到最优参数,为了提高参数设计质量及效果,拟建立系统的非线性规划模型,采用混合优化算法一次性得到全局最优解.然后,通过Multisim仿真及搭建小功率实验样机进行验证和对比分析.

1 自激谐振WPT电路

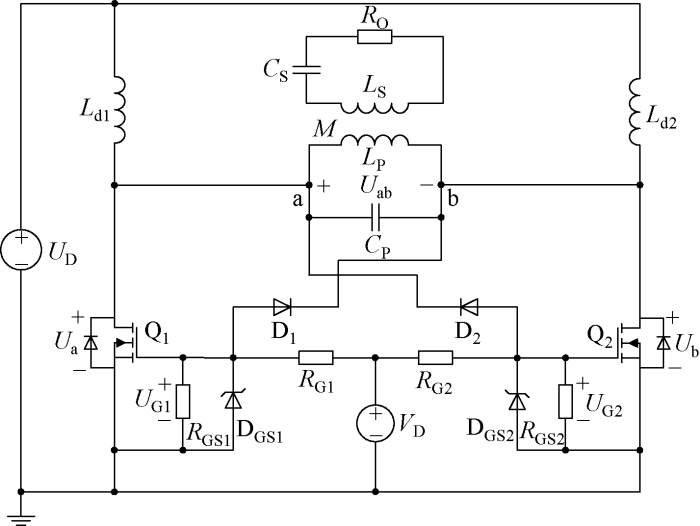
文献[8 ⇓-10]中所用的自激谐振式软开关WPT系统核心电路(原边谐振电路)如图1所示.图中:Q₁、Q₂为工作在互补推挽模式下两个MOSFET开关管;U_D、V_D分别为主直流输入电源电压及MOS管的驱动电源电压;L_d1、L_d2为防止开关管直通短路的扼流电感;L_P、L_S分别为原、副边谐振电感,互感大小为M;C_P、C_S别为原、副边谐振电感的补偿电容,本文采用原边并联-副边串联(Primary Side Parallel-Secondary Side Series, PS)拓扑^[8],虽然文献[9-10]中采用PS拓扑,但不影响原边谐振电路结构的设计改进;二极管D₁、D₂通过实时检测原边并联谐振网络的电压来钳位控制两个开关管交替通断,是实现电路自激推挽谐振的关键器件;R_G1、R_G2分别为Q₁、Q₂的栅级开通限流电阻;R_GS1、R_GS2为MOS管的栅源寄生电容提供放电通道,防止开关管误动作;稳压管D_GS1、D_GS2可以防止Q₁、Q₂栅源过电压而击穿;U_a、U_b分别为Q₁、Q₂的漏源电压.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 自激谐振WPT电路原理图

Fig.1 Schematic diagram of circuit of self-excited resonant WPT

在两个开关管Q₁、Q₂轮流导通下,直流电压U_D经过扼流电感L_d1、L_d2,给原边谐振网络L_P、C_P提供能量,L_P、C_P谐振后的电能以电磁波形式感应给副边谐振网络L_S、C_S,并传输到等效负载R_O.原边谐振网络的高频谐振电压U_ab通过二极管D₁、D₂拉低或抬高Q₁、Q₂的控制电压U_G1、U_G2.

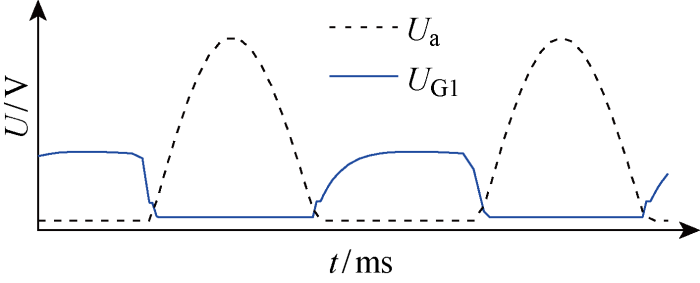
图2为以Q₁开关管为例(Q₁波形移相180°即为Q₂)的自激谐振电路仿真波形.图中:U为电压;t为时间.U_G1为高电平时,Q₁导通,U_a为低电平,二极管D₂导通,拉低U_G2,使Q₂可靠关断;此刻,驱动电压V_d几乎全部加到限流电阻R_G2上,如果按照减小开通损耗要求的电阻配置标准(2~10 Ω),R_G2会产生较多热损耗.当谐振电路使电压U_b低于V_d时,二极管D₁开始导通,U_G1随着U_b的降低而逐渐降低为低电平,使Q₁关断;同时,R_G1上的电流越来越大,U_a电压逐渐升高,当U_a高于V_d时,二极管D₂不导;此刻,R_G2上仍流过电流驱动Q₂,U_G2的电压随着驱动电流的增大而逐渐抬高到接近于V_d,Q₂完全导通.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 自激谐振WPT电路开关管波形

Fig.2 Switch waveform of self-excited resonant WPT circuit

如果R_G1过大,Q₁开通电压上升较为缓慢,增大开通损耗,该电阻在U_G1被拉低时作为二极管D₁的限流电阻,不能太小,一般取值为300 Ω左右,否则长时间工作发热严重.因此,这种电路在开关管的开通损耗及限流电阻的热损耗方面存在一定的矛盾.

2 自激谐振WPT改进电路

通过原理分析可知,图1所示的自激谐振电路中谐振箝位二极管既连接MOS管的控制极又与主谐振电路直接交联,从而导致电路设计中的固有矛盾.改进思路为采用小功率MOS管代替二极管实现主电路与控制电路相对隔离,MOS管驱动电阻不受主电路电流影响;又由于MOS管的导通压降比二极管小很多,所以显著降低主功率MOS管的关断电压,与文献[8]中驱动电路加入电容实现负压关断的方式相比,此电路同样能有效改善电路的ZVS特性.改进的自激谐振WPT电路如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 改进型自激谐振WPT电路

Fig.3 Improved self-excited resonant WPT circuit

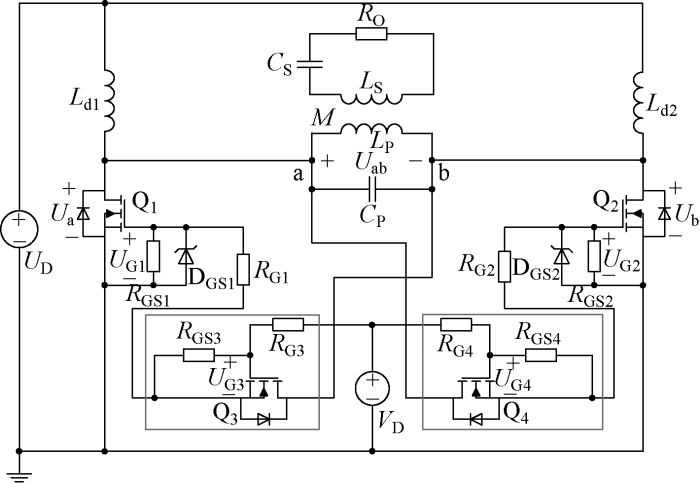
对比图1的原谐振电路,图3增加了Q₃、Q₄两个小功率MOS管分别代替原电路中的二极管实现对主功率管Q₁、Q₂的驱动控制.R_G3、R_G4分别为Q₃、Q₄的驱动限流电阻;R_GS3、R_GS4分别为Q₃、Q₄的栅源极保护电阻;由于Q₃、Q₄实现驱动电源与谐振网络的相对隔离,所以4个开关管的栅极限流电阻可以设置为MOS管的最优范围(2~10 Ω级别),以最大限度减小开通损耗.Q₁~Q₄开关管的栅源电压分别用U_G1~U_G4表示;稳压管D_GS3、D_GS4分别用来限制U_G3、U_G4的驱动过电压.改进型原边电路的总体工作原理与原谐振电路基本相似,在Q₃、Q₄两个开关的辅助驱动下,主功率开关管Q₁、Q₂以180°相位差交错通断,在WPT电路的原边谐振网络中产生高频电压U_ab.以Q₃驱动Q₁的通断为例对电路工作原理进行说明,仿真波形如图4所示,图中分别给出了U_G1与U_a、U_G1与U_G3的波形对比图.将t₀~t₄一个周期波形分为4种模态分析工作原理.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 改进型自激谐振WPT电路开关管波形

Fig.4 Switch waveform of improved self-excited resonant WPT circuit

模态1 t₀~t₁时,Q₃栅源驱动电压U_G3为高电平(约为V_D),Q₃开通,Q₁栅源驱动电压U_G1决定于U_b大小,U_b与U_a波形相位差180°.从U_a波形可以看出,U_b为低电平(地),则U_G1为低电平,Q₁关断(Q₂导通).直流电压U_D沿两条路线到地:一条依次经过L_d2、Q₂,为电感蓄能;另一条依次经过L_d1、原边谐振网络a-b、Q₂,谐振网络充能使U_a按正弦规律变化(见图4).

模态2 t₁~t₂时,为Q₁由关断到导通过渡阶段.t₁时刻,谐振换能使U_b电压开始上升(U_a继续下降),U_G1跟随U_b开始上升,则U_G3电位开始下降,U_G3≈V_D-U_G1.至t₂时刻,U_G3下降至MOS管的门槛电压U_G3,th≈3 V,Q₃临界关断,U_G1的电压被箝位为V_D-U_G1,th,Q₁开关管导通.

模态3 t₂~t₃时,为模态2的t₂时刻后稳定状态.U_G3保持为门槛电压,Q₃保持临界关断,U_G1保持箝位电压V_D-U_G3,th,Q₁持续导通,U_a为低电压(地).Q₄导通使U_G2置为低电平,Q₂关断.直流电源U_d沿两条路线到地:一条经过L_d1、Q₁,为电感蓄能;另一条经过L_d2、原边谐振网络b-a、Q₁,谐振网络充能使U_b按正弦规律变化.

模态4 t₃~t₄时,为Q₁由导通到关断过渡阶段.t₃时刻,电路谐振使U_b下降到能够使U_G3大于门槛电压U_G3,th,U_G3开始上升,Q₃开始导通,U_G1跟随U_b开始下降,Q₁开始关断,U_a开始上升.至t₄时刻,U_b谐振到低电平(地),U_G1也降到低电平,Q₁完全关断,U_G3达到高电平V_D,Q₃完全开通.

在相同的坐标尺度下,对比图2与图4中U_G1与U_a波形,改进前的开关管驱动电压受较大驱动电阻的影响而上升缓慢,改进后的电路开通速度快,开关损耗小;改进前的驱动电压受二极管管压降影响,其低电平难以达到改进后的近地电平,相关研究为改善低电平电压,在驱动电路中串入了电容.改进后的自激振荡电路由于具有较快的开通速度及较低的关断电压,其ZVS特性比改进前电路有较大提高,开关管驱动电阻与主电路的隔离结构使驱动电阻上的热损耗较小,电路长时间工作的器件温度正常.

3 参数优化非线性规划模型

改进型自激谐振WPT系统电路的关键参数如原副边电感、电容、互感等,主要集中于谐振网络中,但在实际电路设计中还需要考虑输出电压的稳压值、输出功率的最大值、电感的最大电流、电容的最高电压、开关管的器件压流容限、谐振频率范围以及直流扼流电感对频率的影响等因素.因此,对系统参数优化问题实质上是一个多变量多约束非线性规划(NonLinear Programming, NLP)问题^[12-13].采用松耦合变压器漏感模型建立PS型谐振网络等效电路模型^[14],如图5所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

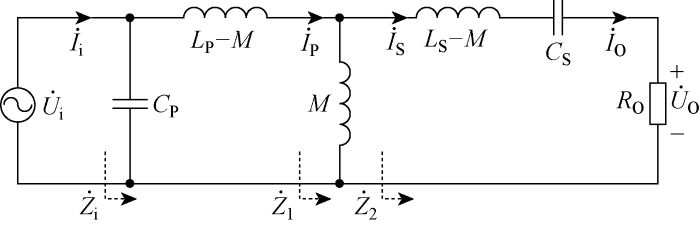
图5 WPT系统PS型谐振网络等效电路

Fig.5 PS-type resonant network equivalent circuit of WPT system

图5中所有线路内阻均简化,U_i为等效输入电压即U_ab;U_O为负载输出电压;I_i、I_P、I_S、I_O分别为原边谐振网络输入电流、原边谐振回路电流、副边电流、负载电流;Z_i、Z₁、Z₂分别为虚线箭头所示区域等效阻抗;电路中原、副边等效电感大小分别为 L_P-M、L_S-M.

基于基波近似原则及阻抗分析方法,根据基尔霍夫电压、电流定律,以副边谐振频率f₀为系统工作频率点,则系统谐振角频率为

(1)ω=2πf₀=1/

\sqrt{L_{S} C_{S}}

在满足式(1)的条件下,可得

(2)

\begin{array}{l} {\overset{\cdot}{Z}}_{1} = ω^{2} M^{2} / R_{O} + j ω M, {\overset{\cdot}{Z}}_{2} = R_{O} - j ω M \\ {\overset{\cdot}{Z}}_{i} = \frac{ω (L_{P} R_{O} - j ω M^{2})}{ω^{3} M^{2} C_{P} + j R_{O} (ω^{2} L_{P} C_{P} - 1)} \end{array}\}

系统原边完全谐振于频率点f₀的条件为 Im ${\overset{\cdot}{Z}}_{i}$ =0,设原副边耦合系数k=M/ $\sqrt{L_{P} L_{S}}$ ,则

(3)L_P=

\frac{C_{S}^{2} R_{O}^{2}}{C_{P} (ω^{2} C_{S}^{2} R_{O}^{2} + k^{4})}

\frac{1}{ω^{2} C_{P} (Q_{S}^{2} k^{4} + 1)}

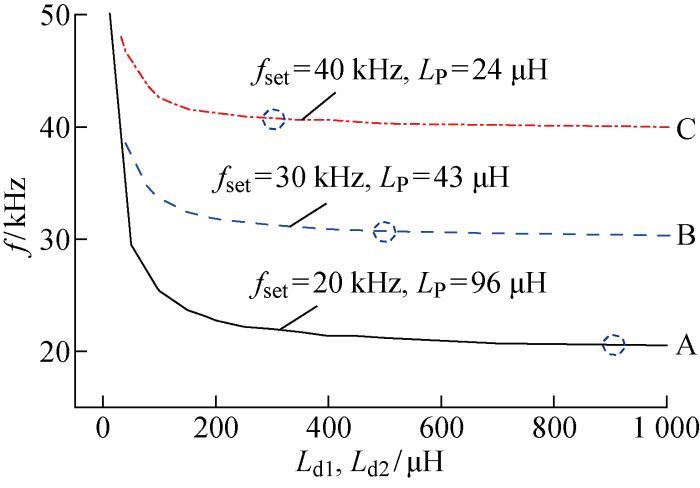
式中:副边品质因数Q_S=ωL_S/R_O.可以看出当Q_Sk²≪1时,即 $Q_{S}^{2}$ k⁴+1≈1,原边电感L_P不受负载变化的影响,那么负载变化对系统的谐振频率点影响最小,可取

(4)Q_Sk²≤0.1

与一般PS拓扑不同,直流扼流电感L_d1及L_d2大小易影响原边谐振频率,与原边谐振电感L_P有一定的约束关系.设计频率f_set根据功率管的频率范围,选择20~40 kHz.频率太小谐振电感的体积就会变大,频率太大开关损耗就会增大.利用仿真数据分析得到在不同的设计频率f_set下,L_d1及L_d2对系统谐振频率(f)的影响如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 扼流电感与谐振电感对系统频率的影响

Fig.6 Effect of choke inductor and resonant inductor on system frequency

图中,A、B、C三条曲线对应设计频率为20、30、40 kHz,在C_P、C_S、k、R_O不变的情况下,不同的设计频率会对应不同的谐振电感值L_P、L_S.仿真分析中发现,L_P与L_d1(L_d2)相差越大,系统真实工作频率与设计频率越接近,设计准确性越好.图6中每条曲线上的虚线圈即为能达到设计频率的最小L_d1(L_d2)值,约为L_P大小的10倍.系统的体积及内阻损耗限制了L_d1及L_d2不能太大,在L_d1(L_d2)确定的前提下,可设L_P的约束为

(5)L_P<L_d1/10

系统输出电压有效值为

(6)U_O=U_ik

\sqrt{C_{P} / C_{S}}

式(6)中,U_i与直流电源电压U_D的关系可通过对扼流电感L_d1及L_d2应用伏秒定理得到,即U_i=πU_D/ $\sqrt{2}$ .

原边谐振网络输入总电流的有效值为

(7)I_i=U_ik²C_P/(C_SR_O)

原、副边电容电压及电流有效值U_CP、U_CS及I_CP、I_CS,原、副边电感电流及负载电流有效值I_LP、I_LS及I_O分别为

(8)

\begin{array}{l} I_{L P} = \frac{U_{i} C_{P}}{C_{S} R_{O}} \sqrt{ω^{2} C_{S}^{2} R_{O}^{2} + k^{4}} \\ I_{L S} = \frac{U_{i} k}{R_{O}} \sqrt{\frac{C_{P}}{C_{S}}} \\ U_{C P} = U_{i}, I_{C P} = U_{i} ω C_{P} \\ U_{C S} = \frac{I_{L S}}{ω C_{S}}, I_{O} = I_{C S} = I_{L S} \end{array}\}

在电路及数学模型的基础上,建立非线性规划模型还需要确定目标函数、优化变量及约束条件.系统忽略内阻完全谐振于副边谐振点时,理论计算的效率接近100%,因此,目标函数以系统能量传输(P_O)最大为目标,取倒数变换成NLP标准模型为

(9)min F(x)=1/P_O=R_O/

U_{O}^{2}

式中:F(x)为目标函数,x为自变量的向量形式,即为待优化的参数变量集,其表达式为

(10)x=(k,f₀,L_P,L_S,C_P,C_S)

式中:k_l<k<k_u、f_0l<f₀<f_0u、L_Pl<L_P<L_Pu、L_Sl<L_S<L_Su、C_Pl<C_P<C_Pu、C_Sl<C_S<C_Su,k_l、k_u分别表示耦合系数k的最小值及最大值,其余参数同理.L_Pu的选择需要考虑与L_d1(L_d2)的约束关系,见式(5);耦合系数在没有磁芯的情况下一般不超过0.25;开关频率受开关损耗限制,在最大开关频率范围内选择合适值;电容需考虑市面常用的高频谐振电容规格;这些最值构成自变量参数的搜索解空间.

系统元器件及线路的电压、电流不能超过最大值,根据式(7)和式(8)及电路系统工作电流、电压容限确定非线性约束条件为

(11)

\begin{array}{l} g_{1} = I_{i} - I_{i u} \leq 0 \\ g_{2} = I_{L P} - I_{L P u} \leq 0 \\ g_{3} = I_{L S} - I_{L S u} \leq 0 \\ g_{4} = U_{C P} - U_{C P u} \leq 0 \\ g_{5} = I_{C P} - I_{C P u} \leq 0 \\ g_{6} = U_{C S} - U_{C S u} \leq 0 \end{array}\}

式中:g_j为不等式约束(j=1, 2, …, 6);I_LPu为原边电感电流I_LP的最大值,其余参数同理.由于副边串联的电感、电容、电阻电流相等,在I_LSu参数的选择上需要一并考虑I_O及I_CS的电流容限.若所设计的系统参数要求负载变化及扼流电感对谐振频率影响较小,则不等式约束还需考虑式(4)和式(5),可得:

(12){g₇=Q_Sk²-0.1≤0, g₈=L_P-0.1I_d1≤0}

自变量之间的等式约束关系可由满足式(4)约束下的式(1)和式(3)得到.设定一个极小数ε= 0.01,将等式约束转换成不等式约束可得:

(13){g₉=|ω²L_SC_S-1|≤ε, g₁₀=|ω²L_PC_P-1|≤ε}

利用式(8)~(12)建立改进型自激谐振变换系统的NLP数学模型,该模型有1个目标函数、6个约束自变量及10个非线性约束.

4 参数混合优化求解

针对非线性规划问题,MATLAB提供了丰富的智能优化算法库,如遗传算法(Genetic Algorithm, GA)、粒子群算法、模式搜索算法、极小化极大算法等^[15].算法优化具有一定的随机性,容易限入局部最优解,一般需要多次运算调整参数才能得到一个稳定的最优值^[16].为了提高优化效率,将基于种群智能决策的遗传算法与梯度算法结合,得到一种混合优化算法(见图7),该算法只需要对种群数量及迭代次数等参数进行简单设置就能稳定得到全局最优解.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 混合优化算法流程图

Fig.7 Flow chart of hybrid optimization algorithm

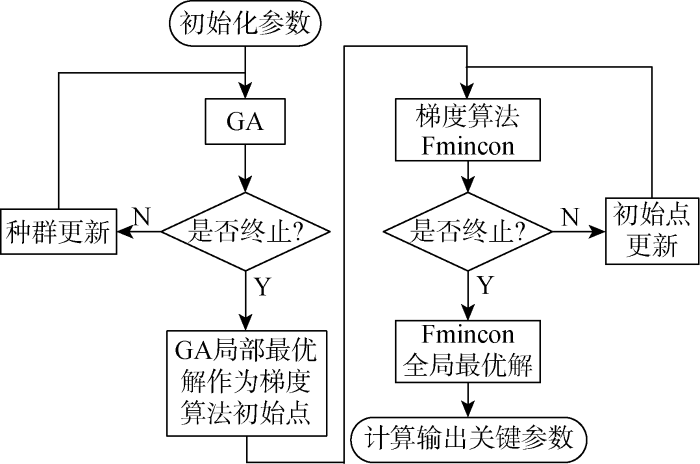
根据算法流程,利用MATLAB实时编辑器编写系统参数优化程序,设计过程如下.

4.1 参数初始化

假设系统基本参数为U_D=24 V、R_O=10 Ω、L_d1=L_d2=300 μH;根据原副边电感、电容等器件的电压、电流容限,设置电流、电压约束最大值为I_iu=5 A、I_LPu=I_LSu=I_CPu=8 A、U_CPu=U_CSu=100 V;6个待优化自变量解空间范围如表1所示.

表1 优化自变量各参数解空间范围

Tab.1 Solution space range of each optimization independent variable

范围	k	f₀/kHz	L_P/μH	L_S/μH	C_P/μF	C_S/μF
下届	0.1	20	10	10	0.1	0.1
上届	0.25	35	100	100	1	1

新窗口打开| 下载CSV

4.2 混合优化算法

在实时编辑器中插入“优化”模块任务,指定问题类型为“非线性”、约束选项前的NLP模型特点选择“下届”“上届”“线性不等式”“非线性”等模块,线性不等式即g₈,求解器选择“遗传算法”;然后分别建立“目标函数”(式(9))、“约束函数”(非线性约束)等局部函数,其中“约束函数”包括非线性不等式约束g₁~g₇及非线性等式约束g₉~g₁₀;GA算法求解器设置参数中,种群大小为200、最大代数为150、非线性约束算法使用罚函数法;GA优化输出变量作为Fmincon算法的初始值x₀.再次插入“优化”模块任务,求解器选择“Fmincon”,初始值选择x₀,其他参数基本同GA.

4.3 参数输出

运行各段代码后,调用“目标函数”及“约束函数”计算并输出最优自变量、非线性约束条件等相关参数.最优自变量优化参数k、f₀、L_P、L_S、C_P、C_S分别为0.245、34.5 kHz、30.92 μH、76.91 μH、0.69 μF、0.28 μF;约束条件优化参数I_i、I_LP、I_LS、U_CP、I_CP、U_CS、Q_S分别为0.8 A、8 A、2.06 A、53.31 V、7.96 A、34.36 V、1.67.自变量均满足表1解空间范围要求,但是L_P比g₈要求的30 μH略大 0.92 μH,由于式(5)所确定的比例是一个预估参数,所以适当误差可以接受;约束条件优化参数均满足设计要求.

计算输出电压U_O=20.61 V,对应的最大输出功率P_O=42.5 W,不考虑直流电源及扼流电感内阻,以原边谐振网络输入为基准,理论计算的系统传输效率约为99.7%.

算法优化过程中发现, GA得到最优稳定值需要重复运行至少7次,最小目标函数为 0.023 5;梯度算法Fmincon得到最优稳定值需要重复运行至少9次,最小目标函数为 0.024 3;而改进的混合优化算法运行3次即可得到稳定最小目标函数为 0.020 7,证明改进型算法有较稳定的优化能力且能更好地突破局部最优点,达到全局最优的优化效果.

5 仿真及实验验证

根据图3所示的改进型自激谐振电路结构,使用Multisim软件建立系统的仿真模型,利用优化参数设置电路中的关键参数k、L_P、L_S、C_P、C_S,实验参数设置存在一定误差.仿真及实验电路中:大功率开关管Q₁、Q₂选用IRF540N(100 V/33 A),小功率开关管Q₃、Q₄选用IRF520N(100 V/9.7 A),MOSFET栅源保护电阻选用10 kΩ金属膜电阻、栅极限流电阻选用5.1 Ω/1 W小功率电阻,驱动过压保护稳压管选用1N4745(16 V).

实验样机如图8所示,样机中包括原ZVS电路以便对比分析,所用谐振二极管采用FR307快恢复二极管,MOSFET驱动电阻采用330 Ω的普通电阻,其余参数同改进型电路.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 实验样机实物

Fig.8 Physical model of experimental prototype

首先测量仿真及实验参数(见表2),并与理论优化参数进行对比,检验系统整体工作状态.

表2 仿真及实验关键参数

Tab.2 Key parameters of simulation and experiment

条件	I_i/A	I_LP/A	I_LS/A	U_CP/V	I_CP/A	U_CS/V
仿真	0.99	7.80	2.06	53.2	8.19	33.1
实验	1.1	8.1	1.9	55.1	8.1	30.2

新窗口打开| 下载CSV

系统输出电压及工作频率分别为:仿真条件下,U_O=20.6 V,f₀=35.3 kHz;实验条件下,U_O=19.6 V,f₀=34.7 kHz.仿真与实验数据与理论计算参数除了工作频率有一定误差,即实验比仿真更接近理论值,其余参数基本一致.频率存在一定误差的原因有:一是扼流电感对系统频率有影响,且原边谐振电感利用近似方式得到;二是实验电路电感内阻、耦合系数等的参数变化影响频率.仿真与实验的直流输入电流分别为1.85、2.0 A,传输效率分别为95.6%、80%,实际电路非理想器件的内阻及参数漂移降低了系统效率.

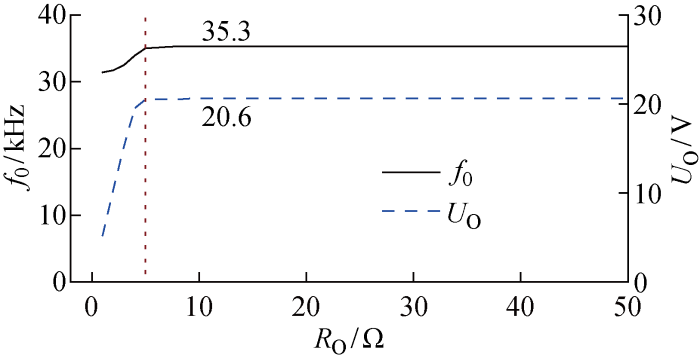
系统设计中原边L_P与C_P采用简化的设计公式(13)中的g₁₀,是为了使系统参数在一定的负载变化范围内具有较强的鲁棒性.改变负载检验系统稳频及稳压效果,得到Multisim仿真结果如图9所示.从仿真图可以看出,在其他参数不变的情况下,负载R_O>5 Ω,即输出功率P_O<85 W范围内系统均具有较强的频率及电压稳定性(仿真中R_O=1 000 Ω时频率及电压稳定性亦不变).利用实验验证不同负载电阻下的频率及电压稳定性^[17-18](见表3).由表3可以看出谐振频率f₀及输出电压U_O能够稳定在一定范围内;由图9可见,实验数据低于仿真值,但是谐振频率较接近理论值,这是由于实际参数与仿真参数不完全一致引起的偏差.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同负载下谐振频率及输出电压仿真图

Fig.9 Simulation diagram of resonant frequency and output voltage at different loads

表3 不同负载电阻下谐振频率及输出电压

Tab.3 Resonant frequency and output voltage with different load resistors

R_O/Ω	5	7	10	20	40
f₀/kHz	34.1	34.3	34.7	34.4	34.4
U_O/V	18.5	18.9	19.6	19.8	20.1

新窗口打开| 下载CSV

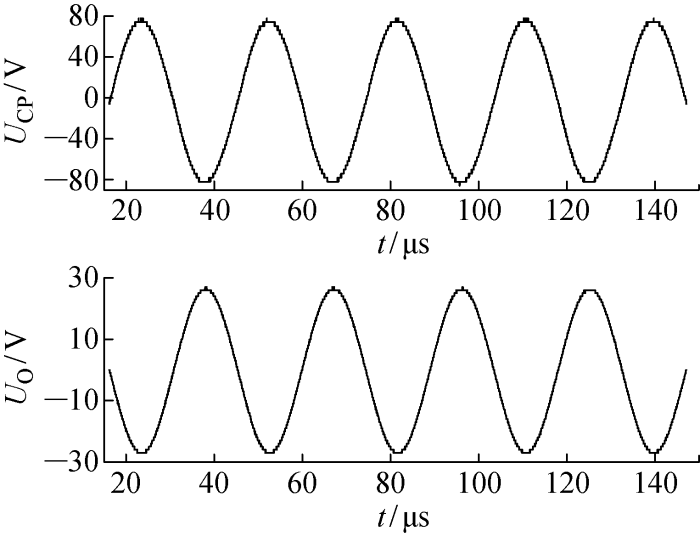
图10给出R_O=7 Ω时输出电压U_O=18.9 V及原边谐振电容电压U_CP=55.8 V波形,波形接近正弦波,呈现完全谐振状态.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 负载为7 Ω时输出及原边谐振电容电压实验波形

Fig.10 Experimental waveforms of output and primary resonant capacitor voltage when the load is 7 Ω

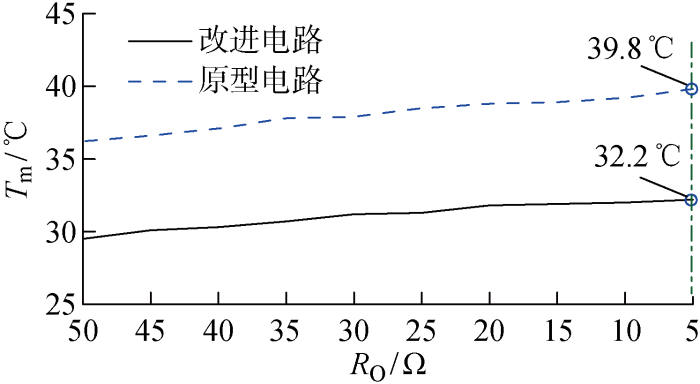
为了验证改进型软开关WPT电路比原自激振荡电路的开关管损耗低、发热少,将负载换成功率滑动变阻器,在相同条件下,负载电阻R_O由50 Ω到5 Ω每隔20 s减小5 Ω,用红外测温仪实时测量MOSFET正面温度(T_m),结果如图11所示.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 两种电路MOSFET温度对比

Fig.11 Comparison of MOSFET temperature of two circuits

对比MOSFET温度发现,改进后的电路与原电路最小温差为6.7 ℃、最大温差为7.6 ℃,平均温差为7.2 ℃;实验测得原电路在R_O=10 Ω时效率约为74%,与改进型电路比较相差约5%,功率越大效率差越大,平均相差至少约为4%.由此可见,改进型谐振WPT电路由于驱动能力更强使开关损耗降低,更适用于高频谐振电路.

改进型电路主开关管栅源电压U_G1及漏源电压U_a波形如图12所示,与理论分析的图4波形基本一致,只是开关管栅源波形受前级驱动影响,波形顶部非理想平直,但基本实现ZVS开关效果.

图12

新窗口打开| 下载原图ZIP| 生成PPT

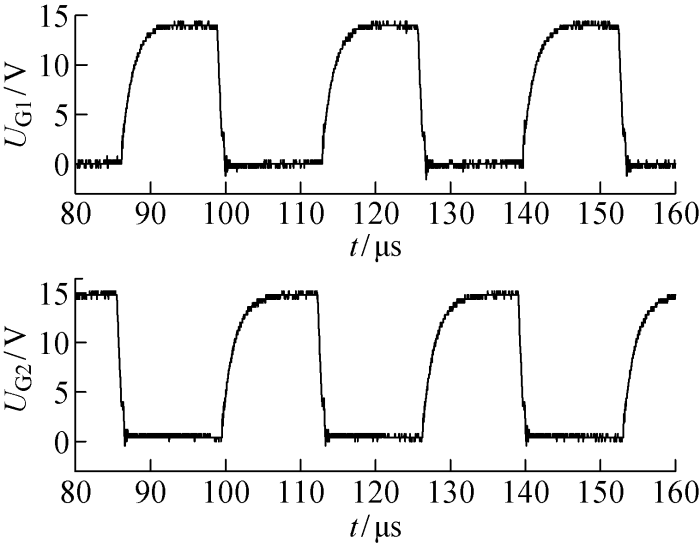
图12 改进型电路主开关管栅源及漏源电压实验波形

Fig.12 Experimental waveforms of gate and drain source voltages of main switch in improved circuit

原电路两个开关管栅源电压驱动波形如图13所示,两路波形互补导通,但由于栅极限流电阻较大,致使栅源导通高电平上升沿较缓.对比图12改进型的驱动电压,电路改进后主功率管栅源驱动脉冲上升沿更加陡直,开关速度更快,开关损耗更低.

图13

新窗口打开| 下载原图ZIP| 生成PPT

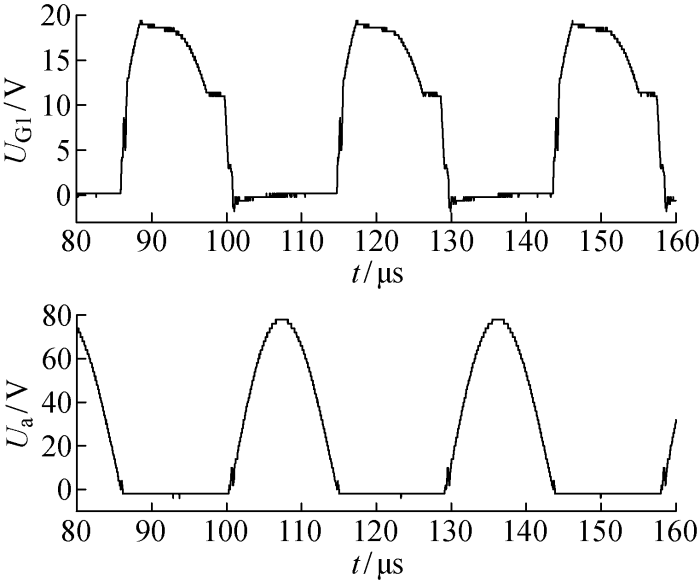
图13 原电路两个开关管栅源电压实验波形

Fig.13 Experimental waveforms of gate-source voltage of two switches in original circuit

6 结论

采用4个MOSFET开关管设计一种改进型低功耗软开关自激振荡WPT系统.分析电路机理并建立电路关键参数的数学模型,为了解决系统多参数多变量多约束优化设计问题,采用非线性规划思想建模并设计了一种“GA+梯度算法”的混合优化算法;该方法能综合考虑系统设计关键因素,一次性得出所有满足要求的最优化参数,克服传统的一次设计仅考虑一个参数最优而难以兼顾参数全局最优的问题;另外,对比分析理论、仿真及实验结果,验证了改进型电路开关管发热量小、系统效率高、软开关特性优良等特点.该型WPT电路在小功率应用场合具有一定优势,但在功率较大时性能达不到设计要求,还需要进一步从设计上进行改进以提高带载能力.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

薛明, 杨庆新, 章鹏程, 等.

无线电能传输技术应用研究现状与关键问题

[J]. 电工技术学报, 2021, 36(8): 1547-1568.

[本文引用: 1]

XUE

Ming

, YANG

Qingxin

, ZHANG

Pengcheng

, et al.

Application status and key issues of wireless power transmission technology

[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.

[本文引用: 1]

[2]

KURS

, KARALIS

, MOFFATT

, et al.

Wireless power transfer via strongly coupled magnetic resonances

[J]. Science, 2007, 317(5834): 83-86.

PMID:17556549 [本文引用: 1]

Using self-resonant coils in a strongly coupled regime, we experimentally demonstrated efficient nonradiative power transfer over distances up to 8 times the radius of the coils. We were able to transfer 60 watts with approximately 40% efficiency over distances in excess of 2 meters. We present a quantitative model describing the power transfer, which matches the experimental results to within 5%. We discuss the practical applicability of this system and suggest directions for further study.

[3]

ZHANG

, PANG

H L

, GEORGIADIS

, et al.

Wireless power transfer-An overview

[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1044-1058.

DOI:10.1109/TIE.41 URL [本文引用: 1]

[4]

高晋阳, 颜国正, 石云波, 等.

肠道微型仿尺蠖式机器人机载供能线圈优化

[J]. 上海交通大学学报, 2020, 54(2): 152-159.

[本文引用: 1]

GAO

Jinyang

, YAN

Guozheng

, SHI

Yunbo

, et al.

Optimization of a powering coil onboard a dime-size inchworm-like robot for exploring the intestine

[J]. Journal of Shanghai Jiao Tong University, 2020, 54(2): 152-159.

[本文引用: 1]

[5]

ZHANG

Q L

, WANG

C F

, YUAN

, et al.

Research on input-parallel single-switch wireless power transfer system with constant-current and constant-voltage output

[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 4817-4830.

DOI:10.1109/TPEL.2021.3118434 URL [本文引用: 1]

[6]

李应智, 魏业文, 王琦婷, 等.

应用于磁耦合谐振式无线电能传输系统的高效率E类逆变电源设计方法

[J]. 电工技术学报, 2019, 34(2): 219-225.

[本文引用: 1]

Yingzhi

, WEI

Yewen

, WANG

Qiting

, et al.

Design method of high efficiency class-E inverter applied to magnetic coupled resonant wireless power transmission system

[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 219-225.

[本文引用: 1]

[7]

徐惠三

. 自激推挽ICPT系统效率分析与优化设计[D]. 西安: 西安科技大学, 2017.

[本文引用: 1]

Huisan

. Efficiency analysis and optimization design of self-oscillatory push-pull ICPT[D]. Xi’an: Xi’an University of Science and Technology, 2017.

[本文引用: 1]

[8]

王尧, 刘卫国, 皇甫宜耿, 等.

基于自激逆变器的无线电能传输系统

[J]. 电工技术学报, 2019, 34(22): 4751-4760.

[本文引用: 4]

WANG

Yao

, LIU

Weiguo

, HUANGFU

Yigeng

, et al.

Wireless power transfer system based on the self-excited inverter

[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4751-4760.

[本文引用: 4]

[9]

张献, 苑朝阳, 杨庆新, 等.

自激推挽式磁耦合无线电能传输系统磁屏蔽特性分析

[J]. 中国电机工程学报, 2018, 38(2): 555-561.

[本文引用: 3]

ZHANG

Xian

, YUAN

Zhaoyang

, YANG

Qingxin

, et al.

Analysis of the magnetic shielding characteristics of magnetic coupling resonant wireless power transmission system based on self-excited push-pull converter

[J]. Proceedings of the CSEE, 2018, 38(2): 555-561.

[本文引用: 3]

[10]

杨晶菁, 陈为, 谢文燕.

自激推挽式无线电能传输系统研究

[J]. 电源学报, 2021, 19(2): 142-152.

DOI:10.13234/j.issn.2095-2805.2021.2.142 [本文引用: 3]

基于对推挽式自激振荡电路原理的详细分析，通过研究发射线圈电压电流的特性，建立了系统的等效电路模型，并采用理论计算和仿真分析验证了系统的性能。同时将自激推挽式无线电能传输系统应用于传感器节点的锂电池变距离无线充电中。最后搭建两线圈系统验证了自激推挽式无线电能传输系统具有频率自适应的能力；在一定范围内变耦合系数时能够输出稳定的功率并保持稳定的效率。当线圈间轴向距离在1～4 cm变化时，自激推挽式无线充电系统可为锂电池提供500 mA的稳定充电电流。

YANG

Jingjing

, CHEN

Wei

, XIE

Wenyan

Research on wireless power transmission system based on self-excited push-pull oscillator

[J]. Journal of Power Supply, 2021, 19(2): 142-152.

DOI:10.13234/j.issn.2095-2805.2021.2.142 [本文引用: 3]

Based on the detailed analysis of the principle for a self-excited push-pull oscillation circuit, an equivalent circuit model of the system was established by studying the voltage and current characteristics of the transmitting coil. In addition, the system performance was verified by theoretical calculation and simulation analysis. Meanwhile, an self-excited push-pull wireless power transmission (WPT) system was applied to the variable-distance wireless charging of lithium batteries at sensor nodes. Finally, a 2-coil system was built to verify the system's frequency self-adaption capability. This system can output stable power and maintain stable efficiency when the coupling coefficient was within a certain range. When the distance between coils varied from 1 to 4 cm, the self-excited push-pull wireless charging system can provide steady charging current of 500 mA for lithium battery.

[11]

H C

, WANG

K P

, FANG

J Y

, et al.

Pulse density modulated ZVS full-bridge converters for wireless power transfer systems

[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 369-377.

DOI:10.1109/TPEL.2018.2812213 URL [本文引用: 1]

[12]

高键鑫, 吴旭升, 高嵬, 等.

非线性规划求解单位功率因数谐振结构参数方法

[J]. 电力系统自动化, 2018, 42(6): 128-134.

[本文引用: 1]

GAO

Jianxin

, WU

Xusheng

, GAO

Wei

, et al.

Non-linear programming method for solving parameters of unity power factor resonant converter

[J]. Automation of Electric Power Systems, 2018, 42(6): 128-134.

[本文引用: 1]

[13]

赵志斌, 王春芳, 骆彬, 等.

单管感应电能传输系统参数全局优化

[J]. 西安交通大学学报, 2018, 52(8): 146-153.

[本文引用: 1]

ZHAO

Zhibin

, WANG

Chunfang

, LUO

Bin

, et al.

Global optimization for parameters in single switch inductive power transmission system

[J]. Journal of Xi’an Jiaotong University, 2018, 52(8): 146-153.

[本文引用: 1]

[14]

朱国荣, 林鹏, 陆江华, 等.

无线能量传输系统双LCC谐振补偿电路研究

[J]. 华中科技大学学报(自然科学版), 2017, 45(5): 104-109.

[本文引用: 1]

ZHU

Guorong

, LIN

Peng

, LU

Jianghua

, et al.

Research on double LCC compensation circuit in inductive power transfer system

[J]. Journal of Huazhong University of Science & Technology (Natural Science Edition), 2017, 45(5): 104-109.

[本文引用: 1]

[15]

孙跃, 夏金凤, 唐春森, 等.

采用元胞遗传算法的无线电能传输网路径寻优

[J]. 西安交通大学学报, 2017, 51(4): 30-36.

[本文引用: 1]

SUN

Yue

, XIA

Jinfeng

, TANG

Chunsen

, et al.

Path optimization for wireless power transfer networks with cellular genetic algorithm

[J]. Journal of Xi’an Jiaotong University, 2017, 51(4): 30-36.

[本文引用: 1]

[16]

REZAZADEH

, KHIALI-MIAB

A two-layer genetic algorithm for the design of reliable cellular manufacturing systems

[J]. International Journal of Industrial Engineering Computations, 2017, 8(3): 315-332.

[本文引用: 1]

[17]

SONG

, LI

Z J

, DU

Z J

, et al.

Design for constant output voltage and current controllability of primary side controlled wireless power transfer system

[C]// 2017 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW). Chongqing, China: IEEE, 2017: 1-6.

[本文引用: 1]

[18]

X H

, CHU

H J

, WONG

S C

, et al.

An IPT battery charger with near unity power factor and load-independent constant output combating design constraints of input voltage and transformer parameters

[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 7719-7727.

DOI:10.1109/TPEL.63 URL [本文引用: 1]

无线电能传输技术应用研究现状与关键问题

2021

... 无线电能传输(Wireless Power Transfer, WPT)系统通过磁场或电场完成原、副边设备的非接触能量传递,克服传统有线输电的磨损、漏电、火花放电等各种问题,增强设备对复杂环境的适应能力,具有广阔的应用前景^[1-2].磁耦合WPT技术在手机、家用电器、穿戴式医疗设备等中小功率产品方面的研究和应用已经成为热点^[3-4].中小功率产品对体积、质量、效率、可靠性、稳定性及性价比等方面都有较高要求,很多学者从电路拓扑结构、耦合变压器优化设计等方面进行了深入研究.文献[5-6]中采用单个开关管实现软开关,降低开关损耗,缺点是复杂的控制电路、辅助电源及检测电路等增大了系统体积质量.文献[7]中采用两个开关管的自激推挽拓扑结构来实现WPT,但为了实现频率跟踪设计了较为复杂的控制激励电路.文献[8⇓-10]中设计的自激推挽谐振式逆变电路的驱动控制电路较为简单,实现了零电压开关(Zero Voltage Switching, ZVS)^[11],具有良好的频率自动跟踪性能,但不足之处有两点:一是功率开关管的驱动电阻过大,参数一般在hΩ级别,而根据金属-氧化物半导体场效应晶体管(Metal Oxide Semiconductor Field Effect Transistor,MOSFET)技术手册及使用经验,要使开关管减小驱动冲击的条件下迅速开通,该驱动电阻选为10 Ω左右即可,过大的驱动电阻会使开关管驱动脉冲上升过缓,造成开关损耗增大;二是该电路虽然实现了软开关ZVS,但由于驱动电阻及谐振互锁二极管导通压降的影响,无论是零电压开通还是零电压关断,开关管漏源电压与栅源驱动电压的交叠区面积还可以进一步减小,以降低开关损耗. ...

无线电能传输技术应用研究现状与关键问题

2021

Wireless power transfer via strongly coupled magnetic resonances

2007

Wireless power transfer-An overview

2019

肠道微型仿尺蠖式机器人机载供能线圈优化

2020

肠道微型仿尺蠖式机器人机载供能线圈优化

2020

Research on input-parallel single-switch wireless power transfer system with constant-current and constant-voltage output

2022

应用于磁耦合谐振式无线电能传输系统的高效率E类逆变电源设计方法

2019

应用于磁耦合谐振式无线电能传输系统的高效率E类逆变电源设计方法

2019

2017

基于自激逆变器的无线电能传输系统

2019

... 文献[8⇓-10]中所用的自激谐振式软开关WPT系统核心电路(原边谐振电路)如图1所示.图中:Q₁、Q₂为工作在互补推挽模式下两个MOSFET开关管;U_D、V_D分别为主直流输入电源电压及MOS管的驱动电源电压;L_d1、L_d2为防止开关管直通短路的扼流电感;L_P、L_S分别为原、副边谐振电感,互感大小为M;C_P、C_S别为原、副边谐振电感的补偿电容,本文采用原边并联-副边串联(Primary Side Parallel-Secondary Side Series, PS)拓扑^[8],虽然文献[9-10]中采用PS拓扑,但不影响原边谐振电路结构的设计改进;二极管D₁、D₂通过实时检测原边并联谐振网络的电压来钳位控制两个开关管交替通断,是实现电路自激推挽谐振的关键器件;R_G1、R_G2分别为Q₁、Q₂的栅级开通限流电阻;R_GS1、R_GS2为MOS管的栅源寄生电容提供放电通道,防止开关管误动作;稳压管D_GS1、D_GS2可以防止Q₁、Q₂栅源过电压而击穿;U_a、U_b分别为Q₁、Q₂的漏源电压. ...

... [8],虽然文献[9-10]中采用PS拓扑,但不影响原边谐振电路结构的设计改进;二极管D₁、D₂通过实时检测原边并联谐振网络的电压来钳位控制两个开关管交替通断,是实现电路自激推挽谐振的关键器件;R_G1、R_G2分别为Q₁、Q₂的栅级开通限流电阻;R_GS1、R_GS2为MOS管的栅源寄生电容提供放电通道,防止开关管误动作;稳压管D_GS1、D_GS2可以防止Q₁、Q₂栅源过电压而击穿;U_a、U_b分别为Q₁、Q₂的漏源电压. ...

... 通过原理分析可知,图1所示的自激谐振电路中谐振箝位二极管既连接MOS管的控制极又与主谐振电路直接交联,从而导致电路设计中的固有矛盾.改进思路为采用小功率MOS管代替二极管实现主电路与控制电路相对隔离,MOS管驱动电阻不受主电路电流影响;又由于MOS管的导通压降比二极管小很多,所以显著降低主功率MOS管的关断电压,与文献[8]中驱动电路加入电容实现负压关断的方式相比,此电路同样能有效改善电路的ZVS特性.改进的自激谐振WPT电路如图3所示. ...

基于自激逆变器的无线电能传输系统

2019

自激推挽式磁耦合无线电能传输系统磁屏蔽特性分析

2018

... ,虽然文献[9-10]中采用PS拓扑,但不影响原边谐振电路结构的设计改进;二极管D₁、D₂通过实时检测原边并联谐振网络的电压来钳位控制两个开关管交替通断,是实现电路自激推挽谐振的关键器件;R_G1、R_G2分别为Q₁、Q₂的栅级开通限流电阻;R_GS1、R_GS2为MOS管的栅源寄生电容提供放电通道,防止开关管误动作;稳压管D_GS1、D_GS2可以防止Q₁、Q₂栅源过电压而击穿;U_a、U_b分别为Q₁、Q₂的漏源电压. ...

自激推挽式磁耦合无线电能传输系统磁屏蔽特性分析

2018

自激推挽式无线电能传输系统研究

2021

... -10]中采用PS拓扑,但不影响原边谐振电路结构的设计改进;二极管D₁、D₂通过实时检测原边并联谐振网络的电压来钳位控制两个开关管交替通断,是实现电路自激推挽谐振的关键器件;R_G1、R_G2分别为Q₁、Q₂的栅级开通限流电阻;R_GS1、R_GS2为MOS管的栅源寄生电容提供放电通道,防止开关管误动作;稳压管D_GS1、D_GS2可以防止Q₁、Q₂栅源过电压而击穿;U_a、U_b分别为Q₁、Q₂的漏源电压. ...

自激推挽式无线电能传输系统研究

2021

Pulse density modulated ZVS full-bridge converters for wireless power transfer systems

2019

非线性规划求解单位功率因数谐振结构参数方法

2018

... 改进型自激谐振WPT系统电路的关键参数如原副边电感、电容、互感等,主要集中于谐振网络中,但在实际电路设计中还需要考虑输出电压的稳压值、输出功率的最大值、电感的最大电流、电容的最高电压、开关管的器件压流容限、谐振频率范围以及直流扼流电感对频率的影响等因素.因此,对系统参数优化问题实质上是一个多变量多约束非线性规划(NonLinear Programming, NLP)问题^[12-13].采用松耦合变压器漏感模型建立PS型谐振网络等效电路模型^[14],如图5所示. ...

非线性规划求解单位功率因数谐振结构参数方法

2018

单管感应电能传输系统参数全局优化

2018

单管感应电能传输系统参数全局优化

2018

无线能量传输系统双LCC谐振补偿电路研究

2017

无线能量传输系统双LCC谐振补偿电路研究

2017

采用元胞遗传算法的无线电能传输网路径寻优

2017

... 针对非线性规划问题,MATLAB提供了丰富的智能优化算法库,如遗传算法(Genetic Algorithm, GA)、粒子群算法、模式搜索算法、极小化极大算法等^[15].算法优化具有一定的随机性,容易限入局部最优解,一般需要多次运算调整参数才能得到一个稳定的最优值^[16].为了提高优化效率,将基于种群智能决策的遗传算法与梯度算法结合,得到一种混合优化算法(见图7),该算法只需要对种群数量及迭代次数等参数进行简单设置就能稳定得到全局最优解. ...

采用元胞遗传算法的无线电能传输网路径寻优

2017

A two-layer genetic algorithm for the design of reliable cellular manufacturing systems

2017

Design for constant output voltage and current controllability of primary side controlled wireless power transfer system

2017

... 系统设计中原边L_P与C_P采用简化的设计公式(13)中的g₁₀,是为了使系统参数在一定的负载变化范围内具有较强的鲁棒性.改变负载检验系统稳频及稳压效果,得到Multisim仿真结果如图9所示.从仿真图可以看出,在其他参数不变的情况下,负载R_O>5 Ω,即输出功率P_O<85 W范围内系统均具有较强的频率及电压稳定性(仿真中R_O=1 000 Ω时频率及电压稳定性亦不变).利用实验验证不同负载电阻下的频率及电压稳定性^[17-18](见表3).由表3可以看出谐振频率f₀及输出电压U_O能够稳定在一定范围内;由图9可见,实验数据低于仿真值,但是谐振频率较接近理论值,这是由于实际参数与仿真参数不完全一致引起的偏差. ...

An IPT battery charger with near unity power factor and load-independent constant output combating design constraints of input voltage and transformer parameters

2019

〈

〉