基于在线LASSO VAR和EGARCH模型的风场功率集成概率预测

doi:10.16183/j.cnki.jsjtu.2021.377

基于在线LASSO VAR和EGARCH模型的风场功率集成概率预测

王鹏, 李艳婷^,, 张宇

上海交通大学机械与动力工程学院,上海 200240

Probabilistic Forecasting of Wind Power Generation Using Online LASSO VAR and EGARCH Model

WANG Peng, LI Yanting^,, ZHANG Yu

School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 李艳婷,副教授,博士生导师; E-mail:ytli@sjtu.edu.cn.

责任编辑: 王历历

收稿日期: 2021-09-26 修回日期: 2021-12-20 接受日期: 2021-12-31

基金资助:

国家自然科学基金面上项目(72072114)

Received: 2021-09-26 Revised: 2021-12-20 Accepted: 2021-12-31

作者简介 About authors

王鹏(1998-),硕士生,研究方向为数据驱动的能源预测等.

摘要

由于风速波动性大,风力发电往往呈现一定的不确定性.传统风能预测模型以均值为0、方差固定的正态分布度量不确定性,但方差可能随时间变化,即具有异方差性.为提升预测精度,基于在线最小绝对收缩和选择算子的向量自回归(LASSO VAR)和指数自回归条件异方差(EGARCH)模型,提出一种考虑异方差性的风场级功率集成概率预测模型.首先使用在线LASSO VAR模型预测风力机的有功功率,再利用自回归条件异方差检验验证残差的异方差性,并利用信息冲击曲线和动态显著线评估正负残差对未来条件方差的不对称影响.然后针对异方差性和不对称性,使用EGARCH模型对单风力机有功功率的残差进行预测,得到有功功率的条件方差.最后,考虑各风力机有功功率的相关性,将风场中各风力机的有功功率求和,得到整个风场总有功功率的概率预测结果.将该方法应用于中国华东某地风场,验证了该模型能有效提高预测精度.

关键词： 在线LASSO VAR; 异方差; 指数条件异方差模型; 概率预测

Abstract

Wind power generation has uncertainty due to the high fluctuation of wind speed. In traditional wind power prediction models, the uncertainty is measured by normal distribution with zero mean and constant variance. However, the variance may vary with time, which means the variance has heteroscedasticity. To improve the prediction accuracy, this paper proposes a new integrated probabilistic wind power prediction model for wind farm considering heteroscedasticity based on online least absolute shrinkage and selection operator and vector autoregression (LASSO VAR) and the exponential generalized autoregressive conditional heteroskedasticity (EGARCH) model. First, online LASSO VAR is used to forecast power output. Then, heteroscedasticity of residuals is validated by autoregressive conditional heteroskedasticity test. Considering heteroscedasticity, the news impact curve and dynamic significance line verify that positive and negative residuals affect future volatility asymmetrically. Thus, the EGARCH model is used to forecast the residuals to obtain the conditional variance of point prediction results. Finally, the probabilistic result of total power output is obtained by summing the power output of turbines in the wind farm considering the correlation of the active wind power of wind turbines. This method is applied to forecast the power output of a wind farm in East China and is proved effective in improving the prediction accuracy.

Keywords： online least absolute shrinkage and selection operator and vector autoregression (LASSO VAR); heteroscedasticity; exponential generalized autoregressive conditional heteroskedasticity (EGARCH) model; probabilistic forecasting

PDF (20159KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王鹏, 李艳婷, 张宇. 基于在线LASSO VAR和EGARCH模型的风场功率集成概率预测[J]. 上海交通大学学报, 2023, 57(7): 845-858 doi:10.16183/j.cnki.jsjtu.2021.377

WANG Peng, LI Yanting, ZHANG Yu. Probabilistic Forecasting of Wind Power Generation Using Online LASSO VAR and EGARCH Model[J]. Journal of Shanghai Jiaotong University, 2023, 57(7): 845-858 doi:10.16183/j.cnki.jsjtu.2021.377

由于传统能源的不可再生性,清洁绿色能源受到越来越广泛的关注.风能作为一种清洁的可再生能源,是近年来全球增长最快的能源之一.风能是重要的可再生能源,风力发电(简称风电)累计装机容量持续增长,从2010年的198 GW增长到2021年的837 GW,预计到2030年将达到 3 200 GW^[1].然而,风速不确定性高、波动性大,这使得风力机有功功率往往也呈现一定的不确定性,因此有必要进行有功功率的概率预测.但传统的概率预测模型未考虑方差可能随时间变化,即具有异方差性的问题,影响了功率预测的准确性.因此,亟需探索新方法以准确预测整个风电场的输出功率.

风电预测模型一般可分为确定性预测和概率预测两类.现有风电预测模型大多是仅提供特定预测值的确定性模型.确定性模型可分为基于数值天气预测的模型^[2-3]、传统统计模型^[4⇓-6]、基于机器学习的模型^[7-8]和这些方法的集成模型^[9-10].不同确定性预测模型的详细概述可见文献[11-12].考虑时空相关的回归模型是同时考虑时间和空间相关性的确定性预测模型,基于最小绝对收缩和选择算子(LASSO)的向量自回归(Vector Autoregression, VAR)模型计算效率较高,是一种常用的时空模型^[13-14].确定性预测模型的一个明显缺点是不能量化预测的不确定性.相反,概率预测模型可以给出预测值的置信区间或预测值的概率分布函数来评估预测的不确定性.

概率预测模型主要分为参数、非参数和集成模型.参数模型需要预测指定数据和参数的分布.高斯分布^[15]和贝塔分布^[16]是描述风电分布的两种合理选择.非参数模型并不需要预先指定数据和参数的分布.分位数回归(Quantile Regression, QR)是广泛应用的非参数风电概率预测模型.文献[17-18]中利用局部QR得到风能的概率预测.核密度估计(Kernel Density Estimation, KDE)模型由于灵活的数据适应性,也常用作非参数概率预测模型.KDE模型可以提供风电预测概率密度函数的所有信息,然而,由于传统的KDE为所有历史数据分配相等的权重,所以会产生具有高同质性的密度函数.因此,有研究提出采用与历史数据相似性相关的加权核密度估计^[19].

近年来,随着基于数值天气预测模型的发展,基于集成的概率预测模型也被应用于一些研究中.其中,贝叶斯模型平均(Bayes Model Averaging, BMA)是最重要的一个.风力机有功功率预测的概率密度函数由几个条件概率密度函数的加权和得到,更高的权重被分配给预测更准确的成员.BMA已成功应用于风速^[20]和风电^[21]的概率预测.集成方法可以基于集成成员的预测结果进行偏差校正,由于条件分布设置灵活,所以具有较高的适应性.

然而,以上概率预测模型未充分考虑异方差性,自回归条件异方差(Autoregressive Conditional Heteroskedasticity, ARCH)族模型为预测方差提供了更好的选择.文献[22]中结合自回归移动平均(Autoregressive Moving Average, ARMA)模型和广义自回归条件异方差(Generalized Autoregressive Conditional Heteroskedasticity, GARCH)模型建立了ARMA-GARCH模型预测风功率数据,并针对不同情况的预测误差给予对应的补偿方案,提升了风电功率的预测精度.文献[23]中首先建立风电波动性与风电预测误差的动态相依性模型,并结合差分整合ARMA模型和GARCH模型建立时变分布边缘模型,最终给出不同波动水平下的风电条件预测误差分布.

综上所述,针对风电不确定性高和现有概率预测模型未充分考虑异方差性的问题,首先使用在线LASSO VAR模型对风电场中多个风力机的有功功率时间序列进行建模,以描述风力机有功功率间的时空相关性,减少预测所需的运行时间并提升预测准确度.同时,考虑风能点预测模型可能存在的异方差问题,使用ARCH检验验证点预测的异方差性,并使用信息冲击曲线和动态显著线验证正负偏差对未来残差波动的不同影响.之后使用指数自回归条件异方差(EGARCH)模型对点预测模型的不确定性建模,追踪点预测模型不确定性的趋势.最后基于风力机功率的空间相关性,对风场中风力机的有功功率进行集成,计算风场总有功功率的均值和方差,得到风场总功率的概率预测.

1 数据集介绍

使用中国华东某地海上风场的数据.该风场共有24台风力机,风力机额定功率为3.6 MW,总装机容量为20.42×10⁴ kW.风场所处位置四季分明,年平均气温为16 ℃,年平均降水量为1 100 mm.风力机的传感器记录风力机所在位置的实时数据,包括风速、风向、有功功率.为了提升后续时序模型的效果,需要使时序数据更加稳定,因此对每小时的数据取平均值以平滑数据.

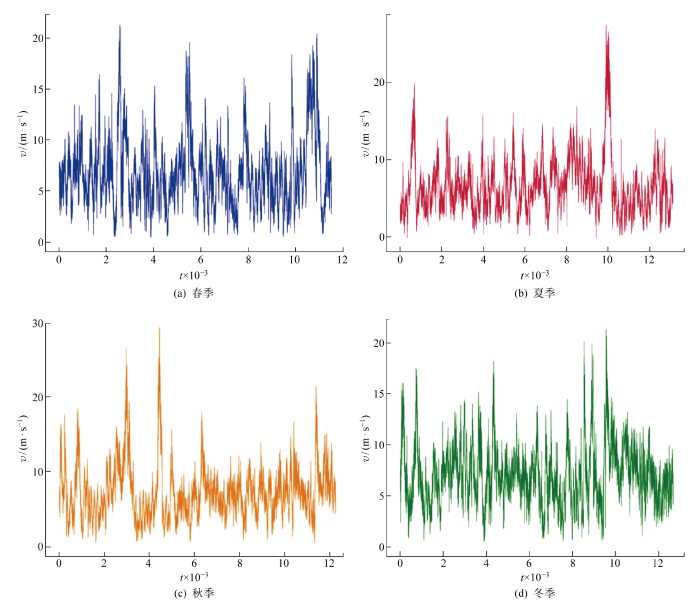
图1为风场一年四季的风速时序图对比.图中:t为相应季节中的时间步索引,每两个时间步的间隔为10 min;v为风速.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 不同季节风速时序图

Fig.1 Time series of wind speed in different seasons

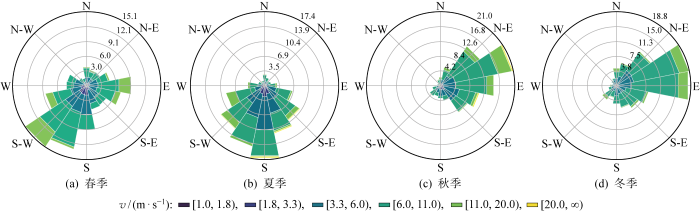
图2为风向玫瑰图对比.风速和风向在不同季节呈现不同趋势和模式.风速在不同季节均具有较大的波动性,与其他季节相比,冬季的风速波动最小.不同季节的盛行风不同,春季盛行西南风,夏季盛行南风,而秋季和冬季主要盛行东风.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 不同季节风向玫瑰图

Fig.2 Rose diagram of wind direction in different seasons

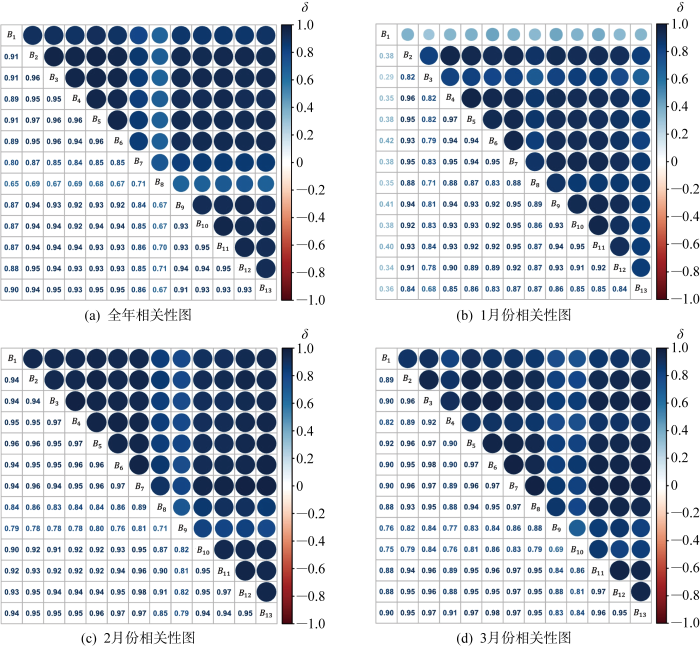
图3展示了不同时期下(全年、1月、2月、3月)前13台风力机(B₁~B₁₃)记录的有功功率相关系数(δ).可以看出,大多数相关系数都在0.8以上,这意味着风力机的有功功率具有较强的空间相关性.因为有功功率可以支撑空间关系的研究,所以仅使用有功功率数据,该特征时间跨度为2019年1月2日至2019年12月31日.在不同时期内,风力机的有功功率相关性也在随时间不断变化.例如1月,1号风力机与其他风力机的相关性较低;2月,1号与其他风力机的相关性都在0.7以上,而9号和13号风力机与其余风力机相关性较1月份明显降低;3月,9号和10号风力机与其余风力机的相关性较低.而从全年来看,8号风力机与其余风力机相关性较低.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 风力机有功功率相关性图

Fig.3 Correlation of power output of turbines

2 研究方法

2.1 在线LASSO VAR模型

VAR模型可以分析风力机有功功率间的空间相关性,并且计算效率高、效果好,可以用于有功功率的点预测^[24],设P_t_,_i为风力机i在时刻t的有功功率,P_t为有功功率向量,包含t时刻所有风力机的有功功率数据,引入VAR模型^[25]则有

(1)$\boldsymbol{P}_{t}=\sum_{l=1}^{L} \boldsymbol{A}_{l} \boldsymbol{P}_{t-l}+\boldsymbol{\epsilon}_{t}$

式中:A_l为系数矩阵;l为滞后阶数;L为模型阶数;白噪声项$\boldsymbol{\epsilon}_{t}$假设服从多元正态分布, $\boldsymbol{\epsilon}_{t}$~(0, Σ),Σ为协方差矩阵.通常,A_l的估计可以通过最小化训练集上的均方误差得到.然而,随着维度增大,所需拟合的参数数量增长速度是非线性的.因此,当训练数据不足时,大量待拟合参数会带来严重的过拟合问题,从而导致预测效果不佳.

LASSO正则化可以有效地解决过拟合问题.文献[26]中提出风能预测中LASSO VAR的应用,LASSO VAR的损失函数为

(2)

\overset{T}{\sum_{t = 1}} {(P_{t} - {\hat{P}}_{t})}_{2}^{2}

+λ

\overset{L}{\sum_{l = 1}} {(A_{l})}_{1}

式中: ${\hat{P}}_{t}$ 为P_t的预测值; ${(\cdot)}_{1}$ 为矩阵1-范数, ${(\cdot)}_{2}$ 为向量2-范数,T为求和的时间长度.式(2)中的损失函数可以使A_l有解析解.正则化参数λ可以控制A_l的稀疏程度,过滤掉部分不重要的相关系数,从而使A_l中只包含对预测影响最明显的部分系数.式(2)的最优化可以由循环坐标下降法求解^[27].循环坐标下降法在每次求解中固定其他系数,只对损失函数求解一个系数的最优值,不断循环迭代直至收敛.在每次求解中,系数A_l_,_i_,_j可由下式更新:

(3)A_l_,_i_,_j=

\frac{S (\overset{T}{\sum_{t = 1}} P_{t - l, j} (P_{t, i} - {\hat{P}}_{t, i} + A_{l, i, j} P_{t - l, j}), λ)}{\overset{T}{\sum_{t = 1}} P_{t - l, j}^{2}}

S(z,λ)=

\{\begin{array}{l} z - λ, & z > 0 且 λ < | z | \\ z + λ, & z < 0 且 λ < | z | \\ 0, & λ > | z | \end{array}

式中: ${\hat{P}}_{t, i}$ 为t时刻风力机i功率的预测值;S(·)为软阈值算子.

为了使模型更好地捕捉到有功功率序列的变动,每当获得新的有功功率数据时,系数矩阵A_l都需要被重新估计.然而,重新估计一个高维的LASSO VAR模型非常耗时.因此,基于文献[28]中的工作,对有功功率LASSO VAR模型采用如下在线估计方法.该方法重新将A_l更新公式表示为

(4)A_l_,_i_,_j=

\frac{S (Λ, λ)}{Z_{l, l, T, j, j}}

(5)

\begin{array}{l} Λ = Z_{0, l, T, i, j} - \overset{L}{\sum_{m = 1}} {Z^{T}}_{m, l, T, j} {A^{T}}_{m, i} + \\ Z_{l, l, T, j, j} A_{l, i, j} \\ Z_{l, l, T, j, j} = \overset{T}{\sum_{t = 1}} P_{t - l, j}^{2} \end{array}\}

式中:Λ为式(3)中软阈值算子的第一项;A_m_,_i为模型的系数矩阵;Z为两台风力机的功率数据相乘并求和后的表示算子,下标的前两项为两风力机历史时间的索引,下标的末两项为两风力机的索引,可以用矩阵表示为

Z_m_,_l_,_T=

\overset{T}{\sum_{t = 1}}

P_t_-_m

{P^{T}}_{t - l}

Z_m_,_l_,_T可以变换为

(6)Z_m_,_l_,_T=Z_m_,_l_,_T_-1+P_T_-_m

{P^{T}}_{T - l}

因为Z_m_,_l_,_T_-1= $\overset{T - 1}{\sum_{t = 1}}$ P_t_-_m ${P^{T}}_{t - l}$ (m=0, 1, …, L; l=1, 2, …, L)可以由之前的时间步直接得到,所以,只需要存储L步的数据与Z_m_,_l_,_T_-1,就可以得到Z_m_,_l_,_T,进而可以快速更新A_l的元素.

超参数λ的选取沿用文献[28]中的方法,即给定一个λ的取值集合,在每一次更新中,挑选出使 $\overset{T - 1}{\sum_{t = 1}} {(P_{t} - {\hat{P}}_{t})}_{2}^{2}$ 最小的λ.

在时刻t,给定系数矩阵A_l,l=1, 2, …, L,在线LASSO VAR在时刻t+1的有功功率预测向量P_t₊₁=[P_t_+1,1P_t_+1,2 … P_t_+1,_Q]^T可以估计为

(7)

{\hat{P}}_{t + 1}

\overset{L}{\sum_{l = 1}}

A_lP_t_+1-_l

2.2 异方差模型

2.2.1 ARCH检验

在线LASSO VAR模型预测有功功率时,假设误差项为白噪声,方差为常数,即$\boldsymbol{\epsilon}_{t}$~N(0, Σ).但实际上,有功功率预测的误差项可能和残差历史值以及时间相关,即具有异方差效应.

传统的检验异方差效应的方法主要包括图示检验法、Breusch-Pagan检验、Goldfeld-Quandt检验等^[29].但上述异方差检验方法主要针对多元回归问题,对时间序列预测问题而言,ARCH检验更合适.因此,采用ARCH检验验证风力机有功功率预测的异方差性.

采用ARCH检验对在线LASSO VAR模型得到的所有风力机有功功率残差向量a_t进行检验.单台风力机对应的有功功率残差值a_t=P_t-E(P_t|F_t_-1),其中P_t为时刻t所有风力机有功功率之和,F_t_-1为时刻t-1时所有信息的信息集,E(P_t|F_t_-1)为时刻t的在线LASSO VAR预测的有功功率值.构造如下自回归模型:

(8)

a_{t}^{2}

=α₀+

\overset{q}{\sum_{l = 1}}

α_l

a_{t - l}^{2}

+e_t, t=q+1, q+2, …, M

式中:e_t为误差项;q为模型阶数;M为样本量.用普通最小二乘法估计自回归模型的参数并计算预测t时刻的残差 ${\hat{e}}_{t}$ ,令回归模型对因变量的拟合程度和残差平方和分别为

e_{S S R_{0}}

\overset{M}{\sum_{t = q + 1}}

(

a_{t}^{2}

-u)²,

e_{S S R_{1}}

\overset{M}{\sum_{t = q + 1}} {\hat{e}}_{t}^{2}

其中u= $\frac{1}{M} \overset{M}{\sum_{t = 1}} a_{t}^{2}$ ,得到检验统计量为

(9)F=

\frac{(e_{S S R_{0}} - e_{S S R_{1}}) / q}{e_{S S R_{1}} / (M - 2 q - 1)}

零假设为参数α₁=α₂=…=α_q=0,零假设成立时F近似服从F(q, M-2q-1);否则,拒绝零假设,认为有功功率预测值存在异方差效应.

2.2.2 EGARCH模型

GARCH模型^[30]是ARCH模型^[31]的推广,可以修正点预测的异方差性,计算点预测的不确定性.GARCH模型对在线LASSO VAR模型的误差项$\boldsymbol{\epsilon}_{t}$建模, GARCH(p', q)过程由下式给出:

(10)

\begin{array}{l} a_{t} | F_{t - 1} = ε_{t} \sqrt{h_{t}} \\ h_{t} = α_{0} + \overset{p'}{\sum_{i = 1}} α_{i} a_{t - i}^{2} + \overset{q}{\sum_{j = 1}} β_{j} h_{t - j} \end{array}\}

式中:ε_t为零均值单位方差的独立同分布白噪声,其分布常取标准正态分布、标准化的t分布、广义误差分布; $a_{t}^{2}$ 的模型阶数p'>0, q≥0, α₀>0, α_i≥0, 自回归部分待求解的模型参数β_j≥0;条件方差D(P_t|F_t_-1)=D(a_t|F_t_-1)=h_t,即有功功率预测的条件方差可以由有功功率残差平方 $a_{t}^{2}$ 滞后值的线性组合表示.

类似于经济学中,回报低于预期时股市波动率往往上升,回报高于预期时股市波动率往往下降^[32];风能概率预测中,有功功率点预测的正负偏差对未来波动率的影响也可能不同,后续将从数据维度进行验证.基于上述分析,因为正负偏差对波动率有不对称影响,所以使用EGARCH模型^[33]对有功功率的条件方差进行建模更合适.

EGARCH(p', q)模型中,有功功率残差a_t的分布与GARCH模型相同,为式(10).令g(ε_t)=αε_t+γ( $|ε_{t}|$ -E $|ε_{t}|$ ),g(ε_t)的期望为0,z'_t=(1, g(ε_t_-1), …, g(ε_t_-_p'), ln h_t_-1, ln h_t_-2, …, ln h_t_-_q),ω^T=(α₀, α₁, …, α_p', β₁, β₂, …, β_q),EGARCH模型的h_t由下式给出:

(11)ln h_t=z'_tω, β₁≡1

式中:z'_t为输入变量,为z_t的转置;α、γ和 ω为待学习的参数.

EGARCH模型的参数通常采用极大似然估计法进行估计.假设ε_t~N(0, 1),EGARCH模型的对数似然损失L(ω)为

(12)

\begin{array}{l} L (ω) = \frac{\overset{M}{\sum_{t = 1}} l_{t} (ω)}{M} \\ l_{t} (ω) = - \frac{1}{2} l n h_{t} - \frac{1}{2} a_{t}^{2} h_{t}^{- 1} \end{array}\}

式中:l_t(ω)为模型参数为ω时t时刻的损失值,对参数ω进行求导有

(13)

\frac{\partial l_{t}}{\partial ω}

\frac{1}{2} h_{t}^{- 1} \frac{\partial h_{t}}{\partial ω} (\frac{a_{t}^{2}}{h_{t}} - 1)

(14)

\frac{\partial h_{t}}{\partial ω}

=h_t

(z_{t} + \overset{p'}{\sum_{j = 1}} α_{j} \frac{\partial g (ε_{t - j})}{\partial ω} + \overset{q}{\sum_{i = 1}} β_{i} \frac{1}{h_{t - i}} \frac{\partial h_{t - i}}{\partial ω})

具体估计细节可以参考文献[34], 另外可以采用文献[35]中提出的迭代步骤来获得极大似然估计量.ω_o表示第o次迭代后的参数值,ω_o₊₁可由下式计算:

(15)ω_o₊₁=ω_o+λ_o

{(\overset{M}{\sum_{t = 1}} \frac{\partial l_{t}}{\partial ω} \frac{\partial l_{t}}{\partial ω'})}^{- 1} \overset{M}{\sum_{t = 1}} \frac{\partial l_{t}}{\partial ω}

式中:∂l_t/∂ω在ω_o处估计,λ_o为一个可变的步长,选定λ_o以最大化给定方向上的似然函数,给定方向由∂l_t/∂ω的T×1向量的最小二乘回归得到.

2.3 风场的有功功率概率预测

一般来说,风场中的风力机作为整体,针对特定区域供电,就风力机风能预测问题而言,更关注整个风场的有功功率预测.因此,在得到单个风力机的有功功率后,需要将所有风力机的有功功率求和.不同风力机间的有功功率相关系数计算公式为

(16)ρ_ij=

\frac{\overset{M}{\sum_{t = 1}} (P_{t, i} - u_{i}) (P_{t, j} - u_{j})}{\sqrt{\overset{M}{\sum_{t = 1}} (P_{t, i} - u_{i})^{2}} \sqrt{\overset{M}{\sum_{t = 1}} (P_{t, j} - u_{j})^{2}}}

式中: ρ_ij为风力机i、j有功功率的相关系数;u_i、u_j分别为风力机i、j有功功率的平均值.而存在相关性的风力机有功功率求和的均值和方差计算公式为

(17)E(

\overset{n}{\sum_{i = 1}}

P_t_,_i|F_t_-1)=E(P_t_{, 1}|F_t_-1)+…+E(P_t_,_n|F_t_-1)

(18)

\begin{array}{l} D (\overset{n}{\sum_{i = 1}} P_{t, i} | F_{t - 1}) = \\ \overset{n}{\sum_{i = 1}} D (P_{t, i} | F_{t - 1}) + 2 \sum_{i \neq j} O_{i, j, t} = \\ \overset{n}{\sum_{i = 1}} h_{t, i} + 2 \sum_{i \neq j} O_{i, j, t} \\ O_{i, j, t} = ρ_{i j} \sqrt{D (P_{t, i} | F_{t - 1})} \times \\ \sqrt{D (P_{t, j} | F_{t - 1})} = \\ ρ_{i j} \sqrt{h_{t, i}} \sqrt{h_{t, j}} \end{array}\}

式中:E(P_t_,_i|F_t_-1)为在线LASSO VAR预测时刻t时风力机i有功功率的条件均值;D(P_t_,_i|F_t_-1)为风力机i有功功率的条件方差;O_i_,_j_,_t为时刻t时风力机i和j有功功率的协方差预测值.由式(17)和式(18)可以得到整个风场有功功率及其不确定性.

3 模型评估

从三方面评估新模型的效果:在线LASSO VAR方法对有功功率的点预测效果、EGARCH模型对单风力机有功功率的概率预测效果、考虑功率相关性的整个风场的点预测与概率预测效果.实例研究的代码基于Windows系统的R version 4.0.2执行.

3.1 在线LASSO VAR有功功率点预测

首先使用在线LASSO VAR对24台风力机2019年全年的有功功率进行建模,时间分辨率为1 h,共有 8402 个观测.为了方便在线LASSO VAR模型与其他时空模型进行对比,将前 7000 个观测归为训练集,最后的 1402 个观测作为测试集.使用均方根误差(RMSE)、平均绝对误差(MAE)与对称平均绝对百分比误差(SMAPE)作为评估指标,其数学表达式如下:

(19)

\begin{array}{l} α_{R M S E} = \sqrt{\frac{1}{M} \overset{M}{\sum_{t = 1}} {(P_{t} - {\hat{P}}_{t})}_{2}^{2}} \\ α_{M A E} = \frac{1}{M} \overset{M}{\sum_{t = 1}} {(P_{t} - {\hat{P}}_{t})}_{1} \\ α_{S M A P E} = \frac{1}{M} \overset{M}{\sum_{i = 1}} \frac{2 | P_{t} - {\hat{P}}_{t} |}{P_{t} + {\hat{P}}_{t}} \end{array}\}

从在线学习、稀疏性、气象数据3个维度验证在线LASSO VAR模型的有效性.在线学习维度中,使用在线自回归(Autoregressive, AR)模型、Batch LASSO VAR模型^[28]进行对比;在稀疏性维度中,使用弹性网(Elastic Net, ENET)、分层稀疏(Hierarchical Sparse)、平滑削边绝对偏离(Smoothly Clipped Absolute Deviation, SCAD)进行对比.在气象数据维度中,使用基于风速和风向的功率曲线进行对比.

表1为在线维度中各时序模型的预测结果.模型后的数字代表模型的最高阶数.Batch LASSO VAR的数学模型与在线LASSO VAR相同,但模型参数只在获得所有训练集数据后更新一次.出于对模型估计效率的考虑,对于VAR模型,令最高时间阶数L为4阶.由表1可见,VAR模型在各个指标上都远远优于非VAR模型,在线AR模型的预测效果在所有模型中最差,这主要由于在线AR模型只考虑单风力机的时间相关性,未考虑多风力机间的空间相关性.上述结果验证了考虑空间相关性的VAR模型的有效性.

表1 在线维度中各模型预测结果

Tab.1 Forecasting results in online dimension

模型	RMSE	MAE	SMAPE
在线LASSO VAR(4)	397.08	272.03	55.65
在线LASSO VAR(3)	397.24	272.27	53.00
在线LASSO VAR(2)	406.98	280.50	54.16
在线LASSO VAR(1)	406.80	280.10	54.04
Batch LASSO VAR(4)	399.05	273.76	53.07
Batch LASSO VAR(3)	399.31	274.03	53.11
Batch LASSO VAR(2)	399.64	274.17	53.16
Batch LASSO VAR(1)	408.54	279.34	53.99
在线AR(4)	420.52	287.19	55.05

新窗口打开| 下载CSV

1阶的两种VAR模型效果相差无几,但更高阶的在线VAR模型优于Batch VAR.同时,由于Batch LASSO VAR模型需要对所有的训练数据进行拟合优化,而在线LASSO VAR每次只需要利用到距离当前时刻最近的一部分训练数据,所以后者的运行效率远远高于前者.拟合一个在线更新的3阶LASSO VAR模型只需要20.8 s,而拟合一个同阶的Batch LASSO VAR模型却需要659.6 s,这验证了在线方法的优越性.

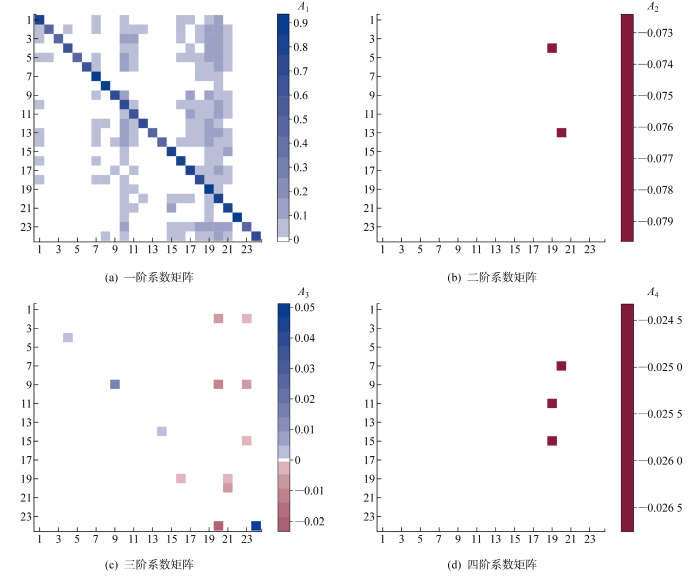
图4为在线LASSO VAR(4)模型的系数矩阵图,A₁~A₄分别为系数.图4(a)和4(c)展示了在线LASSO VAR(4)一阶滞后和三阶滞后的系数矩阵,可以看出大多数系数的绝对值都小于0.2,这表明LASSO VAR削弱了无关风力机间的数据相关性.图4(b)和4(d)为四阶在线LASSO VAR(4)的系数矩阵.空白色块表示等于0的系数,这意味着LASSO确实限制了非零系数的数量.由图4(d)可见,在线LASSO VAR(4)的四阶滞后系数矩阵中非零系数很少,结合预测效果分析,这代表考虑第四阶的滞后已很难从时空样本中提取到有利于改善预测的信息,从而未能明显提升LASSO VAR的效果,因此选择滞后阶数3是合理的.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 在线LASSO VAR(4)的系数矩阵

Fig.4 Coefficient matrix of online LASSO VAR(4)

综合考虑预测精度与运行效率,在线LASSO VAR(3)的表现最优,因此,后续利用该模型的预测结果进行稀疏性、天气数值预测(Numerical Weather Prediction, NWP)数据维度的比较,以及风场总功率的概率预测.

表2为稀疏性、气象数据维度中各时序模型的预测结果.稀疏性方法主要有特征降维和正则化矩阵两种.特征降维主要有主成分分析、T-SNE等,但本文研究的时空预测问题输入为各力风力机的有功功率数据,特征降维得到的新特征解释性差,不适合对输入矩阵进行稀疏处理.针对VAR模型的正则化矩阵主要有LASSO、弹性网、层次稀疏、SCAD等.使用后3种方法替换LASSO重新进行预测,发现SCAD的计算量很大、运行效率低,同样的数据量下,运行时间为LASSO的120倍,不适合进行大规模时空预测的稀疏处理;弹性网和层次稀疏的运行时间与LASSO相近,但没有提升预测结果.因此,使用LASSO稀疏参数矩阵是合理的.

表2 稀疏性、气象数据维度中各模型预测结果

Tab.2 Forecasting results in sparse and meteorological data dimensions

模型	RMSE	MAE	SMAPE
LASSO VAR(3)	399.31	274.03	53.11
ENET VAR(3)	399.03	278.56	53.90
Hierarchical Sparse VAR(3)	418.82	295.31	56.55
气象预测+功率曲线	449.6	308.56	54.22
添加气象数据的LASSO VAR(3)	407.1	280.4	54.12

新窗口打开| 下载CSV

为了研究不使用气象数据是否会影响预测结果,一方面使用在线LASSO VAR(3)模型预测风速和风向,并基于风速和风向构建功率曲线.在线LASSO VAR(3)模型已被证明能有效进行时空预测;基于风速和风向构建功率曲线,预测线性度R²达到0.96.由表2的预测结果可以看出,使用该方法得到的功率预测结果并不好,这主要是因为影响风力机功率输出的因素有很多,只使用风速和风向构造功率曲线,精度很难保证.另一方面,将风力机的风速和风向数据添加到只包含有功功率的输入矩阵中,运行算法发现预测结果反而变差.综上可知,如果各风力机间的功率存在较强的时空相关性,不考虑气象数据不会影响模型预测结果.

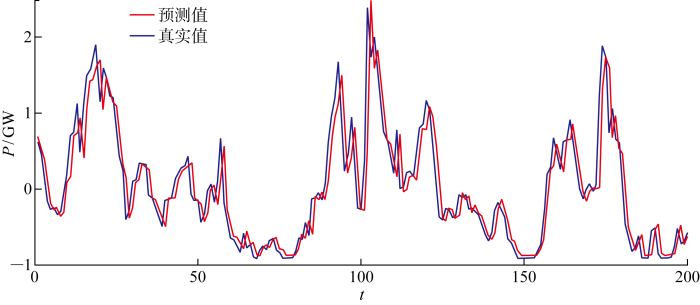
在测试集中,以35号风力机为例,在线LASSO VAR(3)的预测值与真实值对比如图5所示,可以看出,预测值较好地追踪了真实值的趋势,预测结果较好.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 35号风力机的在线LASSO VAR(3)预测结果

Fig.5 Forecasting result of online LASSO VAR (3) of Turbine 35

3.2 EGARCH模型概率预测

可靠度、锐度、预报技巧分和连续概率排位分数(Continuous Ranked Probability Score, CRPS)是评估风场总功率概率预测结果的常用指标^[36],各指标的定义如下.

可靠度的定义为

(20)R^1-^β=

\frac{1}{M} \overset{M}{\sum_{t = 1}} η_{t}^{1 - β}

-(1-β)

式中:1-β为名义覆盖率,其预测区间为 [ ${\hat{q}}_{t}^{β / 2}$ , ${\hat{q}}_{t}^{1 - β / 2}$ ],其中β表示未在置信区间内的概率;P_t为t时刻的风场总功率.当 ${\hat{q}}_{t}^{β / 2}$ <P_t< ${\hat{q}}_{t}^{1 - β / 2}$ 时, $η_{t}^{1 - β}$ =1;其余情况下, $η_{t}^{1 - β}$ =0.

锐度的定义为

(21)S^1-^β=

\frac{1}{M} \overset{M}{\sum_{t = 1}} δ_{t}^{1 - β}

式中: $δ_{t}^{1 - β}$ = ${\hat{q}}_{t}^{1 - β / 2}$ - ${\hat{q}}_{t}^{β / 2}$ .锐度是名义覆盖率预测区间的平均宽度.锐度反映了预测区间凝聚概率信息的能力,相同可靠度下,锐度越小的区间效果越好.

预报技巧分的定义为

(22)K_t=

\overset{r}{\sum_{k = 1}}

(

ξ_{t}^{α_{k}}

-α_k)(P_t-

{\hat{q}}_{t}^{α_{k}}

)

式中:r为预测分位数的个数;α_k为置信度;当P_t≤ ${\hat{q}}_{t}^{α_{k}}$ 时, $ξ_{t}^{α_{k}}$ =1,否则 $ξ_{t}^{α_{k}}$ =0.K_t反映t时刻所有预测分位数的预测效果,技巧分越大代表区间预测越好,最大值为0.

CRPS^[37]的定义为

(23)$\begin{array}{r}C\left(N\left(u, \sigma^{2}\right), x\right)=\sigma\left\{\frac { x - u } { \sigma } \left[2 \Phi\left(\frac{x-u}{\sigma}\right)-\right.\right. \\\left.1]+2 \phi\left(\frac{x-u}{\sigma}\right)-\frac{1}{\sqrt{\pi}}\right\}\end{array}$

式中:u和σ²分别为预测正态分布的均值和方差;x为真实值;ϕ和Φ分别为标准正态分布概率密度函数和累积概率密度函数.

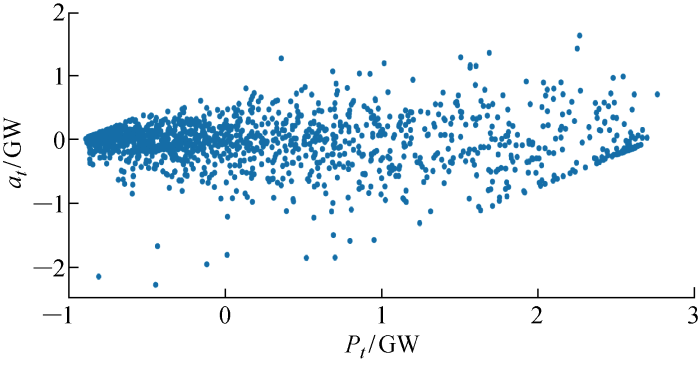
首先对在线LASSO VAR(3)的预测残差进行异方差检验.一是绘制有功功率和残差的散点图,以图6中的35号风力机为例,可以看出,随着有功功率值变大,残差散点整体呈现扩大的趋势,判断可能存在异方差效应.二是对预测残差作ARCH检验,发现24台风力机的检验p值均小于0.05,说明在线LASSO VAR(3)的预测残差存在异方差性.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 35号风力机的有功功率与残差散点图

Fig.6 Forecasting result of online LASSO VAR (3) of Turbine 35

接着使用EGARCH(1, 1)模型对在线LASSO VAR(3)验证集的残差值进行重新预测.假设EGARCH(1, 1)模型的残差服从标准正态分布.35号风力机拟合得到的EGARCH(1, 1)中ln h_t的表达式如下,其中各系数均在0.01水平下显著.

(24)ln h_t=1.255+0.271ε_t_-1+0.422

(|ε_{t - 1}| - \sqrt{\frac{π}{2}})

+0.893ln h_t_-1

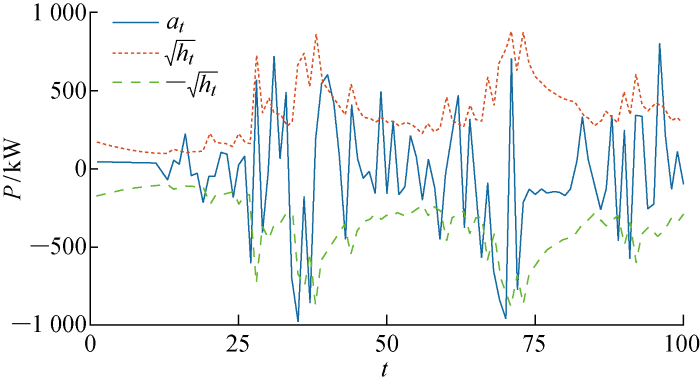
图7为35号风力机的EGARCH(1, 1)模型预测结果.可知,虽在某些极值点中,EGARCH(1, 1)模型没能正确预测,低估了真实值;在某些残差很小的点中,EGARCH(1, 1)高估了真实值,造成一定的浪费;但总体来说,其能较好地追踪残差的趋势,预测结果较好.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 EGARCH(1, 1)模型预测35号风力机残差

Fig.7 Residuals of Turbine 35 predicted by EGARCH (1, 1) model

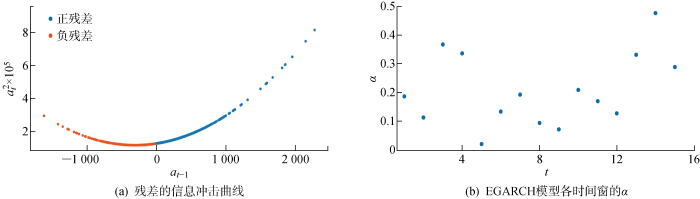
得到EGARCH(1, 1)模型的系数后,使用信息冲击曲线和动态显著线验证EGARCH模型的合理性.使用二次函数拟合残差和未来波动h_t的关系,得到正负残差对未来波动h_t的不对称影响^[38],如图8所示.图8(a)为残差的信息冲击曲线,可以看出,在绝对值相同的情况下,正残差对应的下一个时间点的波动大于负残差对应的下一个时间点的波动.图8(b)为采用长度为500的滑动时间窗的方法,使用不同的残差序列估计EGARCH(1, 1)模型得到的对应α,其中横坐标为残差序列的索引值;可以看出,α均为正值,并且在显著性水平为0.05时均显著.综上可知,图8验证了正负残差对条件方差的不对称影响.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 正负残差对波动性不同影响的验证

Fig.8 Different effects of positive and negative residuals on volatility

假设单个风力机有功功率服从正态分布N(μ,σ²),μ由Online LASSO VAR(3)点预测值估计,σ²由EGARCH(1, 1)模型预测结果估计.考虑风场中各个风力机有功功率间的相关性,对整个风场的总功率输出进行概率预测,并将其与KDE^[39]、BMA方法、QR模型、分位数回归森林(Quantile Regression Forest, QRF)模型^[40]模型进行比较.其中,BMA模型只选取与当前时刻最近的M个观测训练.本文选取M为24和48,分别对应1 d与2 d的数据.

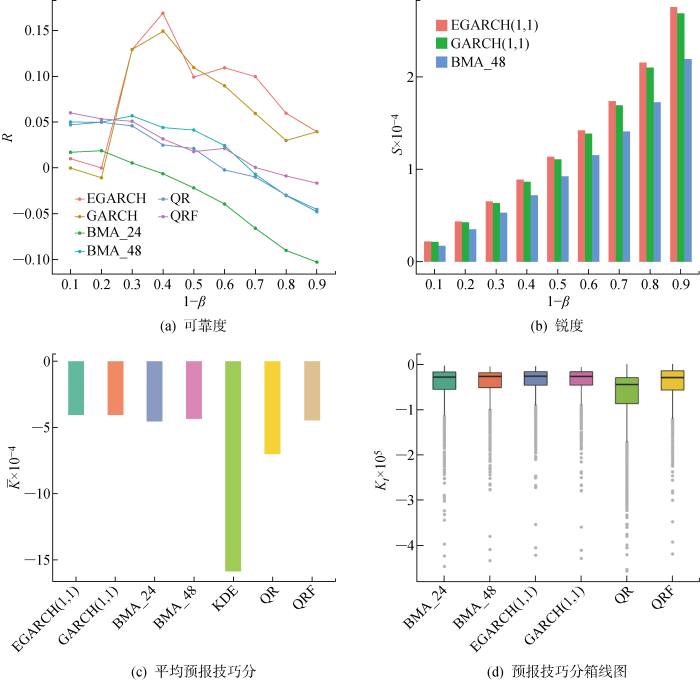
表3为各概率预测模型的结果.可知,考虑异方差的两个模型EGARCH(1, 1)与GARCH(1, 1)的RMSE、预报技巧分、CRPS相较于其他模型都有很大的提高.就RMSE而言,两个异方差模型小于BMA模型;就预报技巧分而言,异方差模型更接近0.同时,就CRPS而言,异方差模型优于其他模型.两个异方差模型相比,在中位数预测相同的情况下,EGARCH(1, 1)模型的预报技巧分和CRPS两个预测指标都要优于GARCH(1, 1).因此,预报技巧分和CRPS的优势表明,EGARCH(1, 1)模型在概率预测上能取得非常好的效果.

表3 EGARCH模型与其他模型的对比

Tab.3 Comparison of EGARCH and other models

模型	中位数预测 RMSE	K_t	CRPS
EGARCH (1, 1)	8019.4	-40401.8	4057.5
GARCH (1, 1)	8019.4	-40532.8	4070.8
BMA_48	8421.7	-43291.0	4389.9
BMA_24	8936.9	-45535.7	4640.5
KDE	32461.5	-158444	11345.67
QR	14918.7	-70989.3	7201.1
QRF	9182.3	-45429.4	4594.0

新窗口打开| 下载CSV

图9为EGARCH模型与其他模型的结果对比图.图9(a)展示了各模型的可靠度.可以看出,除了名义覆盖率为10%和20%,EGARCH模型和GARCH模型真实覆盖率与名义覆盖率的差明显高于其他模型.图9(b)展示了可靠性较高的EGARCH模型、GARCH模型和BMA_48模型的锐度.可以看出,异方差模型给出的区间宽度要高于BMA_48,这可能导致了其预测区间对一些波动较大的点的捕获能力高,最终得到较高的预报技巧分和CRPS.图9(c)展示了各模型的平均预报技巧分( $\bar{K}$ ),可以看出EGARCH模型最优,并且异方差模型要明显好于非异方差模型.图9(d)展示了各模型的预报技巧分箱形图.可以看出,异方差模型的预报技巧分的箱形宽度较小,均值更接近于0,预报技巧分的方差也较小,这表明异方差模型的准确度和鲁棒性均高于其他模型.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 EGARCH模型与其他模型的对比

Fig.9 Comparison of EGARCH and other models

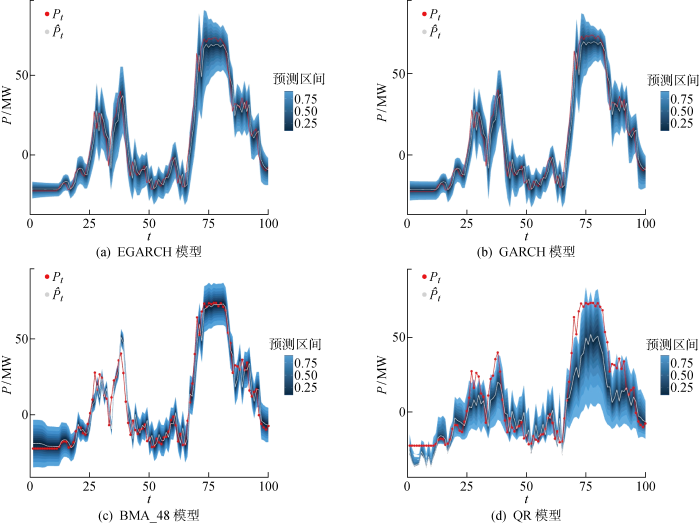
图10展示了各模型在连续测试集上的预测区间,红线表示真实的总功率P_t,灰线表示模型的中位数预测 ${\hat{P}}_{t}$ .名义覆盖率从0.1~0.9的预测区间也由不同的颜色表示,较深的颜色表示较小的区间覆盖率.可以看出,EGARCH模型的预测区间较窄,而且能较好地覆盖真实值,体现了EGARCH模型具有较好的概率预测效果.EGARCH模型相较于GARCH模型,在正偏差时的置信区间更宽、在负偏差时的置信区间更窄,验证了EGARCH模型可以体现出正负残差对波动性的不同影响;并且可以看出,在两段功率明显上升导致正残差的时间段内,EGARCH模型的预测区间比GARCH模型的预测区间宽,覆盖了原始点,这有助于EGARCH模型预测效果的提升.BMA在功率变化较小的连续值中,预测区间宽度较大,而且在 25~50 h中,预测区间很窄,不能很好地覆盖真实值.QR和QRF模型的效果明显不如EGARCH模型和BMA_48模型,其预测区间较宽,而且在部分连续时间段内未能很好地覆盖真实值.综上可以看出,采用EGACH模型度量在线LASSO VAR模型的不确定性,并将风场中各风力机的功率进行集成可以明显改进概率预测结果.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 各模型在连续测试集上的预测区间

Fig.10 Prediction interval of models on continuous test set

4 结论

针对风电不确定性高、现有模型未充分考虑异方差性的问题,使用在线LASSO VAR预测各风力机的有功功率,使用EGARCH预测残差,最终得到风场总有功功率的概率预测结果.将各模型在中国华东某地风场的功率预测效果进行比较,得出以下结论:

(1) 在线LASSO VAR模型进行时空预测,可以考虑到风力机间有功功率相关性的变化,在减小运算量的同时提升点预测的准确性.

(2) EGARCH模型可以针对风能点预测模型的不对称性建模,预测结果相较于GARCH模型得到提升.

(3) 采用EGACH模型预测在线LASSO VAR模型的条件方差,并将各风力机的有功功率求和,得到风场总有功功率,相较于QR、QRF、KDE、BMA直接对总有功功率建模,可以明显改进概率预测结果.

本文对风能区间预测、风能预测异方差处理、正负残差不对称性影响等问题具有一定的参考意义,未来将对时空异方差进行进一步研究.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Global Wind Energy Council.

Global wind report 2022

[R/OL]. (2022-12-31)[2023-02-16]. https://gwec.net/global-wind-report-2022/.

URL [本文引用: 1]

[2]

LANDBERG

, WATSON

S J

Short-term prediction of local wind conditions

[J]. Boundary-Layer Meteorology, 1994, 70(1): 171-195.

DOI:10.1007/BF00712528 URL [本文引用: 1]

[3]

FOCKEN

, LANGE

, WALDL

Previento-A wind power prediction system with an innovative upscaling algorithm

[C/OL]. (2001-01-01)[2021-07-30]. https://www.researchgate.net/publication/250448566_Previento_-_A_Wind_Power_Prediction_System_with_an_Innovative_Upscaling_Algorithm.

URL [本文引用: 1]

[4]

方江晓, 周晖, 黄梅, 等.

基于统计聚类分析的短期风电功率预测

[J]. 电力系统保护与控制, 2011, 39(11): 67-73.