计及建筑热负荷弹性的综合能源系统调度方法

doi:10.16183/j.cnki.jsjtu.2021.534

计及建筑热负荷弹性的综合能源系统调度方法

胡博¹, 程欣², 邵常政^,¹, 黄威¹, 孙悦³, 谢开贵¹

1.重庆大学输配电装备及系统安全与新技术国家重点实验室,重庆 400044

2.国网山西省电力公司经济技术研究院,太原 030001

3.中国长江电力股份有限公司,湖北宜昌,443002

Optimal Dispatch of Integrated Energy System Based on Flexibility of Thermal Load

HU Bo¹, CHENG Xin², SHAO Changzheng^,¹, HUANG Wei¹, SUN Yue³, XIE Kaigui¹

1. State Key Laboratory of Power Transmission Equipment and System Security and New Technology,Chongqing University, Chongqing 400044, China

2. Economic and Technical Research Institute,State Grid Shanxi Electric Power Company, Taiyuan 030001, China

3. China Yangtze Power Co., Ltd., Yichang 443002, Hubei, China

通讯作者: 邵常政,助理研究员;E-mail:cshao@cqu.edu.cn.

责任编辑: 孙伟

收稿日期: 2021-12-28 修回日期: 2022-02-18 接受日期: 2022-04-2

基金资助:

国家自然科学基金项目(52107072)
中国博士后科学基金项目(2021M693711)
中央高校基本科研业务费项目(2021CDJQY-037)

Received: 2021-12-28 Revised: 2022-02-18 Accepted: 2022-04-2

作者简介 About authors

胡博(1983-),教授,博士生导师,从事电力系统可靠性评估及综合能源系统优化运行研究.

摘要

具有一定弹性的建筑热负荷被视为电-热综合能源系统运行优化的重要调节资源.考虑建筑热负荷具有规模大、单体容量小的特点,非侵入式的数据驱动方法成为量化建筑热负荷弹性的有效手段.然而,由于数据不足或模型精度不够,该方法将不可避免地产生误差,给电-热综合能源系统的优化调度带来认知不确定性.因此,提出一种考虑建筑热负荷弹性并兼容相关认知不确定性的电-热综合能源系统优化调度方法.分析基于数据驱动的建筑热负荷需求弹性评估方法,将评估过程中产生的误差建模为认知不确定性,并通过改进的D-S证据理论对多源误差进行融合;采用拉丁超立方抽样方法生成表征热负荷弹性认知不确定性的场景,并通过模糊聚类法进行场景削减;将构造的场景集嵌入电-热综合能源系统的协调优化调度中,实现对建筑热负荷弹性及相关认知不确定性的综合考虑.算例仿真结果表明,考虑建筑热负荷需求弹性及认知不确定性对减少弃风、提高电热综合能源系统的运行灵活性至关重要.

关键词： 需求弹性; 认知不确定性; 电热综合能源系统; 优化调度

Abstract

The flexibility of thermal loads of buildings is a valuable balancing resource for operation of the heat and electricity integrated energy system (HE-IES). Considering the characteristics of large scale and small single load capacity of the themal load, the non-intrusive data-driven method has become an effective means to quantify the flexibility of building thermal load. However, due to the inaccuracy of the model or the lack of data, this method inevitably produces errors and brings epistemic uncertainty to the optimal dispatch of the HE-IES. An optimal dispatch model of the HE-IES that is compatible with the epistemic uncertainty of demand flexibility in the thermal loads of buildings is proposed. First, a data-driven flexible demand assessment method for building thermal load is described. The measurement errors are modeled as epistemic uncertainty and the multiple error sources are combined by using the D-S evidence theory. Then, the representative scenarios are selected to represent the epistemic uncertainty of the demand flexibility based Latin hypercube sampling(LHS) method, and the scenarios are reduced by the fuzzy clustering method. Finally, the representative scenarios are embedded in the coordinated and optimized dispatch of the HE-IES to realize the comprehensive consideration of the thermal load flexibility and related epistemic uncertainty of the building. The results demonstrate that considering the epistemic uncertainties of the thermal load demand is crucial for reducing the wind power curtailments and improving the operational flexibility of HE-IES.

Keywords： demand flexibility; epistemic uncertainty; heat and electricity integrated energy system(HE-IES); optimal dispatch

PDF (4261KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

胡博, 程欣, 邵常政, 黄威, 孙悦, 谢开贵. 计及建筑热负荷弹性的综合能源系统调度方法[J]. 上海交通大学学报, 2023, 57(7): 803-813 doi:10.16183/j.cnki.jsjtu.2021.534

HU Bo, CHENG Xin, SHAO Changzheng, HUANG Wei, SUN Yue, XIE Kaigui. Optimal Dispatch of Integrated Energy System Based on Flexibility of Thermal Load[J]. Journal of Shanghai Jiaotong University, 2023, 57(7): 803-813 doi:10.16183/j.cnki.jsjtu.2021.534

近年来,快速增长的能源需求和日益严峻的环境问题迫使各国积极推进新能源及多能融合技术发展^[1].电热综合能源系统实现电力系统和区域供热系统在能源生产、分配和利用等方面耦合,具有低碳、高效、经济的优点,获得广泛关注和发展^[2].截至2020年底,我国热电联产装机容量达到约 498 GW,未来供热系统和电力系统将有更广泛的互联.

为提高电-热综合能源系统的能源利用率,诸多文献研究建立了电-热综合调度模型,以统一部署电力和供热设备的运行计划^[3].然而,在统一调度过程中,热电联产机组“以热定电”的运行方式限制了电-热综合能源系统的运行灵活性,从而导致系统无法消纳更多的风力资源^[4].为改善这一现象,文献[5 ⇓-7]中提出通过热泵、电锅炉和热电联产机组的联合运行,达到能量在电、热等不同形式之间灵活切换,从而提高电热系统的运行灵活性.另一方面,具有天然弹性的建筑热负荷因其形式灵活、不需要增设额外设备而受到青睐,并广泛应用于电-热综合能源系统的优化调度中,以提高能源利用率和风力发电(简称风电)消纳能力^[8-9].

为量化建筑热负荷的弹性,文献[9]中将建筑热负荷建模为“储能电池”,以电池的充放电代表建筑热负荷功率的调节过程.然而,这类建模方法往往忽略了建筑本身的传热特性,使模型本身失去建筑传热特性物理层面的可解释性.此外,文献[10-11]中提出采用实验方法对建筑传热特性及潜在灵活性进行研究.但工作量较大,限制了该方法的应用^[12].考虑上述方法的缺点,文献[12-13]中提出利用数据驱动的方法量化建筑热负荷的弹性.文献[14 ⇓-16]中基于大规模监测数据和专家信息,构建量化热负荷弹性的关键参数与其影响因素的关系模型,进而实现对建筑热负荷弹性的预测.为提高供热系统的智能化程度,文献[17]中采用混合数据驱动模型对未来1 h的热负荷进行预测建模,文献[18]中建立了基于深度长短期记忆网络的综合能源多负荷联合预测模型.然而,数据驱动方法不可避免地存在数据不足和训练模型不精确的问题,随之带来热负荷弹性量化测量误差,这种误差可能会导致对建筑热负荷需求弹性的过度高估,从而对电-热综合能源系统的协调优化调度构成风险.

基于该背景,本文提出一种考虑建筑热负荷弹性并兼容相关认知不确定性的电-热综合能源系统协调优化调度方法.首先,分析基于数据驱动的建筑热负荷需求弹性评估方法,将评估过程中产生的误差建模为认知不确定性,并通过改进的D-S证据理论对多源误差进行融合,获得描述建筑热负荷需求弹性评估的综合性误差值.然后,采用拉丁超立方抽样方法和模糊聚类法生成代表性场景以表征热负荷弹性及认知不确定性.最后,实现计及建筑热负荷弹性以及相关认知不确定性的电-热综合能源系统协调优化调度.

1 建筑热负荷需求弹性的量化与表征

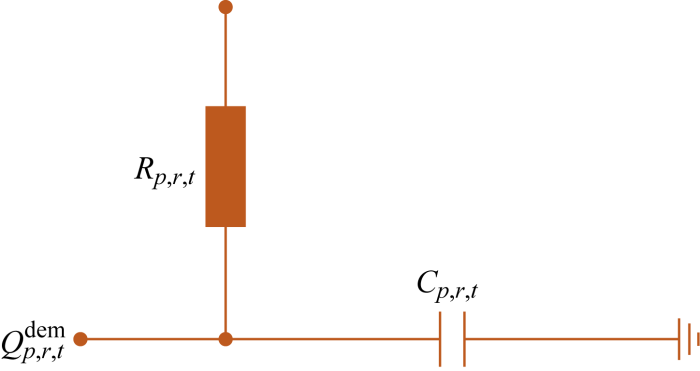
1.1 基于一阶等效热参数模型的热负荷需求建模

在电热综合能源系统中,建筑物存在热动态特性,因此建筑通过各式散热器获取热能后,经过一段时间延迟才可达到预设温度^[19].目前,一阶等效热参数(ETP)模型^[20]被广泛用来描述建筑物的热动态特性,详细揭示了注入的热能与建筑物室内外温度之间的关系,如图1所示.一阶ETP模型的数学关系式如下:

$Q_{p, r, t}^{d e m}$

$Q_{p, r, t}^{l o s s}$

$Q_{p, r, t}^{n e t}$

(1)

$Q_{p, r, t}^{l o s s}$ =

$\frac{τ_{p, r, t}^{i n} - τ_{p, r, t}^{o u t}}{R_{p, r, t}}$ =k_p_,_r_,_tV_p_,_r(

$τ_{p, r, t}^{i n}$ -

$τ_{p, r, t}^{o u t}$ )

(2)

$Q_{p, r, t}^{n e t}$ =

$Q_{p, r, t}^{d e m}$ -

$Q_{p, r, t}^{l o s s}$ =C_p_,_r_,_t

$\frac{d τ_{p, r, t}^{i n}}{d t}$

(3)

式中: $Q_{p, r, t}^{d e m}$ 为t时刻区域供热系统向p区域第r个建筑输送的热能; $Q_{p, r, t}^{l o s s}$ 为建筑热需求基础值; $Q_{p, r, t}^{n e t}$ 为建筑热需求弹性值; $τ_{p, r, t}^{i n}$ 和 $τ_{p, r, t}^{o u t}$ 分别为建筑室内、外温度;R_p_,_r_,_t为建筑等效热阻;k_p_,_r_,_t为建筑传热参数;V_p_,_r为建筑体体积;C_p_,_r_,_t为热惯性参数,表征建筑等效热容的大小,物理层面视作建筑热负荷需求上下浮动的调节能力.化简后各参数关系为

$Q_{p, r, t}^{d e m}$ =k_p_,_r_,_tV_p_,_r(

$τ_{p, r, t}^{i n}$ -

$τ_{p, r, t}^{o u t}$ )+C_p_,_r_,_t

$\frac{d τ_{p, r, t}^{i n}}{d t}$

(4)

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 一阶等效热参数模型

Fig.1 First-order equivalent thermal parameter model

1.2 基于数据驱动的建筑热负荷需求弹性评估

评估建筑热负荷基准值和弹性值的关键参数为k_p_,_r_,_t和C_p_,_r_,_t.k_p_,_r_,_t和C_p_,_r_,_t会随着建筑围护结构及外界天气条件的改变而变化^[21]; 此外,外界天气条件不同,用户的用热需求也存在一定差异^[22].因此,有必要针对同一类建筑揭示k_p_,_r_,_t和C_p_,_r_,_t与气象参数的关系,进而为建筑热负荷需求弹性预测提供较准确的参考,具体包含以下主要步骤:

(1) 提取过程.基于智能监控设备,收集历史建筑热负荷数据和气象参数,并基于历史数据从中提取k_p_,_r_,_t和C_p_,_r_,_t作为后续研究样本.

(2) 训练过程.基于数据驱动算法建立k_p_,_r_,_t和C_p_,_r_,_t与气象参数之间的关系,并利用气象预测数据对k_p_,_r_,_t和C_p_,_r_,_t进行预测,为建筑热负荷需求弹性评估提供指导.

然而,在上述提取和训练过程中,针对k_p_,_r_,_t和C_p_,_r_,_t预测的测量误差不可避免.这些测量误差均可归结为认知不确定性引起的误差.认知不确定性是由于模型不准确或缺乏数据而导致对问题缺乏理解,进而产生的认知偏差^[23].

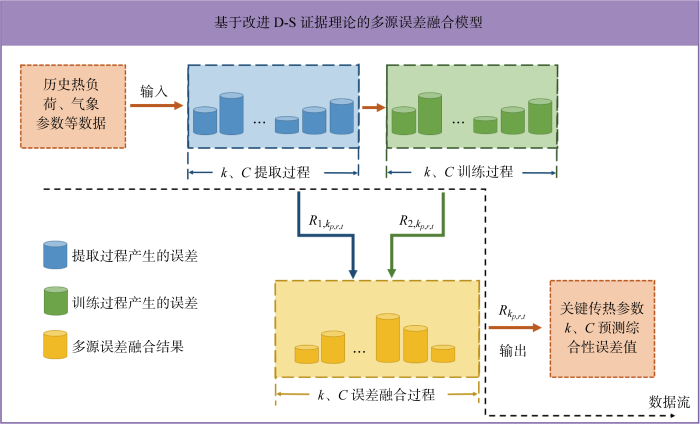
在上述基于数据驱动的预测方法中,导致k_p_,_r_,_t和C_p_,_r_,_t预测误差的认知不确定性主要来源于提取和训练两个过程.因此,预测k_p_,_r_,_t和C_p_,_r_,_t时有必要考虑多源认知不确定性带来的后果.如图2所示,提出基于改进D-S证据理论的多源误差融合模型解决上述问题,其中 $R_{1, k_{p, r, t}}$ 和 $R_{2, k_{p, r, t}}$ 分别为k_p_,_r_,_t在提取和训练过程中认知不确定性导致的相对误差, $R_{k_{p, r, t}}$ 为综合考虑多源认知不确定性后k_p_,_r_,_t的综合性相对误差值.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 建筑热参数k_p_,_r_,_t多源误差融合示意图

Fig.2 Illustration of multi-source measurement errors fusion of k_p_,_r_,_t

2 多源误差认知不确定性建模

合理处理k_p_,_r_,_t和C_p_,_r_,_t预测过程中的多源误差及误差相互之间的关系极其重要.基于改进的D-S证据理论,全面考虑认知不确定性导致的多源误差对k_p_,_r_,_t和C_p_,_r_,_t预测的影响.表1为k_p_,_r_,_t和C_p_,_r_,_t的多误差来源及各误差数量级分析.可知,k_p_,_r_,_t和C_p_,_r_,_t不同来源误差所属数量级存在差异,而针对同一处理过程,k_p_,_r_,_t和C_p_,_r_,_t对应的误差所属数量级也并不相同.这是因为k_p_,_r_,_t和C_p_,_r_,_t对应的建筑热负荷体量存在差异,且受气象参数影响的程度不同,导致同一模型求解所得的k_p_,_r_,_t和C_p_,_r_,_t预测误差存在差异.

表1 k_p_,_r_,_t和C_p_,_r_,_t多源误差来源及数量级分析

Tab.1 Analysis of multi-source error sources and order of magnitude of k_p_,_r_,_t and C_p_,_r_,_t

参数	误差来源(误差数量级)
k_p_,_r_,_t	提取过程(10^-3)
	训练过程(10^-2)
C_p_,_r_,_t	提取过程(10^-6)
	训练过程(10^-3)

新窗口打开| 下载CSV

2.1 多源误差认知不确定性建模

D-S证据理论由Dempster首先提出,它建立在完善的方法论上,可以解决由随机性或模糊性而导致的不确定性问题^[24],并且通过多方信息融合能够综合不同主体信息^[25],得到更加可靠的评估结果,其主要概念定义如下.

设非空集合Θ为识别框架,定义映射m: 2^Θ→ [0, 1]满足

$\begin{array}{l} m (Θ) = 0 \\ \sum_{X \subseteq Θ} m (X) = 1 \end{array}\}$

(5)

式中:m为基本概率分配函数即mass函数,可以理解为对子集X的支持度或信任度.如果m(X)>0,则称X为焦元.

信任函数定义如下:

Bel(A)=

$\sum_{B \subseteq A}$ m(B), ∀A⊆Θ

(6)

根据D-S证据理论的Dempster融合规则,融合后焦元X的mass函数如下:

m(X)=

$\{\begin{array}{l} \frac{\sum_{A = X} m_{1} (X_{1}) m_{2} (X_{2}) m_{3} (X_{3}) \dots m_{n} (X_{n})}{1 - \sum_{A = Θ} m_{1} (X_{1}) m_{2} (X_{2}) m_{3} (X_{3}) \dots m_{n} (X_{n})}, \\ X \neq Θ \\ 0, X = Θ \end{array}$

(7)

式中:A=X₁∩X₂∩…∩X_n;m₁, m₂, …, m_n 为识别框架Θ中不同证人针对n个焦元X提供的mass函数,X₁, X₂, …, X_n为对应焦元.

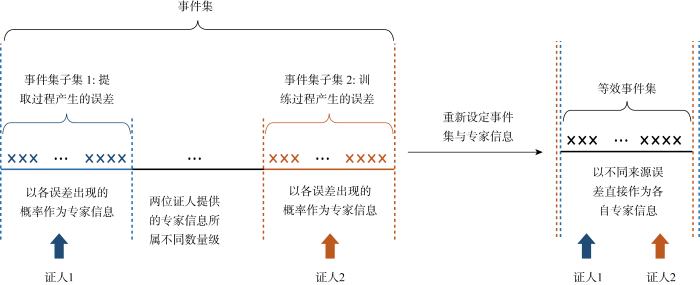
由表1可知,在提取和训练的过程中,k_p_,_r_,_t和C_p_,_r_,_t平均相对误差的数量级具有差异性.根据传统证据理论,将k_p_,_r_,_t和C_p_,_r_,_t的多源误差视作事件集,当各误差出现的概率表征mass函数时,由于k_p_,_r_,_t和C_p_,_r_,_t多源误差所属不同数量级,将导致构造的多源误差对应的事件集无重合区,即不同证人只对指定区域的事件提供专家信息.然而,每位证人只有知悉全局,并给出整个事件集的支持度,才可以提供完整准确的专家信息.因此,上述做法不合逻辑,必然会影响证据融合的结果.

针对以上问题,将认知不确定性导致的k_p_,_r_,_t和C_p_,_r_,_t多源测量误差视作是对同一事件集的多方面证据描述.基于改进的D-S证据理论,多源误差相融合,得到一个描述k_p_,_r_,_t和C_p_,_r_,_t预测误差的综合性结果,具体改进如下.

(1) 构建识别框架:

Θ={X₁,X₂,…,X_d,…,X_n}

(8)

式中:X_d为k_p_,_r_,_t和C_p_,_r_,_t多源相对误差对应的同一等效事件;n为等效事件的数量.

(2) 构建mass函数.k_p_,_r_,_t和C_p_,_r_,_t的测量误差主要来自两个方面,即对于同一事件X_d,存在两个证人提供对应的mass函数值,直接将多源误差视作多位证人对同一等效事件的信任度,具体关系如下:

m₁(X_d)=

$R_{1, k_{p, r, t}}$

(9)

m₂(X_d)=

$R_{2, k_{p, r, t}}$

(10)

m(X_d)=

$R_{k_{p, r, t}}$

(11)

利用式(7)对k_p_,_r_,_t多源相对误差进行融合,得到m(X_d)便可表征k_p_,_r_,_t的综合性相对误差.本文采用 $R_{k_{p, r, t}}$ 表示融合后误差,同样的处理方法可以应用于C_p_,_r_,_t.

图3所示用以说明算法改进前后各方面性能的提升.可知,基于上述方法改进后,在处理k_p_,_r_,_t和C_p_,_r_,_t多源误差融合时,等效事件集数量的减少使得计算负担同步下降;同时各位证人对整个事件集提供专家信息,保证了专家信息的完整性和有效性.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 证据理论方法改进说明

Fig.3 Explanation of improvement of evidence theory method

2.2 基于信息熵融合的改进证据理论

使用基于信息熵特性融合的修正信任函数描述误差融合,从而更准确地估计建筑热负荷的需求弹性^[26-27].

识别框架Θ的mass函数对所有命题都提供支持度或称信任度.Pignistic概率转换方法转换的目的是对系统已获得的各命题信任值进行重新分配,以获得更可靠的决策依据,具体定义如下:

Bet P_m(θ_i)=

$\sum_{θ_{i} \in X_{d}, X_{d} \in Θ} \frac{m (X_{d})}{| X_{d} |}$ , i=1,2,…,l; d=1,2,…,n

(12)

式中:θ_i为焦元X_d包含的信息;|X_d|为焦元X_d中的元素个数.

当信任函数进行信息转移时,子命题的支持度也随之变化,为此定义条件支持度的概念度量信任函数信息转移过程中对子命题的支持度的变化,即:

S_H(θ_j|θ_i)=

$\sum_{\frac{θ_{i} \in X_{d} \subseteq H}{θ_{j} \in X_{d}}} \frac{m (X_{d})}{| X_{d} |}$

(13)

L_H(θ_j|θ_i)=

$\sum_{\frac{θ_{j} \in X_{d} \subseteq H}{θ_{i} \notin X_{d}}} \frac{m (X_{d})}{| X_{d} |}$

(14)

式中:θ_i∈H, H⊆Θ, ∀θ_j(θ_j∈H); S_H(θ_j|θ_i)和L_H(θ_j|θ_i)分别为mass函数在集合H上提取信息θ_i对θ_j的条件支持度和剩余支持度,并且可以进一步得到以下关系:

S_H(θ_j|θ_i)=S_H(θ_i|θ_j)

(15)

S_H(θ_i)=S_H(θ_i|θ_j)+L_H(θ_i|θ_j)

(16)

L_H(θ_i|θ_j)=

$S_{H \ {θ_{j}}}$ (θ_i)

(17)

式(15)说明mass函数在H上对子命题的条件支持度是相互的.式(16)表示当对子命题的无条件支持度一定时,子命题的条件支持度越大,其剩余支持度越小.从式(17)可知,mass函数在H上目标子命题对子命题的剩余支持度即为mass函数在H上提取目标子命题信息后对子命题的无条件支持度.

采用一种新的信任函数信息转移算法,该算法基于Pignistic转换,逐步提取子命题的条件支持度,并将其重点放在无条件支持度大的子命题上,具体算法如下:

(1) 输入事件集Θ={X₁,X₂,…,X_d}和对应的mass函数值{m(X₁), m(X₂), …, m(X_d)}.

(2) 由式(18)计算每一个自命题的无条件支持度,即

S_Θ(θ_i)=

$\sum_{θ_{i} \in X_{d} \subseteq H} \frac{m (X_{d})}{| X_{d} |}$ , i∈H

(18)

(3) 令p_i=S_Θ(θ_i),得到分布(p₁, p₂, …, p_n)为信任函数的初始状态.

(4) 通过式(13)和(14)计算条件支持度与剩余支持度.

(5) 选择信息融合下条件支持度最大的子命题,重新计算每个原子命题的条件支持度,直到所有信息融合完毕.

(6) 修正后的(p₁, p₂, …, p_n)被认为是识别框架Θ的新mass函数值.

基于上述讨论即可获得修正后描述k_p_,_r_,_t 和 C_p_,_r_,_t综合性相对误差的mass函数值.

3 基于代表性场景的电热综合能源系统协调调度模型

3.1 计及建筑热负荷需求弹性及认知不确定性的代表性场景生成

重点介绍计及热负荷需求弹性及认知不确定性的场景生成方法,代表日的选取方法参考文献[28].

3.1.1 考虑k_p_,_r_,_t和C_p_,_r_,_t认知不确定性的场景生成

建筑热负荷需求弹性主要由k_p_,_r_,_t和C_p_,_r_,_t刻画,因此通过抽样k_p_,_r_,_t和C_p_,_r_,_t的误差场景表示各自相对误差的不确定性.目前,蒙特卡罗(MC)抽样和拉丁超立方(LHS)抽样是使用较为广泛的抽样方法^[29].MC抽样技术是完全随机的,在输入分布的范围内,样本可以落在任何位置,但样本更有可能从高发生概率的分布区域中抽取.而LHS抽样根据输入变量的累积分布函数(CDF)生成随机样本数^[30],它从随机变量的整个分布中进行抽样,可以确保小概率事件在模拟的输出中被准确地代表,从而提供更稳定和更精确的估计结果.同时LHS抽样迭代次数少,在抽样效率和运行时间方面的表现均更为优异.因此,采用LHS抽样方法模拟k_p_,_r_,_t和C_p_,_r_,_t的不确定性,应用过程如下:

(1) 确定抽样样本数N_s,将[0,1]分成N_s层,并在每层中随机产生一个随机数.

(2) 根据样本数N_LHS,设置N_LHS个区间.

(3) 判断步骤(1)中抽取的随机数所处N_LHS个区间中的位置.

(4) 若随机数处于第q个区间,则该随机数对应的k_p_,_r_,_t和C_p_,_r_,_t的相对误差可在此区间上利用线性法计算,由此产生N_s个描述k_p_,_r_,_t和C_p_,_r_,_t不确定性的场景.

3.1.2 基于模糊聚类算法的场景缩减技术

LHS抽样方法虽然在一定程度上可以提高建筑热负荷需求弹性不确定性评估的准确性,但也为后续的调度过程带来巨大的计算负担.对此,使用模糊聚类算法进行场景缩减,并生成代表性场景来描述建筑热负荷需求弹性及不确定性.

场景缩减技术根据场景的相似程度将场景分为不同的集群.模糊控制是自动控制领域的经典方法,模糊集引入了隶属度的概念,不遵循经典数学中“非0即1”的约定,而是提供了更灵活的聚类结果^[31].

模糊聚类算法的目标函数是最小化聚类场景与聚类簇中聚类中心之间的欧氏距离,具体如下:

$J_{F C M}^{q'}$ (U,W,G)=

$\overset{z}{\sum_{v = 1}} \overset{g}{\sum_{w = 1}} u_{v w}^{q'} d_{v w}^{2}$ =

$\overset{z}{\sum_{v = 1}} \overset{g}{\sum_{w = 1}} u_{v w}^{q'} {(x_{w} - a_{v})}^{2}$

(19)

式中:U 为z×g隶属度矩阵,z为设定的聚类类别数,g为待选场景的数量;W为聚类中心矩阵;G为候选聚类场景的一维矩阵;u_vw 为场景x_v 对聚类 w 的隶属度;x_w为待聚类的第w个场景;d_vw 为x_w和a_v之间的欧氏距离;a_v为每个聚类的聚类中心;模糊系数q'一般由经验决定,q'值过小或过大均会导致聚类算法的效果变差.各参数需满足的约束条件及算法具体流程见文献[32].

基于上述模型即可生成描述建筑热负荷需求弹性及认知不确定性的代表性场景,并应用于电热协调调度模型中.

3.2 电热综合能源系统协调调度模型

基于上述方法,综合考虑建筑热负荷需求弹性及认知不确定性,将建筑热负荷的灵活需求响应模型纳入电热综合能源系统优化调度模型中,以解决促进风电消纳等能源问题.

融合建筑热负荷灵活需求响应模型的电-热协调调度模型简述如下:

min

$\sum_{s \in S_{g e n}}$ f(

$P_{s, t}^{g e n}$ ,

$Q_{s, t}^{g e n}$ )

(20)

$P_{s, t}^{g e n}$ ,

$Q_{s, t}^{g e n}$ ,

$P_{p, t}^{d e m}$ ,

$Q_{p, t}^{d e m}$ )≤0, ∀s,p,t

(21)

$Q_{p, t}^{d e m}$ =k_p_,_t

$\overset{N_{p, r}}{\sum_{r = 1}}$ (

$τ_{p, t}^{i n}$ -

$τ_{p, t}^{o u t}$ )V_p_,_r+C_p_,_t

$\frac{d τ_{p, t}^{i n}}{d t}$

(22)

$\underline{τ_{p, t}^{i n}}$ ≤

$τ_{p, t}^{i n}$ ≤

$\bar{τ_{p, i}^{i n}}$

(23)

式中: $P_{s, t}^{g e n}$ 和 $Q_{s, t}^{g e n}$ 分别为机组s的电出力如热电联产机组和热出力如燃气机组、锅炉等; $P_{p, t}^{d e m}$ 为电负荷;N_p_,_r为建筑总数;S_gen为机组集合.式(20)为目标函数,其目的为最小化系统运行成本;式(21)表示运行约束;式(22)为建筑热负荷灵活性模型;式(23)给定了室内温度舒适范围.有关电-热系统协调调度模型的目标函数和约束的介绍详见文献[33].

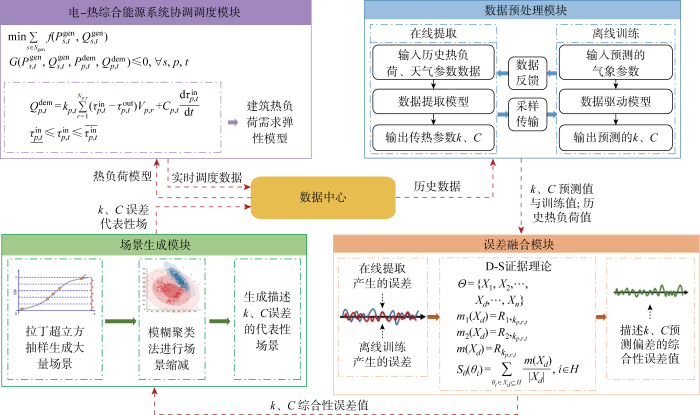
基于上述讨论,提出计及建筑热负荷需求弹性和认知不确定性的电-热综合能源系统协调调度平台如图4所示,其主要分为以下4个子模块,数据交汇中心为各个子模块间数据传递提供桥梁.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 建筑热负荷需求弹性及认知不确定性处理方法及应用

Fig.4 Processing method and application of flexible demand and epistemic uncertainty of building thermal loads

(1) 数据预处理模块.基于历史热负荷数据和气象参数,提取传热参数k和C,并基于数据驱动训练算法,建立k、C与气象参数间的关系,从而实现未来气象条件下k和C的预测.

(2) 误差融合模块.将提取和训练过程中产生的k、C多源测量误差建模为认知不确定性,并采用改进的证据理论将多源测量误差融合以获得描述k和C不确定性的综合性误差值.

(3) 场景生成模块.采用LHS抽样和模糊聚类法生成描述建筑热负荷需求弹性及认知不确定性的代表性场景,用于后续的电热协调调度模块.

(4) 电-热综合能源系统协调调度模块.建筑热负荷的灵活需求响应模型成功嵌入电-热综合能源系统优化调度中,实现计及建筑热负荷需求弹性及认知不确定性的电-热综合能源系统协调调度.

4 算例仿真

构建算例仿真以验证本文方法的准确性和有效性.首先,讨论用于评估建筑热负荷需求弹性及认知不确定性方法的有效性.然后,给出考虑k_p_,_t和C_p_,_t认知不确定性前后建筑热负荷评估结果.此外,使用简单的测试系统与已有调度方法对比,证明融合认知不确定性模型后电热综合能源系统调度灵活性的提升.模型仿真均在 MATLAB R2018b环境下进行,线性优化部分由Gurobi求解器求解.

4.1 k_p_,_t和C_p_,_t的多源误差融合

基于智能监控设备获取300组历史热负荷及天气参数数据集,从中提取k_p_,_t和C_p_,_t并求取对应的认知不确定性导致的偏差,同时给出多源误差的融合结果.

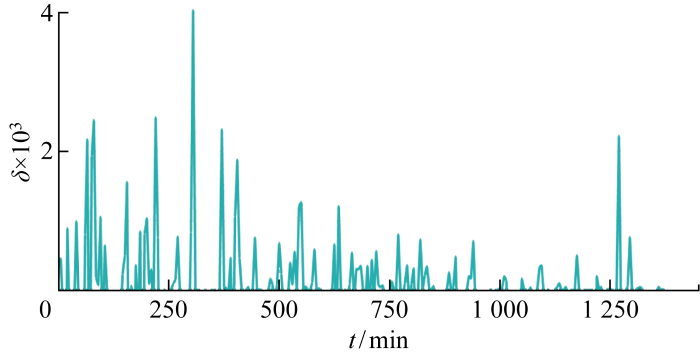
图5和6为热惯性参数C_p_,_t在提取和训练过程中认知不确定性导致的相对误差(δ),可知两个过程产生的误差所属数量级不同.图7为C_p_,_t多源误差融合结果,可知误差融合结果与图5和6各个过程的误差结果存在差异,证明了多源误差融合的必要性.采用同样的方法,k_p_,_t的多源误差融合结果如图8所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 C_p_,_t提取过程中产生的相对误差

Fig.5 Relative error of C_p_,_t during extracting process

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 C_p_,_t训练过程中产生的相对误差

Fig.6 Relative error of C_p_,_t during training process

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 多源误差融合后C_p_,_t的综合性相对误差

Fig.7 Relative error of C_p_,_t after considering error fusion

图8

新窗口打开| 下载原图ZIP| 生成PPT

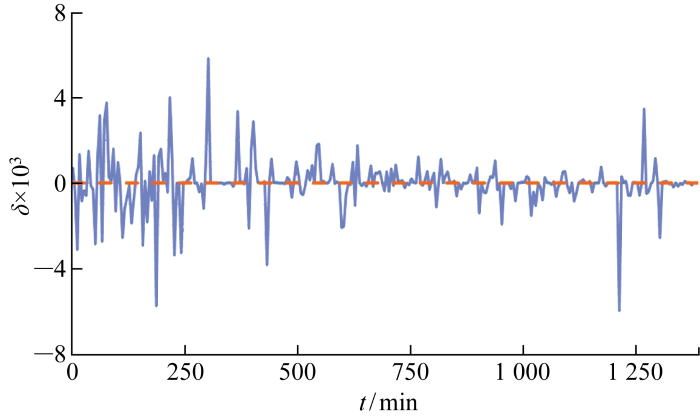
图8 多源误差融合后k_p_,_t的综合性相对误差

Fig.8 Relative error of k_p_,_t after considering error fusion

4.2 多源误差融合的精确性分析

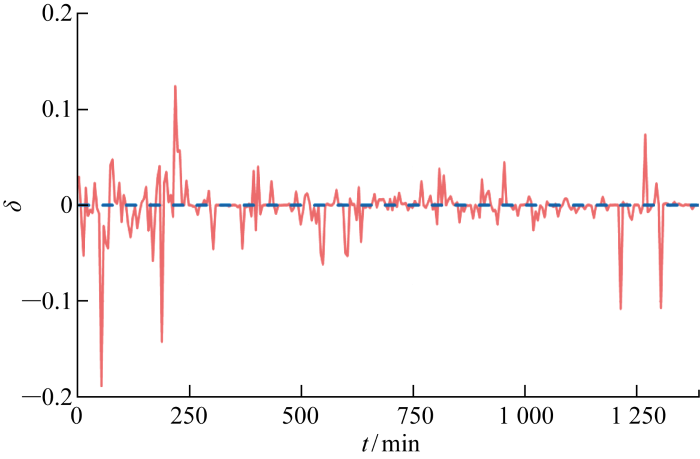
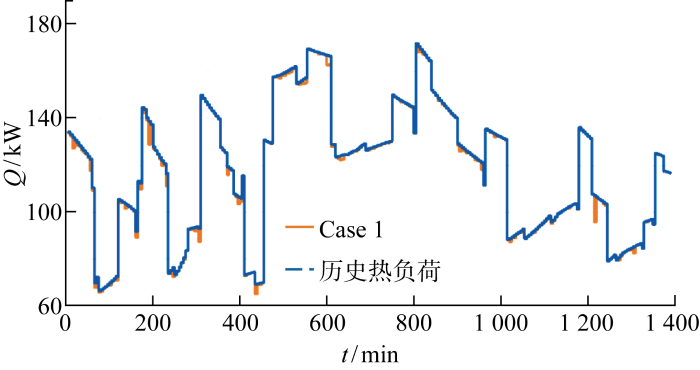
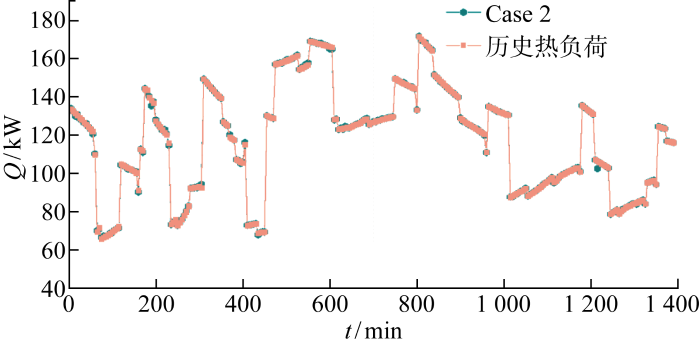
设置两个子算例Case 1和Case 2,通过比较是否考虑k_p_,_t和C_p_,_t多源误差融合时建筑热负荷的估计值,详细说明考虑多源误差融合的必要性,验证认知不确定性处理方法的准确性.其中,Case 1的训练误差作为传热系数k_p_,_t和C_p_,_t的估计误差评估建筑热负荷的需求弹性;Case 2在评价建筑热负荷需求弹性时,考虑k_p_,_t和C_p_,_t多源误差融合.

图9和图10分别为建筑热负荷(Q)的评估结果,可知子算例Case 2的评估精度高于Case 1.此外,Case 1的平均相对误差为0.43%,而Case 2的平均相对误差为0.21%,即考虑参数多源误差融合后,建筑热负荷的评估精度获得到提升,进一步证明了考虑建筑传热参数多源误差融合在评估建筑热负荷需求弹性时的必要性.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 子算例Case 1建筑热负荷评估精度

Fig.9 Thermal loads assessment precision of Case 1

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 子算例Case 2建筑热负荷评估精度

Fig.10 Thermal loads assessment precision of Case 2

4.3 应用

为了说明建筑热负荷的需求弹性可以为系统提供更大的调节空间,将提出的建筑热负荷灵活响应模型应用于实际的电热综合能源系统中.系统结构及参数主要来自文献[34],并在此基础上,增加一台功率为600 MW的风力涡轮机和一台1000 kW的燃气发电机组,电能通过配电网络中每条馈线处的11/0.433 kV 变压器提供给负载;在区域供热系统中,设置3个节点提供热能.

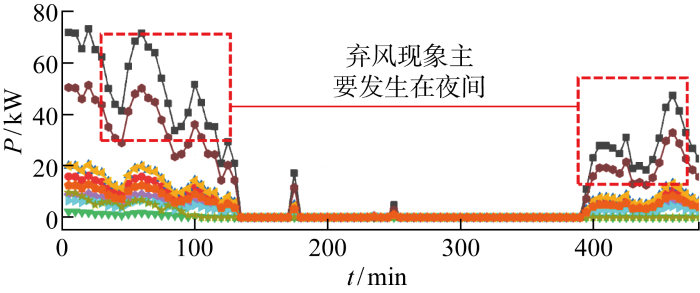
使用LHS抽样生成更多描述建筑热负荷需求弹性及认知不确定性的场景.为了减小计算量,通过模糊聚类技术进行场景缩减.图11为具有代表性的弃风场景结果,其中P为弃风功率.可知,弃风现象主要发生在夜间,这是因为夜晚热负荷需求量增长,热电联产机组“以热定电”的运行方式使得夜间热电联产机组电出力随之增长,而夜间电负荷需求下降,限制了风电上网空间,造成大量的弃风.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 代表性场景弃风现象

Fig.11 Wind curtailment of representative scenarios

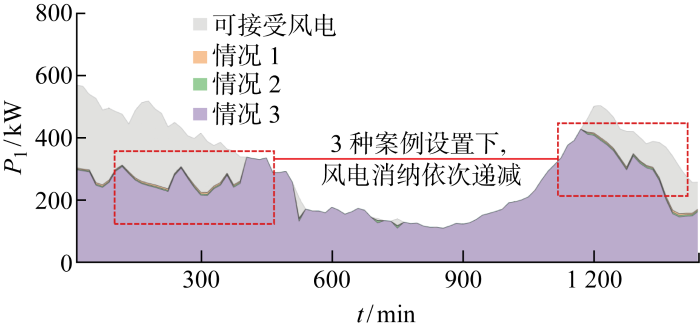
准确评估建筑热负荷的潜在弹性可以提升风电消纳效率.图12为是否考虑建筑热负荷需求弹性及不确定性的调度过程中风电消纳量(P₁)的比较.其中情况1为考虑热负荷需求及不确定性;情况2为考虑热负荷需求但不考虑不确定性;情况3为不考虑热负荷需求弹性.可知,当考虑建筑热负荷需求弹性及不确定性,并将建筑热负荷灵活需求响应模型嵌入电-热综合能源系统优化调度中时,在大部分时间段内系统风电消纳量明显增加.相较于情况2和情况3,情况1在1 d内的弃风率分别降低了2.6%和5.1%.由此得出结论,考虑建筑热负荷弹性可以显著提高风电消纳,进一步证明了本文的热负荷需求弹性不确定性评估模型对提高系统和风电消纳的灵活性是必要且有效的.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 风电消纳情况对比

Fig.12 Comparison of wind integration

5 结语

本文研究了建筑热负荷需求弹性及认知不确定性的处理方法及应用,以促进电热综合能源系统协调优化调度中可变风电的消纳.将基于数据驱动的建筑热负荷需求弹性评估方法过程中产生的多源误差建模为认知不确定性,并通过改进的D-S证据理论对多源误差进行融合;采用拉丁超立方抽样方法和模糊聚类法生成表征热负荷需求弹性及认知不确定性的代表性场景;将构造的场景集嵌入电-热综合能源系统协调调度中,实现对建筑热负荷需求弹性及相关认知不确定性的综合考虑.在后续研究中,将针对建筑热负荷弹性不确定性在能源市场中的应用提出解决方案,即对充分考虑能价激励、用户行为下,建筑热负荷弹性不确定性评估及应用展开进一步研究.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

夏越, 陈颖, 杜松怀, 等.

综合能源系统多时间尺度动态时域仿真关键技术

[J]. 电力系统自动化, 2022, 46(10): 97-110.

[本文引用: 1]

XIA

Yue

, CHEN

Ying

, DU

Songhuai

, et al.

Key technologies for multi-time-scale dynamic time-domain simulation of integrated energy system

[J]. Automation of Electric Power Systems, 2022, 46(10): 97-110.

[本文引用: 1]

[2]

武梦景, 万灿, 宋永华, 等.

含多能微网群的区域电热综合能源系统分层自治优化调度

[J]. 电力系统自动化, 2021, 45(12): 20-29.

[本文引用: 1]

Mengjing

, WAN

Can

, SONG

Yonghua

, et al.

Hierarchical autonomous optimal dispatching of district integrated heating and power system with multi-energy microgrids

[J]. Automation of Electric Power Systems, 2021, 45(12): 20-29.

[本文引用: 1]

[3]

, GU

, MENG

, et al.

Economic dispatch of integrated energy systems with robust thermal comfort management

[J]. IEEE Transactions on Sustainable Energy, 2021, 12(1): 222-233.

DOI:10.1109/TSTE.5165391 URL [本文引用: 1]

[4]

DAI

Y H

, CHEN

, MIN

, et al.

Dispatch model of combined heat and power plant considering heat transfer process

[J]. IEEE Transactions on Sustainable Energy, 2017, 8(3): 1225-1236.

DOI:10.1109/TSTE.2017.2671744 URL [本文引用: 1]

[5]

李健, 李雪峰, 张娜, 等.

计及储热备用效益的电热综合能源系统优化调度模型

[J]. 电网技术, 2021, 45(10): 3851-3859.

[本文引用: 1]

Jian

, LI

Xuefeng

, ZHANG

, et al.

Optimal dispatch model of electricity-heat integrated energy system considering reserved benefits of heat storage

[J]. Power System Technology, 2021, 45(10): 3851-3859.

[本文引用: 1]

[6]

崔杨, 姜涛, 仲悟之, 等.

考虑风电消纳的区域综合能源系统源荷协调经济调度

[J]. 电网技术, 2020, 44(7): 2474-2483.

[本文引用: 1]

CUI

Yang

, JIANG

Tao

, ZHONG

Wuzhi

, et al.

Source-load coordination economic dispatch method for regional integrated energy system considering wind power accommodation

[J]. Power System Technology, 2020, 44(7): 2474-2483.

[本文引用: 1]

[7]

孙娟, 卫志农, 孙国强, 等.

计及P2H的电-热互联综合能源系统概率能量流分析

[J]. 电力自动化设备, 2017, 37(6): 62-68.

[本文引用: 1]

SUN

Juan

, WEI

Zhinong

, SUN

Guoqiang

, et al.

Analysis of probabilistic energy flow for integrated electricity-heat energy system with P2H

[J]. Electric Power Automation Equipment, 2017, 37(6): 62-68.

[本文引用: 1]

[8]

DAI

Y H

, CHEN

, MIN

, et al.

Dispatch model for CHP with pipeline and building thermal energy storage considering heat transfer process

[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 192-203.

DOI:10.1109/TSTE.2018.2829536 URL [本文引用: 1]

[9]

NIU

J D

, TIAN

, LU

Y K

, et al.

Flexible dispatch of a building energy system using building thermal storage and battery energy storage

[J]. Applied Energy, 2019, 243: 274-287.

DOI:10.1016/j.apenergy.2019.03.187 URL [本文引用: 2]

[10]

CHEN

Y B

, XU

, CHEN

, et al.

Experimental investigation of demand response potential of buildings: Combined passive thermal mass and active storage

[J]. Applied Energy, 2020, 280: 115956.

DOI:10.1016/j.apenergy.2020.115956 URL [本文引用: 1]

[11]

W L

, YANG

, JI

, et al.

Estimating demand response potential under coupled thermal inertia of building and air-conditioning system

[J]. Energy and Buildings, 2019, 182: 19-29.

DOI:10.1016/j.enbuild.2018.10.022 URL [本文引用: 1]

[12]

XUE

P N

, JIANG

, ZHOU

Z G

, et al.

Multi-step ahead forecasting of heat load in district heating systems using machine learning algorithms

[J]. Energy, 2019, 188: 116085.

DOI:10.1016/j.energy.2019.116085 URL [本文引用: 2]

[13]

朱继忠, 董瀚江, 李盛林, 等.

数据驱动的综合能源系统负荷预测综述

[J]. 中国电机工程学报, 2021, 41(23): 7905-7924.

[本文引用: 1]

ZHU

Jizhong

, DONG

Hanjiang

, LI

Shenglin

, et al.

Review of data-driven load forecasting for integrated energy system

[J]. Proceedings of the CSEE, 2021, 41(23): 7905-7924.

[本文引用: 1]

[14]

, CHENG

, XU

H L

, et al.

Smart meter data-driven evaluation of operational demand response potential of residential air conditioning loads

[J]. Applied Energy, 2020, 279: 115708.

DOI:10.1016/j.apenergy.2020.115708 URL [本文引用: 1]

[15]

YAN

, LIU

A simplified prediction model for energy use of air conditioner in residential buildings based on monitoring data from the cloud platform

[J]. Sustainable Cities and Society, 2020, 60: 102194.

DOI:10.1016/j.scs.2020.102194 URL [本文引用: 1]

[16]

TENG

, SUN

, OUYANG

, et al.

Optimal operation strategy for combined heat and power system based on solid electric thermal storage boiler and thermal inertia

[J]. IEEE Access, 2019, 7: 180761-180770.

DOI:10.1109/ACCESS.2019.2958877 URL [本文引用: 1]

[17]

王琎

. 基于数据驱动的区域供热系统热负荷预测方法研究[D]. 天津: 天津理工大学, 2020.

[本文引用: 1]

WANG

Jin

. Research on heat load forecasting method of district heating system based on data drive[D]. Tianjin: Tianjin University of Technology, 2020.

[本文引用: 1]

[18]

刘尔佳

. 数据驱动下的综合能源预测及需求响应优化运行研究[D]. 北京: 华北电力大学(北京), 2021.

[本文引用: 1]

LIU

Erjia

. Data-driven integrated energy forecasting and research on optimal operation of integrated demand response[D]. Beijing: North China Electric Power University, 2021.

[本文引用: 1]

[19]

CHEN

X Y

, WANG

J X

, XIE

, et al.

Demand response potential evaluation for residential air conditioning loads

[J]. IET Generation, Transmission & Distribution, 2018, 12(19): 4260-4268.

DOI:10.1049/gtd2.v12.19 URL [本文引用: 1]

[20]

Z G

, WU

W C

, WANG

J H

, et al.

Transmission-constrained unit commitment considering combined electricity and district heating networks

[J]. IEEE Transactions on Sustainable Energy, 2016, 7(2): 480-492.

DOI:10.1109/TSTE.2015.2500571 URL [本文引用: 1]

[21]

邵腾

. 东北严寒地区乡村民居节能优化研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.

[本文引用: 1]

SHAO

Teng

. The energy-saving optimization for rural house in northeast severe cold regions[D]. Harbin: Harbin Institute of Technology, 2018.

[本文引用: 1]

[22]

胡志豪, 冯忠楠, 魏繁荣, 等.

计及热力不确定性的智能建筑电-热联合鲁棒经济调度

[J]. 中国电机工程学报, 2020, 40(12): 3907-3919.

[本文引用: 1]

Zhihao

, FENG

Zhongnan

, WEI

Fanrong

, et al.

Robust dispatch for electrical-thermal combined intelligent building considering impacts of uncertainties on thermal side

[J]. Proceedings of the CSEE, 2020, 40(12): 3907-3919.

[本文引用: 1]

[23]

T P

, KANG

, WEN

M L

Graduation formula: A new method to construct belief reliability distribution under epistemic uncertainty

[J]. Journal of Systems Engineering and Electronics, 2020, 31(3): 626-633.

DOI:10.23919/JSEE.5971804 URL [本文引用: 1]

[24]

时洪会, 蒋文保.

D-S证据理论综述

[J]. 信息化建设, 2015(11): 331.

[本文引用: 1]

SHI

Honghui

, JIANG

Wenbao

A summary of D-S evidence theory

[J]. Informatization Construction, 2015(11): 331.

[本文引用: 1]

[25]

李昌玺, 周焰, 王盛超, 等.

多源信息融合中一种新的证据合成算法

[J]. 上海交通大学学报, 2016, 50(7): 1125-1131.

[本文引用: 1]

Changxi

, ZHOU

Yan

, WANG

Shengchao

, et al.

A novel combination rule of evidence theory in multi-source information fusion

[J]. Journal of Shanghai Jiao Tong University, 2016, 50(7): 1125-1131.

[本文引用: 1]

[26]

徐洪富, 吴根秀, 许才.

基于大焦元的子焦元的信任函数逼近方法

[J]. 江西师范大学学报(自然科学版), 2019, 43(3): 282-286.

[本文引用: 1]

Hongfu

, WU

Genxiu

, XU

Cai

The approximation method of the belief function based on the sub focal elements of the large focal elements

[J]. Journal of Jiangxi Normal University (Natural Science Edition), 2019, 43(3): 282-286.

[本文引用: 1]

[27]

程子成, 吴根秀, 宋姝婷.

基于融合信息熵性质的信任函数概率逼近

[J]. 江西师范大学学报(自然科学版), 2014, 38(5): 534-538.

[本文引用: 1]

CHENG

Zicheng

, WU

Genxiu

, SONG

Shuting

A probability approximations of belief function based on fusion of the properties of information entropy

[J]. Journal of Jiangxi Normal University (Natural Science Edition), 2014, 38(5): 534-538.

[本文引用: 1]

[28]

SCOTT

I J

, CARVALHO

P M S

, BOTTERUD

, et al.

Clustering representative days for power systems generation expansion planning: Capturing the effects of variable renewables and energy storage

[J]. Applied Energy, 2019, 253: 113603.

DOI:10.1016/j.apenergy.2019.113603 URL [本文引用: 1]

[29]

ZHANG

S X

, CHENG

H Z

, ZHANG

L B

, et al.

Probabilistic evaluation of available load supply capability for distribution system

[J]. IEEE Transactions on Power Systems, 2013, 28(3): 3215-3225.

DOI:10.1109/TPWRS.2013.2245924 URL [本文引用: 1]

[30]

JIRUTITIJAROEN

, SINGH

Comparison of simulation methods for power system reliability indexes and their distributions

[J]. IEEE Transactions on Power Systems, 2008, 23(2): 486-493.

DOI:10.1109/TPWRS.2008.919425 URL [本文引用: 1]

[31]

高新波, 谢维信.

模糊聚类理论发展及应用的研究进展

[J]. 科学通报, 1999, 44(21): 2241-2251.

[本文引用: 1]

GAO

Xinbo

, XIE

Weixin

Research progress on the development and application of fuzzy clustering theory

[J]. Chinese Science Bulletin, 1999, 44(21): 2241-2251.

[本文引用: 1]

[32]

YANG

W H

, CAO

M S

, GE

P J

, et al.

Risk-oriented renewable energy scenario clustering for power system reliability assessment and tracing

[J]. IEEE Access, 2020, 8: 183995-184003.

DOI:10.1109/Access.6287639 URL [本文引用: 1]

[33]

SHAO

C Z

, SHAHIDEHPOUR

, DING

Market-based integrated generation expansion planning of electric power system and district heating systems

[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2483-2493.

DOI:10.1109/TSTE.5165391 URL [本文引用: 1]

[34]

LIU

X Z

, WU

J Z

, JENKINS

, et al.

Combined analysis of electricity and heat networks

[J]. Applied Energy, 2016, 162: 1238-1250.

DOI:10.1016/j.apenergy.2015.01.102 URL [本文引用: 1]

综合能源系统多时间尺度动态时域仿真关键技术

2022

... 近年来,快速增长的能源需求和日益严峻的环境问题迫使各国积极推进新能源及多能融合技术发展^[1].电热综合能源系统实现电力系统和区域供热系统在能源生产、分配和利用等方面耦合,具有低碳、高效、经济的优点,获得广泛关注和发展^[2].截至2020年底,我国热电联产装机容量达到约 498 GW,未来供热系统和电力系统将有更广泛的互联. ...

综合能源系统多时间尺度动态时域仿真关键技术

2022

含多能微网群的区域电热综合能源系统分层自治优化调度

2021

含多能微网群的区域电热综合能源系统分层自治优化调度

2021

Economic dispatch of integrated energy systems with robust thermal comfort management

2021

... 为提高电-热综合能源系统的能源利用率,诸多文献研究建立了电-热综合调度模型,以统一部署电力和供热设备的运行计划^[3].然而,在统一调度过程中,热电联产机组“以热定电”的运行方式限制了电-热综合能源系统的运行灵活性,从而导致系统无法消纳更多的风力资源^[4].为改善这一现象,文献[5⇓-7]中提出通过热泵、电锅炉和热电联产机组的联合运行,达到能量在电、热等不同形式之间灵活切换,从而提高电热系统的运行灵活性.另一方面,具有天然弹性的建筑热负荷因其形式灵活、不需要增设额外设备而受到青睐,并广泛应用于电-热综合能源系统的优化调度中,以提高能源利用率和风力发电(简称风电)消纳能力^[8-9]. ...

Dispatch model of combined heat and power plant considering heat transfer process

2017

计及储热备用效益的电热综合能源系统优化调度模型

2021

计及储热备用效益的电热综合能源系统优化调度模型

2021

考虑风电消纳的区域综合能源系统源荷协调经济调度

2020

考虑风电消纳的区域综合能源系统源荷协调经济调度

2020

计及P2H的电-热互联综合能源系统概率能量流分析

2017

计及P2H的电-热互联综合能源系统概率能量流分析

2017

Dispatch model for CHP with pipeline and building thermal energy storage considering heat transfer process

2019

Flexible dispatch of a building energy system using building thermal storage and battery energy storage

2019

... 为量化建筑热负荷的弹性,文献[9]中将建筑热负荷建模为“储能电池”,以电池的充放电代表建筑热负荷功率的调节过程.然而,这类建模方法往往忽略了建筑本身的传热特性,使模型本身失去建筑传热特性物理层面的可解释性.此外,文献[10-11]中提出采用实验方法对建筑传热特性及潜在灵活性进行研究.但工作量较大,限制了该方法的应用^[12].考虑上述方法的缺点,文献[12-13]中提出利用数据驱动的方法量化建筑热负荷的弹性.文献[14⇓-16]中基于大规模监测数据和专家信息,构建量化热负荷弹性的关键参数与其影响因素的关系模型,进而实现对建筑热负荷弹性的预测.为提高供热系统的智能化程度,文献[17]中采用混合数据驱动模型对未来1 h的热负荷进行预测建模,文献[18]中建立了基于深度长短期记忆网络的综合能源多负荷联合预测模型.然而,数据驱动方法不可避免地存在数据不足和训练模型不精确的问题,随之带来热负荷弹性量化测量误差,这种误差可能会导致对建筑热负荷需求弹性的过度高估,从而对电-热综合能源系统的协调优化调度构成风险. ...

Experimental investigation of demand response potential of buildings: Combined passive thermal mass and active storage

2020

Estimating demand response potential under coupled thermal inertia of building and air-conditioning system

2019

Multi-step ahead forecasting of heat load in district heating systems using machine learning algorithms

2019

... .考虑上述方法的缺点,文献[12-13]中提出利用数据驱动的方法量化建筑热负荷的弹性.文献[14⇓-16]中基于大规模监测数据和专家信息,构建量化热负荷弹性的关键参数与其影响因素的关系模型,进而实现对建筑热负荷弹性的预测.为提高供热系统的智能化程度,文献[17]中采用混合数据驱动模型对未来1 h的热负荷进行预测建模,文献[18]中建立了基于深度长短期记忆网络的综合能源多负荷联合预测模型.然而,数据驱动方法不可避免地存在数据不足和训练模型不精确的问题,随之带来热负荷弹性量化测量误差,这种误差可能会导致对建筑热负荷需求弹性的过度高估,从而对电-热综合能源系统的协调优化调度构成风险. ...

数据驱动的综合能源系统负荷预测综述

2021

数据驱动的综合能源系统负荷预测综述

2021

Smart meter data-driven evaluation of operational demand response potential of residential air conditioning loads

2020

A simplified prediction model for energy use of air conditioner in residential buildings based on monitoring data from the cloud platform

2020

Optimal operation strategy for combined heat and power system based on solid electric thermal storage boiler and thermal inertia

2019

2020

2021

Demand response potential evaluation for residential air conditioning loads

2018

... 在电热综合能源系统中,建筑物存在热动态特性,因此建筑通过各式散热器获取热能后,经过一段时间延迟才可达到预设温度^[19].目前,一阶等效热参数(ETP)模型^[20]被广泛用来描述建筑物的热动态特性,详细揭示了注入的热能与建筑物室内外温度之间的关系,如图1所示.一阶ETP模型的数学关系式如下: ...

Transmission-constrained unit commitment considering combined electricity and district heating networks

2016

2018

... 评估建筑热负荷基准值和弹性值的关键参数为k_p_,_r_,_t和C_p_,_r_,_t.k_p_,_r_,_t和C_p_,_r_,_t会随着建筑围护结构及外界天气条件的改变而变化^[21]; 此外,外界天气条件不同,用户的用热需求也存在一定差异^[22].因此,有必要针对同一类建筑揭示k_p_,_r_,_t和C_p_,_r_,_t与气象参数的关系,进而为建筑热负荷需求弹性预测提供较准确的参考,具体包含以下主要步骤: ...

2018

计及热力不确定性的智能建筑电-热联合鲁棒经济调度

2020

计及热力不确定性的智能建筑电-热联合鲁棒经济调度

2020

Graduation formula: A new method to construct belief reliability distribution under epistemic uncertainty

2020

... 然而,在上述提取和训练过程中,针对k_p_,_r_,_t和C_p_,_r_,_t预测的测量误差不可避免.这些测量误差均可归结为认知不确定性引起的误差.认知不确定性是由于模型不准确或缺乏数据而导致对问题缺乏理解,进而产生的认知偏差^[23]. ...

D-S证据理论综述

2015

... D-S证据理论由Dempster首先提出,它建立在完善的方法论上,可以解决由随机性或模糊性而导致的不确定性问题^[24],并且通过多方信息融合能够综合不同主体信息^[25],得到更加可靠的评估结果,其主要概念定义如下. ...

D-S证据理论综述

2015

多源信息融合中一种新的证据合成算法

2016

多源信息融合中一种新的证据合成算法

2016

基于大焦元的子焦元的信任函数逼近方法

2019

... 使用基于信息熵特性融合的修正信任函数描述误差融合,从而更准确地估计建筑热负荷的需求弹性^[26-27]. ...

基于大焦元的子焦元的信任函数逼近方法

2019

... 使用基于信息熵特性融合的修正信任函数描述误差融合,从而更准确地估计建筑热负荷的需求弹性^[26-27]. ...

基于融合信息熵性质的信任函数概率逼近

2014

... 使用基于信息熵特性融合的修正信任函数描述误差融合,从而更准确地估计建筑热负荷的需求弹性^[26-27]. ...

基于融合信息熵性质的信任函数概率逼近

2014

... 使用基于信息熵特性融合的修正信任函数描述误差融合,从而更准确地估计建筑热负荷的需求弹性^[26-27]. ...

Clustering representative days for power systems generation expansion planning: Capturing the effects of variable renewables and energy storage

2019

... 重点介绍计及热负荷需求弹性及认知不确定性的场景生成方法,代表日的选取方法参考文献[28]. ...

Probabilistic evaluation of available load supply capability for distribution system

2013

... 建筑热负荷需求弹性主要由k_p_,_r_,_t和C_p_,_r_,_t刻画,因此通过抽样k_p_,_r_,_t和C_p_,_r_,_t的误差场景表示各自相对误差的不确定性.目前,蒙特卡罗(MC)抽样和拉丁超立方(LHS)抽样是使用较为广泛的抽样方法^[29].MC抽样技术是完全随机的,在输入分布的范围内,样本可以落在任何位置,但样本更有可能从高发生概率的分布区域中抽取.而LHS抽样根据输入变量的累积分布函数(CDF)生成随机样本数^[30],它从随机变量的整个分布中进行抽样,可以确保小概率事件在模拟的输出中被准确地代表,从而提供更稳定和更精确的估计结果.同时LHS抽样迭代次数少,在抽样效率和运行时间方面的表现均更为优异.因此,采用LHS抽样方法模拟k_p_,_r_,_t和C_p_,_r_,_t的不确定性,应用过程如下: ...

Comparison of simulation methods for power system reliability indexes and their distributions

2008

模糊聚类理论发展及应用的研究进展

1999

... 场景缩减技术根据场景的相似程度将场景分为不同的集群.模糊控制是自动控制领域的经典方法,模糊集引入了隶属度的概念,不遵循经典数学中“非0即1”的约定,而是提供了更灵活的聚类结果^[31]. ...

模糊聚类理论发展及应用的研究进展

1999

Risk-oriented renewable energy scenario clustering for power system reliability assessment and tracing

2020

... 式中:U 为z×g隶属度矩阵,z为设定的聚类类别数,g为待选场景的数量;W为聚类中心矩阵;G为候选聚类场景的一维矩阵;u_vw 为场景x_v 对聚类 w 的隶属度;x_w为待聚类的第w个场景;d_vw 为x_w和a_v之间的欧氏距离;a_v为每个聚类的聚类中心;模糊系数q'一般由经验决定,q'值过小或过大均会导致聚类算法的效果变差.各参数需满足的约束条件及算法具体流程见文献[32]. ...

Market-based integrated generation expansion planning of electric power system and district heating systems

2020

... 式中:

$P_{s, t}^{g e n}$

和

$Q_{s, t}^{g e n}$

分别为机组s的电出力如热电联产机组和热出力如燃气机组、锅炉等;

$P_{p, t}^{d e m}$

为电负荷;N_p_,_r为建筑总数;S_gen为机组集合.式(20)为目标函数,其目的为最小化系统运行成本;式(21)表示运行约束;式(22)为建筑热负荷灵活性模型;式(23)给定了室内温度舒适范围.有关电-热系统协调调度模型的目标函数和约束的介绍详见文献[33]. ...

Combined analysis of electricity and heat networks

2016

... 为了说明建筑热负荷的需求弹性可以为系统提供更大的调节空间,将提出的建筑热负荷灵活响应模型应用于实际的电热综合能源系统中.系统结构及参数主要来自文献[34],并在此基础上,增加一台功率为600 MW的风力涡轮机和一台1000 kW的燃气发电机组,电能通过配电网络中每条馈线处的11/0.433 kV 变压器提供给负载;在区域供热系统中,设置3个节点提供热能. ...

〈

〉