调度计划的时间颗粒度指调度计划中一个时段的长度.以风力发电(简称风电)为主的RES高比例、大规模并网,易受气象因素影响而出现RES功率快速波动.如2018年6月纽约上州因风暴致使250 MW风电场在8 min内全部停机;而我国酒泉、江苏等8个107 kW级以上的风电基地出力同时率在90%以上,易受大面积气象事件影响而短时间内出现快速爬坡事件[3].美国联邦能源管理委员会指出小时级时间颗粒度灵活性不足以应对高RES渗透率影响[4],过大的时间颗粒度不能捕捉调度时段内净负荷快速波动,产生大量不平衡功率,造成系统频率偏差、线路过载、弃风弃光等后果.因此,电网净负荷波动率提高的同时,日前调度时间颗粒度也被逐步缩小.20世纪50年代起较长的一段时间内,日前调度计划均以60 min为一个时段[5];至90年代,日前调度开始以30 min为一个调度时段[6];21世纪初至今,日前调度普遍以15 min为一个调度时段[7].
目前已有大量针对日前调度时间颗粒度经济性、安全性以及调度计算量优化的深入研究.文献[8]中对比分析5、15、30和60 min时间颗粒度机组组合,指出缩短时间颗粒度能降低期望运行费用,并且可以缓解风电出力波动的影响.文献[9]中对比分析60、15 min时间颗粒度的随机优化调度,指出15 min时间颗粒度鲁棒性更优,但代价是计算成本显著增加.文献[10-11]中分析调度时间颗粒度内风电出力波动引发的电网线路过载等问题,并提出三阶段预防调度策略.文献[12]中指出由于计算能力的限制以及更高分辨率净负荷数据的缺乏,可能难以大规模缩短时间颗粒度.为缓解缩短时间颗粒度带来的计算成本增长问题,文献[13-14]中统一机组组合和经济调度,从而降低了日前调度和日内调度总计算量.文献[15]中提出自适应时间颗粒度方案,不改变总调度计划时段数的同时,依据净负荷波动剧烈程度选择时间颗粒度,进而控制调度整体计算量.文献[16]中基于净负荷预测准确率随时间变化特征,提出随调度时间增加而增大时间颗粒度的滚动优化调度方案.现有文献优化了调度计算量,并指出高RES渗透率电网应当缩短时间颗粒度来降低调度运营成本和提高系统灵活性,但目前还没有涉及不同净负荷波动率电网如何选择时间颗粒度的具体问题.
针对上述问题,提出一种基于全局灵敏度的日前调度时间颗粒度优化方法,依据电网净负荷波动率优化时间颗粒度.采用全局灵敏度量化不同波动率电网中各时间颗粒度下净负荷波动性、不确定性对优化调度的影响,辨识不同时间颗粒度下影响优化调度的关键因素.并依据波动性、不确定性的灵敏度分析不同波动率电网下缩短时间颗粒度是否会提升优化调度程度和降低调度费用,进而确定不同波动率电网的时间颗粒度优化方案.
1 时间颗粒度特性分析
波动性是指功率随时间而变化的特性,不确定性为功率预测值与实际值之间的偏差.综合考虑对净负荷波动性与不确定性、计算量影响,时间颗粒度主要通过以下3个方面影响日前调度.
(1) 调度计划的精细度.
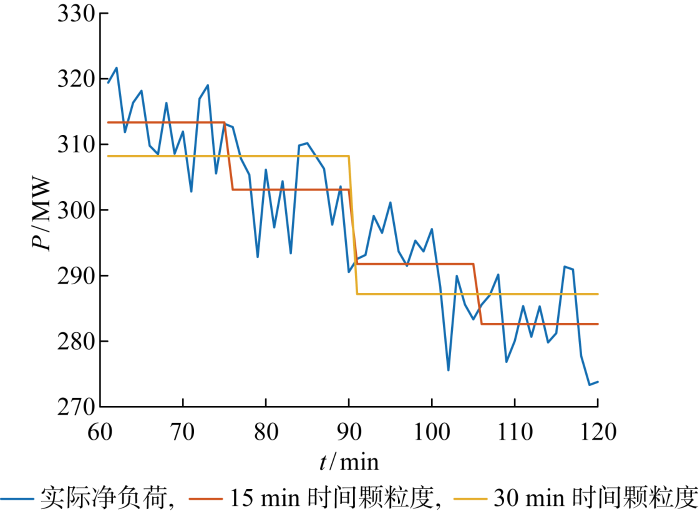
2009年美国德克萨斯州10 min时间尺度下风电功率变化量高达 1 256 MW,占风电场容量的14%[17],光伏发电数十秒的波动量可达60%以上[18].缩短时间颗粒度可以更好地捕捉净负荷波动变化,避免调度计划中预留的爬坡能力不足,产生过大频率偏差甚至电网解列等严重后果.调度计划的滚动修编针对每一采样时刻的净负荷进行优化调度,解决净负荷的持续性偏差问题,不能解决时段内的波动问题.因此,净负荷波动率高的电网中,缩短时间颗粒度十分必要.图1中,相比于30 min时间颗粒度,15 min时间颗粒度可以更精细地描述净负荷变化趋势.缩短时间颗粒度可以降低波动性对优化调度影响,提升调度计划精细度.图中:P为净负荷;t为时间.
图1
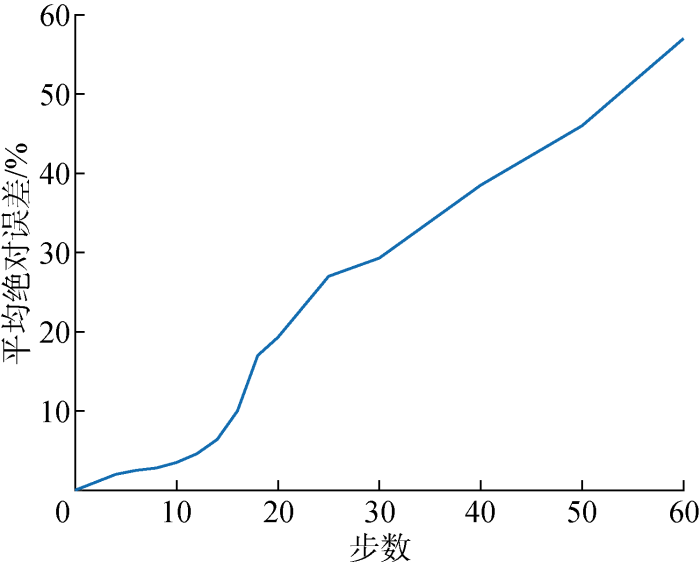
(2) 净负荷预测的准确率.
图2
(3) 优化调度的计算量.
电力系统优化调度问题是一个典型的大规模、非线性、离散的优化问题,大部分决策变量和约束条件均基于时段,例如每个调度时段的机组状态和出力、有功平衡约束、备用约束等.时间颗粒度缩小,将使电力系统优化调度的计算规模成倍扩大.以时间颗粒度从30 min缩短为15 min为例,变量数和约束条件数量大致增加为原来的2倍,调度计划编制时段数翻倍,总的调度计算量将呈指数级增长[20].
净负荷波动性与不确定性、计算资源是影响时间颗粒度选择的3个关键因素.净负荷不确定性取决于现有预测水平与预测手段.由于预测能力短时间内无法提升,所以在计算资源充足情况下,净负荷波动性是选择调度计划时间颗粒度的决定性因素.
2 源荷匹配率与灵活性不足率指标
缩短调度计划时间颗粒度可以有效缓解净负荷波动变化影响,提升调度计划精细度,但同时也会增大净负荷预测误差,使得优化调度效果不一定得到提升.通过定义源荷匹配率与灵活性不足率指标反映系统优化程度和可靠性,源荷匹配率指机组出力曲线与净负荷曲线匹配程度,便于分析净负荷波动性、不确定性综合影响下,缩短时间颗粒度是否会提升系统调度优化;灵活性不足率指电力系统通过调配各种资源响应净负荷波动性、不确定性的能力,可以反映不同时间颗粒度下系统可靠性.
2.1 源荷匹配率
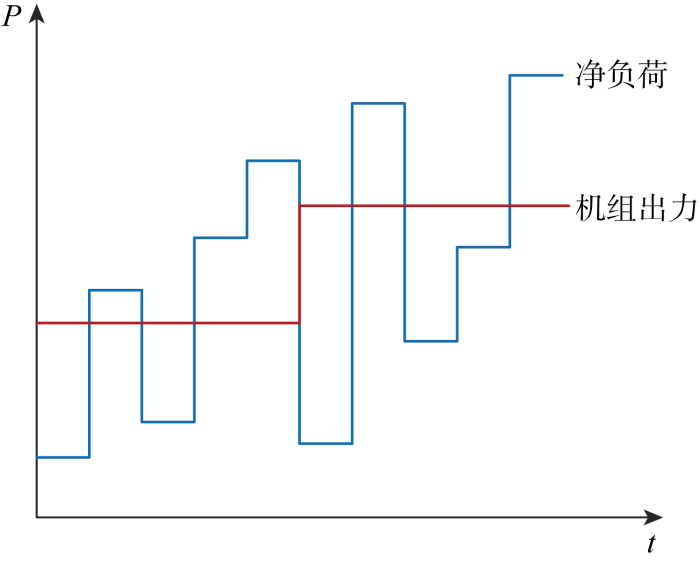
目前,日前调度机制将调度周期划分为24或96个时段,并假定每个时段调度指令对应为该时段净负荷平均值,如图3所示.
图3
图3
净负荷功率功率曲线与调度指令
Fig.3
Net load power power curve and scheduling instructions
机组组合阶梯曲线对净负荷预测曲线拟合程度较低,未充分利用净负荷预测信息且不能体现时间颗粒度内的功率波动变化.机组出力曲线与实际净负荷曲线包络而成的面积为不平衡功率,是调度计划之外的电量,必须通过临时调度或者自动控制系统调节.
不平衡功率总量为
式中: Pl(t)为t时段实时净负荷功率;
为了分析调度的优化程度,反映机组出力与净负荷的匹配程度,参照文献[21]中方法提出源荷匹配率:
式中:n1为调度时段内净负荷功率预测点数;
源荷匹配率反映机组出力跟踪净负荷的能力.该指标越高,表明机组出力能更好地追踪净负荷的变化,产生不平衡功率总量小且调度运营成本低,调度优化程度更高.
2.2 灵活性不足率
式中:
为更好地衡量电网系统灵活性裕度的充足度,建立灵活性不足率作为评价指标如下:
式中:Fup、Fdown分别为电网24 h内的上调灵活性不足率和下调灵活性不足率;a表征考虑不确定性程度;σ为系统净负荷预测误差的标准差;Pmax为最大负荷;Pdown(t)、Pup(t)分别为系统t时段内可能发生的最大向下波动功率和最大向上波动功率;γsum为调度时段总数.
总灵活性不足率F为上调灵活性不足率和下调灵活性不足率之和,该指标反映电网平抑净负荷波动与预测误差的能力,其值越小,系统灵活性裕度越充足,平抑波动性与不确定性能力越强.
2.3 日前调度建模
日前调度中,各风电场对下一日出力计划进行预测并汇报调度中心,调度中心根据风电场汇报信息以及负荷预测信息安排下一日常规机组的启停计划,其目标函数与约束条件如下:
式中:Ns为场景数,取3;πs为第s个场景的概率;um,t,s、
3 基于全局灵敏度的时间颗粒度选择方法
缩小时间颗粒度,一方面可以提高精细化程度,有利于降低临时调度的功率和电量;另一方面,会降低净负荷预测准确率,增加临时调度的功率和电量.优化时间颗粒度的核心是在精细化程度和负荷预测准确率之间取得平衡,使临时调度的功率和电量最小化,达到降低调度成本的目的.因此,需要比较缩短时间颗粒度带来的优化调度提升量与增加预测误差引发的优化调度下降量.灵敏度分析方法是量化输入变量及变量间相互作用对输出变量影响程度的有效手段[24],因此,采用Sobol'方法和多项式混沌展开的全局灵敏度方法,量化不同波动率电网中不同时间颗粒度下净负荷波动性、不确定性对源荷匹配率指标方差的影响程度,利用净负荷波动性、不确定性对源荷匹配率指标的全局灵敏度选择最优时间颗粒度.
3.1 多项式混沌展开
对于含n2个独立随机变量x=[x1 …
式中:i=[i1 …
多项式基函数Φi(x)之间具有正交性,可以分解为各输入变量对应基函数的张量积,即
式中:
实际工程中为便于计算,将式(14)进行有理项截断,限定最高展开阶数为r:
将式(16)改写为向量形式:
式中:基函数向量Φ(x)=[1 Φ1(x) … Φr-1(x)]T;Φ(x)对应展开系数向量a=[a0a1 … ar-1]T.
最高展开阶数r取值越大,展开模型拟合精度越高,但计算量也越大.通常最高展开阶数r取2~3即可满足工程计算精度,为便于计算取r=2,则
对Q组采样样本进行源荷匹配率指标计算,基于最小二乘原理计算式(18)中各展开项系数可表示如下:
式中:x(i)为输入变量第i组采样样本;y(x(i))为第i组采样样本源荷匹配率指标结果.
3.2 基于Sobol'方法和多项式混沌展开全局灵
敏度 首先定义如下下标集合:
Sobol'分解形式为
式中:f0为常数项;fi(xi)为xi的1阶子函数;
结合随机变量方差的定义,f(x)的方差可以表示为
由于各非0阶子函数的期望为0,所以D(f(x))可以进一步用子函数的方差表示:
式中:Di=D(f(xi)),表示1阶子函数f(xi)的方差;Dij为2阶子函数f(xi,xj)的方差;
当随机变量x满足独立分布时,由Sobol'分解的唯一性,可将式(18)唯一化简为Sobol'分解形式:
对比式(17)与式(24)可得:
可得基于多项式混沌展开的各阶全局灵敏度指标:
3.3 算法流程
基于净负荷波动性、不确定性对优化调度指标的灵敏度,针对不同波动率电网选择合适时间颗粒度,流程如下:
(1) 数据输入.包含净负荷波动率、误差率的样本和概率分布信息.
(2) 波动性与不确定性灵敏度计算.采用拉丁方采样得到Q个输入样本,每一个样本点都执行确定性日前调度计算,计算源荷匹配率.基于Sobol'方法和多项式混沌展开分别计算不同波动率电网中,波动性与不确定性在不同时间颗粒度下对源荷匹配率的全局灵敏度指标.
(3) 基于全局灵敏度的不同波动率电网时间颗粒度选择方案.在不同波动率电网中,依据净负荷波动性、不确定性的全局灵敏度分析各时间颗粒度下影响优化调度的主要因素.当波动性为影响优化调度的主要因素时,需缩短时间颗粒度.当不确定性为影响优化调度的主要因素时,需增大时间颗粒度.
4 算例
图4
表1 系统机组参数
Tab.1
| 机组 | am/[美元· (MW2·h)-1] | bm/[美元· (MW·h)-1] | cm/ [美元·h-1] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 470 | 150 | 4.3×10-4 | 21.60 | 958.20 | 120 | -120 | 3000 | 3000 |
| 2 | 460 | 130 | 6.3×10-4 | 21.05 | 1313.60 | 120 | -120 | 3000 | 3000 |
| 3 | 340 | 73 | 5.9×10-4 | 20.81 | 604.97 | 120 | -120 | 2200 | 2200 |
| 4 | 300 | 60 | 7.0×10-4 | 22.90 | 471.60 | 100 | -100 | 1800 | 1800 |
| 5 | 243 | 73 | 7.9×10-4 | 21.62 | 480.29 | 100 | -100 | 900 | 900 |
| 6 | 160 | 57 | 5.6×10-4 | 17.87 | 601.75 | 100 | -100 | 900 | 900 |
| 7 | 130 | 20 | 2.1×10-3 | 16.51 | 502.70 | 50 | -50 | 260 | 260 |
| 8 | 120 | 47 | 4.8×10-3 | 23.23 | 639.40 | 50 | -50 | 260 | 260 |
| 9 | 80 | 20 | 10.9×10-1 | 19.58 | 455.60 | 50 | -50 | 30 | 30 |
| 10 | 55 | 20 | 9.5×10-3 | 22.54 | 629.40 | 50 | -50 | 30 | 30 |
净负荷波动率定义为
式中:Pt,n+1、Pt,n为时段t内第n+1、n个预测点净负荷功率.净负荷数据的分辨率为1 min.
4.1 初始波动率电网灵敏度分析
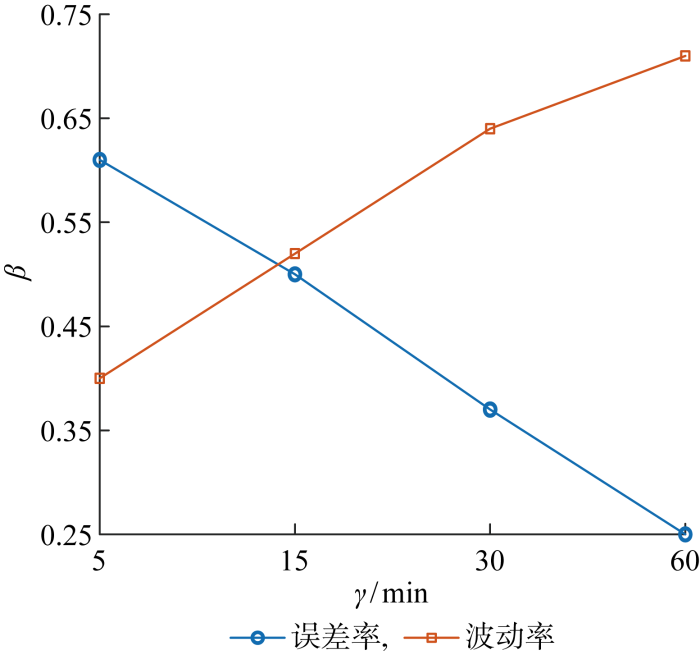
假设净负荷波动率与净负荷预测平均误差无关,波动率与误差率为独立变量.波动率、误差率数据预处理以采用5 min时间颗粒度为例,净负荷波动率方差为7%,误差率为8.5%,假设波动率方差服从N(7%, 7%/3)、误差率服从N(8.5%, 8.5%/3)的正态分布,采用拉丁超立方抽样分别生成100组净负荷波动率方差、误差率数据:(σ1,σ2,…,σ100)、(λ1,λ2,…,λ100),并按照对应波动率方差(σ1,σ2,…,σ100)生成波动率为N(0,σ1),N(0,σ2), …, N(0,σ100)的净负荷数据,预测曲线为实际曲线叠加相应满足N(0,λ1/3), N(0,λ2/3), …, N(0,λ100/3)分布的白噪声,分别计算净负荷的波动率、误差率对源荷匹配率的全局灵敏度.图5为灵敏度(β)与时间颗粒度关系的计算结果.
图5
图5
净负荷预测误差率与波动率灵敏度
Fig.5
Net load forecast error rate and volatility sensitivity
由图5可知,净负荷误差率灵敏度随时间颗粒度增大而减小,波动率灵敏度随时间颗粒度的增大而增大.当误差率与波动率灵敏度之差较大时,则灵敏度高的一方为影响优化调度的主导因素.当误差率为主导因素时,波动率影响较小,应当增大时间颗粒度提升优化调度;当波动率为主导因素时,误差率影响较小,应当缩短时间颗粒度提升优化调度.需在净负荷波动率、误差率之间取得一种平衡.因此,可以采用误差率与波动率灵敏度之差判断是否需要优化时间颗粒度.
表2 灵敏度之差与优化调度效果
Tab.2
| γ/min | Δβ | Psum/(MW·h) | D/% |
|---|---|---|---|
| 5 | 0.21 | 3 230 | 90.74 |
| 15 | 0.10 | 3 187 | 90.87 |
| 30 | 0.27 | 3 247 | 90.70 |
| 60 | 0.46 | 3 281 | 90.60 |
表3 经济性以及灵活性
Tab.3
| γ/min | f1/美元 | f2/美元 | f3/美元 | F/% |
|---|---|---|---|---|
| 5 | 826723 | 83915 | 910640 | 2.02 |
| 15 | 826555 | 82794 | 909350 | 1.93 |
| 30 | 825736 | 84352 | 910090 | 2.09 |
| 60 | 824864 | 85249 | 910110 | 2.17 |
由表3可知,15 min时间颗粒度下总成本最小,且总灵活性不足率也最低.因此,可以通过波动率、误差率灵敏度之差来选择时间颗粒度,灵敏度之差越小,优化调度效果越好,总费用越低,且灵活性更高.净负荷波动率为7%时,15 min为最优时间颗粒度.
4.2 8%波动率电网灵敏度分析
为验证在计算资源充足与现有预测水平情况下,净负荷波动性是选择调度计划时间颗粒度的决定性因素,令净负荷误差率等其他条件不变,将净负荷波动率增大为8%,对净负荷的波动率、误差率进行灵敏度分析,计算结果如图6所示.
图6
图6
净负荷预测误差率与波动率灵敏度
Fig.6
Net load forecast error rate and volatility sensitivity
由图6可知,相比于原波动率为7%的电网,波动率增大为8%后各时间颗粒度下波动率灵敏度均增大,误差率灵敏度均相应缩小.
表4 灵敏度之差与优化调度效果
Tab.4
| γ/min | Δβ | F/% | D/% | f3/美元 |
|---|---|---|---|---|
| 5 | 0.07 | 2.19 | 89.17 | 932860 |
| 15 | 0.11 | 2.30 | 88.87 | 932900 |
| 30 | 0.31 | 2.45 | 88.79 | 933270 |
| 60 | 0.54 | 2.52 | 88.69 | 933480 |
4.3 不同波动率电网最优时间颗粒度
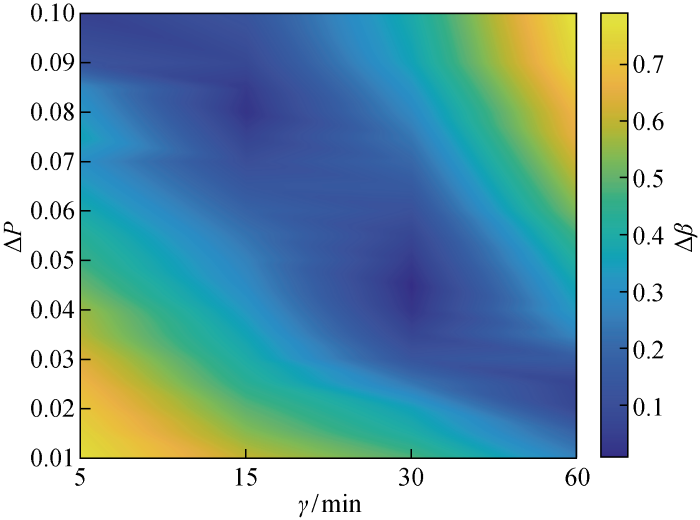
在计算资源充足与现有预测水平情况下,净负荷波动率是优化时间颗粒度的决定性因素.分别计算波动率从1%按步长0.05%增大至10%的不同电网净负荷波动率、误差率灵敏度.净负荷波动率、误差率灵敏度之差如图7所示.
图7
图7
净负荷预测误差率和波动率灵敏度之差
Fig.7
Sensitivity difference between net load forecast error rate and volatility
随着净负荷波动率上升,灵敏度之差最小点不断左移,表明净负荷波动率高的电网中,缩短时间颗粒度可以提升优化调度.波动率越高的电网中,最优时间颗粒度越小.图7中各波动率的最优时间颗粒度分界点为2.909%、5.455%、7.673%.净负荷波动率小于2.909%时,应当选择60 min时间颗粒度;净负荷波动率在[2.909%,5.455%)时,应当选择30 min时间颗粒度;净负荷波动率在[5.455%,7.673%]时,应当选择15 min时间颗粒度;净负荷波动率大于7.673%且计算资源充足时,应当选择5 min时间颗粒度.
5 结语
时间颗粒度优化问题的关键在于权衡净负荷波动性与不确定性.基于波动率、误差率灵敏度之差在负荷波动性与不确定性之间取得一种平衡;并指出高气象敏感RES电网中,波动率为选择时间颗粒度的关键因素,高波动率电网应当缩短时间颗粒度提升优化调度;最后确定各净负荷波动率下的最优时间颗粒.此外,本文方法在计算资源充足的情况下进行时间颗粒度优化,未来将对优化缩短时间颗粒度后的调度计算量展开研究.
参考文献
中国2050高比例可再生能源发展情景暨路径研究
[R].
China 2050 high percentage renewable energy development scenario and pathway study
[R].
Effect of time resolution on unit commitment decisions in systems with high wind penetration
[C]//
考虑风电爬坡事件的鲁棒机组组合
[J].
Robust unit commitment considering wind power ramp events
[J].
Security constrained unit commitment
[J].
Short term scheduling in a wind/diesel autonomous energy system
[J].DOI:10.1109/59.119261 URL [本文引用: 1]
电网安全节能发电日前调度优化模型及算法
[J].
Optimal model and algorithm for day-ahead generation scheduling of transmission grid security constrained convention dispatch
[J].
Stochastic optimization of sub-hourly economic dispatch with wind energy
[J].DOI:10.1109/TPWRS.2015.2410301 URL [本文引用: 1]
Intra-interval security assessment in power systems with high wind penetration
[J].DOI:10.1109/TSTE.5165391 URL [本文引用: 1]
Intra-interval security based dispatch for power systems with high wind penetration
[J].DOI:10.1109/TPWRS.2018.2870667 URL [本文引用: 1]
Economic consequences of alternative solution methods for centralized unit commitment in day-ahead electricity markets
[J].DOI:10.1109/TPWRS.2008.919246 URL [本文引用: 1]
Hidden power system inflexibilities imposed by traditional unit commitment formulations
[J].DOI:10.1016/j.apenergy.2017.01.089 URL [本文引用: 1]
Multiple time resolution unit commitment for short-term operations scheduling under high renewable penetration
[J].DOI:10.1109/TPWRS.2013.2278215 URL [本文引用: 1]
Comparison of advanced power system operations models for large-scale renewable integration
[J].DOI:10.1016/j.epsr.2015.06.025 URL [本文引用: 1]
Multiple time resolution stochastic scheduling for systems with high renewable penetration
[J].
Studying the variability and uncertainty impacts of variable generation at multiple timescales
[J].DOI:10.1109/TPWRS.2012.2185816 URL [本文引用: 1]
Analysis of wind power ramping behavior in ERCOT
[R].
光伏发电置信容量的研究现状与发展趋势
[J].
Current status and development trend on capacity credit of photovoltaic generation
[J].
基于信息熵的历史数据选取对超短期风电功率预测精度影响研究
[J].
Impact of historical data selection on accuracy of ultra-short-term wind power prediction based on prediction information entropy
[J].
Time-adaptive unit commitment
[J].DOI:10.1109/TPWRS.59 URL [本文引用: 1]
考虑自适应实时调度的多电压等级直流配电网能量优化方法
[J].
Energy optimization method of multi-voltage-level DC distribution network considering adaptive real-time scheduling
[J].
Variance-based global sensitivity analysis for power systems
[J].DOI:10.1109/TPWRS.2017.2719046 URL [本文引用: 1]
基于稀疏多项式混沌展开的可用输电能力不确定性量化分析
[J].
Sparse polynomial chaos expansion based uncertainty quantification for available transfer capability
[J].
Particle swarm optimization
[C]//
基于多场景随机规划和MPC的冷热电联合系统协同优化
[J].
Collaborative optimization of combined cooling heating and power system based on multi-scenario stochastic programming and model predictive control
[J].