由于燃油具有比热容大、性质稳定以及代偿损失小等优点[1 ] ,现已被作为热端部件的热沉广泛应用于现代高速飞行器设计中[2 ] .但以燃油作为热沉必须关注燃油的温度变化,如温度过高,不仅容易破坏其热稳定性,而且形成的非溶性沉积物和树脂沉淀物也可能堵塞油箱[3 -4 ] .因此,在储油系统结构设计过程中研究油箱内燃油温度分布尤为重要.试验和数值模拟是获得高速飞行器燃油温度变化的两个重要手段,虽然前者可获得准确的燃油温度数据,但因其无法在储油系统结构设计阶段完成,故基于数值模拟的燃油温度变化预测对储油系统结构设计起重要作用[5 ] .
国内外对燃油温度场计算的研究方法主要包括集总参数法、计算流体动力学(CFD)法和热网络法等.集总参数法假设燃油温度一致,重点关注燃油热平衡分析和边界条件研究.在燃油热平衡分析方面,Teare等[6 ] 提出一种快速的油箱瞬态热分析模型,该模型可以独立分析油箱的结构传热和油箱内部的换热问题;Bodie等[7 ] 提出一种应用于包括燃油管路在内的飞机燃油系统整体网络热分析模型,基于该模型探究了燃油温度的变化情况;Mawid等[8 ] 介绍了一种航空飞行器燃油系统模拟工具Athena,并通过试验验证了其有效性;张兴娟等[9 ] 利用热量平衡方法构建了燃油温度计算模型,分析飞机超声速巡航状态下燃油温度的瞬态变化.在边界条件研究方面,Ai等[10 ] 分析了影响油箱温度场的内部导热、外部对流和辐射等边界条件,并在此基础上建立了燃油瞬态计算模型.集总参数法简单高效,但忽略了燃油温度在空间上的差异,无法得到局部区域上的燃油温度,尤其是无法关注到靠近油箱壁面位置的高温区域油温[11 ] ,因此这一方法难以满足高速飞行器油箱设计的需要.
使用CFD方法可对油箱整体结构建模和计算,从而获得油箱内温度场分布情况.陈悦[4 ] 采用二维和三维的方法模拟了输油箱和供油箱内燃油流动换热过程,获得了油箱内燃油的温度分布特点及燃油出口温度随时间变化而变化的过程;赵璇[11 ] 采用CFD方法分析了超声速飞行器机翼油箱内外流场温度分布,并将CFD方法与集总参数法结果进行对比.CFD方法可以精确捕获油箱温度场分布,但对飞行全过程进行模拟所需的计算开销极大,难以满足油箱设计阶段快速迭代优化的需要.
为解决集总参数法得不到局部温度和CFD方法计算效率过低的问题,热网络法被应用于温度场计算,尤其是在固体温度场计算中,如轴承[12 ] 、电动机及发电机[13 ] 、管路[14 ] 和电路[15 -16 ] 等.康振烨等[17 ] 将热网络法应用于燃油温度场计算,将不同位置的燃油划分到不同的基元模块中,采用MATLAB/Simulink软件搭建飞机油箱稳态热分析仿真模型;吕亚国等[5 ] 在此基础上建立了飞机油箱非稳态热分析模型,结果表明热网络法的计算结果与飞行测试数据吻合良好.上述研究假设油箱基元模块节点之间的传热方式为固体导热,这一假设仅适用于燃油温度较低情况,对于具有高油温的高速飞行器储油系统,燃油内部会存在较强的冷热掺混,假定燃油基元模块间传热方式为固体导热的方法会带来较大误差.不仅如此,目前的热网格法未考虑燃油内部的宏观流动,随着燃油消耗,油箱中燃油存在整体向下的宏观流动,对于每一个位置固定的基元模块,都需要考虑燃油宏观流动带来的传质影响.
针对高速飞行器燃油瞬态温度预测问题,本文基于文献[5 ]和文献[17 ]提出一种满足设计精度的高效修正热网络方法,通过修正热传导方程的方法考虑油箱内部冷热掺混的影响,通过修正热平衡方程的方法考虑燃油宏观流动的影响.基于该热网络法构建了高速飞行器储油系统瞬态热分析模型,在不同的热边界条件和储油系统几何结构下校核其普适性.
1 高速飞行器的油箱模型
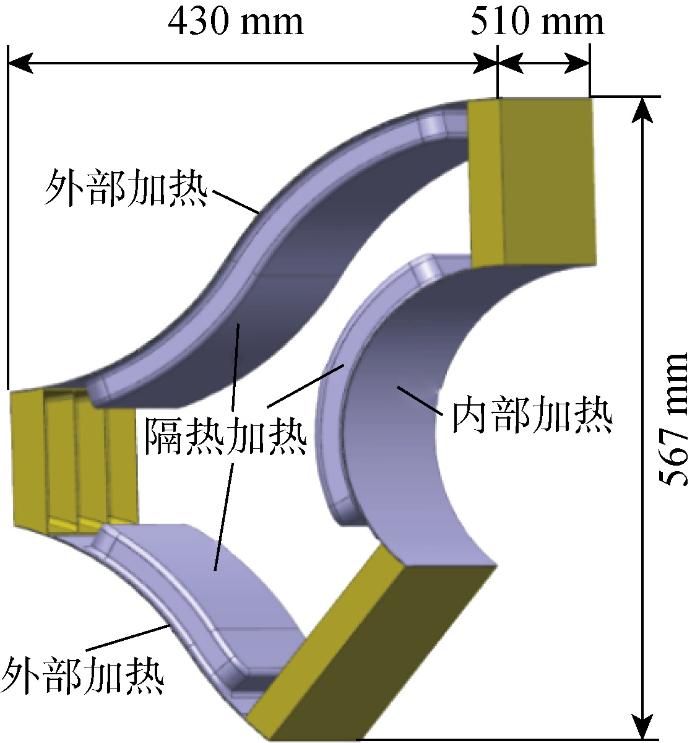
典型高速飞行器油箱结构的三维模型如图1 所示.油箱内侧面装有隔热材料以防止燃油温度过高;油箱左上和左下侧贴近飞机外壁面,飞行过程中会受到高速气流的气动加热作用;油箱右下侧贴近发动机进气道,会受到发动机的热传导加热;其余3个面以及两端端面与其他部件相连,可近似为绝热条件.在飞行过程中,通过高压氮气挤压气囊为发动机提供带有压力的燃油[18 ] .
图1
图1
油箱示意图
Fig.1
Diagram of fuel tank
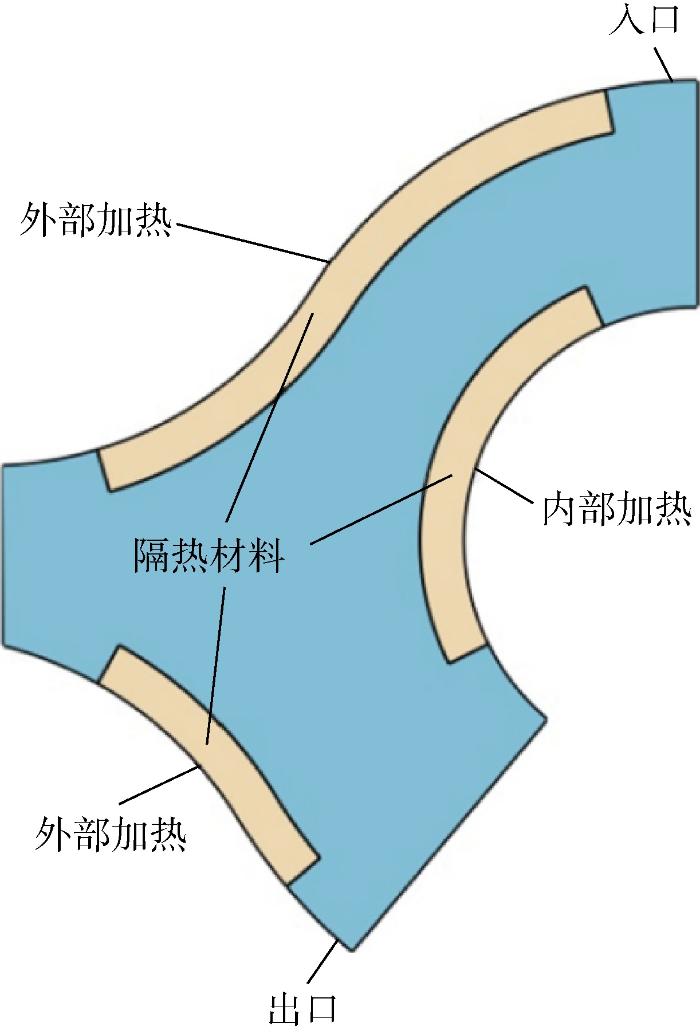
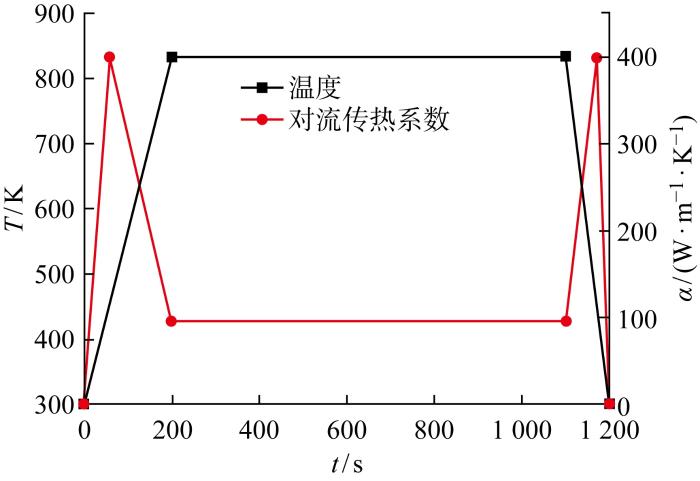
计算中高速飞行器油箱初始条件和模型简化如下:① 油箱在垂直于纸面方向上结构相似,且端面为绝热条件,因此将油箱模型简化为二维模型处理,油箱最上端和最下端表面为燃油入口和出口,如图2 所示;② 初始时刻油箱内充满燃油,燃油和隔热材料温度均为15 ℃,1200 s内燃油均匀消耗完;③ 外部的气动加热效果等效为对流加热边界条件,其对流换热系数和来流温度随时间的变化如图3 所示,t 为时间,T 为温度,α 为对流传热系数;④ 将内部发动机进气道的热传导作用等效为温度边界条件,温度随时间的变化与外部相同;⑤ 忽略气囊、蒙皮等结构对油箱温度场的影响.
图2
图2
油箱计算区域示意图
Fig.2
Diagram of fuel tank calculation domain
图3
图3
随时间变化的边界温度和对流传热系数
Fig.3
Variation of boundary temperature and heat transfer coefficient with time
2 修正热网络方法
2.1 热网络基元模块分类
对基元模块进行分类是因为不同的基元模块存在不同的热平衡方程.油箱内存在燃油和氮气两相,因氮气并非热设计的重点关注对象,在一定范围内可以接受氮气升到比较高的温度,且其密度较小,热扩散系数比较大,温度更易趋于一致,故采用集总参数法的方式处理,即将油箱中填充氮气的区域作为一个完整的基元模块,定义为氮气基元模块.
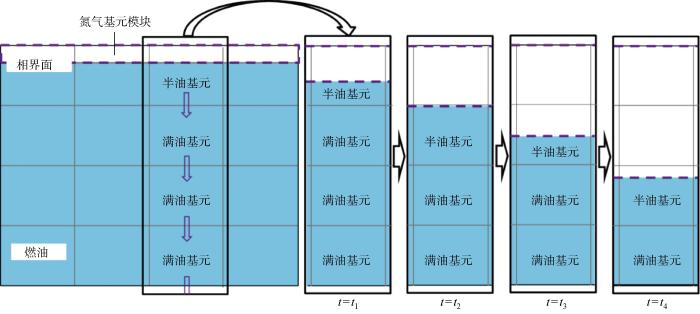
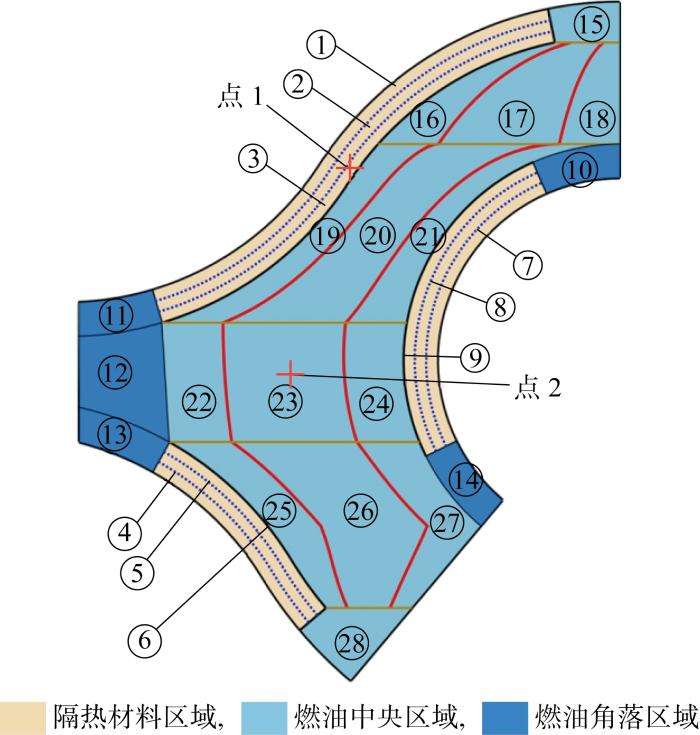
对于燃油则需要对其内部区域进行划分,以其形状规则的油箱结构为例阐述其区域划分,如图4 所示.首先,将油箱腔体等距划分为4×4个区域,将每个区域内的燃油作为一个单独的基元模块,认为每一个基元模块内部温度相同.初始时刻,油箱内充满燃油,随着燃油消耗,油气界面不断下降,处于最上层的燃油基元模块体积不断缩小,其他燃油基元模块体积恒定.根据燃油消耗过程中某一时刻基元模块体积是否发生改变,将燃油基元模块定义为两种类型:体积发生改变的模块定义为半油基元模块;体积恒定不变的模块定义为满油基元模块.随着燃油持续消耗,当油气界面到达基元模块交界面位置时,最上层的燃油基元模块体积变为0后消失,原本处于第二层的满油基元模块转变为半油基元模块,体积不断缩小,处于下层的基元模块仍为满油基元模块,以此类推直至燃油全部耗尽.
图4
图4
半油基元模块和满油基元模块随燃油消耗变化示意图
Fig.4
Variation of partial fuel module and full fuel module with fuel consumption
除了对油箱内部氮气和燃油区域划分基元模块外,对隔热材料区域也可进行划分,将其定义为隔热材料基元模块.
2.2 基元模块热平衡方程
2.2.1 半油基元模块
根据基元模块内能的变化量等于与周围基元模块的传热量和传质量,可将半油基元模块和满油基元模块的热平衡方程表述为
(1) d ( ρ c V i T i ) d t i +Ei
式中:Ti 为基元模块i 的瞬时温度;ρcVi 为基元模块i 的密度、比热容和体积的乘积;Qi 为基元模块i 与周围基元模块之间的传热量;Ei 为由于燃油整体向下流动导致的基元模块i 与周围基元模块之间的传质量.
假定燃油密度和比热容恒定,半油基元模块体积和温度均随时间变化而变化,式(1)左边展开为
(2) d ( ρ c V i T i ) d t ρTi c d V i d t ρcVi d T i d t ρTi cwi d V f u e l d t i d T i d t
式中:wi 为基元模块的相界面面积与总的相界面面积之比;V fuel 为燃油总体积.
假设燃油均匀平稳流出,燃油流线方向与纵向的热网络划分线平行.对于燃油基元模块i ,仅在纵向上存在传质作用,对于半油基元模块仅存在流出项,传质项可以写为
(3) Ei =- d m i d t i =ρ d V i d t i =ρwi d V f u e l d t i
式中:dmi / dt 为流出基元模块i 的质量流量,与基元模块i 质量的变化量ρ dVi / dt 大小相等,符号相反.
(4) d V f u e l d t m · f u e l ρ
式中:m · f u e l
(5) V fuel =V fuel,0 + ∫ 0 t d V f u e l d t
式中:V fuel,0 为初始时刻燃油体积. 对于基元模块i ,其体积变化速率dVi / dt 为总体积变化速率dV fuel / dt 的wi 倍,其体积大小也可通过式(5)的方式积分得到.
将式(2)~(5)带入式(1)可得半油基元模块的热平衡方程为
(6) d T i d t Q i ρ c V i
2.2.2 满油基元模块
满油基元模块热平衡方程的基本形式同式(1),不同的是其体积不随时间发生改变,其传质项除了考虑流出基元模块的质量流量,还应考虑从上方流入的基元模块质量流量:
(7) Ei =-d m i d t cTi +d m i n d t cT in =ρwi d V f u e l d t i -Tin )
式中:dm in / dt 为流入基元模块i 的质量流量,因满油基元模块质量守恒,其值与流出的质量流量dmi / dt 相等;T in 为流入基元模块i 质量流量的温度.
(8) d T i d t Q i ρ c V i w i ( T i - T i n ) d V f u e l d t V i
2.2.3 氮气基元模块
(9) m N 2 V N 2 p R g T N 2 V N 2
式中:p 为压力,保持1.5个标准大气压恒定;R g 为氮气的气体常数;氮气体积V N 2
(10) d m N 2 d t p R g 1 T N 2 d V N 2 d t - V N 2 T N 2 2 d T N 2 d t
式中:T N 2 V N 2 / dt 与燃油体积变化率dV fuel / dt 大小相等,符号相反.
(11) d ( ρ c V V N 2 T N 2 ) d t i + d m N 2 d t P T N 2 , i n
式中:cV 为定容比热容;cP 为定压比热容;T N 2 , i n
(12) d T N 2 d t R g p Q i + T N 2 , i n T N 2 c P - c V d V d t c P V N 2 T N 2 , i n T N 2 2
2.2.4 隔热材料基元模块
对于油箱隔热材料等固体区域,也可以划分热网络,其控制方程为
(13) d T s d t Q s ρ c V s
2.3 油箱基元模块划分
基于燃油的流动方向可将油箱结构离散化,划分为若干个基元模块,热网络划分方式如图5 所示.其中,因隔热材料在平行于边界面方向上温差较小而在边界面法线方向上存在较大温差,故将每个隔热材料在沿边界法向方向上划分为3个等宽度的基元模块,编号为①~⑨;然后,对燃油角落区域的油箱结构进行热网络划分,角落区域直接受到热载荷,其温度与油箱中央区域相差较大,需单独处理,编号为⑩~,同时角落区域控制体流动情况较为复杂,故在计算过程中进行适当简化,在控制方程(1)中不考虑传质项的影响;最后,对燃油中央区域进行基元模块划分.从CFD计算结果来看,中央区域温差不大,基元模块不必划分过多.中央区域基元模块横向划分线为水平线,纵向划分线为穿过横向线的1/4和3/4等分线,即在中央区域任画一条水平线,纵向划分线均穿过其1/4和3/4等分点,编号为~.忽略由温度梯度引起的燃油自然对流,只考虑燃油消耗引起的燃油宏观流动,则燃油流线与纵向划分线趋于平行,因此基元模块之间只需考虑纵向传质.定义氮气区域为编号的基元模块.
图5
图5
油箱基元模块
Fig.5
Cell module of fuel tank
2.4 基元模块间传热量计算
(14) Qi = ∑ j T j - T i R i j
式中:Tj 为相邻基元模块j 的温度;Rij 为基元模块i 和基元模块j 之间的热阻.传热量计算的关键在于两个基元模块之间热阻的计算.隔热材料内部热阻计算公式为
(15) R =L/ (λA )
式中:L 为两基元模块节点之间的距离;λ 为材料的导热系数;A 为导热面积.
因燃油受热之后内部存在冷热掺混,燃油内部之间的热阻若直接按照固体导热热阻计算,内部换热将远高于被看作固体导热时的换热强度,但燃油内部的冷热掺混现象较为复杂,难以直接求解,因此提出掺混系数的概念.将燃油节点之间的导热系数λ 调整为kλ (k >1),掺混系数k 表征由于燃油内部冷热掺混导致的换热量增加,燃油基元模块之间的热阻计算公式表示为
(16) R =L/ (kλA )
(17) R =1/ (αA )
式中:α 可以采用经验公式的方法求解.对于形状复杂的壁面,也可采用CFD计算方法提取或修正经验公式.
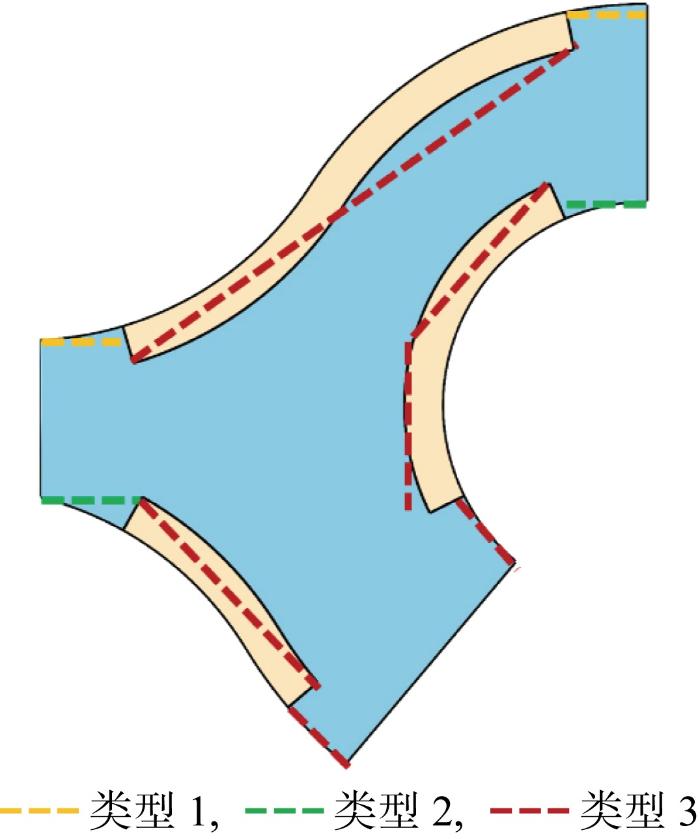
为了将对流传热系数的经验公式用于油箱壁面,将油箱壁面等效为3种类型,如图6 所示.
图6
图6
等效的油箱壁面示意图
Fig.6
Diagram of equivalent fuel tank wall
将图6 中类型1等效为热面朝下的水平壁面,其对流传热系数计算公式[19 ] 为
(18) α = λ D 0 . 25
式中:D 为特征长度;Gr 为格拉斯霍夫;Pr 为普朗特数.
将图6 中类型2等效为热面朝上的水平壁面,其对流传热系数计算公式[20 ] 为
(19) α =λ L . 54 (G r N 2 P r N 2 ) 0 . 25 ,0. 15(G r N 2 r N 2 0 . 33 }
将图6 中类型3等效为与竖直方向夹角为θ 的倾斜平面,其对流传热系数计算公式[20 ] 为
(20) \begin{aligned}\alpha&=\frac{\lambda}{L}\text{max }\left\{0.508Pr^{\frac{1}{2}}(0.92+Pr)^{-\frac{1}{4}}Gr^{\frac{1}{4}},\\\\\text{0. 024 8}\frac{(GrPr)^{\frac{2}{5}}Pr^{\frac{1}{15}}}{(1+0.494Pr^{\frac{2}{3}})^{\frac{2}{5}}}\right\}\end{aligned}
对于燃油与氮气控制体之间的热阻计算,因氮气热阻远高于燃油热阻,故计算过程中仅考虑氮气对流热阻而忽略燃油热阻,对流传热系数由式(19)计算.
2.5 方程求解方法
图7
图7
油箱温度场计算流程图
Fig.7
Flow chart of fuel tank temperature field calculation
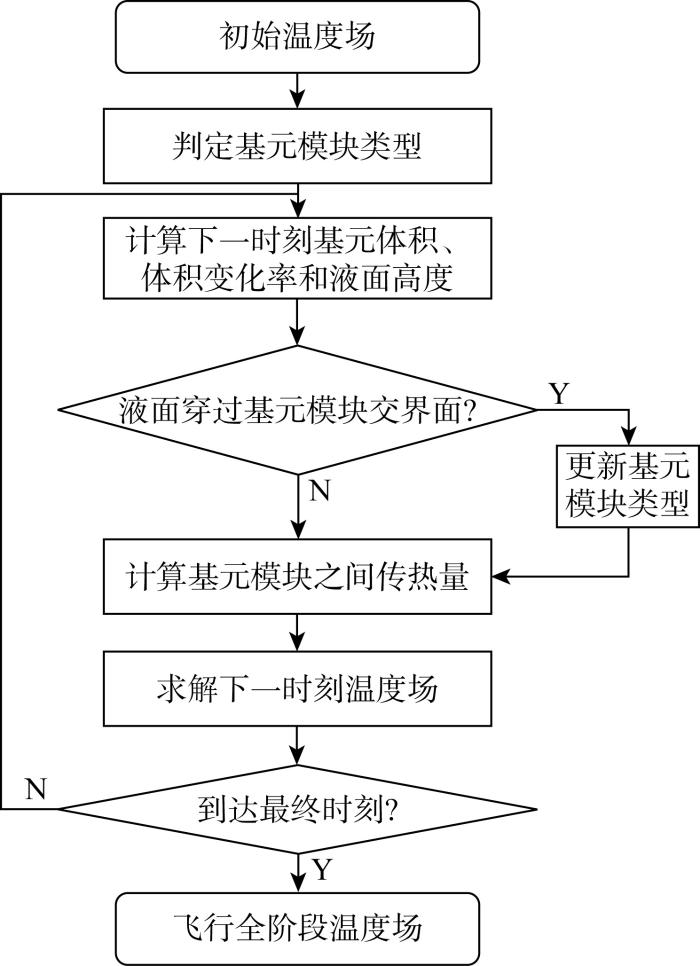
在初始温度场已知情况下,先对各个基元模块的类型加以判定,包括半油基元模块、满油基元模块、氮气基元模块和隔热材料基元模块,然后求解下一时刻基元模块体积和体积变化率,液面高度H 可通过对下式迭代求解得到:
(21) V fuel = ∫ 0 H
式中:A (h )为油箱内高度为h 的位置的横截面面积,在几何模型确定的情况下为已知量.如液面高度经过基元模块交界面,则意味着一些半油模块的消失和一些满油基元模块转变为半油基元模块,此时需要更新燃油区域的基元模块类型;随后,计算各个基元模块之间的传热量;最终,可以得到每个控制体对应的热平衡方程.各个控制体的热平衡方程组成一个常微分方程组:
(22) d T i d t 1 , T2 , …, T i , t)
式中:i =1, 2, …, 29. 方程组的初始条件为Ti =288. 15K. 采用龙格-库塔法求解式(22),最终得到各个基元模块随时间的温度变化.
3 结果与讨论
3.1 燃油温度的CFD计算结果
CFD的结果可以为网格法提供合理的修正系数及方法验证.采用 ANSYS Fluent软件进行高速飞行器燃油温度变化的计算,流场控制方程采用雷诺平均Navier-Stokes方程,湍流模型采用标准k -epsilon湍流模型计算.CFD作为网格法验证的基础,本文首先利用规则形状油箱的实验对采用的CFD计算方法进行验证.
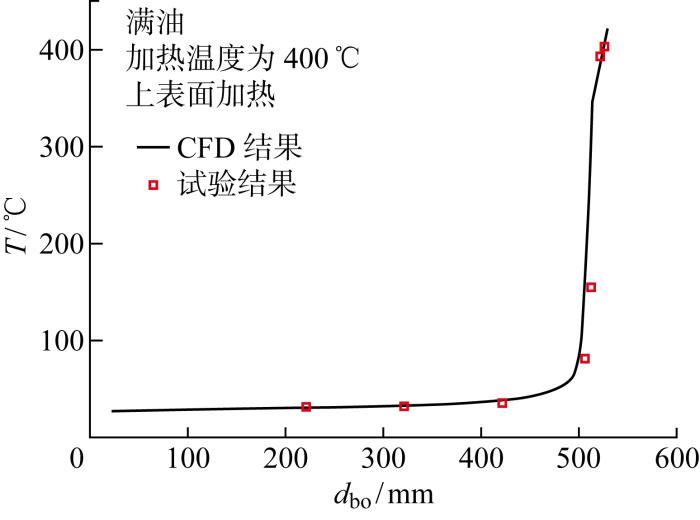
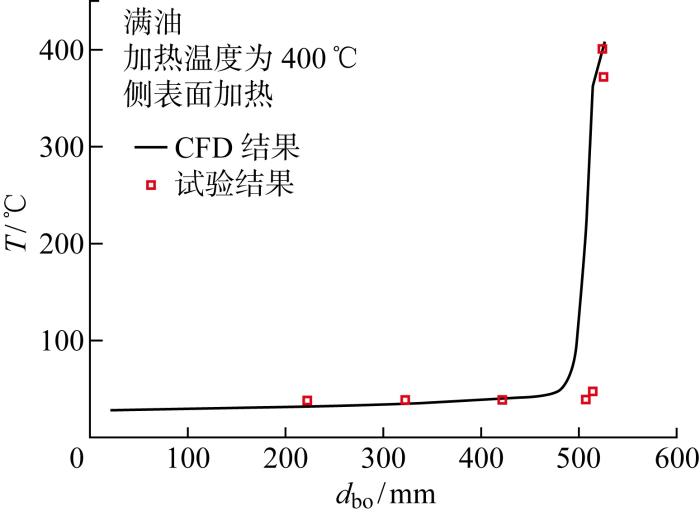
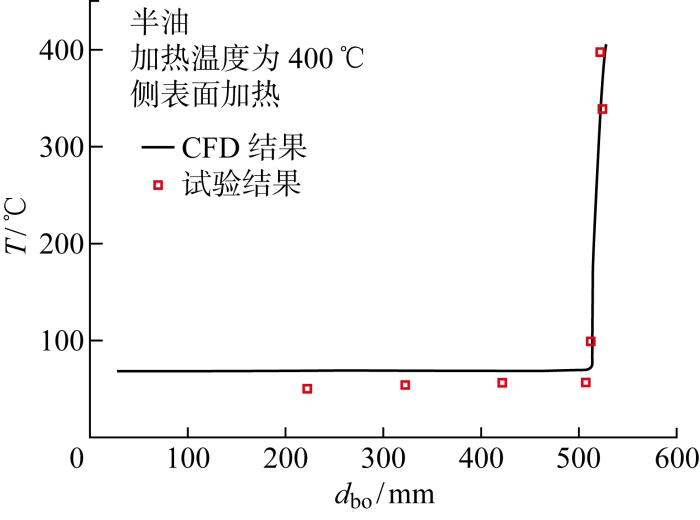
实验中油箱外形尺寸为500 mm×300 mm×500 mm,由侧板、盖板、刚性隔热垫和隔热毡等部件组成,其外形如图8 所示,实验加热系统如图9 所示.实验中加热表面温度保持400 ℃,对比分析上表面加热满油、侧表面加热满油、侧表面加热半油3个实验状态下的温度测量结果和CFD计算的结果,如图10 ~图12 所示(d bo 为距底部距离),得出CFD计算结果与实验结果的趋势一致,温度计算值与实验测量值吻合较好.
图8
图8
实验油箱外形示意图
Fig.8
Schematic diagram of experimental fuel tank
图9
图9
实验加热系统
Fig.9
Experimental heating system
图10
图10
上表面加热满油状态油温分布对比
Fig.10
Comparison of fuel temperature distribution when heated on upper surface with full fuel
图11
图11
侧表面加热满油状态油温分布对比
Fig.11
Comparison of fuel temperature distribution when heated on side surface with full fuel
图12
图12
侧表面加热半油状态油温分布对比
Fig.12
Comparison of fuel temperature distribution when heated on side surface with partial fuel
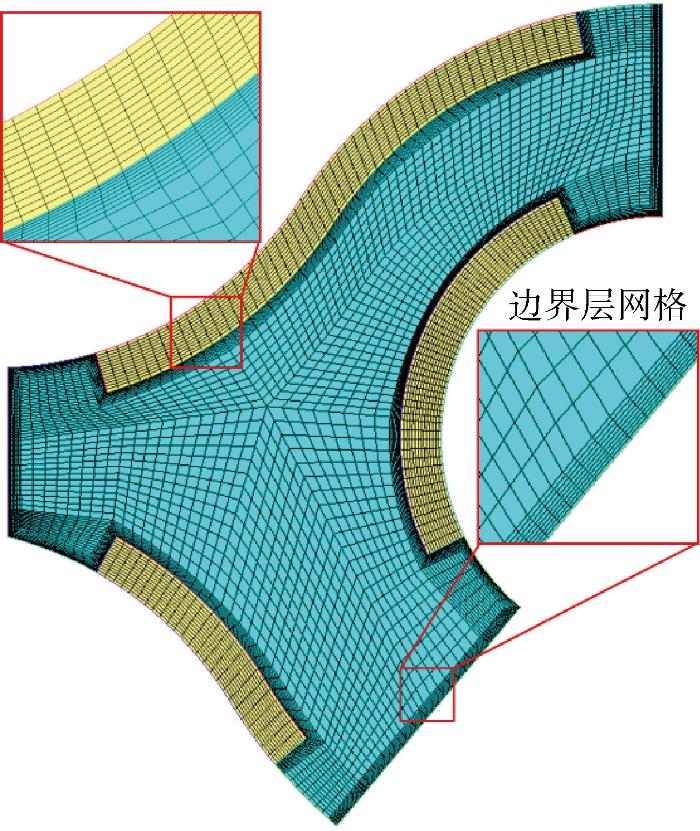
在CFD方法验证基础上,进行实际油箱CFD数值计算,计算网格如图13 所示.对边界层区域网格进行加密处理,网格总数为 17 048 个,满足网格无关性要求.
图13
图13
油箱计算网格
Fig.13
Grid of fuel tank
选取RP-3燃油为研究对象,密度采用Boussinesq假设处理,参考密度为700 kg/m3 ,热膨胀系数为 0.003 128 2 K-1 ,氮气密度按照理想气体方程计算.隔热材料热导率为0.05 W/(m·K),密度为128 kg/m3 ,比热容为929.7 J/(kg·K),入口压力为p ,温度为15 ℃,出口采用速度边界条件以表示燃油匀速率流出.计算中氮气和燃油界面采用流体体积(VOF)多相流模型.
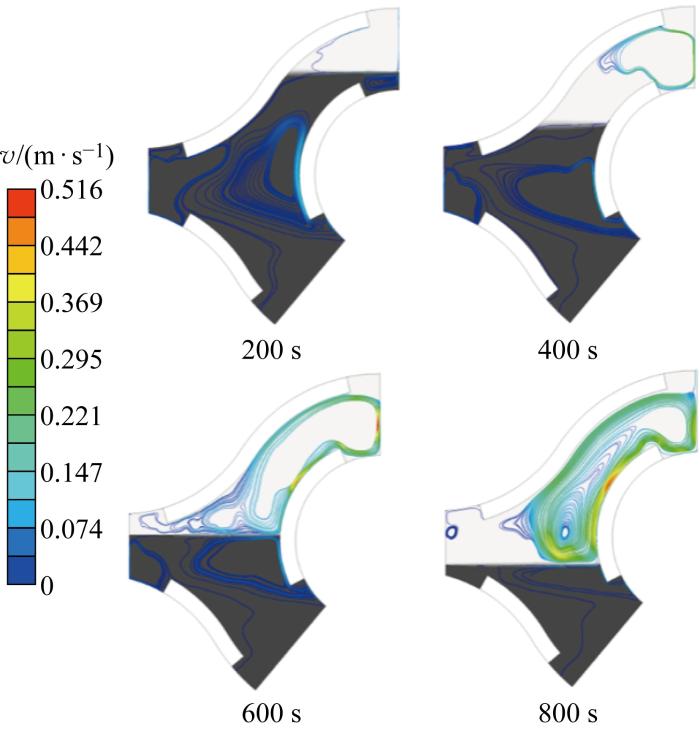
1 200 s 内油箱内氮气和燃油速度(v )分布云图和流线图如图14 所示.从速度云图中可见,由于燃油和氮气受热密度发生变化,二者均产生了明显的自然对流.氮气对流速度约为0.1 m/s,对流较为强烈;燃油内部对流较弱,部分区域特别是底部流动较小,上端对流速度约在0.01 m/s量级.
图14
图14
不同时刻油箱内速度和相界面分布云图
Fig.14
Velocity and phase contours at different times
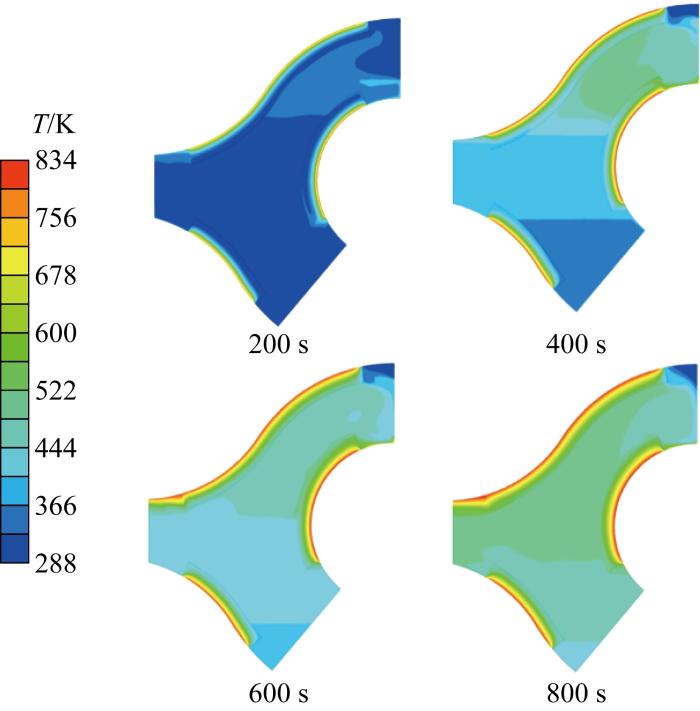
1 200 s 内油箱内温度分布云图如图15 所示,3个隔热材料在边界面法线方向上从边界上的834 K快速过渡到内部的400~500 K,而在平行于边界面方向上温度接近.因氮气具有较大的热扩散系数,边界的热量更容易传输到内部,而燃油热扩散系数较小,热量不容易传入,故总体上氮气温度高于燃油.
图15
图15
不同时刻油箱内温度分布云图
Fig.15
Temperature contours at different times
3.2 与CFD的结果对比及掺混系数影响分析
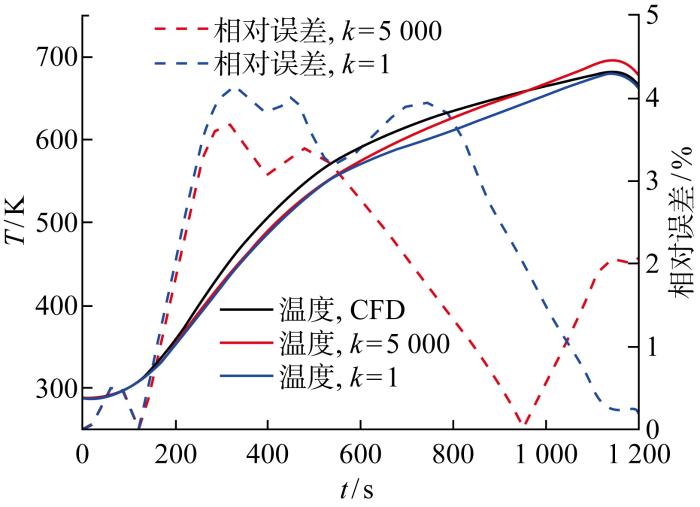
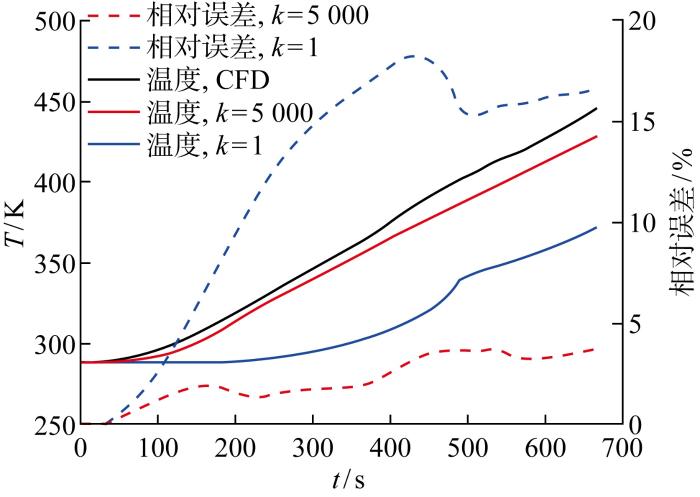
取中心点位于图5 中点1的典型绝热材料基元模块③和中心点位于图5 中点2的燃油基元模块进行结果分析:点1靠近燃油边界区域,可反映油气交界面区域的温度情况;点2位于整个油箱的中心位置,可反映燃油中央区域的温度情况.
典型绝热材料控制体和典型燃油控制体热网络法以及CFD计算结果如图16 和图17 所示.当掺混系数k =1时,将燃油控制体之间的传热方式按照固体传热计算,热网络法得到的隔热材料温度与CFD计算结果相近,但燃油温度显著偏低,这是由于掺混系数k =1时,忽略了燃油对流换热导致的内部换热量增加,从而导致误差较大.
图16
图16
绝热材料基元模块CFD和热网络法计算结果
Fig.16
Calculation results of thermal network method and CFD method for insulator module
图17
图17
燃油基元模块CFD和热网络法计算结果
Fig.17
Calculation results of thermal network method and CFD method for fuel module
(24) f (k )= ∑ t = t m ∑ i = 1 29 T i , C F D - T i , k
式中:tm =100, 200, …, 1 200 s,T i, CFD t 时刻基元模块i 中心区域温度的CFD计算结果;Ti , k t 时刻通过热网络方法得到的掺混系数为k 时基元模块i 的温度计算结果. 最终的掺混系数k 取式(24)中的最小值点,本文中 k =5 000,表明燃油内部存在较为强烈的对流换热,此时CFD计算结果与热网络法计算结果相对误差小于5%,说明引入掺混系数k 的热网络法可以有效对燃油温度场进行计算.
3.3 热网络法对边界条件普适性验证
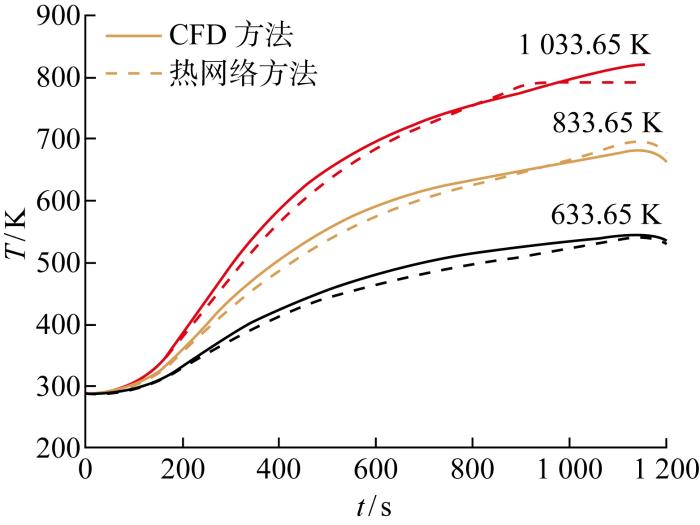
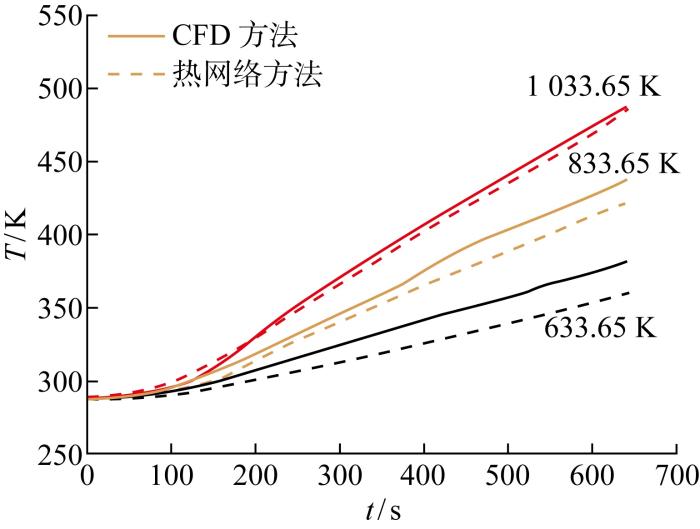
为验证热网络法对不同边界条件的适用性,保持掺混系数k =5 000 不变,取其他可能达到的最高和最低热边界(稳定状态温度增减200 K)条件重新计算,并与CFD结果对比,结果如图18 和图19 所示.
图18
图18
不同边界条件下隔热材料基元模块计算结果
Fig.18
Calculation results for insulator module under different boundary conditions
图19
图19
不同边界条件下燃油基元模块计算结果
Fig.19
Calculation results for fuel module under different boundary conditions
由图可见,当边界条件温度改变后,热网络法仍可准确获得温度计算结果,与CFD结果相比相对误差在5%以内,验证了热网络法在一定边界条件范围内的普适性.如需计算温度偏离较大的情况,则可以改变边界温度重新进行CFD计算获得对应温度下的掺混系数,根据两点或多点的掺混系数值,构造掺混系数关于温度的函数,提高温度适用范围.
3.4 热网络法对几何条件普适性验证
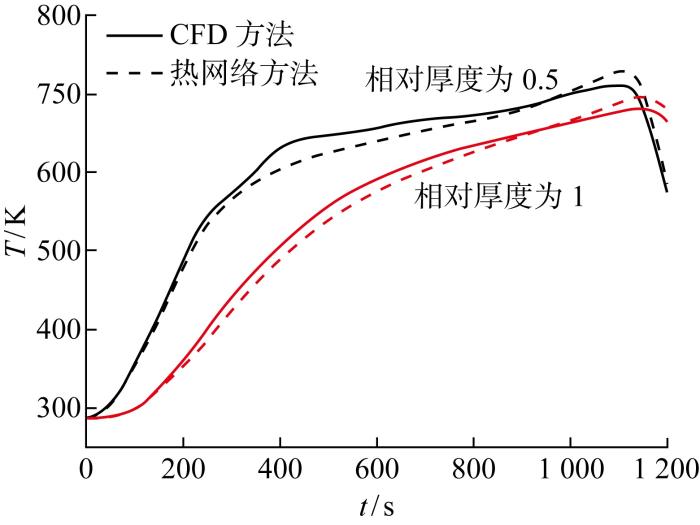
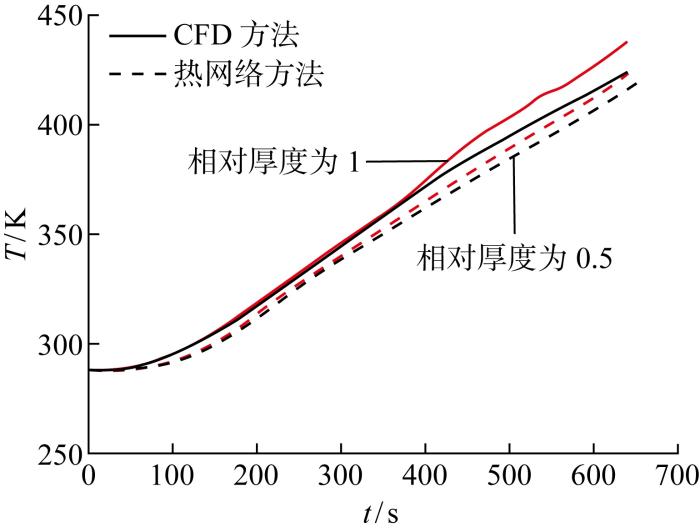
油箱设计过程中,其外形结构受油箱外其他设备限制不会发生很大改变,油箱结构优化设计通常是对隔热材料厚度的微小调整.
为了验证热网络法对不同隔热材料厚度的适用性,保持掺混系数k =5 000 不变,将原本偏厚的隔热材料厚度减少一半重新计算,并与CFD结果对比,计算结果如图20 和图21 所示.
图20
图20
不同隔热材料厚度下隔热材料基元模块计算结果
Fig.20
Calculation results for insulator module with different thicknesses of insulation material
图21
图21
不同隔热材料厚度下燃油基元模块计算结果
Fig.21
Calculation results for fuel module with different thicknesses of insulation material
由图可见,隔热材料厚度减少一半后,热网络法仍可准确获得温度计算结果,与CFD结果相比相对误差在4%以内,同样验证了热网络法对隔热材料厚度的普适性.如需计算几何结构调整较大的情况,可以改变几何结构重新进行CFD计算获得对应几何结构下的掺混系数,根据两点或多点的掺混系数值,构造掺混系数关于几何结构的函数,提高温度适用范围.
此外,CFD计算结果表明,当隔热材料厚度减少后,中央区域燃油温度有所下降,这一结果也被热网络法有效捕捉,这是由于在当前物性和边界条件下,隔热材料厚度减少,燃油总量提升,热沉作用更加明显;另一方面,厚度减少后,隔热材料与燃油的对流换热面积也相应减少,导致燃油温度降低.但隔热材料厚度过小会导致隔热材料和燃油交界面处的燃油温度提升,在油箱热设计过程中需要对上述因素进行权衡考虑.
最后,以CPU主频3.70 GHz、10核运行的计算机比较CFD方法和热网络方法的计算时间.CFD程序单次计算时间约为30~50 h,而使用相同计算机运行单次热网络法程序的计算时间在1 min以内,在计算速度上热网络方法远超CFD方法.从油箱热设计的全周期考虑,在本方法提出前,需要数十次CFD计算获得优化后的几何结构,本方法则仅需少量CFD计算获得修正系数,将优化迭代过程依托于修正热网络方法,从而极大缩短研发周期.
4 结语
针对高速飞行器飞行全阶段燃料温度瞬态预测问题,基于修正的热网络法构建的燃油瞬态热分析模型具有与CFD接近的计算精度,可准确计算出油箱内燃油温度场的分布和变化情况,对不同边界条件、几何条件均有较好普适性,计算效率远高于CFD方法.在实际油箱结构优化过程中,可以通过修正热网络法对油箱结构进行快速迭代设计,寻找满足条件的最优方案.
修正的热网络法中掺混系数k 表征了燃油受热之后内部冷热掺混的剧烈程度,其主要影响因素是燃油物理性质、边界温度和几何条件等.通常情况下,航空燃油种类固定,燃油物性变化不大,掺混系数k 通过一次CFD校正后,在油箱设计的迭代优化过程中无需再次调整.通过将掺混系数调整为与之相关性较强的变量函数,可以将本方法进一步拓展至其他复杂边界条件和几何条件的适用范围,应用于其他形式的高速飞行器油箱温度场计算.
参考文献
View Option
[1]
唐玫 , 吉洪湖 , 胡娅萍 . 超声速飞行器综合热管理系统优化设计
[J]. 推进技术 2022 , 43 (1 ): 50 -60 .
[本文引用: 1]
TANG Mei JI Honghu HU Yaping JOptimal design of comprehensive thermal management system for supersonic vehicle
[J]. Journal of Propulsion Technology 2022 , 43 (1 ): 50 -60 .
[本文引用: 1]
[2]
王文龙 , 王伟 . 下一代战斗机综合环境控制/热管理系统开发现状
[J]. 飞机设计 2004 , 24 (1 ): 74 -76 .
[本文引用: 1]
WANG Wenlong WANG Wei Development of integrated environmental control system/thermal management system for next generation fighter aircraft
[J]. Aircraft Design 2004 , 24 (1 ): 74 -76 .
[本文引用: 1]
[3]
贾真 , 侯凌云 , 龚景松 , 等 . 煤油热沉与热裂解反应特性的试验研究
[J]. 工程热物理学报 2011 , 32 (10 ): 1789 -1792 .
[本文引用: 1]
JIA Zhen HOU Lingyun GONG Jingsong et al Experimental study on heat sink and thermal cracking of kerosene
[J]. Journal of Engineering Thermophysics 2011 , 32 (10 ): 1789 -1792 .
[本文引用: 1]
[4]
陈悦 . 飞机燃油系统热负荷计算及热管理分析 [D]. 南京 : 南京航空航天大学 , 2014 .
[本文引用: 2]
CHEN Yue Heat sink calculation and the analysis of thermal management for aircraft fuel system [D]. Nanjing : Nanjing University of Aeronautics and Astronautics , 2014 .
[本文引用: 2]
[5]
吕亚国 , 任国哲 , 刘振侠 , 等 . 飞机燃油箱热分析研究
[J]. 推进技术 2015 , 36 (1 ): 61 -67 .
[本文引用: 3]
LV Yaguo REN Guozhe LIU Zhenxia et al Thermal analysis of fuel tank for aircraft
[J]. Journal of Propulsion Technology 2015 , 36 (1 ): 61 -67 .
[本文引用: 3]
[6]
TEARE D KUBIK D Integrated cryo-tank thermodynamic analysis method
[C]//2nd International Aerospace Planes Conference Orlando, USA : AIAA , 1990 : 5214 .
[本文引用: 1]
[7]
BODIE M RUSSELL G MCCARTHY K et al Thermal analysis of an integrated aircraft model
[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition Orlando, USA : AIAA , 2013 : 69 -145 .
[本文引用: 1]
[8]
MAWID M ARANA C SEKAR B An engineering analysis tool for high performance combustors and fuel systems
[C]//34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit Cleveland, USA : AIAA , 1998 : 3910 .
[本文引用: 1]
[9]
张兴娟 , 张作琦 , 高峰 . 先进战斗机超声速巡航过程中的燃油温度变化特性分析
[J]. 航空动力学报 2010 , 25 (2 ): 258 -263 .
[本文引用: 1]
ZHANG Xingjuan ZHANG Zuoqi GAO Feng Fuel temperature analysis of advanced fighter aircraft during supersonic cruise
[J]. Journal of Aerospace Power 2010 , 25 (2 ): 258 -263 .
[本文引用: 1]
[10]
AI Q CHEN L XU X et al Analysis method of transient temperature field for fuel tank of nigh-altitude large UAV
[J]. Journal of Harbin Institute of Technology 2016 , 23 (6 ): 41 -46 .
[本文引用: 1]
[11]
赵璇 . 飞行器超音速巡航状态油箱热特性研究 [D]. 南京 : 南京航空航天大学 , 2020 .
[本文引用: 2]
ZHAO Xuan Study on thermal characteristics of wing tank in supersonic cruise state of aircraft [D]. Nanjing : Nanjing University of Aeronautics and Astronautics , 2020 .
[本文引用: 2]
[12]
YAN K HONG J ZHANG J H et al Thermal-deformation coupling in thermal network for transient analysis of spindle-bearing system
[J]. International Journal of Thermal Sciences 2016 , 104 : 1 -12 .
DOI:10.1016/j.ijthermalsci.2015.12.007
URL
[本文引用: 1]
[13]
BOGLIETTI A CAVAGNINO A STATON D et al Evolution and modern approaches for thermal analysis of electrical machines
[J]. IEEE Transactions on Industrial Electronics 2009 , 56 (3 ): 871 -882 .
DOI:10.1109/TIE.2008.2011622
URL
[本文引用: 1]
[15]
HIJAZI A KRECZANIK P BIDEAUX E et al Thermal network model of supercapacitors stack
[J]. IEEE Transactions on Industrial Electronics 2011 , 59 (2 ): 979 -987 .
DOI:10.1109/TIE.2011.2158769
URL
[本文引用: 1]
[16]
BAHMAN A S MA K GHIMIRE P et al A 3-D-lumped thermal network model for long-term load profiles analysis in high-power IGBT modules
[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics 2016 , 4 (3 ): 1050 -1063 .
DOI:10.1109/JESTPE.2016.2531631
URL
[本文引用: 1]
[17]
康振烨 , 刘振侠 , 任国哲 , 等 . 基于MATLAB/Simulink的飞机燃油箱内燃油温度仿真计算
[J]. 推进技术 2014 , 35 (1 ): 62 -69 .
[本文引用: 2]
KANG Zhenye LIU Zhenxia REN Guozhe et al Simulation and calculation of fuel temperature in aircraft fuel tank based on MATLAB/Simulink
[J]. Journal of Propulsion Technology 2014 , 35 (1 ): 62 -69 .
[本文引用: 2]
[18]
韩江锋 , 郑日恒 , 李立翰 , 等 . 冲压发动机油箱传热理论研究
[J]. 推进技术 2013 , 34 (12 ): 1664 -1669 .
[本文引用: 1]
HAN Jiangfeng ZHENG Riheng LI Lihan et al Theoretical study for heat transfer of ramjet fuel tank
[J]. Journal of Propulsion Technology 2013 , 34 (12 ): 1664 -1669 .
[本文引用: 1]
[19]
杨世铭 , 陶文铨 . 传热学 [M]. 第4版 . 北京 : 高等教育出版社 , 2006 .
[本文引用: 1]
YANG Shiming TAO Wenquan Heat transfer [M]. 4th ed. Beijing : Higher Education Press , 2006 .
[本文引用: 1]
[20]
胡小平 , 吴海燕 , 鄢昌渝 . 传热传质分析 [M]. 长沙 : 国防科技大学出版社 , 2011 .
[本文引用: 2]
HU Xiaoping WU Haiyan YAN Changyu Heat and mass transfer analysis [M]. Changsha : National University of Defense Technology Press , 2011 .
[本文引用: 2]
超声速飞行器综合热管理系统优化设计
1
2022
... 由于燃油具有比热容大、性质稳定以及代偿损失小等优点[1 ] ,现已被作为热端部件的热沉广泛应用于现代高速飞行器设计中[2 ] .但以燃油作为热沉必须关注燃油的温度变化,如温度过高,不仅容易破坏其热稳定性,而且形成的非溶性沉积物和树脂沉淀物也可能堵塞油箱[3 -4 ] .因此,在储油系统结构设计过程中研究油箱内燃油温度分布尤为重要.试验和数值模拟是获得高速飞行器燃油温度变化的两个重要手段,虽然前者可获得准确的燃油温度数据,但因其无法在储油系统结构设计阶段完成,故基于数值模拟的燃油温度变化预测对储油系统结构设计起重要作用[5 ] . ...
超声速飞行器综合热管理系统优化设计
1
2022
... 由于燃油具有比热容大、性质稳定以及代偿损失小等优点[1 ] ,现已被作为热端部件的热沉广泛应用于现代高速飞行器设计中[2 ] .但以燃油作为热沉必须关注燃油的温度变化,如温度过高,不仅容易破坏其热稳定性,而且形成的非溶性沉积物和树脂沉淀物也可能堵塞油箱[3 -4 ] .因此,在储油系统结构设计过程中研究油箱内燃油温度分布尤为重要.试验和数值模拟是获得高速飞行器燃油温度变化的两个重要手段,虽然前者可获得准确的燃油温度数据,但因其无法在储油系统结构设计阶段完成,故基于数值模拟的燃油温度变化预测对储油系统结构设计起重要作用[5 ] . ...
下一代战斗机综合环境控制/热管理系统开发现状
1
2004
... 由于燃油具有比热容大、性质稳定以及代偿损失小等优点[1 ] ,现已被作为热端部件的热沉广泛应用于现代高速飞行器设计中[2 ] .但以燃油作为热沉必须关注燃油的温度变化,如温度过高,不仅容易破坏其热稳定性,而且形成的非溶性沉积物和树脂沉淀物也可能堵塞油箱[3 -4 ] .因此,在储油系统结构设计过程中研究油箱内燃油温度分布尤为重要.试验和数值模拟是获得高速飞行器燃油温度变化的两个重要手段,虽然前者可获得准确的燃油温度数据,但因其无法在储油系统结构设计阶段完成,故基于数值模拟的燃油温度变化预测对储油系统结构设计起重要作用[5 ] . ...
下一代战斗机综合环境控制/热管理系统开发现状
1
2004
... 由于燃油具有比热容大、性质稳定以及代偿损失小等优点[1 ] ,现已被作为热端部件的热沉广泛应用于现代高速飞行器设计中[2 ] .但以燃油作为热沉必须关注燃油的温度变化,如温度过高,不仅容易破坏其热稳定性,而且形成的非溶性沉积物和树脂沉淀物也可能堵塞油箱[3 -4 ] .因此,在储油系统结构设计过程中研究油箱内燃油温度分布尤为重要.试验和数值模拟是获得高速飞行器燃油温度变化的两个重要手段,虽然前者可获得准确的燃油温度数据,但因其无法在储油系统结构设计阶段完成,故基于数值模拟的燃油温度变化预测对储油系统结构设计起重要作用[5 ] . ...
煤油热沉与热裂解反应特性的试验研究
1
2011
... 由于燃油具有比热容大、性质稳定以及代偿损失小等优点[1 ] ,现已被作为热端部件的热沉广泛应用于现代高速飞行器设计中[2 ] .但以燃油作为热沉必须关注燃油的温度变化,如温度过高,不仅容易破坏其热稳定性,而且形成的非溶性沉积物和树脂沉淀物也可能堵塞油箱[3 -4 ] .因此,在储油系统结构设计过程中研究油箱内燃油温度分布尤为重要.试验和数值模拟是获得高速飞行器燃油温度变化的两个重要手段,虽然前者可获得准确的燃油温度数据,但因其无法在储油系统结构设计阶段完成,故基于数值模拟的燃油温度变化预测对储油系统结构设计起重要作用[5 ] . ...
煤油热沉与热裂解反应特性的试验研究
1
2011
... 由于燃油具有比热容大、性质稳定以及代偿损失小等优点[1 ] ,现已被作为热端部件的热沉广泛应用于现代高速飞行器设计中[2 ] .但以燃油作为热沉必须关注燃油的温度变化,如温度过高,不仅容易破坏其热稳定性,而且形成的非溶性沉积物和树脂沉淀物也可能堵塞油箱[3 -4 ] .因此,在储油系统结构设计过程中研究油箱内燃油温度分布尤为重要.试验和数值模拟是获得高速飞行器燃油温度变化的两个重要手段,虽然前者可获得准确的燃油温度数据,但因其无法在储油系统结构设计阶段完成,故基于数值模拟的燃油温度变化预测对储油系统结构设计起重要作用[5 ] . ...
2
2014
... 由于燃油具有比热容大、性质稳定以及代偿损失小等优点[1 ] ,现已被作为热端部件的热沉广泛应用于现代高速飞行器设计中[2 ] .但以燃油作为热沉必须关注燃油的温度变化,如温度过高,不仅容易破坏其热稳定性,而且形成的非溶性沉积物和树脂沉淀物也可能堵塞油箱[3 -4 ] .因此,在储油系统结构设计过程中研究油箱内燃油温度分布尤为重要.试验和数值模拟是获得高速飞行器燃油温度变化的两个重要手段,虽然前者可获得准确的燃油温度数据,但因其无法在储油系统结构设计阶段完成,故基于数值模拟的燃油温度变化预测对储油系统结构设计起重要作用[5 ] . ...
... 使用CFD方法可对油箱整体结构建模和计算,从而获得油箱内温度场分布情况.陈悦[4 ] 采用二维和三维的方法模拟了输油箱和供油箱内燃油流动换热过程,获得了油箱内燃油的温度分布特点及燃油出口温度随时间变化而变化的过程;赵璇[11 ] 采用CFD方法分析了超声速飞行器机翼油箱内外流场温度分布,并将CFD方法与集总参数法结果进行对比.CFD方法可以精确捕获油箱温度场分布,但对飞行全过程进行模拟所需的计算开销极大,难以满足油箱设计阶段快速迭代优化的需要. ...
2
2014
... 由于燃油具有比热容大、性质稳定以及代偿损失小等优点[1 ] ,现已被作为热端部件的热沉广泛应用于现代高速飞行器设计中[2 ] .但以燃油作为热沉必须关注燃油的温度变化,如温度过高,不仅容易破坏其热稳定性,而且形成的非溶性沉积物和树脂沉淀物也可能堵塞油箱[3 -4 ] .因此,在储油系统结构设计过程中研究油箱内燃油温度分布尤为重要.试验和数值模拟是获得高速飞行器燃油温度变化的两个重要手段,虽然前者可获得准确的燃油温度数据,但因其无法在储油系统结构设计阶段完成,故基于数值模拟的燃油温度变化预测对储油系统结构设计起重要作用[5 ] . ...
... 使用CFD方法可对油箱整体结构建模和计算,从而获得油箱内温度场分布情况.陈悦[4 ] 采用二维和三维的方法模拟了输油箱和供油箱内燃油流动换热过程,获得了油箱内燃油的温度分布特点及燃油出口温度随时间变化而变化的过程;赵璇[11 ] 采用CFD方法分析了超声速飞行器机翼油箱内外流场温度分布,并将CFD方法与集总参数法结果进行对比.CFD方法可以精确捕获油箱温度场分布,但对飞行全过程进行模拟所需的计算开销极大,难以满足油箱设计阶段快速迭代优化的需要. ...
飞机燃油箱热分析研究
3
2015
... 由于燃油具有比热容大、性质稳定以及代偿损失小等优点[1 ] ,现已被作为热端部件的热沉广泛应用于现代高速飞行器设计中[2 ] .但以燃油作为热沉必须关注燃油的温度变化,如温度过高,不仅容易破坏其热稳定性,而且形成的非溶性沉积物和树脂沉淀物也可能堵塞油箱[3 -4 ] .因此,在储油系统结构设计过程中研究油箱内燃油温度分布尤为重要.试验和数值模拟是获得高速飞行器燃油温度变化的两个重要手段,虽然前者可获得准确的燃油温度数据,但因其无法在储油系统结构设计阶段完成,故基于数值模拟的燃油温度变化预测对储油系统结构设计起重要作用[5 ] . ...
... 为解决集总参数法得不到局部温度和CFD方法计算效率过低的问题,热网络法被应用于温度场计算,尤其是在固体温度场计算中,如轴承[12 ] 、电动机及发电机[13 ] 、管路[14 ] 和电路[15 -16 ] 等.康振烨等[17 ] 将热网络法应用于燃油温度场计算,将不同位置的燃油划分到不同的基元模块中,采用MATLAB/Simulink软件搭建飞机油箱稳态热分析仿真模型;吕亚国等[5 ] 在此基础上建立了飞机油箱非稳态热分析模型,结果表明热网络法的计算结果与飞行测试数据吻合良好.上述研究假设油箱基元模块节点之间的传热方式为固体导热,这一假设仅适用于燃油温度较低情况,对于具有高油温的高速飞行器储油系统,燃油内部会存在较强的冷热掺混,假定燃油基元模块间传热方式为固体导热的方法会带来较大误差.不仅如此,目前的热网格法未考虑燃油内部的宏观流动,随着燃油消耗,油箱中燃油存在整体向下的宏观流动,对于每一个位置固定的基元模块,都需要考虑燃油宏观流动带来的传质影响. ...
... 针对高速飞行器燃油瞬态温度预测问题,本文基于文献[5 ]和文献[17 ]提出一种满足设计精度的高效修正热网络方法,通过修正热传导方程的方法考虑油箱内部冷热掺混的影响,通过修正热平衡方程的方法考虑燃油宏观流动的影响.基于该热网络法构建了高速飞行器储油系统瞬态热分析模型,在不同的热边界条件和储油系统几何结构下校核其普适性. ...
飞机燃油箱热分析研究
3
2015
... 由于燃油具有比热容大、性质稳定以及代偿损失小等优点[1 ] ,现已被作为热端部件的热沉广泛应用于现代高速飞行器设计中[2 ] .但以燃油作为热沉必须关注燃油的温度变化,如温度过高,不仅容易破坏其热稳定性,而且形成的非溶性沉积物和树脂沉淀物也可能堵塞油箱[3 -4 ] .因此,在储油系统结构设计过程中研究油箱内燃油温度分布尤为重要.试验和数值模拟是获得高速飞行器燃油温度变化的两个重要手段,虽然前者可获得准确的燃油温度数据,但因其无法在储油系统结构设计阶段完成,故基于数值模拟的燃油温度变化预测对储油系统结构设计起重要作用[5 ] . ...
... 为解决集总参数法得不到局部温度和CFD方法计算效率过低的问题,热网络法被应用于温度场计算,尤其是在固体温度场计算中,如轴承[12 ] 、电动机及发电机[13 ] 、管路[14 ] 和电路[15 -16 ] 等.康振烨等[17 ] 将热网络法应用于燃油温度场计算,将不同位置的燃油划分到不同的基元模块中,采用MATLAB/Simulink软件搭建飞机油箱稳态热分析仿真模型;吕亚国等[5 ] 在此基础上建立了飞机油箱非稳态热分析模型,结果表明热网络法的计算结果与飞行测试数据吻合良好.上述研究假设油箱基元模块节点之间的传热方式为固体导热,这一假设仅适用于燃油温度较低情况,对于具有高油温的高速飞行器储油系统,燃油内部会存在较强的冷热掺混,假定燃油基元模块间传热方式为固体导热的方法会带来较大误差.不仅如此,目前的热网格法未考虑燃油内部的宏观流动,随着燃油消耗,油箱中燃油存在整体向下的宏观流动,对于每一个位置固定的基元模块,都需要考虑燃油宏观流动带来的传质影响. ...
... 针对高速飞行器燃油瞬态温度预测问题,本文基于文献[5 ]和文献[17 ]提出一种满足设计精度的高效修正热网络方法,通过修正热传导方程的方法考虑油箱内部冷热掺混的影响,通过修正热平衡方程的方法考虑燃油宏观流动的影响.基于该热网络法构建了高速飞行器储油系统瞬态热分析模型,在不同的热边界条件和储油系统几何结构下校核其普适性. ...
Integrated cryo-tank thermodynamic analysis method
1
1990
... 国内外对燃油温度场计算的研究方法主要包括集总参数法、计算流体动力学(CFD)法和热网络法等.集总参数法假设燃油温度一致,重点关注燃油热平衡分析和边界条件研究.在燃油热平衡分析方面,Teare等[6 ] 提出一种快速的油箱瞬态热分析模型,该模型可以独立分析油箱的结构传热和油箱内部的换热问题;Bodie等[7 ] 提出一种应用于包括燃油管路在内的飞机燃油系统整体网络热分析模型,基于该模型探究了燃油温度的变化情况;Mawid等[8 ] 介绍了一种航空飞行器燃油系统模拟工具Athena,并通过试验验证了其有效性;张兴娟等[9 ] 利用热量平衡方法构建了燃油温度计算模型,分析飞机超声速巡航状态下燃油温度的瞬态变化.在边界条件研究方面,Ai等[10 ] 分析了影响油箱温度场的内部导热、外部对流和辐射等边界条件,并在此基础上建立了燃油瞬态计算模型.集总参数法简单高效,但忽略了燃油温度在空间上的差异,无法得到局部区域上的燃油温度,尤其是无法关注到靠近油箱壁面位置的高温区域油温[11 ] ,因此这一方法难以满足高速飞行器油箱设计的需要. ...
Thermal analysis of an integrated aircraft model
1
2013
... 国内外对燃油温度场计算的研究方法主要包括集总参数法、计算流体动力学(CFD)法和热网络法等.集总参数法假设燃油温度一致,重点关注燃油热平衡分析和边界条件研究.在燃油热平衡分析方面,Teare等[6 ] 提出一种快速的油箱瞬态热分析模型,该模型可以独立分析油箱的结构传热和油箱内部的换热问题;Bodie等[7 ] 提出一种应用于包括燃油管路在内的飞机燃油系统整体网络热分析模型,基于该模型探究了燃油温度的变化情况;Mawid等[8 ] 介绍了一种航空飞行器燃油系统模拟工具Athena,并通过试验验证了其有效性;张兴娟等[9 ] 利用热量平衡方法构建了燃油温度计算模型,分析飞机超声速巡航状态下燃油温度的瞬态变化.在边界条件研究方面,Ai等[10 ] 分析了影响油箱温度场的内部导热、外部对流和辐射等边界条件,并在此基础上建立了燃油瞬态计算模型.集总参数法简单高效,但忽略了燃油温度在空间上的差异,无法得到局部区域上的燃油温度,尤其是无法关注到靠近油箱壁面位置的高温区域油温[11 ] ,因此这一方法难以满足高速飞行器油箱设计的需要. ...
An engineering analysis tool for high performance combustors and fuel systems
1
1998
... 国内外对燃油温度场计算的研究方法主要包括集总参数法、计算流体动力学(CFD)法和热网络法等.集总参数法假设燃油温度一致,重点关注燃油热平衡分析和边界条件研究.在燃油热平衡分析方面,Teare等[6 ] 提出一种快速的油箱瞬态热分析模型,该模型可以独立分析油箱的结构传热和油箱内部的换热问题;Bodie等[7 ] 提出一种应用于包括燃油管路在内的飞机燃油系统整体网络热分析模型,基于该模型探究了燃油温度的变化情况;Mawid等[8 ] 介绍了一种航空飞行器燃油系统模拟工具Athena,并通过试验验证了其有效性;张兴娟等[9 ] 利用热量平衡方法构建了燃油温度计算模型,分析飞机超声速巡航状态下燃油温度的瞬态变化.在边界条件研究方面,Ai等[10 ] 分析了影响油箱温度场的内部导热、外部对流和辐射等边界条件,并在此基础上建立了燃油瞬态计算模型.集总参数法简单高效,但忽略了燃油温度在空间上的差异,无法得到局部区域上的燃油温度,尤其是无法关注到靠近油箱壁面位置的高温区域油温[11 ] ,因此这一方法难以满足高速飞行器油箱设计的需要. ...
先进战斗机超声速巡航过程中的燃油温度变化特性分析
1
2010
... 国内外对燃油温度场计算的研究方法主要包括集总参数法、计算流体动力学(CFD)法和热网络法等.集总参数法假设燃油温度一致,重点关注燃油热平衡分析和边界条件研究.在燃油热平衡分析方面,Teare等[6 ] 提出一种快速的油箱瞬态热分析模型,该模型可以独立分析油箱的结构传热和油箱内部的换热问题;Bodie等[7 ] 提出一种应用于包括燃油管路在内的飞机燃油系统整体网络热分析模型,基于该模型探究了燃油温度的变化情况;Mawid等[8 ] 介绍了一种航空飞行器燃油系统模拟工具Athena,并通过试验验证了其有效性;张兴娟等[9 ] 利用热量平衡方法构建了燃油温度计算模型,分析飞机超声速巡航状态下燃油温度的瞬态变化.在边界条件研究方面,Ai等[10 ] 分析了影响油箱温度场的内部导热、外部对流和辐射等边界条件,并在此基础上建立了燃油瞬态计算模型.集总参数法简单高效,但忽略了燃油温度在空间上的差异,无法得到局部区域上的燃油温度,尤其是无法关注到靠近油箱壁面位置的高温区域油温[11 ] ,因此这一方法难以满足高速飞行器油箱设计的需要. ...
先进战斗机超声速巡航过程中的燃油温度变化特性分析
1
2010
... 国内外对燃油温度场计算的研究方法主要包括集总参数法、计算流体动力学(CFD)法和热网络法等.集总参数法假设燃油温度一致,重点关注燃油热平衡分析和边界条件研究.在燃油热平衡分析方面,Teare等[6 ] 提出一种快速的油箱瞬态热分析模型,该模型可以独立分析油箱的结构传热和油箱内部的换热问题;Bodie等[7 ] 提出一种应用于包括燃油管路在内的飞机燃油系统整体网络热分析模型,基于该模型探究了燃油温度的变化情况;Mawid等[8 ] 介绍了一种航空飞行器燃油系统模拟工具Athena,并通过试验验证了其有效性;张兴娟等[9 ] 利用热量平衡方法构建了燃油温度计算模型,分析飞机超声速巡航状态下燃油温度的瞬态变化.在边界条件研究方面,Ai等[10 ] 分析了影响油箱温度场的内部导热、外部对流和辐射等边界条件,并在此基础上建立了燃油瞬态计算模型.集总参数法简单高效,但忽略了燃油温度在空间上的差异,无法得到局部区域上的燃油温度,尤其是无法关注到靠近油箱壁面位置的高温区域油温[11 ] ,因此这一方法难以满足高速飞行器油箱设计的需要. ...
Analysis method of transient temperature field for fuel tank of nigh-altitude large UAV
1
2016
... 国内外对燃油温度场计算的研究方法主要包括集总参数法、计算流体动力学(CFD)法和热网络法等.集总参数法假设燃油温度一致,重点关注燃油热平衡分析和边界条件研究.在燃油热平衡分析方面,Teare等[6 ] 提出一种快速的油箱瞬态热分析模型,该模型可以独立分析油箱的结构传热和油箱内部的换热问题;Bodie等[7 ] 提出一种应用于包括燃油管路在内的飞机燃油系统整体网络热分析模型,基于该模型探究了燃油温度的变化情况;Mawid等[8 ] 介绍了一种航空飞行器燃油系统模拟工具Athena,并通过试验验证了其有效性;张兴娟等[9 ] 利用热量平衡方法构建了燃油温度计算模型,分析飞机超声速巡航状态下燃油温度的瞬态变化.在边界条件研究方面,Ai等[10 ] 分析了影响油箱温度场的内部导热、外部对流和辐射等边界条件,并在此基础上建立了燃油瞬态计算模型.集总参数法简单高效,但忽略了燃油温度在空间上的差异,无法得到局部区域上的燃油温度,尤其是无法关注到靠近油箱壁面位置的高温区域油温[11 ] ,因此这一方法难以满足高速飞行器油箱设计的需要. ...
2
2020
... 国内外对燃油温度场计算的研究方法主要包括集总参数法、计算流体动力学(CFD)法和热网络法等.集总参数法假设燃油温度一致,重点关注燃油热平衡分析和边界条件研究.在燃油热平衡分析方面,Teare等[6 ] 提出一种快速的油箱瞬态热分析模型,该模型可以独立分析油箱的结构传热和油箱内部的换热问题;Bodie等[7 ] 提出一种应用于包括燃油管路在内的飞机燃油系统整体网络热分析模型,基于该模型探究了燃油温度的变化情况;Mawid等[8 ] 介绍了一种航空飞行器燃油系统模拟工具Athena,并通过试验验证了其有效性;张兴娟等[9 ] 利用热量平衡方法构建了燃油温度计算模型,分析飞机超声速巡航状态下燃油温度的瞬态变化.在边界条件研究方面,Ai等[10 ] 分析了影响油箱温度场的内部导热、外部对流和辐射等边界条件,并在此基础上建立了燃油瞬态计算模型.集总参数法简单高效,但忽略了燃油温度在空间上的差异,无法得到局部区域上的燃油温度,尤其是无法关注到靠近油箱壁面位置的高温区域油温[11 ] ,因此这一方法难以满足高速飞行器油箱设计的需要. ...
... 使用CFD方法可对油箱整体结构建模和计算,从而获得油箱内温度场分布情况.陈悦[4 ] 采用二维和三维的方法模拟了输油箱和供油箱内燃油流动换热过程,获得了油箱内燃油的温度分布特点及燃油出口温度随时间变化而变化的过程;赵璇[11 ] 采用CFD方法分析了超声速飞行器机翼油箱内外流场温度分布,并将CFD方法与集总参数法结果进行对比.CFD方法可以精确捕获油箱温度场分布,但对飞行全过程进行模拟所需的计算开销极大,难以满足油箱设计阶段快速迭代优化的需要. ...
2
2020
... 国内外对燃油温度场计算的研究方法主要包括集总参数法、计算流体动力学(CFD)法和热网络法等.集总参数法假设燃油温度一致,重点关注燃油热平衡分析和边界条件研究.在燃油热平衡分析方面,Teare等[6 ] 提出一种快速的油箱瞬态热分析模型,该模型可以独立分析油箱的结构传热和油箱内部的换热问题;Bodie等[7 ] 提出一种应用于包括燃油管路在内的飞机燃油系统整体网络热分析模型,基于该模型探究了燃油温度的变化情况;Mawid等[8 ] 介绍了一种航空飞行器燃油系统模拟工具Athena,并通过试验验证了其有效性;张兴娟等[9 ] 利用热量平衡方法构建了燃油温度计算模型,分析飞机超声速巡航状态下燃油温度的瞬态变化.在边界条件研究方面,Ai等[10 ] 分析了影响油箱温度场的内部导热、外部对流和辐射等边界条件,并在此基础上建立了燃油瞬态计算模型.集总参数法简单高效,但忽略了燃油温度在空间上的差异,无法得到局部区域上的燃油温度,尤其是无法关注到靠近油箱壁面位置的高温区域油温[11 ] ,因此这一方法难以满足高速飞行器油箱设计的需要. ...
... 使用CFD方法可对油箱整体结构建模和计算,从而获得油箱内温度场分布情况.陈悦[4 ] 采用二维和三维的方法模拟了输油箱和供油箱内燃油流动换热过程,获得了油箱内燃油的温度分布特点及燃油出口温度随时间变化而变化的过程;赵璇[11 ] 采用CFD方法分析了超声速飞行器机翼油箱内外流场温度分布,并将CFD方法与集总参数法结果进行对比.CFD方法可以精确捕获油箱温度场分布,但对飞行全过程进行模拟所需的计算开销极大,难以满足油箱设计阶段快速迭代优化的需要. ...
Thermal-deformation coupling in thermal network for transient analysis of spindle-bearing system
1
2016
... 为解决集总参数法得不到局部温度和CFD方法计算效率过低的问题,热网络法被应用于温度场计算,尤其是在固体温度场计算中,如轴承[12 ] 、电动机及发电机[13 ] 、管路[14 ] 和电路[15 -16 ] 等.康振烨等[17 ] 将热网络法应用于燃油温度场计算,将不同位置的燃油划分到不同的基元模块中,采用MATLAB/Simulink软件搭建飞机油箱稳态热分析仿真模型;吕亚国等[5 ] 在此基础上建立了飞机油箱非稳态热分析模型,结果表明热网络法的计算结果与飞行测试数据吻合良好.上述研究假设油箱基元模块节点之间的传热方式为固体导热,这一假设仅适用于燃油温度较低情况,对于具有高油温的高速飞行器储油系统,燃油内部会存在较强的冷热掺混,假定燃油基元模块间传热方式为固体导热的方法会带来较大误差.不仅如此,目前的热网格法未考虑燃油内部的宏观流动,随着燃油消耗,油箱中燃油存在整体向下的宏观流动,对于每一个位置固定的基元模块,都需要考虑燃油宏观流动带来的传质影响. ...
Evolution and modern approaches for thermal analysis of electrical machines
1
2009
... 为解决集总参数法得不到局部温度和CFD方法计算效率过低的问题,热网络法被应用于温度场计算,尤其是在固体温度场计算中,如轴承[12 ] 、电动机及发电机[13 ] 、管路[14 ] 和电路[15 -16 ] 等.康振烨等[17 ] 将热网络法应用于燃油温度场计算,将不同位置的燃油划分到不同的基元模块中,采用MATLAB/Simulink软件搭建飞机油箱稳态热分析仿真模型;吕亚国等[5 ] 在此基础上建立了飞机油箱非稳态热分析模型,结果表明热网络法的计算结果与飞行测试数据吻合良好.上述研究假设油箱基元模块节点之间的传热方式为固体导热,这一假设仅适用于燃油温度较低情况,对于具有高油温的高速飞行器储油系统,燃油内部会存在较强的冷热掺混,假定燃油基元模块间传热方式为固体导热的方法会带来较大误差.不仅如此,目前的热网格法未考虑燃油内部的宏观流动,随着燃油消耗,油箱中燃油存在整体向下的宏观流动,对于每一个位置固定的基元模块,都需要考虑燃油宏观流动带来的传质影响. ...
Modelling steady-state thermal behaviour of double thermal network pipes
1
2017
... 为解决集总参数法得不到局部温度和CFD方法计算效率过低的问题,热网络法被应用于温度场计算,尤其是在固体温度场计算中,如轴承[12 ] 、电动机及发电机[13 ] 、管路[14 ] 和电路[15 -16 ] 等.康振烨等[17 ] 将热网络法应用于燃油温度场计算,将不同位置的燃油划分到不同的基元模块中,采用MATLAB/Simulink软件搭建飞机油箱稳态热分析仿真模型;吕亚国等[5 ] 在此基础上建立了飞机油箱非稳态热分析模型,结果表明热网络法的计算结果与飞行测试数据吻合良好.上述研究假设油箱基元模块节点之间的传热方式为固体导热,这一假设仅适用于燃油温度较低情况,对于具有高油温的高速飞行器储油系统,燃油内部会存在较强的冷热掺混,假定燃油基元模块间传热方式为固体导热的方法会带来较大误差.不仅如此,目前的热网格法未考虑燃油内部的宏观流动,随着燃油消耗,油箱中燃油存在整体向下的宏观流动,对于每一个位置固定的基元模块,都需要考虑燃油宏观流动带来的传质影响. ...
Thermal network model of supercapacitors stack
1
2011
... 为解决集总参数法得不到局部温度和CFD方法计算效率过低的问题,热网络法被应用于温度场计算,尤其是在固体温度场计算中,如轴承[12 ] 、电动机及发电机[13 ] 、管路[14 ] 和电路[15 -16 ] 等.康振烨等[17 ] 将热网络法应用于燃油温度场计算,将不同位置的燃油划分到不同的基元模块中,采用MATLAB/Simulink软件搭建飞机油箱稳态热分析仿真模型;吕亚国等[5 ] 在此基础上建立了飞机油箱非稳态热分析模型,结果表明热网络法的计算结果与飞行测试数据吻合良好.上述研究假设油箱基元模块节点之间的传热方式为固体导热,这一假设仅适用于燃油温度较低情况,对于具有高油温的高速飞行器储油系统,燃油内部会存在较强的冷热掺混,假定燃油基元模块间传热方式为固体导热的方法会带来较大误差.不仅如此,目前的热网格法未考虑燃油内部的宏观流动,随着燃油消耗,油箱中燃油存在整体向下的宏观流动,对于每一个位置固定的基元模块,都需要考虑燃油宏观流动带来的传质影响. ...
A 3-D-lumped thermal network model for long-term load profiles analysis in high-power IGBT modules
1
2016
... 为解决集总参数法得不到局部温度和CFD方法计算效率过低的问题,热网络法被应用于温度场计算,尤其是在固体温度场计算中,如轴承[12 ] 、电动机及发电机[13 ] 、管路[14 ] 和电路[15 -16 ] 等.康振烨等[17 ] 将热网络法应用于燃油温度场计算,将不同位置的燃油划分到不同的基元模块中,采用MATLAB/Simulink软件搭建飞机油箱稳态热分析仿真模型;吕亚国等[5 ] 在此基础上建立了飞机油箱非稳态热分析模型,结果表明热网络法的计算结果与飞行测试数据吻合良好.上述研究假设油箱基元模块节点之间的传热方式为固体导热,这一假设仅适用于燃油温度较低情况,对于具有高油温的高速飞行器储油系统,燃油内部会存在较强的冷热掺混,假定燃油基元模块间传热方式为固体导热的方法会带来较大误差.不仅如此,目前的热网格法未考虑燃油内部的宏观流动,随着燃油消耗,油箱中燃油存在整体向下的宏观流动,对于每一个位置固定的基元模块,都需要考虑燃油宏观流动带来的传质影响. ...
基于MATLAB/Simulink的飞机燃油箱内燃油温度仿真计算
2
2014
... 为解决集总参数法得不到局部温度和CFD方法计算效率过低的问题,热网络法被应用于温度场计算,尤其是在固体温度场计算中,如轴承[12 ] 、电动机及发电机[13 ] 、管路[14 ] 和电路[15 -16 ] 等.康振烨等[17 ] 将热网络法应用于燃油温度场计算,将不同位置的燃油划分到不同的基元模块中,采用MATLAB/Simulink软件搭建飞机油箱稳态热分析仿真模型;吕亚国等[5 ] 在此基础上建立了飞机油箱非稳态热分析模型,结果表明热网络法的计算结果与飞行测试数据吻合良好.上述研究假设油箱基元模块节点之间的传热方式为固体导热,这一假设仅适用于燃油温度较低情况,对于具有高油温的高速飞行器储油系统,燃油内部会存在较强的冷热掺混,假定燃油基元模块间传热方式为固体导热的方法会带来较大误差.不仅如此,目前的热网格法未考虑燃油内部的宏观流动,随着燃油消耗,油箱中燃油存在整体向下的宏观流动,对于每一个位置固定的基元模块,都需要考虑燃油宏观流动带来的传质影响. ...
... 针对高速飞行器燃油瞬态温度预测问题,本文基于文献[5 ]和文献[17 ]提出一种满足设计精度的高效修正热网络方法,通过修正热传导方程的方法考虑油箱内部冷热掺混的影响,通过修正热平衡方程的方法考虑燃油宏观流动的影响.基于该热网络法构建了高速飞行器储油系统瞬态热分析模型,在不同的热边界条件和储油系统几何结构下校核其普适性. ...
基于MATLAB/Simulink的飞机燃油箱内燃油温度仿真计算
2
2014
... 为解决集总参数法得不到局部温度和CFD方法计算效率过低的问题,热网络法被应用于温度场计算,尤其是在固体温度场计算中,如轴承[12 ] 、电动机及发电机[13 ] 、管路[14 ] 和电路[15 -16 ] 等.康振烨等[17 ] 将热网络法应用于燃油温度场计算,将不同位置的燃油划分到不同的基元模块中,采用MATLAB/Simulink软件搭建飞机油箱稳态热分析仿真模型;吕亚国等[5 ] 在此基础上建立了飞机油箱非稳态热分析模型,结果表明热网络法的计算结果与飞行测试数据吻合良好.上述研究假设油箱基元模块节点之间的传热方式为固体导热,这一假设仅适用于燃油温度较低情况,对于具有高油温的高速飞行器储油系统,燃油内部会存在较强的冷热掺混,假定燃油基元模块间传热方式为固体导热的方法会带来较大误差.不仅如此,目前的热网格法未考虑燃油内部的宏观流动,随着燃油消耗,油箱中燃油存在整体向下的宏观流动,对于每一个位置固定的基元模块,都需要考虑燃油宏观流动带来的传质影响. ...
... 针对高速飞行器燃油瞬态温度预测问题,本文基于文献[5 ]和文献[17 ]提出一种满足设计精度的高效修正热网络方法,通过修正热传导方程的方法考虑油箱内部冷热掺混的影响,通过修正热平衡方程的方法考虑燃油宏观流动的影响.基于该热网络法构建了高速飞行器储油系统瞬态热分析模型,在不同的热边界条件和储油系统几何结构下校核其普适性. ...
冲压发动机油箱传热理论研究
1
2013
... 典型高速飞行器油箱结构的三维模型如图1 所示.油箱内侧面装有隔热材料以防止燃油温度过高;油箱左上和左下侧贴近飞机外壁面,飞行过程中会受到高速气流的气动加热作用;油箱右下侧贴近发动机进气道,会受到发动机的热传导加热;其余3个面以及两端端面与其他部件相连,可近似为绝热条件.在飞行过程中,通过高压氮气挤压气囊为发动机提供带有压力的燃油[18 ] . ...
冲压发动机油箱传热理论研究
1
2013
... 典型高速飞行器油箱结构的三维模型如图1 所示.油箱内侧面装有隔热材料以防止燃油温度过高;油箱左上和左下侧贴近飞机外壁面,飞行过程中会受到高速气流的气动加热作用;油箱右下侧贴近发动机进气道,会受到发动机的热传导加热;其余3个面以及两端端面与其他部件相连,可近似为绝热条件.在飞行过程中,通过高压氮气挤压气囊为发动机提供带有压力的燃油[18 ] . ...
1
2006
... 将图6 中类型1等效为热面朝下的水平壁面,其对流传热系数计算公式[19 ] 为 ...
1
2006
... 将图6 中类型1等效为热面朝下的水平壁面,其对流传热系数计算公式[19 ] 为 ...
2
2011
... 将图6 中类型2等效为热面朝上的水平壁面,其对流传热系数计算公式[20 ] 为 ...
... 将图6 中类型3等效为与竖直方向夹角为θ 的倾斜平面,其对流传热系数计算公式[20 ] 为 ...
2
2011
... 将图6 中类型2等效为热面朝上的水平壁面,其对流传热系数计算公式[20 ] 为 ...
... 将图6 中类型3等效为与竖直方向夹角为θ 的倾斜平面,其对流传热系数计算公式[20 ] 为 ...