结构性黏土中球孔扩张不排水解析及其在静力触探中的应用

doi:10.16183/j.cnki.jsjtu.2021.330

结构性黏土中球孔扩张不排水解析及其在静力触探中的应用

张亚国^,^a, 肖书雄^a, 翟张辉^b, 李同录^b

a.长安大学建筑工程学院,西安 710061

b.长安大学地质工程与测绘学院,西安 710061

Undrained Solution for Spherical Cavity Expansion in Structured Clay and Its Application in CPT

ZHANG Yaguo^,^a, XIAO Shuxiong^a, ZHAI Zhanghui^b, LI Tonglu^b

a. School of Civil Engineering, Chang’an University, Xi’an 710061, China

b. School of Geological Engineering and Surveying, Chang’an University, Xi’an 710061, China

责任编辑: 孙启艳

收稿日期: 2021-09-3 修回日期: 2021-11-17 接受日期: 2021-11-29

基金资助:

国家自然科学基金项目(41807242)
国家自然科学基金项目(42072311)
中央高校基本科研业务费专项基金(300102281202)

Received: 2021-09-3 Revised: 2021-11-17 Accepted: 2021-11-29

作者简介 About authors

张亚国(1984-),副教授,现主要从事土力学及基础工程方面的教学和科研工作;E-mail:yaguozhang29@chd.edu.cn.

摘要

圆孔扩张理论被广泛用于静力触探(CPT)和静压沉桩等问题的贯入阻力或挤土位移分析预测中.目前结构性黏土中的圆柱孔扩张解答难以考虑扩孔过程中土体结构破坏或退化影响,一定程度上限制了该理论解答的工程适用范围.将锥尖或桩端贯入作为球形孔的扩张挤土过程,基于结构性黏土剑桥模型和塑性区大应变理论,将球孔扩张不排水问题归结为各有效应力分量的常微分方程组边值问题,以弹塑性边界上应力值为边值条件对该问题进行求解.结果表明,随着土体结构性增强,球孔周围的临界状态区和塑性区范围减小,扩孔应力增大,超固结土的应变软化特征和剪胀性更明显;对于初始应力相同的结构性黏土,各有效应力分量在孔壁附近均趋于对应重塑土中的应力分量,说明土体在扩孔扰动过程中发生了结构破坏或退化.最后将确定的扩孔应力用于CPT贯入阻力及孔隙水压力的理论计算中,与已有解答进行对比分析,发现考虑土体结构性影响后能得到与实测值更接近的预测结果.

关键词： 结构性黏土; 球孔扩张; 不排水; 弹塑性解; 静力触探

Abstract

The cavity expansion theory is widely used in the analysis and prediction of cone resistance and lateral displacements in cone penetration test (CPT) and pile installation. Nowadays, the existing theoretical solutions for cavity expansion in structured clay cannot consider the influences of structure degradation on the mechanical behaviors of soil during the expanding process, which limits its applications in practical engineering to some extent. Therefore, taking the penetration of cone or pile tip as a spherical cavity expansion process in soil, based on the structured Cam-Clay (SCC) model and the large strain theory in plastic zone, the undrained spherical cavity expansion problem could be attributed to a boundary value problem of a system of ordinary differential equations about effective stress components. The equations then could be solved with stresses on the elastic-plastic boundary serving as boundary conditions. The results show that, with strengthening of soil structure, the plastic and critical state zones narrow, the internal cavity stresses increased, and the softening behavior and dilatancy of over-consolidated soil become more significant. For structured clay with the same initial stresses, the effective stress components adjacent to cavity wall overlap with that of the corresponding reconstituted soil, which indicates that the degradation of soil structure occurs during the soil-disruption accompanied expansion process. Finally, the internal cavity stresses derived from the proposed solution were used for theoretical calculation of cone resistance and pore pressure in CPT. A comparison of the existing solution with the results calculated indicates that the results obtained with consideration of soil structure are closer to the measured values.

Keywords： structured clay; spherical cavity expansion; undrained; elastic-plastic solution; cone penetration test(CPT)

PDF (2513KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张亚国, 肖书雄, 翟张辉, 李同录. 结构性黏土中球孔扩张不排水解析及其在静力触探中的应用[J]. 上海交通大学学报, 2023, 57(6): 709-718 doi:10.16183/j.cnki.jsjtu.2021.330

ZHANG Yaguo, XIAO Shuxiong, ZHAI Zhanghui, LI Tonglu. Undrained Solution for Spherical Cavity Expansion in Structured Clay and Its Application in CPT[J]. Journal of Shanghai Jiaotong University, 2023, 57(6): 709-718 doi:10.16183/j.cnki.jsjtu.2021.330

静力触探(CPT)锥尖或桩端贯入挤土过程与土体中球形孔的扩张相似,桩身挤土与旁压试验则与圆柱孔扩张类似,因此圆孔(包括球形孔和圆柱孔)扩张理论被广泛用于CPT贯入及沉桩挤土等工程问题的分析预测中^[1-2].Yu等^[2]对比几种CPT的分析理论后指出,圆孔扩张理论能够充分考虑土体应力状态、应力历史及应力-应变本构关系,因而比基于刚性体假定的极限承载力理论和基于理想塑性假定的应变路径法具有更好的适用性.这一研究促进了扩孔理论在工程贯入问题中的应用,包括用于预测CPT锥尖阻力、孔隙水压力^[3⇓-5]、基于CPT测试结果反演土体参数以及计算沉桩挤土位移和预测桩基承载力等^[6⇓-8],同时实际工程的复杂性也促使该理论不断发展完善.

早期研究中通常假定土体为理想弹塑性体,基于摩尔-库仑(M-C)屈服准则推导球孔扩张解答,分析扩孔过程中土体的塑性变形和屈服特性^[2],但受理想弹塑性模型限制,该解答无法考虑土体应力历史的影响.随着土体本构关系的发展,土体应力历史和应力水平的临界状态模型逐渐被引入到圆孔扩张问题中^[9],例如Chen等^[10]基于统一硬化模型(UH)模拟了球孔扩张过程中超固结土体应变软化特性;Huang等^[11]基于无黏性土中的临界状态模型,分析了球孔扩张过程中土体的剪胀特性对扩孔压力等的影响,并将解答结果在砂土CPT试验中进行了应用;近年来,Chen等^[12]及Sivasithamparam等^[13]分别基于Dafalias及S-CLAY1各向异性本构模型,推导了圆柱孔扩张的不排水解答,以适用于具有各向异性的天然土体.

天然沉积的土体除了上述性质外,往往还具有明显的结构性,因此结构性土中的圆孔扩张问题研究逐渐受到了学者们的重视^[14].沈珠江^[15]曾指出土的结构性数学模型已成为21世纪土力学研究的核心问题;刘维正等^[16]考虑施工因素对软黏土结构性的扰动求解了圆柱孔扩张问题,但该解答通过构造扰动函数描述土体的结构性损伤机理,而非采用考虑土体结构性的力学模型;Sivasithamparam等^[17]基于S-CLAY1S模型,将考虑天然黏土各向异性扩孔解^[13]拓展至能同时考虑土体结构性的扩孔解答,但所采用本构模型的复杂性使得计算过程中需确定的模型参数过多,不便于进行工程应用;李镜培等^[18]和周攀等^[19]基于已有结构性土的本构模型,采用相关联流动法则分别对土体中不排水和排水柱孔扩张机理进行分析,但这些解答仅能反映土体初始结构性的影响,无法考虑扩孔过程中圆柱孔周围土体结构性损伤的影响.

目前结构性土中的扩孔解答多为圆柱孔扩张解答,而锥尖或桩端的挤土过程往往被等效成周围土体球形孔扩张的过程,这些柱形孔扩张的解答难以在CPT和沉桩等贯入问题中直接应用.对此,本研究基于Carter等^[20]提出的结构性黏土剑桥(SCC)模型,推导了结构性黏土中的不排水球孔扩张解答,该解答能够充分考虑土体结构性、应力历史等对球孔周围土体应力大小及分布的影响,也能反映球孔扩张过程中土体发生的结构性损伤及相应的应变软化行为.此外,解答用于预测CPT锥端贯入阻力和孔隙水压力,通过与实测值对比,表明该解答在天然结构性黏土的工程贯入问题中具有更好的适用性.

1 力学模型

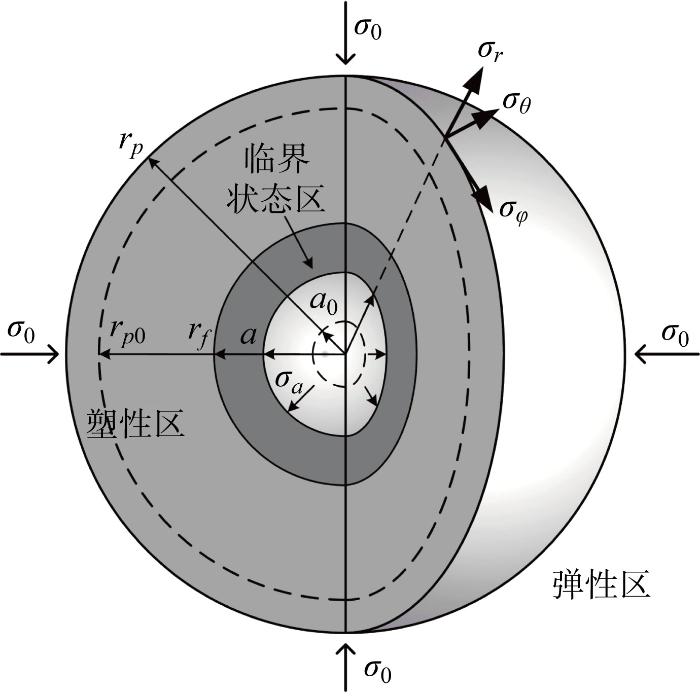
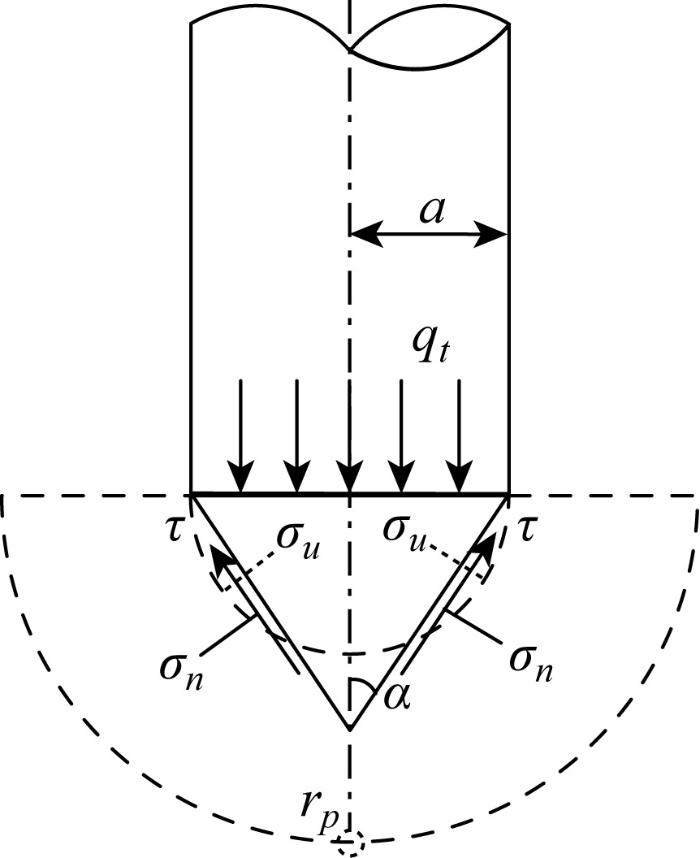
采用球坐标(r, θ, φ)(r为径向方向, θ为切向方向, φ为环向方向)建立不排水条件下黏土中球孔扩张力学模型,σ_r、σ_θ和σ_φ分别表示径向、切向和环向的总应力,如图1所示.假定球孔初始孔径为a₀,孔周的初始应力为 σ_r₀=σ_θ₀=σ_φ₀=σ₀;当孔壁上扩孔应力增至σ_a时,球孔孔径扩至a,孔周形成半径为r_p的塑性区(r_p₀为r_p位置土单元对应的初始半径).扩孔应力增加至一定程度后,孔周土体存在3个应力状态区:①邻近孔壁的临界状态区,a<r≤r_f,r_f为临界状态区半径,其特点是在应力保持恒定的情况下应变持续发展;②塑性区(r_f<r≤r_p)应力和应变呈非线性变化,服从SCC模型;③弹性区(r≥r_p)内应力和应变保持线性关系,服从胡克(Hooke)定律.球孔扩张问题,任意位置处的平衡微分方程可表达为

(1)

\frac{d σ_{r}}{d r}

\frac{σ_{r} - σ_{θ}}{r}

根据临界状态土力学,平均有效应力和偏应力表达式分别为

(2)

\begin{array}{l} p' = (σ'_{r} + σ'_{θ} + σ'_{φ}) / 3 \\ q = [\frac{(σ'_{r} - σ'_{θ})^{2} + (σ'_{r} - σ'_{φ})^{2} + (σ'_{θ} - σ'_{φ})^{2}}{2}]^{\frac{1}{2}} \end{array}\}

式中:σ'_r、σ'_θ和σ'_φ分别为径向、切向和环向有效应力.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 结构性黏土中球孔扩张力学模型

Fig.1 Mechanical model of spherical cavity expansion in structured clay

基于球孔的对称性,可假定θ和φ两个方向的应力应变相等,即σ'_θ=σ'_φ和ε_θ=ε_φ,其中ε_θ和ε_φ分别为切向和环向应变.则式(2)可整理为

(3)

\begin{array}{l} p' = (σ'_{r} + 2 σ'_{θ}) / 3 \\ q = σ'_{r} - σ'_{θ} \end{array}\}

2 SCC模型

2.1 压缩曲线和屈服方程

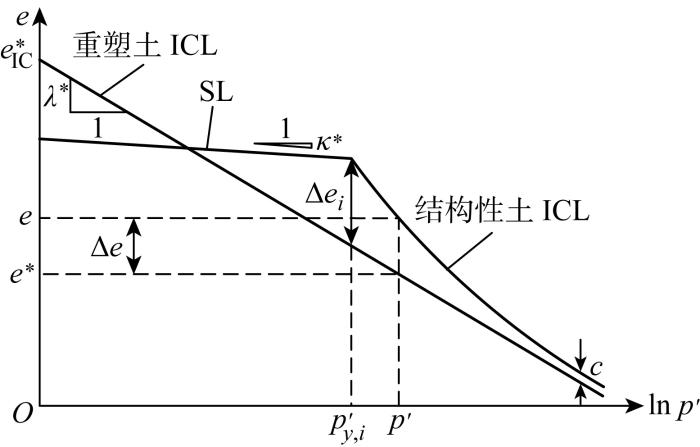
土体的各向同性压缩(ICL)曲线如图2所示.上标*表示与结构土相同应力状态所对应重塑土;e和e^*分别为结构性土和对应重塑土的孔隙比, $e_{I C}^{*}$ 为p'=1时的e^*值;Δe=e-e^*,为土体的结构性大小;p'_y_,_i为各向同性压缩时结构性土的初始屈服应力;Δe_i为p'=p'_y_,_i时的Δe值,即结构性土和重塑土孔隙比差值的最大值;c为p'→∞时的Δe值;λ^*为e-ln p'平面内重塑土ICL线的斜率;κ^*为e-ln p'平面内回弹线(SL)的斜率.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 结构性土与对应重塑土的压缩曲线模型

Fig.2 Idealisation of compression curve of reconstituted and structured clays

图2中结构性土ICL表达式为

(4)e=

e_{I C}^{*}

+(Δe_i-c)

{(\frac{p'_{y, i}}{p'})}^{b}

-λ^*ln p'+c

式中:b为反映结构损伤速率的模型常数.Carter等^[20]基于式(4)得到了结构性土在任意应力路径下的广义压缩曲线,表达式为

(5)e=

e_{I C}^{*}

-κ^*ln p'+(Δe_i-c)

{(\frac{p'_{y, i}}{p'_{s}})}^{b}

-(λ^*-κ^*)ln p'_s+c

式中:p'_s为结构性土的屈服应力.

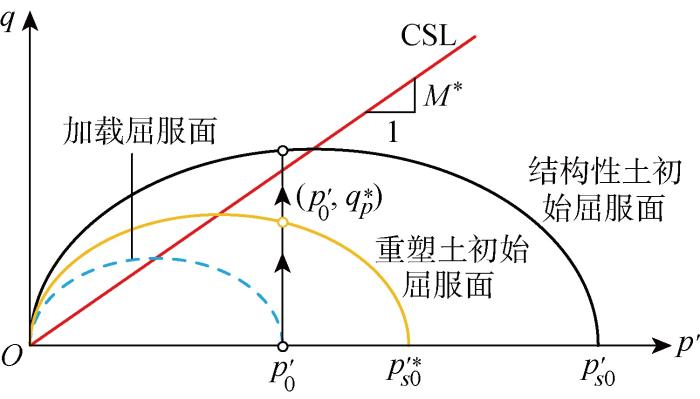
与修正剑桥(MCC)模型类似,SCC模型的屈服方程为

(6)f=q²-M^*²p'(p'_s-p')=0

式中:M^*为p'-q平面内临界状态线(CSL)的斜率.

2.2 塑性流动法则

SCC模型中考虑了结构性对土体塑性体变d $ε_{v}^{p}$ 的影响,硬化函数可表示为

(7)dp'_s=

\frac{(1 + e) p'_{s}}{(λ^{*} - κ^{*}) + b (< Δ e - c > + \frac{γ η Δ e}{M^{*} - η})}

ε_{v}^{p}

式中:<>为Macaulay括号,当x≥0时,<x>=x,当x<0时,<x>=0;η=q/p'为应力比;γ为反映剪切对土体结构性损伤贡献的模型常数;Δe可表达为

(8)Δe=(Δe_i-c)

{(p'_{y, i} / p'_{s})}^{b}

对于结构性土的硬化过程(η<M^*),塑性流动法则为

(9)$\frac{\mathrm{d}\varepsilon_d^p}{\mathrm{d}\varepsilon_v^p}=\frac{2\eta}{\left|M^{-2}-\eta^2\right|+\bar{\omega}\eta^2\left|1-\sqrt{p_e^{\prime}/p_s^{\prime}}\right|}$

式中:为反映结构性对流动法则影响的模型常数;$\mathrm{d}\varepsilon_d^p$为塑性剪应变增量.$ p_{e}^{\prime}$的表达式为

(10)p'_e=exp

(\frac{e_{I C}^{*} - e - κ^{*} l n p'}{λ^{*} - κ^{*}})

对于结构性土的软化过程(η>M^*),考虑结构性损伤引起的软化效应,塑性流动法则为

(11)

\frac{d ε_{d}^{p}}{d ε_{v}^{p}}

=Ω

(12)Ω=

\frac{- (λ^{*} - κ^{*}) - b (< Δ e - c > - \frac{γ η Δ e}{M^{*} - η})}{λ^{*} - κ^{*} + b (< Δ e - c > + \frac{γ η Δ e}{M^{*} - η})}

对于结构性较弱的土,其应力状态到达CSL线时土体结构可能已经完全破坏,即η=M^*且Δe=0,联立式(5)、(8)和(10)可得p'_e=p'_s,此时硬化函数式(7)和流动法则式(9)和(11)与MCC一致,土体进入临界状态,即d $ε_{d}^{p}$ →∞.

对于结构性较强的土,当应力状态到达CSL线时土体结构可能未完全破坏,即η=M^*且Δe≠0,可得p'_e≠p'_s,由式(9)和(11)也可知d $ε_{d}^{p}$ →∞不成立,说明土体未进入临界状态.Carter等^[20]分析不排水剪切试验结果发现,在该情况下继续加载,应力路径在p'-q平面内沿CSL线下滑(dq=M^*dp'<0)直至Δe=0.由于不排水条件下体应变增量dε_v=0,此时塑性应变增量为

(13)$\begin{aligned} & \mathrm{d} \varepsilon_v^p=-\mathrm{d} \varepsilon_v^e=-\frac{\kappa}{1+e} \frac{\mathrm{d} p^{\prime}}{p^{\prime}} \mid \\ & \mathrm{d} \varepsilon_d^p=\frac{2\left|\mathrm{~d} \varepsilon_v^p\right|}{\tilde{\omega}_\eta\left|1-\sqrt{p_e^{\prime} / p_s^{\prime}}\right|} \mid\end{aligned}$

式中:d $ε_{v}^{e}$ 为弹性体应变增量.

联立式(6)和式(13),并结合η=M^*和dp'<0,可得η=M^*且Δe≠0情况下继续加载时土体的硬化和流动法则为

(14)dp'_s=-

\frac{(1 + e) p'_{s}}{κ^{*}}

ε_{v}^{p}

(15)$\frac{\mathrm{d}\varepsilon_d^p}{\mathrm{d}\varepsilon_v^p}=\frac2{\bar{\omega}\eta\mid1-\sqrt{p_e^{\prime}/p_s^{\prime}}}$

3 不排水球孔扩张问题求解

3.1 弹性区解答

弹性区满足小应变假定,服从胡克定律,即应力应变增量关系为

(16)

[\begin{array}{l} d ε_{r}^{e} \\ d ε_{θ}^{e} \end{array}]

\frac{1}{E} [\begin{array}{l} 1 & - 2 ν^{*} \\ - ν^{*} & 1 - ν^{*} \end{array}] [\begin{array}{l} d σ'_{r} \\ d σ'_{θ} \end{array}]

ε_{φ}^{e}

ε_{θ}^{e}

式中:d $e_{r}^{e}$ 、d $ε_{θ}^{e}$ 和d $ε_{φ}^{e}$ 分别为径向、切向和环向的弹性应变增量;ν^*为泊松比;弹性模量E=2G(1+ν^*),其中剪切模量是平均有效应力p'和孔隙比e的函数^[9],为

(17)G=

\frac{3 (1 - 2 ν^{*}) (1 + e) p'}{2 (1 + ν^{*}) κ^{*}}

球孔周围弹性区应力分量和径向位移 ${U_{r}}^{[5]}$ 为

(18)

\begin{array}{l} σ'_{r} = σ'_{0} + (σ'_{r_{p}} - σ'_{0}) (r_{p} {/ r)}^{3} \\ σ'_{θ} = σ'_{0} - \frac{1}{2} (σ'_{r_{p}} - σ'_{0}) {(\frac{r_{p}}{r})}^{3} \\ U_{r} = \frac{σ'_{r_{p}} - σ'_{0}}{4 G_{0}} \frac{r_{p}^{3}}{r^{2}} \end{array}\}

式中:σ $'_{r_{p}}$ 为弹塑性区交界面r_p处的径向有效应力;G₀为初始剪切模量,其值为

(19)G₀=

\frac{3 (1 - 2 ν^{*}) (1 + e) p'_{0}}{2 (1 + ν^{*}) κ^{*}}

式中:p'₀为初始平均有效应力.

3.2 塑性区分析

SCC模型采用非相关联流动法则,塑性应变增量为

(20)

\begin{array}{l} d ε_{v}^{p} = Λ \partial g / \partial p' \\ d ε_{d}^{p} = Λ \partial g / \partial q \end{array}\}

式中:g为塑性势;Λ为塑性应变率.

位于屈服面上的应力点满足塑性一致性条件df=0,即

(21)df=

\frac{\partial f}{\partial p'}

dp'+

\frac{\partial f}{\partial q}

dq+

\frac{\partial f}{\partial p'_{s}} \frac{\partial p'_{s}}{\partial ε_{v}^{p}}

ε_{v}^{p}

式中:各偏导数可根据式(6)、(7)和(14)求得.

根据非相关联流动法则,联立式(20)和式(21)可得径向、切向和环向的塑性应变增量为

(22)

\begin{array}{l} d ε_{r}^{p} = Λ \frac{\partial g}{\partial σ'_{r}} = Λ \frac{\partial g}{\partial p'} \frac{\partial p'}{\partial σ'_{r}} + Λ \frac{\partial g}{\partial q} \frac{\partial q}{\partial σ'_{r}} = \\ \frac{\partial p'}{\partial σ'_{r}} d ε_{v}^{p} + \frac{\partial q}{\partial σ'_{r}} d ε_{d}^{p} = (\frac{\partial p'}{\partial σ'_{r}} + \frac{d ε_{d}^{p}}{d ε_{v}^{p}} \frac{\partial q}{\partial σ'_{r}}) d ε_{v}^{p} = \\ y b_{r} (a_{r} d σ'_{r} + 2 a_{θ} d σ'_{θ}) \\ d ε_{θ}^{p} = Λ \frac{\partial g}{\partial σ'_{θ}} = Λ \frac{\partial g}{\partial p'} \frac{\partial p'}{\partial σ'_{θ}} + Λ \frac{\partial g}{\partial q} \frac{\partial q}{\partial σ'_{θ}} = \\ \frac{\partial p'}{\partial σ'_{θ}} d ε_{v}^{p} + \frac{\partial q}{\partial σ'_{θ}} d ε_{d}^{p} = (\frac{\partial p'}{\partial σ'_{θ}} + \frac{d ε_{d}^{p}}{d ε_{v}^{p}} \frac{\partial q}{\partial σ'_{θ}}) d ε_{v}^{p} = \\ y b_{θ} (a_{r} d σ'_{r} + 2 a_{θ} d σ'_{θ}) \\ d ε_{φ}^{p} = d ε_{θ}^{p} \end{array}\}

(23)

\begin{array}{l} y = - 1 / (\frac{\partial f}{\partial p'_{s}} \frac{\partial p'_{s}}{\partial ε_{v}^{p}}) \\ b_{r} = \frac{\partial p'}{\partial σ'_{r}} + \frac{d ε_{d}^{p}}{d ε_{v}^{p}} \frac{\partial q}{\partial σ'_{r}} = \frac{1}{3} + \frac{d ε_{d}^{p}}{d ε_{v}^{p}} \\ b_{θ} = \frac{\partial p'}{\partial σ'_{θ}} + \frac{d ε_{d}^{p}}{d ε_{v}^{p}} \frac{\partial q}{\partial σ'_{θ}} = \frac{1}{3} - \frac{1}{2} \frac{d ε_{d}^{p}}{d ε_{v}^{p}} \\ a_{r} = \frac{\partial f}{\partial σ'_{r}} = \frac{\partial f}{\partial p'} \frac{\partial p'}{\partial σ'_{r}} + \frac{\partial f}{\partial q} \frac{\partial q}{\partial σ'_{r}} = \\ p' (M^{* 2} - η^{2}) / 3 + 2 q \\ a_{θ} = \frac{\partial f}{\partial σ'_{θ}} = \frac{\partial f}{\partial p'} \frac{\partial p'}{\partial σ'_{θ}} + \frac{\partial f}{\partial q} \frac{\partial q}{\partial σ'_{θ}} = \\ p' (M^{* 2} - η^{2}) / 3 - q \end{array}\}

需要指出的是,求解p'、q关于σ'_r和σ'_θ的偏导数时应根据p'、q的严格定义式(2)进行计算.

另外,塑性区总应变还应包含弹性部分,因此,联立弹性本构式(16)和塑性本构式(22),可得塑性区的弹塑性应力应变增量关系为

(24)

[\begin{array}{l} d ε_{r} \\ d ε_{θ} \end{array}]

[\begin{array}{l} y b_{r} a_{r} + \frac{1}{E} & 2 y b_{r} a_{θ} - \frac{2 v^{*}}{E} \\ y b_{θ} a_{r} - \frac{v^{*}}{E} & 2 y b_{θ} a_{θ} + \frac{1 - v^{*}}{E} \end{array}] [\begin{array}{l} d σ'_{r} \\ d σ'_{θ} \end{array}]

根据大变形(对数应变)理论,径向和切向应变为

(25)

\begin{array}{l} ε_{r} = - l n \frac{d r}{d r_{0}} \\ ε_{θ} = - l n \frac{r}{r_{0}} \end{array}\}

式中:r₀为土单元的初始径向位置.

对ε_r作变换得

(26)ε_r=ln

\frac{d r_{0}}{d r}

=ln

\frac{d (e^{ε_{θ}} r)}{d r}

=ln

(e^{ε_{θ}} + r \frac{d e^{ε_{θ}}}{d r})

由于ε_θ是r/r₀的函数,ε_r是ε_θ的函数,故ε_r也是关于r/r₀的函数.令ℓ=r/r₀,则对数切向应变为

(27)ε_θ=-ln ℓ

不排水条件下体应变ε_v=0,则径向应变为

(28)ε_r=ε_v-2ε_θ=2ln ℓ

由式(24)、(27)和(28)可得控制方程组为

(29)

\begin{array}{l} \frac{d σ'_{r}}{d l} - \frac{m}{Θ l} = 0 \\ \frac{d σ'_{θ}}{d l} - \frac{n}{Θ l} = 0 \end{array}\}

式中:

(30)

\begin{array}{l} m = \frac{2}{E^{2}} [1 - 2 ν^{*} + E y a_{θ} (b_{r} + 2 b_{θ})] \\ n = - \frac{1}{E^{2}} [1 - 2 ν^{*} + E y a_{r} (b_{r} + 2 b_{θ})] \\ Θ = \frac{1}{E^{3}} [1 - ν^{*} - 2 ν^{* 2} + E y (1 - ν^{*}) a_{r} b_{r} + \\ 2 E y a_{θ} b_{θ} + 2 E y ν^{*} (a_{r} b_{θ} + a_{θ} b_{r})] \end{array}\}

在塑性区,式(29)将结构性土中球孔不排水扩张问题归结为σ'_r和σ'_θ的一阶常微分方程组边值问题.为了完成该问题的求解,还需解决以下3个问题:① 边界条件的确定;② 将有效应力与中间变量ℓ的关系转换至与r的关系;③ 超孔隙水压力Δu的确定.

3.3 边界条件

根据平均有效应力p'的定义式(2)和弹性区应力解式(18)可知,弹性区的p'为定值,等于初始有效应力σ'₀.因此,由应力连续性可得弹塑性区交界面处应力为

(31)p'_p=p'₀=σ'₀

将弹塑性边界上应力点(p'₀,q_p)代入屈服方程式(6)中,求得弹塑性区界面上偏应力为

(32)q_p=M^*p'₀

\sqrt{R R_{s} - 1}

式中:R= $p_{s 0}^{' *}$ /p'₀,为各向同性超固结比^[9];结构应力比R_s=p'_s₀/ $p_{s 0}^{' *}$ ,用于反映黏土结构性强弱,其中p'_s₀和 $p_{s 0}^{' *}$ 分别为结构性土和所对应的重塑土的初始屈服应力,如图3所示, $q_{p}^{*}$ 为重塑土中孔周弹塑性边界上的偏应力.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 p'-q平面内的有效应力路径(ESP)

Fig.3 Effective stress path in p'-q plane

由式(3)、式(31)和式(32)可得弹塑性边界处有效应力分量为

(33)

\begin{array}{l} σ'_{r} |_{l = l_{p}} = σ'_{r p} = p'_{0} + \frac{2}{3} q_{p} \\ σ'_{θ} |_{l = l_{p}} = σ'_{θ p} = p'_{0} - \frac{1}{3} q_{p} \end{array}\}

式中:ℓ_p=r_p/r_p₀表示弹塑性边界对应的ℓ值.

根据变形连续性可知,弹塑性交界面处的位移(U_r=r-r₀)仍满足弹性区位移解,根据式(18),ℓ_p可表示为

(34)ℓ_p=

\frac{r_{p}}{r_{p 0}}

{\frac{r}{r - U_{r}}|}_{r = r_{p}}

\frac{4 G_{0}}{4 G_{0} - (σ'_{r p} - σ'_{0})}

3.4 变量转换及超孔隙水压力确定

软黏土中的球孔扩张可视为不排水过程,球孔周围土体的体应变为0,由球体体积算法可知

(35)r³-a³=

r_{0}^{3}

a_{0}^{3}

整理式(35)可得

(36)

\frac{r}{a}

{[\frac{1 - {(a_{0} / a)}^{3}}{1 - 1 / l^{3}}]}^{\frac{1}{3}}

式(36)建立了ℓ与r的转化关系.通过该式,可将式(29)中确定的σ'_r、σ'_θ与ℓ关系转换为应力分量与径向位置r的关系.同样,将ℓ_p代入式(36)则可确定塑性区半径r_p.

基于有效应力原理,在不排水条件下式(1)可写为有效应力的形式:

(37)

\frac{d σ'_{r}}{d r}

\frac{d u}{d r}

\frac{σ'_{r} - σ'_{θ}}{r}

式中:u为孔隙水压力.

当塑性区范围a<r<r_p及应力分量σ'_r和σ'_θ确定后,超孔隙水压力可根据平衡方程式(37)求解.对式(37)积分可得:

(38)Δu=u-u₀=σ'_p-σ'_r-2

\int_{r_{p}}^{r} \frac{σ'_{r} - σ'_{θ}}{r}

式中:u₀为初始孔隙水压力.

4 算例分析与讨论

为探究土体结构性对不排水扩孔应力、孔周应力分布和应力路径的影响,考虑R_s=1,1.2,1.5三种黏土结构性强弱,分别求解了正常、轻超和重超固结黏土(R=1,3,10)中的球孔扩张问题.波士顿黏土(BBC)被广泛用于圆孔扩张理论的分析中^[5,9],为了便于比较,采用文献[9]中BBC黏土的基本物性参数 M^*、λ^*、κ^*、ν^*和初始应力状态参数R、σ'₀、e₀、G₀作为计算参数,结合相对应结构性相关模型参数b、c、$\tilde{w} $和γ在SCC本构模型中的含义以及BBC黏土的性质,根据Carter等^[20]参数确定方法,对结构性参数进行取值,如表1和表2所示.当R_s=1时,表示重塑土与结构性土具有相同的应力状态.

表1 模型计算参数

Tab.1 Calculation parameters of SCC model

基本参数	结构性参数
$M^*=1.2	b=1
λ^*=0.15	c=0
κ^*=0.03	$\tilde{w} $=1
ν^*=0.278	γ=0.5

新窗口打开| 下载CSV

表2 BBC黏土的初始状态参数^[9]

Tab.2 Initial state parameters of BBC clay^[9]

R	σ'₀/kPa	e₀	G₀/kPa	$e_{I C}^{*}$
1	100	1.09	4348	1.781
3	120	0.97	4113	1.820
10	144	0.80	3756	1.822

注:初始孔隙水压力u₀=100 kPa^[9].

新窗口打开| 下载CSV

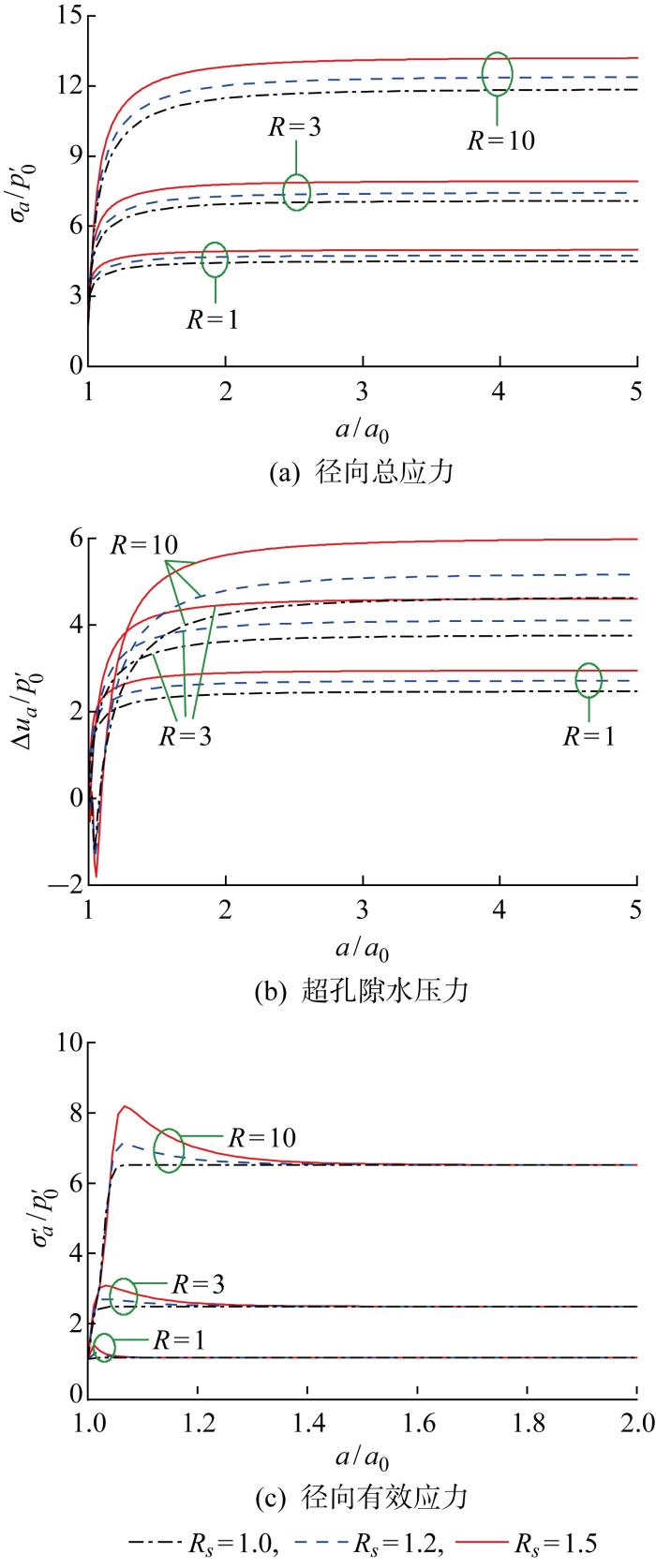
总扩孔应力σ_a、孔壁处超孔压Δu_a以及有效扩孔应力σ'_a随扩孔半径的变化如图4所示,各应力通过p'₀进行了归一化处理.由图4(a)可知,各向同性超固结比R越大, σ_a/p'₀越大;当R相同时,σ_a/p'₀随结构应力比 R_s的增大而增加, 表明土的结构性越强,扩张相同大小球孔时所需的扩孔应力值越大;当R_s=1时,该解答将退化为修正剑桥模型MCC中的解(重塑土中的解答).由图4(b)可见,当R=10时超孔压出现负值,表明在重超固结土扩孔过程中出现一定的剪胀现象.根据图4(c)可知,随着a/a₀增大,重塑土(R_s=1)中σ'_a/p'₀迅速增大至稳定值;结构性土(R_s=1.2,1.5)中σ'_a/p'₀先快速增大至峰值,再逐渐减小至稳定值,说明结构性土扩孔过程中由于土体结构破坏表现出应变软化的特征;对于不同结构性土体,σ'_a/p'₀稳定值与对应的重塑土一致,说明随着孔径的增大,孔壁处土体的结构逐步丧失.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 孔壁处应力值随扩孔半径的变化

Fig.4 Normalized stresses on cavity wall versus cavity radius

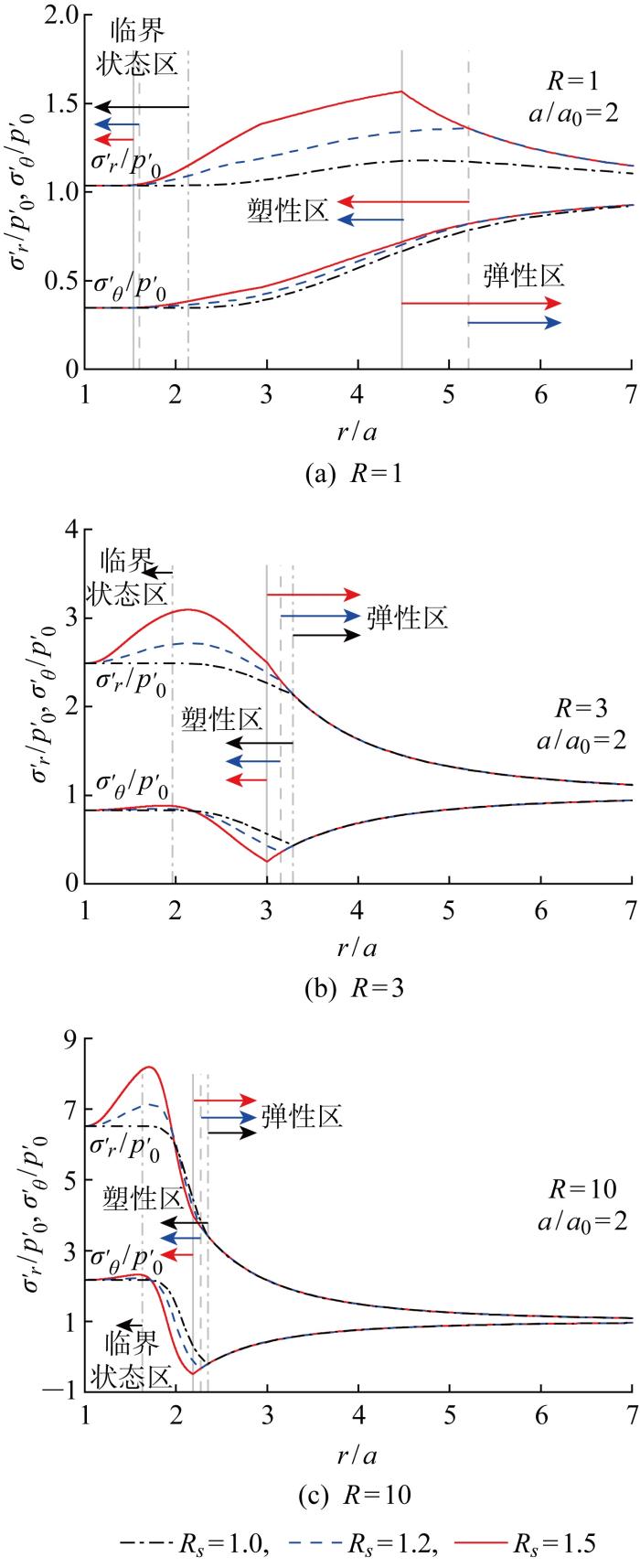
不同结构性土中归一化有效应力σ'_r/p'₀和σ'_θ/p'₀的径向分布如图5所示.对于正常固结土,随着土体结构性增强(R_s增大),扩张球孔周围的塑性区和临界状态区缩小,且随着径向距离减小,塑性区内有效应力单调减小;对于超固结(R=3,10)的结构性土(R_s=1.2,1.5),随着到孔壁(r/a=1)的距离越小,径向应力先增大后减小,结构性越强变化趋势越明显,说明结构性土出现应变软化的特点;切向应力则快速增大至稳定值,结构性影响不显著.此外,当到孔壁的距离逐渐减小时,结构性土中的应力分布与重塑土趋于一致,间接反映了扩孔扰动过程对周围土体结构的影响.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 归一化有效应力的径向变化

Fig.5 Normalized effective stress along radial direction versus R

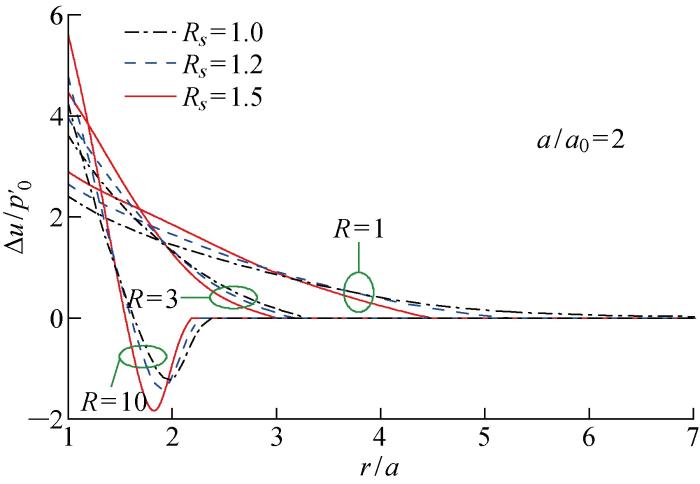
球孔扩张引起的周围土体中超孔隙水压力分布情况如图6所示.距孔壁较远的弹性区Δu/p'₀为0,说明土体弹性变形不会产生超孔隙水压力;在塑性区,Δu/p'₀随着到孔壁距离的减小总体上增大;对于重超固结土,Δu/p'₀在靠近孔壁过程中先减小后增大.需要注意的是,对于具有相同R的土体,结构性越强,超孔隙水压力变化越快,这一定程度上体现了土体结构破坏孔压快速增大的过程.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 归一化超孔隙水压力的径向变化

Fig.6 Variations of normalized excess pore pressure along radial direction

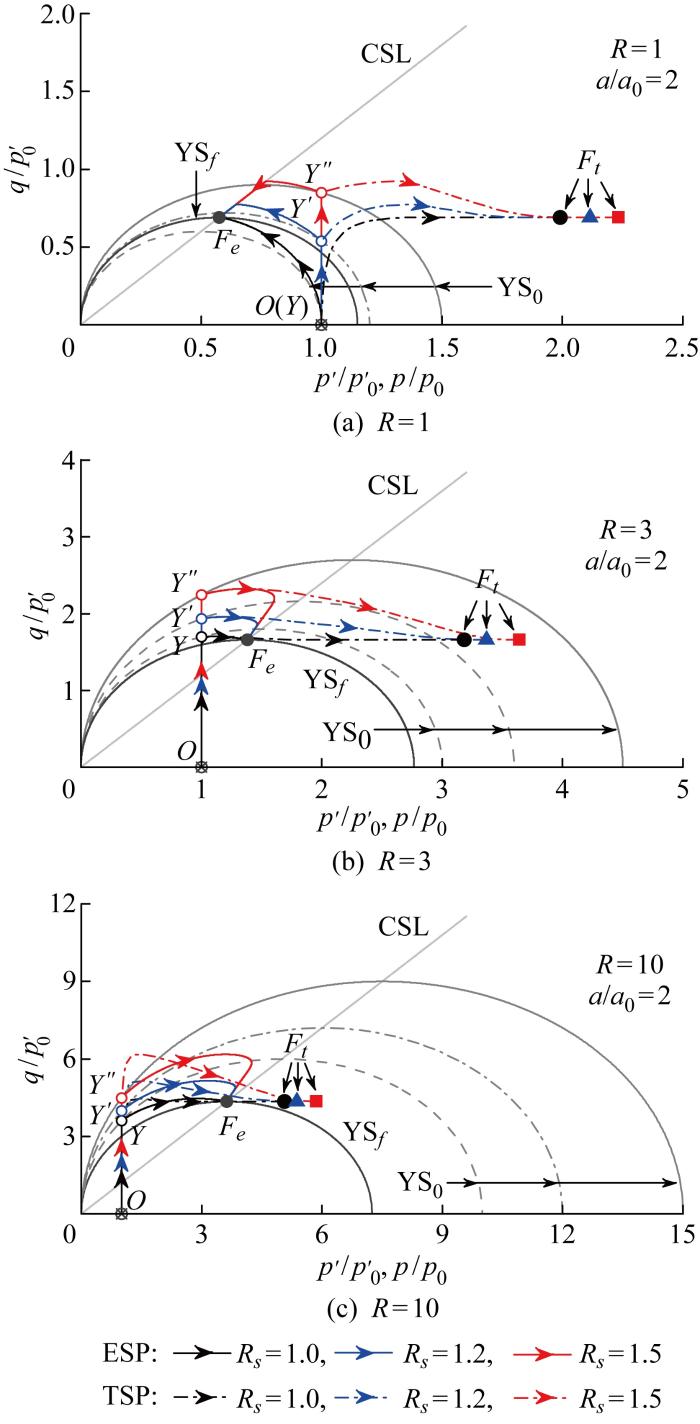
孔壁土单元扩孔过程中的应力路径如图7所示.图中ESP和TSP分别表示有效应力路径和总应力路径;YS₀和YS_f分别表示初始屈服面和最终屈服面;点O、Y、F_e和F_t分别为初始应力点、屈服点、ESP终点和TSP终点.在相同超固结状态下,结构性土的ESP终点与重塑土重合,说明土体在扩孔后丧失了结构性,其有效应力状态最终与对应的重塑土达到一致.此外,最终的总应力p值随R_s增大而增大,因总应力p与对应的有效应力p'的差值即为孔隙水压力,故可知土体结构性越强,扩孔过程中孔壁附近的孔隙水压力越大.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 孔壁土单元的应力路径

Fig.7 Stress path of soil element on cavity wall versus R

根据图7,对于重塑土(R_s=1),ESP在弹性阶段(p'不变,q增加)为线性变化,在塑性阶段发生应变硬化(正常固结)或软化(超固结)到达CSL线;对于结构性土(R_s=1.2,1.5),其弹性阶段应力路径较重塑土增长,塑性阶段与重塑土区别较大;对于正常固结土(R=1),ESP到达CSL线后沿着CSL线下滑(dq=M^*dp'<0),直至应力状态与重塑土重合于点F,说明这种情况下土体先发生了应变硬化,后由于结构损伤出现应变软化现象;对于轻超和重超固结(R=3,10)的结构性土,ESP出现斜率大于M^*的陡降段,说明加载过程中土体出现了明显的应变软化.

5 CPT中的应用分析

球孔扩张理论在CPT试验结果分析方面具有广泛应用^[2⇓-4].将锥头挤土时受到的正应力σ_n看作球形孔的极限扩张应力σ_u,将剪应力τ看作锥面与土的摩阻力,模型如图8所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 静力触探力学模型

Fig.8 Mechanical model for cone penetration test

由锥头受力平衡可得静力触探锥尖阻力^[4]:

(39)q_t=σ_n+τcot α=σ_u+α_ctan ϕ'σ'_ucot α

式中:α为锥面与锥尖轴线的夹角;α_c为锥面与土的摩擦系数;ϕ'为土的有效内摩擦角;σ_u和σ'_u分别为σ_a和σ'_a在a/a₀→∞时所对应的值,见图4(a)和4(c).

锥头贯入过程中的孔隙水压力表示为

(40)u_m=Δu_o+Δu_s+u₀

式中:Δu_o为八面体正应力引起的超孔压,即图4(b)中孔壁处的超孔压Δu_a;Δu_s为剪应力引起的超孔压,可近似于$2s’_{v0}$^[4];u₀为初始孔压.CPT试验中无预钻孔,故在计算扩孔应力和超孔压时初始孔径a₀为0.

通过结构性不明显的Bothkennar黏土和具有较强结构性的Ottawa黏土的CPT结果^[3]验证本研究解答的适用性.CPT锥头的锥角为2α=60°,锥面与土摩擦系数α_c=1,在三向压缩条件下(如土体中球孔扩张过程),天然黏土的塑性应变率Λ=0.75^[3-4].另外,注意到参数e₀、λ^*和κ^*的值未给出,需通过文献[4]中参数转换方法将含有该参数的式(7)、式(10)、式(12)和式(14)转化为已有参数表达式.

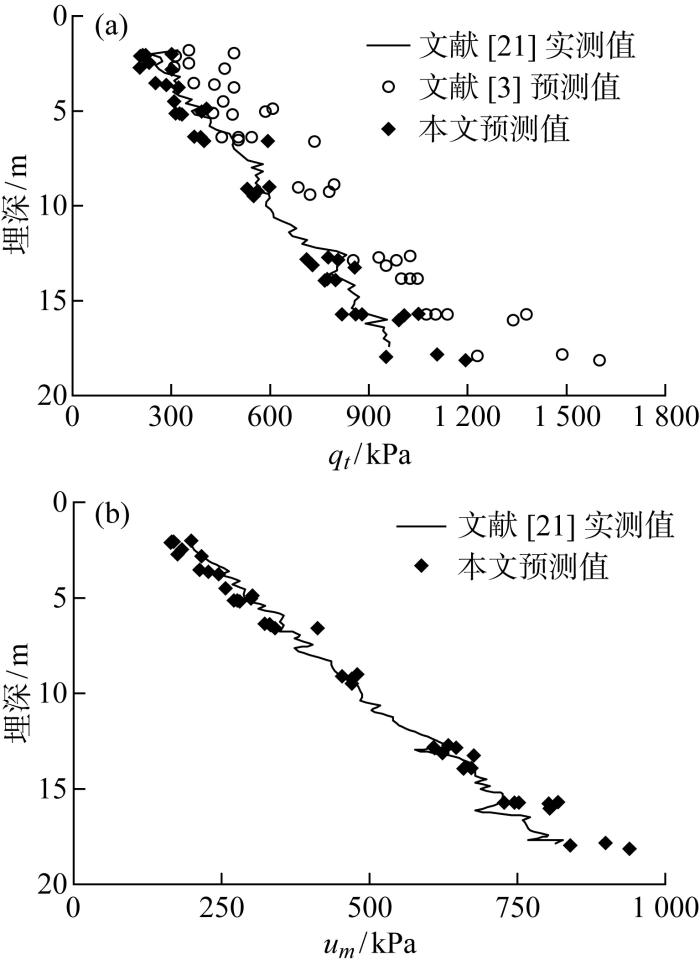
Bothkennar软黏土计算参数^[21]包括ϕ'=34°,M^*=1.37,超固结比OCR为1.4~3.5,σ'_v₀=23.2~124.3 kPa,G₀=2 621.3~8 666.2 kPa,考虑到泊松比对计算结果影响较小,结合黏土性质,此处假定ν^*=0.3,又因Bothkennar黏土结构性不明显^[3,21],故计算过程中结构性参数R_s取1.将利用本文方法确定的极限扩孔应力和超孔隙水压力代入式(39)和式(40),得到CPT锥端贯入阻力q_t和锥尖孔隙水压力u_m,如图9所示.与Chang等^[3]预测的q_t进行对比,本文预测值更接近实测值;由于Chang等^[3]假定塑性区的剪切模量G为常数而非p'的函数(见式(17)),且将塑性区的最终偏应力q近似地看作峰值偏应力q_u,使得预测的q_t偏大.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 Bothkennar黏土中CPT锥端阻力与孔隙水压力预测

Fig.9 Prediction of cone resistance and pore pressure in Bothkennar clay

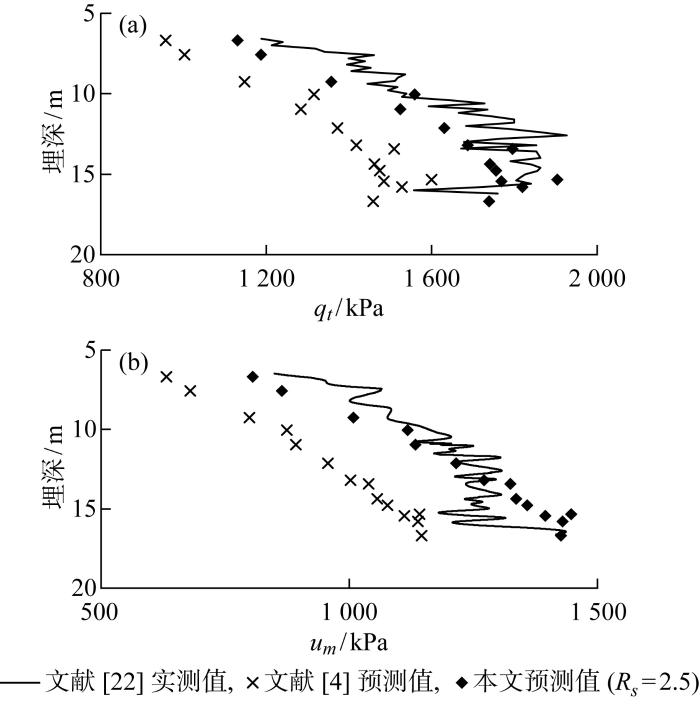
Ottawa黏土是一种具有强结构性的高灵敏性黏土,其基本计算参数^[3,22]为ϕ'=27°,ν^*=0.3,M^*=1.07,OCR为2.2~4.1,σ'_v₀=71.5~165.5 kPa,G₀=17 931.3~23 783.0 kPa.Zhang等^[4]基于球孔扩张理论,对该黏土中CPT锥端贯入阻力和孔隙水压力进行了预测,但该解答中没有考虑土体结构性,使预测值远低于实测值.为此,基于结构性中球孔扩张解答对Ottawa黏土中CPT结果进行预测,由于缺少该黏土结构性相关参数,计算时仍取表1中的b、c、$\tilde{w} $和γ值,并假定R_s=2.5,在考虑黏土结构性影响的情况下,能够得到与实测值较为接近的预测结果,如图10所示.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 Ottawa黏土中CPT锥端阻力与孔隙水压力预测

Fig.10 Prediction of cone resistance and pore pressure in Ottawa clay

6 结论

基于SCC模型和塑性区大变形理论,推导结构性黏土中的球孔扩张不排水精确解,并将该解答在CPT原位测试结果预测中进行应用,得出以下主要结论:

(1) 与重塑土相比,结构性土中由扩孔引起的塑性区和临界状态区范围减小,结构性越强,该趋势表现越明显.

(2) 随着土体结构性增强,总扩孔应力和超孔隙水压力增大,有效扩孔应力先增大后减小至稳定值,说明结构性土在扩孔过程中由于土体结构破坏而表现出应变软化特征.

(3) 从球孔周围土体的应力分布和应力路径可知,重塑土在塑性区仅表现出应变硬化特征;结构性较弱的土一般表现为先硬化后因结构破坏出现一定的软化现象;结构性较强的土体则由于结构破坏直接表现出显著的应变软化特征.结构性土的最终应力状态与重塑土达到一致,说明土体结构在扩孔扰动过程中发生完全破坏.

(4) 将本文解答应用在不同结构性土CPT结果中,发现基于本文球孔扩张解能够较好地预测锥端贯入阻力和孔隙水压力,若不考虑土体结构性时会造成明显低估.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

P Q

, YU

H S

Undrained cavity expansion analysis with a unified state parameter model for clay and sand

[J]. Géotechnique, 2017, 67(6): 503-515.

DOI:10.1680/jgeot.15.P.261 URL [本文引用: 1]

This paper presents a new analytical solution for undrained expansion of spherical and cylindrical cavities in soils with a unified state parameter model for clay and sand (CASM). Large strain and effective stress solutions are derived for soils in the elastic, plastic and critical-state regions. The key advantage of using the state parameter model CASM is that it can model both clay and sand and is generally able to capture overall soil behaviour as observed in the laboratory. The newly developed solution provides the stress and strain fields during the expansion of a cavity from an initial to a final radius. Following the validation with the original Cam Clay solution, a simple parametric study is conducted to investigate the effects of key model parameters on stress distributions and cavity expansion curves. Applications to the analysis of pile installation and self-boring pressuremeter tests highlight some important implications in geotechnical practice.

[2]

H S

, MITCHELL

J K

Analysis of cone resis-tance: Review of methods

[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(2): 140-149.

DOI:10.1061/(ASCE)1090-0241(1998)124:2(140) URL [本文引用: 4]

[3]

CHANG

M F

, TEH

C I

, CAO

L F

Undrained cavity expansion in modified cam clay II: Application to the interpretation of the piezocone test

[J]. Géotechnique, 2001, 51(4): 335-350.

DOI:10.1680/geot.2001.51.4.335 URL [本文引用: 8]

This paper presents an interpretation of the piezocone test in clay based on a simplified theoretical solution of cavity expansion in modified Cam clay. The cone resistance and the pore pressures measured on the cone tip and just behind the cone tip are interpreted using the framework of cavity expansion theories with due consideration of the effect of strain rate and the initial stress state. Methods for estimating the overconsolidation ratio, the undrained shear strength and the rigidity index of clay are proposed. A comparison of results obtained from the proposed methods with published data and limited field data collected in the Singapore marine clay indicates the validity of the proposed analysis methods.

[4]

ZHANG

Y G

, LI

J P

, LIANG

F Y

et al.

Interpretation of cone resistance and pore-water pressure in clay with a modified spherical cavity expansion solution

[J]. Bulletin of Engineering Geology and the Environment, 2016, 75(1): 391-399.

DOI:10.1007/s10064-015-0732-y URL [本文引用: 7]

[5]

RAO

P P

, CHEN

Q S

, LI

et al.

Elastoplastic solution for spherical cavity expansion in modified cam-clay soil under drained condition

[J]. International Journal of Geomechanics, 2017, 17(8): 06017005.

DOI:10.1061/(ASCE)GM.1943-5622.0000925 URL [本文引用: 2]

[6]

邱敏, 袁青, 李长俊,

等.

基于孔穴扩张理论的黏土不排水抗剪强度计算方法对比研究

[J]. 岩土力学, 2019, 40(3): 1059-1066.

[本文引用: 1]

QIU

Min

, YUAN

Qing

, LI

Changjun

et al.

Comparative study of calculation methods for undrained shear strength of clay based on cavity expansion theory

[J]. Rock and Soil Mechanics, 2019, 40(3): 1059-1066.

[本文引用: 1]

[7]

ZHOU

, LI

J P

, LI

et al.

Analysis of the existing pile response induced by adjacent pile driving in undrained clay

[J]. Computers and Geotechnics, 2021, 138: 104319.

DOI:10.1016/j.compgeo.2021.104319 URL [本文引用: 1]

[8]

李镜培, 徐子涵.

长期受荷桩极限承载力的预测

[J]. 上海交通大学学报, 2021, 55(4): 380-386.

[本文引用: 1]

Jingpei

, XU

Zihan

Prediction of ultimate bearing capacity of long-term loaded piles

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(4): 380-386.

[本文引用: 1]

[9]

CHEN

S L

, ABOUSLEIMAN

Y N

Exact undrained elasto-plastic solution for cylindrical cavity expansion in modified cam clay soil

[J]. Géotechnique, 2012, 62(5): 447-456.

DOI:10.1680/geot.11.P.027 URL [本文引用: 8]

This paper presents an exact semi-analytical analysis for cylindrical cavity expansion in modified Cam Clay critical state soil under the undrained condition. By assuming small-strain deformation in the elastic region and large-strain deformation in the plastic region, the formulation of the problem is reduced to solving a system of first-order ordinary differential equations for the radial, tangential and vertical effective stresses in the plastic zone. The pore pressure distribution can subsequently be determined from the radial equilibrium equation in terms of the total stresses. The semi-analytical solution derived in this paper follows the rigorous definitions for the two effective stress invariants instead of approximate ones, as usually assumed in the existing literature, and applies to the more general case where the out-of-plane (vertical) in situ stress may be different from the in-plane (horizontal) one. The results show clearly that the stress history (overconsolidation ratio) has a significant influence on the stress and pore pressure distributions around the cavity. The present solution provides an exact and realistic theoretical framework for predicting the soil behaviour around the cylindrical cavity, with applications to the interpretation of pressuremeter tests and to pile installation problems. It also serves as a valuable benchmark for verifying various cavity expansion numerical methods involving the critical state plasticity model.

[10]

CHEN

H H

, LI

J P

et al.

An elastoplastic solution for spherical cavity undrained expansion in overconsolidated soils

[J]. Computers and Geotechnics, 2020, 126: 103759.

DOI:10.1016/j.compgeo.2020.103759 URL [本文引用: 1]

[11]

HUANG

M S

, TONG

S J

, SHI

Z H

Solution for spherical cavity expansion in state-dependent soils

[J]. Acta Geotechnica, 2021, 16(6): 1773-1788.

DOI:10.1007/s11440-020-01096-3 [本文引用: 1]

[12]

CHEN

S L

, LIU

Undrained cylindrical cavity expansion in anisotropic critical state soils

[J]. Géotechnique, 2019, 69(3): 189-202.

DOI:10.1680/jgeot.16.P.335 URL [本文引用: 1]

This paper develops a rigorous semi-analytical approach for the undrained cylindrical cavity expansion problem using an anisotropic critical state clay plasticity model. The model, originally proposed by Y. F. Dafalias in 1987, is capable of capturing the inherent anisotropy of the soil due to its initial K0 consolidation history, as well as the subsequent stress-induced anisotropy, through the proper incorporation of the rotation and/or distortion of the ellipsoidal yield surface. It is found that the cavity expansion boundary value problem can be eventually reduced to solving a system of six first-order ordinary differential equations in the plastic zone, with the radial, tangential and vertical stresses in association with the three anisotropic variables controlling the yield surface evolution being the basic unknowns. The pore water pressure can be subsequently deduced from the radial equilibrium equation. Extensive parametric studies have been made of the effects of K0 consolidation anisotropy (including also the subsequent stress-induced anisotropy) and past consolidation history (overconsolidation ratio) on the calculated distributions of stress components and excess pore pressure, the progressive development of the stress-induced anisotropy, and on the effective stress trajectory for a soil particle at the cavity surface due to the cavity expansion. The present solution on account of the natural and induced anisotropy is expected to be able to provide more realistic analyses for a variety of geotechnical problems such as the pile installation prediction and interpretation of pressuremeter tests. It can also serve as a benchmark for the finite-element numerical modelling of the cavity expansion problem involving the advanced anisotropic critical state plasticity models.

[13]

SIVASITHAMPARAM

, CASTRO

Undrained expansion of a cylindrical cavity in clays with fabric anisotropy: Theoretical solution

[J]. Acta Geotechnica, 2018, 13(3): 729-746.

DOI:10.1007/s11440-017-0587-4 URL [本文引用: 2]

[14]

梁发云, 陈龙珠.

应变软化Tresca材料中扩孔问题解答及其应用

[J]. 岩土力学, 2004, 25(2): 261-265.

[本文引用: 1]

LIANG

Fayun

, CHEN

Longzhu

Analytical solution to cavity expansion in strain-softening soils with Tesca yield criterion and its applications

[J]. Rock and Soil Mechanics, 2004, 25(2): 261-265.

[本文引用: 1]

[15]

沈珠江.

土体结构性的数学模型: 21世纪土力学的核心问题

[J]. 岩土工程学报, 1996, 18(1): 95-97.

[本文引用: 1]

SHEN

Zhujiang

The mathematic model of structural soils: A key problem of soil mechanics in 21th century

[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(1): 95-97.

[本文引用: 1]

[16]

刘维正, 石名磊, 徐林荣.

考虑软黏土结构性损伤的圆柱孔扩张弹塑性分析

[J]. 岩土工程学报, 2013, 35(3): 487-494.

[本文引用: 1]

LIU

Weizheng

, SHI

Minglei

, XU

Linrong

Elastoplastic analysis of cylindrical cavity expansion in natural sedimentary soft clay with structure damage

[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(3): 487-494.

[本文引用: 1]

[17]

SIVASITHAMPARAM

, CASTRO

Undrained cylindrical cavity expansion in clays with fabric anisotropy and structure: Theoretical solution

[J]. Computers and Geotechnics, 2020, 120: 103386.

DOI:10.1016/j.compgeo.2019.103386 URL [本文引用: 1]

[18]

李镜培, 周攀, 李亮,

等.

饱和结构性黄土不排水柱孔扩张问题弹塑性解

[J]. 同济大学学报(自然科学版), 2021, 49(2): 163-172.

[本文引用: 1]

Jingpei

, ZHOU

Pan

, LI

Liang

et al.

Elastic-plastic solution for undrained expansion of cylindrical cavity in saturated structured loess

[J]. Journal of Tongji University (Natural Science), 2021, 49(2): 163-172.

[本文引用: 1]

[19]

周攀, 李镜培, 李亮,

等.

结构性黄土排水柱孔扩张问题弹塑性解析

[J]. 岩石力学与工程学报, 2021, 40(1): 175-186.

[本文引用: 1]

ZHOU

Pan

, LI

Jingpei

, LI

Liang

et al.

Elastic-plastic solution for drained cylindrical cavity expansion in structured loess

[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(1): 175-186.

[本文引用: 1]

[20]

CARTER

J P

, LIU

M D

Review of the structured cam clay model

[C]//Geo-Frontiers Congress 2005. Reston, VA, USA: American Society of Civil Engineers, 2005: 99-132.

[本文引用: 4]

[21]

HIGHT

D W

, BOND

A J

, LEGGE

J D

Characterization of the bothkennar clay: An overview

[J]. Géotechnique, 1992, 42(2): 303-347.

DOI:10.1680/geot.1992.42.2.303 URL [本文引用: 2]

Following the purchase by the Science and Engineering Research Council of a soft clay test site at Bothkennar in Scotland, work has been carried out to provide data characterizing the clay for the benefit of future research projects. State of the art methods were used to enhance the research value of the characterization project. Fieldwork in 1989 involved high quality sampling using equipment from Laval and Sherbrooke Universities in Canada, and a 100 mm fixed piston sampler operated by the Building Research Establishment. In situ testing to augment earlier work at the site included in situ permeability, hydraulic fracture and field vane tests. Laboratory testing was undertaken by seven institutions in the UK and by Laval University. It involved the measurement of permeability and its variation with void ratio and flow direction, the measurement of yield and compressibility characteristics in oedometer tests, the measurement of stress-strain-strength and yield characteristics using triaxial and simple shear tests and the investigation of progressive destructuring of the clay using triaxial strain path tests. Using the results from this and earlier work, the Paper gives an overview of the ground conditions and the behaviour of the clay. The study also yielded information on the techniques of sampling and testing appropriate to soft naturally structured soils.

[22]

KONRAD

J M

, LAW

K T

Preconsolidation pressure from piezocone tests in marine clays

[J]. Géotechnique, 1987, 37(2): 177-190.

DOI:10.1680/geot.1987.37.2.177 URL [本文引用: 1]

Piezocone penetration tests were carried out at five sites in marine clay with overconsolidation ratios ranging from 1·3 to 4·8 A simple model for the behaviour of these clays indicates that the effective vertical yield stress mobilized along the cone axis during penetration is equal to the difference between the actual induced total vertical stress in the soil and the total porewater pressure. The actual induced total vertical stress can he derived from piezocone test data. Theoretically the ratio of the vertical yield stress inferred from piezocone results and the preconsolidation pressure should correlate with the overconsolidation ratio. This hypothesis is supported by the field and laboratory investigations presented in this study.

Undrained cavity expansion analysis with a unified state parameter model for clay and sand

2017

... 静力触探(CPT)锥尖或桩端贯入挤土过程与土体中球形孔的扩张相似,桩身挤土与旁压试验则与圆柱孔扩张类似,因此圆孔(包括球形孔和圆柱孔)扩张理论被广泛用于CPT贯入及沉桩挤土等工程问题的分析预测中^[1-2].Yu等^[2]对比几种CPT的分析理论后指出,圆孔扩张理论能够充分考虑土体应力状态、应力历史及应力-应变本构关系,因而比基于刚性体假定的极限承载力理论和基于理想塑性假定的应变路径法具有更好的适用性.这一研究促进了扩孔理论在工程贯入问题中的应用,包括用于预测CPT锥尖阻力、孔隙水压力^[3⇓-5]、基于CPT测试结果反演土体参数以及计算沉桩挤土位移和预测桩基承载力等^[6⇓-8],同时实际工程的复杂性也促使该理论不断发展完善. ...

Analysis of cone resis-tance: Review of methods

1998

... [2]对比几种CPT的分析理论后指出,圆孔扩张理论能够充分考虑土体应力状态、应力历史及应力-应变本构关系,因而比基于刚性体假定的极限承载力理论和基于理想塑性假定的应变路径法具有更好的适用性.这一研究促进了扩孔理论在工程贯入问题中的应用,包括用于预测CPT锥尖阻力、孔隙水压力^[3⇓-5]、基于CPT测试结果反演土体参数以及计算沉桩挤土位移和预测桩基承载力等^[6⇓-8],同时实际工程的复杂性也促使该理论不断发展完善. ...

... 早期研究中通常假定土体为理想弹塑性体,基于摩尔-库仑(M-C)屈服准则推导球孔扩张解答,分析扩孔过程中土体的塑性变形和屈服特性^[2],但受理想弹塑性模型限制,该解答无法考虑土体应力历史的影响.随着土体本构关系的发展,土体应力历史和应力水平的临界状态模型逐渐被引入到圆孔扩张问题中^[9],例如Chen等^[10]基于统一硬化模型(UH)模拟了球孔扩张过程中超固结土体应变软化特性;Huang等^[11]基于无黏性土中的临界状态模型,分析了球孔扩张过程中土体的剪胀特性对扩孔压力等的影响,并将解答结果在砂土CPT试验中进行了应用;近年来,Chen等^[12]及Sivasithamparam等^[13]分别基于Dafalias及S-CLAY1各向异性本构模型,推导了圆柱孔扩张的不排水解答,以适用于具有各向异性的天然土体. ...

... 球孔扩张理论在CPT试验结果分析方面具有广泛应用^[2⇓-4].将锥头挤土时受到的正应力σ_n看作球形孔的极限扩张应力σ_u,将剪应力τ看作锥面与土的摩阻力,模型如图8所示. ...

Undrained cavity expansion in modified cam clay II: Application to the interpretation of the piezocone test

2001

... 通过结构性不明显的Bothkennar黏土和具有较强结构性的Ottawa黏土的CPT结果^[3]验证本研究解答的适用性.CPT锥头的锥角为2α=60°,锥面与土摩擦系数α_c=1,在三向压缩条件下(如土体中球孔扩张过程),天然黏土的塑性应变率Λ=0.75^[3-4].另外,注意到参数e₀、λ^*和κ^*的值未给出,需通过文献[4]中参数转换方法将含有该参数的式(7)、式(10)、式(12)和式(14)转化为已有参数表达式. ...

... [3-4].另外,注意到参数e₀、λ^*和κ^*的值未给出,需通过文献[4]中参数转换方法将含有该参数的式(7)、式(10)、式(12)和式(14)转化为已有参数表达式. ...

... Bothkennar软黏土计算参数^[21]包括ϕ'=34°,M^*=1.37,超固结比OCR为1.4~3.5,σ'_v₀=23.2~124.3 kPa,G₀=2 621.3~8 666.2 kPa,考虑到泊松比对计算结果影响较小,结合黏土性质,此处假定ν^*=0.3,又因Bothkennar黏土结构性不明显^[3,21],故计算过程中结构性参数R_s取1.将利用本文方法确定的极限扩孔应力和超孔隙水压力代入式(39)和式(40),得到CPT锥端贯入阻力q_t和锥尖孔隙水压力u_m,如图9所示.与Chang等^[3]预测的q_t进行对比,本文预测值更接近实测值;由于Chang等^[3]假定塑性区的剪切模量G为常数而非p'的函数(见式(17)),且将塑性区的最终偏应力q近似地看作峰值偏应力q_u,使得预测的q_t偏大. ...

... [3]预测的q_t进行对比,本文预测值更接近实测值;由于Chang等^[3]假定塑性区的剪切模量G为常数而非p'的函数(见式(17)),且将塑性区的最终偏应力q近似地看作峰值偏应力q_u,使得预测的q_t偏大. ...

... [3]假定塑性区的剪切模量G为常数而非p'的函数(见式(17)),且将塑性区的最终偏应力q近似地看作峰值偏应力q_u,使得预测的q_t偏大. ...

... Ottawa黏土是一种具有强结构性的高灵敏性黏土,其基本计算参数^[3,22]为ϕ'=27°,ν^*=0.3,M^*=1.07,OCR为2.2~4.1,σ'_v₀=71.5~165.5 kPa,G₀=17 931.3~23 783.0 kPa.Zhang等^[4]基于球孔扩张理论,对该黏土中CPT锥端贯入阻力和孔隙水压力进行了预测,但该解答中没有考虑土体结构性,使预测值远低于实测值.为此,基于结构性中球孔扩张解答对Ottawa黏土中CPT结果进行预测,由于缺少该黏土结构性相关参数,计算时仍取表1中的b、c、

$\tilde{w} $

和γ值,并假定R_s=2.5,在考虑黏土结构性影响的情况下,能够得到与实测值较为接近的预测结果,如图10所示. ...

Interpretation of cone resistance and pore-water pressure in clay with a modified spherical cavity expansion solution

2016

... 由锥头受力平衡可得静力触探锥尖阻力^[4]: ...

... 式中:Δu_o为八面体正应力引起的超孔压,即图4(b)中孔壁处的超孔压Δu_a;Δu_s为剪应力引起的超孔压,可近似于$2s’_{v0}$^[4];u₀为初始孔压.CPT试验中无预钻孔,故在计算扩孔应力和超孔压时初始孔径a₀为0. ...

... 的值未给出,需通过文献[4]中参数转换方法将含有该参数的式(7)、式(10)、式(12)和式(14)转化为已有参数表达式. ...

$\tilde{w} $

和γ值,并假定R_s=2.5,在考虑黏土结构性影响的情况下,能够得到与实测值较为接近的预测结果,如图10所示. ...

Elastoplastic solution for spherical cavity expansion in modified cam-clay soil under drained condition

2017

... 为探究土体结构性对不排水扩孔应力、孔周应力分布和应力路径的影响,考虑R_s=1,1.2,1.5三种黏土结构性强弱,分别求解了正常、轻超和重超固结黏土(R=1,3,10)中的球孔扩张问题.波士顿黏土(BBC)被广泛用于圆孔扩张理论的分析中^[5,9],为了便于比较,采用文献[9]中BBC黏土的基本物性参数 M^*、λ^*、κ^*、ν^*和初始应力状态参数R、σ'₀、e₀、G₀作为计算参数,结合相对应结构性相关模型参数b、c、

$\tilde{w} $

和γ在SCC本构模型中的含义以及BBC黏土的性质,根据Carter等^[20]参数确定方法,对结构性参数进行取值,如表1和表2所示.当R_s=1时,表示重塑土与结构性土具有相同的应力状态. ...

基于孔穴扩张理论的黏土不排水抗剪强度计算方法对比研究

2019

基于孔穴扩张理论的黏土不排水抗剪强度计算方法对比研究

2019

Analysis of the existing pile response induced by adjacent pile driving in undrained clay

2021

长期受荷桩极限承载力的预测

2021

长期受荷桩极限承载力的预测

2021

Exact undrained elasto-plastic solution for cylindrical cavity expansion in modified cam clay soil

2012

... 式中:d

e_{r}^{e}

、d

ε_{θ}^{e}

和d

ε_{φ}^{e}

分别为径向、切向和环向的弹性应变增量;ν^*为泊松比;弹性模量E=2G(1+ν^*),其中剪切模量是平均有效应力p'和孔隙比e的函数^[9],为 ...

... 式中:R=

p_{s 0}^{' *}

/p'₀,为各向同性超固结比^[9];结构应力比R_s=p'_s₀/

p_{s 0}^{' *}

,用于反映黏土结构性强弱,其中p'_s₀和

p_{s 0}^{' *}

分别为结构性土和所对应的重塑土的初始屈服应力,如图3所示,

q_{p}^{*}

为重塑土中孔周弹塑性边界上的偏应力. ...

$\tilde{w} $

... ,为了便于比较,采用文献[9]中BBC黏土的基本物性参数 M^*、λ^*、κ^*、ν^*和初始应力状态参数R、σ'₀、e₀、G₀作为计算参数,结合相对应结构性相关模型参数b、c、

$\tilde{w} $

... BBC黏土的初始状态参数^[9] ...

... Initial state parameters of BBC clay^[9] ...

... 注:初始孔隙水压力u₀=100 kPa^[9]. ...

An elastoplastic solution for spherical cavity undrained expansion in overconsolidated soils

2020

Solution for spherical cavity expansion in state-dependent soils

2021

Undrained cylindrical cavity expansion in anisotropic critical state soils

2019

Undrained expansion of a cylindrical cavity in clays with fabric anisotropy: Theoretical solution

2018

... 天然沉积的土体除了上述性质外,往往还具有明显的结构性,因此结构性土中的圆孔扩张问题研究逐渐受到了学者们的重视^[14].沈珠江^[15]曾指出土的结构性数学模型已成为21世纪土力学研究的核心问题;刘维正等^[16]考虑施工因素对软黏土结构性的扰动求解了圆柱孔扩张问题,但该解答通过构造扰动函数描述土体的结构性损伤机理,而非采用考虑土体结构性的力学模型;Sivasithamparam等^[17]基于S-CLAY1S模型,将考虑天然黏土各向异性扩孔解^[13]拓展至能同时考虑土体结构性的扩孔解答,但所采用本构模型的复杂性使得计算过程中需确定的模型参数过多,不便于进行工程应用;李镜培等^[18]和周攀等^[19]基于已有结构性土的本构模型,采用相关联流动法则分别对土体中不排水和排水柱孔扩张机理进行分析,但这些解答仅能反映土体初始结构性的影响,无法考虑扩孔过程中圆柱孔周围土体结构性损伤的影响. ...

应变软化Tresca材料中扩孔问题解答及其应用

2004

应变软化Tresca材料中扩孔问题解答及其应用

2004

土体结构性的数学模型: 21世纪土力学的核心问题

1996

土体结构性的数学模型: 21世纪土力学的核心问题

1996

考虑软黏土结构性损伤的圆柱孔扩张弹塑性分析

2013

考虑软黏土结构性损伤的圆柱孔扩张弹塑性分析

2013

Undrained cylindrical cavity expansion in clays with fabric anisotropy and structure: Theoretical solution

2020

饱和结构性黄土不排水柱孔扩张问题弹塑性解

2021

饱和结构性黄土不排水柱孔扩张问题弹塑性解

2021

结构性黄土排水柱孔扩张问题弹塑性解析

2021

结构性黄土排水柱孔扩张问题弹塑性解析

2021

Review of the structured cam clay model

2005

... 目前结构性土中的扩孔解答多为圆柱孔扩张解答,而锥尖或桩端的挤土过程往往被等效成周围土体球形孔扩张的过程,这些柱形孔扩张的解答难以在CPT和沉桩等贯入问题中直接应用.对此,本研究基于Carter等^[20]提出的结构性黏土剑桥(SCC)模型,推导了结构性黏土中的不排水球孔扩张解答,该解答能够充分考虑土体结构性、应力历史等对球孔周围土体应力大小及分布的影响,也能反映球孔扩张过程中土体发生的结构性损伤及相应的应变软化行为.此外,解答用于预测CPT锥端贯入阻力和孔隙水压力,通过与实测值对比,表明该解答在天然结构性黏土的工程贯入问题中具有更好的适用性. ...

... 式中:b为反映结构损伤速率的模型常数.Carter等^[20]基于式(4)得到了结构性土在任意应力路径下的广义压缩曲线,表达式为 ...

... 对于结构性较强的土,当应力状态到达CSL线时土体结构可能未完全破坏,即η=M^*且Δe≠0,可得p'_e≠p'_s,由式(9)和(11)也可知d

ε_{d}^{p}

→∞不成立,说明土体未进入临界状态.Carter等^[20]分析不排水剪切试验结果发现,在该情况下继续加载,应力路径在p'-q平面内沿CSL线下滑(dq=M^*dp'<0)直至Δe=0.由于不排水条件下体应变增量dε_v=0,此时塑性应变增量为 ...

$\tilde{w} $

Characterization of the bothkennar clay: An overview

1992

... ,21],故计算过程中结构性参数R_s取1.将利用本文方法确定的极限扩孔应力和超孔隙水压力代入式(39)和式(40),得到CPT锥端贯入阻力q_t和锥尖孔隙水压力u_m,如图9所示.与Chang等^[3]预测的q_t进行对比,本文预测值更接近实测值;由于Chang等^[3]假定塑性区的剪切模量G为常数而非p'的函数(见式(17)),且将塑性区的最终偏应力q近似地看作峰值偏应力q_u,使得预测的q_t偏大. ...

Preconsolidation pressure from piezocone tests in marine clays

1987

$\tilde{w} $

和γ值,并假定R_s=2.5,在考虑黏土结构性影响的情况下,能够得到与实测值较为接近的预测结果,如图10所示. ...

〈

〉