周期DoS攻击下变周期切换正系统的安全控制

doi:10.16183/j.cnki.jsjtu.2021.445

周期DoS攻击下变周期切换正系统的安全控制

刘教^,, 孔祥娜, 张甜甜

河北工业大学人工智能与数据科学学院,天津 300401

Secure Control for Variable Periodic Switched Positive Systems Under Periodic DoS Attack

LIU Jiao^,, KONG Xiangna, ZHANG Tiantian

School of Artificial Intelligence, Hebei University of Technology, Tianjin 300401, China

责任编辑: 李博文

收稿日期: 2021-11-8 修回日期: 2022-12-29 接受日期: 2022-01-11

基金资助:

国家自然科学基金(62103129)

Received: 2021-11-8 Revised: 2022-12-29 Accepted: 2022-01-11

作者简介 About authors

刘教(1987-),讲师,现主要从事复杂系统控制、安全控制的研究,电话(Tel.):022-60203069;E-mail:jiaoliu@hebut.edu.cn.

摘要

周期拒绝服务(DoS)攻击阻止了切换正系统的测量通道与控制通道通过网络进行信息交换.此外,系统切换行为、DoS攻击引起的混杂行为以及正性约束增加了安全控制研究的困难.针对遭受周期DoS攻击的网络化切换正系统,提出一种基于切换行为的建模方法并研究其安全控制问题.在变周期切换条件下,通过限定切换周期与DoS攻击周期的关系,构造多线性余正Lyapunov函数,并得到闭环系统为正系统以及渐近稳定条件,进而基于正系统理论设计安全状态反馈控制器.在此基础上,讨论周期DoS攻击下系统进行恒定周期切换的情形.最后,通过仿真示例验证结果的有效性.

关键词： 切换正系统; 周期拒绝服务攻击; 多线性余正Lyapunov函数; 安全控制

Abstract

Periodic denial-of-service (DoS) attack prevents the information exchange of measurement channel and control channel for switched positive systems through the network. Moreover, the coupling of system switching behavior and hybrid behavior due to DoS attack and positive constraint also increase the difficulty in secure control research. The secure control problem of networked switched positive systems under periodic DoS attack is studied and a modeling method based on switching behavior is proposed in this paper. Under variable periodic switching, the multiple linear copositive Lyapunov function is constructed to obtain the positive and asymptotically stable condition for the closed-loop system by limiting the relationship between the switching period and the DoS attack period, and a secure state feedback controller based on the positive system theory is designed, based on which, the constant periodic switching case is also discussed by using the positive system theory. Finally, the validity of the results is verified by a simulation example.

Keywords： switched positive systems; periodic denial-of-service (DoS) attack; multiple linear copositive Lyapunov function; secure control

PDF (689KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘教, 孔祥娜, 张甜甜. 周期DoS攻击下变周期切换正系统的安全控制[J]. 上海交通大学学报, 2023, 57(5): 624-630 doi:10.16183/j.cnki.jsjtu.2021.445

LIU Jiao, KONG Xiangna, ZHANG Tiantian. Secure Control for Variable Periodic Switched Positive Systems Under Periodic DoS Attack[J]. Journal of Shanghai Jiaotong University, 2023, 57(5): 624-630 doi:10.16183/j.cnki.jsjtu.2021.445

网络化系统通过无线网络传输信息摆脱了地域限制,但无线网络的开放性使得系统完整性以及可用性遭受破坏,导致系统性能降低甚至失去稳定性.从网络系统安全控制的角度来说,网络攻击主要分为两类,一类是拒绝服务(DoS)攻击,另一类是欺骗攻击. DoS攻击旨在阻断网络通信,破坏信息交换.如文献[1]中考虑了攻击者间歇发起DoS攻击以破坏测量通道数据可用性的情况.欺骗攻击则是通过在前向通道或反馈通道注入精心设计的错误数据,以破坏系统状态.如文献[2]中提出将欺骗攻击同时注入传感器到控制器的通道和控制器到执行器的通道来破坏系统完整性,进而探究网络系统的安全问题.相较于欺骗攻击, DoS攻击是众多网络攻击中出现频率最高、危害最大、最易实现的攻击手段^[3-4].因此,近年来这方面研究成果较多^[5-6].

攻击者能量有限造成DoS攻击不能一直发生,因此,能量有限且方便实施的周期DoS攻击引起了学者们的广泛关注.文献[7-8]中研究了周期DoS攻击下网络系统的安全控制问题. 文献[9]中将遭受周期DoS攻击的系统建模为切换系统,利用相对成熟的切换理论^[10-11]研究DoS攻击下系统的安全问题.但是对于遭受DoS攻击的切换系统而言,系统本身的切换特性与DoS攻击引起的切换特性相互耦合,这将导致混杂问题难以处理.针对此问题许多学者进行了研究,文献[12]中提出限制DoS攻击的持续区间以及发生频率,通过构造满足平均驻留时间的切换信号,以稳定遭受DoS攻击的切换系统.文献[13]中采取合适的事件触发机制将 DoS攻击下的网络化切换系统建模为新型切换系统,实现安全控制.

另外,由于实际生活中常存在取值为非负的特殊物理量,例如细菌群落数量、森林覆盖率以及有机物浓度等,将这类物理量作为状态变量可得正系统.与一般系统不同,正系统是指初始状态和系统输入都为非负时,任意时刻的系统状态与输出都能保持非负的动态系统.近年来,描述特定切换法则、掌管模态切换的一类正系统被称为切换正系统,由于该系统具有可靠性强、应用范围广等优点,受到学者们的关注^[14-15],常应用于通信系统^[16]、编队飞行^[17]、流行病学^[18]等不同领域.对于遭受DoS攻击的切换正系统,DoS攻击阻止了测量通道与控制通道之间的信息传递,导致系统稳定性及正性均受影响.同时系统状态的非负特性、子系统之间切换特性及DoS攻击引起的切换特性相互耦合,这更增加了问题解决的难度.因此,在遭受DoS攻击情形下,设计一种安全控制器使得切换正系统依然能够保证其正性及稳定性尤为重要.目前,针对遭受DoS攻击的切换正系统的研究鲜有成果.

基于以上讨论,本文主要研究在周期DoS攻击及变周期切换信号下,网络化切换正系统的安全控制问题.研究过程中面临如下挑战,首先,系统的正性约束使得二次型Lyapunov方法体系中的线性矩阵不等式等理论均不再适用,需要寻找新的研究方法.其次,需要对周期DoS攻击下变周期切换正系统的切换行为进行建模.最后,需要考虑子系统之间切换特性和DoS攻击引起的切换特性相互耦合对安全控制造成的影响.

1 问题描述及预备知识

考虑如下切换系统:

(1)(t)=A_σ₍_t₎x(t)+B_σ₍_t₎u(t)

式中:x(t)∈Rⁿ,u(t)∈R^m分别表示系统状态与控制输入;σ(t): [0,∞)→M={1,2,…,N}为系统切换信号,N表示子系统个数.当第l个子系统被激活时,切换信号σ(t)=l,对应的参数矩阵为A_l∈Rⁿ^×ⁿ, B_l∈Rⁿ^×^m,A_l为Metzler矩阵.

为保证系统(1)的正性及稳定性,设计如下状态反馈控制器:

(2)u(t)=K_σ₍_t₎x(t)

式中:K_σ₍_t₎为待设计状态反馈控制器增益矩阵.

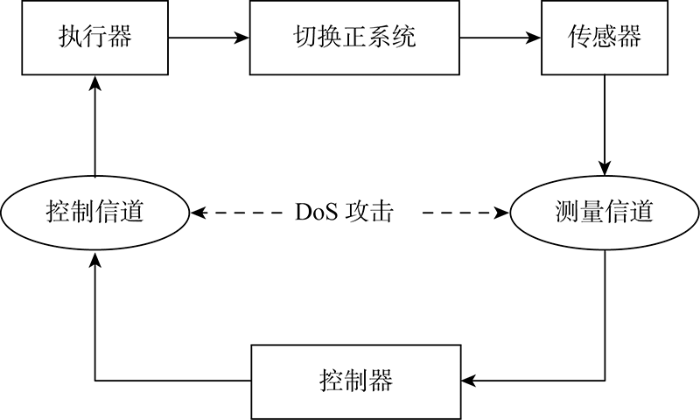
网络化切换正系统的控制信道和测量信道通过开放共享的无线网络传递信息,因此信息在传输过程中易因遭受DoS攻击而无法正常更新.故以切换正系统为研究对象,在传感器到控制器以及控制器到执行器之间的通道通过共享网络传递信息的情况下,设计DoS攻击下网络化切换正系统框架,如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 DoS攻击下网络化切换正系统框架

Fig.1 Architecture of networked switched positive system under DoS attack

假设DoS攻击同时作用于控制信道和测量信道.DoS攻击及切换信号分别满足下列两个假设.

假设1: DoS攻击的周期恒定,一个完整DoS攻击周期固定为T_DoS.

假设2: 切换信号的周期是变化的,第k个切换区间的长度T_k与DoS攻击周期T_DoS关系为T_k=m_kT_DoS, m_k∈{1,2,…,m_max},其中m_k为DoS攻击周期个数.

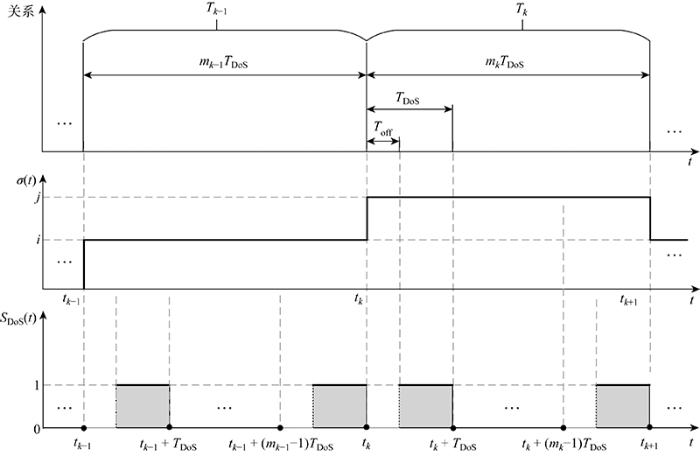
切换正系统遭受周期DoS攻击时,切换信号与DoS攻击信号S_DoS(t)关系如图2所示.其中,序列{t_k_-1,t_k,t_k₊₁,…}表示系统切换时刻.假设在区间[t_k_-1,t_k)内,为第i个子系统运行;在区间[t_k,t_k₊₁)内,为第j个子系统运行,期间有m_k个DoS攻击周期;序列{t_k, t_k+T_DoS, …, t_k+(m_k-1)T_DoS}分别表示DoS攻击周期的起始时刻.每个DoS攻击周期分为长度为T_off的休眠期和长度为T_DoS-T_off的激活期. DoS攻击信号S_DoS(t)满足:

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 切换信号σ(t)与DoS攻击信号S_DoS(t)关系图

Fig.2 Relationship between system switching signal σ(t) and DoS attack signal S_DoS(t)

(3)S_DoS(t)=

\{\begin{array}{l} 1, & t \in [t_{k} + (κ - 1) T_{D o S}, \\ t_{k} + (κ - 1) T_{D o S} + T_{o f f}) \\ 0, & t \in [t_{k} + (κ - 1) T_{D o S} + T_{o f f}, \\ t_{k} + κ T_{D o S}) \end{array}

式中:κ∈{1,2,…,m_k}为DoS攻击周期次序.S_DoS(t)=1表示DoS攻击处于休眠期,此时进行正常通信;S_DoS(t)=0表示DoS攻击处于激活期,此时通信中断.周期DoS攻击下执行器的输出^[19]可表示为

(4)u(t)=

\{\begin{array}{l} K_{σ (t)} x (t), & S_{D o S} (t) = 1 \\ 0, & S_{D o S} (t) = 0 \end{array}

根据式(1)、(3)和(4)可得遭受周期DoS攻击的闭环系统为

(5)

\overset{\cdot}{x}

(t)=

\{\begin{array}{l} A_{σ (t)} x (t) + B_{σ (t)} K_{σ (t)} x (t), \\ t \in [t_{k} + (κ - 1) T_{D o S}, \\ t_{k} + (κ - 1) T_{D o S} + T_{o f f}) \\ A_{σ (t)} x (t), \\ t \in [t_{k} + (κ - 1) T_{D o S} + T_{o f f}, t_{k} + κ T_{D o S}) \end{array}

2 稳定性分析及控制器设计

给出在周期DoS攻击下闭环系统的稳定性条件并设计相应的安全控制器.

定理1 对于系统(5),给定常数α>0,β>0,μ>1,s>0,I表示单位阵.当i,j∈M且i≠j时,若存在向量p_j≻0及矩阵K_j使得当β(T_DoS-T_off)≤αT_off时,式(6)~(10)成立,或者当β(T_DoS-T_off)>αT_off时,式(6)~(9)及(11)成立,则系统(5)是正系统且渐近稳定,其中“≻”或“≺”表示向量中每个元素都有大于或小于关系.

(6)A_j+B_jK_j+sI≻0

(7) (A_j+B_jK_j)^Tp_j+αp_j≺0

(8)p_j-βp_j≺0

(9)p_j≺μp_i

(10)

\begin{array}{l} l n μ + β (T_{D o S} - T_{o f f}) - α T_{o f f} < 0 \\ β (T_{D o S} - T_{o f f}) \leq α T_{o f f} \end{array}\}

(11)

\begin{array}{l} l n μ + m_{m a x} [β (T_{D o S} - T_{o f f}) - α T_{o f f}] < 0 \\ β (T_{D o S} - T_{o f f}) > α T_{o f f} \end{array}\}

证明由式(5)可知,在DoS攻击休眠期有 $\overset{\cdot}{x}$ (t)=(A_σ₍_t₎+B_σ₍_t₎K_σ₍_t₎)x(t).由A_j+B_jK_j为Metzler矩阵得此区间系统为正系统.在DoS攻击激活期有 $\overset{\cdot}{x}$ (t)=A_σ₍_t₎x(t),由A_j为Metzler矩阵得此区间系统为正系统,因此系统(5)是正系统.

为证明系统渐近稳定性,选择如下多线性余正Lyapunov函数:

(12)V_σ₍_t₎(t)=x^T(t)p_σ₍_t₎

当DoS攻击处于休眠期,即t∈[t_k+(κ-1)T_DoS, t_k+(κ-1)T_DoS+T_off)时,沿着系统(5)的轨迹对式(12)求导有

(13)(t)=x^T(t)(A_j+B_jK_j)^Tp_j

因而有

(14) (t)+αV_j(t)=x^T(t)[(A_j+B_jK_j)^Tp_j+αp_j]

由不等式(7)知:

(15)(t)<-αV_j(t)

对不等式(15)在区间[t_k+(κ-1)T_DoS, t_k+(κ-1)T_DoS+T_off)内求积分得到:

(16)V_j[t_k+(κ-1)T_DoS+T_off]<V_j[t_k+(κ-1)T_DoS]

当DoS攻击处于激活期,即t∈[t_k+(κ-1)T_DoS+T_off, t_k+κT_DoS)时,沿着系统(5)的轨迹对式(12)求导可得:

(17)(t)-βV_j(t)=x^T(t)(p_j-βp_j)

由不等式(8)知:

(18)(t)<βV_j(t)

对不等式(18)在区间[t_k+(κ-1)T_DoS+T_off, t_k+κT_DoS)内求积分得:

(19)V_j(t_k+κT_DoS)<V_j[t_k+(κ-1)T_DoS+T_off]

结合不等式(16)和(19),可得整个DoS攻击周期Lyapunov函数的变化关系为

(20)V_j(t_k+κT_DoS)<V_j[t_k+(κ-1)T_DoS]

考虑整个切换区间[t_k,t_k₊₁),该切换区间内含有m_k个DoS攻击周期,可得:

(21)

V_{σ (t_{k})}

(t_k₊₁)<

e^{m_{k} [β (T_{D o S} - T_{o f f}) - α T_{o f f}]} V_{σ (t_{k})}

(t_k)

由式(9)可得切换时刻t_k处Lyapunov函数的变化为

(22)

V_{σ (t_{k + 1})}

(t_k₊₁)≤μ

V_{σ (t_{k})}

(t_k₊₁)

结合式(21)~(22)可得:

(23)

V_{σ (t_{k + 1})}

(t_k₊₁)≤μ

e^{m_{k} [β (T_{D o S} - T_{o f f}) - α T_{o f f}]} V_{σ (t_{k})}

(t_k)

推广到0初始状态,可得:

(24)

V_{σ (t_{k})}

(t_k)≤μ^k

e^{\overset{k - 1}{\sum_{θ = 0}} m_{θ, k} [β (T_{D o S} - T_{o f f}) - α T_{o f f}]}

V_σ₍₀₎(0)

由于系统为变周期切换,第k个切换区间内含有的攻击周期数目m_θ_,_k(θ=0,1,…,k-1)不同,所以需要对式(24)中的 $\overset{k - 1}{\sum_{θ = 0}}$ m_θ_,_k[β(T_DoS-T_off)-αT_off]进行放缩,主要对β(T_DoS-T_off)与αT_off的大小进行讨论:

当β(T_DoS-T_off)≤αT_off时,令η₁=ln μ+β(T_DoS-T_off)-αT_off, 由m_θ_,_k>0及式(10)可得:

(25)

V_{σ (t_{k})}

(t_k)≤

e^{[l n μ + β (T_{D o S} - T_{o f f}) - α T_{o f f}] k}

V_σ₍₀₎(0)=

e^{η_{1} k}

V_σ₍₀₎(0), η ₁<0

当β(T_DoS-T_off)>αT_off时,令η₂=ln μ+m_max[β(T_DoS-T_off)-αT_off],由m_θ_,_k<m_max及式(11)可得:

(26)

V_{σ (t_{k})}

(t_k)≤

e^{{l n μ + m_{m a x} [β (T_{D o S} - T_{o f f}) - α T_{o f f}]} k}

V_σ₍₀₎(0)=

e^{η_{2} k}

V_σ₍₀₎(0), η ₂<0

令η=max{η₁,η₂},有 $V_{σ (t_{k})}$ (t_k)≤e^ηkV_σ₍₀₎且η<0.因为每个DoS攻击周期内Lyapunov函数最大值在攻击结束的时刻得到,所以对于∀t∈[t_k,t_k₊₁)有

(27)

V_{σ (t_{k})}

(t)≤

\underset{κ \in 0,1, \dots, m_{k}}{m a x} e^{κ [β (T_{D o S} - T_{o f f}) - α T_{o f f}]} V_{σ (t_{k})}

(t_k)≤

\underset{κ \in 0,1, \dots, m_{k}}{m a x}

{

e^{[β (T_{D o S} - T_{o f f}) - α T_{o f f}]}

e^{m_{m a x} [β (T_{D o S} - T_{o f f}) - α T_{o f f}]}

}×

V_{σ (t_{k})}

(t_k)

此外,令c= $\underset{κ \in 0,1, \dots, m_{k}}{m a x}$ { $e^{β (T_{D o S} - T_{o f f}) - α T_{o f f}}$ , $e^{m_{m a x} [β (T_{D o S} - T_{o f f}) - α T_{o f f}]}$ },可得:

(28)

V_{σ (t_{k})}

(t)≤c

V_{σ (t_{k})}

(t_k)≤ce^ηkV_σ₍₀₎(0)

由于

(29)V_σ₍₀₎(0)≤ε₁

‖x_{σ (0)} (0)‖

(30)V_σ₍_t₎(t)≤ε₂

‖x_{σ (t)} (t)‖

其中ε₁= $\underset{j \in M}{m a x}$ p_j,ε₂= $\underset{j \in M}{m i n}$ p_j.因此有

(31)

‖x_{σ (t)} (t)‖

≤

\frac{ε_{1}}{ε_{2}}

ce^η⁽^k⁺¹⁾

‖x_{σ (0)} (0)‖

由ce^η⁽^k⁺¹⁾<1可以看出整个系统的能量呈现全局递减的趋势,即系统全局渐近稳定.

定理2 对于系统(5),给定向量 ${\tilde{v}}_{j}$ 和常数α>0,λ>0,μ>1,若存在适当维数矩阵z_j和p_j,使得当β(T_DoS-T_off)>αT_off时,式(8)~(10)及式(31)~(33)成立或者当β(T_DoS-T_off)<αT_off时,式(8)~(9)和(11)及式(31)~(33)成立时,则在控制器即式(34)的作用下,系统(5)是正系统且渐近稳定.

(32)

{\tilde{v}}^{T}_{j} {B^{T}}_{j}

p_jA_j+B_j

{\tilde{v}}_{j} {z^{T}}_{j}

+λI≻0

(33)

{\tilde{v}}^{T}_{j} {B^{T}}_{j}

p_j≻0

(34)

{A^{T}}_{j}

p_j+z_j+αp_j≺0

(35)u(t)=K_jx(t)=

\frac{1}{{\tilde{v}}^{T}_{j} {B^{T}}_{j} p_{j}} {\tilde{v}}_{j} {z^{T}}_{j}

x(t)

证明在式(31)两侧同时除以式(32),可得:

(36)A_j+B_j

\frac{1}{{\tilde{v}}^{T}_{j} {B^{T}}_{j} p_{j}} {\tilde{v}}_{j} {z^{T}}_{j}

\frac{λ}{{\tilde{v}}^{T}_{j} {B^{T}}_{j} p_{j}}

I≻0

令z_j= ${K^{T}}_{j} {B^{T}}_{j}$ p_j,s= $\frac{λ}{{\tilde{v}}^{T}_{j} {B^{T}}_{j} p_{j}}$ ,代入式(35)有

(37)A_j+B_jK_j+sI≻0

另将z_j代入式(33)中,可得:

(38)

{A^{T}}_{j}

p_j+

{K^{T}}_{j} {B^{T}}_{j}

p_j+αp_j≺0

式(37)即转化为式(7),此时结合定理1可得系统(5) 为正系统且渐近稳定.

为求解控制器增益, 设计如下算法.

算法

1. 给定矩阵A_j与B_j,以及参数α,β,μ,T_DoS,T_off的值并设定 ${\tilde{v}}_{j}$ 的值.

2. 通过定理1获得切换正系统稳定性条件.

3. 根据定理1计算出p_j与z_j的数值.

4. 通过定理2设计出状态反馈控制器增益为

K_j= $\frac{1}{{\tilde{v}}^{T}_{j} {B^{T}}_{j} p_{j}} {\tilde{v}}_{j} {z^{T}}_{j}$

推论1 在定理1中,若m_k=κ,则对于式(5)所描述系统,给定常数α>0,β>0,μ>1,s>0,若存在适当维数矩阵p_j>0和控制器增益K_j,常数λ>0和适当维数的矩阵z_j(j∈M),使得式(6)~(9)和式(31)~(33)及下列不等式成立:

(39)ln μ+κ[β(T_DoS-T_off)-αT_off]<0

(40)u(t)=K_jx(t)=

\frac{1}{{\tilde{v}}^{T}_{j} {B^{T}}_{j} p_{j}} {\tilde{v}}_{j} {z^{T}}_{j}

x(t)

则在控制器(39)的作用下,系统(5)为正系统且渐近稳定.

3 仿真实例

考虑连续时间切换正系统(1)中含有如下两个子系统:

A₁= $[\begin{array}{l} - 0.17 & 0.20 \\ 0 & - 0.90 \end{array}]$ , B₁= $[\begin{array}{l} 0.28 & 0.58 \\ 0.30 & 0.11 \end{array}]$

A₂= $[\begin{array}{l} - 0.14 & 0.34 \\ 0.06 & - 0.70 \end{array}]$ , B₂= $[\begin{array}{l} 0.16 & 0.31 \\ 0.69 & 0.35 \end{array}]$

选择DoS攻击信号的攻击周期T_DoS=10 s,休眠期T_off=6 s,给定初始条件x(0)=[1 3]^T.考虑变周期切换,即系统(1)的每个切换区间所受到的攻击次数不同,选择m_max=10, α=0.10, β=0.10, μ=1.20,λ=10.60, ${\tilde{v}}_{1}$ =[0.23 0.19]^T, ${\tilde{v}}_{2}$ =[0.19 0.3]^T.此时满足条件式(10),由此可得控制器增益矩阵:

K₁= $[\begin{array}{l} 0.006 2 & 0.006 2 \\ 0.005 8 & 0.005 8 \end{array}]$

K₂= $[\begin{array}{l} 0.003 5 & 0.003 5 \\ 0.006 9 & 0.006 9 \end{array}]$

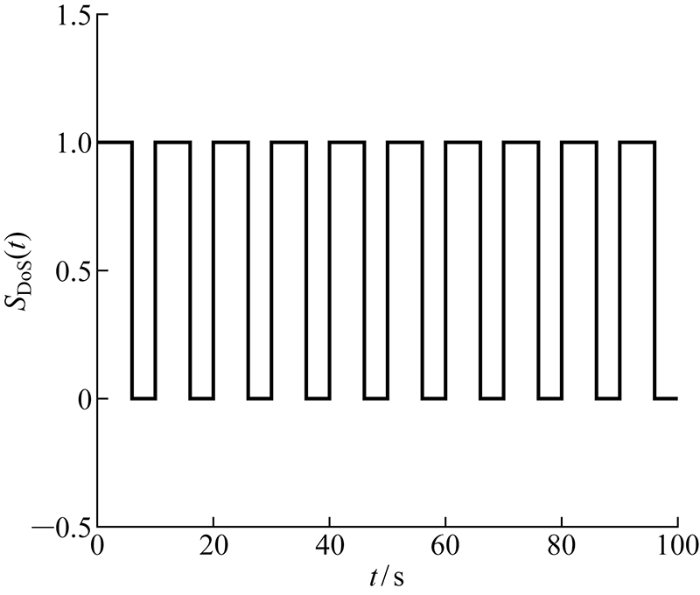
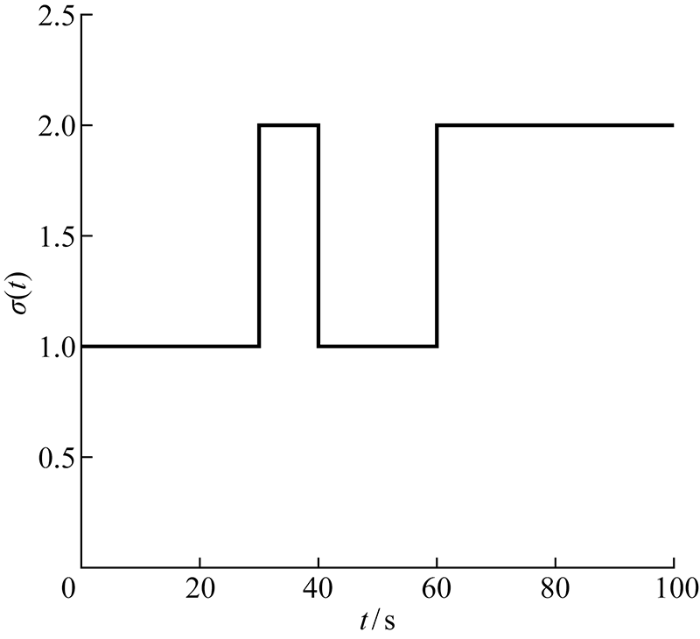
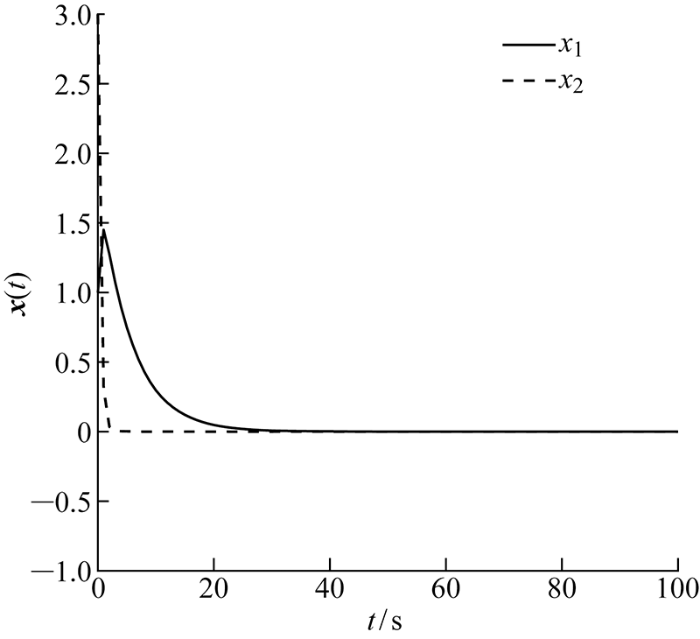
周期DoS攻击信号如图3所示.此外在图4中,系统共有4个切换区间,但每个切换区间的长度不同,每个子系统运行时受到的周期DoS攻击次数不同.系统的状态轨迹曲线如图5所示,即在受到周期DoS攻击情况下,尽管系统为变周期切换,仍可以在控制器的作用下趋于稳定且保持非负状态,验证了定理2的有效性.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 DoS攻击信号

Fig.3 DoS attack signal

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 切换信号

Fig.4 Switching signal

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 系统状态轨迹

Fig.5 System state trajectory

4 结语

切换正系统是控制理论和工程领域研究的热点问题.针对网络化切换正系统的测量信道和控制信道同时存在周期DoS攻击问题,研究了变周期切换的安全控制问题.将攻击时长、攻击次数等相关参数转化为切换区间的长度,得到相应系统数学模型.利用切换方法对周期DoS攻击下的切换正系统进行合理建模,设计出安全控制器保证DoS攻击下系统的正性及稳定性,借助Metzler矩阵和多Lyapunov函数法从攻击周期、切换区间、切换时刻分析了系统的正性和全局渐近稳定性.最后,通过仿真实例验证了安全控制器的有效性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

YAN

J J

, YANG

G H

Switching resilient control scheme for cyber-physical systems against DoS attacks

[J]. Journal of the Franklin Institute, 2021, 358(8): 4257-4276.

DOI:10.1016/j.jfranklin.2021.03.020 URL [本文引用: 1]

[2]

DING

, TANG

, WANG

, et al.

Secure synchronization of complex networks under deception attacks against vulnerable nodes

[J]. Applied Mathematics and Computation, 2021, 399: 126017.

DOI:10.1016/j.amc.2021.126017 URL [本文引用: 1]

[3]

王志文, 刘伟.

拒绝服务攻击下信息物理系统事件触发广义预测控制

[J]. 上海交通大学学报, 2020, 54(9): 910-915.

[本文引用: 1]

WANG

Zhiwen

, LIU

Wei

Event-triggered generalized predictive control of cyber-physical systems under denial-of-service attacks

[J]. Journal of Shanghai Jiao Tong University, 2020, 54(9): 910-915.

[本文引用: 1]

[4]

YANG

, GU

, TIAN

E G

, et al.

Event-based switching control for networked switched systems under nonperiodic DoS jamming attacks

[J]. IET Control Theory & Applications, 2020, 14(19): 3097-3106.

DOI:10.1049/cth2.v14.19 URL [本文引用: 1]

[5]

ZHU

Y Z

, ZHENG

W X

Observer-based control for cyber-physical systems with periodic DoS attacks via a cyclic switching strategy

[J]. IEEE Transactions on Automatic Control, 2020, 65(8): 3714-3721.

DOI:10.1109/TAC.9 URL [本文引用: 1]

[6]

XING

M P

, LU

J Q

, QIU

J L

, et al.

Synchronization of complex dynamical networks subject to DoS attacks: An improved coding-decoding protocol

[J]. IEEE Transactions on Cybernetics, 2023, 53(1): 102-113.

DOI:10.1109/TCYB.2021.3090406 URL [本文引用: 1]

[7]

WANG

P B

, REN

X M

, ZHENG

D D

Event-triggered resilient control for cyber-physical systems under periodic DoS jamming attacks

[J]. Information Sciences, 2021, 577: 541-556.

DOI:10.1016/j.ins.2021.07.002 URL [本文引用: 1]

[8]

, SONG

Y B

Optimal periodic DoS attack with energy harvester in cyber-physical systems

[J]. Neurocomputing, 2020, 390: 69-77.

DOI:10.1016/j.neucom.2020.01.075 URL [本文引用: 1]

[9]

S L

, HAN

Y X

, CHEN

X L

, et al.

Event-triggered H∞ filtering over wireless sensor networks under unknown periodic DoS jamming attacks

[C]// 2018 Chinese Control and Decision Conference. Shenyang, China: IEEE, 2018: 1433-1438.

[本文引用: 1]

[10]

宋秀兰, 俞立.

一类约束线性切换系统的滚动优化控制

[J]. 上海交通大学学报, 2015, 49(11): 1635-1640.

[本文引用: 1]

SONG

Xiulan

, YU

Receding optimization control for a class of constrained linear switched systems

[J]. Journal of Shanghai Jiao Tong University, 2015, 49(11): 1635-1640.

[本文引用: 1]

[11]

REN

H L

, ZONG

G D

, LI

T S

Event-triggered finite-time control for networked switched linear systems with asynchronous switching

[J].

IEEE Transactions on Systems, Man, and

Cybernetics: Systems, 2018, 48(11): 1874-1884.

[本文引用: 1]

[12]

H Q

, ZHAO

Stabilisation of switched linear systems under denial of service

[J]. IET Control Theory & Applications, 2020, 14(11): 1438-1444.

DOI:10.1049/cth2.v14.11 URL [本文引用: 1]

[13]

HAN

Y C

, LIAN

, HUANG

Event-triggered H∞ control of networked switched systems subject to denial-of-service attacks

[J]. Nonlinear Analysis: Hybrid Systems, 2020, 38: 100930.

DOI:10.1016/j.nahs.2020.100930 URL [本文引用: 1]

[14]

LIU

, YANG

Y K

, LI

H C

, et al.

Stabilisation for switched positive systems under extended asynchronous switching

[J]. IET Control Theory & Applications, 2019, 13(16): 2702-2709.

DOI:10.1049/cth2.v13.16 URL [本文引用: 1]

[15]

J J

, LIU

D X

, XIA

D B

, et al.

Robust stabilization of switched positive discrete-time systems with asynchronous switching and input saturation

[J]. Optimal Control Applications and Methods, 2019, 40(1): 105-118.

[本文引用: 1]

[16]

OGURA

, PRECIADO

V M

Stability of spreading processes over time-varying large-scale networks

[J]. IEEE Transactions on Network Science and Engineering, 2016, 3(1): 44-57.

DOI:10.1109/TNSE.2016.2516346 URL [本文引用: 1]

[17]

SON

J H

, AHN

H S

Formation coordination for the propagation of a group of mobile agents via self-mobile localization

[J]. IEEE Systems Journal, 2015, 9(4): 1285-1298.

DOI:10.1109/JSYST.2014.2326795 URL [本文引用: 1]

[18]

RAMI

M A

, TADEO

Controller synthesis for positive linear systems with bounded controls

[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2007, 54(2): 151-155.

[本文引用: 1]

[19]

KUZMANOVIC

, KNIGHTLY

E W

Low-rate TCP-targeted denial of service attacks and counter strategies

[J]. IEEE/ACM Transactions on Networking, 2006, 14(4): 683-696.

DOI:10.1109/TNET.2006.880180 URL [本文引用: 1]

Switching resilient control scheme for cyber-physical systems against DoS attacks

2021

... 网络化系统通过无线网络传输信息摆脱了地域限制,但无线网络的开放性使得系统完整性以及可用性遭受破坏,导致系统性能降低甚至失去稳定性.从网络系统安全控制的角度来说,网络攻击主要分为两类,一类是拒绝服务(DoS)攻击,另一类是欺骗攻击. DoS攻击旨在阻断网络通信,破坏信息交换.如文献[1]中考虑了攻击者间歇发起DoS攻击以破坏测量通道数据可用性的情况.欺骗攻击则是通过在前向通道或反馈通道注入精心设计的错误数据,以破坏系统状态.如文献[2]中提出将欺骗攻击同时注入传感器到控制器的通道和控制器到执行器的通道来破坏系统完整性,进而探究网络系统的安全问题.相较于欺骗攻击, DoS攻击是众多网络攻击中出现频率最高、危害最大、最易实现的攻击手段^[3-4].因此,近年来这方面研究成果较多^[5-6]. ...

Secure synchronization of complex networks under deception attacks against vulnerable nodes

2021

拒绝服务攻击下信息物理系统事件触发广义预测控制

2020

拒绝服务攻击下信息物理系统事件触发广义预测控制

2020

Event-based switching control for networked switched systems under nonperiodic DoS jamming attacks

2020

Observer-based control for cyber-physical systems with periodic DoS attacks via a cyclic switching strategy

2020

Synchronization of complex dynamical networks subject to DoS attacks: An improved coding-decoding protocol

2023

Event-triggered resilient control for cyber-physical systems under periodic DoS jamming attacks

2021

... 攻击者能量有限造成DoS攻击不能一直发生,因此,能量有限且方便实施的周期DoS攻击引起了学者们的广泛关注.文献[7-8]中研究了周期DoS攻击下网络系统的安全控制问题. 文献[9]中将遭受周期DoS攻击的系统建模为切换系统,利用相对成熟的切换理论^[10-11]研究DoS攻击下系统的安全问题.但是对于遭受DoS攻击的切换系统而言,系统本身的切换特性与DoS攻击引起的切换特性相互耦合,这将导致混杂问题难以处理.针对此问题许多学者进行了研究,文献[12]中提出限制DoS攻击的持续区间以及发生频率,通过构造满足平均驻留时间的切换信号,以稳定遭受DoS攻击的切换系统.文献[13]中采取合适的事件触发机制将 DoS攻击下的网络化切换系统建模为新型切换系统,实现安全控制. ...

Optimal periodic DoS attack with energy harvester in cyber-physical systems

2020

Event-triggered H∞ filtering over wireless sensor networks under unknown periodic DoS jamming attacks

2018

一类约束线性切换系统的滚动优化控制

2015

一类约束线性切换系统的滚动优化控制

2015

IEEE Transactions on Systems, Man, and

2018

Stabilisation of switched linear systems under denial of service

2020

Event-triggered H∞ control of networked switched systems subject to denial-of-service attacks

2020

Stabilisation for switched positive systems under extended asynchronous switching

2019

... 另外,由于实际生活中常存在取值为非负的特殊物理量,例如细菌群落数量、森林覆盖率以及有机物浓度等,将这类物理量作为状态变量可得正系统.与一般系统不同,正系统是指初始状态和系统输入都为非负时,任意时刻的系统状态与输出都能保持非负的动态系统.近年来,描述特定切换法则、掌管模态切换的一类正系统被称为切换正系统,由于该系统具有可靠性强、应用范围广等优点,受到学者们的关注^[14-15],常应用于通信系统^[16]、编队飞行^[17]、流行病学^[18]等不同领域.对于遭受DoS攻击的切换正系统,DoS攻击阻止了测量通道与控制通道之间的信息传递,导致系统稳定性及正性均受影响.同时系统状态的非负特性、子系统之间切换特性及DoS攻击引起的切换特性相互耦合,这更增加了问题解决的难度.因此,在遭受DoS攻击情形下,设计一种安全控制器使得切换正系统依然能够保证其正性及稳定性尤为重要.目前,针对遭受DoS攻击的切换正系统的研究鲜有成果. ...

Robust stabilization of switched positive discrete-time systems with asynchronous switching and input saturation

2019

Stability of spreading processes over time-varying large-scale networks

2016

Formation coordination for the propagation of a group of mobile agents via self-mobile localization

2015

Controller synthesis for positive linear systems with bounded controls

2007

Low-rate TCP-targeted denial of service attacks and counter strategies

2006

... 式中:κ∈{1,2,…,m_k}为DoS攻击周期次序.S_DoS(t)=1表示DoS攻击处于休眠期,此时进行正常通信;S_DoS(t)=0表示DoS攻击处于激活期,此时通信中断.周期DoS攻击下执行器的输出^[19]可表示为 ...

〈

〉