三电平双有源混合全桥DC-DC变换器最小回流功率控制

doi:10.16183/j.cnki.jsjtu.2021.493

三电平双有源混合全桥DC-DC变换器最小回流功率控制

陶海军^,¹^,², 张金生¹, 肖群星¹, 郑征¹^,²

1.河南理工大学电气工程与自动化学院,河南焦作 454003

2.河南省智能装备直驱技术与控制国际联合实验室,河南焦作 454003

Minimum Return Power Control for Three-Level Dual Active Hybrid Full-Bridge DC-DC Converters

TAO Haijun^,¹^,², ZHANG Jinsheng¹, XIAO Qunxing¹, ZHENG Zheng¹^,²

1. School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454003, Henan, China

2. Henan International Joint Laboratory of Direct Drive and Control of Intelligent Equipment, Jiaozuo 454003, Henan, China

责任编辑: 王一凡

收稿日期: 2021-12-7 修回日期: 2022-07-3 接受日期: 2022-10-17

基金资助:

国家自然科学基金(U1804143)
河南省科技攻关项目(222102220014)
河南省高校基本科研业务费专项资金资助(NSFRF210409)

Received: 2021-12-7 Revised: 2022-07-3 Accepted: 2022-10-17

作者简介 About authors

陶海军(1980-),副教授﹐从事大功率开关电源及其控制的研究;E-mail:taohj99@hpu.edu.cn.

摘要

三电平双有源混合全桥(H-TLFB)DC-DC变换器通过引入三电平桥臂提高输入电压范围.针对该变换器在传统双重移相控制下具有较大的功率回流、较高的电流应力等问题,提出一种最小回流功率控制策略.首先分析H-TLFB DC-DC变换器功率传输特性,比较变换器在两种不同工作模式下回流功率值的大小,并根据回流功率与电压比、移相比、传输功率的数学关系,计算出回流功率达到最小时对应的最优移相比,并设计相应优化控制策略.与传统双重移相控制策略相比,最小回流功率控制策略下的回流功率可以在全功率传输范围内达到最小值,并且在一定的电压比范围内,回流功率、电流应力可以同时得到优化.最后,通过实验验证设计控制策略的正确性和可行性.

关键词： 三电平双有源混合全桥DC-DC变换器; 移相控制; 回流功率; 传输效率; 电流应力

Abstract

Hybrid three-level full bridge (H-TLFB) DC-DC converters increase the input voltage range by introducing a three-level bridge arm. Aimed at the problems of large power return and high current stress in the traditional dual phase shift control, a minimum return power control strategy is proposed. First, the power transmission characteristics of H-TLFB DC-DC converter are analyzed, the size of the return power value of the converter in two different operating modes is compared, and the optimal shift of the return power is calculated according to the mathematical relationship between the return power and the voltage ratio, the shift and the transmission power. The corresponding optimal shift of the return power is calculated, and the corresponding optimization control strategy is designed. Compared with the traditional dual phase shift control strategy, the return power in the minimum return power control strategy can reach the minimum value in the full power transmission range, and within a certain voltage ratio range, the return power and current stress can be optimized at the same time. Finally, the correctness and feasibility of the design control strategy are verified by experiments.

Keywords： hybrid three-level full bridge (H-TLFB) DC-DC converter; phase shift control; backflow power; transmission efficiency; current stress

PDF (5890KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

陶海军, 张金生, 肖群星, 郑征. 三电平双有源混合全桥DC-DC变换器最小回流功率控制[J]. 上海交通大学学报, 2023, 57(5): 521-532 doi:10.16183/j.cnki.jsjtu.2021.493

TAO Haijun, ZHANG Jinsheng, XIAO Qunxing, ZHENG Zheng. Minimum Return Power Control for Three-Level Dual Active Hybrid Full-Bridge DC-DC Converters[J]. Journal of Shanghai Jiaotong University, 2023, 57(5): 521-532 doi:10.16183/j.cnki.jsjtu.2021.493

近年来,随着可再生能源的发展,双有源全桥(Dual Active Bridge,DAB)DC-DC变换器因其较高的功率密度、能量可以双向流动、易于实现模块化等优点,得到了越来越广泛的应用^[1⇓-3].

目前,许多学者对两电平DAB(2L-DAB)进行了比较深入的研究,其中,单移相控制^[4-5]因易于实现的特点被广泛应用在DAB中.但在这种控制方式下,DAB中会出现较大的功率回流现象和较大的电流应力,导致功率传输效率降低,变换器中开关器件的使用寿命也会被缩短.为解决这一问题,扩展移相控制、双重移相控制、三重移相控制等被相继提出.其中,扩展移相通过在变压器原边全桥内增加一个移相角来调节变换器,文献[6]中对比了扩展移相下和传统单移相控制下回流功率的大小,发现在扩展移相下变换器的功率传输更广,回流功率更小,但文中并未提及最小回流功率的优化方法.文献[7]中在双重移相控制的基础上分析变换器软开关特性,并建立其动态小信号模型,在实现变换器软开关的基础上,减小了回流功率.文献[8-9]中基于扩展移相控制分析变换器电流应力与移相比之间的数学关系,提出一种优化电流应力的控制方案,并基于该方案与双重移相、三重移相下的电流应力进行对比,发现该控制策略不仅实现了在各种工况下电流应力最小化,而且在全功率传输范围内实现了开关管的零电压开通,但文中并未对变换器的回流功率优化进行分析.此外,相较于双重移相控制,扩展移相在变换器副边全桥内缺少控制自由度,存在一定局限性.

因此,文献[10]中基于双重移相控制建立两电平DAB的电流应力数学模型,分析计算出电流应力最小值,并设计出相应的控制方案,使变换器在稳态运行时,尤其是在轻载条件下,具有最小的电流应力,但变换器的效率却没有达到最优值,还需要进一步的优化.文献[11]中提出了一种最小回流功率优化算法,通过实时采样输入电压、输出电压、输出电流计算出传输功率P₀、电压比k,并通过设计最优控制器计算出最优移相比,使变换器回流功率达到最小值,但该文中对回流功率的优化分析仅在一种工作模式下开展,分析不够全面.文献[12-13]中为减小变换器回流功率在三重移相控制的基础上设计一种回流功率优化方案,提高了系统的响应速度,但其控制策略较为复杂,难以实现.

为了使DAB可以更好地应用在高电压场合,可以在DAB中引入三电平桥臂,使三电平变换器^[14]的开关管承受的电压应力降低,同时可以在器件选型时选择耐压等级较低的开关管来降低成本.文献[15 ⇓-17]中在DAB拓扑中引入了三电平半桥结构,并提出相应控制策略,有效降低了变换器的导通损耗.文献[18-19]中提出一种脉冲宽度调制(PWM)与移相结合的控制方式,使回流功率达到最小值的同时也实现了软开关.文献[20]中在两电平DAB中引入三电平全桥,分析了不同模式下开关管实现软开关时移相比与输入电压、输出电压之间的关系,并提出相应的调制策略,实现了两边全桥开关管的软开关,使变换器可以获得更宽的电压转换增益,但对于变换器传输功率、回流功率之间的关系未作出具体分析.

综上所述,本文以基于双重移相控制的三电平双有源混合全桥(H-TLFB)DC-DC变换器为研究对象,以减小变换器回流功率,提高变换器功率传输效率为目标,首先分析变换器功率传输特性,确定变换器功率传输范围,其次,分析变换器在特定电压比、特定传输功率下回流功率随移相比变化的趋势,在此基础上,设计最优移相比算法,提出最小回流功率控制策略.最后进行实验,验证了本文理论分析的正确性、可行性.

1 三电平混合全桥DC-DC变换器功率传输特性分析

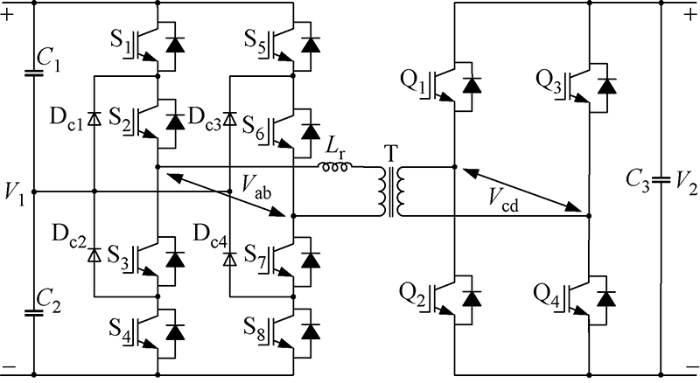
H-TLFB DC-DC变换器的拓扑结构如图1所示,由输入电压V₁、输出电压V₂、高频变压器T、传输电感L_r(原边全桥串联电感加变压器漏感)、输入端带钳位二极管的三电平全桥、输出端两电平全桥、高压侧分压电容C₁、高压侧分压电容C₂、支撑电容C₃组成.图中:S₁~S₈为输入端三电平全桥的开关管;Q₁~Q₄为输出端两电平全桥的开关管;D_c1~D_c4为输入端全桥的钳位二极管;V_ab为输出桥臂电压;V_cd为传输到副边桥的桥臂电; $i_{L_{r}}$ 为流经电感L_r的电流.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 三电平混合全桥DC-DC变换器

Fig.1 H-TLFB DC-DC converter

图2所示为H-TLFB DC-DC变换器在双重移相控制下的脉冲序列.图中:T_hs为半个开关周期;T_h为一个开关周期;n为变压器的匝数比;D₁为原边桥内移相比;D₂为副边桥相对于原边桥的外移相比.由于两个移相角大小不同,H-TLFB DC-DC变换器移相控制可分为模式A(0≤D₁≤D₂≤1)和模式B(0≤D₂≤D₁≤1),且0≤D₁+D₂≤1.为简化分析,本文假设功率从V₁侧向V₂侧传递,定义电压比k=V₁/(nV₂),且k>1.变换器主要工作模式如图3所示,其中t'₁为电感电流过0时刻.

图2

新窗口打开| 下载原图ZIP| 生成PPT

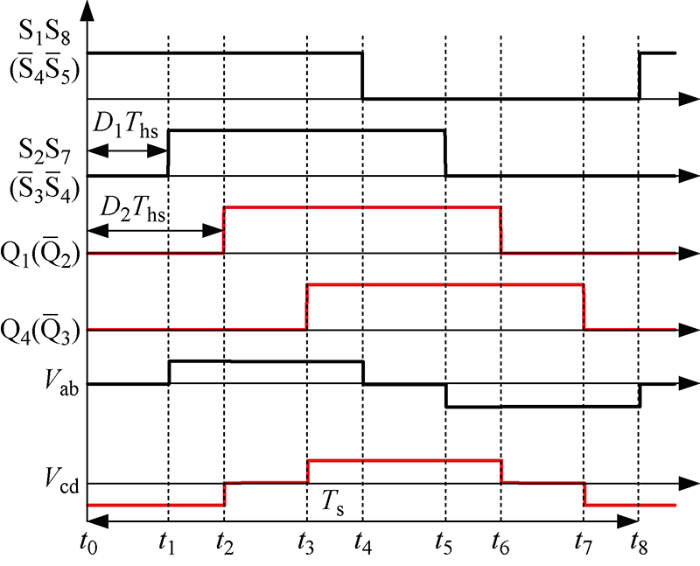
图2 H-TLFB DC-DC变换器在双重移相控制下的脉冲序列

Fig.2 Pulse train of H-TLFB DC-DC converter in dual phase shift control

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 H-TLFB DC-DC变换器主要工作模式

Fig.3 Main operating mode of H-TLFB DC-DC converter

由图2和图3可知,在不同时间段,电感的端电压与端电流均存在如下关系:

$\frac{d i_{L_{r}} (t)}{d t}$

$\frac{V_{a b} - n V_{c d}}{L_{r}}$

(1)

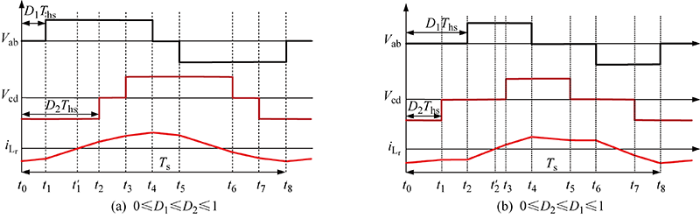
H-TLFB DC-DC变换器工作在稳定状态时,根据电感电流的对称性,可得:

$i_{L_{r}}$ (t₀)=-

$i_{L_{r}}$ (t₄)

(2)

结合图2和图3,并根据式(1)和式(2),可得出H-TLFB DC-DC变换器在两种模式下各时刻电感电流表达式,如表1和表2所示.表中:f_s为H-TLFB DC-DC变换器开关频率.

表1 模式A下等效电感电流值

Tab.1 Equivalent inductance current in Mode A

$i_{L_{r}}$ (t)	0≤D₁≤D₂≤1
$i_{L_{r}}$ (t₀)	[V₁(D₁-1)-nV₂(D₁+2D₂-1)]/(4L_rf_s)
$i_{L_{r}}$ (t₁)	[V₁(D₁-1)-nV₂(-D₁+2D₂-1)]/(4L_rf_s)
$i_{L_{r}}$ (t₂)	[V₁(-D₁+2D₂-1)-nV₂(D₁-1)]/(4L_rf_s)
$i_{L_{r}}$ (t₃)	[V₁(D₁+2D₂-1)-nV₂(D₁-1)]/(4L_rf_s)

新窗口打开| 下载CSV

表2 模式B下等效电感电流值

Tab.2 Equivalent inductance current in Mode B

$i_{L_{r}}$ (t)	0≤D₂≤D₁≤1
$i_{L_{r}}$ (t₀)	[V₁(D₁-1)-nV₂(D₁+2D₂-1)]/(4L_rf_s)
$i_{L_{r}}$ (t₁)	[V₁(D₁-1)+nV₂(1-D₁)]/(4L_rf_s)
$i_{L_{r}}$ (t₂)	[V₁(D₁-1)+nV₂(1-D₁)]/(4L_rf_s)
$i_{L_{r}}$ (t₃)	[V₁(D₁+2D₂-1)+nV₂(1-D₁)]/(4L_rf_s)

新窗口打开| 下载CSV

根据文献[11]对2L-DAB功率表达式的分析,可得传输功率标幺值 $P_{t}^{*}$ 、回流功率标幺值 $P_{c}^{*}$ :

$P_{t}^{*}$ =

$\frac{1}{T_{h s}} \int_{0}^{T_{h s}}$ V_ab(t)

$i_{L_{r}}$ (t)dt

$\frac{1}{P_{N}}$

(3)

$P_{c}^{*}$ =

$\frac{1}{T_{h s}} \int_{t_{1}}^{t'_{1}}$ V₁(t)

$i_{L_{r}}$ (t)dt

$\frac{1}{P_{N}}$

(4)

式中:P_N为H-TLFB DC-DC变换器单移相控制(D₁=0)下的最大传输功率,

P_N=

$\frac{n V_{1} V_{2}}{8 L_{r} f_{s}}$

(5)

由表1~2,并结合式(3)可以得出变换器功率传输表达式如表3和表4所示.

根据表3~4可以得到H-TLFB DC-DC变换器传输功率关于移相角的变化曲线,如图4所示,两种工作模式对应的功率传输范围分别为[0,1]P_N、[0,2/3]P_N.此外,相对于传统单移相控制,H-TLFB DC-DC变换器增加了一个控制变量,提高了变换器调节的灵活性,在同一传输功率下,有多组D₁、D₂可供选择,但大多数自由度(D₁、D₂)的组合存在较大的回流功率,因此,需要计算出最优的移相比组合使变换器的回流功率达到最小.

表3 模式A下变换器传输功率、回流功率值

Tab.3 Transmission power and reflux power values of converter in Mode A

模式A	功率表达式
$P_{t}^{*}$	4D₂-4 $D_{2}^{2}$ -2 $D_{1}^{2}$
$P_{c}^{*}$	[k(1-D₁)+2D₂-D₁-1]²/[2(k+1)]

新窗口打开| 下载CSV

表4 模式B下变换器传输功率、回流功率值

Tab.4 Transmission power and reflux power values of converter in Mode B

模式B	功率表达式
$P_{t}^{*}$	4D₂-4D₁D₂-2 $D_{2}^{2}$
$P_{c}^{*}$	[(k-1)(1-D₁)]²/(2k)

新窗口打开| 下载CSV

图4

新窗口打开| 下载原图ZIP| 生成PPT

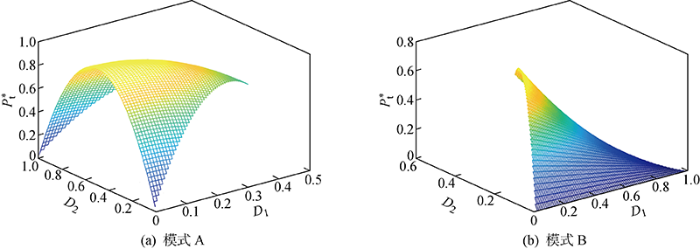
图4 H-TLFB DC-DC变换器功率传输范围

Fig.4 Power transmission range of H-TLFB DC-DC converter

2 变换器回流功率优化分析

2.1 回流功率数学模型建立

设H-TLFB DC-DC变换器移相控制下的传输功率为P₀,结合表3~4可得:

D_1-_MA=

$\sqrt{2 D_{2} - 2 D_{2}^{2} - \frac{P_{0}}{2}}$

(6)

D_1-_MB=1-

$\frac{1}{2}$ D₂-

$\frac{P_{0}}{4 D_{2}}$

(7)

式中:D_1-MA、D_1-MB分别为模式A、模式B下的D₁值.

将式(6)~(7)分别代入到表3~4中回流功率的表达式中可得:

$P_{c, M A}^{*}$

$\frac{{[(k + 1) (1 - \sqrt{2 D_{2} - 2 D_{2}^{2} - \frac{P_{0}}{2}}) + 2 D_{2} - 2]}^{2}}{2 (k + 1)}$

(8)

$P_{c, M B}^{*}$

$\frac{{[(k - 1) (\frac{1}{2} D_{2} + \frac{P_{0}}{4 D_{2}})]}^{2}}{2 k}$

(9)

式中: $P_{c, M A}^{*}$ 、 $P_{c, M B}^{*}$ 分别为模式A、模式B下的回流功率.

在特定传输功率P₀=0.6的条件下,结合式(8)~(9)可以得到回流功率 $P_{c}^{*}$ 关于移相比D₂、电压比k的变化曲线,如图5所示.电压比k一定时,回流功率曲线随外移相比D₂的增加呈现出先减小后增加的趋势.电压比k增加时,在两种工作模式下,变换器回流功率值均增大.电压比k=1时,模式A与模式B的回流功率值均达到最小,变换器在模式B的工作条件下回流功率可以降低为0.

图5

新窗口打开| 下载原图ZIP| 生成PPT

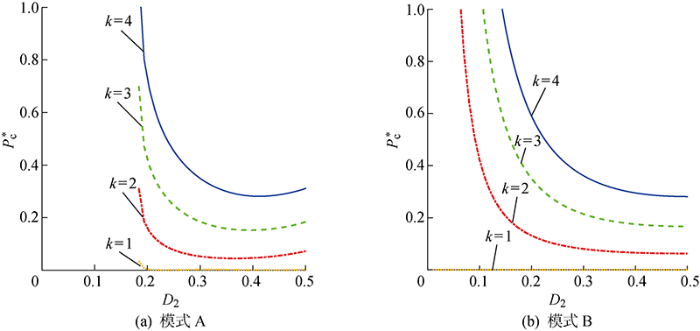
图5 特定电压比下变换器回流功率变化曲线

Fig.5 Backflow power curves of converter at a specific voltage ratio

在特定电压比k=2.5的条件下,结合式(8)~(9)可以得到回流功率 $P_{c}^{*}$ 关于移相比D₂、传输功率P₀的变化曲线,如图6所示.由图可见,当外移相角D₂一定时,回流功率值随着传输的功率值的增大而增大.传输功率P₀一定时,与图5类似,变换器的回流功率曲线随着移相比D₂的增加呈现出先减小后增加的趋势.在理想条件下,可以取曲线的最低点,即回流功率最小值点的工作条件来使变换器的回流功率达到最小值,但考虑到两种工作模式下的限制条件0≤D₁≤D₂≤1、0≤D₂≤D₁≤1,得出变换器回流功率最小值点如图6中圆形标记所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

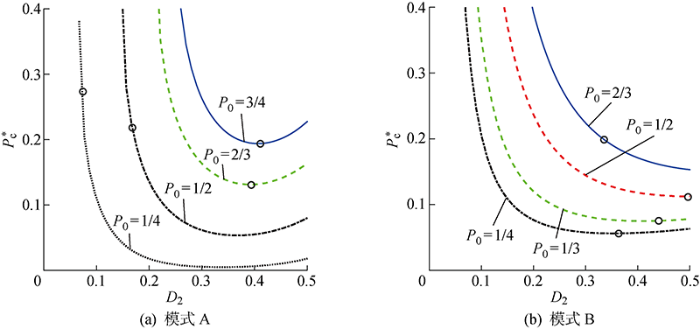
图6 特定传输功率下变换器回流功率变化曲线

Fig.6 Backflow power curves of converter at a specific transmission power

对比图6(a)和6(b),在特定传输功率P₀=1/4时,模式A下对应的最小回流功率值大于模式B,当P₀=2/3时,模式B下对应的最小回流功率值大于模式A,由此可知,变换器在相同的传输功率下,选择不同的工作模式,最小回流功率值也会发生变化.因此,需要分别求解出两种工作模式下的最小回流功率,并作出对比,得到变换器的最小回流功率值.

2.2 最小回流功率求解

为简化分析,仅描述模式A下最小回流功率求解过程.根据表3,可得:

D₂=

$\frac{1}{2} - \frac{1}{2} \sqrt{1 - 2 D_{1}^{2} - P_{0}}$

(10)

结合表3,将D₂值代入到回流功率表达式中并对其进行求导得到最优移相比组合:

$\begin{array}{l} D_{1} = (k + 1) \sqrt{\frac{1 - P_{0}}{2 {(k + 1)}^{2} + 4}} \\ D_{2} = \frac{1}{2} - \sqrt{\frac{1 - P_{0}}{2 {(k + 1)}^{2} + 4}} \end{array}\}$

(11)

但在模式A下需要满足条件0≤D₁≤D₂≤1,可得:

f(k,P₀)=(2P₀-1)k²+(8P₀-6)k+8P₀-5≥0

(12)

解方程(12),从而有a和Δ:

$\begin{array}{l} a = 2 P_{0} - 1 \\ Δ = 16 - 24 P_{0} \end{array}\}$

(13)

根据拉格朗日算法,a与Δ的取值共分为下列4种情况.

(1) a>0, Δ≤0.即P₀≥2/3时,对于任意k值,均满足f(k, P₀)≥0,此时的最优移相比为

$\begin{array}{l} D_{1} = (k + 1) \sqrt{\frac{1 - P_{0}}{2 {(k + 1)}^{2} + 4}} \\ D_{2} = \frac{1}{2} - \sqrt{\frac{1 - P_{0}}{2 {(k + 1)}^{2} + 4}} \end{array}\}$

(14)

(2) a>0,Δ>0.即1/2<P₀<2/3时,对f(k, P₀)=0进行求解k值,可得:

$\begin{array}{l} k_{1} = \frac{3 - 4 P_{0} - \sqrt{4 - 6 P_{0}}}{2 P_{0} - 1} \\ k_{2} = \frac{3 - 4 P_{0} + \sqrt{4 - 6 P_{0}}}{2 P_{0} - 1} \end{array}\}$

(15)

根据传输功率P₀所处范围确定电压比k的范围:若1/2<P₀≤5/8,则k₁<0,k₂>1;若5/8<P₀<2/3,则0<k₁<1,k₂>1.两种情况下,k₂的值均大于1.

当f(k, P₀) <0时,取D₁=D₂,结合表3中回流功率的表达式,可得:

$\begin{array}{l} D_{1 +} = D_{2 +} = \frac{2 + \sqrt{4 - 6 P_{0}}}{6} \\ D_{1 -} = D_{2 -} = \frac{2 - \sqrt{4 - 6 P_{0}}}{6} \\ P_{c}^{*} = \frac{[(k - 1) (1 - D_{1} {)]}^{2}}{2 (k + 1)} \end{array}\}$

(16)

从式(16)中可以得出,D₁值越大,回流功率 $P_{c}^{*}$ 越小,即 $P_{c}^{*}$ (D₁₊)< $P_{c}^{*}$ (D_1-).

若k∈[1,(3-4P₀ $\sqrt{4 - 6 P_{0}}$ )/(2P₀-1)),则f(k, P₀)<0, $P_{c}^{*}$ (D₁₊)< $P_{c}^{*}$ (D_1-),此时的最优移相比组合为

D₁=D₂=

$\frac{2 + \sqrt{4 - 6 P_{0}}}{6}$

(17)

若k∈[(3-4P₀+ $\sqrt{4 - 6 P_{0}}$ )/(2P₀-1),+∞),则f(k, P₀)≥0,此时的最优移相比为

$\begin{array}{l} D_{1} = (k + 1) \sqrt{\frac{1 - P_{0}}{2 {(k + 1)}^{2} + 4}} \\ D_{1} = \frac{1}{2} - \sqrt{\frac{1 - P_{0}}{2 {(k + 1)}^{2} + 4}} \end{array}\}$

(18)

(3) a≤0,Δ>0.即0≤P₀≤1/2时,在k≥1的条件下,f(k, P₀)<0.考虑限制条件0≤D₁+D₂≤1,此时的最优移相比组合为

D₁=D₂=

$\frac{2 - \sqrt{4 - 6 P_{0}}}{6}$

(19)

(4) a≤0,Δ≤0.经分析,该情况下,最优移相比无解.

根据以上对模式A下最优移相比的求解过程,同理可以得到模式B下不同传输功率范围对应的最优移相比,取值如表5所示.表中:D_1,Bmin、D_2,Bmin为H-TLFB DC-DC变换器工作在模式B下回流功率达到最小值时对应的移相比.

表5 模式B下对应的最优移相比组合

Tab.5 Optimal shift comparison combinations in Mode B

P₀	D_1,Bmin	D_2,Bmin
0<P₀≤1/2	1- $\sqrt{P_{0} / 2}$	$\sqrt{P_{2} / 2}$
1/2<P₀≤2/3	$\frac{2 + \sqrt{4 - 6 P_{0}}}{6}$	$\frac{2 + \sqrt{4 - 6 P_{0}}}{6}$

新窗口打开| 下载CSV

根据2.1节对回流功率传输特性的分析,再结合以上对H-TLFB DC-DC变换器在不同工作模式下最小回流功率的求解,得出变换器在不同功率传输范围、电压比下,可以选取不同的工作模式,确定一组最优移相比,使得变换器在全功率传输范围内回流功率达到最小值.设D_1,min、D_2,min分别为变换器回流功率取得最小值时的移相比.由式(11)、(13)、(15)、(16)及表3、表5可以得到H-TLFB DC-DC变换器在移相控制下不同P₀、k的分布范围以及对应范围内的最优移相比,如表6所示.

表6 不同传输功率范围对应的最优移相比

Tab.6 Optimal shift comparison of different transmission power ranges

P₀	k	D_1,min
0<P₀≤1/2	k≥1	1- $\sqrt{P_{0} / 2}$
1/2<P₀<2/3	1≤k<k₂	$\frac{2 + \sqrt{4 - 6 P_{0}}}{6}$
	k≥k₂	(1+k) $\sqrt{\frac{1 - P_{0}}{2 {(k + 1)}^{2} + 4}}$
2/3≤P₀≤1	k≥1	(1+k) $\sqrt{\frac{1 - P_{0}}{2 {(k + 1)}^{2} + 4}}$

新窗口打开| 下载CSV

设 $P_{c, m i n}^{*}$ 为H-TLFB DC-DC变换器在最优相移下的最小回流功率,结合表3和表6, $P_{c, m i n}^{*}$ 取值如表7所示.

表7 最优移相比对应的最小回流功率值

Tab.7 Optimal shift corresponding to minimum return power value

D_1,min	D_2,min	$P_{c, m i n}^{*}$
1- $\sqrt{P_{0} / 2}$	$\sqrt{P_{0} / 2}$	$\frac{P_{0} {(k - 1)}^{2}}{4 k}$
$\frac{2 + \sqrt{4 - 6 P_{0}}}{6}$	$\frac{2 + \sqrt{4 - 6 P_{0}}}{6}$	$\frac{[(k - 1) {(4 - \sqrt{4 - 6 P_{0}})]}^{2}}{72 (k + 1)}$
(1+k) $\sqrt{\frac{1 - P_{0}}{2 {(k + 1)}^{2} + 4}}$	$\frac{1}{2} - \sqrt{\frac{1 - P_{0}}{2 {(k + 1)}^{2} + 4}}$	$\frac{{[k - \sqrt{\frac{(1 - P_{0}) (k^{2} + 2 k + 3)}{2}}]}^{2}}{2 (k + 1)}$

新窗口打开| 下载CSV

3 最优移相比下变换器性能分析

3.1 最小回流功率优化分析

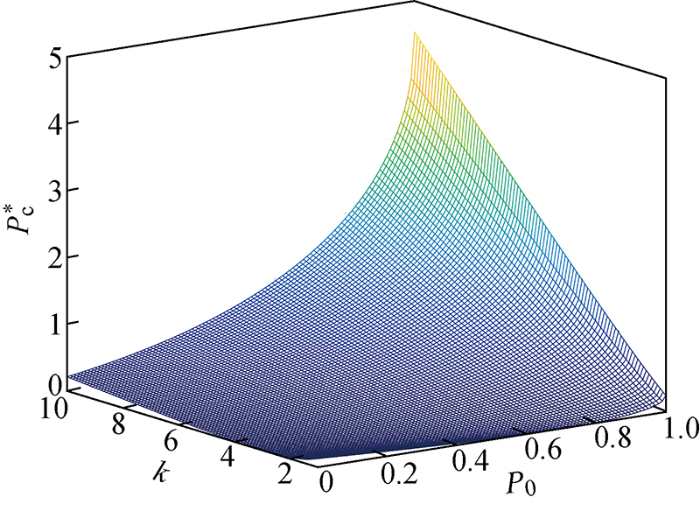
图7给出了最小回流功率变化的三维图.由图可见,电压比k、传输功率P₀增大时,最小回流功率值会随之增大.电压比k=1时,回流功率值最小,与2.1节中分析结果一致.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 最小回流功率变化曲线

Fig.7 Change curve of minimum reflux power

图8所示为回流功率的变化曲线,传输功率P₀=0.4,图中曲线从上至下D₁的值依次增大.由图可见,电压比k一定时,随着D₁的减小,变换器回流功率值增大,D₁=0时,即变换器在单移相控制下的回流功率值最大.在同一控制策略下,电压比k增大,回流功率值随之增大,其中,在最小回流功率控制策略下,回流功率值可以在全电压比范围内降到最小.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 传统移相与最小回流功率控制下的最小回流功率

Fig.8 Minimum reflux power in conventional phase shiftand minimum reflux power control

3.2 电流应力优化分析

以P₀=0.2为例,图9对比了变换器在最小回流功率控制策略和传统移相控制下电流应力的变化曲线.表1~2给出了变换器在两种不同工作模式下各个时刻的电流值,通过对比得到,在两种工作模式下,电流均在t₄时刻达到峰值,即变换器的电流应力为

图9

新窗口打开| 下载原图ZIP| 生成PPT

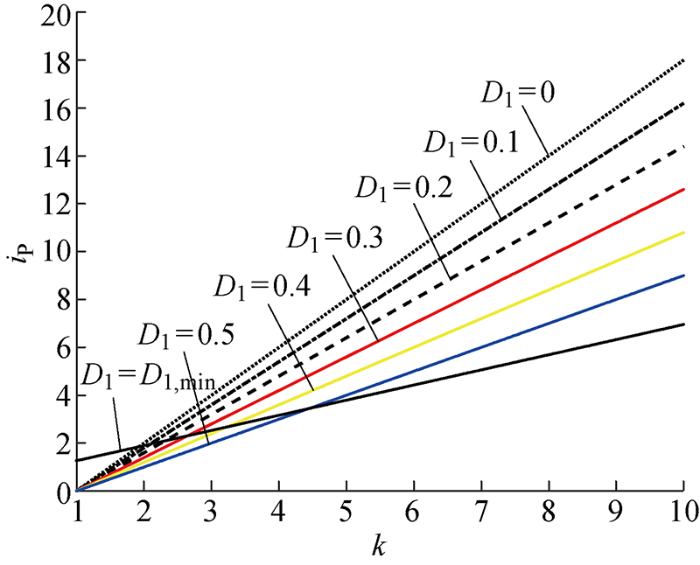
图9 传统移相与最小回流功率控制下的电流应力

Fig.9 Current stress in conventional phase shift and minimum reflux power control

I_P=

$\frac{n V_{2} [(1 - D_{1}) (k - 1) + 2 D_{2}]}{4 L_{r} f_{s}}$

(20)

为了简化分析,将I_P进行标幺化:

$\begin{array}{l} i_{N} = \frac{n V_{2}}{8 L_{r} f_{s}} \\ i_{P} = \frac{I_{P}}{i_{N}} = 2 [(1 - D_{1}) (k - 1) + 2 D_{2}] \end{array}\}$

(21)

式中:i_N为变换器稳态工作下的额定传输电流.

从图9中可以看出,当传输功率P₀=0.2时,变换器电流应力随电压比k的增大而增大,在传统双重移相控制下,随着内移相角D₁的增大,变换器承受的电流应力减小.低电压比下,在最小回流功率控制策略下电流应力值高于传统移相控制,但当电压比增大到一定值时,最小回流功率控制策略可以同时实现对电流应力、回流功率的优化.

3.3 优化控制策略

根据第1节对传输功率的分析,并结合式(5)可得:

P₀=

$\frac{V_{2} I_{2}}{P_{N}}$ =

$\frac{8 f_{s} L_{r} I_{2}}{n V_{1}}$

(22)

$\frac{V_{1}}{n V_{2}}$

(23)

式中:I₂为变换器副边输出电流.

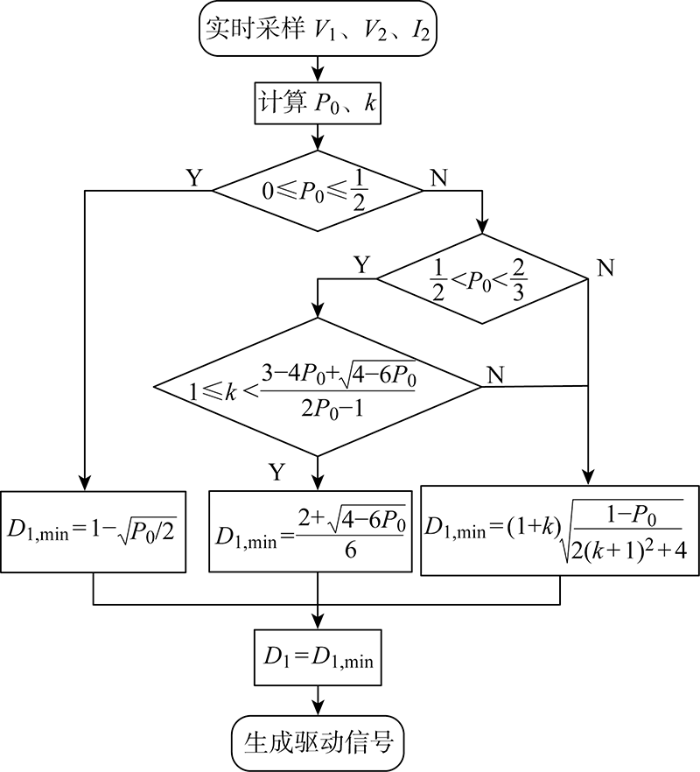
根据2.3节中对最小回流功率的求解,设计出最小回流功率控制器,控制器的算法流程如图10所示.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 最优移相比算法流程图

Fig.10 Flow chart of optimal shift comparison algorithm

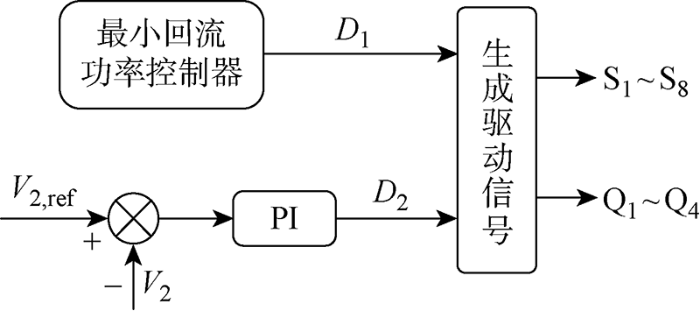
图11为变换器最小回流功率的控制框图.外移相角D₂由目标输出电压V_2,_ref与实时输出电压的误差信号经过比例积分(PI)调节器给出,以保证变换器输出电压的稳定,再结合最小回流功率控制器实时给定的D₁,使变换器工作在最小回流功率状态.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 系统总体控制框图

Fig.11 Overall control block diagram of system

4 实验验证

为验证本文所提最小回流功率控制策略的正确性与有效性,搭建一台实验样机(见图12)对以上理论分析进行实验验证,具体电路参数如表8所示.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 实验样机

Fig.12 Experimental prototype platform

表8 H-TLFB DC-DC变换器具体电路参数

Tab.8 Specific circuit parameters of H-TLFB DC-DC converter

主电路参数	取值
f_s/kHz	10
n	1
L_r/μH	60
C₁, C₂/mF	0.25
C₃/mF	1

新窗口打开| 下载CSV

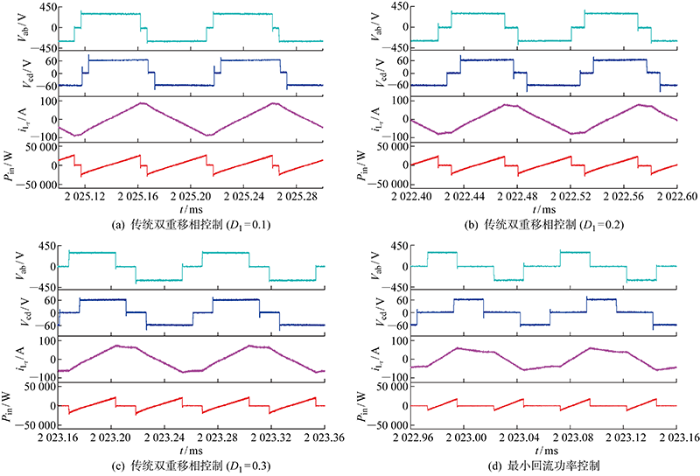
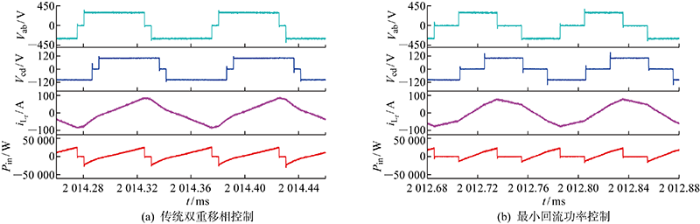
图13给出了在相同传输功率下,变换器在不同运行条件下稳定运行的波形.图中:P_in为变换器瞬时输入功率.直流输入电压为300 V,输出电压为60 V.传统双重移相控制下,D₁=0.1时,回流功率为5.39 kW,电感电流幅值为87 A;D₁=0.2时,回流功率为3.98 kW(计及一个周期内出现的两次功率回流现象),电感电流幅值为80 A;D₁=0.3时,回流功率为3.34 kW,电感电流幅值为72 A.在最小回流功率控制下,回流功率为1.12 kW,电感电流幅值为58 A.通过对比,在传统双重移相控制策略下的回流功率、电流应力值较大,内移相角D₁增大,电流应力、回流功率值随之减小,最小回流功率控制下,变换器电流应力、回流功率值最小.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 变换器稳态输出波形

Fig.13 Steady-state output waveform of converter

图14给出了在最小回流功率控制策略下,变换器在不同电压比下稳定运行的波形.图13(a)中,输入电压为360 V、输出电压为60 V,此时电压比k=6,传输功率P₀=0.33,该工况下变换器的回流功率为1.44 kW,电感电流幅值为63 A.图13(b)中,输入电压为300 V、输出电压为60 V,此时电压比k=5,传输功率P₀=0.39,该工况下变换器的回流功率为1.12 kW,电感电流幅值为58 A.通过对比可以得出,最小回流功率控制策略下,电压比k增大,变换器回流功率和电流应力值会随之增加,与图5、图9中分析结果一致.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 不同电压比下变换器的回流功率

Fig.14 Reflux power of converters at different voltage ratios

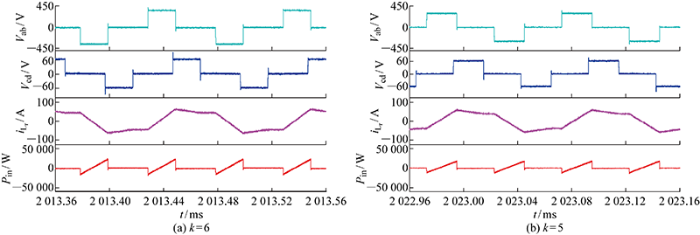
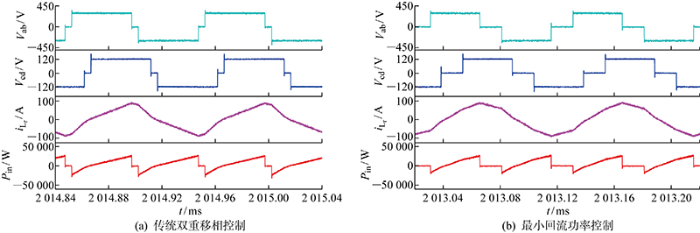
图14(a)和14(b)分别给出了传输功率P₀=0.33、P₀=0.39(0<P₀≤1/2)时变换器稳态输出波形,为进一步验证所提最小回流功率控制策略在全功率传输范围内有效,图15和16分别给出了不同控制下变换器在P₀=0.66(1/2<P₀<2/3)、P₀=0.78(2/3≤P₀≤1)时的稳态输出波形.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 P₀=0.66时回流功率优化对比图

Fig.15 Comparison of reflux power optimization at P₀=0.66

如图15所示,输入电压为300 V、输出电压为100 V,此时变换器传输功率P₀=0.66 (1/2<P₀<2/3),传统双重移相控制下,回流功率为4.26 kW,电感电流幅值为86.5 A.最小回流功率控制下,回流功率为1.40 kW,电感电流幅值为78.5 A.对比图15(a)和15(b)可知,在最小回流功率控制下,回流功率得到大幅优化的同时,电流应力也被减小.

如图16所示,输入电压为300 V、输出电压为120 V, 此时变换器传输功率P₀=0.78(1/2<P₀<2/3),传统双重移相控制下,回流功率为3.16 kW,电感电流幅值为88.5 A.最小回流功率控制下,回流功率为1.85 kW,电感电流幅值为89.5 A.对比图16(a)和16(b)可知,当P₀=0.78时,在最小回流功率控制下,回流功率被减小的同时电流应力没有得到优化,但变换器效率值大小由回流功率、电流应力共同决定,整体而言,变换器在最小回流功率控制下,其效率值增大.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 P₀=0.78时回流功率优化对比图

Fig.16 Comparison of reflux power optimization at P₀=0.78

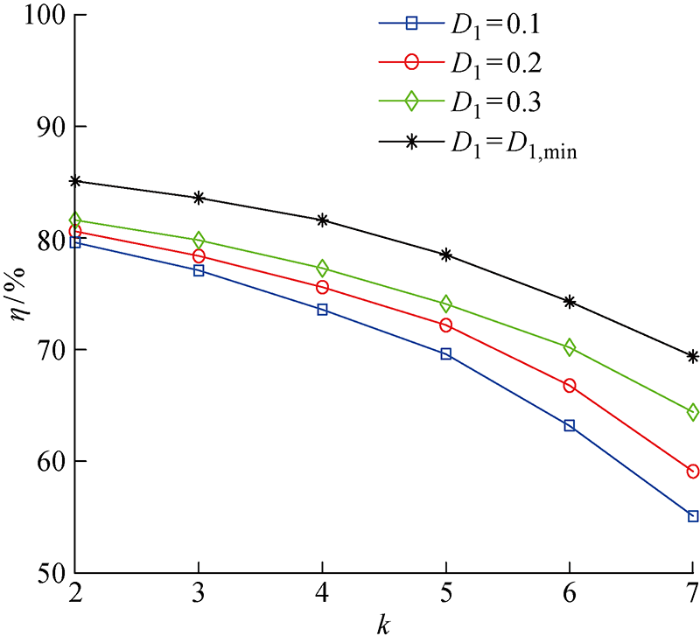
图17所示为变换器功率传输效率(η)曲线.由图可见,在不同的控制策略下,保持闭环输出电压50 V不变,提升输入电压,随着k值的增大,系统回流功率与电流应力增大,系统效率值降低,与图14中分析结果一致.此外,最小回流功率控制下的效率曲线始终高于传统双重移相控制,验证了本文所提控制策略的有效性.

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 变换器在不同控制下的功率传输效率曲线

Fig.17 Power transmission efficiency curves of converter in different controls

5 结论

针对H-TLFB DC-DC变换器,提出最小回流功率控制策略,通过分析H-TLFB DC-DC变换器 0≤D₁≤D₂≤1与0≤D₂≤D₁≤1两种不同的工作模式,建立变换器电流应力与移相比、电压比之间的数学模型,进而求解出H-TLFB DC-DC变换器在不同运行条件下达到最小回流功率的最优移相比组合,得出在一定的电压比范围内,变换器回流功率和电流应力值可以同时得到优化.理论分析和实验结果表明:

(1) 采用分段控制算法计算出最优移相比,使H-TLFB DC-DC变换器在全功率传输范围内均具有最小的回流功率.

(2) 最小回流功率控制策略下,在一定的电压比范围内,变换器回流功率、电流应力可以同时得到优化.

(3) 保证输入电压不变,提高输出电压,最小回流功率控制策略下,该策略对回流功率、电流应力的优化效果随着传输功率的增加而降低.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

DING

, YANG

, ZHANG

, et al.

A novel soft-switching multiport bidirectional DC-DC converter for hybrid energy storage system

[J]. IEEE Transactions on Power Electronics, 2013, 29(4): 1595-1609.

DOI:10.1109/TPEL.2013.2264596 URL [本文引用: 1]

[2]

KRISMER

, KOLAR

J W

Efficiency-optimized high-current dual active bridge converter for automotive applications

[J]. IEEE Transactions on Industrial Electronics, 2011, 59(7): 2745-2760.

DOI:10.1109/TIE.2011.2112312 URL [本文引用: 1]

[3]

SHI

, LI

, XUE

, et al.

Optimized operation of current-fed dual active bridge DC-DC converter for PV applications

[J]. IEEE Transactions on Industrial Electronics, 2015, 62(11): 6986-6995.

DOI:10.1109/TIE.2015.2432093 URL [本文引用: 1]

[4]

KHERALUWALA

M N

, GASCOIGNE

R W

, DIVAN

D M

, et al.

Performance characterization of a high-power dual active bridge DC-to-DC converter

[J]. IEEE Transactions on Industry Applications, 1992, 28(6): 1294-1301.

DOI:10.1109/28.175280 URL [本文引用: 1]

[5]

殷晓东, 罗登, 李祖勇, 等.

一种双向隔离DC-DC变换器二次纹波电压抑制方法

[J]. 电工技术学报, 2018, 33(6): 1356-1363.