随着“碳达峰、碳中和”的目标被提出,可再生能源大规模并网,直流配网具有新能源消纳能力强、供电功率大、线路损耗小、运行效率高等优势,是配电网发展的方向之一[1-2].直流配网中分布式电源占比高,换流设备数量大,极易产生大量谐波,其原因是:① 单相逆变器二次脉动功率[3]、交流侧三相不平衡通过换流器在直流侧产生谐波分量[4],其谐波属性与换流器类型有关,换流器为电流源型,则谐波属性为电流特性;② 交直流非线性负载主要产生谐波电流,经线路阻抗后伴随产生谐波电压.据分析,二倍频分量是直流配网谐波的主要成分之一,其频次低、含量大,增加线路损耗,严重影响了直流系统供电质量,危害设备安全、使用寿命与系统效率,间接导致碳排量增加.二倍频谐波治理已成为直流配电网应用过程中亟需解决的关键技术问题[5].
直流配网谐波治理主要分为集中式以及分布式两类.集中式治理在直流母线上并联大电容、LC谐振电路或有源滤波器集中滤除母线上的谐波分量[6-7].但无源滤波器体积大、功率密度低,电感电容参数的匹配问题容易放大高频次的谐波[8].集中式治理方法可改变二次谐波电流的分配,适用于系统规模小、谐波含量少或谐波源单一的场景.分布式治理可分为有无额外辅助电路两种方式.文献[9]提出在换流器控制回路内增加虚拟阻抗,改变二次谐波电流的分配情况;文献[10-11]提出改变换流器结构,实现二次谐波电流的抑制,但是其控制复杂,难以实现;上述方法改变换流器的拓扑或控制方式来抑制谐波,考虑了母线电压稳定,但没有彻底抑制低频谐波.直流有源滤波器(DC Active Power Filter, DC-APF)主要为buck-boost型电路,可以针对不同谐波源进行安装,就地消除谐波源的特定次的谐波[12].相比于上述方法,分布式DC-APF能够就近补偿谐波电流,减少流过线路阻抗上的谐波电流,从源头上抑制谐波电压的产生.但是随着直流配电网规模的增大,系统中谐波源数量也在不断增加,为保证供电质量,系统配置的DC-APF的数量也随之增加;滤波器控制回路之间存在耦合干扰,使滤波器之间存在交互影响,导致滤波性能下降,系统中的谐波含量超出预期的指标.
目前,直流滤波装置之间的交互影响分析主要有阻抗分析法和相对增益矩阵分析方法(Relative Gain Array, RGA)等.文献[13-14]建立换流站和滤波器的等效阻抗模型,分析等效阻抗变化对系统中谐波分布的影响,但没有具体分析影响阻抗变化的因素;文献[15]建立多APF系统的等效模型,通过传递函数分析APF之间的交互影响,提出增加电感或减小比例或积分增益来抑制耦合干扰;文献[16]建立多逆变器并网模型,利用RGA分析引起多逆变器并网振荡的影响因素,并通过改变拓扑参数抑制交互影响.上述文献对交流系统中电力电子装置间的交互影响进行分析,其研究方法与结论不完全适用于多直流滤波器交互影响的研究.
本文针对直流配电网中多个DC-APF的复杂交互影响,利用等效输出阻抗法,建立多直流滤波器并网模型.利用相对增益矩阵的分析方法,分析直流配电网存在多个谐波源、多个滤波器工作时,电网电气参数、滤波器控制器参数等对滤波器稳定工作产生的影响,并提出合理选择控制器参数的参考方法.在PSCAD/EMTDC与RT-LAB软件中建立含多DC-APF的直流配网模型,对不同参数条件下多DC-APF工作的直流母线二次谐波含量进行测试,仿真结果验证了多滤波器交互影响机理分析方法的有效性.
1 直流配电网与直流滤波器
1.1 直流配电网
直流配电网的典型结构如图1所示.上级交流电网通过变压器与双向AC/DC换流器接入直流母线,稳定直流母线电压;直流电源包括光伏和储能设备,光伏通过DC/DC换流器接入直流母线,储能设备经过双向DC/DC接入直流配网,根据需求灵活配置输出功率;负荷侧包括直流负荷和交流负荷.
图1
直流电压谐波或者电流谐波是指在直流电压或电流中含有的交流分量.一方面,随着电力电子技术的快速发展,配电网中交直流功率变换器的性能不断提升,设备自身产生的二次谐波电流含量很低;另一方面,交流侧非线性负荷产生的谐波通常以就地的交流滤波器来滤除.因此,本文主要考虑单相电流源型逆变器和三相不对称负载在直流侧产生的二次谐波电流.考虑DC-APF的分布式配置时,主要从谐波源个数以及谐波源产生的谐波电流大小两个方面综合考虑.对于较大的谐波源,建议单独配置DC-APF;对较小的谐波源,可以馈线为单位配置DC-APF.通过DC-APF吸收二次谐波电流,抑制流经线路阻抗和负载阻抗的谐波电流,减小直流母线的谐波电压.
1.2 直流滤波器
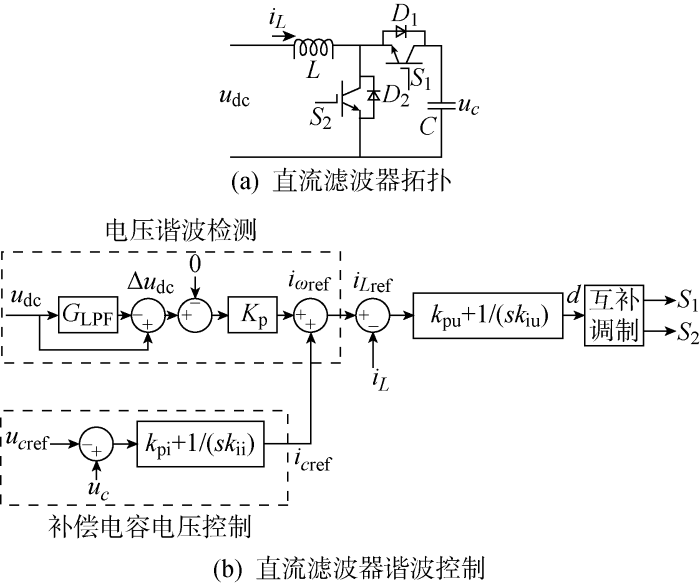
直流滤波器的典型拓扑结构与控制方法如图2所示.图中:udc为连接点电压;
图2
DC-APF的控制方法主要分为两个部分,如图2(b)所示.图中:GLPF为低通滤波器传递函数;kpu和kiu分别是补偿电容电压PI(线性控制器)调节器的比例系数和积分系数;kpi和kii分别是电流内环PI调节器的比例系数和积分系数;Kp为纹波电压放大系数;d为占空比调制信号;s表示复频率.第1部分为谐波检测,电压udc经过低通滤波器得到谐波分量Δudc,经过放大系数Kp得到谐波电流参考值iωref,ω表示角频率;第2部分为补偿控制,即补偿电容电压参考值ucref与实际值uc的差值经过PI调节得到谐波电流修正量icref.上述两个参考电流之和iLref与iL的差值经过PI调解器得到控制开关管信号S1、S2的占空比,使DC-APF产生相位相反的电流,补偿安装位置处的二次谐波电流.
如图2(b)所示,根据小信号模型可以计算DC-APF各环节的传递函数,并由各环节传递函数以及闭环控制模式下参数之间的关系计算出DC-APF闭环输出阻抗如下:
式中:
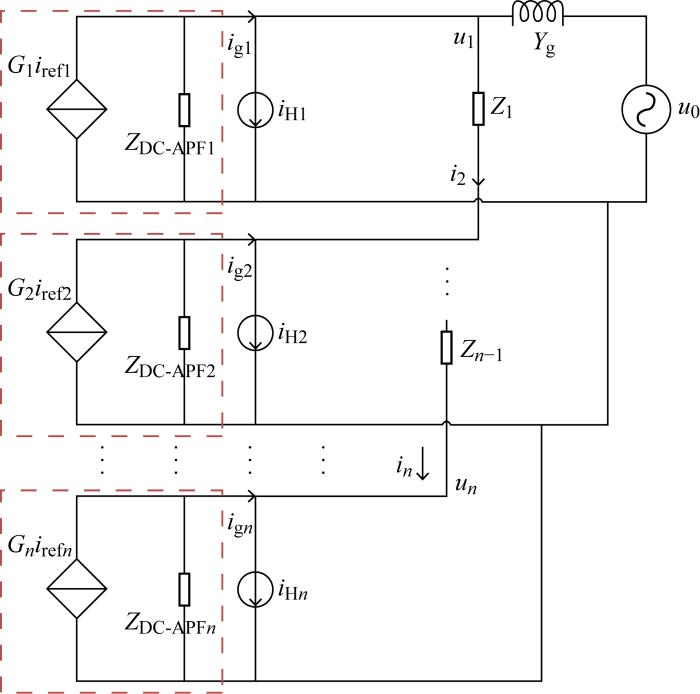
由闭环输出阻抗与直流滤波器的输出特性,将单DC-APF简化成诺顿等效电路,其等效模型如图3虚线框内所示.将图1中多个直流滤波器并网的模型,采用该诺顿简化模型替换并网[17],并将谐波源等效为谐波电流源,则多直流滤波器并网模型如图3所示.图中:
图3
由于DC-APF难以完全补偿谐波电流,未补偿的谐波电流流经负载或线路阻抗,在滤波器并网点产生谐波电压.滤波器控制参数决定了滤波器并网点二次谐波电压幅值与相角,参数匹配时滤波器并网点的二次谐波电压幅值与相角几乎相等,则不会引起二次谐波环流,从而避免了相互干扰.
由于直流母线电压中存在二倍频谐波电压才会对直流滤波器产生激励影响,故在理论分析时将u0近似认为等于0.根据基尔霍夫定律可以得到该模型的数学关系为
2 基于相对增益矩阵理论的交互影响机理分析方法
2.1 相对增益矩阵原理
相对增益矩阵(RGA)被广泛运用于分析多变量控制系统交互影响.其基本原理为:对于一个g输入和k输出的系统, 输入
式中:分子表示所有控制均开环的模式;分母表示除uj-yi回路闭环控制外,其他所有控制均开环的模式.
λij表示当其他控制回路加入时,对uj-yi回路的影响程度.当λij=1时,表示uj-yi的回路与其他控制回路没有交互影响,
式中:⊗表示矩阵的Hadamard乘积;G(jω)表示任意频率下的传递函数矩阵.
2.2 DC-APF并网相对增益矩阵
首先分析图3中两台DC-APF并网工作的场景,该场景下的数学模型如下:
建立DC-APF输出电流与母线电压以及谐波源电流的传递函数矩阵G2×3为
直流配电网中每多接入一个滤波器则会形成一个新系统,新系统与原系统的数学模型存在一定的递推关系,因此可由两台APF并网系统传递函数递推至n台APF并网系统传递函数.n个DC-APF并网系统(即系统中直流滤波器数量为n,且m=2,3,…,n-1)与n-1个DC-APF并网系统的递推关系如下:
每个直流滤波器的输出电流为
将式(8)代入式(7)以及n-1个DC-APF并网传递函数矩阵G(n-1)×n,可以推导出n个DC-APF并网传递函数矩阵Gn×(n+1).传递函数矩阵推导关系如图4所示.
图4
利用式(5)可以计算得到多直流滤波器控制回路的相对增益矩阵:
式中:
2.3 基于RGA的多直流滤波器工作交互影响分析
基于典型的直流配电网系统,在电网中针对不同的谐波源安装多个直流滤波器.基于RGA理论,分析滤波器内的控制器参数以及电网电气参数对滤波器交互影响大小的关系.
图5
图5
不同参数对λc的幅值及相位的影响
Fig.5
Influence of different parameters on amplitude and phase of λc
表1
DC-APF1控制器参数以及电气参数对
Tab.1
| 参数 | 参数变化趋势 | λc变化趋势 |
|---|---|---|
| Z1 | 增大 | 逐渐减小至1 |
| Kp | 增大 | 从λc>1逐渐减小至λc<1 |
| kpu | 增大 | 不变 |
| kiu | 增大 | 不变 |
图6
图7
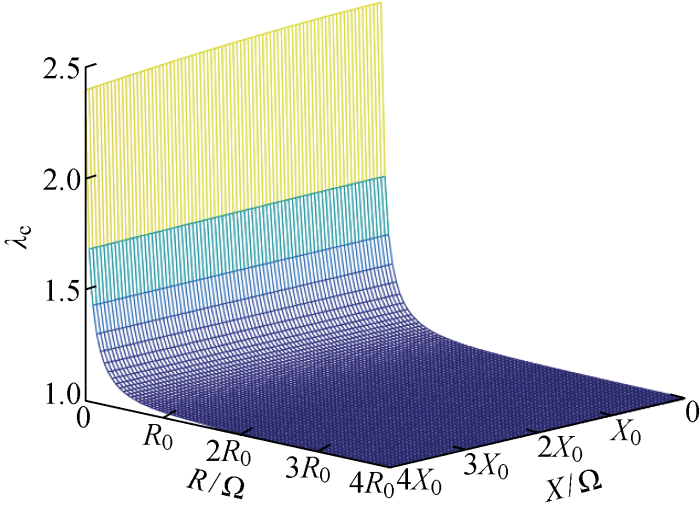
图7
电气距离电阻和电抗对λc的影响
Fig.7
Influence of electrical distance resistance and reactance on λc
表2
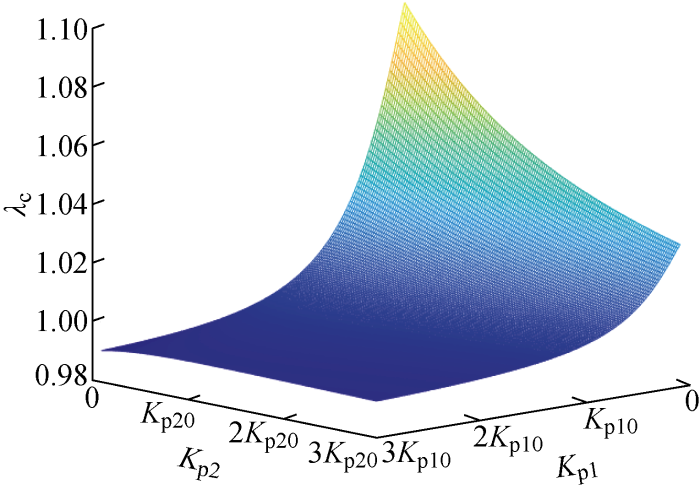
滤波器控制器及电气参数对
Tab.2
| 参数 | 参数变化趋势 | λc幅值变化 |
|---|---|---|
| Kp1 | 增大 | 从λc>1减少至λc<1 |
| Kp2 | 增大 | 从λc>1减少至λc<1 |
| R/Ω | 增大 | 逐渐减少至1 |
| X/Ω | 增大 | 不变 |
3 算例分析
表3 系统主要参数
Tab.3
| 设备名称 | 参数 | 取值 |
|---|---|---|
| AC/DC1 | udc/V | 1 000 |
| 开关频率fs/kHz | 10 | |
| 直流侧稳压电容Cac/μF | 2 200 | |
| AC/DC2 | udc/V | 1 000 |
| fs/kHz | 2 | |
| Cac/μF | 2 200 | |
| 负荷 | 直流电阻性负荷Rdc/Ω | 30 |
| P/kW | 10 | |
| 交流系统 | 电压U/kV | 0.6 |
| 光伏电源 | 输出功率Pout/kW | 5 |
| 线路 | R/(Ω·km-1) | 0.4 |
| X/(μH·km-1) | 500 |
表4 滤波器参数
Tab.4
| 设备 | 参数 | 取值 |
|---|---|---|
| DC-APF1 | L/mH | 12.5 |
| C/μF | 2 200 | |
| uc/V | 1 300 | |
| DC-APF2 | L/mH | 10 |
| DC-APF3 | C/μF | 2 200 |
| uc/V | 1 300 |
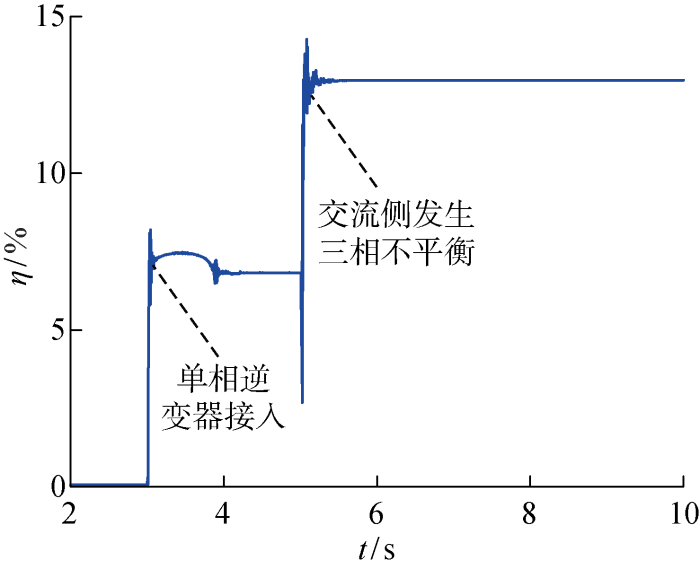
图8
图8
正常运行下的二次谐波电压含量
Fig.8
Second harmonic voltage content under normal operation
正常运行时,母线上二次谐波电压含量较低,t=3 s时,单相逆变器的接入使得二次谐波电压含量增加至7.1%;t=5 s时设置交流侧三相不平衡,二次谐波电压含量增加至12.5%,严重影响电网的正常运行.
3.1 仿真工况1
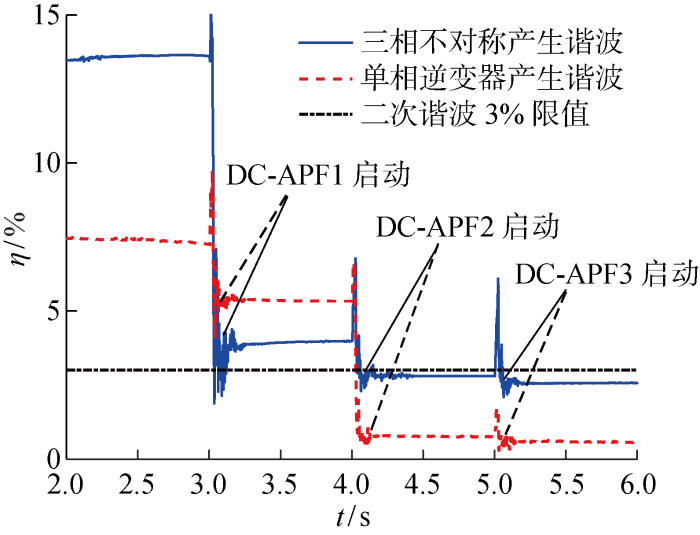
直流配网中,针对三相不平衡与单相换流器产生的二次谐波分量,接入多个分布式DC-APF进行滤波,直流母线上的二次谐波电压含量如图9所示.以交流侧发生三相不平衡为例,t=3 s时投入使用DC-APF1,t=4 s时投入使用DC-APF2,t=5 s时投入使用DC-APF3.图9中,以三相不平衡产生的二次谐波为例,DC-APF1抑制了大部分二次谐波,稳定时谐波含量为4.0%,DC-APF2启动后使得谐波含量降为2.7%;DC-APF3启动后直流母线二次谐波含量降为2.5%.治理单相逆变器产生的二次谐波时,直流母线电压谐波含量变化情况相似.两个场景中,与谐波源距离较近的滤波器抑制谐波效率高,而距离较远的滤波器有一定的辅助治理效果.
图9
图9
不同谐波源工况下直流母线二次谐波电压含量
Fig.9
Second harmonic voltage content of DC bus under different harmonic sources
当系统中同时存在多种谐波源时,分别采用分布式DC-APF和集中式DC-APF进行谐波治理,两个场景中DC-APF的总容量相同,直流母线二次谐波电压含量如图10所示.当采用分布式DC-APF治理方法时,DC-APF2启动后,系统中二次谐波含量为1.4%,低于采用集中式DC-APF治理后4.2%的二次谐波含量,且满足单次谐波电压含量低于3%的要求.同样,距离谐波源较远的DC-APF3有一定的辅助治理作用.因此,在多谐波源场景下,分布式谐波治理方法要优于集中式谐波治理方法.
图10
图10
不同谐波治理方式下直流母线二次谐波电压含量
Fig.10
Second harmonic voltage content of DC bus under different harmonic control methods
仿真工况1说明在多谐波源场景下,分布式滤波器能够有效抑制各谐波源产生的谐波电流,降低母线上的谐波电压.但控制器参数选择不当时,滤波器的滤波效果变化幅度较大,其原因为控制器之间产生耦合干扰,具体影响参数分析见仿真工况2.
3.2 仿真工况2
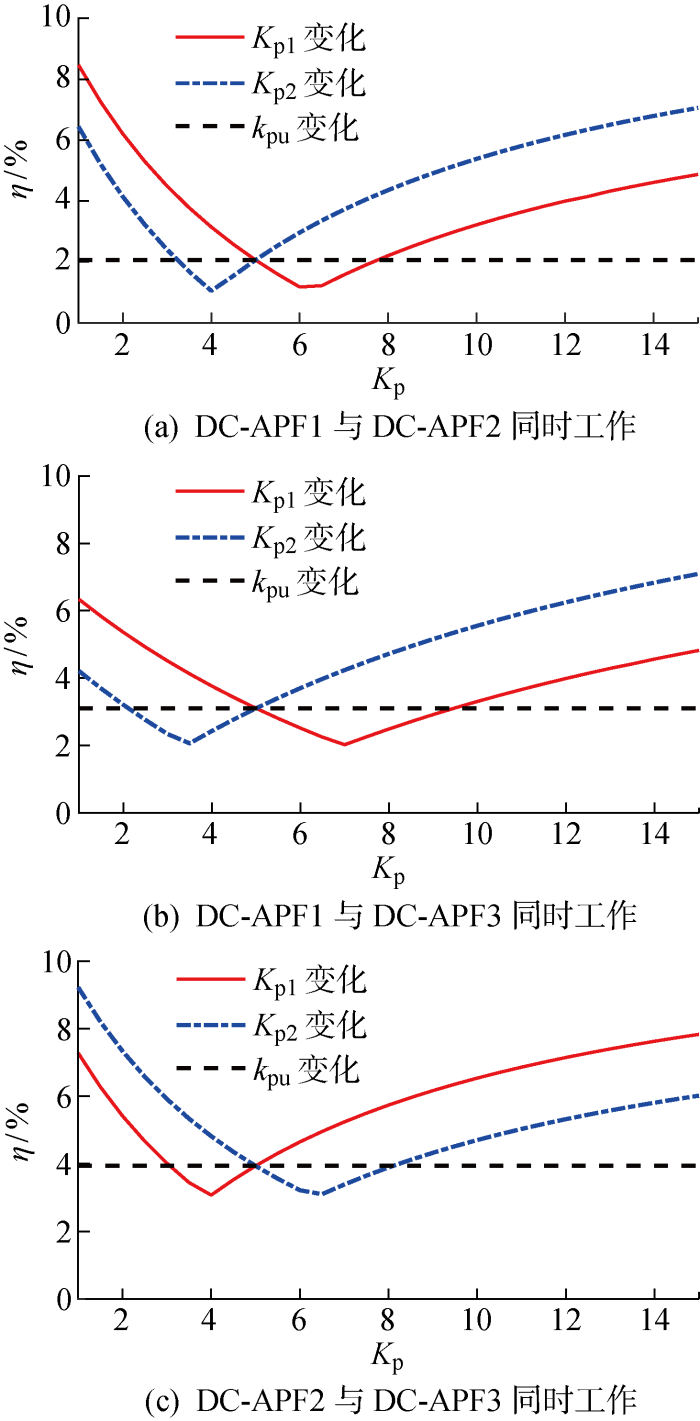
仿真工况2为在该直流配电网系统中使用两个不同的分布式DC-APF工作,分析控制器参数以及电网参数对交互影响的仿真验证.图11和图12分别为改变两个滤波器之间的电气距离Z1,DC-APF的放大系数Kp、PI控制器参数kpu并且系统稳定时,直流母线上的二次谐波电压含量,kiu变化情况与kpu相同,图中不再重复表示.图11中,DC-APF1与DC-APF2的组合滤波效果明显优于其他两个组合;随着电气距离的增加,直流母线二次谐波电压越来越小,滤波器之间的交互影响越小,滤波效果越好.图12中,直流电压谐波检测放大系数Kp存在一个临界值,当小于该临界值时,滤波效果变化较小,能有效去除谐波,随着Kp的不断增大,滤波器组合工作的滤波性能越来越差,当系数超过一定裕度时,严重影响系统供电可靠性;无论PI控制器参数kpu(kiu)如何变化,直流母线二次谐波电压幅值变化均较小,改变该参数对交互影响的变化可以忽略;上述仿真分析结果与理论分析结果相似.表5、表6为3种场景下,投入使用DC-APF1与DC-APF2,不同Z1和Kp1所对应的直流母线中二次谐波含量(ηh,h=1, 2, 3,表示场景数),其变化趋势分别与图11、图12类似.其中场景1为电网内仅设置交流侧三相不平衡产生的二次谐波;场景2为电网内仅接入单相逆变器产生的二次谐波;场景3为电网内两种二次谐波源均存在.
图11
图11
电气距离Z1变化时直流母线二次谐波电压含量(Kp=5,kpu=15,kiu=0.1)
Fig.11
DC bus second harmonic voltage content at variation in power distance Z1 (Kp=5,kpu=15,kiu=0.1)
图12
图12
比例系数变化时直流母线二次谐波电压含量
Fig.12
DC bus second harmonic voltage content at variation controller parameters
表5
Tab.5
| Z1/Ω | η1/% | η2/% | η3/% |
|---|---|---|---|
| 0.4 | 2.15 | 1.50 | 2.71 |
| 0.8 | 1.36 | 1.00 | 1.69 |
| 1.5 | 0.78 | 0.57 | 1.06 |
| 2.0 | 0.59 | 0.48 | 0.78 |
表6
Tab.6
| Kp1 | η1/% | η2/% | η3/% |
|---|---|---|---|
| 1 | 5.33 | 3.58 | 6.43 |
| 5 | 1.76 | 1.10 | 2.06 |
| 8 | 3.82 | 2.26 | 4.36 |
| 12 | 4.83 | 3.42 | 6.17 |
电气距离越大,DC-APF间耦合干扰越弱,与交流系统中滤波器交互影响机理分析结论具有一致性.交流滤波器与直流滤波器拓扑和控制不同,控制器参数对耦合干扰的影响存在差异.
由于实际场景中电气距离变化范围有限,因此可通过调节Kp来降低滤波器之间交互影响,最优情况可使得λc为1,此时母线上二次谐波量最少.后续网架结构或DC-APF需要重新安装时,根据新的拓扑重新建立等效模型,并计算相应的相对增益矩阵对Kp进行重新整定.
3.3 实验验证
为验证所提交互影响机理分析方法的有效性,搭建了RT-LAB半实物仿真实验,实验平台如图13所示,其对应的实验参数与仿真参数一致.
图13
图14中,场景1为滤波器控制器参数无优化时直流母线电压,场景2为滤波器控制器参数优化后直流母线电压.在DC-APF启动之前,直流母线谐波电压含量为8.9%;t=0.38 s时,DC-APF1启动后,谐波电压含量降到4.6%,能够有效吸收一定的谐波电流,降低谐波电压;t=0.68 s时,DC-APF2启动,直流母线电压稳定后,场景1和场景2中二次谐波电压含量分别为3.3%、2.0%,优化的参数能有效提升滤波器的协同滤波能力.
图14
由实验结果可知,对DC-APF放大系数Kp进行优化配置,能在一定程度上减小滤波器之间的耦合干扰,增强协同滤波能力.
4 结论
针对直流配网二次谐波滤波器间存在交互影响的问题,本文根据直流有源滤波器的拓扑结构和控制方法,建立了多滤波器诺顿等效并网模型,基于相对增益矩阵,提出了多滤波器的电气距离和控制参数影响滤波效果的分析方法.在PSCAD/EMTDC和RT-LAB软件中分别建立了直流配网仿真模型和半实物仿真模型,验证了分析方法的有效性和适用性,主要结论如下:
(1) 通过对相对增益矩阵对角线元素的频谱分析,滤波器间电气距离和直流电压谐波检测放大系数对滤波器的耦合干扰存在一定影响,而PI控制器参数无影响.
(2) 电气距离对滤波器耦合干扰的影响呈线性关系;随着电气距离的增大,耦合干扰逐渐减少.而直流电压谐波检测放大系数对耦合干扰的影响存在拐点;放大系数的选择离拐点越近,耦合干扰越小.
(3) 在电气距离一定的情况下,合理选择各个滤波器的谐波检测放大系数可有效减小滤波器之间的交互影响,实现直流母线二次谐波抑制效果最佳.
所提方法可为直流配电网多滤波器选址、控制参数选择提供理论依据,有效减少滤波器间的耦合干扰,具有良好的应用价值与前景.
参考文献
光储直流配电网灵活虚拟惯性控制策略
[J].
Flexible virtual inertial control strategy for optical storage DC distribution network
[J].
柔性直流配电网故障分析
[J].
Failure analysis of flexible DC distribution network
[J].
Power quality assessment in shipboard microgrids under unbalanced and harmonic AC bus voltage
[J].DOI:10.1109/TIA.28 URL [本文引用: 1]
直流侧电压高二次纹波率条件下的单相逆变器谐波削弱调制
[J].
Single-phase inverter harmonic attenuation modulation under the condition of high secondary ripple rate of DC side voltage
[J].
混合微电网虚拟联合谐波抑制器控制策略
[J].
Control strategy of virtual joint harmonic suppressor for hybrid microgrid
[J].
基于测量值的无源滤波器设计新方法及其应用
[J].
New method and application of passive filter design based on measured value
[J].
混合型有源滤波器接入LCC-HVDC后的谐振分析及抑制方法
[J].
Resonance analysis and suppression method of hybrid active filter connected to LCC-HVDC
[J].
AC filterless flexible LCC HVDC with reduced voltage rating of controllable capacitors
[J].DOI:10.1109/TPWRS.59 URL [本文引用: 1]
A DC-link modulation scheme with phase-shifted current control for harmonic cancellations in multidrive applications
[J].
Mitigation of low-frequency current ripple in fuel-cell inverter systems through waveform control
[J].DOI:10.1109/TPEL.2012.2205407 URL [本文引用: 1]
A power decoupling method based on four-switch three-port DC-DC-AC converter in DC microgrid
[J].DOI:10.1109/TIA.2014.2327162 URL [本文引用: 1]
含滤波器的多换流站谐波阻抗模型与谐波交互影响研究
[J].
Research on harmonic impedance model and harmonic interaction of multi-converter stations with filters
[J].
多馈入直流输电系统谐波交互影响分析
[J].
Harmonic interaction analysis of multi-infeed DC transmission system
[J].
Dynamic interaction analysis of APF systems
[J].DOI:10.1109/TIE.2013.2289896 URL [本文引用: 1]
基于频域RGA原理的多并联三相逆变器间交互影响分析
[J].
Interaction analysis of multi-parallel three-phase inverters based on frequency domain RGA principle
[J].