作为有效节省产线投资、聚焦核心生产、统筹外包维护的先进制造模式,延伸传统制造价值链的租赁化生成正逐渐成为制造业转型升级的新趋势[1].为多区域企业提供最优的运维规划与调度决策,是出租方“产品+服务”整体解决方案中的关键环节[2].随着广域服务型制造的广泛应用,承租企业规模不断扩大,进而带动维护外包服务的全球多区域化发展.因此,出租方需要设立多个维护中心以满足各承租企业的动态运维需求[3].同时,面向制造产线集群的运维规划不是独立作业,而是与维护人员调度和服务路线优化紧密相连且相互影响[4].综上所述,面向多中心租赁服务网络的运维调度需要综合考虑维护能力、资源协同、运输成本及延期惩罚等约束对全局性决策的影响,并进一步考虑多中心维护团队之间的协同调度优化,以确保多中心租赁网络的运行可靠性和运维经济性.
目前面向租赁服务网络的运维策略已受到学术界的热点关注,Camci[5]提出了一种基于故障概率预测的租赁设备集群维护规划与人员派遣模型,利用遗传算法最小化故障风险成本与维护成本,得到成本最优的维护方案.López-Santana等[6]针对租赁设备集群的维护调度与路由问题,提出了一种两阶段迭代求解模型,首先通过最小化总预期成本得到各设备的维护需求,接着基于设备地理位置与维护团队信息,动态输出各维护团队的服务路线与各维护作业的开始时刻.Irawan等[7]提出了一种针对海上风力发电(简称风电)场维护调度问题的优化模型,以输出最小维护成本的最佳维护团队路线.在此基础上,一些学者们将维护调度与路由问题由单租赁设备集群拓展至多设备制造系统集群.Nguyen等[8]通过考虑设备间的经济相关性与地理相关性,动态输出总成本结余最大的维护调度与路由方案.司国锦等[9]通过对多设备制造系统集群运维调度问题的分析与建模,建立三层机会维护策略,利用最早的设备预知维护机会进行系统维护成组并得出团队的最佳服务路线.此外,Diaz-Ramirez等[10]针对飞机维护调度中的单一维护中心单个团队路径规划问题,通过建立飞机与人员综合优化模型得出最佳路径方案.
上述研究主要集中于单一维护中心的运维调度问题,尚未考虑多个维护中心之间的维护团队协同共享.随着多中心网络的发展,越来越多的学者们通过研究多个中心之间的维护团队协同调度以实现资源共享与配置优化.Schrotenboer等[11]针对海上风电机组的多服务中心人员分配与路由规划问题,通过开发自适应领域搜索算法以得出最优的维护船只路线,进而减少船舶航行次数.韩笑乐等[12]针对集装箱进出口码头泊位-堆场的调度问题,通过设计两阶段禁忌搜索算法以最小化船舶总在港时间.Li等[13]针对农机运维的非对称多中心路径优化问题,输出最优服务方案,以同时满足上门维护服务时的节点服务如零件更换和有向弧服务(将故障的农用机械从农场位置运至制定的维护中心)需求.辜勇等[14]针对多中心协同配送的车辆路径问题,设计一种三阶段求解算法,输出总成本最小的配送方案.Wang等[15]针对资源共享和温度控制约束下的多中心冷链物流协同配送问题,通过最小化总成本与运输车辆数目输出最佳物流运营策略.
上述多中心协同调度研究主要是对传统车辆路径问题的拓展研究,且普遍涉及给定服务需求的路由决策,尚未考虑系统成组维护与团队协同调度的综合优化.然而在多中心租赁服务网络中,维护需求动态变化大、约束条件类型多,将成组维护决策与团队协同调度优化同时考虑,根据不同承租方企业的实际维护需求,统筹维护能力、资源协同、运输成本及延期惩罚等要素,通过协同规划输出各维护团队的出发点与服务路线,降本增效潜能更大.因此,本文提出一种多中心协同维护调度(MCMS)策略.首先在系统层考虑成组维护决策优化,综合考虑设备维护停机、累积失效损失以及系统组合选取对维护决策的影响,通过最小化总维护成本得出各承租方串联系统的成组维护集合.然后基于系统层输出的成组维护集合,进一步考虑各企业地理位置与各维护中心团队数目,输出总调度成本最小的各中心维护团队的服务路线.最后通过算例验证所提出策略的有效性.
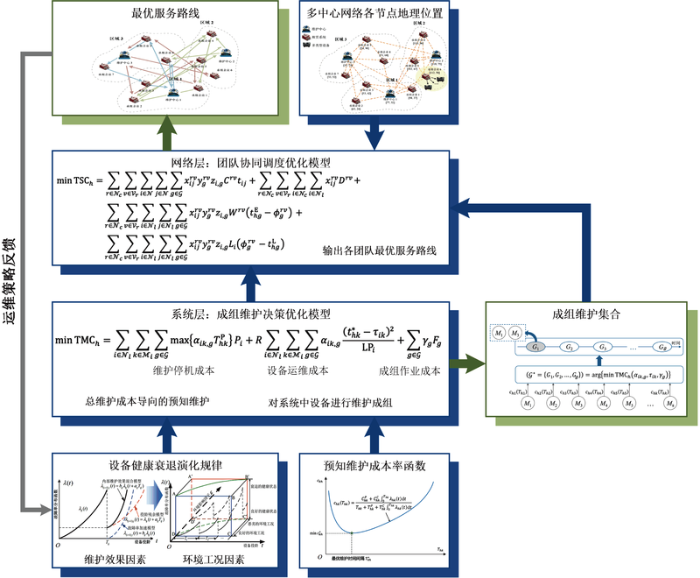
1 问题描述
本文所研究的多中心运维调度问题主要面向由地理分布的串联租赁系统集群与多个维护中心构成的多中心租赁服务网络,针对服务型制造转型升级下出租方全球多中心运维带来的维护资源调度挑战,为解决系统成组维护需求与维护团队协同共享等问题造成的运维复杂度难点,提出了系统层、网络层动态交互的MCMS策略.旨在确保各承租方制造系统正常运作的同时,灵活调配各中心的维护团队资源,以降低总成本并提升维护团队利用效率.首先,在系统层针对不同类型设备的衰退模型与串联系统结构,考虑设备之间的经济依赖性,优化各串联系统的成组维护方案以减少不必要的系统维护停机.然后,基于优化得出的成组维护方案,在网络层通过平衡跨中心维护团队共享与局域内维护需求响应之间的相互制约关系,输出各中心维护团队的最佳服务路线,以实现跨区域的维护团队资源共享.双层交互的MCMS策略的建模框架如图1所示,各层交互决策优化流程如下.
图1
(1) 针对包含多设备串联系统群组的系统层,基于设备的衰退演化规律建模预知维护的成本率函数,综合考虑设备维护停机、累积失效损失以及系统组合选取对维护决策的影响,对同一系统内的设备进行维护成组,建立成组维护优化模型并输出总维护成本最小的成组维护集合.
(2) 针对全球分布的多个承租方系统与多个维护中心构成的网络层,实时拉动系统层各租赁系统的成组维护集合,整合多中心租赁服务网络各中心的维护团队资源与各节点维护需求,进一步考虑服务路由优化、团队派遣选取和维护响应速度对调度决策的影响,输出最小化总调度成本所对应的各团队最优服务路线,以帮助各中心的维护人员提前安排所需工具与备件,并基于优化路线及时地实施维护作业.
2 租赁系统的成组维护决策优化
针对各租赁系统的维护需求评估,系统层研究的成组维护优化可描述为:多中心租赁服务网络有L个待维护的租赁系统,各系统由Mi个租赁设备串联构成.基于各设备的故障率函数,综合考虑设备维护停机、累积失效损失以及系统组合选取对维护决策的影响,构建由维护停机成本、设备运维成本和成组作业成本构成的总维护成本.通过最小化总维护成本,得到租赁系统的最优维护时间窗.系统层所涉及的符号如表1所示.
表1 成组维护决策优化模型的符号及含义
Tab.1
| 符号类别 | 符号 | 含义 |
|---|---|---|
| 集合与索引 | Mi | 租赁系统i中的设备集合(索引k∈Mi= |
| Nl | 租赁系统集合(索引i, j∈Nl= | |
| G | 成组维护集合(索引g∈G= | |
| 模型参数 | λhk(t) | 设备k在第h个维护周期的故障率函数 |
| chk(Thk) | 设备k在第h个维护周期内的成本率函数 | |
| 设备k在第h个维护周期的预知维护作业时长 | ||
| Pi | 租赁系统i单位时间的维护停机损失 | |
| R | 设备运维成本的系数项 | |
| LPi | 租赁系统i的租赁服务期时长 | |
| Fg | 各成组维护集合的固定成本 | |
| wg | 维护时间窗的窗宽 | |
| 各成组维护集合对应的维护时间窗 | ||
| nhg | 各成组维护集合中所需维护的设备数目 | |
| 执行各成组维护集合所需的维护时长 | ||
| 决策变量 | αik, g | 租赁系统i的设备k在成组维护集g中时为1,否则为0 |
| τik | 租赁系统i的设备k的预知维护作业开始时间 | |
| γg | 成组维护集g中有待维护的设备时为1,否则为0 |
针对各租赁系统中的设备k,在第1个维护周期即h=1时,故障率函数服从运维领域设备常用的威布尔分布.在h≥2的维护周期中,综合考虑内部维护效果和外部环境工况,引入役龄残余因子ahk和环境影响因子bhk,构建设备k的故障率函数,具体的表达式如下:
式中:βk和ηk为设备k威布尔分布的形状和位置参数;T'(h-1)k为网络层团队协同调度方案执行后所更新的设备维护周期.
各设备的预知维护间隔Thk表示设备k在第h-1个预知维护作业和第h个预知维护作业之间的运行周期.对于单个租赁设备而言,每个预知维护间隔Thk内的成本项包括一次预知维护作业的成本
式中:
对于由多台设备串联组成的租赁系统而言,针对多机系统的维护优化不仅需要考虑各台设备的实时衰退趋势,还需要系统性地分析设备之间的相互依赖性,依据现有维护资源对各系统的维护作业进行规划,以满足企业降低维护成本的需求.而将同一系统中的多台设备进行成组维护不仅可以避免因维护导致的系统频繁停机,而且可以减少维护团队的重复派遣.基于各设备的独立维护时点
上述优化模型的目标函数式(4)表示最小化总维护成本,具体包括维护停机成本、设备运维成本和成组作业成本.约束式(5)确保每台租赁设备的预知维护作业由一个成组维护集合执行,且只执行一次.约束式(6)限制成组维护集合个数的取值范围,即不小于租赁系统总数I且不大于总设备数目.确保每个成组维护集合中至少有一台设备且不超过一个系统内的设备总数.约束式(7)保证每个成组维护集合仅包含同一系统的多台设备,而不涉及不同地理分布设备间的成组维护规划.约束式(8)~(9)给出了决策变量集的定义域.
通过求解上述优化模型,获得总维护成本最小的成组维护方案,即每个成组维护集合内的设备信息、维护作业时长和维护开始时间.为符合实际工业场景,将得出的维护开始时间点拓展至维护时间窗,则各成组维护集合对应的维护时间窗[
基于上述优化模型求解和维护时间窗拓展,对于任意一个非空的成组维护集合g∈G,包含以下3项维护需求信息:① 所需维护的设备数目nhg=
3 多中心网络的团队协同调度优化
基于系统层优化得出的成组维护集合G,网络层的团队协同调度优化问题可作如下数学描述:多中心租赁服务网络可用有向图G=(N, A)表示.其中点集合N=Nc∪Nl包括维护中心集合Nc={1, 2, …, C}和承租方集合Nl={1, 2, …, L},其中各承租方网络节点为多类型设备组成的串联产线系统.弧集合A={(i, j)|i, j∈N, i≠j}表示维护中心与租赁系统之间的可行路线.同时每一条维护团队的服务派遣路线都必须开始和截止于同一维护中心.Vr={1, 2, …, Vr}表示维护中心 r∈Nc处的维护团队集合,且所有的维护团队可表示为V=
表2 团队协同调度优化模型的符号及含义
Tab.2
| 符号类别 | 符号 | 含义 |
|---|---|---|
| 模型参数 | Crv | 维护团队v∈Vr的单位时间路由成本 |
| tij | 租赁系统i到租赁系统j的路由时间 | |
| Drv | 维护团队v∈Vr的固定派遣成本 | |
| Wrv | 维护团队v∈Vr的单位时间的等待成本 | |
| Li | 维护团队v∈Vr的单位时间的延时惩罚成本 | |
| qrv | 维护团队v∈Vr一次派遣的最大可维护的设备数目 | |
| 决策变量 | 维护团队v∈Vr由租赁系统i前往租赁系统j时为1,否则为0 | |
| 维护团队v∈Vr被派遣以执行成组维护集合g时为1,否则为0 | ||
| zi,g | 成组维护集合g由系统i中的设备组成时为1,否则为0 | |
| 维护团队v∈Vr执行成组维护集合g的实际开始时点 |
基于系统层优化模型得出的成组维护集合g∈G,以及对应的维护数据nhg、维护时长
上述优化模型的目标函数式(11)表示最小化总维护成本,具体包括团队路由成本、固定派遣成本、服务等待成本和延时惩罚成本.约束式(12)保证每个派遣的维护团队必须从维护中心出发并最终回到同一个维护中心.约束式(13)表明每一只维护团队所对应的服务路径进入各租赁系统,也需要从该节点出来.约束式(14)旨在将派遣的团队数目限制在该维护中心现有的技术人员团队的总数之内.约束式(15)限制维护团队所能执行维护作业的设备总数目.约束式(16)~(17)为各成组维护集合实际开始时点的计算公式.约束式(18)~(19)给出了决策变量集的定义域.
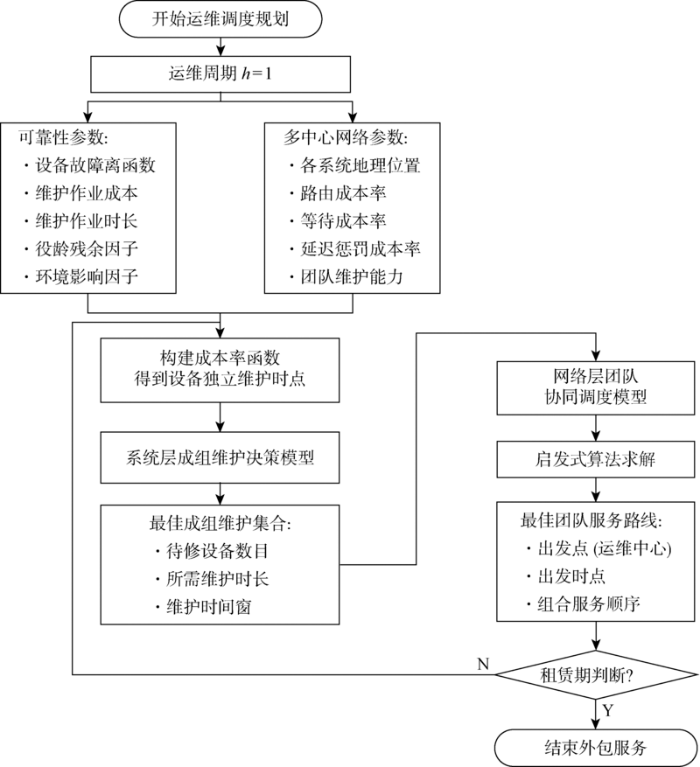
4 策略流程
首先,基于各设备的故障率函数与预知维护成本率函数,通过综合考虑设备维护停机、累积失效损失以及系统组合选取对维护决策的影响,建立系统层的成组维护决策优化模型.考虑租赁系统内设备的经济相关性,系统层优化模型的目标是对各串联租赁系统内所有设备的预知维护作业进行成组,由于不同区域系统之间的成组维护不存在相关制约与影响,所以可以通过并行地优化各系统内设备的成组维护,并运用精确求解算法得出最优解集.然后,基于系统层优化模型的求解结果,得到成组集合的nhg、
图2
图2
多中心协同维护调度策略的流程图
Fig.2
Flow chart of multi-center collaborative maintenance scheduling strategy
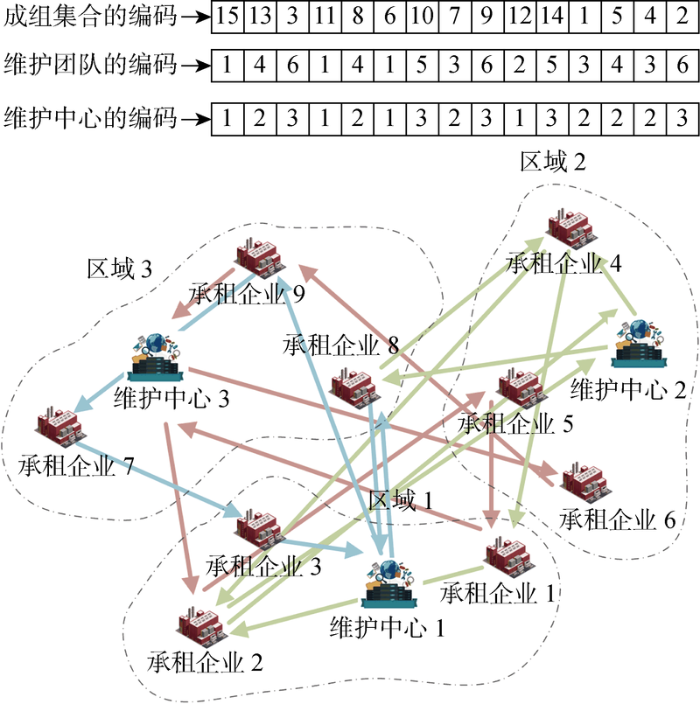
为了高效求解网络层团队协同调度优化模型,获得成本有效的团队服务路线方法,运用遗传算法进行优化求解.本文运用3个实数对路由决策进行编码,一个代表成组维护集合,一个代表执行维护作业的维护团队,一个代表维护团队的出发点,具体实例如图3所示.该编码实例表示有15个优化得出的成组维护集合,以及6支维护团队的服务路线.例如,维护团队1从维护中心1出发,依次服务承租系统9、7和3,最后返回维护中心1.
图3
5 算例分析
表3 各租赁设备的可靠性和维护参数
Tab.3
| k | i | βk | ηk | bhk | ahk | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3.15 | 5 600 | 1.05 | 0.025 | 6 500 | 18 000 | 20 | 66 |
| 2 | 1.70 | 4 900 | 1.036 | 0.016 | 9 000 | 30 000 | 25 | 74 | |
| 3 | 2.51 | 5 500 | 1.02 | 0.018 | 6 000 | 17 000 | 14 | 48 | |
| 4 | 2 | 1.94 | 4 200 | 1.015 | 0.023 | 3 900 | 8 800 | 10 | 38 |
| 5 | 1.85 | 6 400 | 1.03 | 0.038 | 4 600 | 21 000 | 12 | 68 | |
| 6 | 2.95 | 5 300 | 1.025 | 0.048 | 3 200 | 6 800 | 8 | 18 | |
| 7 | 3 | 2.57 | 6 100 | 1.03 | 0.038 | 6 700 | 28 000 | 12 | 68 |
| 8 | 1.83 | 6 000 | 1.04 | 0.036 | 4 600 | 22 000 | 10 | 22 | |
| 9 | 2.97 | 4 300 | 1.025 | 0.048 | 3 900 | 7 000 | 8 | 19 | |
| 10 | 4 | 1.84 | 4 200 | 1.015 | 0.023 | 4 300 | 8 200 | 10 | 39 |
| 11 | 1.72 | 5 500 | 1.03 | 0.038 | 7 600 | 26 000 | 12 | 68 | |
| 12 | 1.83 | 3 800 | 1.04 | 0.036 | 9 800 | 16 000 | 10 | 22 | |
| 13 | 5 | 1.74 | 4 300 | 1.036 | 0.016 | 9 000 | 20 000 | 25 | 72 |
| 14 | 2.51 | 5 500 | 1.02 | 0.018 | 6 000 | 17 000 | 14 | 48 | |
| 15 | 3.13 | 4 600 | 1.018 | 0.036 | 7 000 | 13 000 | 16 | 40 | |
| 16 | 6 | 2.93 | 4 700 | 1.025 | 0.048 | 4 000 | 6 800 | 8 | 18 |
| 17 | 1.83 | 3 500 | 1.04 | 0.036 | 9 800 | 16 000 | 10 | 22 | |
| 18 | 1.84 | 4 500 | 1.04 | 0.018 | 8 200 | 21 000 | 25 | 74 | |
| 19 | 7 | 2.62 | 5 000 | 1.05 | 0.025 | 6 000 | 15 000 | 20 | 66 |
| 20 | 2.34 | 5 300 | 1.027 | 0.046 | 7 000 | 22 000 | 22 | 60 | |
| 21 | 2.89 | 4 200 | 1.04 | 0.036 | 9 800 | 16 000 | 10 | 24 | |
| 22 | 8 | 2.25 | 5 500 | 1.03 | 0.038 | 9 600 | 28 000 | 12 | 68 |
| 23 | 1.78 | 3 600 | 1.04 | 0.036 | 9 800 | 16 000 | 10 | 22 | |
| 24 | 1.76 | 5 600 | 1.036 | 0.016 | 8 000 | 30 000 | 25 | 74 | |
| 25 | 9 | 3.29 | 4 400 | 1.018 | 0.036 | 7 000 | 13 000 | 16 | 40 |
| 26 | 2.51 | 5 200 | 1.02 | 0.018 | 6 000 | 17 000 | 14 | 48 | |
| 27 | 1.84 | 4 200 | 1.015 | 0.023 | 3 600 | 8 800 | 10 | 38 |
表4 多中心租赁网络中任意节点之间的路由时间
Tab.4
| 节点 | i1 | i2 | i3 | i4 | i5 | i6 | i7 | i8 | i9 | r1 | r2 | r3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i1 | — | 29 | 23 | 30 | 15 | 10 | 34 | 21 | 35 | 11 | 22 | 37 |
| i2 | — | 11 | 49 | 37 | 37 | 15 | 26 | 34 | 18 | 46 | 25 | |
| i3 | — | 40 | 28 | 30 | 11 | 16 | 24 | 13 | 37 | 18 | ||
| i4 | — | 15 | 23 | 45 | 24 | 28 | 36 | 11 | 39 | |||
| i5 | — | 10 | 36 | 16 | 27 | 22 | 9 | 34 | ||||
| i6 | — | 40 | 23 | 35 | 20 | 13 | 40 | |||||
| i7 | — | 21 | 22 | 24 | 44 | 11 | ||||||
| i8 | — | 14 | 18 | 24 | 18 | |||||||
| i9 | — | 31 | 33 | 13 | ||||||||
| r1 | — | 30 | 30 | |||||||||
| r2 | — | 42 | ||||||||||
| r3 | — |
表5 系统层与网络层的模型参数设置
Tab.5
| 系统层模型参数设置 | 网络层模型参数设置 | |||
|---|---|---|---|---|
| 参数 | 取值 | 参数 | 取值 | |
| Pi/(元·h-1) | 300 | Crv/(元·h-1) | 200 | |
| R/元 | 6 000 | Drv/元 | 20 000 | |
| Fg/元 | 4 000 | Wrv/(元·h-1) | 200 | |
| wg/h | 24 | Li/(元·h-1) | 300 | |
| LPi/h | 17 520 | qrv/台 | 7 | |
| ∑Vr(r∈Nc)/个 | 6 | |||
表6 第1个周期的系统层成组维护决策
Tab.6
| 序号 | i | 成组维护集合 | nhg | [ | |
|---|---|---|---|---|---|
| 1 | 1 | {1, 3} | 2 | 20 | [2 898, 2 922] |
| 2 | 1 | {2} | 1 | 25 | [3 167, 3 191] |
| 3 | 2 | {4, 6} | 2 | 10 | [3 069, 3 093] |
| 4 | 2 | {5} | 1 | 12 | [2 845, 2 869] |
| 5 | 3 | {7} | 1 | 12 | [3 261, 3 285] |
| 6 | 3 | {8, 9} | 2 | 10 | [2 865, 2 889] |
| 7 | 4 | {10} | 1 | 10 | [2 799, 2 823] |
| 8 | 4 | {11, 12} | 2 | 12 | [3 253, 3 277] |
| 9 | 5 | {13, 14, 15} | 3 | 25 | [3 170, 3 194] |
| 10 | 6 | {16, 17, 18} | 3 | 25 | [3 011, 3 035] |
| 11 | 7 | {19, 20, 21} | 3 | 22 | [2 912, 2 936] |
| 12 | 8 | {22} | 1 | 12 | [2 833, 2 857] |
| 13 | 8 | {23, 24} | 2 | 25 | [3 113, 3 137] |
| 14 | 9 | {25} | 1 | 16 | [3 069, 3 093] |
| 15 | 9 | {26, 27} | 2 | 14 | [2 864, 2 888] |
| 总维护成本 TMC1=155 017元 | |||||
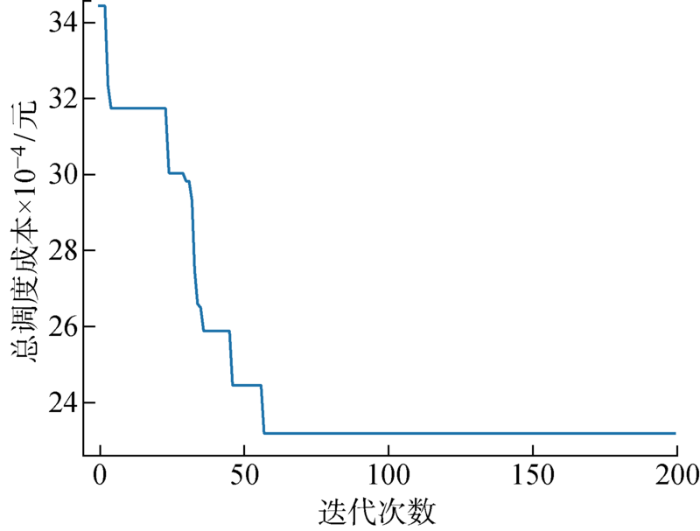
所有算法均使用Python3运行,实验平台操作系统的具体配置为2.00 GHz Intel Core i5处理器,16 GB运行内存.利用相应曲面法进行算法参数优化与实验测试,遗传算法参数设置如下:种群规模取160,迭代次数取200代,变异概率为0.85,交叉概率为0.1,并选用轮盘赌选择、两点互换变异、单点交叉等操作.基于表6得到的各串联租赁系统的维护需求,运用遗传算法对网络层的优化模型进行求解,在满足各团队的维护能力约束条件下,得到总调度成本最小对应的各团队服务路线,如表7所示.同时,遗传算法的收敛曲线如图4所示,且一次运行的时间约为65 s,符合出租方实际运维管理要求.可以看出,遗传算法结果在50代以内快速下降,60代左右算法逐渐收敛于最优结果.
表7 第1个周期的网络层团队协同调度方案
Tab.7
| 团队序号 | 出发点 | 出发时点 | 组合服务顺序 | 租赁系统服务路线 |
|---|---|---|---|---|
| 1 | 维护中心r1 | 3 011 | (3, 14, 10) | r1→2→9→6→r1 |
| 2 | 维护中心r1 | 3 113 | (13, 2, 9) | r1→8→1→5→r1 |
| 3 | 维护中心r2 | 2 865 | (6, 11) | r2→3→7→r2 |
| 4 | 维护中心r2 | 3 253 | (8, 5) | r2→4→3→r2 |
| 5 | 维护中心r3 | 2 799 | (7, 12, 15, 1, 4) | r3→4→8→9→1→2→r3 |
| 总调度成本TSC1=237 200 元 | ||||
图4
图4
第1个周期网络层模型动态寻优的收敛曲线
Fig.4
Convergence curve of the network-level dynamic optimization at the first cycle
在得出当前第h个周期的维护方案后,根据各设备的实际开始维护时间更新各设备的维护周期T'hk,并对下一个h+1周期设备的故障率函数进行更新λ(h+1)k(t).决策者基于更新后的设备故障率函数,对多中心租赁服务网络的各系统进行成组维护与团队协同调度,以实现长期的“产品+服务”运维管理.本文考虑两年的租赁期,则剩下各周期的维护方案如表8所示.
表8 贯序各周期的维护方案
Tab.8
| h | 成组维护集合G | 最优服务路线 | 对应的团队出发点 |
|---|---|---|---|
| 1 | {1, 3}{2}{4, 6}{5}{7}{8, 9}{10}{11, 12}{13, 14, 15} {16, 17, 18}{19, 20, 21}{22}{23, 24}{25}{26, 27} | (2→9→6, 8→1→5, 3→7, 4→3, 4→8→9→1→2) | (1, 2, 3, 2, 1) |
| 2 | {1, 3}{2}{4, 6}{5}{7}{8, 9}{10}{11, 12}{13, 14, 15} {16, 17, 18}{19, 20, 21}{22}{23, 24}{25}{26, 27} | (8→3→9, 3→4, 8→9, 6→2, 1→5, 4→1→7→2) | (3, 1, 3, 1, 2, 1) |
| 3 | {1, 3}{2}{4, 6}{5}{7}{8, 9}{10}{11, 12}{13, 14}{15} {16, 17}{18}{19, 20, 21}{22}{23}{24}{25}{26}{27} | (3→4→5, 6→2→7, 8→9→4, 1→3→9, 6→1, 9→8→2→8→5) | (2, 1, 2, 1, 1, 2) |
| 4 | {1, 3}{2}{4}{5}{6}{7}{8}{9}{10}{11}{12}{13, 14}{15} {16, 17}{18}{19}{20, 21}{22}{23}{24}{25}{26}{27} | (5→4, 3→6→1→3→7, 9→5→9, 2→9→8→3→6, 8→4, 7→1→2) | (2, 3, 3, 1, 2, 3) |
| 5 | {1, 3}{2}{4}{5}{6}{7}{8}{9}{10}{11}{12}{13}{14}{15} {16, 17}{18}{19}{20}{21}{22}{23}{24}{25}{26}{27} | (9→6→8, 7→8→2→4→6, 4→5, 8→3→5→3→2→7→1, 9, 1→3→2→9→7) | (3, 1, 2, 1, 3, 3) |
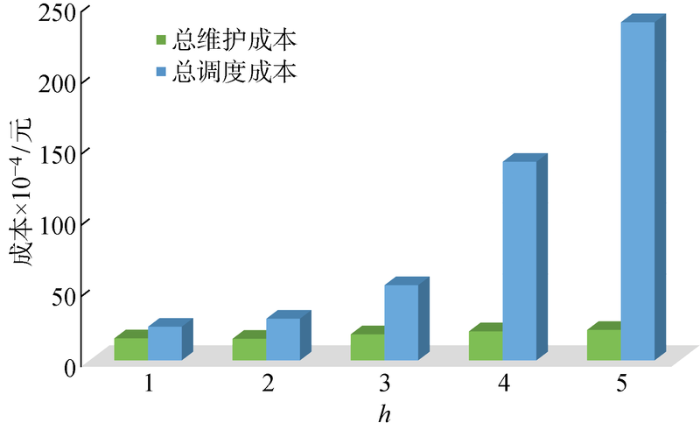
同时,上述各周期的成本表现如图5所示.本算例通过设定每个周期所派遣的总维护团队个数,验证所提出MCMS策略在多维护中心团队资源规划中的利用效率.在运维服务开始时(h=1),仅需要派遣5支维护团队即可满足出租方的外表服务.随着运维服务时间递增,各租赁设备的独立维护时间点逐渐分散,即需要增加维护团队的个数以权衡服务等待成本和固定派遣成本.同时,由于本算例中的总维护团队数目限制,所以随着服务周期h的增加,进而形成由服务等待成本项增加而导致的总调度成本激增.
图5
图5
各周期维护方案的成本表现
Fig.5
Cost performance of MCMS policy in each maintenance scheme
为了验证本文所提出的MCMS策略在求解面向多中心租赁服务网络的维护调度与路由问题的有效性,将MCMS策略与目前常用的两种策略进行对比,以验证MCMS策略在经济上具有突出优势.具体策略描述为:
(1) 贯序成组维护(SGM)策略.为了减少团队重复派遣和系统频繁停机,该策略利用最早的设备独立维护时点对同一系统中的所有设备进行维护成组,各中心的维护团队则通过考虑跨区域资源共享以执行所有成组作业.
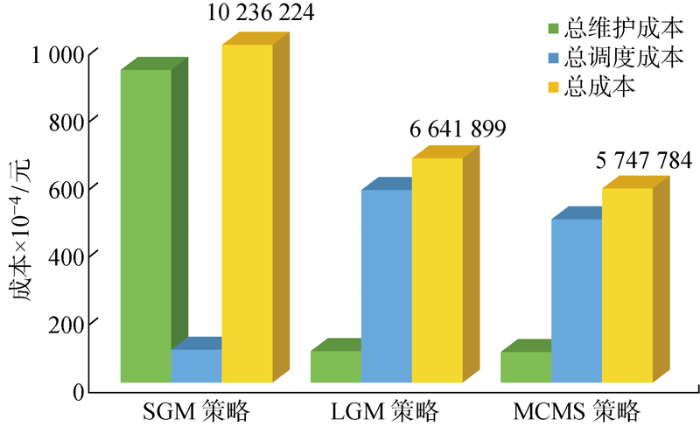
(2) 局部成组维护(LGM)策略.与提出的MCMS策略系统层部分相同,都是通过最小化总维护成本得到各租赁系统的成组维护集合,但在网络层仅考虑各区域内部维护团队的服务路线优化,不考虑跨区域的服务团队资源共享.为了确保上述3种维护策略的成本有效性对比,考虑为期两年的运维调度服务,对应的总维护成本、总调度成本以及总成本如图6所示.成本对比结果显示,总体上MCMS策略可以有效降低总成本,具体原因可分析如下:一方面,通过与SGM策略对比显示,MCMS策略可以有效地对各租赁系统的设备进行维护成组,而非单一成组系统内的所有设备,进而大幅度降低总维护成本;另一方面,通过与LGM策略对比显示,MCMS策略可以进一步统筹各中心的维护团队资源,以优化各周期的维护团队派遣个数.具体而言,由LGM策略得出的第一周期的方案需要6个维护团队进行维护作业,而MCMS策略优化仅需5个维护团队.
图6
总体而言,提出的MCMS策略可以显著降低维护与调度成本,确保广域运维服务的及时性,并进一步利用现有维护团队资源.不同的租赁设备退化趋势、维护相关参数、承租方地理位置和维护团队资源都将会影响运维调度优化,进而生成完全不同的整体解决方案.所提出的MCMS策略机制可以很好地适应这些变化,并获取自适应的运维方案.一方面,系统层的成组维护优化可以通过权衡提前维护与延迟维护,对相近维护需求的设备进行成组,以确定各系统最合适的维护时机;另一方面,网络层通过有目的地对各团队的出发点与服务顺序进行优化,以减少服务路由成本并降低维护团队等待时间.通过动态比较每个可行解的总调度成本,选择总调度成本最低的解决方案作为该周期的运维方案.
6 结语
针对出租方拓展全球“产品+服务”整体解决方案中存在的多中心运维调度问题,提出了系统层、网络层动态交互的多中心协同维护调度策略.在系统层综合考虑设备维护停机、累积失效损失以及系统组合选取对维护决策的影响,对同一串联租赁系统内的设备进行维护成组优化,得出总维护成本最小的成组维护方案和维护时间窗;在网络层进一步考虑服务路由优化、团队派遣选取和维护响应速度对调度决策的影响,输出最小化总调度成本所对应的各团队最优服务路线.算例结果表明,与现有的两种维护调度策略相比,本文所提出的多中心协同维护调度策略可以充分利用各运维中心的维护团队资源,有效降低成本的同时确保计算效率,更加符合出租方实际的运维调度服务.此外,所提出的系统层与网络层动态交互的模型可以根据不同承租方企业的实际维护需求,对多中心协同维护调度策略进行适当调整,以适用于各类不同场景的广域服务型制造,并拓展应用于风电机场、制造工厂和电力装备等的多中心运维调度规划,具备一定应用前景.同时,本文所提出的多中心运维调度问题尚未考虑设备随机失效约束、复杂系统结构约束和维护人力资源约束对维护调度决策的影响,因此综合考虑多种约束并开发高效求解算法将是下一步的研究重点.
参考文献
Service-oriented manufacturing: A new product pattern and manufacturing paradigm
[J].DOI:10.1007/s10845-009-0301-y URL [本文引用: 1]
A service-oriented dynamic multi-level maintenance grouping strategy based on prediction information of multi-component systems
[J].DOI:10.1016/j.jmsy.2019.09.005 URL [本文引用: 1]
面向串并联生产系统机会维护的产能平衡导向租赁利润优化策略
[J].
Capacity balancing-oriented leasing profit optimization of opportunistic maintenance for leased series-parallel production system
[J].
Service-oriented global optimization integrating maintenance grouping and technician routing for multi-location multi-unit production systems
[J].DOI:10.1080/24725854.2021.1957181 URL [本文引用: 1]
Maintenance scheduling of geographically distributed assets with prognostics information
[J].DOI:10.1016/j.ejor.2015.03.023 URL [本文引用: 1]
On the combined maintenance and routing optimization problem
[J].DOI:10.1016/j.ress.2015.09.016 URL [本文引用: 1]
Optimisation of maintenance routing and scheduling for offshore wind farms
[J].DOI:10.1016/j.ejor.2016.05.059 URL [本文引用: 1]
Dynamic maintenance grouping and routing for geographically dispersed production systems
[J].DOI:10.1016/j.ress.2018.12.031 URL [本文引用: 1]
面向租赁服务网络广域运维的3层机会维护调度策略
[J].
Triple-level opportunistic maintenance optimization policy for multi-location operation and maintenance of leasehold service network
[J].
Aircraft maintenance, routing, and crew scheduling planning for airlines with a single fleet and a single maintenance and crew base
[J].DOI:10.1016/j.cie.2014.05.027 URL [本文引用: 1]
Coordinating technician allocation and maintenance routing for offshore wind farms
[J].
集装箱进出口码头泊位-堆场协同分配的动态决策
[J].
Dynamic decision making for the intergrated allocation of berth and import/export container terminals
[J].
Discrete firefly algorithm with compound neighborhoods for asymmetric multi-depot vehicle routing problem in the maintenance of farm machinery
[J].
带时间窗的多中心半开放式车辆路径问题
[J].
DOI:10.3969/j.issn.1004-132X.2020.14.013
[本文引用: 1]

针对多中心协同配送下的车辆路径问题,建立了总成本最小化模型,所建模型满足多中心、多需求点和半开放式的特征。考虑到问题的复杂性,设计了一种三阶段求解算法:将K-mediods聚类算法用于原始数据分解,将原规模较大的多配送中心路径问题转换成多个单配送中心路径问题;设计了改进多蚁群算法来求解单配送中心路径问题,得到初始方案;在调整阶段,利用节约算法优化初始方案。分析了算例,并同其他文献的算法求解结果进行对比,结果表明,所提算法比GA-ACO算法求解得到的单中心配送最优路径值减小32.16%,总成本减小30.42%;比狼群算法解得的最优路径值和总成本均减小8.99%;比蚁群算法求得的最优路径值减小24.76%,最小配送成本减小3.40%,从而验证了所建模型的合理性和所设计多阶段算法的有效性。
Multi-depot half open vehicle routing problem with time windows
[J].
DOI:10.3969/j.issn.1004-132X.2020.14.013
[本文引用: 1]

Aiming at the vehicle routing problem under multi-depot collaborative distribution, a minimization model of total costs was established. The model satisfied the characteristics of multi-depot, multi-demand points and half-open. Considering the complexity of the problem, a three-stage solution algorithm was designed. K-mediods clustering algorithm was used to decompose the original data. The original large-scale multi-depot VRP was transformed into multiple single distribution center routing problems. Then, an improved multi-ant colony algorithm was designed to solve the single distribution center routing problem, and the initial scheme was obtained. In the adjustment stages, the initial scheme was optimized by using the saving mileage method. At last, the simulation results were compared with ones of the other methods. The results show that the proposed algorithm is better than GA-ACO algorithm, wolf pack algorithm and ant colony algorithm. The optimal path is optimized by 32.16%, 8.99% and 24.76% respectively, and the total cost is optimized by 30.42%, 8.99% and 3.40% separately, which verifies the rationality of the model and the effectiveness of the multi-stage algorithm design.
Collaborative multiple centers fresh logistics distribution network optimization with resource sharing and temperature control constraints
[J].