上海交通大学学报

上海交通大学学报, 2023, 57(2): 213-220 doi: 10.16183/j.cnki.jsjtu.2021.365

材料科学与工程

膜结构在暴雨积水时材料模型研究

庞妍, 卿强, 王沙沙, 张翔宇, 龚景海,

上海交通大学 船舶海洋与建筑工程学院,上海 200240

Material Model of Membrane Structure in Rainstorm

PANG Yan, QING Qiang, WANG Shasha, ZHANG Xiangyu, GONG Jinghai,

School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 龚景海,博士生导师;E-mail:gongjh@sjtu.edu.cn.

责任编辑: 李博文

收稿日期: 2021-09-23   修回日期: 2021-12-14   接受日期: 2022-02-7  

Received: 2021-09-23   Revised: 2021-12-14   Accepted: 2022-02-7  

作者简介 About authors

庞妍(1997-),博士生,主要研究方向为膜结构数值模拟研究.

摘要

在遭遇暴雨时,坡度比较小的膜面容易积水,准确模拟出此时膜面的变形有助于保障结构安全,现有研究采用的膜材线性本构模型不适用于模拟膜结构在暴雨下的变形.通过在膜结构上进行均布荷载加载试验,模拟膜面遭遇暴雨作用下的力学行为,获得结构积水时的变形形态.采用膜材线性与双折线本构模型,分别建立膜结构有限元模型并进行荷载分析,通过对比有限元模型和实际结构的变形,选取适合模拟膜结构在暴雨下变形的膜材本构模型.数值模拟结果显示:与采用线性本构模型模拟的结构变形相比,采用膜材双折线本构模型模拟出的结构变形更接近试验测得的变形.研究成果可为膜结构在暴雨积水作用下的膜材本构模型选用和分析计算提供参考.

关键词： 膜结构; 积水; 膜材材料模型; 数值模拟; 变形预测

Abstract

When encountering heavy rain, the membrane surface with a relatively small slope is easy to accumulate water. Accurately simulating the deformation of the membrane surface at this time will help ensure the safety of the structure. The linear constitutive model of membrane material used in existing research is not suitable for simulating the deformation of membrane structure in rainstorm. This study conducts a uniform load test on a membrane structure to simulate the mechanical behavior of the membrane surface in rainstorm and obtains the deformation form of the structure when water is accumulated. The linear constitutive model and the double broken line constitutive model of membrane material are used in the finite element model of the membrane structure for load analysis. By comparing the deformation of the finite element model and the actual structure, it selects the constitutive model suitable for simulating the deformation of the membrane structure in heavy rain. The numerical simulation results show that the structural deformation simulated by the double broken line constitutive model is closer to the deformation measured in the experiment than the linear constitutive model. The research results can provide a reference for the selection of the membrane constitutive model and the analysis of membrane structure in rainstorm.

Keywords： membrane structure; water accumulation; membrane material model; numerical simulation; deformation prediction

PDF (7018KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

庞妍, 卿强, 王沙沙, 张翔宇, 龚景海. 膜结构在暴雨积水时材料模型研究[J]. 上海交通大学学报, 2023, 57(2): 213-220 doi:10.16183/j.cnki.jsjtu.2021.365

PANG Yan, QING Qiang, WANG Shasha, ZHANG Xiangyu, GONG Jinghai. Material Model of Membrane Structure in Rainstorm[J]. Journal of Shanghai Jiaotong University, 2023, 57(2): 213-220 doi:10.16183/j.cnki.jsjtu.2021.365

膜结构具有质量轻、强度高的特点,被广泛应用于体育馆、机场、煤棚等结构.坡度较小、较平整的膜结构易在暴雨天气下发生积水而导致结构破坏,因此模拟膜结构遭遇暴雨影响具有必要性.膜材本构模型会直接影响膜面计算变形的大小,但目前在数值模拟中采用的膜材本构模型往往不能准确地反映出实际工作中膜面的形态变化.

膜结构技术规程[1]中建议采用正交比例加载进行重复拉伸试验确定膜材的弹性模量,因为双轴拉伸试验更符合膜材的受力情况.在膜结构和膜材性能的相关研究中[2⇓⇓⇓-6],通常选择经过双轴循环拉伸多次之后已经稳定的曲线作为膜材模型.孙战金等[7]在预张力测量技术的研究中指出,聚酯纤维类膜材经过多次反复张拉,在消除大部分残余应变后,膜材的弹性模量基本稳定在一个固定值,通过计算加载曲线的斜率来确定膜材弹性模量,建立膜材线性本构模型;张其林等[8]将第五循环的加载曲线拟合后得到的直线斜率作为试验所得的弹性模量;黄赛帅等[9]将膜材第二、第三次加载试验曲线进行拟合得到直线,并取两次加载的平均值,最终确定膜材的弹性模量和泊松比;Yang等[10]提出了膜材的二阶非线性模型,与线性模型相比,该模型能更好地模拟测试数据.

现有文献多采用循环多次后稳定的加载曲线进行线性化拟合,求解膜材弹性模量,以及建立膜材线性本构模型[11⇓⇓⇓-15],但并不适用于所有情况.实际上,膜结构在施工完毕后,在遭遇暴雨作用时,膜材并不满足循环加载多次后已经稳定的要求.进行模拟分析时,膜结构采用的膜材材料模型是否能准确反映膜材实际情况,对结构的安全性有关键性影响.若采用的膜材弹性模量与实际值偏差大,则膜面变形的计算结果误差较大,结构在暴雨天气下将有被破坏的危险.

为模拟膜结构受暴雨作用时的受力变形特性,本文在某临时顶盖样机上进行均布荷载加载试验,选择较平整的膜面区域进行加载,模拟膜面的积水变形.通过膜材的单轴拉伸及双轴拉伸建立了膜材的线性和双折线材料模型.基于不同膜材材料模型建立有限元模型进行计算,将数值模拟结果与试验测得的结果进行比较分析,判断材料模型选用的合理性,为膜结构的分析设计及遭遇暴雨的数值模拟提供参考.

1 试验模型

1.1 试验对象

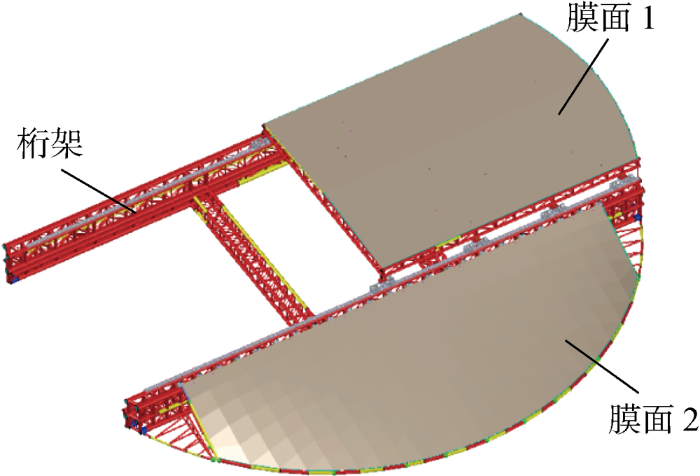
试验对象为一跨度为40 m的圆形核电站临时顶盖,采用骨架式膜结构,整体模型如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   模型整体示意图

Fig.1   Schematic diagram of overall model


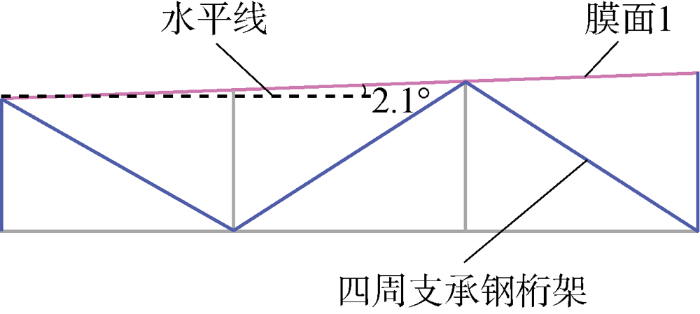
由于排水需求,膜面有一定坡度.如图2所示,膜面1与平面夹角为2.1°,坡度较小,膜面较平,容易在暴雨天气下产生积水,引起膜面较大变形.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   膜面1坡度示意图

Fig.2   Schematic diagram of slope of membrane Surface 1


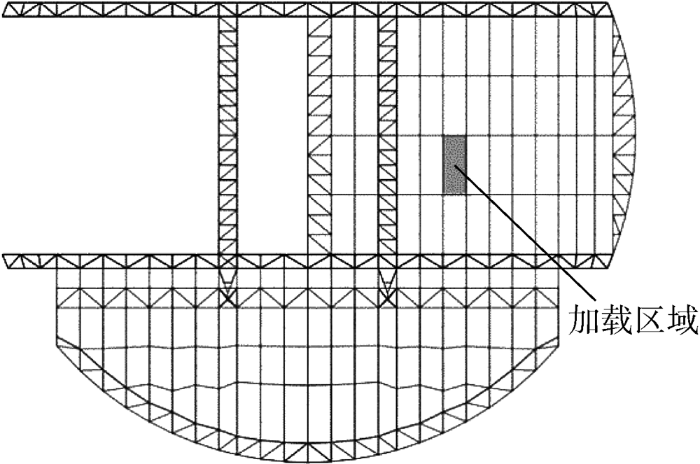
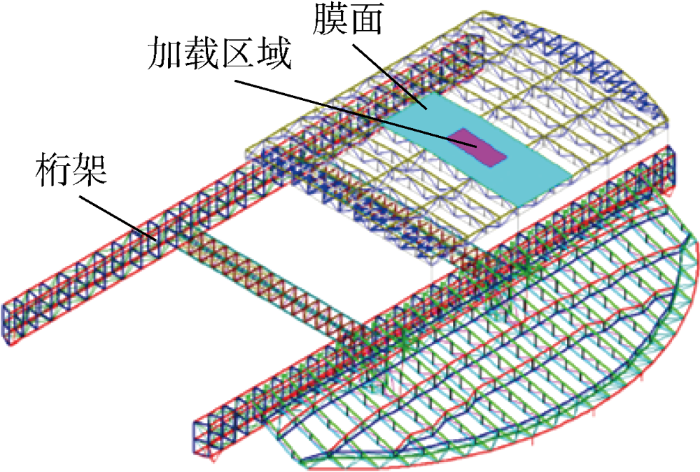
选取膜面1作为试验加载区域.在暴雨时,雨水作为均布荷载作用在膜面上,因此在膜面上施加均布荷载,模拟其遭遇暴雨时的结构变化.为观测膜面在均布荷载作用下的变形,采用局部加载的方法,在膜面上选取加载区域如图3所示,加载区域长3.295 m,宽1.52 m,四周均有钢桁架支承.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   加载区域示意图

Fig.3   Schematic diagram of loading area


1.2 膜材参数

试验模型的膜面采用Ferrari1202S2膜材,密度为 1 050 g/m2,经纬向拉伸强度均为112 kN/m,经向撕裂强度为800 N,纬向撕裂强度为650 N,黏结强度为2.4 kN/m.根据设计,膜面张拉后预应力为1 kN/m.

1.3 膜材材料模型

对膜材进行单轴拉伸试验和应力比(经向:纬向)分别取1∶1、2∶1、1∶2、1∶0、0∶1下的双轴拉伸试验,如图4和图5所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   单轴拉伸试验

Fig.4   Uniaxial tensile test


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   双轴拉伸试验

Fig.5   Biaxial tensile test


由单轴拉伸强度试验可得到膜材的经、纬向极限抗拉强度,分别为102.85和103.71 kN/m,与膜材材料参数显示的112 kN/m接近.膜结构技术规程[1]规定膜面应力不允许超过膜材极限抗拉承载力的1/4,故双轴拉伸试验的应力峰值为膜材抗拉极限强度的1/4,取26 kN/m.

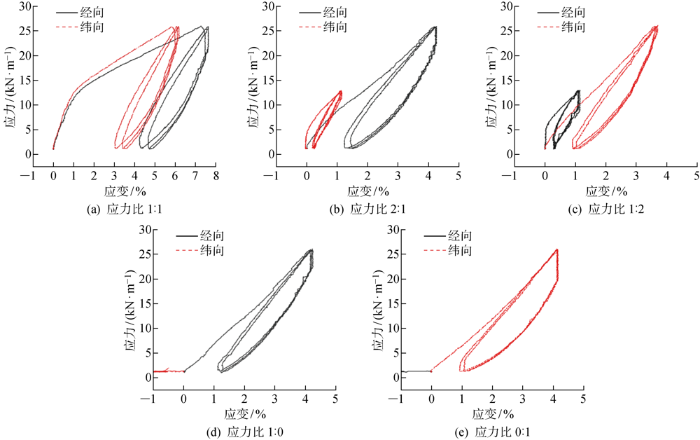
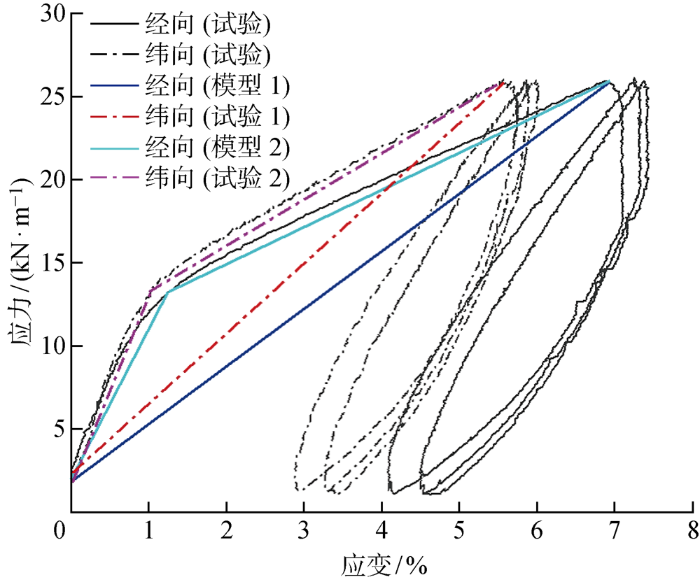
在双轴拉伸试验中,各应力比下均进行3次有效试验,取3次试验计算的平均值作为最终结果,膜材在不同应力比下双轴拉伸的经纬向应力-应变曲线如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   不同应力比下的应力-应变曲线

Fig.6   Strain-stress curves at different stress ratios


通过试验可确定膜材双轴本构模型的力学参数,该结构中Ferrari膜材为正交各向异性弹性材料,本构关系由下式确定:

εw=NwEwt-NfEftνfεf=NfEft-NwEwtνw

式中:Nw、Nf分别为十字形膜材试样经向、纬向荷载;Ew、Ef分别为膜材的经向、纬向弹性模量;εw、εf分别为经向、 纬向应变;νw、νf分别为经向、纬向泊松比;t为膜材厚度.

采用最小二乘法,根据下式可得:

S=∑[E11Nwi+E12Nfi-εwi2+ E22Nfi+E12Nwi-εfi2]
E11= 1Ewt
E22= 1Eft
E12= νwEwt= νfEft

式中:S为最小二乘法所对应的函数;E11、E22和E12为最小二乘法的待定系数;i为角标,代表双轴拉伸试验中测得的每一组数据.

考虑膜材为正交异性材料,E11、E22和E12之间相互独立,故有

∂S∂E11=∂S∂E22=∂S∂E12=0

从而得到3个相互独立的方程:

∂S∂E11=∑NwiE11Nwi+E12Nfi-εwi=0
∂S∂E22=∑NfiE22Nfi+E12Nwi-εfi=0
∂S∂E12=∑[E11NwiNfi+E22NwiNfi+ E12Nwi2+Nfi22-Nwiεfi-Nfiεwi]=0

将应力比为1∶1、2∶1、1∶2、1∶0、0∶1下双轴拉伸试验的应力、应变增量代入式(7)~(9)中,求解线性方程组,即可得到膜材的弹性模量和泊松比.

目前研究多采用膜材线性本构模型,即取应力-应变曲线循环加载段的起点和终点作割线,由割线斜率求得膜材模量.但由图6可以看出,在第一次加载时,膜材的应力-应变曲线呈现出明显的非线性.在加载的初始阶段,曲线斜率最大,随着应力的增大,曲线斜率减小即膜材经、纬向弹性模量减小.

建立以下两种本构模型:线性与双折线本构模型,分别记为模型1和模型2.模型1为线性模型,取应力-应变曲线第一次循环加载段的起点和终点作割线;模型2为双折线模型,第一阶段取应力-应变曲线第一次循环加载段的起点到应力13 kN/m处作割线,第二阶段取应力13 kN/m处到终点作割线.以应力比1∶1时的应力-应变曲线为例,模型1和模型2的割线如图7所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   试验膜材应力-应变曲线(应力比1∶1)

Fig.7   Stress-strain curve at a stress ratio of 1∶1 of membrane material


利用应力比1∶1、2∶1、1∶2、1∶0、0∶1下的应力-应变曲线,分别进行差值计算得到模型1和模型2的膜材力学参数,如表1所示,其中G为切变模量.

表1   膜材试件弹性模量及泊松比计算结果

Tab.1  Calculation results of elastic modulus and Poisson’s ratio of membrane specimen

材料模型Ew/
(kN·m-1)		Ef/
(kN·m-1)		νwνfG/
(kN·m-1)
模型1428.0513.00.1500.17921.4
模型2第一阶段498.2601.40.3910.47224.9
第二阶段410.2495.80.1200.14520.5

新窗口打开| 下载CSV


2 均布荷载加载试验

2.1 试验过程

试验采用均布荷载模拟膜面遭遇暴雨作用.顶盖结构具有抵抗17级台风的需求,因此均布荷载的取值考虑了台风强度.17级台风对应的风压力为2.0 kN/m2,风荷载标准值为5.67 kN/m2,设计值为1.5×5.67 kN/m2=8.505 kN/m2.试验所施加的均布荷载需大于风荷载设计值,加载时选用30 kg沙袋,分3级进行加载.为模拟均布荷载的效果,以布满一层为1级荷载,不断往上叠加沙袋,总共加载193袋.第1级荷载为4.2 kN/m2,第2级荷载为3.3 kN/m2,第3级荷载为2.2 kN/m2,加载完毕后,该膜面所承受的最大荷载即本试验场布荷载为9.7 kN/m2.膜面上的荷载加载过程如图8所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   均布加载过程图

Fig.8   Uniform load loading process diagram


在加载前以及每一级荷载加载完毕后,待膜面变形稳定,采用PENTAX型全站仪对膜面测点的位置进行测量,测点取加载区域的中心点.

2.2 试验结果

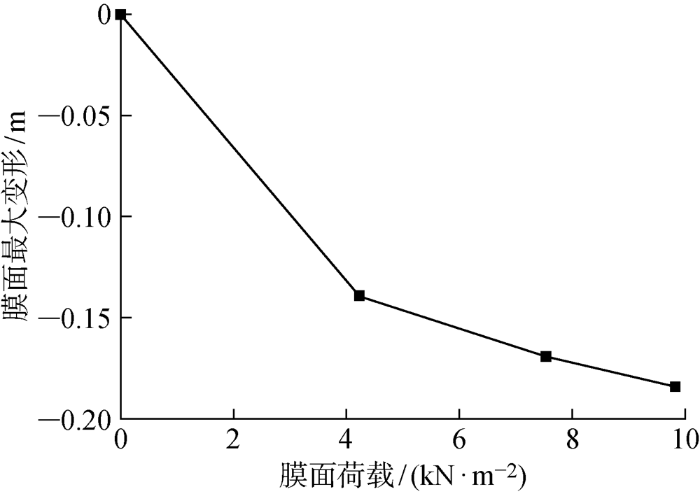
在各级荷载作用下,膜面最大变形与荷载的关系如图9所示.在第1级荷载加载时,膜面的高度变化最大,在随后加载过程中,高度变化速度变慢.在3级荷载加载完毕时,膜面最低点的竖向变形已达到0.184 m.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   膜面最大变形与荷载的关系图

Fig.9   Maximum deformation of membrane surface versus load


3 数值模拟

3.1 有限元数值模拟

使用STCAD软件建立试验对象的有限元分析模型, 如图10所示.图中,加载区域膜面的尺寸为 3.92 m×1.52 m,此处采用三节点膜单元,网格划分为36×12,如图11所示.该区域边缘处膜单元的节点与桁架单元的节点耦合平动方向的自由度.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   有限元模型

Fig.10   Finite element model


图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   膜单元网格划分示意图

Fig.11   Diagram of meshing of membrane elements


采用模型1和模型2分别进行膜材材料模型分析,与材料模型1和模型2对应的有限元模型分别称为模型A和模型B.

由于本试验的膜结构在施工时,按设计要求施加经、纬向1 kN/m的初始预应力,故在有限元模型中,对膜面赋予同样的预应力进行加载过程的受力分析.采用非线性有限元法分析加载过程中的荷载变化和结构受力状态.

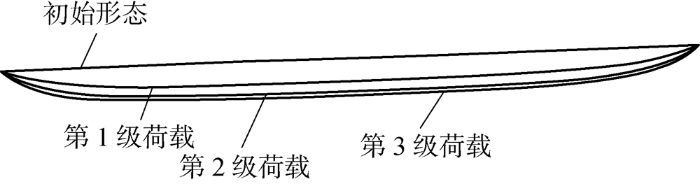
两个模型在3级荷载加载过程中的变形变化规律一致,第1级荷载加载后膜面变形增量最大,随后,变形的速度减慢,各级荷载下加载区域膜面的变形如图12所示.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   各级荷载下加载区域膜面的变形

Fig.12   Deformation of membrane surface of loading area at different loads


模型A与模型B的最大变形对比如图13所示,两模型变形形态相似.模型A的最大变形为 195.03 mm,模型B的最大变形为181.20 mm,比模型A小7.09%.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   模型A与模型B最大变形对比图

Fig.13   Comparison of maximum deformation between model A and model B


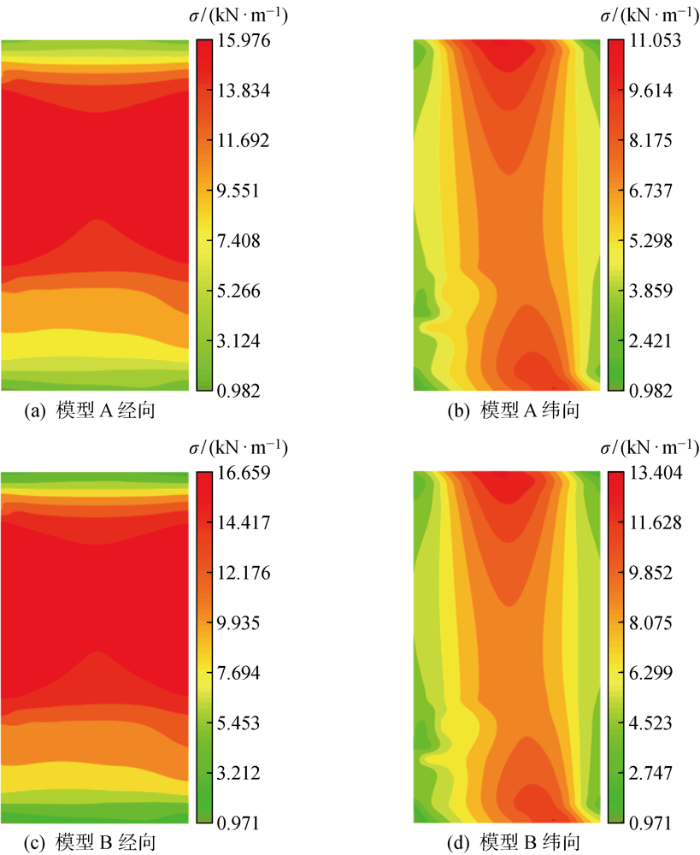
模型A和模型B的加载区域膜面应力(σ)云图如图14所示.在第3级荷载作用下,模型A和模型B的膜面经向应力均大于13 kN/m,达到膜材双折线本构模型的第二阶段.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14   加载区域膜面的应力云图

Fig.14   Stress cloud image of loading area of membrane


3.2 有限元分析结果与试验结果对比

试验和有限元模型得到的膜面最大变形与荷载的关系如图15 所示.由图可知,在初始状态到第3级荷载9.7 kN/m2的加载过程中,有限元模型与试验的膜面变形变化规律一致.在加载初期,曲线的斜率大,随着荷载的增加,膜面高度变化大;在加载后期,膜面的高度变化逐渐减缓.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15   膜面最大变形与荷载的关系

Fig.15   Maximum deformation of membrane surface versus load


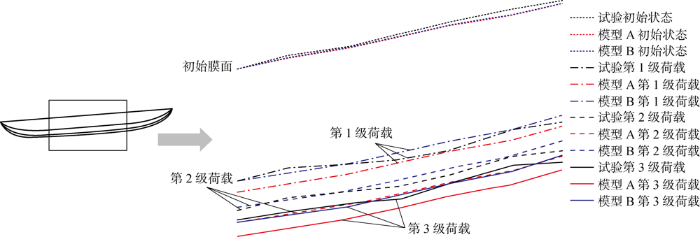
试验测得的膜面最大变形为184 mm,模型A的最大变形为195.03 mm,比试验结果大5.99%,模型B的最大变形为181.20 mm,比试验结果小1.52%.模型B的变形比模型A更接近试验值.局部区域在荷载作用下的试验与模型A、模型B膜面位置对比如图16所示.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16   试验与有限元模型膜面位置图

Fig.16   Membrane surface of test and finite element models


在整个加载过程中,模型A的变形大于试验变形,模型B的变形小于模型A.在施加第1级荷载后,两个有限元模型与实际结构的变形都较为接近,但模型B比模型A更接近.施加第2级荷载后,模型B的变形值仍接近试验值,而模型A的变形值已明显偏离试验值.随着荷载增加,模型B分析结果与试验值越来越接近,模型A的分析结果与试验值的偏差越来越大.

3.3 膜材本构模型的选择

在工程设计中,常常采用膜材模型1即膜材线性本构模型,但实际上,膜材在加载过程中经、纬向应力不断增大,膜材的弹性模量会随应力水平的变化而变化.本文分析表明,考虑该影响的双折线本构模型可以更好地拟合出膜结构受荷载作用后的变形,其分析结果比线性本构模型更合理.

根据有限元分析结果与试验结果的对比分析,采用膜材模型2的有限元模型与试验的实际变形更接近.由图6的应力-应变曲线可知,在加载的初始阶段,膜材经、纬向弹性模量最大,随着应力的增大,膜材弹性模量减小.在本试验中,若采用膜材线性本构模型,在加载的初始阶段,弹性模量偏小,导致结构分析结果的变形偏大,应力偏小,不利于准确模拟膜结构受荷载作用后的变形和内力状态.

4 结论

通过对膜结构模型的加载试验与试验过程的有限元模拟,得到以下主要结论:

(1) 相较于线性材料本构模型,采用膜材双折线本构模型更能准确模拟膜结构在荷载作用下的变形.建议在实际工程中,采用考虑应力水平影响的膜材双折线本构模型,有利于结构的安全.

(2) 实际工程遭受暴雨时,较平的膜面易产生变形和积水,对结构造成危害和危险.因此,当膜材产生一定的变形时,有必要通过张紧装置将膜材重新张紧,避免产生过大变形.

(3) 采用膜材双折线本构模型的有限元分析所预测的膜面变形结果较为准确,但在加载的初始阶段,有限元模型的变形与试验结果有一定差值.膜材的弹性模量随应力比的变化而不断改变,在下一步的研究中,将对膜材特性进行深入研究,建立更合理的膜材非线性本构模型.

参考文献

中国工程建设标准化协会.

膜结构技术规程: CECS 158—2015

[S]. 北京: 中国计划出版社, 2016.

[本文引用: 2]

China Association for Engineering Construction Standardization.

Technical specification for membrane structures: CECS 158—2015

[S]. Beijing: China Planning Press, 2016.

[本文引用: 2]

于沁灵, 龚景海, 郭晓, 等.

涂层织物类膜材的拉伸试验及力学参数研究

[J]. 空间结构, 2020, 26(4): 64-69.

[本文引用: 1]

YU Qinling, GONG Jinghai, GUO Xiao, et al.

Tensile test and mechanical parameters of coated fabric membrane

[J]. Spatial Structures, 2020, 26(4): 64-69.

[本文引用: 1]

SHI T B, HU J H, CHEN W J, et al.

Biaxial tensile behavior and strength of architectural fabric membranes

[J]. Polymer Testing, 2020, 82: 106230.

DOI:10.1016/j.polymertesting.2019.106230      URL     [本文引用: 1]

GAO C J, CHEN W J, SHI T B, et al.

Response surface characterization for biaxial tensile properties of envelope fabrics under multiple stress ratios

[J]. Composite Structures, 2019, 230: 111482.

DOI:10.1016/j.compstruct.2019.111482      URL     [本文引用: 1]

GAO C J, CHEN W J, HU J H, et al.

A new constitutive model on biaxial tensile behavior of architectural fabrics

[J]. Polymer Testing, 2020, 87: 106519.

DOI:10.1016/j.polymertesting.2020.106519      URL     [本文引用: 1]

卫东, 王臣, 向阳, 等.

建筑膜材的材性试验研究

[J]. 空间结构, 2002, 8(1): 37-43.

[本文引用: 1]

WEI Dong, WANG Chen, XIANG Yang, et al.

Experimental study on material properites of structural fabric

[J]. Spatial Structures, 2002, 8(1): 37-43.

[本文引用: 1]

孙战金, 张其林, 杨宗林.

采用数值计算进行膜材预张力测量方法初探

[J]. 振动、测试与诊断, 2005, 25(1): 31-35.

[本文引用: 1]

SUN Zhanjin, ZHANG Qilin, YANG Zonglin.

Preliminary study on membrane pretension measurement by numerical calculations

[J]. Journal of Vibration, Measurement & Diagnosis, 2005, 25(1): 31-35.

[本文引用: 1]

张其林, 倪佳女.

涂层织物类膜材弹性模量试验研究及有限元分析

[C]// 第十二届空间结构学术会议论文集. 北京: 中国土木工程学会桥梁及结构工程分会空间结构委员会, 2008: 275-279.

[本文引用: 1]

ZHANG Qilin, NI Jianü.

Experimental research and finite element analysis of elastic modulus of coated fabrics

[C]// The 12th Space Structure Academic Conference. Beijing, China: Spatial structure committee of bridge and structural engineering branch of china civil engineering society, 2008: 275-279.

[本文引用: 1]

黄赛帅, 陈务军, 董石麟.

飞艇囊体膜材弹性常数双向拉伸测试与分析方法

[J]. 空间结构, 2011, 17(2): 84-89.

[本文引用: 1]

HUANG Saishuai, CHEN Wujun, DONG Shilin.

Bi-axial tensile test method and analytical algorithm of elastic constants for the airship envelope fabric

[J]. Spatial Structures, 2011, 17(2): 84-89.

[本文引用: 1]

YANG B, YU Z L, ZHANG Q L, et al.

The nonlinear orthotropic material model describing biaxial tensile behavior of PVC coated fabrics

[J]. Composite Structures, 2020, 236: 111850.

DOI:10.1016/j.compstruct.2019.111850      URL     [本文引用: 1]

张丽, 陈务军, 董石麟.

PVDF/PES建筑织物膜力学性能单双轴拉伸试验

[J]. 空间结构, 2012, 18(3): 41-48.

[本文引用: 1]

ZHANG Li, CHEN Wujun, DONG Shilin.

Mechanical properties analysis of architectural PVDF/PES fabrics with uni-tensile and bi-axial test

[J]. Spatial Structures, 2012, 18(3): 41-48.

[本文引用: 1]

XU J H, ZHANG Y Y, WU M, et al.

A phenomenological material model for PTFE coated fabrics

[J]. Construction and Building Materials, 2020, 237: 117667.

DOI:10.1016/j.conbuildmat.2019.117667      URL     [本文引用: 1]

WAKEFIELD D S.

Engineering analysis of tension structures: Theory and practice

[J]. Engineering Structures, 1999, 21(8): 680-690.

DOI:10.1016/S0141-0296(98)00023-6      URL     [本文引用: 1]

DINH T D, REZAEI A, PUYSTIENS S, et al.

A study of tension fabric membrane structures under in-plane loading: Nonlinear finite element analysis and validation

[J]. Composite Structures, 2015, 128: 10-20.

DOI:10.1016/j.compstruct.2015.03.055      URL     [本文引用: 1]

COELHO M, ROEHL D.

A finite-strain elastoplasticity material model for ETFE membrane structures

[J]. Computers & Structures, 2019, 217: 36-44.

DOI:10.1016/j.compstruc.2019.03.007      URL     [本文引用: 1]

/

〈 〉