单向热塑性复合材料层压板偏轴拉伸试验及其数值模拟

图1 偏轴拉伸试验的试验设备

Fig.1 Test equipment for off-axis tensile test

1.2 试验结果及分析

采用ASTM D3039/D3039M-17^[25]提出的方法对试验数据进行处理,拉伸应力的计算公式为

(1)σ_i=

\frac{P_{i}}{A}

式中:σ_i为第i个点的拉伸应力;P_i为第i个点的力;A为试验件的横截面积.

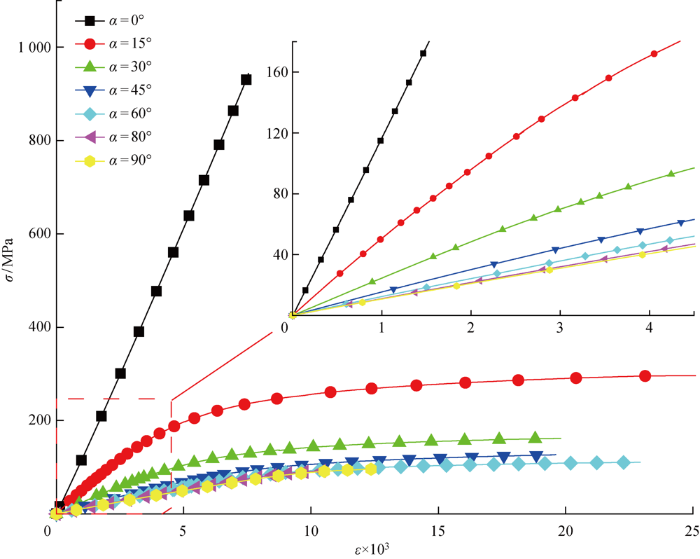
偏轴拉伸试验的应力-应变(σ-ε)曲线如图2所示.从应力-应变曲线可知,当偏轴角度为α=0°时,试验件在破坏前的力学行为都表现为线弹性;随着偏轴角度的逐渐增加,试验件的力学行为首先表现为线弹性,在应力超过一定范围后表现出明显的非线性行为;当偏轴角度在80°~90°之间时,试验件的力学行为只有一小段的线弹性行为,随后发生断裂,原因是这些偏轴角度纤维已经不能承受足够的载荷,在表现出塑性变形前基体已经发生了断裂破坏.

图2

图2 偏轴拉伸应力-应变曲线

Fig.2 Stress-strain curves of off-axis tensile

不同铺层的破坏模式、破坏部位和断裂面角度总结如表1所示.对比不同试验件的断裂面角度和偏轴角度,断裂面角度与偏轴角度的差异在 -1°~2°之间.破坏后的试验件图片如图3(a)所示,断裂面的显微照片如图3(b)所示.断裂面内观察到的主要是基体的断裂,在基体的断裂处可以观察到裸露的纤维,纤维只有少数发生了断裂,未发生断裂的纤维没有观察到明显的偏转.对断裂面的观察和分析表明,断裂面角度与偏轴角度存在差异的原因为在试验件的制造过程中, 层压板的铺层角度与设定的角度存在一定的误差.

表1 不同铺层的破坏模式、破坏部位及断裂面角度^[25]

Tab.1 Failure modes, locations, and fracture plane angles of different specimens^[25]

铺层	破坏模式	破坏部位	断裂面角度/(°)
[0]₈	纵向劈裂	工作段中部	-
[15]₂₀	倒角	工作段中部	15.95
[30]₂₀	倒角	工作段顶部	30.76
[45]₂₀	倒角	工作段顶部和加强段内	46.68
[60]₂₀	倒角	工作段中部	59.38
[80]₂₀	倒角	工作段中部	79.59
[90]₁₆	横向破坏	工作段中部	90.91

图3

图3 试验结束后的试验件及断裂面

Fig.3 Test specimens and fracture surface after test

2 数值模拟设置

2.1 三维弹塑性损伤模型

由试验结果可知,单向AS4/PEEK层压板在偏轴拉伸载荷作用下存在显著的由塑性变形引起的非线性力学行为及破坏行为.为了准确模拟上述行为,需要建立一个包含弹性模型、塑性模型和损伤起始及演化模型的三维弹塑性损伤模型.

2.1.1 弹性模型

在线弹性阶段,本构关系采用三维模型.对于正交各向异性层压板,其典型的应力-应变关系为

(2)

[\begin{array}{l} σ_{11} \\ σ_{22} \\ σ_{33} \\ σ_{12} \\ σ_{23} \\ σ_{13} \end{array}]

[\begin{array}{l} C_{11} & C_{12} & C_{13} & 0 & 0 & 0 \\ C_{12} & C_{22} & C_{23} & 0 & 0 & 0 \\ C_{13} & C_{23} & C_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{66} \end{array}] [\begin{array}{l} ε_{11} \\ ε_{22} \\ ε_{33} \\ ε_{12} \\ ε_{23} \\ ε_{13} \end{array}]

式中:

(3)C₁₁=

\frac{E_{1} (1 - ν_{23} ν_{32})}{1 - ν_{12} ν_{21} - ν_{32} ν_{23} - ν_{13} ν_{31} - 2 ν_{13} ν_{32} ν_{21}}

(4)C₂₂=

\frac{E_{2} (1 - ν_{13} ν_{31})}{1 - ν_{12} ν_{21} - ν_{32} ν_{23} - ν_{13} ν_{31} - 2 ν_{13} ν_{32} ν_{21}}

(5)C₃₃=

\frac{E_{3} (1 - ν_{12} ν_{21})}{1 - ν_{12} ν_{21} - ν_{32} ν_{23} - ν_{13} ν_{31} - 2 ν_{13} ν_{32} ν_{21}}

(6)C₁₂=

\frac{E_{1} (ν_{21} + ν_{23} ν_{31})}{1 - ν_{12} ν_{21} - ν_{32} ν_{23} - ν_{13} ν_{31} - 2 ν_{13} ν_{32} ν_{21}}

(7)C₁₃=

\frac{E_{1} (ν_{31} + ν_{21} ν_{32})}{1 - ν_{12} ν_{21} - ν_{32} ν_{23} - ν_{13} ν_{31} - 2 ν_{13} ν_{32} ν_{21}}

(8)C₂₃=

\frac{E_{2} (ν_{32} + ν_{12} ν_{31})}{1 - ν_{12} ν_{21} - ν_{32} ν_{23} - ν_{13} ν_{31} - 2 ν_{13} ν_{32} ν_{21}}

(9)C₄₄=G₁₂

(10)C₅₅=G₂₃

(11)C₆₆=G₁₃

(12)

\frac{ν_{i j}}{E_{i}}

\frac{ν_{j i}}{E_{j}}

(i, j=1, 2, 3, i≠j)

式中:E₁、E₂和E₃为弹性模量;G₁₂、G₂₃和G₁₃为剪切模量;ν₁₂、ν₁₃和ν₂₃为泊松比;σ_ij(i, j=1, 2, 3)为材料坐标系下的应力;ε_ij(i, j=1, 2, 3)为材料坐标系下的应变.

2.1.2 塑性模型

本模型采用的塑性屈服函数为

(13)F(σ,

{\bar{ε}}^{p}

)=F^p(σ)-κ(

{\bar{ε}}^{p}

)

式中:σ为应力张量; ${\bar{ε}}^{p}$ 为等效塑性应变;F^p(σ)为塑性势函数;κ( ${\bar{ε}}^{p}$ )为强化函数,用于描述屈服面的大小.屈服函数中的塑性势函数采用Sun等^[21]提出的三维塑性势函数.Weeks等^[26]假设复合材料纤维方向为线弹性,而在2-3面内为横观各向异性,故将三维塑性势函数简化为

(14)F^p(σ)=

\sqrt{\frac{3}{2} (σ_{22}^{2} + σ_{33}^{2}) - 3 σ_{22} σ_{33} + 6 σ_{23}^{2} + 3 a_{66} σ_{12}^{2} + 3 a_{66} σ_{13}^{2}}

式中:a₆₆为复合材料各向异性程度的参数,假定其值与材料有关.

等效应力定义为

(15)

\bar{σ}

=F^p

采用关联流动法则确定塑性应变增量为

(16)d

{ε^{p}}_{i j}

=dλ

\frac{\partial F}{\partial σ_{i j}}

(i, j=1, 2, 3)

式中:dλ为比例因子.

为保证单位体积塑性功率(dW^p)相等,有

(17)dW^p=∑σ_ijd

{ε^{p}}_{i j}

\bar{σ}

{\bar{ε}}^{p}

式中:d ${\bar{ε}}^{p}$ 为等效塑性应变增量.将式(14)~式(16)代入式(17)可得

(18)d

{\bar{ε}}^{p}

=dλ

强化函数采用Sun等^[21]提出的幂函数形式的各向同性强化函数,为

(19)κ(

{\bar{ε}}^{p}

)=β(

{\bar{ε}}^{p}

)ⁿ

式中:β和n为材料参数,可通过拟合等效应力-等效塑性应变曲线得到.

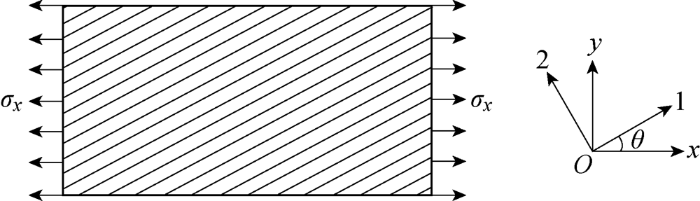
塑性势函数中的参数a₆₆可以通过偏轴拉伸试验得到^[21,27].如图4所示,x-y坐标系为整体坐标系,1-2坐标系为材料坐标系,x轴和1轴之间有一个大小为θ的夹角,在平行于x轴的拉伸载荷的作用下,复合材料层压板的受力状态视为平面应力状态.将层压板在整体坐标系的应力转换到材料坐标系,转换公式为

(20)σ₁₁=cos²θσ_x

(21)σ₂₂=sin²θσ_x

(22)σ₁₂=-sin θcos θσ_x

式中:σ_x为x方向的应力.将式(20)~式(22)代入式(15)可得等效应力为

(23)

\bar{σ}

=h(θ)σ_x

式中:

(24)h(θ)=

{[\frac{3}{2} (s i n^{4} θ + 2 a_{66} s i n^{2} θ c o s^{2} θ)]}^{\frac{1}{2}}

图4

图4 偏轴拉伸试验示意图

Fig.4 Schematic diagram of off-axis tensile test

由塑性应变增量的坐标转换可得

(25)d

{ε^{p}}_{x}

=cos²θd

{ε^{p}}_{11}

+sin²θd

{ε^{p}}_{22}

-sin θcos θd

{ε^{p}}_{12}

式中:d ${ε^{p}}_{x}$ 为x方向的塑性应变增量.将式(14)、式(16)、式(18)、式(20)~(22)代入式(25)可得

(26)d

{\bar{ε}}^{p}

\frac{d {ε^{p}}_{x}}{h (θ)}

假设材料具有显著的塑性效应,且满足小变形假设,则总应变增量可以分解为弹性应变增量和塑性应变增量两部分^[8],即

(27)dε_ij=d

{ε^{e}}_{i j}

{ε^{p}}_{i j}

(i, j=1, 2, 3)

故x方向的塑性应变增量可以表示为

(28)d

{ε^{p}}_{x}

ε_{x}^{t o t a l}

\frac{d σ_{x}}{E_{x}}

式中:d $ε_{x}^{t o t a l}$ 为x方向的总应变增量;dσ_x为x方向的应力增量;E_x的计算公式为

(29)

\frac{1}{E_{x}}

\frac{1}{E_{1}}

cos⁴θ+

(\frac{1}{G_{12}} - \frac{2 ν_{12}}{E_{1}})

sin²θcos²θ+

\frac{1}{E_{2}}

sin⁴θ

通过上述变换,可将偏轴拉伸试验获得的应力-应变曲线转换为等效应力-等效塑性应变曲线.对于不同角度的偏轴拉伸试验,经过转换后的等效应力-等效塑性应变曲线应该是一致的,故可以通过选取适当的a₆₆的值使得不同角度的等效应力-等效塑性应变曲线重合.对于a₆₆的选取,目前有试错法^[21]和信任域反射算法^[28]等计算方法.本文采用Jang等^[28]提出的信任域反射算法进行计算.具体计算流程为:首先设定a₆₆的初值,此处设定为0.5,然后采用式(20)~式(29)将试验获得的不同角度的应力和应变数据变换为等效应力和等效塑性应变数据,将等效应力视为等效塑性应变的函数,通过最小化目标函数来获得a₆₆.目标函数的形式为

(30)f(a₆₆)=

\sqrt{\sum_{{\bar{ε}}^{p}} ({\bar{σ}}_{θ_{1}} ({\bar{ε}}^{p}) - {\bar{σ}}_{θ_{2}} ({\bar{ε}}^{p} {))}^{2}}

(θ₁, θ₂=15°, 30°, 45°, 60°, 80°, 90°)

式中: ${\bar{σ}}_{θ_{1}}$ 和 ${\bar{σ}}_{θ_{2}}$ 为不同角度的等效应力.

2.1.3 损伤起始及演化模型

对于纤维拉伸损伤,本模型采用最大应力准则来预测,即

(31)f_ft=

\frac{σ_{11}}{X_{t}}

(σ₁₁>0)

式中:X_t为纤维方向的拉伸强度.当f_ft≥1时,发生纤维拉伸损伤.

为了预测基体损伤,本模型采用LaRC05准则^[23].该准则认为基体损伤的发生只与潜在断裂面上的正应力(σ_n)和两个剪应力(σ_nT和σ_nL)有关,表达式为

(32)

\begin{array}{l} σ_{n} (ϑ) = \frac{σ_{22} + σ_{33}}{2} + \frac{σ_{22} - σ_{33}}{2} c o s 2 ϑ + \\ σ_{23} s i n 2 ϑ \\ σ_{n T} (ϑ) = \frac{σ_{22} - σ_{33}}{2} s i n 2 ϑ + σ_{23} c o s 2 ϑ \\ σ_{n L} (ϑ) = σ_{12} c o s ϑ + σ_{13} s i n ϑ \end{array}\}

(33)f_mt=

{(\frac{σ_{n T} (ϑ)}{S_{T} - μ_{T} σ_{n} (ϑ)})}^{2}

{(\frac{σ_{n L} (ϑ)}{S_{L} - μ_{L} σ_{n} (ϑ)})}^{2}

{(\frac{σ_{n} (ϑ)}{Y_{T}})}^{2}

(σ_n(ϑ)>0)

(34)

\begin{array}{l} μ_{T} = - \frac{1}{t a n 2 φ_{0}} \\ S_{T} = \frac{Y_{c}}{2 t a n φ_{0}} \\ μ_{L} = S_{L} \frac{μ_{T}}{S_{T}} \end{array}\}

式中:ϑ为潜在断裂面角度,范围为0°~180°;S_T为横向剪切强度;S_L为纵向剪切强度;μ_T为横向摩擦系数;μ_L为纵向摩擦系数;Y_T为基体抗拉强度;Y_c为基体抗压强度;φ₀为纯横向压缩破坏的断裂面的角度,对于碳纤维增强复合材料,试验^[29]测定其值范围为φ₀=53°±2°.当基体最大应力f_mt≥1时,发生基体拉伸损伤.

在使用失效准则对复合材料的损伤模式进行预测后,需要采用适当的损伤变量来模拟复合材料发生损伤后的力学行为.本模型使用的损伤变量包括纤维拉伸损伤变量(d_ft)和基体拉伸损伤变量(d_mt),损伤变量从损伤起始时的0逐渐演化为完全退化时的1^[30].损伤变量的更新采用Donadon等^[31]提出的形式,即

(35)d^t^+Δ^t=max{0, d^t, min{1, 1-

\frac{ε^{0}}{\bar{ε}}

[1+κ²(2κ-3)]}}

式中:d^t^+Δ^t为当前增量步的损伤变量;d^t为前一增量步的损伤变量; $\bar{ε}$ 为当前增量步的等效应变;ε⁰为损伤起始时的应变;κ的计算公式为

(36)κ=

\frac{\bar{ε} - ε^{0}}{ε^{f} - ε^{0}}

式中:ε^f为最终失效时的应变.

对于纤维的损伤,当前增量步的等效应变对应于1方向上的应变分量,损伤开始时的应变和最终失效时的应变的计算公式为

(37)

ε_{f t}^{0}

\frac{X_{t}}{E_{1}}

(38)

ε_{f t}^{f}

\frac{2 G_{f t}}{X_{t} L}

式中:G_ft为纤维拉伸破坏断裂能;L为特征长度.

对于基体的损伤,由于在断裂面上的拉应力会促进基体的损伤,损伤开始时的应变和最终失效时的应变的计算相对更加复杂.当满足式(33)的失效准则时,基体发生损伤,此时的等效应力和等效应变为

(39)

σ_{m}^{0}

\sqrt{< σ_{n} >^{2} + σ_{n L}^{2} + σ_{n T}^{2}}

_{d_{m t}^{t + Δ t} = 0}

(40)

ε_{m}^{0}

\sqrt{< ε_{n} >^{2} + ε_{n L}^{2} + ε_{n T}^{2}} |_{d_{m t}^{t + Δ t} = 0}

式中:ε_n、ε_nL和ε_nT分别为断裂面上的正应变和切应变; $d_{m t}^{t + Δ t}$ 为当前增量步的基体拉伸损伤变量;<x'>为Macaulay算符,定义为<x'>=max (0,x').发生损伤后,基体在当前增量步的等效应变为

(41)ε_m=

\sqrt{< ε_{n} >^{2} + ε_{n L}^{2} + ε_{n T}^{2}}

_{d_{m t}^{t + Δ t} > 0}

对于混合失效情形,基体失效的断裂能为

(42)G_m=G_Ic<

\frac{σ_{n}^{d}}{σ_{m}^{0}}

>²+G_IIc

{(\frac{σ_{n L}^{d}}{σ_{m}^{0}})}^{2}

+G_IIc

{(\frac{σ_{n T}^{d}}{σ_{m}^{0}})}^{2}

式中:G_Ic和G_IIc分别为 I 型断裂和 II 型断裂的断裂能; $σ_{n}^{d}$ 、 $σ_{n L}^{d}$ 和 $σ_{n T}^{d}$ 分别为基体开始发生破坏时断裂面上的应力.故基体最终失效时的应变为

(43)

ε_{m}^{f}

\frac{2 G_{m}}{σ_{m}^{0} L}

(43)

当层压板发生基体损伤时,通过式(32)将应力旋转到断裂面上,对断裂面上的应力进行软化,为了考虑反向载荷对裂纹闭合的影响,断裂面上的正应力只在其为拉伸应力时进行软化,断裂面上的应力软化式为

(44)

\begin{array}{l} σ'_{n} = σ_{n} (1 - d_{m t}) |_{σ_{n} > 0} \\ σ'_{n L} = σ_{n L} (1 - d_{m t}) \\ σ'_{n T} = σ_{n T} (1 - d_{m t}) \end{array}\}

式中:σ'_n、σ'_nL和σ'_nT为断裂面上软化后的正应力和切应力.经过软化后的应力通过式(32)的逆变换将断裂面上的应力转换成原坐标系下的应力.

Matzenmiller等^[32]认为纤维的断裂、屈曲和压缩破坏会对基体的损伤演化产生影响,故纤维损伤导致的应力软化计算公式为

(45)

[\begin{array}{l} σ ″_{11} \\ σ ″_{22} \\ σ ″_{33} \\ σ ″_{12} \\ σ ″_{23} \\ σ ″_{13} \end{array}]

=(1-d_ft)

[\begin{array}{l} σ'_{11} \\ σ'_{22} \\ σ'_{33} \\ σ'_{12} \\ σ'_{23} \\ σ'_{13} \end{array}]

式中:σ'_ij(i, j=1, 2, 3)为发生基体破坏后进行了软化后的应力;σ″_ij(i, j=1, 2, 3)为发生纤维破坏后进行了软化后的应力.

2.2 数值模拟设置

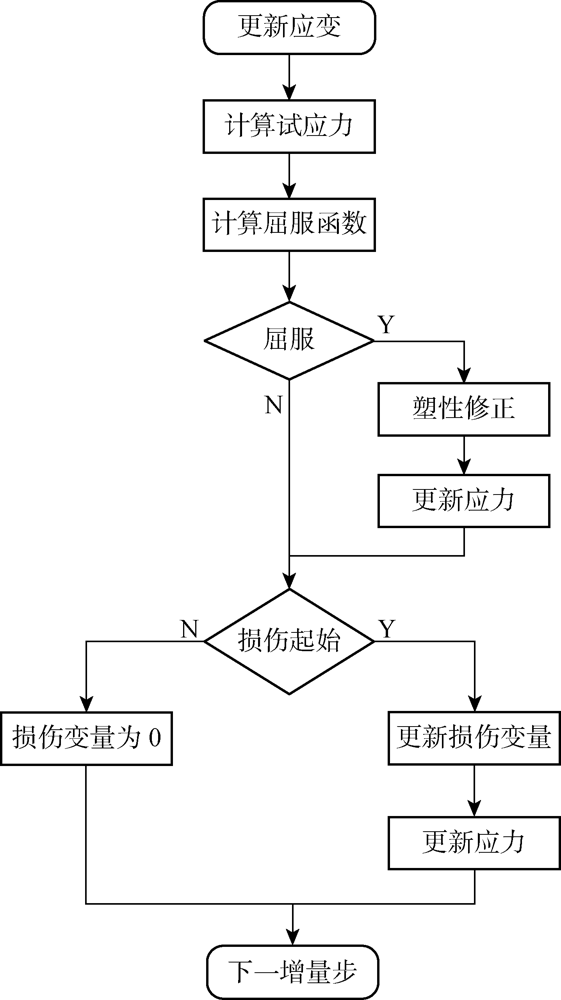
依据三维弹塑性损伤模型的数值算法编写基于Abaqus的用户自定义材料子程序VUMAT,其计算流程如图5所示.

图5

图5 VUMAT计算流程图

Fig.5 Flow chart of subroutine VUMAT

计算过程采用位移增量逐级加载的方式,在第n+1步的具体计算步骤如下.

(1) 初始条件:Δε_n₊₁、 ε_n、 ${ε^{p}}_{n}$ 和 ${\bar{ε}}^{p}_{n}$ ,其中Δε_n₊₁为第n+1步的应变张量增量,ε_n、 ${ε^{p}}_{n}$ 和 ${\bar{ε}}^{p}_{n}$ 分别为第n步的应变张量、塑性应变张量和等效塑性应变.

(2) 假定当前增量步的塑性应变张量和等效塑性应变与上一增量步一致,计算试应力为

(46)

\begin{array}{l} ε_{n + 1}^{p, t r} = {ε^{p}}_{n} \\ {\bar{ε}}_{n + 1}^{p, t r} = {\bar{ε}}^{p}_{n} \\ ε_{n + 1} = ε_{n} + Δ ε_{n + 1} \\ σ_{n + 1}^{t r} = C : (ε_{n + 1} - ε_{n + 1}^{p, t r}) \end{array}\}

式中: $ε_{n + 1}^{p, t r}$ 和 ${\bar{ε}}_{n + 1}^{p, t r}$ 分别为第n+1步的试塑性应变张量和试等效塑性应变;C为刚度张量; $σ_{n + 1}^{t r}$ 为第n+1步的试应力张量.

(3) 检查屈服条件:

(47)F_n₊₁(

σ_{n + 1}^{t r}

{\bar{ε}}_{n + 1}^{p, t r}

)=F^p(

σ_{n + 1}^{t r}

)-κ(

{\bar{ε}}_{n + 1}^{p, t r}

)

如果F_n₊₁( $σ_{n + 1}^{t r}$ , ${\bar{ε}}_{n + 1}^{p, t r}$ )≤0,则第n+1步的塑性应变张量 ${ε^{p}}_{n + 1}$ 、等效塑性应变 ${\bar{ε}}^{p}_{n + 1}$ 和应力张量σ_n₊₁分别为 ${ε^{p}}_{n + 1}$ = ${ε^{p}}_{n}$ 、 ${\bar{ε}}^{p}_{n + 1}$ = ${\bar{ε}}^{p}_{n}$ 和σ_n₊₁= $σ_{n + 1}^{t r}$ ,跳至第5步;否则,跳至第4步进行塑性应变修正.

(4) 采用Newton-Raphson方法迭代求解非线性方程:

(48)F_n₊₁(σ_n₊₁(Δλ_n₊₁),

{\bar{ε}}^{p}_{n + 1}

(Δλ_n₊₁))=0

首先初始化参量:

(49)

\begin{array}{l} k = 0 \\ Δ λ_{n + 1}^{0} = 0 \\ ε_{n + 1}^{p, 0} = ε_{n + 1}^{p, t r} \\ {\bar{ε}}_{n + 1}^{p, 0} = {\bar{ε}}_{n + 1}^{p, t r} \\ σ_{n + 1}^{0} = σ_{n + 1}^{t r} \end{array}\}

式中:Δ $λ_{n + 1}^{k}$ 、 $ε_{n + 1}^{p, k}$ 、 ${\bar{ε}}_{n + 1}^{p, k}$ 和 $σ_{n + 1}^{k}$ 分别为第k次迭代的比例因子增量、塑性应变张量、等效塑性应变和应力张量.

其次计算第k+1次迭代的比例因子增量为

(50)Δ

λ_{n + 1}^{k + 1}

=Δ

λ_{n + 1}^{k}

\frac{F_{n + 1} (σ_{n + 1}^{k} (Δ λ_{n + 1}^{k}), {\bar{ε}}_{n + 1}^{p, k} (Δ λ_{n + 1}^{k}))}{\partial F_{n + 1} (σ_{n + 1}^{k} (Δ λ_{n + 1}^{k}), {\bar{ε}}_{n + 1}^{p, k} (Δ λ_{n + 1}^{k})) / \partial Δ λ_{n + 1}^{k}}

并更新第k+1次迭代的塑性应变张量和等效塑性应变为

(51)

\begin{array}{l} ε_{n + 1}^{p, k + 1} = ε_{n + 1}^{p, k} + \\ Δ λ_{n + 1}^{k + 1} \frac{\partial F_{n + 1} (σ_{n + 1}^{k} (Δ λ_{n + 1}^{k}), {\bar{ε}}_{n + 1}^{p, k} (Δ λ_{n + 1}^{k}))}{\partial σ_{n + 1}^{k}} \\ {\bar{ε}}_{n + 1}^{p, k + 1} = {\bar{ε}}_{n + 1}^{p, k} + Δ λ_{n + 1}^{k + 1} \end{array}\}

再次计算试应力为

(52)

σ_{n + 1}^{k + 1}

=C: (ε_n₊₁-

ε_{n + 1}^{p, k + 1}

)

最后计算F_n₊₁( $σ_{n + 1}^{k + 1}$ (Δ $λ_{n + 1}^{k + 1}$ ), ${\bar{ε}}_{n + 1}^{p, k + 1}$ (Δ $λ_{n + 1}^{k + 1}$ )),如果存在:

F_n₊₁( $σ_{n + 1}^{k + 1}$ (Δ $λ_{n + 1}^{k + 1}$ ), ${\bar{ε}}_{n + 1}^{p, k + 1}$ (Δ $λ_{n + 1}^{k + 1}$ ))≤F_tol(=10^-6)

则 ${ε^{p}}_{n + 1}$ = $ε_{n + 1}^{p, k + 1}$ 、 ${\bar{ε}}^{p}_{n + 1}$ = ${\bar{ε}}_{n + 1}^{p, k + 1}$ 和σ_n₊₁= $σ_{n + 1}^{k + 1}$ ,跳至第5步;否则,令k=k+1,跳至式(50).

(5) 判断是否发生损伤起始.

首先计算f_ft,如果f_ft≥1,则计算纤维损伤变量d_ft;否则d_ft=0.

然后计算f_mt,如果f_mt≥1,则计算基体损伤变量d_mt;否则d_mt=0.

(6) 更新应力,进入下一增量步.

AS4/PEEK材料的性能参数、强度及断裂能^[33⇓-35]如表2和表3所示.其中,G_fc为纤维压缩压

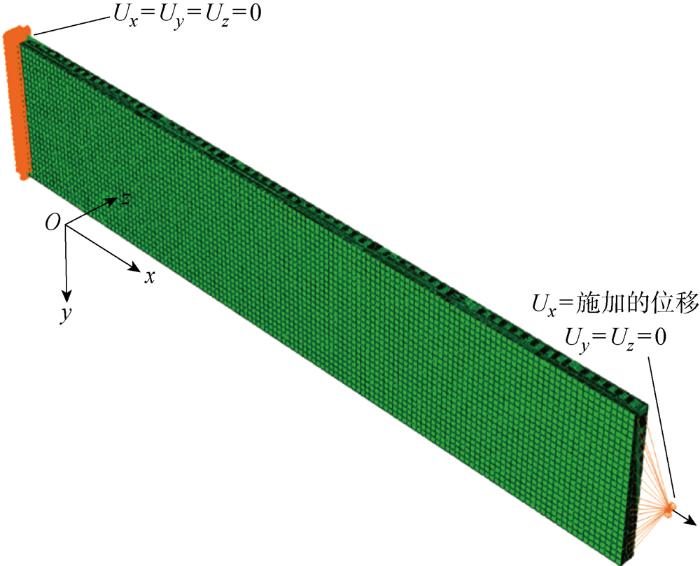
缩破坏断裂能,X_c为纤维压缩破坏断裂能.为了减少计算量,有限元模型不考虑加强片部分,模型长度为200 mm,其余尺寸与试验件尺寸一致,模型的铺层包含试验件的7种铺层.有限元模型的单元类型为C3D8R,厚度方向的单元尺寸为0.14 mm,长度和宽度方向的单元尺寸为1 mm.在加载过程中,如图1(b)所示试验件的上边界在x、y和z的3个方向的位移保持一致,对试验前后的试验件的上边界横截面尺寸进行测量,上边界横截面尺寸变形微小,可以将试验件的上边界视作刚性平面,故有限元模型的边界条件为一端约束x、y和z方向的位移U_x、U_y和U_z,另一端与参考点耦合, 在参考点上施加x方向位移并约束y和z方向的位移.将一组节点耦合至参考点并在参考点施加位移载荷已在文献[10,34,36]中使用广泛.包含边界条件的有限元模型如图6所示.

表2 AS4/PEEK性能参数

Tab.2 Properties of AS4/PEEK

E₁/GPa	E₂/GPa	E₃/GPa	G₁₂/GPa	G₁₃/GPa	G₂₃/GPa	ν₁₂	ν₁₃	ν₂₃
127.00	10.30	10.30	6.00	6.00	3.45	0.32	0.32	0.49

表3 AS4/PEEK的强度及断裂能

Tab.3 Strength and fracture energy of AS4/PEEK

X_t/MPa	X_c/MPa	Y_t/MPa	Y_c/MPa	S_L/MPa	G_Ic/(kJ·m²)	G_IIc/(kJ·m²)	G_ft/(kJ·m²)	G_fc/(kJ·m²)
2023.0	1234.0	92.7	176.0	82.6	1.7	2.0	218.0	104.0

图6

图6 包含边界条件的有限元模型

Fig.6 Finite element model with boundary conditions

3 数值模拟结果及分析

3.1 塑性参数的确定

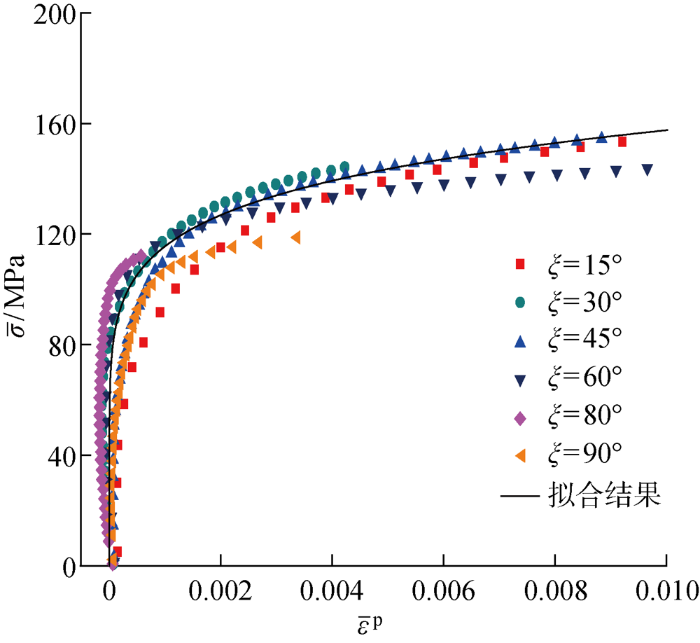
利用MATLAB软件编写程序进行塑性参数的求解.模型假设纤维方向是线弹性的,故[0]₈铺层的数据未考虑,对其余铺层获得的应力-应变曲线进行计算,最优化目标函数后获得的塑性参数为a₆₆=1.50,拟合等效应力-等效塑性应变曲线获得的硬化函数的参数值为β=292.67,n=0.1346.选取上述值绘制的等效应力-等效塑性应变曲线如图7所示,其中ξ为铺层角度.拟合得到的等效应力-等效塑性应变曲线与试验值存在误差的原因有两个:一是试验测量获得的应力和应变数据存在一定的测量误差;二是在进行数值优化过程中存在的舍入误差.

图7

图7 等效应力-等效塑性应变曲线

Fig.7 Equivalent stress-equivalent plastic strain curve

3.2 数值模拟结果

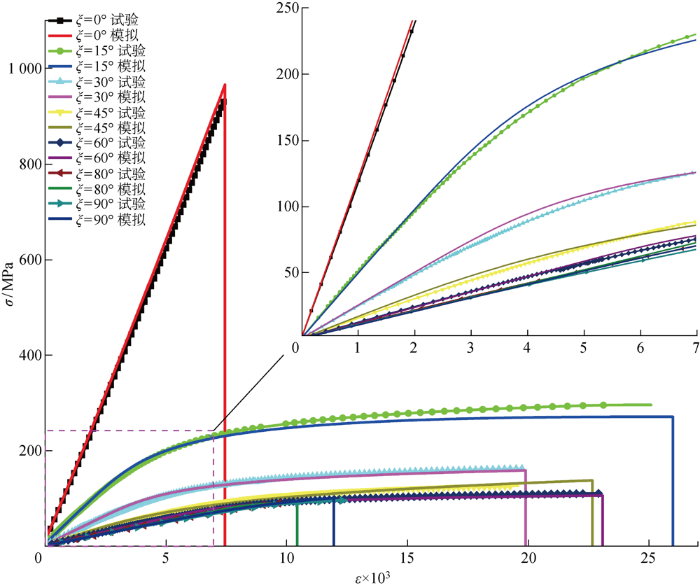
数值模拟获得的不同角度的应力-应变曲线与试验获得的应力-应变曲线的对比如图8所示,可以看出数值模拟获得的应力-应变曲线与试验获得的应力-应变曲线吻合较好,表明本模型能够较为准确地模拟单向AS4/PEEK层压板的塑性效应.

图8

图8 数值模拟与试验的应力-应变曲线对比

Fig.8 Comparison of stress-strain curves between numerical simulation and test

试验和数值模拟预测的拉伸强度见表4,表中实验值为5件试验件的拉伸强度的平均值.从表4可知,在试验件厚度相同的情况下,随着偏轴角度的增加,拉伸强度逐渐下降.数值模拟预测的拉伸强度与实验值的最大误差为19.05%,不超过20%,表明该模型适用于预测单向AS4/PEEK层压板偏轴拉伸的拉伸强度.

表4 拉伸强度及误差的对比

Tab.4 Comparison of tensile strength and error

铺层	实验值/MPa	预测值/MPa	误差/%
[0]₈	896.35	966.21	7.79
[15]₂₀	298.41	271.04	-9.17
[30]₂₀	138.78	158.85	14.46
[45]₂₀	120.50	137.99	14.51
[60]₂₀	114.37	106.28	-7.07
[80]₂₀	76.96	91.62	19.05
[90]₁₆	97.13	101.04	4.03

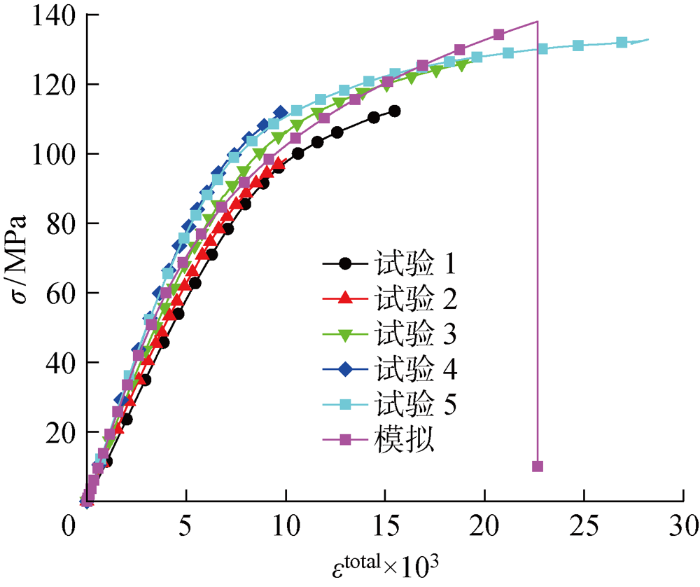
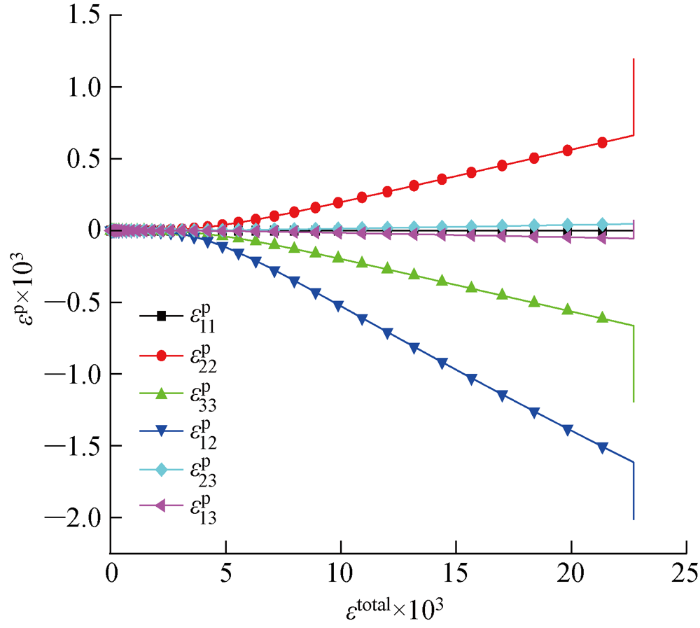
[45]₂₀铺层数值模拟和试验获得的应力-总应变(ε^total)曲线对比如图9所示.结合图10的塑性应变(ε^p)-总应变曲线可知,当总应变在 1.5×10^-3 以下时,各个方向都不存在塑性变形,此时层压板表现为线弹性;随着总应变的增大,除纤维方向外其余方向的塑性变形逐渐增大,使得层压板表现出明显的非线性力学行为;当总应变达到 22.7×10^-3时,应力出现急剧下降,表明此时层压板已经完全破坏.从图10可以看出,塑性变形主要发生在1-2平面内和3方向,且1-2平面内的剪切塑性应变约为2方向和3方向的塑性应变的3倍,表明剪切变形在塑性变形中处于主导地位.

图9

图9 [45]₂₀铺层试验与数值模拟应力-总应变曲线对比

Fig.9 Comparison of stress-total strain curves between experiment and numerical simulation of [45]₂₀ specimens

图10

图10 塑性应变-总应变曲线

Fig.10 Plastic strain-total strain curve

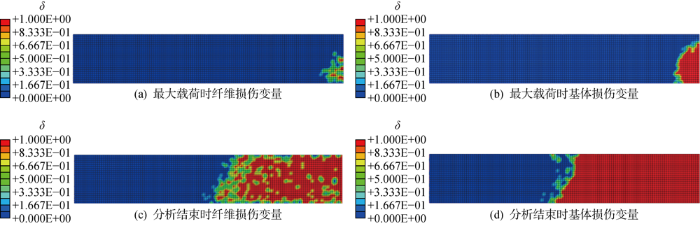
最大载荷和分析结束时的损伤变量(δ)云图如图11所示,当损伤变量值为0时表示未发生破坏,损伤变量值为1时表示已经完全破坏.模拟结果表明,当载荷达到7.34 kN时,层压板首先在端部的边缘发生基体破坏;随着载荷的增加,在基体的破坏部位附近发生纤维破坏,然后基体破坏和纤维破坏开始向未破坏的部位传播;当载荷达到最大值9.66 kN时,基体破坏已经扩展至层压板端部的另一边缘;计算结束时,基体破坏和纤维破坏已经扩展到试验件的中部,此时的层压板已完全失去承载能力.

图11

图11 [45]₂₀铺层损伤变量

Fig.11 Damage variables of [45]₂₀ specimens

4 结论

通过对[0]₈、[15]₂₀、[30]₂₀、[45]₂₀、[60]₂₀、[80]₂₀和[90]₁₆共7种铺层进行偏轴拉伸试验,获得了相应的应力-应变曲线及拉伸强度.对不同铺层角度的断裂面角度进行测量,测得的断裂面角度与铺层角度的差异在 -1°~2°之间,对断裂面的观察和分析表明导致此差异的原因为AS4/PEEK层压板在制造过程中铺层角度和设计角度存在误差.

对于AS4/PEEK层压板在加载过程中表现出显著的非线性力学行为和破坏行为,提出一个同时考虑塑性效应和损伤累计的三维弹塑性损伤本构模型,并开发了基于Abaqus的用户材料子程序VUMAT.塑性模型中的参数使用信任域反射算法计算得到,其值为a₆₆=1.50,β=292.67和n=0.1346.

将三维弹塑性损伤本构模型应用于单向AS4/PEEK层压板的偏轴拉伸数值模拟,预测得到的应力-应变曲线与试验获得的应力-应变曲线吻合良好,表明该模型能够较为准确地模拟单向AS4/PEEK层压板的塑性效应.对加载过程中的各方向的塑性应变的分析表明,1-2平面内的剪切塑性应变在塑性变形中占主导地位.对比数值模拟与试验测量的拉伸强度,在相同的厚度下,随着偏轴角度的增大,拉伸强度逐渐下降,预测的拉伸强度与实际的拉伸强度的最大误差不超过20%,表明该模型适用于预测单向AS4/PEEK层合板的偏轴拉伸强度.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

沈观林, 胡更开.

复合材料力学[M]. 北京: 清华大学出版社, 2006.

SHEN

Guanlin

, HU

Gengkai

Mechanics of composite materials[M]. Beijing: Tsinghua University Press, 2006.

[2]

王昌斌, 方程, 李晔.

国内外连续玻纤增强热塑性复合材料现状

[J]. 汽车文摘, 2020(9): 12-16.

WANG

Changbin

, FANG

Cheng

, LI

Current status of continuous glass fiber reinforced thermoplastic composites at home and abroad

[J]. Automotive Digest, 2020(9): 12-16.

[3]

刘士琦, 周红霞, 王玉, 等.

热塑性复合材料的应用研究

[J]. 化学与粘合, 2021, 43(1): 72-75.

LIU

Shiqi

, ZHOU

Hongxia

, WANG

, et al.

Research progress in the application of environment friendly thermoplastic composite materials

[J]. Chemistry and Adhesion, 2021, 43(1): 72-75.

[4]

见雪珍, 杨洋, 袁协尧, 等.

商用客机连续纤维增强热塑性复合材料的现状及其发展趋势

[J]. 上海塑料, 2015(2): 17-22.

JIAN

Xuezhen

, YANG

Yang

, YUAN

Xieyao

, et al.

Status and development trend of continuous fiber reinforced thermoplastic composites in commercial aircraft

[J]. Shanghai Plastics, 2015(2): 17-22.

DOI:10.1016/0266-3538(94)90176-7 URL [本文引用: 1]

[5]

LAFARIE-FRENOT

M C

, TOUCHARD

Comparative in-plane shear behaviour of long-carbon-fibre composites with thermoset or thermoplastic matrix

[J]. Composites Science and Technology, 1994, 52(3): 417-425.

[6]

WANG

S Y

, ZHANG

J Z

, FANG

G D

, et al.

Mathematical description of mechanical behavior of woven fabric reinforced PPS-based composites at high temperature

[J]. Polymer Composites, 2019, 40(3): 1097-1103.

DOI:10.1002/pc.24807 URL [本文引用: 1]

[7]

TAN

, FALZON

B G

Modelling the nonlinear behaviour and fracture process of AS4/PEKK thermoplastic composite under shear loading

[J]. Composites Science and Technology, 2016, 126: 60-77.

DOI:10.1016/j.compscitech.2016.02.008 URL [本文引用: 1]

[8]

陈静芬.

基于弹塑性损伤本构模型的复合材料层合板破坏荷载预测

[J]. 复合材料学报, 2017, 34(4): 545-557.

[本文引用: 4]

CHEN

Jingfen

Failure loads prediction of composite laminates using a combined elastoplastic damage model

[J]. Acta Materiae Compositae Sinica, 2017, 34(4): 545-557.

[本文引用: 4]

[9]

胡祎乐, 余音, 汪海, 等.

纤维增强复合材料机翼长桁压缩破坏预测方法

[J]. 上海交通大学学报, 2012, 46(9): 1471-1475.

Yile

, YU

Yin

, WANG

Hai

, et al.

A failure prediction method of fiber-reinforced composite wing stringer subjected to compressive loading

[J]. Journal of Shanghai Jiao Tong University, 2012, 46(9): 1471-1475.

[10]

刘魏光, 余音, 汪海.

考虑剪切非线性的复合材料渐进损伤模型

[J]. 上海交通大学学报, 2016, 50(2): 194-199.

[本文引用: 2]

LIU

Weiguang

, YU

Yin

, WANG

Hai

A damage model considering shear nonlinearity for progressive failure analysis of composite laminates

[J]. Journal of Shanghai Jiao Tong University, 2016, 50(2): 194-199.

[本文引用: 2]

[11]

拓宏亮, 马晓平, 卢智先.

基于连续介质损伤力学的复合材料层合板低速冲击损伤模型

[J]. 复合材料学报, 2018, 35(7): 1878-1888.

TUO

Hongliang

, MA

Xiaoping

, LU

Zhixian

A model for low velocity impact damage analysis of composite laminates based on continuum damage mechanics

[J]. Acta Materiae Compositae Sinica, 2018, 35(7): 1878-1888.

[12]

兰剑, 谢官模, 夏俊康, 等.

复合材料开孔层合板双轴拉伸的渐进损伤

[J]. 材料科学与工程学报, 2020, 38(2): 214-219.

LAN

Jian

, XIE

Guanmo

, XIA

Junkang

, et al.

Progressive damage of composite perforated laminates under biaxial tensile loading

[J]. Journal of Materials Science and Engineering, 2020, 38(2): 214-219.

[13]

何柏灵, 葛东云.

复合材料连续损伤力学模型在螺栓接头渐进失效预测中的应用

[J]. 复合材料学报, 2020, 37(8): 2065-2075.

Boling

, GE

Dongyun

Application of continuum damage mechanics model for composites in progressive failure prediction of bolted joints

[J]. Acta Materiae Compositae Sinica, 2020, 37(8): 2065-2075.

DOI:10.1016/j.compstruct.2019.111210 URL [本文引用: 1]

[14]

ZHUANG

F J

, ARTEIRO

, FURTADO

, et al.

Mesoscale modelling of damage in single-and double-shear composite bolted joints

[J]. Composite Structures, 2019, 226: 111210.

[15]

ZHOU

J J

, WEN

P H

, WANG

S N

Finite element analysis of a modified progressive damage model for composite laminates under low-velocity impact

[J]. Composite Structures, 2019, 225: 111113.

DOI:10.1016/j.compstruct.2019.111113 URL [本文引用: 1]

[16]

MOHAMMADI

, MAHMOUDI

Developing a new model to predict the fatigue life of cross-ply laminates using coupled CDM-entropy generation approach

[J]. Theoretical and Applied Fracture Mechanics, 2018, 95: 18-27.

DOI:10.1016/j.tafmec.2018.02.012 URL [本文引用: 1]

[17]

, MA

D Y

, LIU

H F

, et al.

Assessment of failure criteria and damage evolution methods for composite laminates under low-velocity impact

[J]. Composite Structures, 2019, 207: 727-739.

DOI:10.1016/j.compstruct.2018.09.093 URL [本文引用: 1]

[18]

MAA

R H

, CHENG

J H

A CDM-based failure model for predicting strength of notched composite laminates

[J]. Composites Part B: Engineering, 2002, 33(6): 479-489.

DOI:10.1016/S1359-8368(02)00030-6 URL [本文引用: 2]

[19]

XIAO

X R

Modeling energy absorption with a damage mechanics based composite material model

[J]. Journal of Composite Materials, 2009, 43(5): 427-444.

DOI:10.1177/0021998308097686 URL [本文引用: 1]

[20]

LADEVEZE

, LEDANTEC

Damage modelling of the elementary ply for laminated composites

[J]. Composites Science and Technology, 1992, 43(3): 257-267.

DOI:10.1016/0266-3538(92)90097-M URL [本文引用: 1]

[21]

SUN

C T

, CHEN

J L

A simple flow rule for characterizing nonlinear behavior of fiber composites

[J]. Journal of Composite Materials, 1989, 23(10): 1009-1020.

DOI:10.1177/002199838902301004 URL [本文引用: 6]

[22]

HASHIN

Failure criteria for unidirectional fiber composites

[J]. Journal of Applied Mechanics, 1980, 47(2): 329-334.

DOI:10.1115/1.3153664 URL [本文引用: 1]

[23]

PINHO

S T

, DARVIZEH

, ROBINSON

, et al.

Material and structural response of polymer-matrix fibre-reinforced composites

[J]. Journal of Composite Materials, 2012, 46(19/20): 2313-2341.

DOI:10.1177/0021998312454478 URL [本文引用: 2]

[24]

BAŽANT

Z P

, OH

B H

Crack band theory for fracture of concrete

[J]. Matériaux et Construction, 1983, 16(3): 155-177.

DOI:10.1007/BF02486267 URL [本文引用: 1]

[25]

ASTM.

Standard test method for tensile properties of polymer matrix composite materials: D3039/D3039M-17[S/OL]. (2017-12-11) [2021-09-14]. https://www.astm.org/d3039_d3039 m-17.html.

URL [本文引用: 4]

[26]

WEEKS

C A

, SUN

C T

Modeling non-linear rate-dependent behavior in fiber-reinforced composites

[J]. Composites Science and Technology, 1998, 58(3/4): 603-611.

DOI:10.1016/S0266-3538(97)00183-8 URL [本文引用: 1]

[27]

WANG

, XIAO

Some improvements on Sun-Chen’s one-parameter plasticity model for fibrous composites. Part I: Constitutive modelling for tension-compression asymmetry response

[J]. Journal of Composite Materials, 2017, 51(3): 405-418.

DOI:10.1177/0021998316644853 URL [本文引用: 1]

[28]

JANG

, JEON

S Y

, CHOI

J H

, et al.

Mechanical analysis of fiber-reinforced plastics using an elastoplastic-damage constitutive equation considering asymmetric material behavior

[J]. Composite Structures, 2021, 272: 114268.

DOI:10.1016/j.compstruct.2021.114268 URL [本文引用: 2]

[29]

PINHO

S T

, IANNUCCI

, ROBINSON

Physically based failure models and criteria for laminated fibre-reinforced composites with emphasis on fibre kinking. Part II: FE implementation

[J]. Composites Part A: Applied Science and Manufacturing, 2006, 37(5): 766-777.

DOI:10.1016/j.compositesa.2005.06.008 URL [本文引用: 1]

[30]

EGAN

Finite element modelling and high speed testing of countersunk composite aircraft joints[D]. Limerick: University of Limerick, 2014.

[31]

DONADON

M V

, DE

ALMEIDA S F M

, ARBELO

M A

, et al.

A three-dimensional ply failure model for composite structures

[J]. International Journal of Aerospace Engineering, 2009, 2009: 486063.

DOI:10.1016/0167-6636(94)00053-0 URL [本文引用: 1]

[32]

MATZENMILLER

, LUBLINER

, TAYLOR

R L

A constitutive model for anisotropic damage in fiber-composites

[J]. Mechanics of Materials, 1995, 20(2): 125-152.

[33]

LIU

H B

, LIU

, KABOGLU

, et al.

Experimental and numerical studies on the behaviour of fibre-reinforced composites subjected to soft impact loading

[J]. Procedia Structural Integrity, 2019, 17: 992-1001.

DOI:10.1016/j.prostr.2019.08.132 URL [本文引用: 1]

[34]

REN

, LE

G G

, ZHONG

J L

, et al.

Numerical research on elasto-plastic behaviors of fiber-reinforced polymer based composite laminates

[J]. Composite Structures, 2019, 207: 364-372.

DOI:10.1016/j.compstruct.2018.09.027 URL [本文引用: 2]

[35]

LIU

H B

, LIU

, DING

Y Z

, et al.

A three-dimensional elastic-plastic damage model for predicting the impact behaviour of fibre-reinforced polymer-matrix composites

[J]. Composites Part B: Engineering, 2020, 201: 108389.

DOI:10.1016/j.compositesb.2020.108389 URL [本文引用: 1]

[36]

李璇, 陈秀华, 史晓辉, 等.

考虑双模量影响的复合材料销钉连接失效分析

[J]. 上海交通大学学报, 2015, 49(1): 101-108.

Xuan

, CHEN

Xiuhua

, SHI

Xiaohui

, et al.

Effect of bimodularity on failure behaviors of pinned-joint composite laminates

[J]. Journal of Shanghai Jiao Tong University, 2015, 49(1): 101-108.