波浪是近岸水域重要的水动力之一,波浪力是海洋(海岸)工程结构设计中必须考虑的环境荷载,精准预报这一波浪条件是工程设计的前提.水平波浪力是波浪压力沿水深方向的积分,与波浪波面下的速度分布息息相关,因此对速度场的研究具有重要的学术和工程应用价值.
波浪速度的研究多采用理论分析、数值模型模拟和物理模型试验模拟等方法,其中数值模型模拟省时且成本低,是最常用的方式.作为一种典型的势流模型,多数Boussinesq方程将复杂的三维水波问题简化为二维问题,大大降低了模型求解难度,促使这类方程在海岸波浪水动力研究中得以长足发展.Boussinesq模型的理论发展经历了从弱非线性到强非线性等过程,最新方程的适用水深已得到大幅度拓展[1-2],甚至在Liu等[2]的研究中已完全摆脱了水深限制.文献[1]首次对两层水体中间位置的水平和垂直方向速度沿垂向坐标z做泰勒(Taylor)展开,进而利用计算速度取代中间位置处的速度,最终推导出最大空间导数为3的双层Boussinesq方程,该方程在1%误差内的最大适用水深达kh=53.1(k为波数,h为静水深);文献[2]进一步将文献[1]拓展成多层,并给出空间导数为2和5的多层Boussinesq水波方程,4层空间导数为5的方程在1%误差下的适用水深达kh=7600.关于Boussinesq水波方程在理论性能、数值格式和数值应用的研究进展可参见文献[3⇓-5].Madsen等[6]的最新研究认为多数高阶Boussinesq水波方程因色散精度不足,存在波谷不稳定的缺点,并证明了文献[2]最高导数为3的4层水波方程的稳定范围最大.
Liu等[7]分析了最高空间导数为2的多层Boussinesq水波方程的线性和非线性性能,1%误差内,2层模型色散适用水深(相速度)可达kh=19.7,而沿水深分布的水平速度的适用水深仅为kh=5.1,前者是后者的3.86倍;3层和4层色散适用水深分别是其水平速度的3.65倍和2.57倍,可见多层模型速度的适用水深远小于相速度,这一现象也存在于多数常用Boussinesq水波方程中.林鹏程等[8]针对不同非线性、不同水深情况和线性入射条件,研究了最高空间导数为3的单层Boussinesq水波方程垂向分布的速度特征,得出的速度分布与Stokes线性波、二阶波和三阶波解析解存在一定的差异;刘必劲等[9]采用单层Boussinesq水波方程模拟聚焦波和稳态波,发现单层Boussinesq水波方程能够胜任波面的模拟,但无法给出精确的速度轮廓.文献[8-9]采用的单层Boussinesq水波方程是文献[1]双层模型的简化版,相关模拟结果也说明单层Boussinesq水波方程的速度精度远小于色散精度.
1 速度公式的修正
文献[2]将垂向水体分为2层,推导了最高导数为2的双层Boussinesq方程.在立面二维情况下,速度表达式分为从自由表面到静水位、从静水位到连接面以及连接面到水底共3段.
从静水位到连接面的速度场为
式中:u, w为水平、垂向速度;z为垂向坐标,0点起始置于静水位处,向上为正;
从连接面到水底的速度场为
式中:
从自由表面到静水位的速度场为
式中:u10, w10分别为静水位处的水平和垂向速度.
式中:β为常系数,其取值需通过与速度解析解做优化获取.式(7)~(10)中最后一项是3阶导数项的修正,此3阶项可在方程推导过程中直接得到.当速度位于z=zα1,z=zα2时,该项自动为0;当不在这两处时,乘以β后相当于修正.式(5)~(10)简称为改进公式.
水平速度误差和垂直速度误差采用Liu等[2]给出的表达式
式中:us(0)和ws(0) 为静水位处的水平和垂向速度;us(z)和 ws(z)为Stokes线性波速度场.取 0<kh<8,利用上式可优化得到β=0.78.
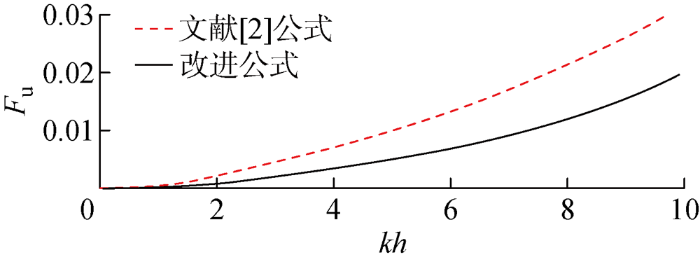
图1
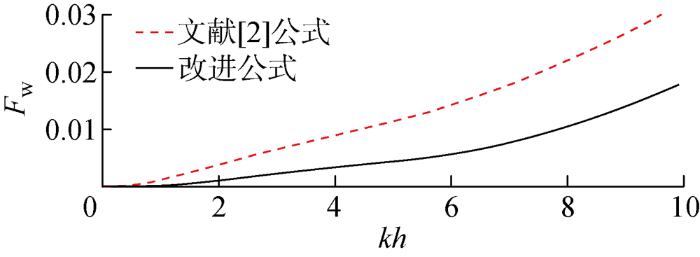
图2
图3
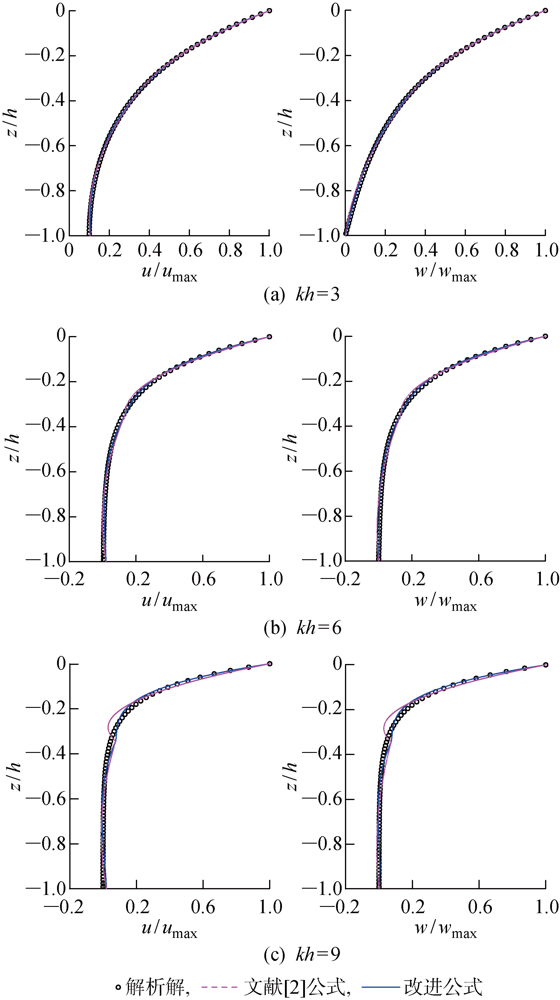
图3
水平和垂向速度与Stokes线性波解析解比较
Fig.3
Comparisons of velocity profiles between numerical results and Stokes linear wave solution
2 数值模型及验证
2.1 数值模型
2.2 与流函数波浪速度场的比较
图3仅给出了线性波条件的速度解析对比,对于较强非线性情况下的速度场是否能够胜任,还需通过数值模拟加以印证.以流函数波浪速度为比较对象,利用解析解验证改进前后计算结果的差异,进一步验证本文公式的有效性.
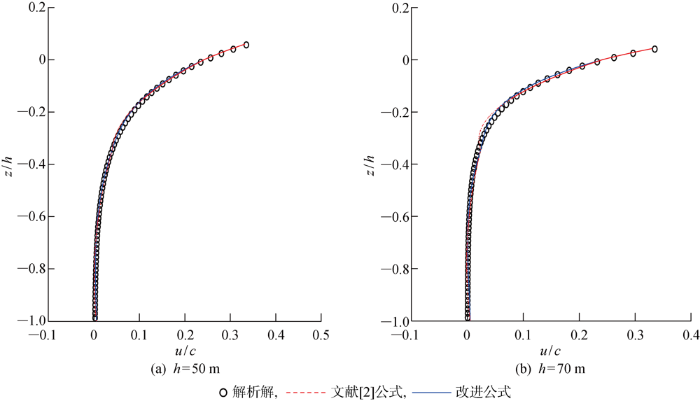
设计静水深h分别为50 m和70 m的两个工况,流函数波浪周期为T=6 s、波高H=5 m.数值模拟中,L为流函数波浪对应的非线性波长,计算区域采用10L,空间步长采用L/32,时间步长采用0.05 s.改进公式和文献[2]公式计算结果与解析解的比较如图4所示,其中c为流函数波浪的相速度.与文献[2]公式相比,改进公式计算得到的速度场与解析解吻合程度更佳,特别是在水深为70 m时,波浪流函数的波长为60.171 m,反算得出kh=7.31.结合图1,当kh=7.31时,文献[2]公式的水平速度积分误差为1.83%,远大于改进公式的积分误差0.99%.数值结果表明,改进的速度场计算结果明显优于文献[2]公式的结果.
图4
图4
计算波峰面下的速度场与波浪流函数解析速度场比较
Fig.4
Comparison of computed velocity profile with analytical solution of wave stream function under wave crest
2.3 聚焦波最大波峰面下的水平速度剖面
Baldock等[12]进行了深水聚焦波演化试验的研究,将最大和最小周期分为29份,每个频率的波幅取值相同,其中B组为宽谱,T=0.6~1.4 s,kh=1.568~7.825;D组为窄谱,T=0.8~1.2 s,kh=2.026~4.403.
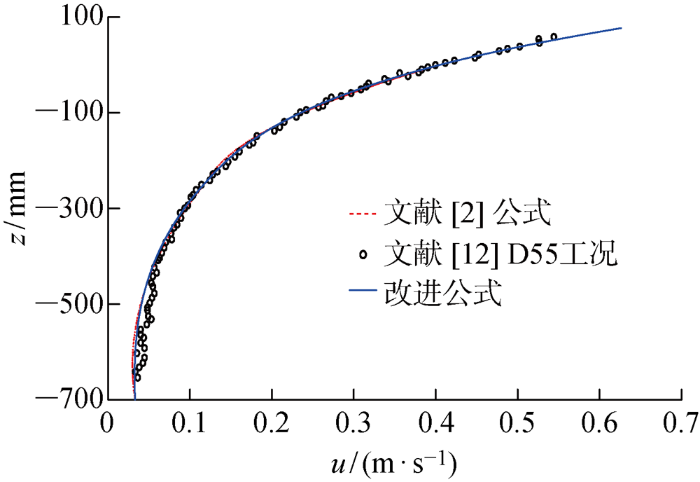
图5
图5
文献[2]公式和改进公式的计算水平速度剖面与D55工况试验结果的比较
Fig.5
Comparisons of calculated horizontal velocity profiles from the present formula and the original formula with D55 experimental data
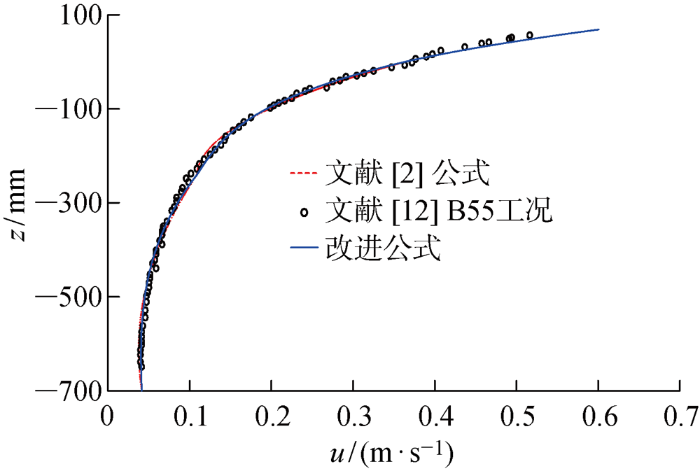
图6
图6
文献[2]公式和改进公式的计算水平速度剖面与B55工况试验结果的比较
Fig.6
Comparisons of calculated horizontal velocity profiles from the present formula and the original formula with B55 experimental data
由图可见,改进公式优于文献[2]公式的计算结果.D55窄谱情况下,波数范围在kh= 2.026~4.403之间,结合图1结果可知,文献[2]中水平速度在1%误差内适用的最大水深为kh=5.1,表明文献[2]公式也能满足所有频率的垂向积分误差都低于1%.因此,针对D55工况,改进前后的计算结果不存在明显差异.B55宽谱情况下,波数范围在kh=1.568~7.825之间,结合图1结果可知,在1%误差内,文献[2]中水平速度计算公式不能涵盖全部频域,kh=7.825的误差约为2%,本文水平速度在1%误差内适用的最大水深为kh=7.34,kh=7.825的误差约为1.14%,可见改进公式的多数频率范围的误差均能控制在1%左右,因此得到的速度剖面更为精确.在自由表面(波面)附近的结果比试验结果大,一方面数值模拟中的衰减现象比物理模型试验中的衰减现象弱;另一方面,物理模型试验中的测量方法很难精确捕捉到自由表面处的速度,其他一些学者采用势流理论模型进行求解也得到类似结果.在水底附近数值模拟的水平速度与试验结果存在一定差异,主要是数值模拟采用Boussinesq水波方程,其在物理机制上与物理模型试验中的衰减现象并不完全一致.
3 结论
提出一种改进方程速度精度的方法,即在双层Boussinesq水波方程的速度公式基础上,引入带有常系数β的三阶项,不改变原始Boussinesq水波方程,利用新的公式即可获取更高精度的速度场.通过理论分析和数值验证,主要得出以下结论:
(1) 双层Boussinesq水波方程的速度场可以在一定程度上得到改进,常系数β=0.78时,在1%误差内,水平速度和垂向速度的最大适用水深得到了较大幅度改进,其中水平速度由原来的kh=5.1提高到kh=7.34,垂向速度由原来的kh=4.5提高到kh=7.83.
(2) 利用模型模拟强非线性聚焦波和流函数波浪(稳态波)演化,发现改进的水平速度剖面与试验结果的吻合度更高,从数值角度展示了理论改进方式的有效性.
此外,本文的改进方法可为其他Boussinesq水波方程改进提供重要参考,有关详细的分析与讨论有待更深入的研究.
参考文献
A new two-layer Boussinesq model for coastal waves from deep to shallow water: Derivation and analysis
[J].DOI:10.1016/j.wavemoti.2016.07.002 URL [本文引用: 4]
A new multi-layer irrotational Boussinesq-type model for highly nonlinear and dispersive surface waves over a mildly sloping seabed
[J].DOI:10.1017/jfm.2018.99 URL [本文引用: 27]
Boussinesq models and their application to coastal processes across a wide range of scales
[J].DOI:10.1061/(ASCE)WW.1943-5460.0000350 URL [本文引用: 1]
Boussinesq相位解析的海岸水动力学数学模型研究进展
[J].
Review of Boussinesq phase-resolving coastal hydrodynamic model
[J].
关于Boussinesq型水波方程理论和应用研究的综述
[J].
A review on the theory and application of Boussinesq-type equations for water waves
[J].
Trough instabilities in Boussinesq formulations for water waves
[J].DOI:10.1017/jfm.2020.76 URL [本文引用: 1]
A multi-layer Boussinesq-type model with second-order spatial derivatives: Theoretical analysis and numerical implementation
[J].DOI:10.1016/j.oceaneng.2019.106545 URL [本文引用: 5]
基于Boussinesq数值模型的波浪速度垂向分布模拟研究
[J].
Simulation of vertical distribution of wave velocity field based on Boussinesq numerical model
[J].
基于Boussinesq水波模型的聚焦波模拟
[J].
Simulating the evolution of a focused wave group by a Boussinesq-type model
[J].
Effect of the coefficient on the performance of a two-layer boussinesq-type model
[J].DOI:10.1007/s13344-021-0004-5 URL [本文引用: 1]
Numerical verification of a two-layer Boussinesq-type model for surface gravity wave evolution
[J].DOI:10.1016/j.wavemoti.2018.11.007 URL [本文引用: 1]
A laboratory study of nonlinear surface waves on water
[J].Philosophical Transactions of the Royal Society A: Mathematical
DOI:10.1098/rsta.1996.0022 URL [本文引用: 2]