上海交通大学学报

上海交通大学学报, 2023, 57(2): 127-137 doi: 10.16183/j.cnki.jsjtu.2021.448

船舶海洋与建筑工程

基于BESO算法的大型海洋垂直轴风力机支撑结构优化

何文君1, 苏捷1, 周岱1, 韩兆龙,1,2, 包艳1, 赵永生1,2, 许玉旺1, 涂佳黄3

1.上海交通大学 船舶海洋与建筑工程学院;海洋工程国家重点实验室, 上海 200240

2.上海交通大学 极地深海技术研究院;海洋装备研究院, 上海 200240

3.湘潭大学 土木工程与力学学院,湖南 湘潭 411105

Supporting Structure Optimization of Offshore Large-Scale Vertical Axis Wind Turbine Based On BESO Algorithm

HE Wenjun1, SU Jie1, ZHOU Dai1, HAN Zhaolong,1,2, BAO Yan1, ZHAO Yongsheng1,2, XU Yuwang1, TU Jiahuang3

1. School of Naval Architecture, Ocean and Civil Engineering; State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. Institute of Polar and Ocean Technology; Institute of Marine Equipment, Shanghai Jiao Tong University, Shanghai 200240, China

3. College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, Hunan, China

通讯作者: 韩兆龙,教授,博士生导师;E-mail:han.arkey@sjtu.edu.cn.

责任编辑: 李博文

收稿日期: 2021-11-7   修回日期: 2021-12-15   接受日期: 2021-12-23  

基金资助: 国家自然科学基金(52271284)
国家自然科学基金(52122110)
国家自然科学基金(42076210)
国家自然科学基金(51879160)
上海市科委重大研究计划(2019-01-07-00-02-E00066)
上海市曙光计划(19SG10)
上海交通大学深蓝计划(SL2020PT201)
上海交通大学深蓝计划(SL2020PT302)
湖南省自然科学基金(2021JJ50027)

Received: 2021-11-7   Revised: 2021-12-15   Accepted: 2021-12-23  

作者简介 About authors

何文君(1997-),硕士生,从事垂直轴风力机结构减振研究.

摘要

大型海洋垂直轴风力机的研究对发展海洋风能具有重要意义,研究大型垂直轴风力机的合理支撑结构形式对风力发电结构安全至关重要.基于变删除率的双向渐进结构优化(BESO)算法,对大型海洋垂直轴风力机进行支撑结构优化,并通过风力机的动力响应特性分析,验证结构优化方法的可靠性.结果表明:反比例型变删除率的BESO算法能有效改善优化迭代速率,适用于垂直轴风力机的支撑结构优化设计;相比于初始结构,拓扑出的新结构模型在风荷载作用下的风致动力响应显著降低.研究成果可用于垂直轴风力机支撑结构设计优化.

关键词： 垂直轴风力机; 双向渐进结构优化算法; 动力响应; 减振

Abstract

The research on large-scale offshore vertical axis wind turbine is of great significance to the development of ocean wind energy. For the safety of wind power, it is very important to study the reasonable supporting structure of the large-scale wind turbine. In this paper, an supporting structure optimization of a large-scale vertical axis wind turbine based on the variable deletion rate bidirectional evolutionary structural optimization (BESO) algorithm is proposed, and the reliability of structural optimization is verified by analyzing the dynamic response. The results show that this inverse proportional BESO algorithm can effectively improve the optimization iteration rate, and has a wide applicability to the optimal design of vertical axis wind turbine supporting structure. Compared with the initial structure, the wind-induced dynamic response of the topological new structure model under wind load is significantly reduced. The findings can be used to optimize the structural design of vertical axis wind turbine.

Keywords： vertical axis wind turbine; bidirectional evolutionary structural optimization (BESO) algorithm; dynamic response; vibration reduction

PDF (12945KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

何文君, 苏捷, 周岱, 韩兆龙, 包艳, 赵永生, 许玉旺, 涂佳黄. 基于BESO算法的大型海洋垂直轴风力机支撑结构优化[J]. 上海交通大学学报, 2023, 57(2): 127-137 doi:10.16183/j.cnki.jsjtu.2021.448

HE Wenjun, SU Jie, ZHOU Dai, HAN Zhaolong, BAO Yan, ZHAO Yongsheng, XU Yuwang, TU Jiahuang. Supporting Structure Optimization of Offshore Large-Scale Vertical Axis Wind Turbine Based On BESO Algorithm[J]. Journal of Shanghai Jiaotong University, 2023, 57(2): 127-137 doi:10.16183/j.cnki.jsjtu.2021.448

自“碳达峰、碳中和”目标提出以来,“能源革命”浪潮势不可挡,风力发电(以下简称风电)在可再生能源结构中占据重要地位,是目前最具竞争力的可再生能源之一[1-2].大型垂直轴风力机不仅可以提高风能利用率、有效降低发电成本,还具有多向受风[3-4]、重心低[5-6]、噪声小[7-8]等优点,在我国能源发展战略中发挥重要作用.因此,大兆瓦级海上垂直轴风力机将成为未来研究领域的重点.

合理的风力机支撑结构是保障海上风电结构安全的关键[9].大型H型垂直轴风力机一般由3~6片与转轴平行的叶片组成,其支撑结构必将承受风荷载和高速旋转引起的离心力[10].叶片和主轴间不合理的支撑形式会导致风力机存在局部结构强度较低、叶片位移过大、易产生振动等问题.近年来,学者们对大型H型垂直轴风力机的支撑结构开展了研究[11⇓-13],Dwiyantoro等[14]对小型垂直轴风力机结构关键部位进行数值模拟分析,研究表明缩短主轴可以显著提高结构强度;Hara等[15]通过改变支撑截面形式研究其对H型垂直轴风力机性能的影响;Islam等[16]在分析垂直轴风力机的设计参数时,描述了支撑臂类型、横截面形状的重要性;Li等[17]使用实验和数值模拟研究了垂直轴风力机支撑臂的影响,指出应选择阻力系数较小的截面形式以减少能量损耗;何大伟等[18]对垂直轴风力机主轴建立参数化模型并对主轴内径、支承跨距等进行优化计算;高振勋等[19]分析了能充分利用风能的多层塔式垂直轴风力机的布置方案;蒋周伟[20]针对H型垂直轴风力机主轴和叶臂结构的不足,在分析风力机风振特性影响因素基础上提出加设纤绳的结构优化方案.但这些研究只能针对特定风力机结构形式进行参数分析和局部优化,虽然对风力机结构稳定性有一定程度提高,但设计空间普遍具有局限性.相比于参数优化,拓扑优化方法具有更多的设计自由度.

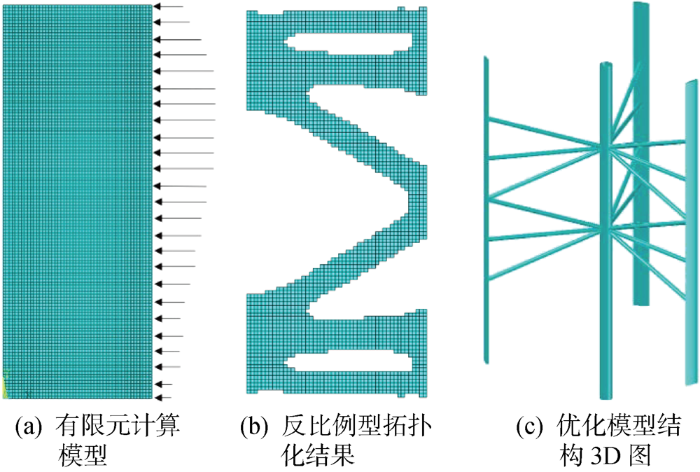
目前结构拓扑优化方法已广泛应用于各个领域,其中双向渐进结构优化(BESO)算法是经典拓扑优化算法之一.文永蓬等[21]基于BESO算法对直辐板车轮进行拓扑优化建模,提出一种新颖的城市轨道车轮辐板结构;才琪等[22]提出了可以应用于桁架结构优化的桁架-双向渐进结构优化算法;刘昆等[23]以船体梁腹板开孔为研究对象,基于BESO算法提出一种适用于船体结构孔型的优化方法.尽管结构拓扑优化技术在众多领域已广泛应用,但在大型海洋垂直轴风力机支撑结构的拓扑优化方面还鲜有研究,因此基于BESO拓扑优化方法研究大型海洋垂直轴风力机支撑结构具有重要意义.

本文将变删除率的BESO算法应用于大型漂浮式垂直轴风力机的支撑结构找形,通过ANSYS参数化设计语言(APDL)进行二次开发,在ANSYS有限元软件中实现大型垂直轴风力机支撑结构的优化,得到一种更符合风力机受力特点的支撑结构形式,该支撑结构可以大大减小风力机由动力响应产生的风振问题.

1 风力机模型

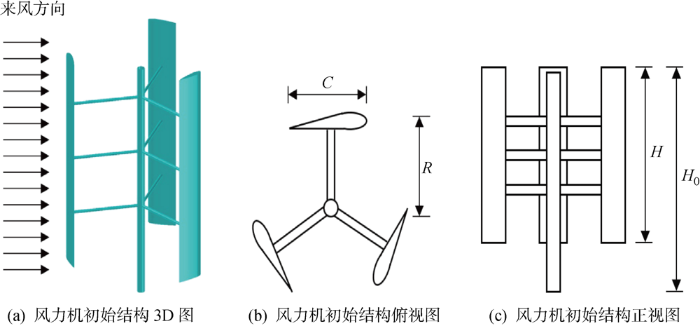
参照Hand等[24]的设计,本文中优化使用的5 MW风力机模型形式为3叶片、3层支撑的垂直轴风力机,叶片翼型截面选择DU-06-W-200,叶片结构为箱型主梁加蒙皮结构,具体几何模型如图1所示.其中,风力机半径R=48.5 m,叶片高度H=127 m,叶片弦长C=6.4 m,主轴高度H0=140 m,叶片安装角为2°.主轴材料选用40Cr合金钢[25],密度ρ0=7.85 g/m3,弹性模量E0=211 N/m2.蒙皮及支撑杆处的材料选择碳纤维环氧树脂,材料密度ρ1=1.62 g/m3,弹性模量E1=120 N/m2,泊松比μ=0.3.考虑最不利荷载工况情况,采用计算流体动力学(CFD)计算气动荷载时,速度入口采用均匀来流,不考虑风剪切,参照文献[26-27]计算入口风速和切出风速均为25 m/s.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   垂直轴风力机几何模型

Fig.1   Geometric model of vertical axis wind turbine


2 数值方法

2.1 气动荷载

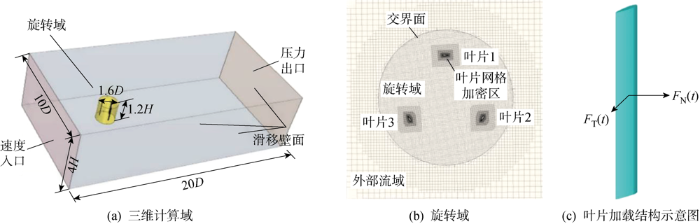
本文大型H型垂直轴风力机叶片所受气动荷载的研究基于CFD方法[28],利用STAR-CCM+软件实现.为减少边界条件对结果的影响,采用长方体计算域和切割体网格,如图2所示.图2(a)中,参照文献[29]计算域长度、宽度和高度分别为20D、10D和4H,旋转域直径为1.6D,高度为1.2H.旋转域和静止域设置交界面,采用滑移网格技术实现风轮旋转,如图2(b)所示.为确保无量纲化壁面距离y+<1满足网格要求,叶片表面采用棱柱层网格,延伸因子为1.3,总厚度为0.08 m,总计网格数为2 625万.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   风场计算域和边界条件

Fig.2   Computation domain and boundary condition of wind field


在转动6~10圈后,风力机的各项性能才趋于稳定,本文风力机的旋转周期为9.46 s,时间步长Δt为0.05 s,且气动荷载随时间变化具有周期性.为方便加载和后续结构动力响应模拟分析,将CFD模拟的气动荷载拟合成时间函数进行结构动力加载.

为使气动荷载模拟更精确,在建模时沿叶片高度方向将叶片分为100份,同时在STAR-CCM+软件中对每段叶片都建立局部坐标系,最终得到每份叶片的气动荷载.再按照力的等效原则将不均匀的气动荷载分别等效加载到叶片的顶部、中部和底部.风力机具有对称性,因此以叶片1中部加载点为例,利用CFD计算得到叶片1中部加载点在一个周期内的切向力和法向力气动数据后,采用多阶正弦函数方法对风力机法向力和切向力进行时程曲线拟合[30],得到风力机叶片加载点上任意时间序列的荷载函数方程为

FN(t)=a0+ ∑j=16(ajcos ω jt+bjsin ω jt)
FT(t)=c0+ ∑j=16(cjcos ω jt+djsin ω jt)

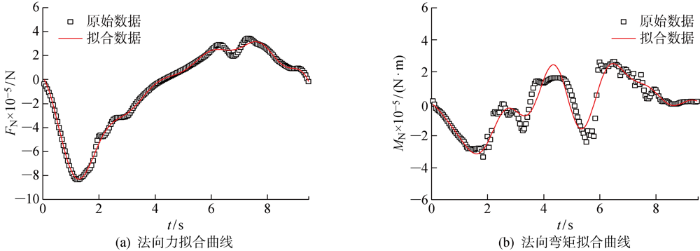
式中:FN(t)和FT(t)分别为t时间下叶片的法向力和切向力;a0、aj、bj、c0、cj、dj为傅里叶系数;ωj为基波圆频率; j∈N*.以叶片中部加载点为例,其受到的法向力和法向弯距(MN)拟合曲线如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   叶片中部加载点处荷载拟合曲线

Fig.3   Applied load curve at the middle loading point of the blade


除风荷载产生的气动荷载外,风力机叶片以角速度ω0绕风力机主轴旋转也会产生离心力,垂直轴风力机旋转时,叶片产生的离心力为

Fω0=mbω02R

式中:mb为叶片质量.

2.2 振动响应分析

风力机的结构振动响应分析在ANSYS软件中实现,采用Newmark-β法[31]中的平均常加速度法进行瞬态分析,参数γ取值为0.5,参数β为0.25.风力机采用瑞利阻尼形式,取刚度阻尼系数为0.03[32].风力机在荷载激励下的振动方程[33]为

$M\ddot{u}(t) + C\dot{u}(t)+ Ku(t) = F_I (t) + F_C (t) + F_K$(t)

式中:M、C、K分别为大型垂直轴风力机的质量、阻尼和刚度矩阵;$ \ddot{u}(t)$、$\dot{u}(t)$、u(t)分别为垂直轴风力机的加速度、速度和位移响应矩阵;FI(t)、FC(t)、FK(t)分别为风力机的惯性力、阻尼力和恢复力矩阵,文中所有结构动力响应计算均由APDL编程实现.

2.3 基于变删除率的BESO算法

将大型垂直轴支撑结构优化问题转化为以结构静刚度最大为目标和结构体积为约束的数学模型[34],如下式:

min C'=C'(x)=uTKu/2
s.t. ∑i=1nxivi-V*=0, xi∈{xmin,1}

式中:C'为结构平均柔顺度;vi为第i个单元的体积;V*为目标体积;xi为第i个单元的相对密度,作为设计变量;xmin和1分别代表某一单元在设计域内缺失或存在.

风力机结构具有对称性,因此以风力机的其中一段叶片与主轴间的支撑形式为例,将三维支撑优化转化为二维平面优化问题.以风力机主轴高度方向和半径方向围成的平面作为初始设计域,取H=127.14 m,宽度B=48.43 m,采用4节点Plane182单元对模型进行网格划分.设置左端为固定端约束,外部风荷载取t=0.89 s时所对应的最不利气动荷载.采用反比例型删除率模型[35]对垂直轴风力机支撑结构进行拓扑优化,结果如图4所示.反比例型删除率模型为

λ=λmax11-V*1-VVi× 1-λminλmax+λmin

式中:λ为删除率;λmin为给定的最小删除率;λmax为给定的最大删除率;Vi为优化过程中每一步迭代过程的体积.当λmin从0.01增加至0.02时,迭代步数下降速率最快,如图4(a)所示,故λmin取0.02;由图4(b)可知λmax在0.06时迭代速度较快,且删除率越小,越能保证拓扑结果的准确性,故λmax取0.06.基于对不同目标体积分数拓扑结果对比,可知V*取0.4时拓扑所得结构较优,因此本文取V*为0.4进行优化.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   删除率对迭代步数的影响

Fig.4   Impact of deletion rate on iteration steps


3 大型垂直轴风力机支撑拓扑优化

3.1 气动荷载

当采用STAR-CCM+对风力机叶片气动荷载进行模拟时,将来流视为不可压缩流体,采用隐式非定常分离流数值离散格式,求解k-ω SST湍流模型.采用二阶精度差分法离散Navier-Stokes方程,采用压力耦合方程组的半隐式方法(SIMPLE)耦合速度和压力.以叶片1为例,其旋转一周形成的法向力和切向力的时程曲线如图5所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   叶片1旋转一周法向力和切向力

Fig.5   Normal and tangential forces of blade 1 rotation


采用Hand等[24]的模拟数据对CFD可靠性进行验证,基于CFD计算模拟和文献[24]气动力模拟数据的功率系数(CP)对比曲线如图6所示.两者整体趋势一致,误差在可接受范围内.因此可以采用此数值模拟方法进行风力机气动荷载的准确计算和下一步研究.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   CFD模型和文献[24]的功率系数对比曲线

Fig.6   Comparison curves of power coefficients between CFD model and that in reference [24]


3.2 支撑优化后的结构形式

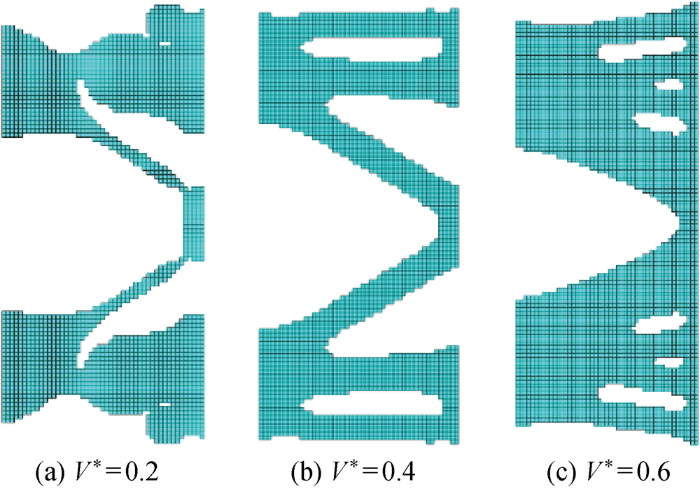
分别对单元删除量(体积)、平均柔顺度、迭代步数的变化历程进行对比分析,如图7所示.传统的BESO算法均采用固定删除率,即以稳定的删除率删除单元应力较小的部分[36].由表1可知,与固定删除率的模型相比,反比例型删除率模型计算效率提高了44.2%.当迭代稳定时,固定删除率模型平均柔顺度为69.19 N·m,而反比例型模型为45.12 N·m.由于平均柔顺度越小,结构刚度越大, 所以反比例型模型迭代出的结构形式更好且更快趋于稳定,后续将选择反比例函数模型拓扑出的优化结构为优化模型与初始模型进行结构动力响应对比分析.拓扑结构初期,单元删除率较大,结构拓扑形式变化较明显,随着拓扑结果向目标体积逼近,结构形式趋于稳定.不同体积目标函数下的拓扑结果如图8所示,典型迭代步骤下风力机支撑拓扑优化结果如图9所示,风力机最终支撑拓扑优化结果示意图如图10所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   优化后结构平均柔顺度和体积分数变化

Fig.7   Average flexibility and volume fraction of optimized structure


表1   反比例型与固定删除率模型对比

Tab.1  Comparison of inverse model and fixed deletion rate

函数模型迭代
步数		计算效率
提高/%		优化后结构平均
柔顺度/(N·m)		平均柔顺度
变化/%
反比例型2944.245.1234.79
固定删除率52-69.19-

新窗口打开| 下载CSV


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   不同体积目标函数下的拓扑结果

Fig.8   Topological results of different volume objective functions


图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   典型迭代步骤下的拓扑进程

Fig.9   Topology processes under typical iterative steps


图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   拓扑优化结果

Fig.10   Topology optimization results


3.3 风力机结构动力响应分析

本文仅针对定常风即速度入口采用均匀来流.考虑最不利荷载工况下,风力机计算入口风速和切出速度均为25 m/s,对转速为0.664 rad/s工况下所受的气动荷载进行分析.风力机叶片选择箱型主梁加蒙皮的结构形式,风力机运动周期为9.463 s.为了简化计算,在进行动力分析时,叶片仅考虑箱型主梁刚度.在保持结构体积相同,其他因素不变的情况下,改变支撑结构形式,运用ANSYS17软件对5 MW风力机初始结构和优化模型进行动力响应分析,其中优化模型由反比例型函数拓扑获得.

风力机在转动6~10圈后气动性能更加稳定,因此选取风力机转动的第80~200 s进行分析.分析发现t=89 s时风力机的结构振幅较大,故对比t=89 s时3种结构在各方向的位移(Ux、Uy、Uz)情况,t=89 s时3个模型对应的位移云图如图11所示.由图11(a)可知,初始模型即未优化模型在x方向位移最大为1.23 m,而优化后模型最大位移为0.56 m,可见优化模型在最危险时的叶片顶端x向位移明显小于初始结构.由图11(b)可知,初始模型在y方向位移最大为1.35 m,而优化后模型最大位移为0.15 m,对叶片顶端y向位移也有明显改善.由图11(c)可知,初始模型的Uz分布在 -0.48~0.01 m之间,优化模型的Uz分布在 -0.15~0.17 m之间.初始模型和优化模型在x、y、z方向位移的最大、最小值均发生在叶片顶端或底端,且x、y向位移较大,z向位移较小.综上分析可知,优化模型相较于初始模型在x、y、z方向的位移均有明显改善.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   风力机结构3向位移云图对比

Fig.11   Comparison of three-way displacement contour maps of vertical axis wind turbine


4 优化结果对比

为进一步分析初始模型和优化模型在动力响应下的减振效果,选取初始模型P点为分析对象,研究两种模型在风力机叶片顶端的风致响应,如图12所示.风力机刚开始运动时不够稳定,因此选取动力响应计算过程的80~200 s进行分析.两种模型在P点处x、y、z向位移时程曲线如图13所示.由图13(a)可知,初始模型在x向出现了非对称变形,位移时程曲线波峰为1.23 m,波谷为-0.58 m,平衡位置在0.50 m左右,而优化模型在x向位移分布在-0.58~0.60 m之间,x向正负幅值较对称;由图13(b)可知,初始模型在y向位移分布为-1.17~0.70 m, 平衡位置接近-0.20 m,而优化模型在y向位移分布为-0.55~0.42 m,y向位移幅值较初始模型显著减小;由图13(c)可知,虽然初始模型和优化模型z向位移的量级均较小,初始模型为-0.54~0.19 m,但优化模型在z向位移幅值为-0.23~0.19 m,负向最大幅值仍有改善.因此,可进一步证明优化模型在动力响应下的减振效果显著.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   两种模型3D结构示意图

Fig.12   3D structure diagram of two models


图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   两模型在节点P的位移时程曲线对比

Fig.13   Comparison of displacement time history curve of two models at node P


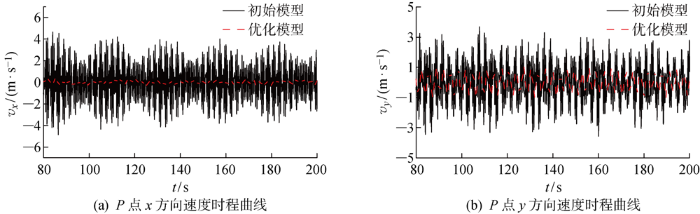
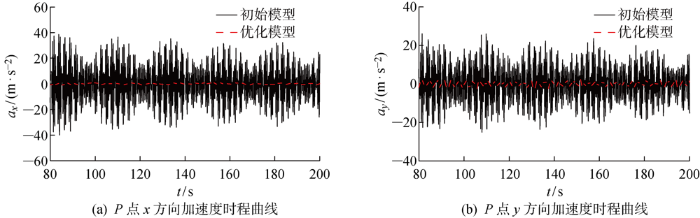
风力机结构位移振幅的变化与叶片顶端运动速度和加速度有关.因此进一步对叶片顶端P点的速度与加速度进行分析.动力响应分析中风力机z向位移较小,因此仅考虑主要位移x、y方向的速度(vx、vy)与加速度(ax、ay)时程曲线.风力机在 80~200 s内叶片顶端P点的速度时程曲线如图14所示.由图可知,相比于初始模型,优化模型在P点的速度显著改善,x向速度浮动范围由 -4.86~4.67 m/s 变为 -0.40~0.36 m/s;y向速度浮动范围由 -3.60~3.70 m/s变为 -1.03~1.03 m/s.风力机在80~200 s内叶片顶端P点的加速度时程曲线如图15所示.由图可知,优化模型在P点的加速度得到显著改善,由x方向上最大值38.67 m/s2变为1.06 m/s2,y方向上最大值26.12 m/s2变为3.06 m/s2.可知,在保持与初始模型体积相同的情况下,优化模型的结构刚度远大于初始模型,风荷载作用下的风致效应显著减小,具有良好的减振效果,同时验证了变删除率的BESO算法对风力机支撑结构拓扑优化的可行性.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14   两模型在节点P的速度时程曲线对比

Fig.14   Comparison of velocity time history curve of two models at node P


图15

新窗口打开| 下载原图ZIP| 生成PPT

图15   两模型在节点P的加速度时程曲线对比

Fig.15   Comparison of acceleration time history curve of two models at node P


在80~200 s动力响应中,两种模型在节点P处的3轴方向位移优化率统计如表2所示.可知,与初始模型相比,优化模型在x、y、z向的位移优化率分别为51.22%、54.70%和61.11%,在P点对应的最大速度和加速度值也显著减小,减振效果明显.因此,基于反比例函数的BESO算法能更好地应用于大型海洋垂直轴风力机的支撑结构优化.

表2   两种模型在节点P处3轴方向位移统计

Tab.2  Triaxial displacement statistics of two models at node P

模型坐标轴最大
位移/m		最大速度/
(m·s-1)		最大加速度/
(m·s-2)		位移
优化率/%
初始模型x1.234.8638.67
y1.173.726.12
z0.54——
优化模型x0.600.41.0651.22
y0.531.033.0654.70
z0.21——61.11

注:“—”表示忽略不计;“空白”表示无数据.

新窗口打开| 下载CSV


5 结论

大型垂直轴风力机支撑结构刚度分布不均匀,风力机结构振动响应明显.本文以某5 MW大型海洋垂直轴风力机支撑结构模型为对象,基于CFD方法,运用STAR-CCM+软件和MATLAB软件拟合风力机气动荷载,提出基于反比例型函数删除率模型的BESO算法对支撑结构进行拓扑优化,并进一步通过ANSYS软件APDL编程实现风力机的动力响应特性分析,验证结构优化的可靠性,主要结论如下:

(1) 基于反比例型函数删除率的BESO算法能明显提高风力机支撑结构的优化效率.与固定删除率的优化模型相比,基于反比例型函数删除率的BESO拓扑算法更适用于大型垂直轴风力机支撑的结构优化,优化效率能提高44.2%.

(2) 优化后的新型结构可以明显减小风致效应的影响.在结构体积相同的情况下,经过拓扑优化的新型垂直轴风力机支撑结构明显提高了风力机的整体结构刚度,叶片在x、y、z向位移分别减小51.22%、54.70%和61.11%.

(3) 基于反比例型函数删除率的BESO拓扑优化算法可以得到垂直轴风力机的较优支撑结构形式.通过初始结构与优化结构的振动响应对比分析验证了该方法的可靠性和有效性,可用于垂直轴风力机支撑结构拓扑优化.

(4) 仅针对反比例型BESO算法拓扑出的结构与原始结构进行动力响应分析对比,后续将针对其他类型函数拓扑出的结构进行分析对比.

参考文献

WANKHADE Y M, BOLKE M R, KANADE S A, et al.

A review of wind energy technology

[J]. Modern Engineering Research, 2016, 6(2): 2249-6645.

[本文引用: 1]

HENDERSON A R.

Offshore wind in Europe

[J]. Refocus, 2002, 3(2): 14-17.

[本文引用: 1]

ZAMANI M, NAZARI S, MOSHIZI S A, et al.

Three dimensional simulation of J-shaped Darrieus vertical axis wind turbine

[J]. Energy, 2016, 116: 1243-1255.

DOI:10.1016/j.energy.2016.10.031      URL     [本文引用: 1]

FIEDLER A J, TULLIS S.

Blade offset and pitch effects on a high solidity vertical axis wind turbine

[J]. Wind Engineering, 2009, 33(3): 237-246.

DOI:10.1260/030952409789140955      URL     [本文引用: 1]

ROLIN V F C, PORTÉ-AGEL F.

Experimental investigation of vertical-axis wind-turbine wakes in boundary layer flow

[J]. Renewable Energy, 2018, 118: 1-13.

DOI:10.1016/j.renene.2017.10.105      URL     [本文引用: 1]

MACPHEE D W, BEYENE A.

Fluid-structure interaction analysis of a morphing vertical axis wind turbine

[J]. Journal of Fluids and Structures, 2016, 60: 143-159.

DOI:10.1016/j.jfluidstructs.2015.10.010      URL     [本文引用: 1]

BALDUZZI F, BIANCHINI A, CARNEVALE E A, et al.

Feasibility analysis of a Darrieus vertical-axis wind turbine installation in the rooftop of a building

[J]. Applied Energy, 2012, 97: 921-929.

DOI:10.1016/j.apenergy.2011.12.008      URL     [本文引用: 1]

ZHANG B S, SONG B W, MAO Z Y, et al.

A novel wake energy reuse method to optimize the layout for Savonius-type vertical axis wind turbines

[J]. Energy, 2017, 121: 341-355.

DOI:10.1016/j.energy.2017.01.004      URL     [本文引用: 1]

孟珣, 李华军, 包兴先.

采油平台在海上风电支撑体系中的应用研究

[J]. 应用基础与工程科学学报, 2010, 18(4): 626-636.

[本文引用: 1]

MENG Xun, LI Huajun, BAO Xingxian.

Feasible study on oil jacket platforms in supporting structural systems of OWTs

[J]. Journal of Basic Science and Engineering, 2010, 18(4): 626-636.

[本文引用: 1]

金浩, 胡以怀, 冯是全.

垂直轴风力机在风力发电中的应用现状及展望

[J]. 环境工程, 2015, 33 (Sup.1): 1033-1038.

[本文引用: 1]

JIN Hao, HU Yihuai, FENG Shiquan.

Current situation and prospect on vertical axis wind turbine in wind power generation

[J]. Environmental Engineering, 2015, 33 (Sup.1): 1033-1038.

[本文引用: 1]

HENDERSON AR, WITCHER D, MORGAN C A.

Floating support structures enabling new markets for offshore wind energy

[C/OL]// European Wind Energy Conference 2009. (2009-03-16)[2021-11-08]. https://www.researchgate.net/profile/Andrew-Henderson/publication/228523769_Floating_support_structures_enabling_new_markets_for_offshore_wind_energy/links/550c3e6f0cf212874160852f/Floating-support-structures-enabling-new-markets-for-offshore-wind-energy.pdf.

URL     [本文引用: 1]

TANG Y G, HU J, LIU L Q.

Study on the dynamic response for floating foundation of offshore wind turbine

[C]// Proceedings of ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering. Rotterdam, Netherlands: ASME, 2011: 929-933.

[本文引用: 1]

刘利琴, 韩袁昭, 肖昌水, 等.

新型浮式基础的海上风机系统动力响应研究

[J]. 海洋工程, 2018, 36(1): 19-26.

[本文引用: 1]

LIU Liqin, HAN Yuanzhao, XIAO Changshui, et al.

Research on dynamic response of offshore wind turbine system based on new semisubmersible-spar hybrid floating foundation

[J]. The Ocean Engineering, 2018, 36(1): 19-26.

[本文引用: 1]

DWIYANTORO A, YUWONO T, SUPHANDANI V.

Structural design optimization of vertical axis wind turbine type darrieus-savonius bambang

[J]. ARPN Journal of Engineering and Applied Sciences, 2016, 11(2): 1073-1077.

[本文引用: 1]

HARA Y, HORITA N, YOSHIDA S, et al.

Numerical analysis of effects of arms with different cross-sections on straight-bladed vertical axis wind turbine

[J]. Energies, 2019, 12(11): 2106.

DOI:10.3390/en12112106      URL     [本文引用: 1]

ISLAM M, FARTAJ A, CARRIVEAU R.

Analysis of the design parameters related to a fixed-pitch straight-bladed vertical axis wind turbine

[J]. Wind Engineering, 2008, 32: 491-507.

DOI:10.1260/030952408786411903      URL     [本文引用: 1]

LI Y, CALISAL S M.

Three-dimensional effects and arm effects on modeling a vertical axis tidal current turbine

[J]. Renewable Energy, 2010, 35(10): 2325-2334.

DOI:10.1016/j.renene.2010.03.002      URL     [本文引用: 1]

何大伟, 吴国庆, 陆彬, 等.

垂直轴风力发电机主轴结构优化设计

[J]. 机械设计与制造, 2018(2): 199-201.

[本文引用: 1]

HE Dawei, WU Guoqing, LU Bin, et al.

Vertical axis wind turbine spindle structure optimization design

[J]. Machinery Design & Manufacture, 2018(2): 199-201.

[本文引用: 1]

高振勋, 蒋崇文, 唐金龙, 等.

多层塔式H型立轴风机的性能分析

[J]. 电力与能源, 2011, 32(5): 402-407.

[本文引用: 1]

GAO Zhenxun, JIANG Chongwen, TANG Jinlong, et al.

Performance evaluation of the multi-stage tower-type vertical-axis wind turbine

[J]. Power & Energy, 2011, 32(5): 402-407.

[本文引用: 1]

蒋周伟. H型垂直轴风力发电机风振特性与结构优化研究[D]. 武汉: 武汉理工大学, 2012.

[本文引用: 1]

JIANG Zhouwei. Study on vibration characteristics and structure optimization of H-type wind power generator with vertical axis[D]. Wuhan: Wuhan University of Technology, 2012.

[本文引用: 1]

文永蓬, 郑晓明, 吴爱中, 等.

基于BESO算法的城市轨道车轮拓扑优化

[J]. 机械工程学报, 2020, 56(10): 191-199.

DOI:10.3901/JME.2020.10.191      [本文引用: 1]

城市轨道车轮的结构优化大多集中于参数优化，设计空间普遍有一定的局限性。以降低城市轨道车轮辐板处的结构应力为目标，利用双向渐进结构优化算法对直辐板车轮进行拓扑优化建模，提出一种新颖的城市轨道车轮辐板结构。重点针对城市轨道车轮受力最恶劣的曲线工况，对直辐板车轮的设计域进行2D拓扑设计，在满足体积约束条件下，通过对删除率、进化率、增加率进行设定，使体积比经过反复振荡从而达到较好的性能优化指标，提高了城市轨道车轮的应力性能，获得了城市轨道车轮的优秀拓扑结构。通过与成熟有限元软件计算结果对比，优化后的静强度和疲劳强度均满足要求，证明了双向渐进结构优化算法的有效性和可靠性。研究结果表明，双向渐进结构优化算法对城市轨道车轮的优化设计是适用的；优化车轮的辐板形式由直辐板进化为曲辐板，且单元向中间圆弧处靠拢，辐板具有不等厚特征；在不增加车轮重量的前提下，优化车轮在辐板处的最大结构应力降低了17%。所做工作对城市轨道车轮结构应力性能的提升具有重要的参考价值。

WEN Yongpeng, ZHENG Xiaoming, WU Aizhong, et al.

Topology optimization of urban rail wheel based on BESO algorithm

[J]. Journal of Mechanical Engineering, 2020, 56(10): 191-199.

DOI:10.3901/JME.2020.10.191      [本文引用: 1]

The structural optimization of urban rail wheels is mostly focused on parameter optimization, and the design space has generally certain limitations. To reduce the structural stress at the plate of urban rail wheels, using bidirectional evolutionary structural optimization algorithm, the topology optimization modeling of straight spoke wheel is carried out. New urban rail wheel plate structure is proposed. The study focuses on the worst-case curve conditions of the urban rail wheels, utilizing 2D topological design of the design domain of the straight plate wheels. Under the constraint of volume, the volume ratio is repeatedly oscillated to achieve better performance optimization indicators by setting the deletion rate, the evolution rate and the increase rate, the stress performance of urban rail wheel can be improved and obtained an excellent topology of the urban rail wheels. By comparing with the calculation results of mature finite element software, the optimized static strength and fatigue strength meet the requirements. It proved the effectiveness and reliability of the bi-directional evolutionary structure optimization algorithm. The research results show that evolutionary structure optimization algorithm is suitable for the optimization design of urban rail wheels. Optimizing the form of the plate of the wheel from a straight plate to a curved plate, and the elements are close to the middle arc, the web has unequal thickness characteristics; Without increasing the weight of the wheel, optimized the maximum structural stress of the wheel at the plate was reduced by 17%. This research has important reference value for improving the structural stress performance of the urban rail wheels.

才琪, 冯若强.

基于改进双向渐进结构优化法的桁架结构拓扑优化

[J]. 建筑结构学报, 2022, 43(4): 68-76.

[本文引用: 1]

CAI Qi, FENG Ruoqiang.

Topology optimization of truss structure based on improved bi-directional evolutionary structural optimization method

[J]. Journal of Building Structures, 2022, 43(4): 68-76.

[本文引用: 1]

刘昆, 郭德松, 王仁华, 等.

基于改进BESO方法的多工况船体开孔孔形优化

[J]. 中国海洋平台, 2021, 36(4): 1-8.

[本文引用: 1]

LIU Kun, GUO Desong, WANG Renhua, et al.

Shape optimization of hull structure hole opening under multiple conditions based on improved BESO method

[J]. China Offshore Platform, 2021, 36(4): 1-8.

[本文引用: 1]

HAND B, CASHMAN A.

Conceptual design of a large-scale floating offshore vertical axis wind turbine

[J]. Energy Procedia, 2017, 142: 83-88.

DOI:10.1016/j.egypro.2017.12.014      URL     [本文引用: 5]

刘利琴, 赵海祥, 袁瑞, 等.

H型浮式垂直轴风力机刚—柔耦合多体动力学建模及仿真

[J]. 海洋工程, 2018, 36(3): 1-9.

[本文引用: 1]

LIU Liqin, ZHAO Haixiang, YUAN Rui, et al.

Modeling and simulation of H-type floating VAWT on rigid-flexible coupling and multi-body dynamics

[J]. The Ocean Engineering, 2018, 36(3): 1-9.

DOI:10.1016/j.oceaneng.2008.12.005      URL     [本文引用: 1]

TRAN T T, KIM D H.

Fully coupled aero-hydrodynamic analysis of a semi-submersible FOWT using a dynamic fluid body interaction approach

[J]. Renewable Energy, 2016, 92: 244-261.

DOI:10.1016/j.renene.2016.02.021      URL     [本文引用: 1]

CHEN Z W, WANG X D, GUO Y Z, et al.

Numerical analysis of unsteady aerodynamic performance of floating offshore wind turbine under platform surge and pitch motions

[J]. Renewable Energy, 2021, 163: 1849-1870.

DOI:10.1016/j.renene.2020.10.096      URL     [本文引用: 1]

张建, 杨庆山.

基于标准k-ε模型的平衡大气边界层模拟

[J]. 空气动力学学报, 2009, 27(6): 729-735.

[本文引用: 1]

ZHANG Jian, YANG Qingshan.

Application of standard k-ε model to simulate the equilibrium ABL

[J]. Acta Aerodynamica Sinica, 2009, 27(6): 729-735.

[本文引用: 1]

雷航. 垂直轴风力机非定常空气动力特性数值模拟分析[D]. 上海: 上海交通大学, 2019.

[本文引用: 1]

LEI Hang. Numerical simulation of the unsteady aerodynamic performance for vertical axis wind turbines[D]. Shanghai: Shanghai Jiao Tong University, 2019.

[本文引用: 1]

杨梦姚, 毛璐璐, 韩兆龙, 等.

三叶片H型垂直轴风力机风振与减振研究

[J]. 上海交通大学学报, 2021, 55(4): 347-356.

[本文引用: 1]

YANG Mengyao, MAO Lulu, HAN Zhaolong, et al.

Wind vibration and vibration reduction of a H-rotor type three-bladed vertical axis wind turbine

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(4): 347-356.

[本文引用: 1]

KATONA M C, ZIENKIEWICZ O C.

A unified set of single step algorithms part 3: The beta-m method, a generalization of the Newmark scheme

[J]. International Journal for Numerical Methods in Engineering, 1985, 21(7): 1345-1359.

DOI:10.1002/nme.1620210713      URL     [本文引用: 1]

WANG K, MOAN T, HANSEN M O L.

Stochastic dynamic response analysis of a floating vertical-axis wind turbine with a semi-submersible floater

[J]. Wind Energy, 2016, 19(10): 1853-1870.

DOI:10.1002/we.1955      URL     [本文引用: 1]

张森文, 曹开彬.

计算结构动力响应的状态方程直接积分法

[J]. 计算力学学报, 2000, 17(1): 94-97.

[本文引用: 1]

ZHANG Senwen, CAO Kaibin.

Direct integration of state equation method for dynamic response of structure

[J]. Chinese Journal of Computational Mechanics, 2000, 17(1): 94-97.

[本文引用: 1]

HUANG X, XIE Y M.

Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method

[J]. Finite Elements in Analysis and Design, 2007, 43(14): 1039-1049.

DOI:10.1016/j.finel.2007.06.006      URL     [本文引用: 1]

罗静, 张大可, 李海军, 等.

基于一种动态删除率的ESO方法

[J]. 计算力学学报, 2015, 32(2): 274-279.

[本文引用: 1]

LUO Jing, ZHANG Dake, LI Haijun, et al.

ESO method based on a kind of dynamic deletion rate

[J]. Chinese Journal of Computational Mechanics, 2015, 32(2): 274-279.

[本文引用: 1]

荣见华, 姜节胜, 胡德文, 等.

基于应力及其灵敏度的结构拓扑渐进优化方法

[J]. 力学学报, 2003, 35(5): 584-591.

[本文引用: 1]

RONG Jianhua, JIANG Jiesheng, HU Dewen, et al.

A structural topology evolutionary optimization method based on stresses and their sensitivity

[J]. Acta Mechanica Sinica, 2003, 35(5): 584-591.

[本文引用: 1]

/

〈 〉