基于此,提出CEEMDAN·MPE-INHT时频分析算法,该算法实现分两步.第1步抑制噪声干扰,对EMD进行双重改进,为控制低频噪声改进EMD得到自适应补充集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,CEEMDAN),为控制高频噪声引入多尺度排列熵(Multiscale Permutation Entropy, MPE),即通过CEEMDAN·MPE控制噪声干扰.第2步排除Bedrosian定理的限制,优化Hilbert变换,得到改进归一化Hilbert变换(Improved Normalized Hilbert Transform, INHT).
首先,通过混有噪声的仿真振动信号验证该算法不仅可有效抑制EMD固有的模态混淆现象,同时得到具有实际物理意义的瞬时频率.再将该算法用于实际工程获得的含噪振动信号时频分析中,发现该算法得到的时频谱在时域和频域均具有较高的分辨率,可有效提取振动信号时频能特征参数,提高了时频分析参数提取精度,对振动信号危害控制具有一定的指导作用.
1 CEEMDAN·MPE-INHT时频分析算法
1.1 CEEMDAN
CEEMDAN[14]是在分解的每一阶段添加有限次自适应白噪声,实现在减少分解次数的同时减小重构误差.通过算法原理分析,发现CEEMDAN对监测中混入低频噪声的控制源于所添加自适应白噪声的抵消能力.
1.2 MPE
1.3 改进归一化Hilbert变换
传统的Hilbert变换受Bedrosian定理的约束,在处理非平稳、多分量信号时会得到负值瞬时频率.针对此现象,Huang等[17]提出归一化希尔伯特-黄变换(Normalized Hilbert Transform, NHT),以此来提高瞬时频率的计算精度.本文在NHT的基础上做出了改进,Huang等[17]用于NHT的IMF来自于EMD或集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)[18-19],但EMD和EEMD在进行含噪信号分解时不可避免会产生模态混淆的问题.而本文IMF由CEEMDAN·MPE得到,对IMF模态混淆进行了抑制.对此类IMF进行NHT,便可实现改进归一化Hilbert变换(INHT).INHT的操作和NHT十分相似,区别在于,NHT所用的IMF来源是EMD或EEMD,而INHT使用的IMF来自于CEEMDAN·MPE,因此这里不加累述,具体可参考文献[17],将其中的IMF替换成CEEMDAN·MPE得到的IMF即可实现INHT.
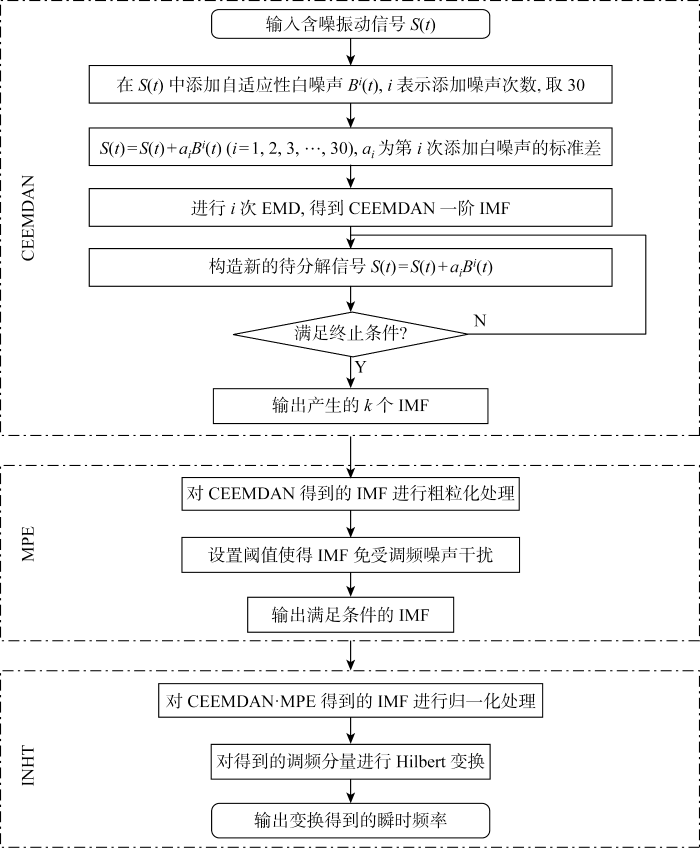
1.4 CEEMDAN·MPE-INHT时频分析算法流程图解
CEEMDAN·MPE-INHT算法的建立思路是对含噪振动信号时频分析时遇到影响其精度的问题进行逐一改进,前述1.1节~1.3节简单说明了组成CEEMDAN·MPE-INHT的每一部分单独算法的运行原理,并未详细展开,为增加论文的可读性,将CEEMDAN·MPE-INHT时频分析算法的运算流程图进行展示,如图1所示.
图1
图1
CEEMDAN·MPE-INHT时频分析算法流程图
Fig.1
Flow chart of CEEMDAN·MPE-INHT time-frequency analysis algorithm
2 仿真信号CEEMDAN·MPE-INHT时频分析
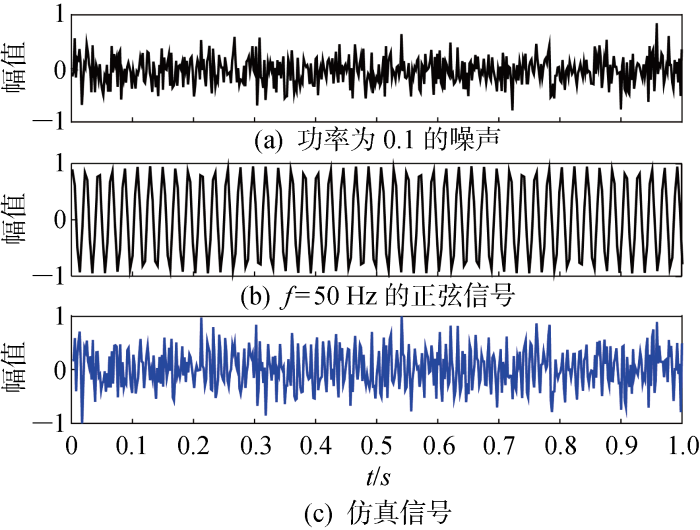
2.1 仿真信号的建立
图2
2.2 仿真信号模态分解
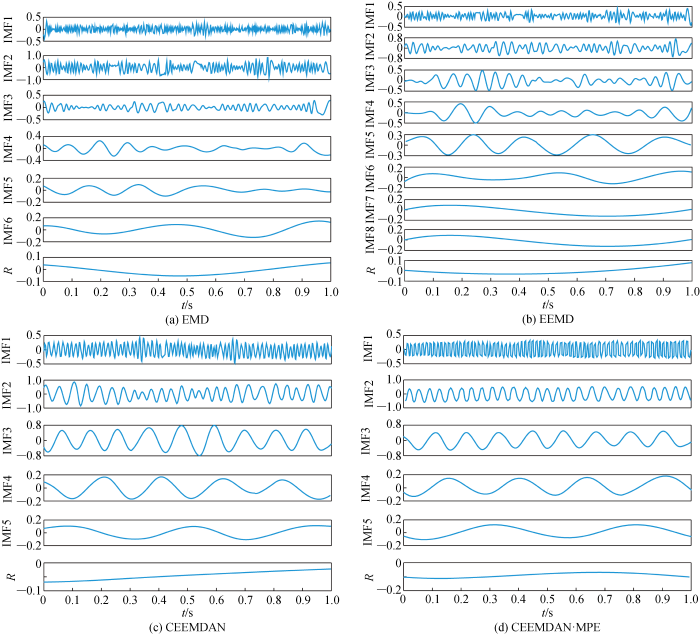
为突出CEEMDAN·MPE对EMD模态混淆的抑制作用,分别采用EMD、EEMD、CEEMDAN和CEEMDAN·MPE对S(t)进行模态分解,分解结果如图3所示.图中:IMF为不同模态分解方法得到的固有模态函数;R为不同模态分解方法得到的余项.图3(a)为EMD结果,不难发现IMF1是难以除去的噪声信号;IMF高频模态混淆严重,如IMF2在t=0.24,0.42,0.54,0.80 s附近都出现高频向中频发展的现象;中频模态混淆有所缓解,如IMF3在t=0.42 s及右端点附近存在向低频发展的趋势;低频相对稳定,如IMF6.图3(b)为EEMD结果,高频IMF模态混淆相比EMD有所缓解,但依旧存在,如IMF1在t=0.42 s处向中频发展;中频相对稳定,如IMF4和IMF5;低频出现模态分裂[17],该现象是模态混淆的第2种现象,即相同的模态分量出现在不同的固有模态函数中,如IMF7和IMF8.图3(c)为CEEMDAN结果,低频分布稳定,高频IMF1出现了模态混淆,出现在t=0.42,0.64 s附近;图3(d)为CEEMDAN·MPE结果,分解得到的IMF从高频向低频依次排列,未见明显模态混淆现象.
图3
图3
仿真信号经不同方法的分解结果
Fig.3
Results of decomposition of simulation signals by different methods
2.3 仿真信号Hilbert变换和INHT对比分析
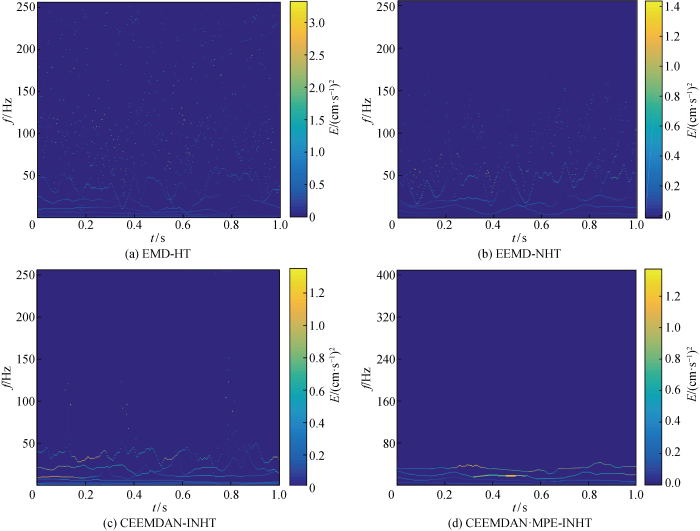
图4
图4(a)为EMD-HT时频谱,可发现时频谱出现了50 Hz以上的虚假分量,该分量较发散,难以识别,时频谱在时间和频率这两个维度的分辨率都不高.图4(b)为EEMD-HT时频谱,可发现50 Hz以上的虚假分量相比EMD-HT少,频率分辨率有所提高.图4(c)为CEEMDAN-INHT得到的时频谱图,基本未见低频模态混淆,50 Hz以下时频谱频率分辨率高,但是在t=0.12,0.36,0.80 s附近出现了高频噪声干扰导致频率分辨率降低.对比图4(a)、图4(b)和图4(c)时频谱在高频和低频处的分辨率,可以发现CEEMDAN相比EMD和EEMD,对低频噪声具有很好的抑制作用,但对高频噪声缺乏控制力度.图4(d)所示为CEEMDAN·MPE-INHT得到的时频谱图,该时频谱在时间和频率维度均具有较高分辨率,未见高频和低频模态混淆.再次表明CEEMDAN对噪声信号引起的低频模态混淆具有良好的抑制作用,MPE也能有效控制噪声信号引起的高频模态混淆,同时CEEMDAN·MPE得到的IMF经过INHT能够得到具有实际物理意义的时频信息,即CEEMDAN·MPE-INHT时频分析算法不仅可有效抑制噪声信号引起的EMD模态混淆,同时得到时频分辨率双高的信号频谱图.
3 基于 CEEMDAN·MPE-INHT 的含噪振动信号时频分析
振动信号在自然界分布极广,本文实际应用中,以含噪爆破地震波振动信号作为研究对象,重点研究CEEMDAN·MPE-INHT算法的实际含噪振动信号时频分析.
为满足交通运输需求,将福建某原有双向四车道隧道原位扩建为双向八车道隧道,相关设计参数如表1所示.施工要求右侧隧道在封闭施工过程中左侧隧道依然保持正常通车状态,因此,在右侧隧道进行爆破施工时,有必要对左侧通车隧道进行动态跟踪监测.
表1 隧道扩建前后设计参数
Tab.1
| 项 目 | 扩建前楼山隧道 | 扩建后楼山隧道 |
|---|---|---|
| 断面形式 | 双向四车道 | 双向八车道 |
| 双洞最小距离/m | 29~35 | 25~31 |
| 行车道宽度/m | 2×3.75 | 2×3.5+2×3.75 |
| 侧向宽度/m | 0.5 | 0.5 |
| 检修道宽/m | 0.75 | 0.75 |
| 总宽度/m | 10.25 | 17.25 |
| 隧道净空高/m | 5 | 5 |
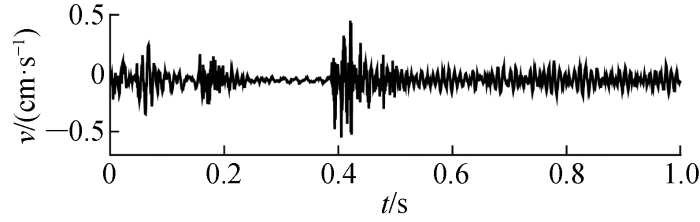
采用UBOX-5016爆破振动智能监测仪对左侧通车隧道进行监测,选取监测点中一条典型爆破振动信号作为研究对象,如图5所示.图中:v为速度;采样时间t=1.0 s;采样点为 1 500.
图5
图5
实际爆破地震波监测信号波形图
Fig.5
The waveform of the actual blasting seismic wave monitoring signal
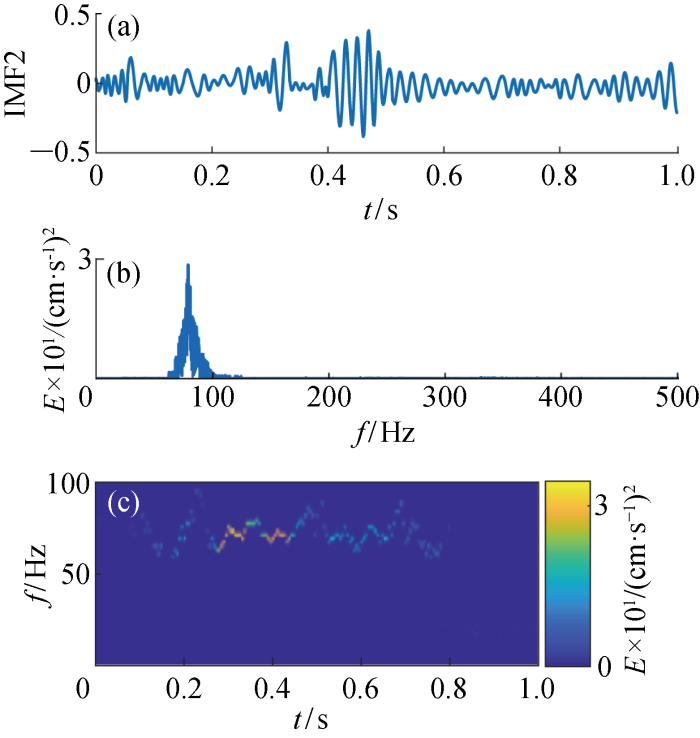
图6
图7
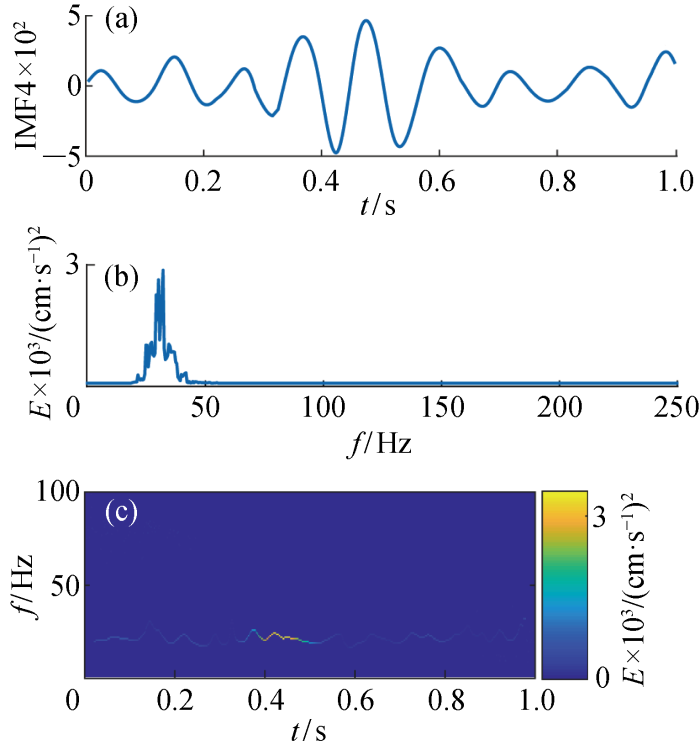
图8
图9
图10
图11
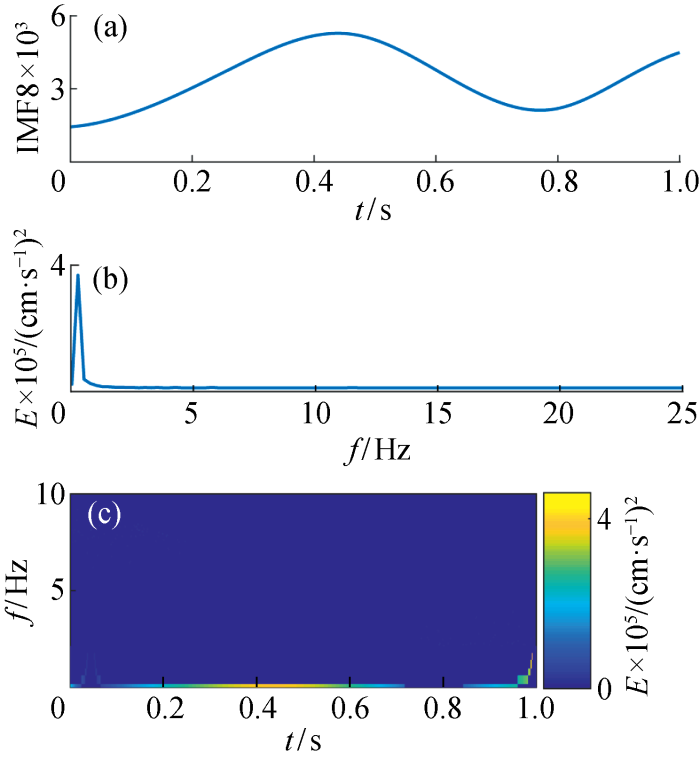
图12
图13
观察图6~图13可发现,基于CEEMDAN·MPE-INHT时频分析算法得到的时频谱图在时域和频域都拥有很高的分辨率.其中IMF1频率范围为100~300 Hz,持续时间0.00~1.00 s;IMF2频率范围为60~100 Hz,持续时间0.10~0.80 s;IMF3频率范围为40~60 Hz,持续时间0.00~0.80 s;IMF4频率范围为20~40 Hz,持续时间0.00~1.00 s;IMF5频率范围为10~20 Hz,持续时间0.08~0.80 s;IMF6频率范围为5~10 Hz,持续时间0.00~1.00 s;IMF7和IMF8频率最低,主要在0~5 Hz,持续时间0.00~1.00 s.通过分析图6~图13可发现,信号能量主要集中在IMF1和IMF2中,其次在IMF3和IMF4中,地震波信号频率主要分布在100~300 Hz,能量也主要集中在高频.
图14
图14
爆破地震波监测信号时间-频率-能量三维图
Fig.14
Time-frequency-energy three-dimensional diagram of blasting seismic wave monitoring signal
综上所述,基于CEEMDAN·MPE-INHT的含噪振动信号时频分析算法,不仅有助于抑制含噪监测信号引起传统EMD固有的模态混淆现象,同时CEEMDAN·MPE得到的IMF经INHT得到的时频图和三维时频能量图可清晰展示振动信号内在所蕴含的频率-能量之间的对应关系,即得到的时频信息具有清晰的物理意义.对含噪振动信号特征参数提取、振动危害控制及科学制定防护措施具有重要的意义.
4 结论
(1) 通过CEEMDAN·MPE-INHT算法在含噪仿真振动信号和实际含噪振动信号时频分析中的应用,验证了该算法可抑制EMD固有的模态混淆现象,并得到时频分辨率均高的时频谱图,谱图对应的时频参数实际物理意义明确.
(2) INHT得到的瞬时频率为IMF的调频分量Hilbert变换得到的,使得传统的Hilbert变换免受Bedrosian定理的限制,因此INHT相比Hilbert变换得到的瞬时频率真实性更高.
(3) 基于CEEMDAN·MPE-INHT含噪振动信号时频分析算法,可得出含噪振动信号内在所蕴含的时间-频率-能量之间的对应关系,该对应关系有助于含噪振动信号内在特征的识别和实际工程振动危害控制.
参考文献
Application of the empirical mode decomposition-Hilbert spectrum method to identify near-fault ground-motion characteristics and structural responses
[J].DOI:10.1785/0120000715 URL [本文引用: 1]
Analysis of acoustic wave frequency spectrum characters of rock mass under blasting damage based on the HHT method
[J].
Stochastic resonance in a special type of asymmetric nonlinear system driven by correlated noise
[J].
The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis
[J].
爆破振动信号的Hilbert-Huang变换分析与应用研究
[J].
Analysis of blasting vibration signal by HHT transform
[J].
Seismic attribute extraction based on HHT and its application in a marine carbonate area
[J].DOI:10.1007/s11770-010-0279-z URL [本文引用: 1]
基于改进MP-WVD算法的核电厂建设爆破振动信号处理方法
[J].
Blasting vibration signal analysis technology of construction of nuclear power plant based on improved MP-WVD algorithm
[J].
单薄山体岩质高边坡爆破振动响应分析及安全控制
[J].
Blasting vibration response and control of high rock slopes of thin mountain
[J].
EMD和FSWT组合方法在爆破振动信号分析中的应用研究
[J].
Application of EMD and FSWT combination method in blasting vibration signal analysis
[J].
改进的EEMD方法及其在滚动轴承故障诊断中的应用
[J].
An improved EEMD method and its application in rolling bearing fault diagnosis
[J].
基于改进的集合经验模态方法振动信号分解
[J].
Vibration signal decomposition based on an improved ensemble empirical mode decomposition method
[J].
Analysis and research on blasting network delay of deep-buried diversion tunnel crossing fault zone based on EP-CEEMDAN-INHT
[J].DOI:10.1007/s10706-021-01968-9 [本文引用: 1]
爆破振动信号分析中模态混叠和虚假分量消除的改进方法
[J].
An improved method to eliminate modal aliasing and false component in blast vibration signals
[J].
A complete ensemble empirical mode decomposition with adaptive noise
[C]//
Multivariate multiscale fractional order weighted permutation entropy of nonlinear time series
[J].DOI:10.1016/j.physa.2018.09.165 URL [本文引用: 1]
改进多尺度排列熵及模糊算法的JTC状态检测
[J].
JTC state detection based on improved multi-scale permutation entropy and fuzzy algorithm
[J].
On instantaneous frequency
[J].
DOI:10.1142/S1793536909000096
URL
[本文引用: 4]

Instantaneous frequency (IF) is necessary for understanding the detailed mechanisms for nonlinear and nonstationary processes. Historically, IF was computed from analytic signal (AS) through the Hilbert transform. This paper offers an overview of the difficulties involved in using AS, and two new methods to overcome the difficulties for computing IF. The first approach is to compute the quadrature (defined here as a simple 90° shift of phase angle) directly. The second approach is designated as the normalized Hilbert transform (NHT), which consists of applying the Hilbert transform to the empirically determined FM signals. Additionally, we have also introduced alternative methods to compute local frequency, the generalized zero-crossing (GZC), and the teager energy operator (TEO) methods. Through careful comparisons, we found that the NHT and direct quadrature gave the best overall performance. While the TEO method is the most localized, it is limited to data from linear processes, the GZC method is the most robust and accurate although limited to the mean frequency over a quarter wavelength of temporal resolution. With these results, we believe most of the problems associated with the IF determination are resolved, and a true time–frequency analysis is thus taking another step toward maturity.
Ensemble empirical mode decomposition: A noise-assisted data analysis method
[J].
DOI:10.1142/S1793536909000047
URL
[本文引用: 1]

A new Ensemble Empirical Mode Decomposition (EEMD) is presented. This new approach consists of sifting an ensemble of white noise-added signal (data) and treats the mean as the final true result. Finite, not infinitesimal, amplitude white noise is necessary to force the ensemble to exhaust all possible solutions in the sifting process, thus making the different scale signals to collate in the proper intrinsic mode functions (IMF) dictated by the dyadic filter banks. As EEMD is a time–space analysis method, the added white noise is averaged out with sufficient number of trials; the only persistent part that survives the averaging process is the component of the signal (original data), which is then treated as the true and more physical meaningful answer. The effect of the added white noise is to provide a uniform reference frame in the time–frequency space; therefore, the added noise collates the portion of the signal of comparable scale in one IMF. With this ensemble mean, one can separate scales naturally without any a priori subjective criterion selection as in the intermittence test for the original EMD algorithm. This new approach utilizes the full advantage of the statistical characteristics of white noise to perturb the signal in its true solution neighborhood, and to cancel itself out after serving its purpose; therefore, it represents a substantial improvement over the original EMD and is a truly noise-assisted data analysis (NADA) method.
Smooth model of blasting seismic wave signal denoising based on two-stage denoising algorithm
[J].DOI:10.1080/12269328.2020.1778543 URL [本文引用: 1]