在众多不锈钢截面产品中,冷弯不锈钢管在结构工程中的应用最为广泛[18],既有不锈钢截面构件的腹板压跛性能研究亦主要集中于冷弯不锈钢方矩管[17,19].Talja等[20]系统地研究了冷弯奥氏体不锈钢矩形管的受力性能,对构件的腹板压跛极限承载力开展了试验研究;Gardner等[21]通过试验考察了冷弯高强奥氏体不锈钢方矩管的腹板压跛极限承载力,评价了设计规范的适用性.Zhou等[15,22]通过试验,研究了奥氏体、高强奥氏体和双相型不锈钢方矩管的腹板压跛性能,提出了针对相应不锈钢材料的腹板压跛极限承载力经验计算公式;在试验基础上,Zhou等[23-24]建立了冷弯不锈钢方矩管的平面屈服线理论模型,综合理论和回归分析,提出了半理论半经验的腹板压跛极限承载力计算公式.陈希湘等[25]对奥氏体不锈钢方矩管进行了局部承压试验,考察了荷载工况、承压长度、腹板高厚比等因素对空心管构件腹板压跛极限承载力的影响.Li等[17,26]通过试验和有限元参数分析,对冷弯铁素体不锈钢方矩管的腹板压跛性能进行了研究,给出了铁素体不锈钢方矩管腹板压跛极限承载力的经验计算方法,并提出了基于直接强度法的腹板压跛极限承载力计算理论,发展了冷弯不锈钢方矩管的腹板压跛极限承载力计算方法.近期,Cai等[27-28]针对冷弯节镍双相型不锈钢方矩管系统地开展了参数分析算例计算,评价了既有规范计算公式及直接强度法[17,26]对于冷弯节镍双相型不锈钢方矩管腹板压跛极限承载力计算的适用性.
目前我国建筑工程领域中,主要应用的不锈钢材为奥氏体和双相型不锈钢.不同种类、不同牌号的不锈钢材料因化学成分不同,力学性能可能存在显著差异.国产奥氏体S30408和双相型S22053是最典型的结构用不锈钢牌号,其构件及连接节点的力学性能得到了广泛研究[2-3,9].为了研究国产冷弯不锈钢方矩管的腹板压跛极限承载力计算方法,本文以奥氏体S30408及双相型S22053不锈钢方矩管为研究对象,在已有试验的基础上[22],采用有限元软件Abaqus开展了数值研究,并利用验证后的有限元模型建立了224组参数分析算例,根据参数分析算例结果,评价了既有腹板压跛极限承载力计算方法对于国产冷弯不锈钢方矩管的适用性,提出了相关设计建议.
1 有限元模型的建立与验证
1.1 试验概述
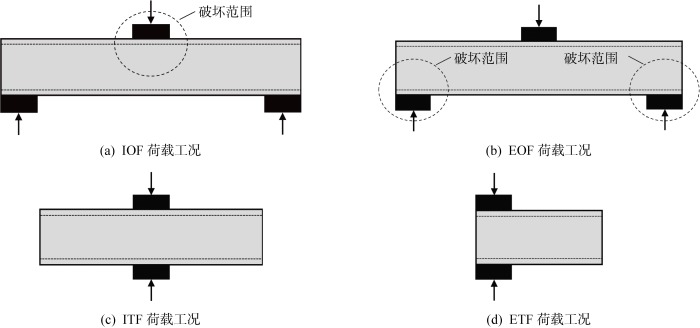
针对腹板压跛问题,各国冷弯型钢结构设计规范[29⇓⇓⇓-33]和冷弯不锈钢结构设计规范[34⇓-36]均界定了4种典型腹板压跛荷载工况(Web Crippling Loading Condition):内部单翼缘(Interior One-Flange, IOF)、端部单翼缘(End One-Flange, EOF)、内部双翼缘(Interior Two-Flange, ITF)和端部双翼缘(End Two-Flange, ETF),如图1所示.本文基于Zhou等[22]在4种荷载工况下开展的32组冷弯不锈钢方矩管腹板压跛试验进行有限元模型的建立与验证.该试验包含了4种截面尺寸的冷弯不锈钢方矩管,考虑了奥氏体和双相型两种不锈钢材料.
图1
图2
1.2 有限元模型的建立
采用通用有限元软件Abaqus建立精细化三维有限元模型,并充分考虑不锈钢材料的非线性本构关系和冷弯截面构件的材料特征.为模拟不锈钢材料的应力-应变关系,有限元模型中材料本构关系采用CECS 410: 2015[10]给出的两阶段Ramberg-Osgood(R-O)模型,本构关系如下:
式中:σ为应力;ε为应变;f0.2为名义屈服强度;fu为抗拉极限强度;E为初始弹性模量;E0.2为σ=f0.2时对应的切线模量;n为应变强化系数;m为计算系数;εu为极限应变.
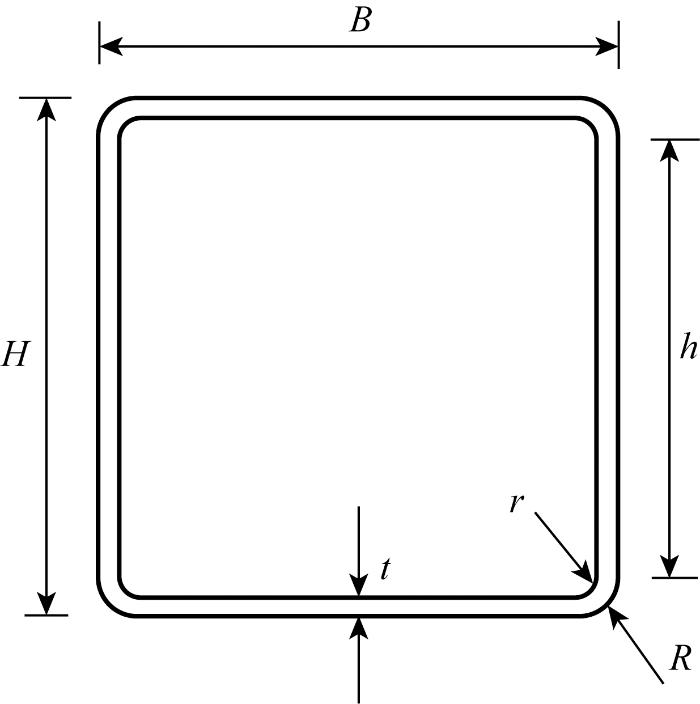
冷弯不锈钢方矩管成型过程中会产生塑性变形,导致材料应变硬化,提高了材料的强度.研究表明[37],冷弯不锈钢方矩管成型过程带来的强度提高不仅限于圆弧弯角处,还会向平板区域延伸约两倍的截面壁厚(2t).为此,在有限元建模中将不锈钢方矩管划分为弯角段及平板段:圆弧弯角及其相邻2t区域内归于弯角段,其余定义为平板段.平板段材料采用Zhou等[22]的材性拉伸试验结果.弯角段材料的名义屈服强度依文献[38]中的建议,取为平板段材料极限强度的85%;弯角段材料的极限强度根据文献[39]中推荐的经验公式计算获得.弯角段材料弹性模量与平板段相同,n依据CECS 410: 2015[10]取值.平板段和弯角段的相关材性参数如表1所示.基于表1所示的材性参数,结合式(1)~(4)的材料本构关系,获得平板段及弯角段材料的名义应力应变关系,再将其转化为真实应力-塑性应变关系输入Abaqus.
表1 有限元模型材性参数取值
Tab.1
| 截面 | 平板段[22] | 弯角段 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| E/GPa | f0.2/MPa | fu/MPa | n | E/GPa | f0.2/MPa | fu/MPa | n | |||
| A150×150×3 | 189 | 448 | 699 | 6 | 189 | 594 | 732 | 6 | ||
| A150×150×6 | 194 | 497 | 761 | 6 | 194 | 647 | 762 | 6 | ||
| D140×80×3 | 212 | 486 | 736 | 5 | 212 | 626 | 839 | 5 | ||
| D160×80×3 | 208 | 536 | 766 | 5 | 208 | 651 | 836 | 5 | ||
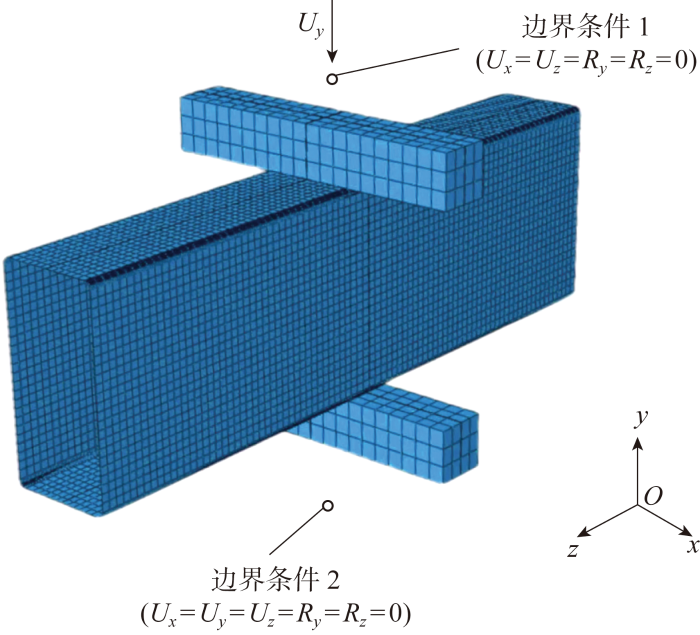
按照Zhou等[22]试验的实际情况,进行32组有限元模型的建立.冷弯不锈钢方矩管试件采用S4R壳单元进行模拟,用于施加荷载的刚性承压板则用离散刚体单元进行模拟.承压板与试件之间的接触使用表面-表面的接触对来模拟,刚度较大的承压板确定为主表面,试件接触面设置为从表面,承压板与试件上下翼缘的接触面在法线方向上设为“硬”接触,在切线方向上采用“罚”的摩擦方式,摩擦因数取为0.4[17,26⇓-28,40].为提高计算的精度,对网格划分进行敏感度分析,最终将方矩管网格划分尺寸统一取为7.5 mm×7.5 mm,圆弧弯角处采用更精细的网格划分,将其划分为20个单元.有限元模型的加载方法及边界条件同试验一致,采用位移加载模式,并对相应的自由度进行释放.研究表明,初始缺陷和残余应力对冷弯型钢腹板压跛性能影响较小[40],建立有限元模型时,可忽略初始缺陷及残余应力对腹板压跛极限承载力的影响[17,26⇓-28,40].以ITF荷载工况为例,其有限元模型如图3所示,Ux、Uy、Uz为沿坐标轴x、y、z方向的位移,Rx、Ry、Rz为绕坐标轴的转动.
图3
1.3 有限元模型的验证
图4
| 试件编号 | PExp/kN | PFEA/kN | 试件编号 | PExp/kN | PFEA/kN | ||
|---|---|---|---|---|---|---|---|
| EOF-A150×150×3-N150 | 47.2 | 44.6 | 1.06 | ETF-A150×150×3-N150 | 28.2 | 27.5 | 1.03 |
| EOF-A150×150×3-N75 | 28.8 | 30.4 | 0.95 | ETF-A150×150×3-N75 | 20.0 | 20.3 | 0.99 |
| EOF-A150×150×6-N150 | 184.6 | 209.4 | 0.88 | ETF-A150×150×6-N150 | 148.3 | 140.9 | 1.05 |
| EOF-A150×150×6-N75 | 124.3 | 132.3 | 0.94 | ETF-A150×150×6-N75 | 95.8 | 89.7 | 1.07 |
| EOF-D140×80×3-N75 | 37.6 | 38.3 | 0.98 | ETF-D140×80×3-N75 | 23.4 | 26.3 | 0.89 |
| EOF-D140×80×3-N50 | 33.6 | 32.9 | 1.02 | ETF-D140×80×3-N50 | 20.6 | 23.0 | 0.90 |
| EOF-D160×80×3-N75 | 32.4 | 35.3 | 0.92 | ETF-D160×80×3-N75 | 23.1 | 24.4 | 0.95 |
| EOF-D160×80×3-N50 | 29.6 | 29.8 | 0.99 | ETF-D160×80×3-N50 | 20.7 | 21.7 | 0.95 |
| IOF-A150×150×3-N150 | 59.3 | 56.7 | 1.05 | ITF-A150×150×3-N150 | 62.1 | 65.3 | 0.95 |
| IOF-A150×150×3-N75 | 51.4 | 47.2 | 1.09 | ITF-A150×150×3-N75 | 54.1 | 52.1 | 1.04 |
| IOF-A150×150×6-N150 | 228.9 | 205.6 | 1.11 | ITF-A150×150×6-N150 | 275.1 | 251.4 | 1.09 |
| IOF-A150×150×6-N75 | 207.0 | 185.0 | 1.12 | ITF-A150×150×6-N75 | 223.7 | 197.1 | 1.14 |
| IOF-D140×80×3-N75 | 51.4 | 54.5 | 0.94 | ITF-D140×80×3-N75 | 61.1 | 62.4 | 0.98 |
| IOF-D140×80×3-N50 | 49.0 | 50.7 | 0.97 | ITF-D140×80×3-N50 | 56.1 | 56.6 | 0.99 |
| IOF-D160×80×3-N75 | 52.5 | 51.3 | 1.02 | ITF-D160×80×3-N75 | 63.1 | 59.5 | 1.06 |
| IOF-D160×80×3-N50 | 49.1 | 47.6 | 1.03 | ITF-D160×80×3-N50 | 56.6 | 53.6 | 1.06 |
| 荷载工况 | PExp/PFEA | |
|---|---|---|
| 平均值 | 变异系数 | |
| EOF* | 0.98 | 0.050 |
| ETF | 0.98 | 0.069 |
| IOF | 1.04 | 0.062 |
| ITF | 1.04 | 0.060 |
注:EOF-A150×150×6-N150试件试验中未能发生腹板压跛破坏,故平均值及变异系数计算中未考虑该数据点.
2 参数分析算例
表4 参数分析算例材性参数取值
Tab.4
| 材料 | 平板段 | 弯角段 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| E/GPa | f0.2/MPa | fu/MPa | n | E/GPa | f0.2/MPa | fu/MPa | n | ||
| S30408 | 193 | 205 | 515 | 6 | 193 | 438 | 680 | 6 | |
| S22053 | 200 | 450 | 620 | 5 | 200 | 527 | 767 | 5 | |
表5 参数分析算例有限元结果
Tab.5
| 试件系列 | PFEA/kN | 试件系列 | PFEA/kN | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EOF | IOF | ETF | ITF | EOF | IOF | ETF | ITF | |||
| A80×80×1.5-N80 | 8.8 | 11.7 | 5.9 | 11.6 | D80×80×1.5-N80 | 14.5 | 19.2 | 9.3 | 19.4 | |
| A80×80×1.5-N40 | 5.8 | 9.7 | 4.1 | 10.2 | D80×80×1.5-N40 | 9.4 | 15.5 | 6.6 | 17.0 | |
| A80×80×2-N80 | 14.2 | 18.7 | 9.9 | 18.8 | D80×80×2-N80 | 24.6 | 30.6 | 16.7 | 31.9 | |
| A80×80×2-N40 | 9.6 | 15.6 | 7.0 | 16.4 | D80×80×2-N40 | 15.5 | 24.5 | 11.4 | 26.6 | |
| A80×80×3-N80 | 27.5 | 35.1 | 20.1 | 36.9 | D80×80×3-N80 | 33.5* | 56.6 | 34.7 | 60.9 | |
| A80×80×3-N40 | 18.8 | 30.3 | 14.2 | 31.6 | D80×80×3-N40 | 29.7 | 46.5 | 23.1 | 50.4 | |
| A100×100×2-N100 | 15.2 | 20.5 | 10.4 | 20.2 | D100×100×2-N100 | 25.5 | 33.8 | 16.6 | 34.0 | |
| A100×100×2-N50 | 10.1 | 17.0 | 7.3 | 17.8 | D100×100×2-N50 | 16.4 | 27.2 | 11.7 | 29.5 | |
| A100×100×2.5-N100 | 22.1 | 29.4 | 15.5 | 29.3 | D100×100×2.5-N100 | 38.2 | 48.3 | 26.0 | 49.8 | |
| A100×100×2.5-N50 | 14.8 | 24.6 | 10.9 | 25.6 | D100×100×2.5-N50 | 24.0 | 38.7 | 17.8 | 41.6 | |
| A100×100×3-N100 | 29.8 | 39.1 | 21.3 | 39.6 | D100×100×3-N100 | 51.8 | 63.9 | 36.7 | 67.0 | |
| A100×100×3-N50 | 20.2 | 33.2 | 15.1 | 34.4 | D100×100×3-N50 | 32.4 | 51.6 | 24.7 | 55.3 | |
| A150×150×2-N150 | 16.4 | 23.1 | 10.7 | 22.6 | D150×150×2-N150 | 24.9 | 37.8 | 15.4 | 35.6 | |
| A150×150×2-N75 | 10.8 | 18.8 | 7.6 | 20.2 | D150×150×2-N75 | 17.1 | 31.5 | 11.4 | 32.2 | |
| A150×150×4-N150 | 54.9 | 72.4 | 39.0 | 73.4 | D150×150×4-N150 | 94.5 | 119.0 | 66.2 | 124.7 | |
| A150×150×4-N75 | 36.8 | 60.6 | 27.5 | 64.0 | D150×150×4-N75 | 59.8 | 95.5 | 45.0 | 103.6 | |
| A150×150×6-N150 | 106.4 | 135.6 | 78.7 | 144.7 | D150×150×6-N150 | 167.1* | 217.4 | 135.6 | 236.8 | |
| A150×150×6-N75 | 72.6 | 118.0 | 55.6 | 123.1 | D150×150×6-N75 | 115.5 | 181.4 | 89.9 | 194.6 | |
| A200×100×2-N100 | 11.9 | 20.1 | 8.1 | 23.1 | D200×100×2-N100 | 17.7 | 33.5 | 11.7 | 36.1 | |
| A200×100×2-N50 | 8.7 | 16.8 | 6.9 | 18.6 | D200×100×2-N50 | 13.8 | 26.9 | 9.9 | 30.0 | |
| A200×100×4-N100 | 40.7 | 63.4 | 30.2 | 71.2 | D200×100×4-N100 | 67.8 | 100.8 | 49.6 | 116.8 | |
| A200×100×4-N50 | 29.4 | 54.1 | 24.2 | 59.7 | D200×100×4-N50 | 45.8 | 82.2 | 39.1 | 91.8 | |
| A200×100×6-N100 | 81.0 | 123.2 | 61.9 | 136.8 | D200×100×6-N100 | 130.9 | 188.4 | 102.2 | 216.6 | |
| A200×100×6-N50 | 58.4 | 107.3 | 48.6 | 118.9 | D200×100×6-N50 | 88.1 | 160.6 | 75.7 | 181.1 | |
| A250×150×2-N150 | 12.6 | 22.9 | 8.8 | 23.6 | D250×150×2-N150 | 17.4 | 37.9 | 11.0 | 34.3 | |
| A250×150×2-N75 | 9.5 | 18.8 | 6.9 | 20.6 | D250×150×2-N75 | 13.9 | 31.1 | 9.3 | 32.3 | |
| A250×150×3-N150 | 27.9 | 45.0 | 19.3 | 49.9 | D250×150×3-N150 | 43.7 | 74.8 | 28.6 | 79.5 | |
| A250×150×3-N75 | 20.1 | 37.3 | 15.7 | 40.9 | D250×150×3-N75 | 32.4 | 59.7 | 23.5 | 65.7 | |
注:D80×80×3-N80及D150×150×6-N150系列的EOF试件未发生腹板压跛破坏.
3 腹板压跛极限承载力计算方法与比较
3.1 美国《冷弯不锈钢结构设计规范》方法
美国《冷弯不锈钢结构设计规范》(SEI/ASCE 8-02)[35]的腹板压跛极限承载力计算方法直接取自1986年版的美国《冷弯型钢结构设计规范》[31],采用的是基于冷弯普通碳钢截面构件腹板压跛极限承载力试验结果拟合而得的纯经验设计公式,并未考虑不锈钢的材料特点.对于常用C形(卷边槽钢)、U形(非卷边槽钢)、Z形、帽形和方矩管截面,《冷弯不锈钢结构设计规范》(SEI/ASCE 8-02)[35]未加以区分,采用了相同的承载力计算公式,没有考虑截面形式不同带来的腹板压跛极限承载力差异.此外,需要指出,该规范针对EOF、IOF、ETF和ITF共4种典型荷载工况,提供了形式冗杂且不同的承载力计算公式,不便于设计人员使用.
式中:Pn表示腹板压跛极限承载力名义值(不考虑分项系数);C为腹板压跛整体确定系数;Cr为内弯角半径系数;CN为承压长度系数;Ch为腹板高厚比系数;θ为腹板倾角.其中,C、Cr、CN、Ch为经验系数.
对于C形、U形、Z形、帽形、工字形拼合截面和压型钢板,SEI/ASCE 8-22[36]采用了与AISI S100-16[33]相同的腹板压跛经验系数,即C、Cr、CN、Ch.对于冷弯方矩管,SEI/ASCE 8-22[36]基于既有冷弯不锈钢方矩管试验数据,标定了适用于冷弯不锈钢方矩管腹板压跛极限承载力计算的经验系数.针对冷弯不锈钢方矩管的经验系数如表6所示,其适用范围为r/t≤2,h/t≤60,N/t≤55,N/h≤3.参与公式经验系数标定的试验数据共计243组,覆盖了欧美国家常用的奥氏体、铁素体、双相型3类不锈钢,包括AISI 304、AISI 301LN、AISI 441、AISI 410L、EN 1.4162、EN 1.4062等多个牌号.
表6 方矩管腹板压跛极限承载力经验系数取值
Tab.6
| 荷载工况 | C | Cr | CN | Ch |
|---|---|---|---|---|
| ETF | 1 | 0.35 | 2.60 | 0.050 |
| ITF | 4 | 0.21 | 0.75 | 0.010 |
| EOF | 2 | 0.32 | 1.60 | 0.040 |
| IOF | 1 | 0.04 | 2.30 | 0.001 |
3.2 《冷弯型钢结构技术规范》(征求意见稿)方法
我国现行CECS 410: 2015[10]尚缺乏常用冷弯不锈钢构件局部承压下的腹板压跛极限承载力计算方法.针对普钢结构,我国现行《冷弯薄壁型钢结构技术规范》(GB 50018—2002)[29]第7.1.7条给出了压型钢板局部承压下的腹板压跛极限承载力验算公式;其条文说明中指出:腹板压跛涉及因素较多,很难用理论精确分析,设计条例提供的计算公式是根据大量试验结果给出的,该式取自欧洲规范.我国《冷弯型钢结构技术规范》(征求意见稿)[32]在受弯构件条目下增加了全新的腹板压跛极限承载力计算方法,新的方法同AISI S100-16[33]保持统一,故腹板压跛极限承载力(规范中表述为:腹板局部受压承载力)计算公式同式(5)一致.需要指出的是,《冷弯型钢结构技术规范》(征求意见稿)[32]给出了计算冷弯C形、U形、Z形及工字形拼合截面构件腹板压跛极限承载力的经验系数,未提供冷弯方矩管的经验系数取值规定.既有研究结果表明,C形截面与方矩管截面具有类似的腹板压跛破坏模式[15,26].本文采用《冷弯型钢结构技术规范》(征求意见稿)[32]给出的C形截面构件经验系数(见表7),以探究该腹板压跛极限承载力计算方法对冷弯不锈钢方矩管的适用性.
表7 C形截面构件腹板压跛极限承载力经验系数取值
Tab.7
| 荷载工况 | C | Cr | CN | Ch |
|---|---|---|---|---|
| ETF | 7.5 | 0.08 | 0.12 | 0.048 |
| ITF | 20 | 0.10 | 0.08 | 0.031 |
| EOF | 4 | 0.14 | 0.35 | 0.020 |
| IOF | 13 | 0.23 | 0.14 | 0.010 |
3.3 直接强度法
直接强度法(Direct Strength Method, DSM)是冷弯型钢结构构件承载力计算的先进方法,SEI/ASCE 8-22[36]将其与传统有效宽度法并列纳入规范正文,可用以计算构件受压、受弯和受剪下的极限承载力.该方法亦被纳入《冷弯型钢结构技术规范》(征求意见稿)[32]的附录C中以验算受压、受弯和压弯构件的承载力.需要指出,目前国际上未有设计规范给出针对构件局部承压下腹板压跛极限承载力计算的直接强度法.Li等[17]通过稳定理论和屈服线理论提出了适用于冷弯方矩管腹板压跛屈曲荷载和屈服荷载的计算公式,建立了适用于各典型荷载工况下冷弯方矩管腹板压跛极限承载力计算的直接强度法,可由下式表示:
式中:PDSM为局部承压下的腹板压跛极限承载力;Py为腹板压跛屈服荷载;Pcr为腹板压跛屈曲荷载;λ=
式中:Nm为屈服线长度,EOF、ETF荷载工况下,Nm=N+2.5R+0.5 h,IOF、ITF荷载工况下,Nm=N+5R+h;αp为屈服荷载计算系数,EOF和IOF荷载工况下,
ETF和ITF荷载工况下,
ks=2R/t-1,αpm=1/ks+0.5/kv,kv=h/t,均为计算系数.
腹板压跛屈曲荷载Pcr可通过下式计算得到[17]:
式中:αc为折减系数,
EOF和ETF荷载工况下,λn取(3.8h/t)×
| 荷载工况 | a | b | n | λk | γ |
|---|---|---|---|---|---|
| EOF | 0.96 | 0.23 | 0.51 | 0.584 | 1.00 |
| IOF | 0.93 | 0.30 | 0.41 | 0.600 | 0.77 |
| ETF | 0.66 | 0.17 | 0.55 | 0.447 | 0.94 |
| ITF | 0.73 | 0.01 | 0.35 | 0.480 | 1.20 |
3.4 计算方法对比
表9 有限元结果与设计方法预测值对比
Tab.9
| 荷载工况 | 统计量 | 奥氏体 | 双向型 | |||||
|---|---|---|---|---|---|---|---|---|
| PFEA/PASCE | PFEA/PGB | PFEA/PDSM | PFEA/PASCE | PFEA/PGB | PFEA/PDSM | |||
| EOF | 平均值 | 1.21 | 1.32 | 0.97 | 1.00 | 1.10 | 1.02 | |
| 变异系数 | 0.079 | 0.114 | 0.056 | 0.086 | 0.144 | 0.070 | ||
| IOF | 平均值 | 1.40 | 1.08 | 1.07 | 1.17 | 0.90 | 1.03 | |
| 变异系数 | 0.081 | 0.129 | 0.044 | 0.063 | 0.108 | 0.045 | ||
| ETF | 平均值 | 1.32 | 1.10 | 1.00 | 1.08 | 0.89 | 1.05 | |
| 变异系数 | 0.091 | 0.189 | 0.090 | 0.067 | 0.125 | 0.067 | ||
| ITF | 平均值 | 1.27 | 0.94 | 1.04 | 1.07 | 0.78 | 1.05 | |
| 变异系数 | 0.103 | 0.218 | 0.081 | 0.074 | 0.159 | 0.068 | ||
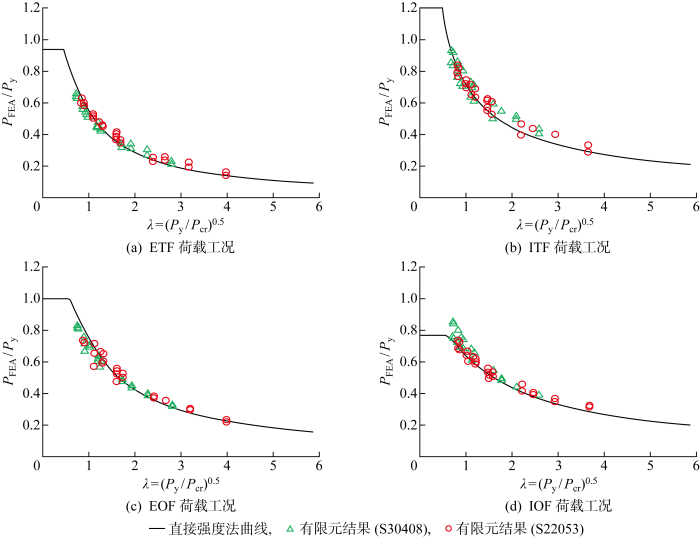
图5
图6
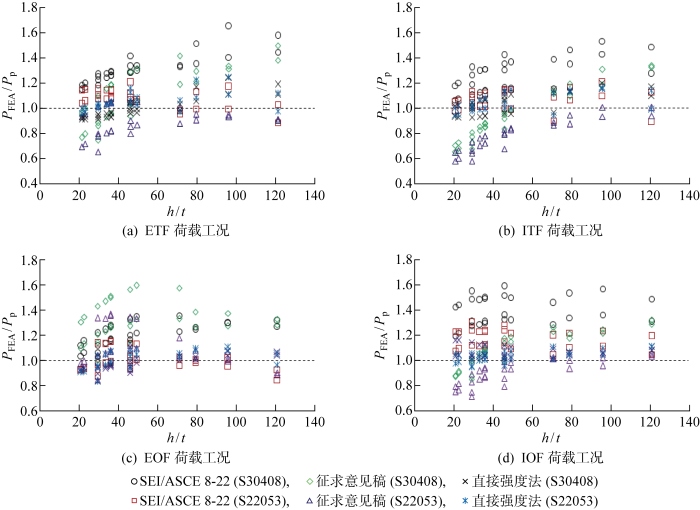
可以看出,对于冷弯奥氏体S30408不锈钢方矩管,SEI/ASCE 8-22的预测结果整体保守且具有较小的离散程度,4种荷载工况下有限元结果与规范预测值的平均比值介于1.21~1.40区间,变异系数在0.079~0.103范围内.对于冷弯双相型S22053不锈钢方矩管,SEI/ASCE 8-22在ETF、ITF和EOF荷载工况下提供了较为准确的腹板压跛极限承载力预测,有限元模拟结果与规范预测结果的平均误差在8%以内,而在IOF荷载工况下,SEI/ASCE 8-22的预测结果则偏保守.此外,由参数分析算例的参数范围及对比结果可得,当构件截面尺寸超出经验参数适用范围(60<h/t≤121,55<N/t≤75)时,SEI/ASCE 8-22的经验参数对于预测冷弯奥氏体S30408和双相型S22053不锈钢方矩管的腹板压跛极限承载力仍具有适用性.因而,美国《冷弯不锈钢结构设计规范》(SEI/ASCE 8-22)[36]中腹板压跛验算公式的经验参数可用于冷弯奥氏体S30408和双相型S22053不锈钢方矩管的腹板压跛极限承载力计算,经验参数适用范围可由h/t≤60,N/t≤55扩展至h/t≤121,N/t≤75.
对于冷弯奥氏体S30408和双相型S22053不锈钢方矩管,在4种荷载工况下,有限元模拟结果与直接强度法预测结果的平均误差在7%以内,变异系数均小于0.090,预测结果总体上与有限元模拟结果比较接近,具有较高的精确度.由此可见,Li等[17]提出的直接强度法适用性强,可用以计算不同种类冷弯不锈钢方矩管的腹板压跛极限承载力.
4 结论
采用有限元软件Abaqus建立了冷弯奥氏体和双相型不锈钢方矩管腹板压跛性能分析的有限元模型,模拟了试验结果,并进行了224组参数分析算例计算.研究得到如下结论:
(1) 建立的有限元模型考虑了不锈钢材料非线性本构关系和冷弯效应,有限元模拟得到的构件破坏模式与试验结果保持一致.同时,有限元模拟获得的腹板压跛极限承载力与试验值的平均误差在4%以内,所建立的有限元模型能够准确地预测冷弯不锈钢方矩管在4种典型腹板压跛荷载工况下的腹板压跛极限承载力.
(3) 美国《冷弯不锈钢结构设计规范》(SEI/ASCE 8-22)[36]中给出的腹板压跛极限承载力计算方法适用于国产冷弯奥氏体S30408和双相型S22053不锈钢方矩管.此外,规范界定的经验参数适用范围可由h/t≤60,N/t≤55扩展至h/t≤121,N/t≤75.
(4) Li等[17]提出的直接强度法具有良好的精确度,可应用于冷弯奥氏体和双相型不锈钢方矩管的腹板压跛极限承载力计算.
参考文献
不锈钢结构的应用和研究现状
[J].
A review of current applications and research of stainless steel structure
[J].
卷边C形截面不锈钢短柱承载力直接强度法
[J].
Direct strength method of capacity of stainless steel lipped C section stub columns
[J].
热轧不锈钢圆管柱轴心受压构件整体稳定性能试验研究
[J].
Experimental investigation on the overall stability of hot-rolled stainless steel tubular columns under axial compression
[J].
焊接双相型不锈钢工字形受弯构件整体稳定性能研究
[J].
Study on the lateral-torsional buckling of duplex stainless steel welded I-section flexural members
[J].
冷成型不锈钢矩形管截面受弯构件挠度计算方法
[J].
A calculation method for the deflections of cold-formed stainless steel flexural members with rectangular hollow sections
[J].
不锈钢压弯构件平面内稳定承载力计算方法研究
[J].
In-plane stability design method of stainless steel beam-columns
[J].
不锈钢焊接箱形截面压弯构件弯曲屈曲试验研究
[J].
Experimental research on flexural buckling of stainless steel welded box-section beam-columns
[J].
不锈钢构件螺栓连接摩擦面抗滑移系数试验
[J].
Experimental research on slip factor in bolted connection with stainless steel
[J].
常温和高温下不锈钢圆柱头栓钉抗剪性能研究
[J].
Shear performance of stainless cylindral head steel stud at room and high temperatures
[J].
《不锈钢结构技术规程》的编制及内容简介
[J].
Introduction to the establishment background and content of Techinical Specification for Stainless Steel Structures
[J].
Recent research on stainless steel tubular structures
[J].DOI:10.1016/S0143-974X(99)00052-8 URL [本文引用: 1]
Cold-formed steel design
[M].
Cold-formed stainless steel sections subjected to web crippling
[J].DOI:10.1061/(ASCE)0733-9445(2006)132:1(134) URL [本文引用: 3]
Study of web crippling in ferritic stainless steel cold formed sections
[J].DOI:10.1016/j.tws.2013.03.015 URL [本文引用: 1]
Web crippling of cold-formed ferritic stainless steel square and rectangular hollow sections
[J].DOI:10.1016/j.engstruct.2018.08.076 URL [本文引用: 14]
Recent research on stainless steel tubular structures
[C]//
Strength curves for web crippling design of cold-formed stainless steel hat sections
[J].DOI:10.1016/j.tws.2014.07.021 URL [本文引用: 1]
Design of stainless steel RHS beams, columns and beam-columns
[R].
Structural design of high-strength austenitic stainless steel
[J].DOI:10.1016/j.tws.2006.04.014 URL [本文引用: 1]
Cold-formed high-strength stainless steel tubular sections subjected to web crippling
[J].DOI:10.1061/(ASCE)0733-9445(2007)133:3(368) URL [本文引用: 12]
Yield line mechanism analysis on web crippling of cold-formed stainless steel tubular sections under two-flange loading
[J].DOI:10.1016/j.engstruct.2005.10.021 URL [本文引用: 1]
考虑单侧翼缘受载腹板屈曲的不锈钢钢管设计
[J].
Design of stainless steel tubular sections subjected to web crippling under one-flange loading
[J].
不锈钢管局部承压性能试验研究
[J].
Experimental investigation on mechanical behavior of stainless steel tube under local axial compression
[J].
Cold-formed ferritic stainless steel tubular structural members subjected to concentrated bearing loads
[J].DOI:10.1016/j.engstruct.2017.05.022 URL [本文引用: 5]
Web crippling design of lean duplex stainless steel tubular members under interior loading conditions
[J].DOI:10.1016/j.engstruct.2021.112192 URL [本文引用: 3]
Design of lean duplex stainless steel tubular sections subjected to concentrated end-bearing loads
[J].
Strength enhancements induced during cold forming of stainless steel sections
[J].DOI:10.1016/j.jcsr.2008.04.014 URL [本文引用: 1]
Experiments on stainless steel hollow sections—Part 1: Material and cross-sectional behaviour
[J].DOI:10.1016/j.jcsr.2003.11.006 URL [本文引用: 1]
Full-range stress-strain curves for stainless steel alloys
[J].DOI:10.1016/S0143-974X(02)00018-4 URL [本文引用: 1]
Web crippling failure using quasi-static FE models
[J].DOI:10.1016/j.tws.2014.05.003 URL [本文引用: 3]
Web crippling of cold formed steel sections
[R].
Strength enhancements in cold-formed structural sections — Part II: Predictive models
[J].DOI:10.1016/j.jcsr.2012.12.007 URL [本文引用: 1]