自由落体状态下二维结构物砰击载荷计算

doi:10.16183/j.cnki.jsjtu.2022.189

自由落体状态下二维结构物砰击载荷计算

孙哲^,¹, 眭旭鹏¹, KOROBKIN Alexander², 邓彦增³, 张桂勇¹, 宗智¹, 姜宜辰¹

1.大连理工大学船舶工程学院,辽宁大连 116024

2.东安格利亚大学数学学院,英国诺维奇 NR47TJ

3.中国空气动力研究与发展中心计算空气动力研究所,四川绵阳 621000

Dynamic Characteristics of Two-Dimensional Structures Slamming Under Free Fall Condition

SUN Zhe^,¹, SUI Xupeng¹, KOROBKIN Alexander², DENG Yanzeng³, ZHANG Guiyong¹, ZONG Zhi¹, JIANG Yichen¹

1. School of Naval Architecture and Ocean Engineering, Dalian University of Technology, Dalian 116024, Liaoning, China

2. School of Mathematics, University of East Anglia, Norwich NR47TJ, United Kingdom

3. Computational Aerodynamics Institute, China Aerodynamics Research and Devilment Center, Mianyang 621000, Sichuan, China

责任编辑: 王一凡

收稿日期: 2022-06-1 修回日期: 2022-10-30 接受日期: 2022-11-10

基金资助:

国家重点研发计划(2021YFC2801701)
国家重点研发计划(2021YFC2801700)
国家自然科学基金(52171295)
国家自然科学基金(52061135107)
中央高校基本科研业务费专项(DUT20TD108)
中央高校基本科研业务费专项(DUT20LAB308)
深海矿产资源开发利用技术国家重点实验室开放项目(SH-2020-KF-A01)
辽宁省“兴辽英才计划”项目(XLYC1908027)
大连市重点领域创新团队支持计划(2020RT03)
大连市青年科技之星项目(2020RQ006)

Received: 2022-06-1 Revised: 2022-10-30 Accepted: 2022-11-10

作者简介 About authors

孙哲(1986-),副教授,主要从事粒子类无网格计算方法、水弹性流固耦合问题方面研究;E-mail:zsun@dlut.edu.cn.

摘要

将各类砰击入水的解析理论模型与时域上的精细积分法相结合,研究了在自由落体状态下具有任意对称形状的二维结构物的砰击过程.通过对解析理论模型的数学表达式进行分析,物体所受的砰击力可以分解为两项,分别为速度相关项和加速度相关项.将本文提出的模型与试验和其他数值模拟方法进行对比,验证结果良好.此外,针对轻质结构物或者具有较大入水速度的物体,可以合理地忽略自身的重力,那么对于指定形状和质量的二维物体,自由落体状态下其在砰击过程中的最大加速度或砰击力峰值总是发生在同一个浸没深度处,而与初始的入水速度无关.

关键词： 解析模型; 砰击力分解; 精细积分法; 自由落体

Abstract

The slamming process of two-dimensional structures under free fall condition with arbitrary symmetrical shapes is investigated by combining various analytical models for slamming and the precise integration method in the time domain. By closely analyzing the mathematical expression of analytical models, the total slamming force acting on the body can be decomposed into two terms which are dependent on the velocity and the acceleration respectively. The developed model proposed in this paper is validated against the results from experiments and other numerical methods. Moreover, it is found that if the gravity of body is ignored, which is a reasonable assumption for situations such as structures with light weight or large entry velocity, the maximum acceleration (or the peak slamming force) for a free fall body will always occur at the certain penetration depth for a particular shape and mass, regardless of the initial slamming velocity.

Keywords： analytical model; slamming force decomposition; precise integration method; free fall

PDF (1402KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

孙哲, 眭旭鹏, KOROBKIN Alexander, 邓彦增, 张桂勇, 宗智, 姜宜辰. 自由落体状态下二维结构物砰击载荷计算[J]. 上海交通大学学报, 2023, 57(11): 1410-1420 doi:10.16183/j.cnki.jsjtu.2022.189

SUN Zhe, SUI Xupeng, KOROBKIN Alexander, DENG Yanzeng, ZHANG Guiyong, ZONG Zhi, JIANG Yichen. Dynamic Characteristics of Two-Dimensional Structures Slamming Under Free Fall Condition[J]. Journal of Shanghai Jiaotong University, 2023, 57(11): 1410-1420 doi:10.16183/j.cnki.jsjtu.2022.189

在现如今的船舶与海洋工程领域,对于多体船或者剖面曲率很大的船舶,较大的航行速度会使船体受到很大的砰击力,这会导致十分严重的结构损伤甚至发生海上事故^[1].因此,砰击现象的研究对于船舶和海洋结构物的性能以及强度具有重要的意义.

砰击入水的开创性工作可以追溯到von Karman^[2]和Wagner^[3]对于楔形体入水过程的研究.基于经典Wagner模型,众多学者对其进行了不同程度的发展和完善.Dobrovol’skaya^[4]研究了具有自由液面流体的相似流动,并提出了入水砰击问题的数学积分表达式.在Zhao等^[5]的模型中,自由液面是线性的而物体边界和伯努利方程保持非线性.Cointe等^[6]、Howison等^[7]和Oliver^[8]通过匹配渐近展开法将整个流场分成3部分并进行了深入的研究.段文洋等^[9]提出了通过辅助线来构建在流动分离发生后的虚拟物体表面,以便快速地预报砰击力.除了对于楔形体的一系列研究,Tassin等^[10]对抛物线物体的入水模型开展研究,而Korobkin^[11-12]则研究了具有任意形状物体的入水过程.

试验方法是研究砰击过程的特征以及验证解析理论模型的重要手段^[13],其中楔形体是被研究最多的模型.典型的研究工作包括Panciroli等^[14-15]对刚性和弹性对称楔形体的砰击过程进行试验和计算.近年来,众多学者对楔形体的倾斜砰击入水以及非对称楔形体的砰击入水进行了试验^[16⇓-18].对于更复杂的船体结构,比如船艏部分,Aarsnes^[19]所进行的自由落体试验是其后数值方法验证^[20-21]中引用最多的研究成果之一.

如今,数值模拟方法以数据可靠、计算速度快等特点成为砰击基础理论研究和实际应用中最常用的工具.边界元法(BEM)是最早应用于砰击模拟的数值方法之一,比如Sun^[20]、Bao等^[22]和Wu等^[23]的研究工作.尽管在数值模拟中可以考虑自由液面的非线性效应和流体的黏度,但计算成本过高使其并不适用于海洋结构物设计的初期.

目前的解析理论研究大多数集中在匀速入水或控制入水.然而,在这种情况下物体所受的砰击力可能会与其在自由落体入水情况下所受的砰击力大不相同.同时,自由落体入水情况更适用于实际工程领域中的结构强度评估.此外,虽然数值模拟方法同样能够应用于结构物自由落体砰击入水的模拟,但解析理论模型更易于从物理学的角度分析砰击力的组成和特性,在时间成本方面解析理论模型相较于数值模拟方法更具有明显的优势,同样也能避免在数值模拟的过程中进行网格划分操作或者物理模型选取不当带来的主观误差.尽管大多只适用于流动分离之前的砰击入水阶段,但是目前的解析理论模型依旧是工程领域预报结构物砰击入水初期阶段的运动响应以及砰击力峰值最有效率的工具.

鉴于上述背景,将时域上的精细积分法与砰击力计算的解析理论模型相结合,将物体的运动控制方程转换为一组常微分方程组,在提升计算精度和减少计算时间的同时,对二维结构物在砰击过程中的砰击载荷进行研究.

1 砰击入水的解析理论模型

1.1 理论基础

本文使用的解析理论模型均基于势流理论,即流体被视为不可压缩且无黏流体.由于砰击是一个在极短时间内发生的高速动态过程,所以可以合理忽略流体的重力对于物体砰击过程的影响^[24-25].同时,流体的表面张力也被忽略.

典型的二维对称物体砰击示意图如图1所示.图中:f(y)为物体的形状函数;ξ(t)为物体在t时刻的浸没深度,且ξ(t)≥0, $\overset{\cdot}{ξ}$ (t)≥0;c(t)为物体湿表面边界投影在y轴上的坐标,且c(t)≥0.在起始时刻,水面保持静止且位于z=0平面.当物体接触水面时,开始计时,同时将接触点视为坐标原点O,以物体的对称轴为z轴,建立yOz坐标系.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 二维对称物体砰击示意图

Fig.1 Sketch of a two-dimensional symmetric structure slamming

t时刻物体表面任意一点的垂向坐标可表示为

z=f(y)-ξ(t)

物体关于z轴对称,因此其湿表面在y轴上的投影长度是2c(t),其中c(t)可以由Wagner条件^[11,25]计算得到:

(1)

\int_{0}^{π / 2}

f(c(t)sin γ)dγ=

\frac{π}{2}

ξ(t)

于是,c(t)对时间的导数 $\overset{\cdot}{c}$ (t)可表示为

\overset{\cdot}{c}

(t)=

\frac{π}{2} \overset{\cdot}{ξ}

(t)/

\int_{0}^{π / 2}

f'(c(t)sin γ)sin γdγ

流体动力学采用基于平板撞击假设的Wagner理论^[3]进行求解,计算区域由物体湿表面在y轴上的投影和未受扰动的自由液面构成.流体的速度势函数φ^W可通过如下控制方程和边界条件求解:

(2)

\begin{array}{l} Δ^{2} φ^{W} = 0, & z < 0 \\ φ^{W} = 0, & z = 0, |y| \geq c \\ \frac{\partial φ^{W}}{\partial z} = - \overset{\cdot}{ξ} (t), & z = 0, |y| < c \\ φ^{W} \to 0, & y^{2} + z^{2} \to \infty \end{array}\}

式(2)的解φ^W(y,0,t)可表示为

(3)$\begin{array}{c}\varphi^{\mathrm{W}}(y, 0, t)=-\dot{\xi}(t) \sqrt{c^{2}(t)-y^{2}} \\-c \leqslant y \leqslant c\end{array}$

1.2 砰击压力计算

物体沿着湿表面的压力分布是通过伯努利方程计算的:

p_B(y,z,t)=-ρ

[\frac{\partial φ}{\partial t} + \frac{1}{2} {(Δ φ)}^{2}]

式中:φ(y,z,t)为z≤0区域的速度势函数;ρ为液体的密度.在基于Wagner理论的不同砰击解析理论模型中,通过不同的近似方法处理非线性效应和湿表面形状来计算物体所受的压力.

(1) 经典Wagner模型(OWM)^[26-27].

在OWM中,仅考虑伯努利方程的线性项,将速度势函数式(3)代入,得到压力表达式:

$\begin{aligned}p(y, t)= & p_{\mathrm{B}}(y, 0, t) \approx-\rho \frac{\partial \varphi^{\mathrm{W}}}{\partial t}= \\& \rho\left(\frac{\dot{\xi} \dot{c} c}{\sqrt{c^{2}-y^{2}}}+\ddot{\xi} \sqrt{c^{2}-y^{2}}\right)\end{aligned}$

(2) 基于非线性伯努利方程的Wagner模型(WN)^[26].

在WN模型中,考虑了伯努利方程的非线性项,同样将速度势函数式(3)代入,得到压力表达式:

p(y,t)=p_B(y,0,t)≈-ρ $[\frac{\partial φ^{W}}{\partial t} + \frac{1}{2} (Δ φ^{W})^{2}]$ =

ρ $(\frac{\overset{\cdot}{ξ} \overset{\cdot}{c} c}{\sqrt{c^{2} - y^{2}}} - \frac{1}{2} \frac{{\overset{\cdot}{ξ}}^{2} c^{2}}{c^{2} - y^{2}} + \ddot{ξ} \sqrt{c^{2} - y^{2}})$

(3) Logvinovich模型(OLM)^[25,28].

在OLM中,在考虑了非线性项的同时,将压力的计算放置在物体浸没深度所处的平面上(即z=-ξ(t)), 而不是在未受扰动的自由液面上.同时,将速度势函数φ表示为Wagner解φ^W(y,0,t)在z=0处的泰勒展开式,并将式(2)中的第3个方程作为边界条件.于是,速度势函数φ可以改写为

ϕ(y,t)=φ(y,-ξ(t),t)≈φ^W(y,0,t)+ $\overset{\cdot}{ξ}$ (t)ξ(t)=

- $\overset{\cdot}{ξ}$ (t) $\sqrt{c^{2} (t) - y^{2}}$ + $\overset{\cdot}{ξ}$ (t)ξ(t)

物体沿湿表面的OLM压力计算公式可最终表示为

p(y,t)=

ρ $(\frac{\overset{\cdot}{ξ} \overset{\cdot}{c} c}{\sqrt{c^{2} - y^{2}}} - \frac{1}{2} \frac{{\overset{\cdot}{ξ}}^{2} c^{2}}{c^{2} - y^{2}} + \ddot{ξ} \sqrt{c^{2} - y^{2}} - \ddot{ξ} ξ)$

(4) 改进的Logvinovich模型(MLM)^[25].

在MLM中,Korobkin^[25]提出通过考虑物体的形状来进一步提高OLM的计算精度,即抛开之前的平板碰撞假设,使压力的计算在真实的物体湿表面上进行.与OLM的处理方法类似,速度势函数φ也表示为φ^W(y,0,t)在z=0处的泰勒展开式,并将式(2)中的第3个方程作为边界条件.于是,速度势函数φ可以改写为

ϕ(y,t)=- $\overset{\cdot}{ξ}$ (t) $\sqrt{c^{2} (t) - y^{2}}$ - $\overset{\cdot}{ξ}$ (t)(f(y)-ξ(t))

物体沿湿表面的MLM压力计算公式可最终表示为

p(y,t)=ρ[ $\frac{\overset{\cdot}{ξ} \overset{\cdot}{c} c}{\sqrt{c^{2} - y^{2}}}$ - $\frac{1}{2} \frac{c^{2}}{c^{2} - y^{2}} \frac{{\overset{\cdot}{ξ}}^{2}}{1 + f_{y}^{2}}$ -

$\frac{1}{2} \frac{{\overset{\cdot}{ξ}}^{2} f_{y}^{2}}{1 + f_{y}^{2}}$ + $\ddot{ξ} \sqrt{c^{2} - y^{2}}$ + $\ddot{ξ}$ (f-ξ)]

式中:f_y为f函数对y的导数.

(5) 广义Wagner模型(GWM)^[25].

在GWM中,速度势和压力的计算放置在物体和流体交界高度附近的物体湿表面上,其余对于速度势φ函数的处理与MLM一致.于是,速度势函数φ可以改写为

ϕ(y,t)≈φ^W(y,0,t)+(f(y)-f(c(t)))×

$\frac{\partial φ^{W} (y, 0, t)}{\partial z}$ =- $\overset{\cdot}{ξ}$ (t) $\sqrt{c^{2} (t) - y^{2}}$ -

$\overset{\cdot}{ξ}$ (t)(f(y)-f(c(t)))

物体沿湿表面的GWM压力计算公式可最终表示为

p(y,t)=ρ[ $\frac{\overset{\cdot}{ξ} \overset{\cdot}{c} c}{\sqrt{c^{2} - y^{2}}}$ - $\frac{1}{2} \frac{c^{2}}{c^{2} - y^{2}} \frac{{\overset{\cdot}{ξ}}^{2}}{1 + f_{y}^{2}}$ -

$\frac{1}{2} \frac{{\overset{\cdot}{ξ}}^{2} f_{y}^{2}}{1 + f_{y}^{2}}$ - $\overset{\cdot}{ξ}$ f_y(c) $\overset{\cdot}{c}$ + ${\overset{\cdot}{ξ}}^{2}$ +

$\ddot{ξ} \sqrt{c^{2} - y^{2}}$ + $\ddot{ξ}$ (f-f(c))]

1.3 砰击力计算

在物体砰击过程中,作用在物体上的砰击力是通过沿物体湿表面对其所受的压力进行积分获得的.不过,压力表达式中的速度相关项包含了一个奇异项,1/(c²-y²), 这使得在y=c附近压力变为负值且不可积分^[27].根据Korobkin^[25]的建议,这一速度相关项的砰击压力应在区域-c^*≤y≤c^*进行积分,其中c^*是距y=c处最近且满足p_v(c^*,t)=0的点.

对于具有任意形状的物体,其形状函数可以表示为物面上均匀分布的离散点的线性差值,如下式所示:

(4)f(y)=f(y_n)+

\frac{f (y_{n + 1}) - f (y_{n})}{y_{n + 1} - y_{n}}

(y-y_n)

之后,根据1.2节所述各个解析理论模型的压力计算公式和式(4),逐个对分段进行积分,便可得到物体所受的砰击力.

为了描述物体在砰击入水过程中的运动状态,借助牛顿第二定律并对其进行改写:

(5)-m

\ddot{ξ}

=F_H-mg=F_v+F_a-mg

式中:m为物体的质量;g为重力加速度,本文取9.81 m/s²;F_v和F_a分别为组成物体所受砰击力F_H的两部分,F_v为速度v的相关项,F_a为加速度a的相关项,

(6)F_v(t)=

\int_{- c^{*}}^{c^{*}}

p_vdy=ρ(a_v₁

\overset{\cdot}{ξ}

+a_v₂

{\overset{\cdot}{ξ}}^{2}

)

(7)F_a(t)=

\int_{- c}^{c}

p_ady=ρ(a_a₁

\ddot{ξ}

+a_a₂

\ddot{ξ}

ξ)

p_v为物体所受砰击压力中的速度相关项部分;p_a为物体所受砰击压力中的加速度相关项部分;a_v₁、a_v₂、a_a₁和a_a₂为砰击力系数.对于不同的解析理论模型,a_v₁、a_v₂、a_a₁和a_a₂的表达式各不相同,如表1所示.表中:

I₁= $\int_{- c^{*}}^{c^{*}} \frac{d y}{(c^{2} - y^{2}) (1 + f_{y}^{2})}$

I₂= $\int_{- c^{*}}^{c^{*}} \frac{f_{y}^{2} d y}{1 + f_{y}^{2}}$

I₃= $\int_{- c}^{c}$ fdy

I₄= $\int_{- c^{*}}^{c^{*}} \frac{d y}{c^{2} - y^{2}}$

表1 不同理论模型下的砰击力系数

Tab.1 Slamming force coefficients for different analytical models

模型	a_v₁	a_v2	a_a1	a_a2
OWM	π $\overset{\cdot}{c}$ c	0	$\frac{π c^{2}}{2}$	0
WN	2 $\overset{\cdot}{c}$ carcsin $\frac{c^{*}}{c}$	- $\frac{c^{2} I_{4}}{2}$	$\frac{π}{2}$ c²	0
OLM	2 $\overset{\cdot}{c}$ carcsin $\frac{c^{*}}{c}$	- $\frac{c^{2} I_{4}}{2}$	$\frac{π}{2}$ c²	-2c
MLM	2 $\overset{\cdot}{c}$ carcsin $\frac{c^{*}}{c}$	- $\frac{c^{2} I_{1} + I_{2}}{2}$	I₃+ $\frac{π}{2}$ c²	-2c
GWM	2 $\overset{\cdot}{c}$ carcsin $\frac{c^{}}{c}$ -2c^f_y(c) $\overset{\cdot}{c}$	- $\frac{c^{2} I_{1} + I_{2}}{2}$ +2c^*	I₃+ $\frac{π}{2}$ c²-c^*f(c)	0

新窗口打开| 下载CSV

2 时域上的精细积分法

在计算获得物体所受的砰击力F_v和F_a之后,物体的动力学控制方程,即式(5),可以通过精细积分法^[29]进行求解.在精细积分法中,动力学控制方程可重新表示为

(8)$\begin{array}{l}M \ddot{\xi}+G \dot{\xi}+K \xi=r \\r=\rho\left(a_{v 2} \dot{\xi}^{2}+a_{a 2} \ddot{\xi} \xi\right) \\M=m+\rho a_{a 1} \\G=\rho a_{v 1} \\K=0\end{array}$

接着,引入一个新的相空间变量:

v=[ξ ζ]^T

其中ζ表示为

ζ=M

\overset{\cdot}{ξ}

\frac{1}{2}

Gξ

于是,式(8)可进一步表示为

(9)$\begin{aligned}\dot{v} & =\boldsymbol{H} \boldsymbol{v}+\boldsymbol{f} \\\boldsymbol{f} & =\left[\begin{array}{ll}0 & r\end{array}\right]^{\mathrm{T}} \\\boldsymbol{H} & =\left[\begin{array}{ll}A & D \\B & C\end{array}\right] \\A & =-\frac{1}{2} M^{-1} G, \quad B=\frac{1}{4} G M^{-1} G-K \\C & =-\frac{1}{2} G M^{-1}, \quad D=M^{-1}\end{aligned}$

对于式(9)所描述的物体动力学系统,若已知第k个时间步的变量v_k,则下一个时间步中的变量v_k₊₁可通过如下所示的Duhamel积分得到:

(10)$\begin{aligned}\boldsymbol{v}_{k+1}= & \exp (\boldsymbol{H} \eta) \boldsymbol{v}_{k}+ \\& { }_{0}^{\eta} \exp [\boldsymbol{H}(\eta-\tau)] \boldsymbol{f}\left(t_{k}+\tau\right) \mathrm{d} \tau\end{aligned}$

式中:η为时间间隔.

在时域上使用精细积分法求解物体运动特征的关键在于计算指数矩阵exp(Hη).该计算包含了两个步骤.首先,使用指数矩阵的附加定理将矩阵扩展为如下形式:

(11)exp(Hη)=exp(Hδ)^m, δ=η/m, m=2^N

通常选择20作为N的取值,于是应用附加定理之后的时间间隔δ可被视为一个非常小的值,因此前4阶泰勒展开式可以用来作为exp(Hδ)的表达形式:

(12)$\begin{array}{l}\exp \left(\boldsymbol{H}_{\delta}\right) \quad \boldsymbol{I}+\boldsymbol{R} \\\boldsymbol{R}=\boldsymbol{H}_{\delta}+\left(\boldsymbol{H}_{\delta}\right)^{2} / 2 !+\left(\boldsymbol{H}_{\delta}\right)^{3} / 3+\left(\boldsymbol{H}_{\delta}\right)^{4} / 4 !\end{array}$

将式(12)代入式(11), exp(Hδ)可近似表示为

(13)$\exp (\boldsymbol{H} \eta)=(\boldsymbol{I}+\boldsymbol{R})^{2^{N}}=\left(\boldsymbol{I}+2 \boldsymbol{R}+\boldsymbol{R}^{2}\right)^{2^{N-1}}$

为了避免由于I的值远大于R_n的增量而导致计算精度的下降,并不是直接对式(13)连续地进行平方,而是使用下式来表征增量的部分:

$\boldsymbol{R}_{n}=2 \boldsymbol{R}_{n-1}+\boldsymbol{R}_{n-1}^{2}$

在重复N次上述操作后,指数矩阵exp(Hδ)最终可以表示为

$\exp (\boldsymbol{H} \eta)=\boldsymbol{I}+\boldsymbol{R}_{N}$

如式(10)所示,为了得到第k+1个时间步中的变量v_k₊₁,还需要确定f的值,而这可以通过“预估-校正”的方法获得.方法的具体细节详见文献[30].

3 结果与讨论

3.1 模型验证

首先验证精细积分法在砰击问题上的时间收敛性.选取5个不同的时间步长Δt并结合MLM模拟了一个二维楔形体的自由落体砰击过程.楔形体的半宽为0.11 m、底升角为25°.加速度随时间变化的预报结果如图2所示,当时间步长小于 0.000 1 s 后,所得结果几乎没有差异.因此,对于之后的所有模拟,均使用 0.000 1 s 作为时间步长.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 基于MLM模型的时间步长收敛性验证

Fig.2 Time step convergence verification based on MLM

接着,将1.2节所述的各类解析理论模型与精细积分法相结合,研究楔形体在砰击过程中的运动状态.具体而言,将上文所述形状的楔形体置于3个不同的高度处,使其进行自由落体运动.在此,定义物体初始入水速度为v₀,则这3个不同初始高度对应的物体初始入水速度分别为v₀= 2.2,3.1,3.6 m/s.在本文中,所研究的物体均为二维物体,因此取楔形体的单位长度质量为2.125 kg/m.预报楔形体在砰击过程中加速度随时间的变化,并将所得结果与文献[14]中的实验结果进行对比,对比结果如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 自由落体状态下楔形体在不同入水速度情况时的加速度变化

Fig.3 Acceleration of wedge under free fall condition at different slamming speeds

观察图3可以发现,OWM给出了与其他4种模型相比过高的预测值,这与文献[14,25]中所指出的现象相一致.而其他考虑了非线性因素或物体表面影响的模型得到了更加准确的预报结果,尤其是MLM和GWM.当v₀= 2.2,3.1 m/s时,MLM预测的加速度峰值与实验结果基本一致,而当v₀= 3.6 m/s时,非线性模型预测的加速度峰值较试验结果高出10%~20%.

为了检验该方法是否适用于形状更加复杂的二维剖面,选取如图4所示的船体剖面模型进行验证.同样地,选取3个不同的高度使其进行自由落体运动,对应的入水速度分别为v₀= 0.61,1.48,2.43 m/s.船体剖面的单位长度质量为261 kg/m.将不同解析理论模型得到的垂向砰击力F随时间变化的预报结果与Aarsnes^[19]的试验结果以及Sun^[20]的BEM数值模拟结果进行对比,对比结果如图5所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 船体剖面示意图

Fig.4 Sketch of ship section

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 自由落体状态下船体剖面在不同入水速度情况时的砰击力变化

Fig.5 Slamming force of ship section under free fall condition at different slamming speeds

观察图5可以发现,虽然在入水初期,解析理论模型与试验以及BEM得到的结果吻合良好,但如果湿表面到达船体剖面上部的末端, 即当c等于剖面半宽之后,解析理论模型便不再能够预报流体和船体剖面的运动变化.然而,砰击理论指出,砰击力会在流体发生流动分离之后立刻达到峰值,这意味着解析理论模型能够相对可靠地预报砰击过程中物体所受的砰击力峰值的大小.对于不同模型的计算结果,OWM依然明显地过度预测了垂向砰击力,而其他模型的结果更接近Aarsnes^[19]的试验结果和Sun^[20]的BEM结果.总体来说,如同上文根据楔形体模型得到的推论一致,对于所有的工况,MLM提供了最准确的预测.

3.2 自由落体状态下的砰击力特性研究

解析理论模型的优点之一是易于研究砰击过程中主要的影响因素和物理机理.Korobkin^[31]通过解析方法研究了椭圆抛物线物体在自由落体状态下的砰击载荷和运动状态变化,Scolan等^[32]通过研究发现,无论是在二维模型还是三维模型,当物体的入水速度恒定,流体能量在砰击过程中会均匀地传递到抬升与飞溅的液体中.在本节中,研究物体在自由落体状态下所受砰击力的特性,即砰击力和物体浸没深度之间的关系.

根据式(1),楔形体湿表面的半宽可以表示为一个浸没深度的函数,即c=c(ξ),因此,c对时间的导数可以写成 $\overset{\cdot}{c}$ = $\overset{\cdot}{c}$ (ξ) $\overset{\cdot}{ξ}$ .若将各类解析理论模型中的c和 $\overset{\cdot}{c}$ 按照上述形式进行改写,式(6)和(7)可表示为

$\begin{array}{l}F_{v}=\rho\left(a_{v 1} \dot{\xi}+a_{v 2} \dot{\xi}^{2}\right)=\rho A_{v} \dot{\xi}^{2} \\F_{a}=\rho\left(a_{a 1} \ddot{\xi}+a_{a 2} \ddot{\xi} \xi\right)=\rho A_{a} \ddot{\xi}\end{array}$

其中:系数A_v和A_a是浸没深度ξ的函数, 即A_v=A_v(ξ), A_a=A_a(ξ).

对于砰击水动力在物体所受的流体载荷中占主导地位的情况,即对于轻质物体或具有较大入水速度的物体,物体自身的重力可以合理地忽略不计.因此,通过系数A_v和A_a,便可以将自由落体状态下物体的动力学方程式(5)重新表述为

(14)-m

\ddot{ξ}

=ρA_v

{\overset{\cdot}{ξ}}^{2}

+ρA_a

\ddot{ξ}

之后,式(14)可以进一步表示为

(15)

\frac{\ddot{ξ}}{\overset{\cdot}{ξ}}

\frac{ρ A_{v} \overset{\cdot}{ξ}}{ρ A_{a} + m}

(16)

\frac{d}{d t}

(ln

\overset{\cdot}{ξ}

)=-

\frac{A_{v}}{A'_{a}} \frac{d}{d t}

[ln(ρA_a+m)]

式中:A'_a 表示系数A_a对浸没深度ξ的导数.对于底升角为β的楔形体,系数A_v和A_a可表示为

(17)A_v=ξC_v

(18)A_a=ξ²C_a

式中:C_v和C_a为两个仅与楔形体底升角有关的常数.在OWM中,C_v和C_a可通过下式计算得到:

$C_{v}=2 C_{a}=\frac{\pi^{3}}{4 \tan ^{2} \beta}$

而在MLM中,C_v和C_a的表达式非常复杂,具体形式可参照Korobkin等^[33]的研究成果,这里不再赘述.通过对式(16)的两侧在时域上进行积分,物体在砰击入水过程中的速度^[31]可表示为

(19)

\overset{\cdot}{ξ}

=v₀

{(\frac{ρ C_{a}}{m} ξ^{2} + 1)}^{- \frac{C_{v}}{2 C_{a}}}

之后,将式(19)代入式(14)或式(15),便可得到物体的加速度表达式:

\ddot{ξ}

\frac{ρ C_{v} v_{0}^{2} ξ}{m} {(\frac{m}{ρ C_{a} ξ^{2} + m})}^{1 + \frac{C_{v}}{C_{a}}}

进一步地,加速度绝对值的最大值|ξ|_max可表示为

$\begin{array}{l}|\xi|_{\max }= \\2 v_{0}^{2} \sqrt{\frac{\rho C_{a}}{m}} \frac{C_{v}}{2 \sqrt{2 C_{v} C_{a}+C_{a}^{2}}}\left(\frac{2 C_{v}+C_{a}}{2 C_{v}+2 C_{a}}\right)^{1+\frac{C_{v}}{C_{a}}}\end{array}$

最大加速度所对应的浸没深度 $\overset{⌒}{ξ}$ 可以通过令d $\ddot{ξ}$ /dξ=0来确定.于是,可以得到:

(20)

\overset{⌒}{ξ}

\sqrt{\frac{m}{2 ρ (C_{v} + C_{a})}}

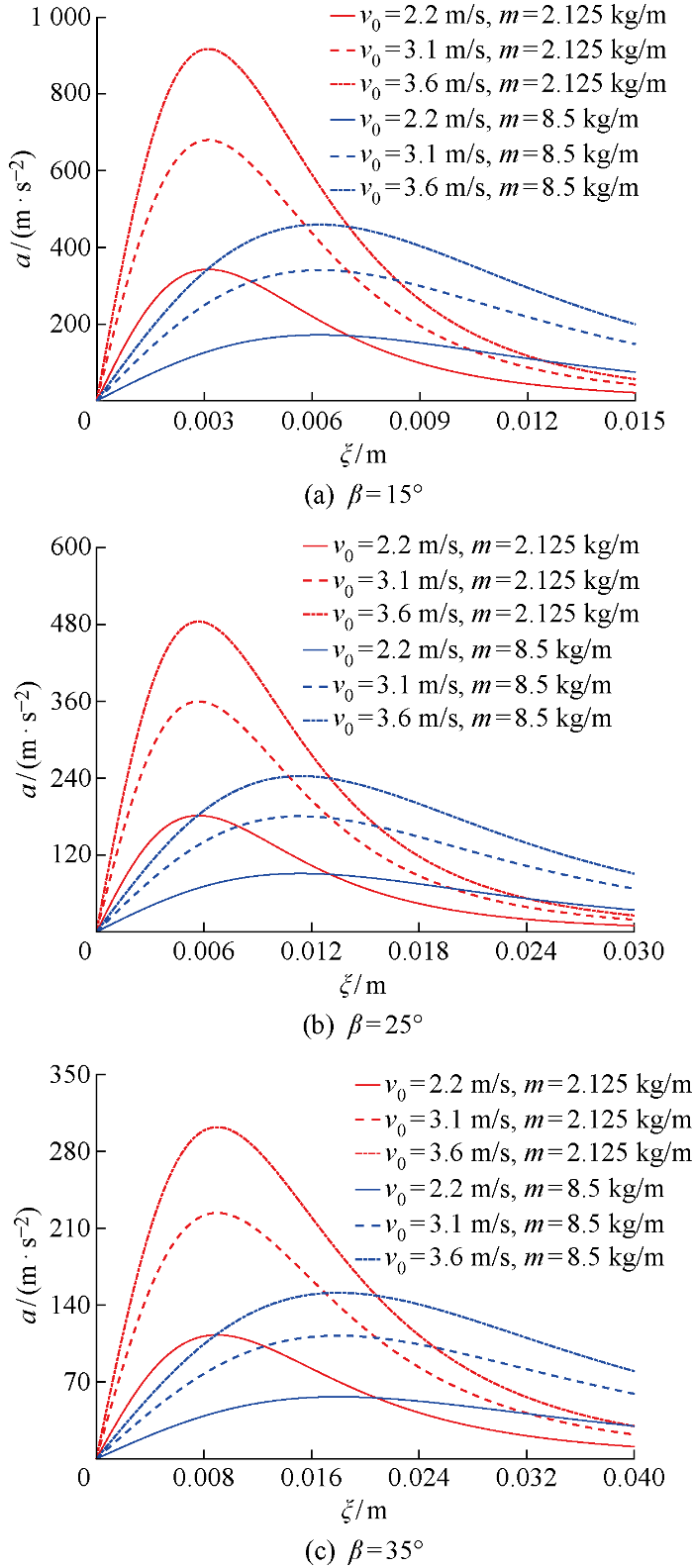
观察式(20)可以发现,在不考虑物体重力的情况下,对于指定底升角的楔形体,其在砰击入水过程中最大加速度或砰击力峰值发生的浸没深度由质量决定,而不受初始入水速度的影响(假设楔形体在此浸没深度之前不会发生流动分离).

选取半宽为0.11 m,底升角分别为β= 15°,25°,35° 的二维楔形体模型作为研究对象,使用MLM计算了其从不同的高度处在自由落体状态下的砰击过程,并预报了物体加速度随浸没深度的变化.在计算过程中,物体自身的重力忽略不计.不同下落高度所对应的物体初始入水速度分别为v₀= 2.2,3.1,3.6 m/s.同时,针对不同底升角的楔形体模型,选取了两个不同的单位长度质量进行研究,分别为2.125和8.5 kg/m.

计算所得到的结果如图6所示,其展示的结果与式(20)一致,即虽然物体在砰击过程中最大加速度或砰击力峰值的数值会随初始入水速度改变,但是其所对应的浸没深度却与初始入水速度无关.此外,在砰击入水过程中,物体的加速度或受到的砰击力会随着底升角的减小或者自身质量的增大而减小.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 自由落体状态下楔形体的加速度变化

Fig.6 Acceleration of wedges under free fall condition

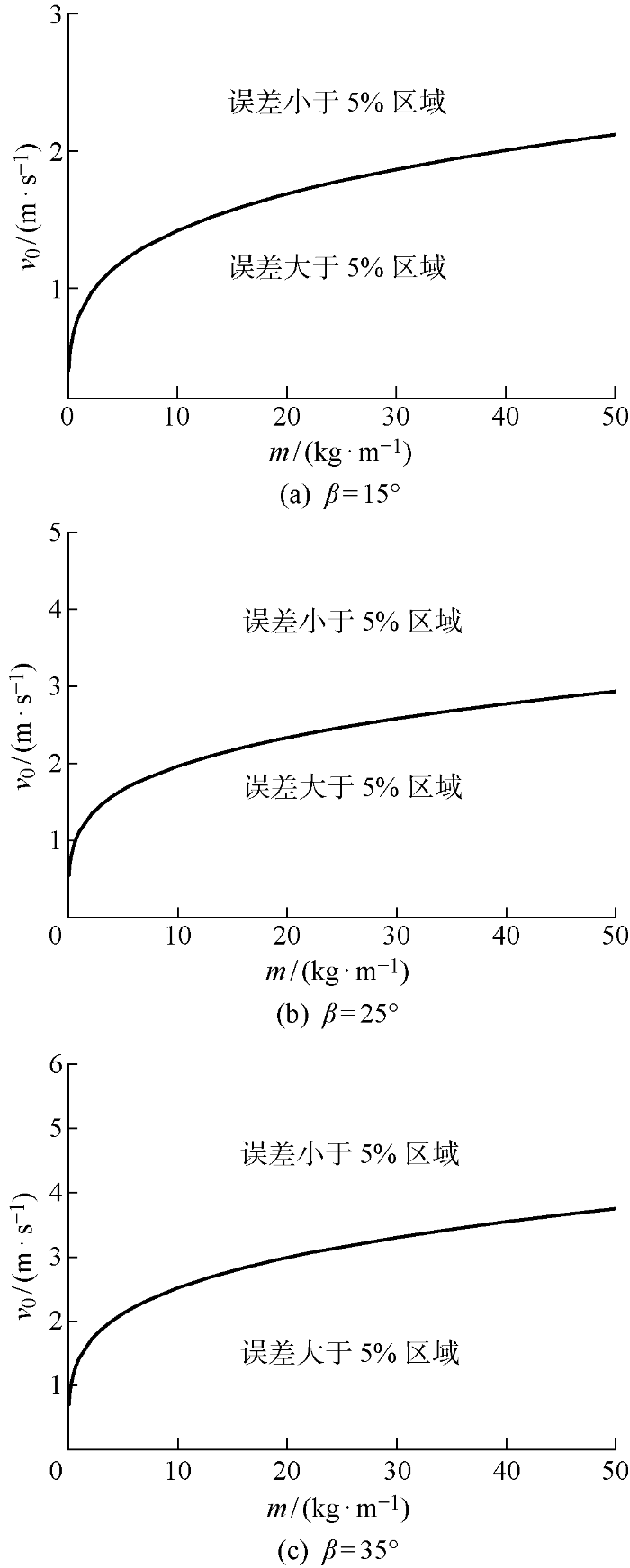
不过随着物体质量的增加或者初始入水速度的减小,物体自身的重力相较于所受到的砰击水动力不再是小量.此时,忽略物体重力会导致计算结果存在误差.若以5%作为误差的阈值来判断预报计算结果的准确性,则针对每一个不同底升角的楔形体模型,依据其质量和初始入水速度绘制能够忽略物体自身质量的临界曲线.在此,物体单位长度质量的研究范围选取为0.05~50 kg/m,各楔形体模型的临界曲线如图7所示.从展示的结果来看,随着物体质量或者底升角的增大,满足误差要求的临界初始入水速度也随之增大.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 各楔形体模型的临界曲线

Fig.7 Critical curves for each wedge model

不过,对于任意复杂形状的物体,不同于上述研究的楔形体模型,很难再从式(15)得到类似式(19)这样的简单表达式,因为式(17)和式(18)不再是必要的.然而,通过对式(16)进行多次分部积分,可以得到:

(21)$\begin{array}{r}\ln \frac{\dot{\xi}}{v_{0}}=A_{0}(\xi) \ln \left(\rho A_{a}+m\right)-A_{0}(0) \ln m+ \\\quad{ }_{i=1}^{N}(-1)^{i} A_{i} \xi+(-1)^{N+1} A_{N}^{\prime} \dot{\xi} \xi \mathrm{d} t\end{array}$

式中:A₀=-A_v/A'_a,A₁=A'₀ln(A_a+m), A_i=A'_i_-1ξ, i=1,2,…,N, 上标'表示关于浸没深度ξ的导数.可以合理地认为,对于指定形状的物体,A_i对ξ的导数,即A'_i,在足够多次的求导之后应该趋于0.因此,式(21)的右侧可以被认为是一个仅与物体质量、形状和浸没深度相关的函数.于是,用F_f(ξ,m)表示.将F_f(ξ,m)代入式(21)的右侧,并将 $\overset{\cdot}{ξ}$ 代回式(14)或式(15),则物体的加速度 $\ddot{ξ}$ 可表示为

(22)

\ddot{ξ}

\frac{ρ V_{0}^{2} A_{v}}{ρ A_{a} + m} e^{2 F_{f} (ξ, m)}

观察式(22)可以发现,上述对于楔形体的结论对于任意复杂形状的物体仍然适用,即在忽略物体重力的情况下,最大加速度或砰击力峰值对应的浸没深度仅与物体的质量和形状相关.

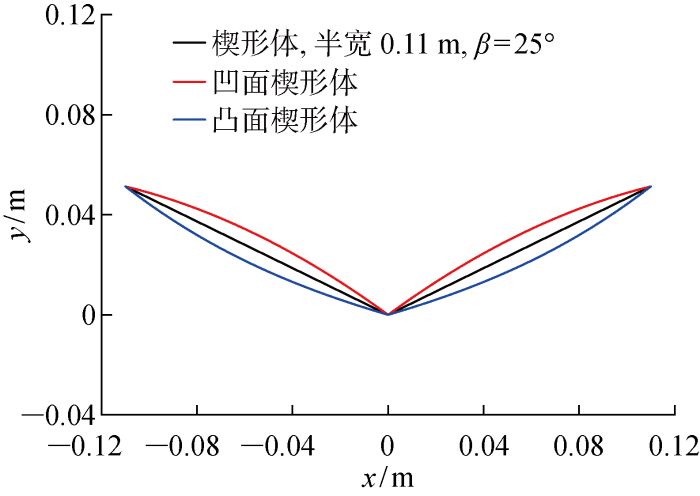
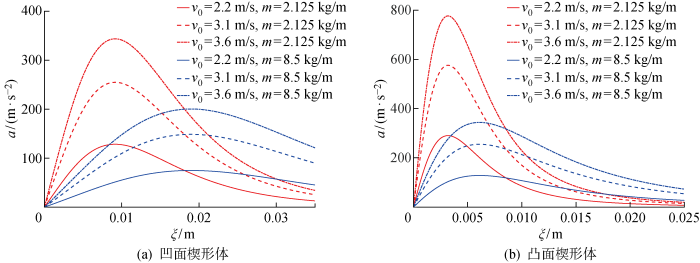
选择半宽均为0.11 m的两个不同形状的曲线楔形体作为验证此结论的模型,其中一个为凸面形状,另一个为凹面形状,模型的具体构型如图8所示.与上述方法类似,在整个砰击入水的过程中,物体同样处于自由落体状态,物体的单位长度质量分别取2.125和8.5 kg/m,物体初始入水速度分别为v₀= 2.2,3.1,3.6 m/s,选择MLM进行预报物体加速度随浸没深度的变化,同时不考虑物体自身的重力.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 曲线型楔形体形状示意图

Fig.8 Sketch of curved wedges

计算所得到的结果如图9所示,所得到的结论与前文对于楔形体模型的分析一致,即虽然最大加速度或砰击力峰值的数值取决于物体的初始入水速度,但是其发生的浸没深度却与初始入水速度无关.此外,对比图8中3类不同形状楔形体所得的结果可以发现,剖面的肥瘦程度在很大程度上会影响物体加速度(或砰击力)和加速度峰值(或砰击力峰值)所对应的浸没深度.剖面越“肥胖”,物体加速度或砰击力越大,加速度峰值或砰击力峰值越早来临.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 自由落体状态下曲线型楔形体的加速度变化

Fig.9 Acceleration of curved wedges under free fall condition

对于此类曲线形状的物体,不同于楔形体模型,增大物体质量或者减小初始入水速度并非会使得计算结果的误差单调增加,因此绘制出能够忽略物体自身质量的临界曲线十分困难.于是,在此仅给出“物体的初始入水速度需要大于1 m/s”作为能忽略物体自身质量的近似前提条件.

4 结论

采用基于势流理论的砰击解析理论模型,研究了自由落体条件下任意二维对称剖面在砰击过程中的动力学特性.使用了几种典型的解析理论模型,从经典Wagner模型到更复杂的MLM和GWM等.

为了求解物体在自由落体状态下的运动状态,将精细积分法与解析模型相结合,并在时域上进行积分.若二维剖面的形状为复杂的曲线形状,那么该物体的表面则通过在物面上生成均匀离散的点并在点与点之间进行线性插值进行处理.

之后,选取两种不同的二维模型,即楔形体和船体剖面,将按照上述方法得到的结果与现有文献中的试验和其他数值模拟结果进行了对比.对比结果表明,考虑非线性因素和湿表面形状的解析理论模型通常能够得到更为精确的结果,尤其是MLM.不过解析理论模型固有的局限性使其无法分析流体在发生流动分离之后的动态变化,但这些模型仍然可以正确地预报流动分离发生前物体所受的砰击力峰值.

此外,对于在砰击过程中可以忽略物体重力的情况,即对于轻质物体而言,砰击力占其所受水动力载荷的主要成分,如果保证物体在自由落体入水过程中产生的最大加速度或砰击力峰值发生在流体发生流动分离之前,那么物体在最大加速度或砰击力峰值发生时的浸没深度仅仅由物体的形状和质量有关,而与其初始的入水速度无关.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

LAVROFF

, DAVIS

M R

, HOLLOWAY

D S

et al.

Wave impact loads on wave-piercing catamarans

[J]. Ocean Engineering, 2017, 131: 263-271.

DOI:10.1016/j.oceaneng.2016.11.015 URL [本文引用: 1]

[2]

VON

KARMAN T

The impact on seaplane floats during landing

[R]. Washington, USA: National Advisory Committee for Aeronautics, 1929.

[本文引用: 1]

[3]

WAGNER

Uber stoss-und gleitvorgange an der oberflache von flussigkeiten

[J]. Zeitschrift für Angewandte Mathematik und Mechanik, 1932, 12(4): 193-215.

DOI:10.1002/zamm.v12:4 URL [本文引用: 2]

[4]

DOBROVOL’SKAYA

Z N

On some problems of similarity flow of fluid with a free surface

[J]. Journal of Fluid Mechanics, 1969, 36(4): 805-829.

DOI:10.1017/S0022112069001996 URL [本文引用: 1]

The paper presents the method of solving a class of two-dimensional problems of the similarity flow of an incompressible fluid with a free surface. The fluid is assumed to be non-viscous and weightless. We consider two-dimensional irrotational similarity flows with dimensionless hydrodynamic characteristics depending only on the ratiosx/v0t, y/v0t, wherex, yare Cartesian co-ordinates,tis time andv0is a constant of the velocity dimension.

[5]

ZHAO

, FALTINSEN

, AARSNES

Water entry of arbitrary two-dimensional sections with and without separation

[C]// 21st Symposium on Naval Hydrodynamics. Washington, USA: The National Academies Press, 1996: 408-423.

[本文引用: 1]

[6]

COINTE

, ARMAND

J L

Hydrodynamic impact analysis of a cylinder

[J]. Journal of Offshore Mechanics Arctic Engineering, 1987, 107: 237-243.

[本文引用: 1]

[7]

HOWISON

S D

, OCKENDON

J R

, WILSON

S K

Incompressible water-entry problems at small deadrise angles

[J]. Journal of Fluid Mechanics, 1991, 222: 215-230.

DOI:10.1017/S0022112091001076 URL [本文引用: 1]

[8]

OLIVER

M J

Water entry and related problems[D]. Oxford, UK: University of Oxford, 2002.

[本文引用: 1]

[9]

段文洋, 朱鑫, 倪阳,

等.

考虑流动分离的有限宽楔形剖面匀速入水受力分析

[J]. 船舶力学, 2013, 17(8): 911-919.

[本文引用: 1]

DUAN

Wenyang

, ZHU

Xin

, NI

Yang

et al.

Constant velocity water entry of finite wedge section with flow separation

[J]. Journal of Ship Mechanics, 2013, 17(8): 911-919.

[本文引用: 1]

[10]

TASSIN

, PIRO

D J

, KOROBKIN

A A

et al.

Two-dimensional water entry and exit of a body whose shape varies in time

[J]. Journal of Fluids and Structures, 2013, 40: 317-336.

DOI:10.1016/j.jfluidstructs.2013.05.002 URL [本文引用: 1]

[11]

KOROBKIN

A A

Water impact problems in ship hydrodynamics

[M]. Southampton, UK: Computational Mechanics Publications, 1996.

[本文引用: 2]

[12]

KOROBKIN

A A

Formulation of penetration problem as a variational inequality

[J]. Dinamika Sploshnoi Sredy, 1982, 58: 73-79.

[本文引用: 1]

[13]

KOROBKIN

A A

, PUKHNACHOV

V V

Initial stage of water impact

[J]. Annual Review of Fluid Mechanics, 1988, 20(1): 159-185.

DOI:10.1146/fluid.1988.20.issue-1 URL [本文引用: 1]

[14]

PANCIROLI

, PORFIRI

Evaluation of the pressure field on a rigid body entering a quiescent fluid through particle image velocimetry

[J]. Experiments in Fluids, 2013, 54: 1360.

[本文引用: 3]

[15]

PANCIROLI

, PORFIRI

Analysis of hydroelastic slamming through particle image velocimetry

[J]. Journal of Sound and Vibration, 2015, 347: 63-78.

DOI:10.1016/j.jsv.2015.02.007 URL [本文引用: 1]

[16]

BARJASTEH

, ZERAATGAR

, JAVAHERIAN

M J

An experimental study on water entry of asymmetric wedges

[J]. Applied Ocean Research, 2016, 58: 292-304.

DOI:10.1016/j.apor.2016.04.013 URL [本文引用: 1]

[17]

SHAMS

, JALALISENDI

, PORFIRI

Experiments on the water entry of asymmetric wedges using particle image velocimetry

[J]. Physics of Fluids, 2015, 27(2): 027103.

DOI:10.1063/1.4907745 URL [本文引用: 1]

In this work, we experimentally characterize the water entry of an asymmetric wedge into a quiescent fluid through particle image velocimetry (PIV). The wedge enters the water surface with an orthogonal velocity falling from a fixed height. We systematically vary the heel angle to elucidate the effect of asymmetric impact on the flow physics and on the fluid-structure interaction. The pressure field in the fluid is reconstructed from PIV data by integrating the Poisson equation. We find that the impact configuration significantly influences both the velocity and the pressure field, ultimately, regulating the hydrodynamic loading on the wedge. Specifically, as the heel angle increases, the location of maximum velocity of the flow moves from the pile-up region to the keel. At the same time, the pressure field significantly decreases in the vicinity of the keel, reaching values smaller than the atmospheric pressure. The spatiotemporal evolution of the hydrodynamic loading is thus controlled by the heel angle, with larger heel angles resulting into more rapid and sustained impacts.

[18]

RUSSO

, JALALISENDI

, FALCUCCI

et al.

Experimental characterization of oblique and asymmetric water entry

[J]. Experimental Thermal and Fluid Science, 2018, 92: 141-161.

DOI:10.1016/j.expthermflusci.2017.10.028 URL [本文引用: 1]

[19]

AARSNES

J V

Drop test with ship sections-effect of roll angle

[R]. Trondheim, Norway: Norwegian Marine Technology Research Institute, 1996.

[本文引用: 3]

[20]

SUN

A boundary element method applied to strongly nonlinear wave-body interaction problems[D]. Trondheim, Norway: Norwegian University of Science and Technology, 2007.

[本文引用: 4]

[21]

ZHU

X Y

Application of the CIP method to strongly nonlinear wave-body interaction problems[D]. Trondheim, Norway: Norwegian University of Science and Technology, 2006.

[本文引用: 1]

[22]

BAO

C M

, WU

G X

, XU

Water entry of a finite width wedge near a floating body

[J]. Applied Ocean Research, 2019, 84: 12-31.

DOI:10.1016/j.apor.2019.01.002 [本文引用: 1]

The problem of a two-dimensional finite-width wedge entering water near a freely floating body is considered through the velocity potential theory for the incompressible liquid with the fully nonlinear boundary conditions on the free surface. The problem is solved by using the boundary element method in the time domain. The numerical process is divided into two phases based on whether the interaction between the wedge and floating body is significant. In the first phase, when the single wedge enters water at initial stage, only a small part near its tip is in the fluid, the problem is studied in a stretched coordinate system and the presence of the floating body has no major effect. In the second phase, the disturbance by water entry of the wedge has reached the floating body, and both are considered together in the physical system. The auxiliary function method is adopted to decouple the nonlinear mutual dependence between the motions of the wedge and floating body, both in three degrees of freedom, and the fluid flow, as well as the interaction effects between them. Case studies are undertaken for a wedge entering water in forced or free fall motion, vertically or obliquely. Results are provided for the accelerations, velocities, pressure distribution and free surface deformation, and the interaction effects are discussed.

[23]

G X

, SUN

, HE

Y S

Numerical simulation and experimental study of water entry of a wedge in free fall motion

[J]. Journal of Fluids and Structures, 2004, 19(3): 277-289.

DOI:10.1016/j.jfluidstructs.2004.01.001 URL [本文引用: 1]

[24]

G D

, DUAN

W Y

, WU

G X

Simulation of water entry of a wedge through free fall in three degrees of freedom

[J]. Proceedings of the Royal Society A, 2010, 466: 2219-2239.

[本文引用: 1]

[25]

KOROBKIN

A A

Analytical models of water impact

[J]. European Journal of Applied Mathematics, 2004, 15(6): 821-838.

DOI:10.1017/S0956792504005765 URL [本文引用: 8]

[26]

TASSIN

, JACQUES

, EL

MALKI

et al.

Assessment and comparison of several analytical models of water impact

[J]. The International Journal of Multiphysics, 2010, 4(2): 125-140.

DOI:10.1260/1750-9548.4.2.125 URL [本文引用: 2]

[27]

KOROBKIN

A A

, KHABAKHPASHEVA

, MALENICA

et al.

A comparison study of water impact and water exit models

[J]. International Journal of Naval Architecture and Ocean Engineering, 2014, 6(4): 1182-1196.

DOI:10.2478/IJNAOE-2013-0238 URL [本文引用: 2]

[28]

LOGVINOVICH

G V

Hydrodynamics of flows with free boundaries

[R]. Washington, USA: U. S. Department of Commerce, 1972.

[本文引用: 1]

[29]

ZHONG

W X

On precise integration method

[J]. Journal of Computational and Applied Mathematics, 2004, 163(1): 59-78.

DOI:10.1016/j.cam.2003.08.053 URL [本文引用: 1]

[30]

吕和祥, 于洪洁, 裘春航.

精细积分的非线性动力学积分方程及其解法

[J]. 固体力学学报, 2001, 22(3): 303-308.

[本文引用: 1]

Hexiang

, YU

Hongjie

, QIU

Chunhang

An integral equation of non-linear dynamics and its solution method

[J]. Acta Mechanica Solida Sinica, 2001, 22(3): 303-308.

[本文引用: 1]

[31]

KOROBKIN

A A

The entry of an elliptical paraboloid into a liquid at variable velocity

[J]. Journal of Applied Mathematics and Mechanics, 2002, 66(1): 39-48.

DOI:10.1016/S0021-8928(02)00006-0 URL [本文引用: 2]

[32]

SCOLAN

Y M

, KOROBKIN

A A

Energy distribution from vertical impact of a three-dimensional solid body onto the flat free surface of an ideal fluid

[J]. Journal of Fluids and Structures, 2003, 17(2): 275-286.

DOI:10.1016/S0889-9746(02)00118-4 URL [本文引用: 1]

[33]

KOROBKIN

A A

, MALENICA

Modified Logvinovich model for hydrodynamic loads on asymmetric contours entering water

[C]//Grue J. 20th International Workshop on Water Waves and Floating Bodies. Longyearbyen, Norway: University of Oslo, 2005: 50-54.

[本文引用: 1]

Wave impact loads on wave-piercing catamarans

2017

... 在现如今的船舶与海洋工程领域,对于多体船或者剖面曲率很大的船舶,较大的航行速度会使船体受到很大的砰击力,这会导致十分严重的结构损伤甚至发生海上事故^[1].因此,砰击现象的研究对于船舶和海洋结构物的性能以及强度具有重要的意义. ...

The impact on seaplane floats during landing

1929

... 砰击入水的开创性工作可以追溯到von Karman^[2]和Wagner^[3]对于楔形体入水过程的研究.基于经典Wagner模型,众多学者对其进行了不同程度的发展和完善.Dobrovol’skaya^[4]研究了具有自由液面流体的相似流动,并提出了入水砰击问题的数学积分表达式.在Zhao等^[5]的模型中,自由液面是线性的而物体边界和伯努利方程保持非线性.Cointe等^[6]、Howison等^[7]和Oliver^[8]通过匹配渐近展开法将整个流场分成3部分并进行了深入的研究.段文洋等^[9]提出了通过辅助线来构建在流动分离发生后的虚拟物体表面,以便快速地预报砰击力.除了对于楔形体的一系列研究,Tassin等^[10]对抛物线物体的入水模型开展研究,而Korobkin^[11-12]则研究了具有任意形状物体的入水过程. ...

Uber stoss-und gleitvorgange an der oberflache von flussigkeiten

1932

... 流体动力学采用基于平板撞击假设的Wagner理论^[3]进行求解,计算区域由物体湿表面在y轴上的投影和未受扰动的自由液面构成.流体的速度势函数φ^W可通过如下控制方程和边界条件求解: ...

On some problems of similarity flow of fluid with a free surface

1969

Water entry of arbitrary two-dimensional sections with and without separation

1996

Hydrodynamic impact analysis of a cylinder

1987

Incompressible water-entry problems at small deadrise angles

1991

2002

考虑流动分离的有限宽楔形剖面匀速入水受力分析

2013

考虑流动分离的有限宽楔形剖面匀速入水受力分析

2013

Two-dimensional water entry and exit of a body whose shape varies in time

2013

Water impact problems in ship hydrodynamics

1996

... 物体关于z轴对称,因此其湿表面在y轴上的投影长度是2c(t),其中c(t)可以由Wagner条件^[11,25]计算得到: ...

Formulation of penetration problem as a variational inequality

1982

Initial stage of water impact

1988

... 试验方法是研究砰击过程的特征以及验证解析理论模型的重要手段^[13],其中楔形体是被研究最多的模型.典型的研究工作包括Panciroli等^[14-15]对刚性和弹性对称楔形体的砰击过程进行试验和计算.近年来,众多学者对楔形体的倾斜砰击入水以及非对称楔形体的砰击入水进行了试验^[16⇓-18].对于更复杂的船体结构,比如船艏部分,Aarsnes^[19]所进行的自由落体试验是其后数值方法验证^[20-21]中引用最多的研究成果之一. ...

Evaluation of the pressure field on a rigid body entering a quiescent fluid through particle image velocimetry

2013

... 接着,将1.2节所述的各类解析理论模型与精细积分法相结合,研究楔形体在砰击过程中的运动状态.具体而言,将上文所述形状的楔形体置于3个不同的高度处,使其进行自由落体运动.在此,定义物体初始入水速度为v₀,则这3个不同初始高度对应的物体初始入水速度分别为v₀= 2.2,3.1,3.6 m/s.在本文中,所研究的物体均为二维物体,因此取楔形体的单位长度质量为2.125 kg/m.预报楔形体在砰击过程中加速度随时间的变化,并将所得结果与文献[14]中的实验结果进行对比,对比结果如图3所示. ...

... 观察图3可以发现,OWM给出了与其他4种模型相比过高的预测值,这与文献[14,25]中所指出的现象相一致.而其他考虑了非线性因素或物体表面影响的模型得到了更加准确的预报结果,尤其是MLM和GWM.当v₀= 2.2,3.1 m/s时,MLM预测的加速度峰值与实验结果基本一致,而当v₀= 3.6 m/s时,非线性模型预测的加速度峰值较试验结果高出10%~20%. ...

Analysis of hydroelastic slamming through particle image velocimetry

2015

An experimental study on water entry of asymmetric wedges

2016

Experiments on the water entry of asymmetric wedges using particle image velocimetry

2015

Experimental characterization of oblique and asymmetric water entry

2018

Drop test with ship sections-effect of roll angle

1996

... 为了检验该方法是否适用于形状更加复杂的二维剖面,选取如图4所示的船体剖面模型进行验证.同样地,选取3个不同的高度使其进行自由落体运动,对应的入水速度分别为v₀= 0.61,1.48,2.43 m/s.船体剖面的单位长度质量为261 kg/m.将不同解析理论模型得到的垂向砰击力F随时间变化的预报结果与Aarsnes^[19]的试验结果以及Sun^[20]的BEM数值模拟结果进行对比,对比结果如图5所示. ...

... 观察图5可以发现,虽然在入水初期,解析理论模型与试验以及BEM得到的结果吻合良好,但如果湿表面到达船体剖面上部的末端, 即当c等于剖面半宽之后,解析理论模型便不再能够预报流体和船体剖面的运动变化.然而,砰击理论指出,砰击力会在流体发生流动分离之后立刻达到峰值,这意味着解析理论模型能够相对可靠地预报砰击过程中物体所受的砰击力峰值的大小.对于不同模型的计算结果,OWM依然明显地过度预测了垂向砰击力,而其他模型的结果更接近Aarsnes^[19]的试验结果和Sun^[20]的BEM结果.总体来说,如同上文根据楔形体模型得到的推论一致,对于所有的工况,MLM提供了最准确的预测. ...

2007

... 如今,数值模拟方法以数据可靠、计算速度快等特点成为砰击基础理论研究和实际应用中最常用的工具.边界元法(BEM)是最早应用于砰击模拟的数值方法之一,比如Sun^[20]、Bao等^[22]和Wu等^[23]的研究工作.尽管在数值模拟中可以考虑自由液面的非线性效应和流体的黏度,但计算成本过高使其并不适用于海洋结构物设计的初期. ...

2006

Water entry of a finite width wedge near a floating body

2019

Numerical simulation and experimental study of water entry of a wedge in free fall motion

2004

Simulation of water entry of a wedge through free fall in three degrees of freedom

2010

... 本文使用的解析理论模型均基于势流理论,即流体被视为不可压缩且无黏流体.由于砰击是一个在极短时间内发生的高速动态过程,所以可以合理忽略流体的重力对于物体砰击过程的影响^[24-25].同时,流体的表面张力也被忽略. ...

Analytical models of water impact

2004

... 物体关于z轴对称,因此其湿表面在y轴上的投影长度是2c(t),其中c(t)可以由Wagner条件^[11,25]计算得到: ...

... (3) Logvinovich模型(OLM)^[25,28]. ...

... (4) 改进的Logvinovich模型(MLM)^[25]. ...

... 在MLM中,Korobkin^[25]提出通过考虑物体的形状来进一步提高OLM的计算精度,即抛开之前的平板碰撞假设,使压力的计算在真实的物体湿表面上进行.与OLM的处理方法类似,速度势函数φ也表示为φ^W(y,0,t)在z=0处的泰勒展开式,并将式(2)中的第3个方程作为边界条件.于是,速度势函数φ可以改写为 ...

... (5) 广义Wagner模型(GWM)^[25]. ...

... 在物体砰击过程中,作用在物体上的砰击力是通过沿物体湿表面对其所受的压力进行积分获得的.不过,压力表达式中的速度相关项包含了一个奇异项,1/(c²-y²), 这使得在y=c附近压力变为负值且不可积分^[27].根据Korobkin^[25]的建议,这一速度相关项的砰击压力应在区域-c^*≤y≤c^*进行积分,其中c^*是距y=c处最近且满足p_v(c^*,t)=0的点. ...

Assessment and comparison of several analytical models of water impact

2010

... (1) 经典Wagner模型(OWM)^[26-27]. ...

... (2) 基于非线性伯努利方程的Wagner模型(WN)^[26]. ...

A comparison study of water impact and water exit models

2014

... (1) 经典Wagner模型(OWM)^[26-27]. ...

Hydrodynamics of flows with free boundaries

1972

... (3) Logvinovich模型(OLM)^[25,28]. ...

On precise integration method

2004

... 在计算获得物体所受的砰击力F_v和F_a之后,物体的动力学控制方程,即式(5),可以通过精细积分法^[29]进行求解.在精细积分法中,动力学控制方程可重新表示为 ...

精细积分的非线性动力学积分方程及其解法

2001

... 如式(10)所示,为了得到第k+1个时间步中的变量v_k₊₁,还需要确定f的值,而这可以通过“预估-校正”的方法获得.方法的具体细节详见文献[30]. ...

精细积分的非线性动力学积分方程及其解法

2001

... 如式(10)所示,为了得到第k+1个时间步中的变量v_k₊₁,还需要确定f的值,而这可以通过“预估-校正”的方法获得.方法的具体细节详见文献[30]. ...

The entry of an elliptical paraboloid into a liquid at variable velocity

2002

... 解析理论模型的优点之一是易于研究砰击过程中主要的影响因素和物理机理.Korobkin^[31]通过解析方法研究了椭圆抛物线物体在自由落体状态下的砰击载荷和运动状态变化,Scolan等^[32]通过研究发现,无论是在二维模型还是三维模型,当物体的入水速度恒定,流体能量在砰击过程中会均匀地传递到抬升与飞溅的液体中.在本节中,研究物体在自由落体状态下所受砰击力的特性,即砰击力和物体浸没深度之间的关系. ...

... 而在MLM中,C_v和C_a的表达式非常复杂,具体形式可参照Korobkin等^[33]的研究成果,这里不再赘述.通过对式(16)的两侧在时域上进行积分,物体在砰击入水过程中的速度^[31]可表示为 ...

Energy distribution from vertical impact of a three-dimensional solid body onto the flat free surface of an ideal fluid

2003

Modified Logvinovich model for hydrodynamic loads on asymmetric contours entering water

2005

〈

〉