低雷诺数变截面细长柔性结构流固耦合能量交换特征分析

doi:10.16183/j.cnki.jsjtu.2022.133

低雷诺数变截面细长柔性结构流固耦合能量交换特征分析

邓秀兵^,¹, 于曰旻², 庞玺源³

1.浙江省水利水电勘测设计院有限责任公司,杭州 310000

2.海南大学土木建筑工程学院, 海口 570228

3.上海交通大学船舶海洋与建筑工程学院,上海 200240

Analysis of Fluid-Structure Coupling Energy Transfer Characteristics Slender Structure with Variable Cross-Section at Low Reynolds Number

DENG Xiubing^,¹, YU Yuemin², PANG Xiyuan³

1. Zhejiang Design Institute of Water Conservancy and Hydro-Electric Power Co., Ltd., Hangzhou 310000, China

2. School of Civil and Architectural Engineering, Hainan University, Haikou 570228, China

3. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

责任编辑: 王一凡

收稿日期: 2022-04-29 修回日期: 2022-07-4 接受日期: 2022-07-12

基金资助:

海南省自然科学基金(519MS026)

Received: 2022-04-29 Revised: 2022-07-4 Accepted: 2022-07-12

作者简介 About authors

邓秀兵(1981-),高级工程师,主要从事道桥设计研究,电话(Tel.):0571-87422943;E-mail:dengxiubing@foxmail.com.

摘要

波浪形变截面柱体结构具有良好的流动减阻特性,然而尚不清楚这种变截面柔性结构的流致振动特性.基于高精度谱单元法建立了细长柔性结构的流固耦合力学模型和高精度算法,对在低速均匀流作用和驻波初始动力激励下的流致振动机理进行了数值分析,阐明了波浪形细长柔性结构的尾流特性、结构动力响应特性、能量传递规律、涡脱频率的展向变化特征,也对减阻、减振机理进行了初步探讨.数值模拟结果表明,在合适截面扰动波高下波浪形变截面柔性结构能够大幅抑制涡激振动响应,并发现在波浪形细长结构两侧形成的特殊涡结构会稳定绕流剪切层,拉长涡旋形成区长度,从而降低尾流结构与结构的流固耦合效应,抑制涡激振动响应.

关键词： 波浪形截面; 流致振动; 细长柔性结构

Abstract

The wavy deformed cross-section cylindrical structure has excellent properties of drag reduction in fluid flow, but the flow-induced vibration characteristics of flexible structure with such variable cross-section are still unclear. In this paper, based on the high-performance spectral element method, a fluid-structure coupled mechanistic model and a numerical algorithm for slender structures are established. The wake characteristics, structural dynamic responses, energy transfers, and spanwise variations of vortex shedding frequencies are discussed. The numerical simulation results show that slender structure with the wavy-deformed cross-section can greatly suppress the vortex-induced vibration response at an appropriate cross-section disturbance wave height, and the special vortex structure formed on both sides of the wavy-shaped slender structure can stabilize the flow around the shear layer and elongate the vortex formation length, thereby reducing the fluid-structure coupling effect between the wake structure and the slender structure, and suppressing the vortex-induced vibration response.

Keywords： wavy cross-section; fluid-induced vibration; slender structure

PDF (18587KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

邓秀兵, 于曰旻, 庞玺源. 低雷诺数变截面细长柔性结构流固耦合能量交换特征分析[J]. 上海交通大学学报, 2023, 57(11): 1400-1409 doi:10.16183/j.cnki.jsjtu.2022.133

DENG Xiubing, YU Yuemin, PANG Xiyuan. Analysis of Fluid-Structure Coupling Energy Transfer Characteristics Slender Structure with Variable Cross-Section at Low Reynolds Number[J]. Journal of Shanghai Jiaotong University, 2023, 57(11): 1400-1409 doi:10.16183/j.cnki.jsjtu.2022.133

在土木工程领域,风、浪、流等环境动力荷载作用下的细长结构物受损甚至破坏屡见不鲜.比如,悬索桥中的主缆索作为典型的细长柔性结构,在来风作用下将产生涡激振动,甚至发生疲劳损坏;又如,在主缆索施工过程中,缆索截面形式发生非对称性变化,当风速超过临界值后,将产生空气动力负阻尼,使得缆索振动逐渐增强,甚至超负荷振幅而破坏.因此,科学评估和有效抑制细长结构的流致动力响应是风、浪、流敏感细长柔性结构设计必须考虑的内容.然而,当前细长柔性结构的流固耦合效应方面研究不足,尤其精准模拟和分析细长结构流致振动响应的力学模型和算法方面仍较缺乏,且亟待深入理解其流固耦合机理并建立系统的分析方法与手段^[1].

波浪形变截面圆柱体结构具有良好的流动减阻效果.近年来,国内外学者对该类型结构的绕流特性开展了较多研究,发现波浪形变截面能够延后剪切层的相互作用,从而有效减小阻力.Ahmed等^[2]采用实验方法研究了波浪形圆柱的边界层分离线和尾流结构,发现波浪形圆柱流动分离线呈现明显的三维特性,在分离节点附近形成流向涡,且发生边界层“上卷”现象,从而延迟或抑制剪切层中湍流的生成和发展.Lam等^[3]利用多种流动显示技术对波浪形圆柱的近尾迹进行了实验研究,给出了平均速度和波动速度分量沿流向、展向和横向的分布特征.实验结果表明,波浪形柱涡旋平均形成长度比大于光滑圆柱.湍流统计分析也表明,光滑圆柱尾迹中的涡街更为规则,而由于波浪形圆柱后面的涡具有较强的三维效应,使得由湍流掺混增强而尾迹表现出更强的非相干流动结构.

目前变截面结构绕流分析主要集中在静止或弹性支承的刚性波浪形结构的减阻和涡激振动特性方面.然而在实际土木工程中,缆索等细长结构的刚度系数通常较小,因此这种结构的柔性作用对流动减阻作用以及涡激振动响应的影响需要进一步研究,包括对初始动力激励的敏感性方面也需要深入分析.在文献[4 ⇓⇓-7]的基础上,针对这一问题,本研究采用基于高精度谱单元方法的流固耦合分析方法,建立了细长变截面柔性圆柱体结构的涡激振动力学模型,对其在低速均匀流作用和驻波初始动力激励下的流致振动机理进行了量化分析,获得了包括波浪形结构的尾流特性、结构动力响应特性、能量传递规律、涡脱频率展向变化特征,并对其在驻波扰动下的减阻、减振机理进行了深入探讨,对波浪形变截面细长结构的工程设计和应用提供参考.

1 数值算法

细长结构的流致振动是一种典型的流固耦合问题.求解流固耦合的基本方法通常有两大类,分别为界面匹配法和非界面匹配法,包括经典的任意拉格朗日-欧拉(ALE)方法和浸入边界法(IBM).本文采用另一种由Dimas等^[8]提出的随体坐标系(Body-fitted Coordinates)方法,该方法在惯性坐标系中求解N-S方程,再通过坐标转换至非惯性坐标系中,从而不需要动网格和浸泡边界近似.

N-S方程和连续性方程在惯性坐标系(x', y', z')内可描述为

(1)

\frac{\partial u'}{\partial t}

+(u'·Δ')u'=-

\frac{1}{ρ_{f}}

Δ'p'+

\frac{1}{R e}

Δ'²u'

(2)Δ'·u'=0

式中:u'=(u', v', w'),表示在惯性坐标系内3个方向的流速;t为时间;p'表示动压力;ρ_f表示流体的密度;Δ'表示惯性坐标系内的梯度算子;雷诺数 Re=U_∞D/ν,U_∞为均匀来流速度大小,D代表波浪形截面柱的平均直径,ν为流体黏性系数.

由惯性坐标系至非惯性坐标系的坐标转换采用如下关系式:

(2)x=x'-ζ_x(z, t), y=y'-ζ_y(z, t)

式中:ζ_x(z, t)和ζ_y(z, t)分别表示结构在顺流向和横流向的位移.相应地,速度项和压力项采用以下变换:

(4)

\begin{array}{l} u = u' - \frac{\partial ζ_{x}}{\partial t} - w' \frac{\partial ζ_{x}}{\partial z} \\ v = v' - \frac{\partial ζ_{y}}{\partial t} - w' \frac{\partial ζ_{y}}{\partial z} \\ w = w' \\ p = p' \end{array}\}

因此,将式(3)和(4)代入N-S方程式(1)和(2)可得:

(5)

\frac{\partial u}{\partial t}

+(u·Δ)u=-

\frac{1}{ρ_{f}}

Δp+

\frac{1}{R e}

Δ²u+A(u, p, ζ)

(6)Δ·u=0

式中:Δ为微分算子;附加项A(u, p, ζ)是由坐标转换引起的附加加速度项,该值在3个坐标方向的计算通过下式得到,

(7)

\begin{array}{l} A_{x} = - \frac{d^{2} ζ_{x}}{d t^{2}} + \frac{1}{R e} [\frac{\partial^{2}}{\partial z^{' 2}} (u + \frac{\partial ζ_{x}}{\partial z} w) - \\ \frac{\partial^{2} u}{\partial z^{2}} + \frac{\partial ζ_{x}}{\partial z} Δ_{x y}^{2} w + \frac{\partial^{3} ζ_{x}}{\partial t \partial z^{2}}] \\ A_{y} = - \frac{d^{2} ζ_{y}}{d t^{2}} + \frac{1}{R e} [\frac{\partial^{2}}{\partial z^{' 2}} (v + \frac{\partial ζ_{y}}{\partial z} w) - \\ \frac{\partial^{2} v}{\partial z^{2}} + \frac{\partial ζ_{y}}{\partial z} Δ_{x y}^{2} w + \frac{\partial^{3} ζ_{y}}{\partial t \partial z^{2}}] \\ A_{z} = \frac{1}{ρ_{f}} \frac{\partial ζ_{x}}{\partial z} \frac{\partial p}{\partial x} + \frac{1}{ρ_{f}} \frac{\partial ζ_{y}}{\partial z} \frac{\partial p}{\partial y} + \\ \frac{1}{R e} (\frac{\partial^{2} w}{\partial z^{' 2}} - \frac{\partial^{2} w}{\partial z^{2}}) \end{array}\}

在此定义:

(8)

\begin{array}{l} \frac{d}{d t} \equiv \frac{\partial}{\partial t} + u \frac{\partial}{\partial x} + v \frac{\partial}{\partial y} + w \frac{\partial}{\partial z} \\ \frac{\partial}{\partial z'} \equiv \frac{\partial}{\partial z} - \frac{\partial ζ_{x}}{\partial z} \frac{\partial}{\partial x} - \frac{\partial ζ_{y}}{\partial z} \frac{\partial}{\partial y} \\ Δ_{x y}^{2} \equiv \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} \end{array}\}

此外,本文采用线性张力梁模型描述细长柔性结构的动力学行为,该模型采用小变形假设,可写成:

(9)ρ_c

\frac{\partial^{2} ζ}{\partial t^{2}}

\frac{\partial ζ}{\partial t}

\frac{\partial^{2} ζ}{\partial z^{2}}

+F(z, t)

式中:ρ_c,k和T分别表示结构的单位长度的质量、阻尼比和张力.需要指出的是,张力T的大小将影响相速度c,c=(T/ρ_c)¹^/²;ζ(z, t)=(ζ_x, ζ_y)表示结构在顺流向和横流向的位移;F(z, t)是作用于结构上的流体力,通过对压力和黏性力项沿结构固壁表面积分获得,

(10)F(z, t)=∮[-pn+ν(Δu+Δu^T)·n]ds

n为指向结构外向的法线单位向量;s为结构表面微分.此外,假设结构的动力响应满足沿展向的周期性条件,则对流场和结构变量可采用傅里叶级数(Fourier Expansion)表示,即

(11)

[\begin{array}{l} u (x, y, z, t) \\ v (x, y, z, t) \\ w (x, y, z, t) \\ p (x, y, z, t) \end{array}]

\overset{M - 1}{\sum_{m = 0}} [\begin{array}{l} u_{m} (x, y, t) \\ v_{m} (x, y, t) \\ w_{m} (x, y, t) \\ p_{m} (x, y, t) \end{array}]

eⁱ^βmz

(12)

[\begin{array}{l} ζ_{x} (z, t) \\ ζ_{y} (z, t) \end{array}]

\overset{M - 1}{\sum_{m = 0}} [\begin{array}{l} ζ_{x, m} (t) \\ ζ_{y, m} (t) \end{array}]

eⁱ^βmz

式中:β=2π/L_z表示展向的波数,L_z为结构长度;M为展开式中傅里叶模态个数;m为各阶模态.将式(11)和(12)代入式(5)和(6)可获得解耦后的二维模态方程:

(13)$\begin{aligned}\frac{\boldsymbol{u}_{m}}{t}+ & {[(\boldsymbol{u} \cdot \boldsymbol{\nabla}) \boldsymbol{u}]_{m}=} \\& -\frac{1}{\rho_{\mathrm{f}}} \boldsymbol{\nabla} p_{m}+\frac{1}{R e}\left(\boldsymbol{\nabla}_{x y}^{2}-\beta^{2} m^{2}\right) \boldsymbol{u}_{m}+\boldsymbol{A}_{m}\end{aligned}$

(14)

\dot{Δ}

·u_m=0

式中: $\dot{Δ}$ ≡ $(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, i β m)$ .相应地,对应于每阶模态m,结构的解耦常微分方程表述为

(15)ρ_c

{\ddot{ζ}}_{m}

{\overset{\cdot}{ζ}}_{m}

+β²m²Tζ_m=F_m(t)

对结构运动的解耦方程式(15),采用二阶Newmark-β方法进行求解.对不定常流场模态方程式(13)和(14),采用Karniadakis等^[9]提出的高阶分步格式进行时间离散.具体地,对每一时间迭代步对速度和压力进行解耦计算.

第1步,考虑非线性项(u·Δ)u和A(u, p, ζ),通过J阶强稳定化算法获得中间速度场 ${\hat{u}}_{m}$ :

(16)

\frac{{\hat{u}}_{m} - \overset{J - 1}{\sum_{q = 0}} α_{q} u_{m}^{n - q}}{Δ t}

\overset{J - 1}{\sum_{q = 0}}

β_q[-(u·Δ)u+A

]_{m}^{n - q}

式中:α_q和β_q均为与强稳定化积分(Stiffly Stable Integration)有关的参数.

第2步,将考虑压力梯度的作用修正速度场,并施加连续性约束条件和纽曼边界条件:

(17)

\frac{{\hat{\hat{u}}}_{m} - {\hat{u}}_{m}}{Δ t}

\dot{Δ}

p_m

第3步,考虑黏性项更新下一步的速度场:

(18)

\frac{γ_{0} u_{m}^{n + 1} - {\hat{\hat{u}}}_{m}}{Δ t}

\frac{1}{R e}

(

Δ_{x y}^{2}

-β²m²)u_m

式中:γ₀为强稳定计算过程中向后差分系数(Backwards Differentiation Coefficient).

对上述时间离散后的模态方程,根据Karniadakis等^[9-10]将(x, y)平面的二维空间域离散为四边形有限元单元,并采用高斯-洛巴托-勒让德(GLL)高阶正交拉格朗日多项式作为形函数进行空间离散.

2 数值模型

2.1 物理模型

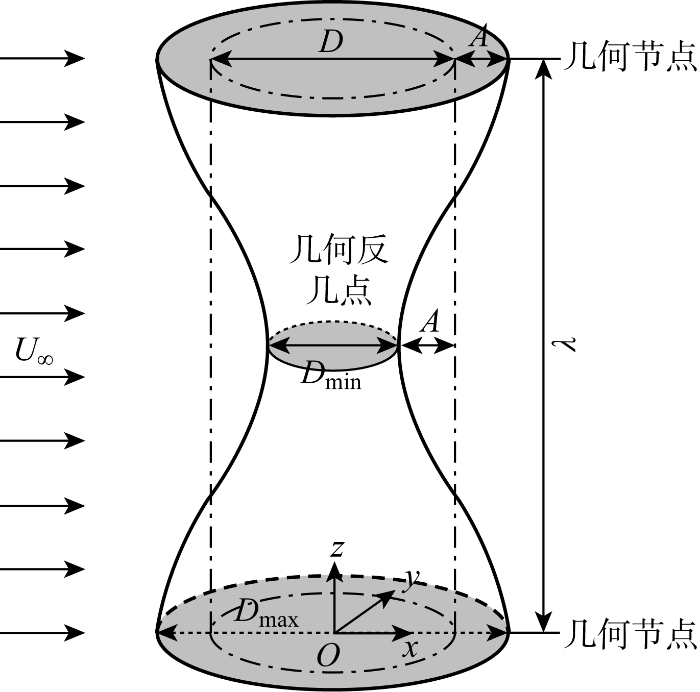
考虑在均匀来流作用下的波浪形变截面圆柱(见图1),其直径沿展向变化由下式确定:

(19)D_z=D+Acos

\frac{2 π z}{λ}

式中:D_z为展向相应位置的圆截面直径.由于波浪形柱直径在展向呈余弦变化,平均直径为D=(D_max+D_min)/2.基于平均直径和均匀来流速度的雷诺数取值为100,因此本文考虑的流动为层流流动.定义波浪形柱直径最大截面所在的展向位置为几何节点,波浪柱直径最小截面所在的对应位置为几何鞍点.A代表波状表面的波高,取值范围为0.1D~0.3D;展向波长设置为λ=4πD.A=0对应于光滑圆柱,也作为基准工况用于与波浪形柱工况进行对比分析.参照 Newman等^[11]的研究,可以通过规定圆柱的初始振幅和速度来确定其初始条件,本研究中初始扰动为驻波:ζ_y(z, t)=acos(ωt)cos(2πz/L_z),其中a为振幅,ω为振动频率,ω=2π/(cL_z).

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 均匀流下截面直径沿展向余弦变化的波浪柱几何示意图

Fig.1 Schematic view of uniform flow past wavy cylinder with the diameter varying along the spanwise direction

二维平面网格划分如图2所示.计算域几何形状为C形,由圆柱上游半径为20D的半圆弧和下游矩形组成,其流向长度为30D,在横流向长度设置为40D,圆柱放置在计算域横流向的中心位置.在(x, y)平面内采用了877个基础网格;由于对每一基础单元再用6阶正交多项式(P=6)对速度和压力场进行近似,所以每个基础网格再细分为5×5个高阶网格.此外,根据文献[11-12],沿展向采用64个傅里叶模态,满足本文雷诺数下的精度要求.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 二维网格拓扑结构

Fig.2 2D mesh topology

流体计算域的边界条件设置如下:入口边界为均匀来流条件,来流速度为(U_∞,0,0);在出口边界上采用纽曼边界条件,令出口边界上∂u/∂x=∂v/∂x=∂w/∂x=0以及p=0.在上、下部边界上指定(u, v, w)=(U_∞,0,0)的远场边界条件;在圆柱固壁采用无滑移和不可渗透边界条件,即流固耦合边界条件 $\frac{\partial ζ}{\partial t}$ =v.通过假设无限长波浪柱的展向周期性,在波浪柱的两端实施了只允许横向运动的自由边界条件^[11].

2.2 模型验证

为了验证力学模型和数值模拟方法的适用性,首先获得了均匀来流作用下细长光滑圆柱涡激振动模拟结果,并与已有文献结果进行对比分析.本模拟中质量比设置为m^*=6.0,而其他模拟参数均与Newman等^[11]相同.图3所示为光滑圆柱在驻波和行波初始激励下的横向振幅(ξ_y)、阻力系数(C_d)和升力系数(C_l)模拟结果,与Newman等^[11]结果吻合良好.尤其在驻波初始激励下本模拟结果与Newman等^[11]结果在展向节点(响应振幅最大的点)和反节点(响应振幅最小的点)位置坐标完全相同.在行波初始激励下的行波响应幅值和行波速度等均与Newman等^[11]结果一致,故说明本文力学模型和模拟方法的可靠性.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 柔性光滑圆柱涡激振动拟结果

Fig.3 Temporal and spatial evolution contour of transverse vibration and hydrodynamic coefficient of smooth cylinder

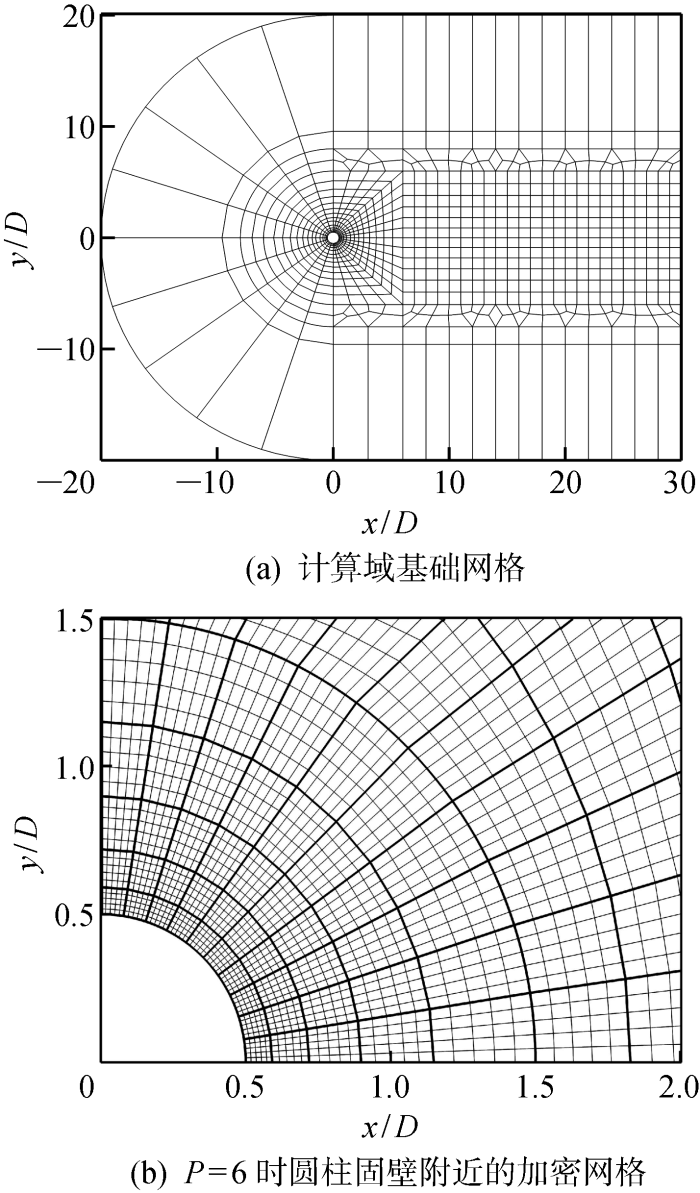
接着正交多项式阶数对计算结果的影响进行验证分析.通过变化多项式阶数P改变高阶网格的疏密;在展向上通过改变傅里叶模态个数,改变展向网格的疏密.由计算结果表明:P=6, M=64时模拟结果足够收敛至精确解.

3 结果与讨论

3.1 运动响应与水动力系数

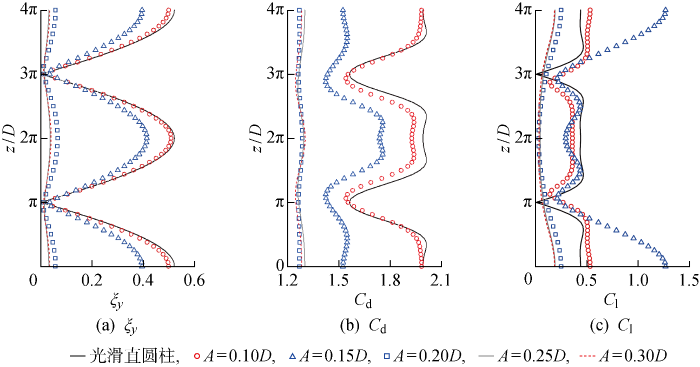
图4所示为ξ_y、C_d和C_l沿细长结构展向的均方根值模拟结果.阻力系数和升力系数分别定义为C_d=2F_d/(ρ_f $U_{\infty}^{2}$ D) 和C_l=2F_l/(ρ_f $U_{\infty}^{2}$ D),其中F_d和F_l分别代表结构受到的顺流和横流向流体力分量.随着扰动波高A的增加,结构的横向振幅逐渐减小,尤其是在A≥0.20D时,结构振动几乎完全被抑制,与无表面扰动或光滑表面结构相比减小了90%.另一方面,当A<0.20D时横向振幅沿展向分布特性与光滑表面结构类似,并且幅值基本相同.阻力系数均方根值,也随着扰动波高的增加而减小,并且在A≥0.20D时,阻力系数相比于光滑表面结构明显降低;而当A<0.20D时其分布特征类似,但在展向各位置处的阻力系数均有小幅减小.升力系数均方根计算结果显示,当A<0.20D时,升力系数相比于光滑表面结构有所升高,而A≥0.20D时,升力系数会显著下降.由此可知,变截面结构的表面扰动波高对振动幅值和水动力系数均有显著影响,并且在A≥0.20D时,结构响应得到有效抑制,且水动力特性得到明显改善.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 ξ_y、C_d和C_l沿展向的均方根值分布

Fig.4 Distribution of root mean square (RMS) value of ξ_y, C_d, and C_l

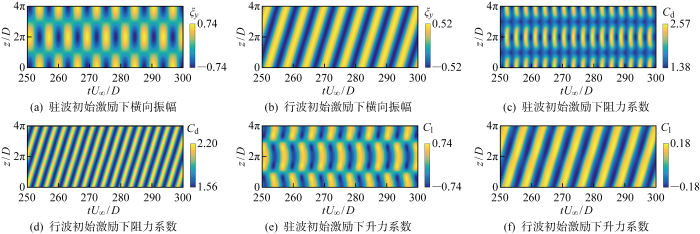
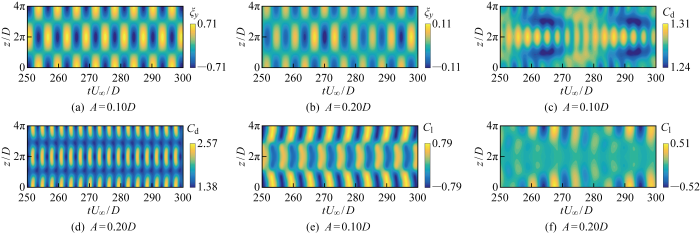
图5为在A=0.10D,0.20D时的结构横向振动响应时程模拟结果.由图可知,两种工况下节点和反节点的展向位置与光滑截面结构相同,即节点位于z/D=0, 2π, 4π,反节点位于z/D=π, 3π处,表明该工况下结构振动模式均与光滑表面结构相同.阻力系数在A=0.10D时其随时间演化特征与光滑表面结构基本相同,均在节点处取得最大值,在反节点处取最小值.然而A=0.20D工况下的阻力系数时空分布则与光滑表面结构完全不同,在阻力系数分布中看不到明显的驻波效应.在z/D=0, 4π时阻力系数并未取得最大值,且最大阻力系数仅有光滑表面结构的50%,表明A=0.20D扰动波高具有良好的减阻效果.进一步观察升力系数时程可知,A=0.10D工况下波形柱在展向π<z/D<3π范围内的升力系数较光滑表面结构有所下降,而在其他展向位置处升力系数有所升高,这与局部雷诺数的增大有关.而当A=0.20D时升力系数时空演化特征发生显著改变,不仅最大升力系数绝对值明显降低,且在两个节点中间的拓扑结构发生显著变化.根据波形柱在驻波初始激励下对横向振幅的抑制效果和对升、阻力特性的影响特征, 大致确定出控制失效范围(A<0.10D)以及控制有效范围(0.20D≤A<0.30D).

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 结构响应与水动力系数计算结果

Fig.5 Temporal and spatial evolution of vibration and hydrodynamic coefficients

3.2 尾流特性

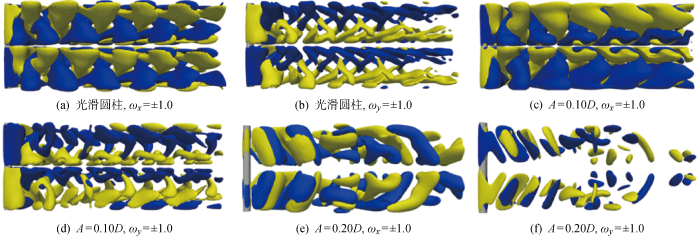
为了进一步了解扰动表面波高对结构振动响应的影响机理,需要对柔性波形柱和柔性光滑柱近尾迹三维涡结构进行对比分析.图6给出了不同扰动波高时展向涡量等值面(ω_z=±1.0)计算结果.其中,图6(a)~6(c)为柔性光滑柱展向涡量等值面透视图,图6(d)~6(f)为俯视图,与Newman等^[11]计算结果吻合良好.驻波初始激励下柔性光滑柱展向涡量中存在明显的交织结构.这种交织涡结构的展向特征是,在z/D=0, 2π截面处形成交错脱落的卡门涡街结构;而在z/D=π, 3π截面处上、下表面同时脱落的完全对称型涡结构.图6中分别给出A=0.10D时模拟结果,显然在z/D=π, 3π截面处的涡结构也呈现对称分布.值得注意的是,在此工况下几何节点处的展向涡量幅值较大从而升力系数幅值也随之增大,而几何鞍点处涡量幅值较小从而升力系数幅值也随之减小,这与图5所示结果一致.图6中分别给出A=0.20D时模拟结果,在该工况下交织涡结构完全消失,弯曲涡管以交错方式从波浪形表面上、下侧分别脱离,并且在尾流中迅速消失.更重要的是,与柔性光滑柱相比,此时波形柱表面剪切层的卷曲和相互作用明显较弱,使得涡形成区长度进一步增大.Lin 等^[13]用数值方法研究了亚临界雷诺数条件下具有相对较大展向波长的刚性波形柱周围的流动特征,也得到了类似的结果.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 展向涡量瞬时等值面(ω_z=±1.0)的透视图和横流向俯视图

Fig.6 Perspective and cross-flow view of the instantaneous isosurface of the spanwise vorticity (ω_z=±1.0)

图7所示为不同扰动波高条件下的涡量场顺流向(ω_x=±1.0)与横流向(ω_y=±1.0)分量瞬时等值面云图.从该图可清晰分辨出顺流向涡结构和横流向涡结构在尾迹附近的演化特征.显然,与柔性光滑柱和A=0.10D扰动波高工况相比,A=0.20D时结构附近涡结构完全不同且涡量强度相对较低,并且沿下游耗散较快.Lin等^[13]指出,附加流向涡在波形柱表面几何鞍点和节点处分别诱导出上涌流和下涌流,使得在几何鞍点处产生宽尾流,而在几何节点处产生窄尾流.这与本文模拟结果非常一致,表明波形结构的涡激振动抑制和减阻效应的力学机理有相同之处.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 3种工况下的顺流向(ω_x=±1.0)与横流向(ω_y=±1.0)瞬时等值面

Fig.7 Instantaneous isosurface of flow direction (ω_x=±1.0) and cross flow direction (ω_y=±1.0) under three working conditions

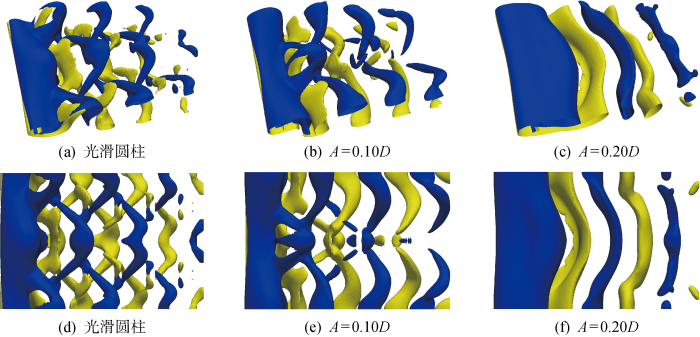
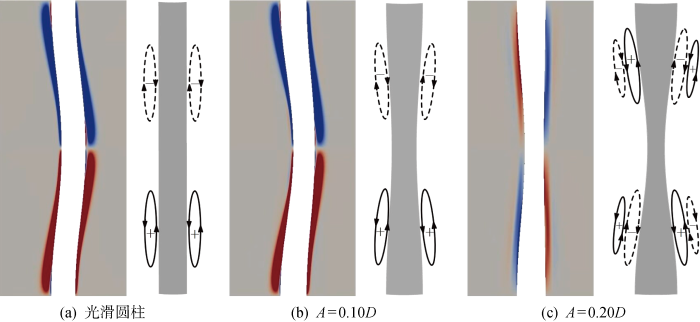
为了进一步研究流向涡对结构响应的影响,图8中给出了3种工况下(x, y)平面内流向涡量切片图;其中图7中分别为柔性光滑柱和在A=0.10D,0.20D时柔性波形柱的模拟结果.该结果表明,柔性光滑柱两侧和A=0.10D波形柱两侧均形成一对同向旋转涡结构,而沿结构展向上、下侧分布的两对涡旋转方向刚好相反.然而,在A=0.20D情况下,在同一展向位置处柔性波形柱两侧生成一对较强的反向旋转涡,在这对反向旋转涡的外侧还分布着一对与各自强涡旋转方向相反的弱涡.Lin 等^[13]指出,最优控制波形柱附加产生的反向流向涡对剪切层稳定性具有重要作用,能够防止剪切层与强涡结构的相互作用,使得涡旋形成长度增大.在A=0.20D的情况下观察到的反向旋转涡旋也稳定了剪切层,拉长了涡旋形成区长度,与本文之前观察到的现象一致.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 3种工况下(x, y)平面内圆柱周围的瞬时等值面和相应的流向涡量示意图

Fig.8 Schematic diagram of instantaneous isosurface and corresponding streamwise vorticity around a cylinder in the plane (x, y) under three working conditions

3.3 能量转换特征与频谱特性

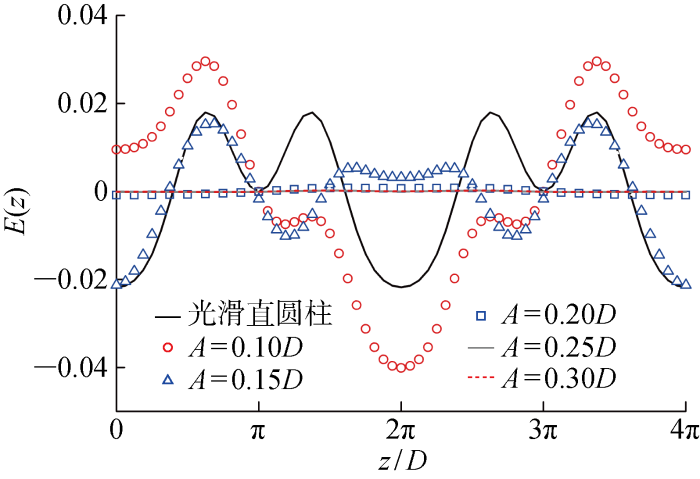
结构的运动响应与流体与结构之间的能量转化特征密切相关,根据 Newman 等^[11]的研究,一个旋涡脱落周期的无量纲时均能量E(z)可定义为

(20)E(z)=

\frac{2}{ρ_{f} U_{\infty}^{2} D^{2} T} \int_{0}^{Γ}

W_ldt

式中:Γ代表无量纲脱落周期;W_l代表升力产生能量的功率,即W_l=∂ζ_y/∂t.当E(z)为正值时,代表能量从流体转移至结构,E(z)为负值则转移方向相反.Newman等^[11]和Zhu等^[12]研究指出对于驻波响应,E(z)取值与展向位置有关,而与无量纲时间无关.同时,E(z)在一个脱落周期内沿整数波长的积分应该为0,表明在一个旋涡脱落周期内,结构从流体中得到的能量和在流体中做功耗散的能量相同,在没有外界能量输入的前提下,整个流体和结构系统满足能量守恒.因此,时均能量代表结构与流体进行能量交换的强度,其值越大则相应结构与流体之间的能量交换越频繁,反映到实际工程中,就会引起结构的疲劳,加速结构的老化.

图9所示为所有工况下时均能量随展向分布计算结果.由图9可知,A=0.10D柔性波形柱的时均能量比柔性光滑柱显著增大,当扰动波面高度增至A=0.15D其时均能量相比于柔性光滑柱维持在同一水准.而当A≥0.20D时,E(z)始终在0附近小幅振荡,说明在上述3种工况下波形柱与流体之间的能量交换接近于0,从能量角度验证了波形柱与流体之间的动力响应被显著抑制.同时,在z/D=0.37π~1.62π以及z/D=2.37π~3.62π之间柔性光滑柱E(z)为正值,在其余位置E(z)为负值;而A=0.10D波浪形结构在两端E(z)为正值,而在跨中附近E(z)为负值, 完全消除初始瞬态效应后,对3种典型工况下横向位移和升力系数时程进行了频域分析.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 细长柔性结构涡激振动时的无量纲时均能量分布

Fig.9 Nondimensional mean time energy distribution of slender structure undergoing vortex-induced vibration

图10中分别为柔性光滑柱横向位移和升力系数功率谱密度(PSD)展向分布计算结果,可以据此确定旋涡脱落频率为fD/U_∞=0.163,此外,在PSD的展向分布云图中可观察到,谱峰幅值与圆柱展向波长密切相关.Bourguet等^[14]研究了长径比为200的细长柔性结构涡激振动问题,并也报道了类似现象.由此可以进一步证实,结构的振动响应与波长相关.此外,阻力频率(这里没有显示)是升力频率的两倍,说明尾迹是经典的2S模式.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 光滑圆柱无量纲时均能量分布

Fig.10 Smooth cylinder power spectral density

图11中分别为A=0.10D柔性波浪柱横向位移和升力系数PSD展向分布模拟结果,可以得知其主频为fD/U_∞=0.161,略小于光滑柱时相应频率.从图11(b)可以看到,与光滑柱相比,A=0.10D柔性波形柱振动时程在跨中对应的PSD值明显减小,表明该位置附近升力的波动强度显著减小,与图5显示的现象一致.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 A=0.1D波浪柱无量纲时均能量分布

Fig.11 Wavy cylinder power spectral density at A=0.1D

图12中分别为A=0.20D柔性波形柱横向位移和升力系数PSD的展向分布计算结果.对于A=0.20D柔性波形柱,除了主频fD/U_∞=0.161外,在fD/U_∞=0.126处也可识别出次峰频率,在图12用白色虚线表示.这种低频次生频率,在PSD-C_l中比在PSD-ζ_y中更强.次生频率产生的原因涉及流固耦合的非线性问题,其机理有待进一步探讨.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 A=0.2D波浪柱无量纲时均能量分布

Fig.12 Wavy cylinder power spectral density at A=0.2D

4 结论

采用基于高精度谱单元方法的流固耦合分析方法,建立了细长柔性波形柱体结构的涡激振动力学模型,对其在低速均匀流作用和驻波初始动力激励下的流致振动机理进行了量化分析.结果显示,当扰动波高A≥0.20D时,柔性波形柱横向振幅相比于光滑柱明显减小,升阻力系数显著降低,水动力特性得到明显改善,表明在合适波高下,柔性波形柱具有良好的流致振动抑制作用.进一步比较扰动波高分别为A=0.10D,0.20D的结构横向振幅和水动力系数的时空演变特征,大致确定出波形柱抑制涡激振动的控制失效范围(A<0.10D)以及控制有效范围(0.20D≤A<0.30D).

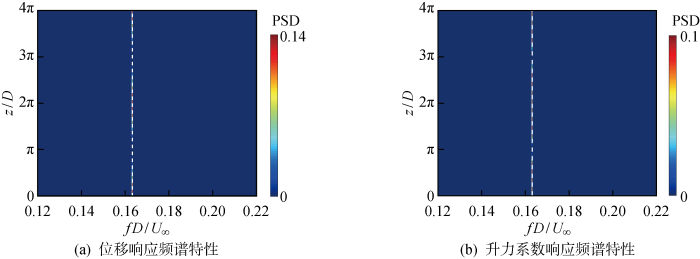
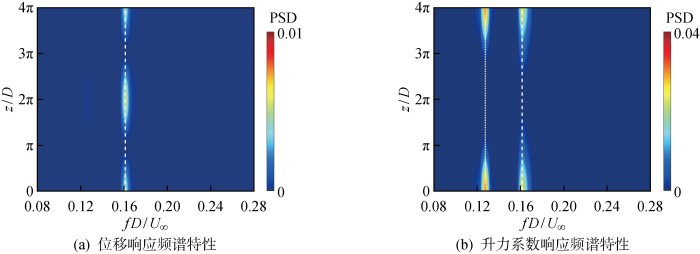
为了探究扰动表面波高对结构振动响应的影响机理,对扰动表面结构和无扰动表面结构近尾迹三维涡结构进行了对比分析.结果表明,与柔性光滑柱相比,A=0.20D工况下交织涡结构完全消失,使得波形扰动截面剪切层的卷曲和相互作用明显较弱,涡形成区长度进一步增大.对柔性光滑柱在A=0.10D,0.20D时波形柱的流向涡结构瞬时等值面进行了模拟比较,结果表明在A=0.20D的情况下观察到的反向旋转涡旋也稳定了剪切层,拉长了涡旋形成区长度.比较了所有工况下时均能量的展向分布计算结果,发现当A≥0.20D时,E(z)始终在0附近小幅振荡,从能量转移角度进一步验证柔性波形柱对涡激振动的抑制作用.在完全消除初始瞬态效应后,对3种典型工况下横向位移和升力系数时程进行了频域分析,确定了3种工况下的漩涡脱落频率,对于A=0.20D波形柱工况下观察到的次生频率,其产生的原因涉及流固耦合的非线性问题,有待对其机理进行进一步探讨.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

陈伟民, 付一钦, 郭双喜.

海洋柔性结构涡激振动的流固耦合机理和响应

[J]. 力学进展, 2017, 47(1): 25-91.

[本文引用: 1]

CHEN

Weimin

, FU

Yiqin

, GUO

Shuangxi

Review on fluid-solid coupling and dynamic response of vortex-induced vibration of slender ocean cylinders

[J]. Advances in Mechanics, 2017, 47(1): 25-91.

[本文引用: 1]

[2]

AHMED

, KHAN

M J

, BAYS-MUCHMORE

Experimental investigation of a three-dimensional bluff-body wake

[J]. AIAA Journal, 1993, 31(3): 559-563.

DOI:10.2514/3.11365 URL [本文引用: 1]

[3]

LAM

, WANG

F H

, SO

R M C

Three-dimensional nature of vortices in the near wake of a wavy cylinder

[J]. Journal of Fluids and Structures, 2004, 19(6): 815-833.

DOI:10.1016/j.jfluidstructs.2004.04.004 URL [本文引用: 1]

[4]

ZHU

H B

, ZHOU

, BAO

et al.

Wake characteristics of stationary catenary risers with different incoming flow directions

[J]. Ocean Engineering, 2018, 167: 142-155.

DOI:10.1016/j.oceaneng.2018.05.030 URL [本文引用: 1]

[5]

ZHU

H B

, WANG

, BAO

et al.

Flow over a symmetrically curved circular cylinder with the free stream parallel to the plane of curvature at low Reynolds number

[J]. Journal of Fluids and Structures, 2019, 87: 23-38.

DOI:10.1016/j.jfluidstructs.2019.03.012 URL [本文引用: 1]

[6]

WANG

, ZHU

H B

, BAO

et al.

Modification of three-dimensional instability in the planar shear flow around two circular cylinders in tandem

[J]. Physics of Fluids, 2019, 31(10): 104110.

DOI:10.1063/1.5120564 URL [本文引用: 1]

Direct stability analysis based on the Floquet theory has been employed to clarify the effects of planar shear on three-dimensional instabilities in the wake of two identical circular cylinders of diameter D in tandem arrangement. The center-to-center separation (Lx) in the range of 1.2 ≤ Lx/D ≤ 2.5 was considered. The onset of the three-dimensional instabilities was calculated, and the critical Reynolds number and corresponding spanwise wavenumber varying with the separation were discussed for different shear rates. Representative configurations were chosen to illustrate different transition scenarios, with the three-dimensional instabilities studied in detail for each case. It was found that three different effects of planar shear on the three-dimensional synchronous instability originally present in the otherwise uniform flow were identified depending on the separation. A subharmonic mode referred to as mode SS was observed to develop in the wake due to the flow asymmetry caused by the planar shear. This subharmonic mode differs from the C-type mode in terms of both the spatial structure and critical spanwise wavelength. Furthermore, the mode SS instability was found to be intensified as the shear becomes stronger, and it develops more rapidly than the synchronous modes.

[7]

WANG

, BAO

, ZHOU

et al.

Flow instabilities in the wake of a circular cylinder with parallel dual splitter plates attached

[J]. Journal of Fluid Mechanics, 2019, 874: 299-338.

DOI:10.1017/jfm.2019.439 URL [本文引用: 1]

In this paper, instabilities in the flow over a circular cylinder of diameter $D$ with dual splitter plates attached to its rear surface are numerically investigated using the spectral element method. The key parameters are the splitter plate length $L$, the attachment angle $\\unicode[STIX]{x1D6FC}$ and the Reynolds number $Re$. The presence of the plates was found to significantly modify the flow topology, leading to substantial changes in both the primary and secondary instabilities. The results showed that the three instability modes present in the bare circular cylinder wake still exist in the wake of the present configurations and that, in general, the occurrences of modes A and B are delayed, while the onset of mode QP is earlier in the presence of the splitter plates. Furthermore, two new synchronous modes, referred to as mode A$^{\\prime }$ and mode B$^{\\prime }$, are found to develop in the wake. Mode A$^{\\prime }$ is similar to mode A but with a quite long critical wavelength. Mode B$^{\\prime }$ shares the same spatio-temporal symmetries as mode B but has a distinct spatial structure. With the exception of the case of $L/D=0.25$, mode A$^{\\prime }$ persists for all configurations investigated here and always precedes the transition through mode A. The onset of mode B$^{\\prime }$ occurs for $\\unicode[STIX]{x1D6FC}>20^{\\circ }$ with $L/D=1.0$ and for $L/D>0.5$ with $\\unicode[STIX]{x1D6FC}=60^{\\circ }$. The characteristics of all the transition modes are analysed, and their similarities and differences are discussed in detail in comparison with the existing modes. In addition, the physical mechanism responsible for the instability mode B$^{\\prime }$ is proposed. The weakly nonlinear feature of mode B$^{\\prime }$, as well as that of mode A$^{\\prime }$, is assessed by employing the Landau model. Finally, selected three-dimensional simulations are performed to confirm the existence of these two new modes and to investigate the nonlinear evolution of the three-dimensional modes.

[8]

DIMAS

A A

, TRIANTAFYLLOU

G S

Baroclinic-barotropic instabilities of the Gulf Stream extension

[J]. Journal of Physical Oceanography, 1995, 25(5): 825-834.

DOI:10.1175/1520-0485(1995)025<0825:BIOTGS>2.0.CO;2 URL [本文引用: 1]

[9]

KARNIADAKIS

G E

, ISRAELI

, ORSZAG

S A

High-order splitting methods for the incompressible Navier-Stokes equations

[J]. Journal of Computational Physics, 1991, 97(2): 414-443.

[本文引用: 2]

[10]

KARNIADAKIS

G E

, SHERWIN

Spectral/hp element methods for computational fluid dynamics

[M]. Oxford, UK: Oxford University Press, 2013: 414-418.

[本文引用: 1]

[11]

NEWMAN

D J

, KARNIADAKIS

G E

A direct numerical simulation study of flow past a freely vibrating cable

[J]. Journal of Fluid Mechanics, 1997, 344: 95-136.

DOI:10.1017/S002211209700582X URL [本文引用: 10]

We present simulation results of flow-induced vibrations of an \ninfinitely long flexible \ncable at Reynolds numbers Re = 100 and Re = 200, \ncorresponding to laminar and \nearly transitional flow states, respectively. The question as to what \ncable motions and \nflow patterns prevail is investigated in detail. Both standing wave \nand travelling wave \nresponses are realized but in general the travelling wave is the preferred response. \nA standing wave cable response produces an interwoven pattern of vorticity, while a \ntravelling wave cable response produces oblique vortex shedding. A sheared inflow \nproduces a mixed standing wave/travelling wave cable response and chevron-like \npatterns with vortex dislocations in the wake. The lift force on the \ncable as well as its \nmotion amplitudes are larger for the standing wave response. At Re = 200, \nthe cable and wake response are no longer periodic, and the maximum \namplitude of the cable \nis about one cylinder diameter, in agreement with experimental results.

[12]

ZHU

H B

, WANG

, BAO

et al.

Flow over a symmetrically curved circular cylinder with the free stream parallel to the plane of curvature at low Reynolds number

[J]. Journal of Fluids and Structures, 2019, 87: 23-38.

DOI:10.1016/j.jfluidstructs.2019.03.012 URL [本文引用: 2]

[13]

LIN

Y F

, BAI

H L

, ALAM

M M

et al.

Effects of large spanwise wavelength on the wake of a sinusoidal wavy cylinder

[J]. Journal of Fluids and Structures, 2016, 61: 392-409.

DOI:10.1016/j.jfluidstructs.2015.12.004 URL [本文引用: 3]

[14]

BOURGUET

, MODARRES-SADEGHI

, KARNIADAKIS

et al.

Wake-body resonance of long flexible structures is dominated by counterclockwise orbits

[J]. Physical Review Letters, 2011, 107(13): 134502.

DOI:10.1103/PhysRevLett.107.134502 URL [本文引用: 1]

海洋柔性结构涡激振动的流固耦合机理和响应

2017

... 在土木工程领域,风、浪、流等环境动力荷载作用下的细长结构物受损甚至破坏屡见不鲜.比如,悬索桥中的主缆索作为典型的细长柔性结构,在来风作用下将产生涡激振动,甚至发生疲劳损坏;又如,在主缆索施工过程中,缆索截面形式发生非对称性变化,当风速超过临界值后,将产生空气动力负阻尼,使得缆索振动逐渐增强,甚至超负荷振幅而破坏.因此,科学评估和有效抑制细长结构的流致动力响应是风、浪、流敏感细长柔性结构设计必须考虑的内容.然而,当前细长柔性结构的流固耦合效应方面研究不足,尤其精准模拟和分析细长结构流致振动响应的力学模型和算法方面仍较缺乏,且亟待深入理解其流固耦合机理并建立系统的分析方法与手段^[1]. ...

海洋柔性结构涡激振动的流固耦合机理和响应

2017

Experimental investigation of a three-dimensional bluff-body wake

1993

... 波浪形变截面圆柱体结构具有良好的流动减阻效果.近年来,国内外学者对该类型结构的绕流特性开展了较多研究,发现波浪形变截面能够延后剪切层的相互作用,从而有效减小阻力.Ahmed等^[2]采用实验方法研究了波浪形圆柱的边界层分离线和尾流结构,发现波浪形圆柱流动分离线呈现明显的三维特性,在分离节点附近形成流向涡,且发生边界层“上卷”现象,从而延迟或抑制剪切层中湍流的生成和发展.Lam等^[3]利用多种流动显示技术对波浪形圆柱的近尾迹进行了实验研究,给出了平均速度和波动速度分量沿流向、展向和横向的分布特征.实验结果表明,波浪形柱涡旋平均形成长度比大于光滑圆柱.湍流统计分析也表明,光滑圆柱尾迹中的涡街更为规则,而由于波浪形圆柱后面的涡具有较强的三维效应,使得由湍流掺混增强而尾迹表现出更强的非相干流动结构. ...

Three-dimensional nature of vortices in the near wake of a wavy cylinder

2004

Wake characteristics of stationary catenary risers with different incoming flow directions

2018

... 目前变截面结构绕流分析主要集中在静止或弹性支承的刚性波浪形结构的减阻和涡激振动特性方面.然而在实际土木工程中,缆索等细长结构的刚度系数通常较小,因此这种结构的柔性作用对流动减阻作用以及涡激振动响应的影响需要进一步研究,包括对初始动力激励的敏感性方面也需要深入分析.在文献[4⇓⇓-7]的基础上,针对这一问题,本研究采用基于高精度谱单元方法的流固耦合分析方法,建立了细长变截面柔性圆柱体结构的涡激振动力学模型,对其在低速均匀流作用和驻波初始动力激励下的流致振动机理进行了量化分析,获得了包括波浪形结构的尾流特性、结构动力响应特性、能量传递规律、涡脱频率展向变化特征,并对其在驻波扰动下的减阻、减振机理进行了深入探讨,对波浪形变截面细长结构的工程设计和应用提供参考. ...

Flow over a symmetrically curved circular cylinder with the free stream parallel to the plane of curvature at low Reynolds number

2019

Modification of three-dimensional instability in the planar shear flow around two circular cylinders in tandem

2019

Flow instabilities in the wake of a circular cylinder with parallel dual splitter plates attached

2019

Baroclinic-barotropic instabilities of the Gulf Stream extension

1995

... 细长结构的流致振动是一种典型的流固耦合问题.求解流固耦合的基本方法通常有两大类,分别为界面匹配法和非界面匹配法,包括经典的任意拉格朗日-欧拉(ALE)方法和浸入边界法(IBM).本文采用另一种由Dimas等^[8]提出的随体坐标系(Body-fitted Coordinates)方法,该方法在惯性坐标系中求解N-S方程,再通过坐标转换至非惯性坐标系中,从而不需要动网格和浸泡边界近似. ...

High-order splitting methods for the incompressible Navier-Stokes equations

1991

... 对结构运动的解耦方程式(15),采用二阶Newmark-β方法进行求解.对不定常流场模态方程式(13)和(14),采用Karniadakis等^[9]提出的高阶分步格式进行时间离散.具体地,对每一时间迭代步对速度和压力进行解耦计算. ...

... 对上述时间离散后的模态方程,根据Karniadakis等^[9-10]将(x, y)平面的二维空间域离散为四边形有限元单元,并采用高斯-洛巴托-勒让德(GLL)高阶正交拉格朗日多项式作为形函数进行空间离散. ...

Spectral/hp element methods for computational fluid dynamics

2013

A direct numerical simulation study of flow past a freely vibrating cable

1997

... 式中:D_z为展向相应位置的圆截面直径.由于波浪形柱直径在展向呈余弦变化,平均直径为D=(D_max+D_min)/2.基于平均直径和均匀来流速度的雷诺数取值为100,因此本文考虑的流动为层流流动.定义波浪形柱直径最大截面所在的展向位置为几何节点,波浪柱直径最小截面所在的对应位置为几何鞍点.A代表波状表面的波高,取值范围为0.1D~0.3D;展向波长设置为λ=4πD.A=0对应于光滑圆柱,也作为基准工况用于与波浪形柱工况进行对比分析.参照 Newman等^[11]的研究,可以通过规定圆柱的初始振幅和速度来确定其初始条件,本研究中初始扰动为驻波:ζ_y(z, t)=acos(ωt)cos(2πz/L_z),其中a为振幅,ω为振动频率,ω=2π/(cL_z). ...

... 二维平面网格划分如图2所示.计算域几何形状为C形,由圆柱上游半径为20D的半圆弧和下游矩形组成,其流向长度为30D,在横流向长度设置为40D,圆柱放置在计算域横流向的中心位置.在(x, y)平面内采用了877个基础网格;由于对每一基础单元再用6阶正交多项式(P=6)对速度和压力场进行近似,所以每个基础网格再细分为5×5个高阶网格.此外,根据文献[11-12],沿展向采用64个傅里叶模态,满足本文雷诺数下的精度要求. ...

... 流体计算域的边界条件设置如下:入口边界为均匀来流条件,来流速度为(U_∞,0,0);在出口边界上采用纽曼边界条件,令出口边界上∂u/∂x=∂v/∂x=∂w/∂x=0以及p=0.在上、下部边界上指定(u, v, w)=(U_∞,0,0)的远场边界条件;在圆柱固壁采用无滑移和不可渗透边界条件,即流固耦合边界条件

\frac{\partial ζ}{\partial t}

=v.通过假设无限长波浪柱的展向周期性,在波浪柱的两端实施了只允许横向运动的自由边界条件^[11]. ...

... 为了验证力学模型和数值模拟方法的适用性,首先获得了均匀来流作用下细长光滑圆柱涡激振动模拟结果,并与已有文献结果进行对比分析.本模拟中质量比设置为m^*=6.0,而其他模拟参数均与Newman等^[11]相同.图3所示为光滑圆柱在驻波和行波初始激励下的横向振幅(ξ_y)、阻力系数(C_d)和升力系数(C_l)模拟结果,与Newman等^[11]结果吻合良好.尤其在驻波初始激励下本模拟结果与Newman等^[11]结果在展向节点(响应振幅最大的点)和反节点(响应振幅最小的点)位置坐标完全相同.在行波初始激励下的行波响应幅值和行波速度等均与Newman等^[11]结果一致,故说明本文力学模型和模拟方法的可靠性. ...

... [11]结果吻合良好.尤其在驻波初始激励下本模拟结果与Newman等^[11]结果在展向节点(响应振幅最大的点)和反节点(响应振幅最小的点)位置坐标完全相同.在行波初始激励下的行波响应幅值和行波速度等均与Newman等^[11]结果一致,故说明本文力学模型和模拟方法的可靠性. ...

... [11]结果在展向节点(响应振幅最大的点)和反节点(响应振幅最小的点)位置坐标完全相同.在行波初始激励下的行波响应幅值和行波速度等均与Newman等^[11]结果一致,故说明本文力学模型和模拟方法的可靠性. ...

... [11]结果一致,故说明本文力学模型和模拟方法的可靠性. ...

... 为了进一步了解扰动表面波高对结构振动响应的影响机理,需要对柔性波形柱和柔性光滑柱近尾迹三维涡结构进行对比分析.图6给出了不同扰动波高时展向涡量等值面(ω_z=±1.0)计算结果.其中,图6(a)~6(c)为柔性光滑柱展向涡量等值面透视图,图6(d)~6(f)为俯视图,与Newman等^[11]计算结果吻合良好.驻波初始激励下柔性光滑柱展向涡量中存在明显的交织结构.这种交织涡结构的展向特征是,在z/D=0, 2π截面处形成交错脱落的卡门涡街结构;而在z/D=π, 3π截面处上、下表面同时脱落的完全对称型涡结构.图6中分别给出A=0.10D时模拟结果,显然在z/D=π, 3π截面处的涡结构也呈现对称分布.值得注意的是,在此工况下几何节点处的展向涡量幅值较大从而升力系数幅值也随之增大,而几何鞍点处涡量幅值较小从而升力系数幅值也随之减小,这与图5所示结果一致.图6中分别给出A=0.20D时模拟结果,在该工况下交织涡结构完全消失,弯曲涡管以交错方式从波浪形表面上、下侧分别脱离,并且在尾流中迅速消失.更重要的是,与柔性光滑柱相比,此时波形柱表面剪切层的卷曲和相互作用明显较弱,使得涡形成区长度进一步增大.Lin 等^[13]用数值方法研究了亚临界雷诺数条件下具有相对较大展向波长的刚性波形柱周围的流动特征,也得到了类似的结果. ...

... 结构的运动响应与流体与结构之间的能量转化特征密切相关,根据 Newman 等^[11]的研究,一个旋涡脱落周期的无量纲时均能量E(z)可定义为 ...

... 式中:Γ代表无量纲脱落周期;W_l代表升力产生能量的功率,即W_l=∂ζ_y/∂t.当E(z)为正值时,代表能量从流体转移至结构,E(z)为负值则转移方向相反.Newman等^[11]和Zhu等^[12]研究指出对于驻波响应,E(z)取值与展向位置有关,而与无量纲时间无关.同时,E(z)在一个脱落周期内沿整数波长的积分应该为0,表明在一个旋涡脱落周期内,结构从流体中得到的能量和在流体中做功耗散的能量相同,在没有外界能量输入的前提下,整个流体和结构系统满足能量守恒.因此,时均能量代表结构与流体进行能量交换的强度,其值越大则相应结构与流体之间的能量交换越频繁,反映到实际工程中,就会引起结构的疲劳,加速结构的老化. ...

Flow over a symmetrically curved circular cylinder with the free stream parallel to the plane of curvature at low Reynolds number

2019

Effects of large spanwise wavelength on the wake of a sinusoidal wavy cylinder

2016

... 图7所示为不同扰动波高条件下的涡量场顺流向(ω_x=±1.0)与横流向(ω_y=±1.0)分量瞬时等值面云图.从该图可清晰分辨出顺流向涡结构和横流向涡结构在尾迹附近的演化特征.显然,与柔性光滑柱和A=0.10D扰动波高工况相比,A=0.20D时结构附近涡结构完全不同且涡量强度相对较低,并且沿下游耗散较快.Lin等^[13]指出,附加流向涡在波形柱表面几何鞍点和节点处分别诱导出上涌流和下涌流,使得在几何鞍点处产生宽尾流,而在几何节点处产生窄尾流.这与本文模拟结果非常一致,表明波形结构的涡激振动抑制和减阻效应的力学机理有相同之处. ...

... 为了进一步研究流向涡对结构响应的影响,图8中给出了3种工况下(x, y)平面内流向涡量切片图;其中图7中分别为柔性光滑柱和在A=0.10D,0.20D时柔性波形柱的模拟结果.该结果表明,柔性光滑柱两侧和A=0.10D波形柱两侧均形成一对同向旋转涡结构,而沿结构展向上、下侧分布的两对涡旋转方向刚好相反.然而,在A=0.20D情况下,在同一展向位置处柔性波形柱两侧生成一对较强的反向旋转涡,在这对反向旋转涡的外侧还分布着一对与各自强涡旋转方向相反的弱涡.Lin 等^[13]指出,最优控制波形柱附加产生的反向流向涡对剪切层稳定性具有重要作用,能够防止剪切层与强涡结构的相互作用,使得涡旋形成长度增大.在A=0.20D的情况下观察到的反向旋转涡旋也稳定了剪切层,拉长了涡旋形成区长度,与本文之前观察到的现象一致. ...

Wake-body resonance of long flexible structures is dominated by counterclockwise orbits

2011

... 图10中分别为柔性光滑柱横向位移和升力系数功率谱密度(PSD)展向分布计算结果,可以据此确定旋涡脱落频率为fD/U_∞=0.163,此外,在PSD的展向分布云图中可观察到,谱峰幅值与圆柱展向波长密切相关.Bourguet等^[14]研究了长径比为200的细长柔性结构涡激振动问题,并也报道了类似现象.由此可以进一步证实,结构的振动响应与波长相关.此外,阻力频率(这里没有显示)是升力频率的两倍,说明尾迹是经典的2S模式. ...

〈

〉