HFS-SDST问题的调度涉及工件的排序和机器分配,是典型的组合优化问题,已经证明HFS-SDST是非确定性多项式难(NP-hard)的问题[5].因此,利用精确算法理论上可以求解,但随着问题规模的增大出现组合爆炸问题,几乎不可能在合理的时间内找到最优调度解,难以满足实际生产需要.启发式算法依据某些规则对调度解进行构造,大大缩短了寻找调度解的时间,Moccellin等[6]提出基于最短处理时间(SPT)和最长处理时间(LPT)规则的启发式算法,求解针对机器阻塞、顺序依赖、顺序独立准备时间的HFS问题,结果证明了对于HFS-SDST问题,最长处理和准备时间(LPS)规则优于其他规则.然而,对于较大规模的复杂调度问题,启发式规则构造的调度解质量不高,因此,采用智能优化算法为快速求解组合优化问题提供了可能;文献[7]中提出基于超启发式学习增强的迭代贪心算法求解HFS-SDST问题,采用该算法对一个实际生产实例的设备数据进行求解可以达到较好的效果;周炳海等[8]提出蚁群算法求解双目标HFS问题,但该算法仅限于求解较小规模的问题;文献[9]中提出基于代理的改进遗传算法,融合了多智能体和遗传算法的优点求解HFS-SDST问题,并通过实验得到一些算例的下限值;Pan等[10]列出6个局部搜索算法和3个群智能优化算法,其中3个群智能算法为改进的果蝇优化算法(FOA)、改进的候鸟迁徙优化(IMBO)和离散人工蜂群(DABC)算法,并给出一种协同优化策略,通过仿真测试对比可知,对于大部分算例,DABC优于其他8个算法;Tian等[11]提出基于pareto的自适应变邻域搜索算法,证明了变邻域搜索求解HFS-SDST问题的有效性;Khare等[12]提出了混合松鼠搜索、反向鲸鱼及离散灰狼3个群智能算法,并且为了提高算法的性能,在松鼠算法中引入变邻域搜索和混合局部搜索,在鲸鱼算法中引入反向学习策略,优化目标为总提早和拖期.文献[10,12]中为群智能算法求解HFS-SDST问题的有效性提供了依据.虽然针对HFS-SDST问题已有一些研究,但算法方面还未形成系统理论成果,因此,研究更高性能的调度算法具有深刻的理论和实际应用意义.
Duman等[13]在2012年提出的候鸟迁徙优化(MBO)算法,因调整参数少、结构简单等优点,得到了广泛应用,但该算法容易早熟收敛且不能直接应用于组合优化问题,因此,Pan等[14]和Han等[15]分别提出改进的离散MBO算法求解HFS问题,且在此基础上,Pan等[10]对文献[14]中提出的IMBO进行了改进.Sioud等[3]针对带SDST的置换流水车间调度(PFSP)问题提出增强的候鸟迁徙优化(EMBO)算法,利用禁忌表控制混合邻域策略产生邻域解的多样性;Meng等[16]和汤洪涛等[17]分别提出采用和声搜索(HS)策略以及变邻域搜索策略产生邻域解的离散MBO,求解批量流车间调度问题.然而,MBO算法是一种邻域搜索算法,因此邻域的选择对算法的优化效果影响较大,而变邻域搜索是一种可以系统地利用邻域变化思想的算法;Báez等[18]提出结合贪心随机自适应力(GRASP)和变邻域搜索的混合算法求解带SDST的平行机调度问题.为了改善MBO的早熟收敛问题,文献[3]中采用重置机制提高算法的全局搜索能力,此外,采用多种群智能优化算法为提高该能力提供了另一种思路;Han等[19]提出改进的多种群离散差分进化算法,求解多用途批处理设备调度问题;Gao等[20]提出一种动态洗牌的多微种群候鸟迁徙优化(SM2-MBO)算法,利用多微子种群并行搜索,求解多资源约束柔性作业车间调度问题,但该算法不能在子种群信息交互时产生更好新个体;Tongur等[21]提出了基于粒子群优化(PSO)算法的改进多种群MBO(IMFMBO)算法,在多种群MBO框架下,通过另一种算法促进子种群之间的信息交互,提高算法的全局搜索能力.因此,本文结合候鸟迁徙优化、子种群交互策略和多种群并行搜索思想,提出IMMBO算法求解HFS-SDST问题.
1 HFS-SDST问题
HFS-SDST问题描述如下:n个工件在m个阶段的流水线上加工,每个工件j(j=1, 2, …, n)依次按相同的顺序通过阶段k(k=1, 2, …, m),m个阶段至少有一个阶段的机器数量Mk>1,每个工件可以在阶段k的任意一台机器上加工.加工过程满足假设:①任意时刻每个工件只能在一台机器上加工;②每台机器同一时间只能加工一个工件;③工件在某阶段机器上一旦开始加工不允许中断.优化目标为通过确定工件的加工顺序以及每阶段工件在机器上的分配情况,使工件的最大加工完成时间(makespan)即Cmax最小.
考虑SDST,n个工件在第1阶段机器上的加工顺序一旦确定,依据工件在可用机器上的加工完成时间最短的标准,工件在后续阶段机器上的加工顺序会相应确定.若工件在第1阶段的加工顺序为π, π=(π1, π2, …, πn),则给出如下HFS-SDST问题的数学模型.
若第1阶段和阶段k(k=2, 3, …, m)的第i(i=1, 2, …, Mk)台机器没有加工过其他工件,则工件πj的完成时间
式中:
如果阶段k的第i台机器加工πj前已经加工过其他工件,则工件πj的加工完成时间为
式中:
其作业完成时间为
最后一个工件在最后阶段机器上的加工完成时间的最大值为
优化调度的目标为找到Cmax最小的n个工件在第1阶段机器上的加工顺序,即π*=(
2 IMMBO
IMMBO算法把初始化种群分成多个子种群,各个子种群利用MBO机制平行搜索,子种群之间利用离散鲸鱼优化策略对各子种群的领飞鸟优化完成信息交互;同时设计局部搜索增强和种群多样化控制机制提高算法的探索和开发能力,IMMBO算法框架如下.
步骤1 设置算法相关参数.利用MNEH算法初始化种群,并把最好的1/3 分到每个子种群作为其领飞鸟,剩下2/3个体随机分配到各子种群,每个子种群包括两个跟飞鸟.
步骤2 保存本代最优个体.
步骤3 子种群领飞鸟利用串行变邻域搜索策略产生邻域个体,若邻域个体中最好的优于领飞鸟,替换领飞鸟.
步骤4 子种群跟飞鸟利用并行变邻域搜索策略产生邻域个体,若邻域个体中最好的优于该跟飞鸟,替换跟飞鸟,若跟飞鸟优于本群的领飞鸟,二者交换.
步骤5 检查是否达到巡回次数,若未达到,转到步骤3,否则转到步骤6.
步骤6 各子种群领飞鸟利用离散鲸鱼优化策略进行交叉,完成子种群之间的信息交互.
步骤7 对种群中的最优个体执行局部搜索(LS).
步骤8 更新各子种群领飞鸟的年龄变量,若某子种群的领飞鸟年龄达到设定年龄限制,启动多样化控制机制,重新产生一个个体放入种群.
步骤9 判断算法迭代是否达到最大迭代次数,若未达到,转到步骤2,否则,算法结束,输出最优个体及其Cmax值.
2.1 编码和解码
连续的优化算法不能直接应用于组合优化问题HFS-SDST,故需要设计离散形式的优化算法,而设计离散优化算法需要对算法中个体进行离散编码和解码.针对HFS问题,常用的编码和解码方法有矩阵和向量两种,本文在考虑SDST的同时采用向量编码,即基于所有工件的一个调度顺序对个体编码[12],然后,将工件按照排列的顺序分配到第1阶段的空闲机器上加工.解码方法为:考虑准备时间,工件在第1阶段按照编码顺序加工,第k(k=2, …, m)阶段的工件加工顺序则依据在该阶段加工完成时间最短的原则,重新排列得到工件在阶段k的加工顺序.
2.2 初始化种群
NEH启发式规则是依据工件在所有阶段机器上的总加工时间越短,优先级别越高的原则得到的工件排序,适用于调度目标为最大完成时间的流水车间调度问题,若考虑带SDST的车间调度问题,不仅需要考虑总加工时间,同时需要考虑SDST.针对带SDST的平行机调度,对于未开始工作的机器,工件j的加工完成时间ψ1, j=s1, j, j+p1, j,其中s1, j, j和p1, j分别为工件j在平行机上的准备时间和加工时间,求出每个工件的完成时间后,按照由小到大的顺序进行加工可以使加工完成时间最短.但对于多阶段的HFS-SDST问题,需要考虑工件j在所有阶段的加工完成时间和ψj,令ψj=
(1) 计算每个工件的ψj,对ψj升序排列,得到工件在第1阶段的排序π=(π1, π2, …, πn).
(2) 依据第1阶段的机器数M1,把π分成两个子序列π1=(π1, π2, …,
(3) 随机调换π2中工件的顺序得到π2',与π1合并得到一个新的第1阶段工件的排序π'=π1∪π2'.
(4) 重复(3), 得到与种群规模相同的工件在第 1 阶段机器上的加工顺序,并分别求出其Cmax.
针对初始种群,按种群中个体的Cmax值升序排列,其中前1/3分配到各个子种群,作为领飞鸟;其余2/3随机分配到各子种群,作为跟飞鸟.子种群的规模为3,即1个领飞鸟和2个跟飞鸟.
2.3 子种群领飞鸟进化
领飞鸟是一个子种群中最好的个体,领飞鸟的质量决定子种群的搜索方向.各子种群中的领飞鸟通过其邻域个体更新.文献[22]中已经证明插入、交换及迭代贪婪(IG)算法中的破坏重建(DC)操作在流水车间调度问题中是较好的邻域解产生策略,因此,领飞鸟的邻域个体由插入、交换以及DC串联起来的串行变邻域搜索策略产生,即依次执行插入、交换和DC,只要采用某一策略能够产生更好的邻域个体就继续使用,反之,则执行下一个策略,直到结束.
串行变邻域策略伪代码如下:

输入π; 输出π
k=1
while k<=3
switch k
case 1 随机选择位置r1上的工件,1≤r1≤n,插入到π的所有可能位置,并依据指标Cmax,找到最好的π'
如果 Cmax(π')<Cmax(π)
π=π', k=1
否则
k=k+1
case 2 随机选择位置r1上的工件,1≤r1≤n,与π的其他所有位置上工件交换,并依据指标Cmax,找到最好的π'
如果Cmax(π')<Cmax(π)
π=π', k=2
否则
k=k+1
case 3 对π执行破坏重建(DC),得到π'
如果Cmax(π')<Cmax(π)
π=π', k=3
否则
k=k+1
End switch
End while

2.4 子种群跟飞鸟进化
产生跟飞鸟邻域个体的策略,要兼具邻域个体的质量和多样性,因此子种群中的跟飞鸟领域个体采用并行变邻域搜索产生,即按照一定概率选择插入或交换两种邻域之一产生跟飞鸟邻域个体.在生产调度问题中,插入更易产生较好的邻域个体,因此,设置选择插入邻域结构的概率设为Pm=0.6,即产生一个随机数r,r∈[0,1],如果r<Pm,执行插入操作直到该跟飞鸟不能更新为止,否则执行交换.对邻域个体采用贪婪选择,只要产生的邻域个体优于跟飞鸟,则跟飞鸟被替换;同时,在跟飞鸟被替换后,若跟飞鸟优于其领飞鸟,二者交换,完成子种群中领飞鸟和跟飞鸟的信息交互.
2.5 巡回
多个子种群领飞鸟和跟飞鸟依据2.3节和2.4节循环G次,利用其邻域解,完成领飞鸟和跟飞鸟的充分开发.
2.6 子种群信息交互
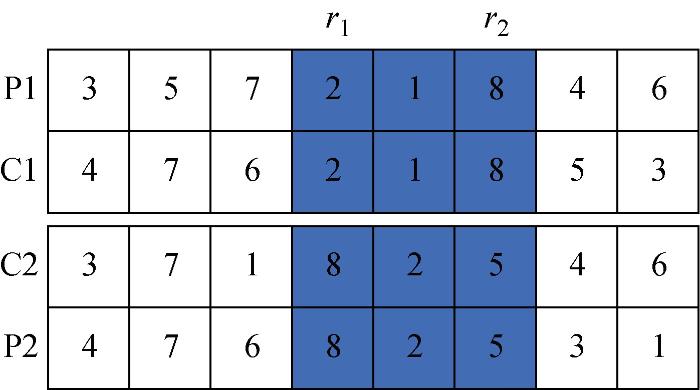
IMMBO算法采用多种群并行搜索,但随着算法的执行,子种群内部个体失去多样性,因此需要通过子种群之间的信息交互,产生更好的个体.鲸鱼优化算法(WOA)[23]是最优个体引领搜索方向的算法,这是利用鲸鱼可以通过螺旋上升过程中泡泡网围攻以及随机搜索猎物完成捕食过程.因此,设计离散鲸鱼优化算法(DWOA)完成子种群之间的信息交互.最优个体存在于各子种群的领飞鸟中,因此,DWOA只对它们优化,同时利用3种交叉策略模拟鲸鱼的捕食过程.鲸鱼围攻和螺旋上升过程分别利用当前个体和最优个体进行次序交叉和两段交叉模拟,分别以50%的概率完成局部搜索,产生一个随机数p,p∈[0,1],若p<0.5,执行次序交叉,否则执行两段交叉;随机搜索猎物过程则利用当前个体和种群中随机个体进行随机交叉模拟完成全局搜索.3种交叉的具体操作如图1~3所示,其中P1和P2为两个父代个体,C1和C2为两个子代交叉个体.
图1
图2
图3
(1) 次序交叉(OX).
步骤1 随机选择两个交叉点r1和r2,且 1≤r1<r2≤n.
步骤2 把P1和P2中r1~r2的工件分别复制到C1和C2中的r1~r2位置.
步骤3 把P1不包含在C2中的工件依次复制到C2; 把P2不包含在C1中的工件依次复制到C1.
步骤4 将C1和C2中Cmax值较小的作为交叉结果.
(2) 随机交叉(JBX).
步骤1 构造两个子序列S1,S2.
步骤2 把P1中对应S1的元素复制到C1;把P2中对应S2的元素复制到P2.
步骤3 把P2中对应S2的元素复制到C1;把P1中对应的S1的元素复制到C2.
步骤4 将C1和C2中Cmax值较小的作为交叉结果.
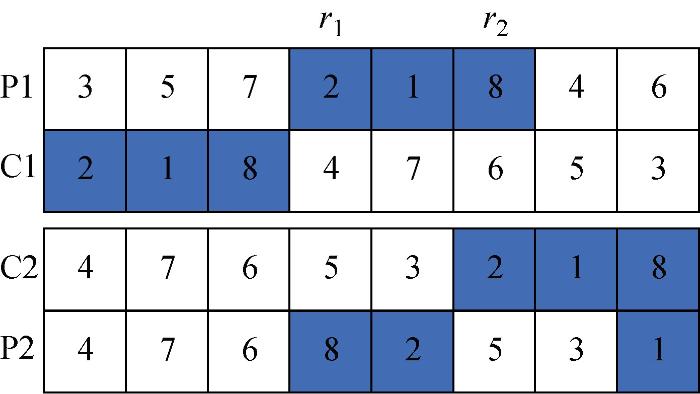
(3) 两段交叉(TSX).
步骤1 随机选择两个交叉点r1和r2,且1≤r1<r2≤n.
步骤2 把P1中r1~r2的工件复制到子序列sub1;从P2中去除sub1中工件,剩余的工件作为子序列sub2.
步骤3 把子序列sub1和sub2复制到C1,把子序列sub2和sub1复制到C2.
步骤4 如果r<0.5,C1作为交叉结束,否则C2作为交叉结果.
在DWOA中,LS和全局搜索平衡至关重要.为达到更好的优化效果,通过一个选择概率Pb完成算法探索和开发的切换,Pb采用非线性的正弦函数替代WOA[23]中的线性函数,由下式给出:
式中:

For 每个个体
如果 p<0.5
如果 r>Pb
种群最优个体与当前个体执行次序交叉(OX)
否则
当前个体与随机选择个体进行随机交叉(JBX)
End if
否则
种群最优个体与当前个体执行两段交叉(TSX)
End if
End for

2.7 LS能力增强
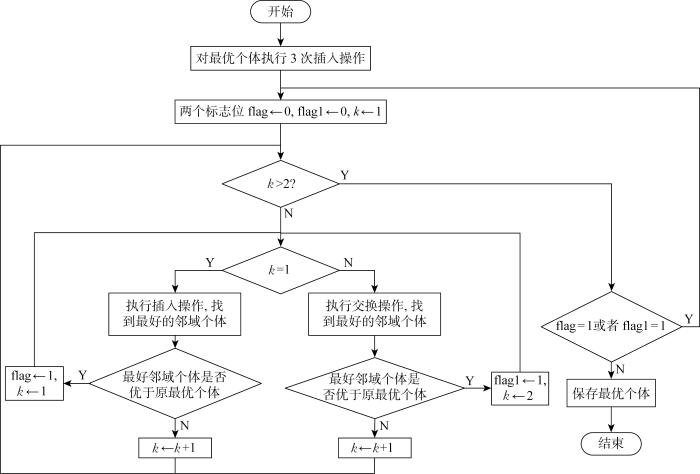
为了进一步提高全局最优个体的质量,对其进行LS.但最优个体是经过多次进化所得,直接进行LS可能进入循环搜索,因此,首先对最优个体进行干扰,然后再执行LS.LS算法流程图如图4所示.
图4
2.8 种群多样化控制
随着IMMBO算法进化,种群中个体失去多样性,因此,为各子种群的领飞鸟设置一个年龄变量,可记录其更新程度,年龄越大,说明更新能力越差.年龄变量初始值为0,如果个体更新,年龄变量清0,否则增加1,并与设置的最大年龄限制,即alimit比较,当某个体年龄大于该值时,可能在它的邻域循环搜索,此时,启动种群多样化控制机制,产生一个新的个体替换该个体.但随机产生的个体质量可能更差,导致算法收敛速度下降,而且被放弃的个体进化了多代,必然携带较好个体信息,其邻域可能就是更好的可行区域.为兼顾随机性和质量,对被放弃的个体执行3次插入干扰,产生一个领域个体,但该邻域个体很难保证质量.为了找到较好的邻域个体,使算法朝着期望的区域搜索,重复上述操作τ次,产生τ个邻域个体,将其中最好的一个个体放入种群替换原个体.考虑新个体的质量和算法效率,将τ设置为10.
3 仿真研究
3.1 仿真环境和算例
算法采用MATLAB R2016b 编写,并在Intel(R) Core(TM) i5-9600KF/3.7 GHz/ 16.0 GB,系统为Windows 10的平台运行.
为了验证实验效果,选择适用于带SDST的流水或HFS问题的算例,即基于Ta的自适应算例[24],通过测试该算例进行参数调整及算法的有效性验证.
3.2 参数调整
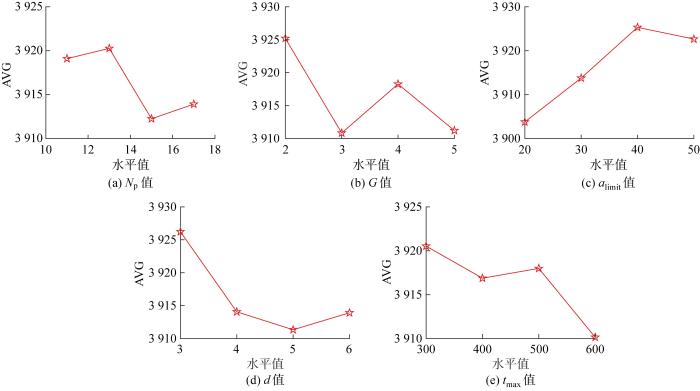
参数设置对于智能优化算法性能影响较大,为了使IMMBO算法在最佳状态下对HFS-SDST问题求解,需要对其参数进行调整.参数调整通过测试中等规模的Ta42衍生的8个自适应算例进行,Ta42算例的工件数n为50,阶段数m为10,每个阶段的机器数有2种情况:3台(P3)或者服从1~3台(P13)之间的统一分布,同时准备时间考虑4种情况,分别为平均加工时间的10%(SSD10)、50%(SSD50)、100%(SSD100)、125%(SSD125).根据上述每个阶段机器数和准备时间情况产生的8个自适应算例记作:SSD10_P13_50、SSD50_P13_50、SSD100_P13_50、SSD125_P13_50、SSD10_P3_50、SSD50_P3_50、SSD100_P3_50和SSD125_P3_50.IMMBO算法中涉及参数较多,通过前期测试,可知对算法优化效果影响较大的5个参数及其大致范围.为了确定参数的值,采用正交实验法对算法中的5个参数的4个水平进行测试.5个参数分别为子种群个数Np、巡回次数G、 最大年龄alimit、破坏重建中的破坏程度d和最大进化代数tmax.正交表如表1所示.
表1 正交实验参数/水平表
Tab.1
| 水平 | Np | G | alimit | d | tmax |
|---|---|---|---|---|---|
| 1 | 11 | 2 | 20 | 3 | 300 |
| 2 | 13 | 3 | 30 | 4 | 400 |
| 3 | 15 | 4 | 40 | 5 | 500 |
| 4 | 17 | 5 | 50 | 6 | 600 |
如果对IMMBO算法的5个参数的4个水平全部组合进行测试,需要进行45=1 024 组实验,但采用正交实验法只需测试42=16组,即可为算法选出合适的参数值,显然,用正交实验法可以使参数选择效率大幅度提高.16种参数组合及测试上述8个算例的结果如表2所示.
表2 L16(45)正交表和实验结果
Tab.2
| 序号 | Np | G | alimit | d | tmax | 平均值 |
|---|---|---|---|---|---|---|
| 1 | 11(1) | 2(1) | 20(1) | 3(1) | 300(1) | 3929.29 |
| 2 | 11(1) | 3(2) | 30(2) | 4(2) | 400(2) | 3909.13 |
| 3 | 11(1) | 4(3) | 40(3) | 5(3) | 500(3) | 3926.50 |
| 4 | 11(1) | 5(4) | 50(4) | 6(4) | 600(4) | 3911.50 |
| 5 | 13(2) | 2(1) | 30(2) | 5(3) | 600(4) | 3915.21 |
| 6 | 13(2) | 3(2) | 20(1) | 6(4) | 500(3) | 3901.25 |
| 7 | 13(2) | 4(3) | 50(4) | 3(1) | 400(2) | 3938.75 |
| 8 | 13(2) | 5(4) | 40(3) | 4(2) | 300(1) | 3925.88 |
| 9 | 15(3) | 2(1) | 40(3) | 6(4) | 400(2) | 3928.04 |
| 10 | 15(3) | 3(2) | 50(4) | 5(3) | 300(1) | 3912.08 |
| 11 | 15(3) | 4(3) | 20(1) | 4(2) | 600(4) | 3892.96 |
| 12 | 15(3) | 5(4) | 30(2) | 3(1) | 500(3) | 3915.92 |
| 13 | 17(4) | 2(1) | 50(4) | 4(2) | 500(3) | 3928.29 |
| 14 | 17(4) | 3(2) | 40(3) | 3(1) | 600(4) | 3920.92 |
| 15 | 17(4) | 4(3) | 30(2) | 6(4) | 300(1) | 3914.88 |
| 16 | 17(4) | 5(4) | 20(1) | 5(3) | 400(2) | 3891.58 |
注:( )内数值表示水平编号.
表3 参数等级及均值响应
Tab.3
| 水平 | Np | G | alimit | d | tmax |
|---|---|---|---|---|---|
| 1 | 3919.1 | 3925.21 | 3903.77 | 3926.22 | 3920.53 |
| 2 | 3920.27 | 3910.84 | 3913.78 | 3914.06 | 3916.88 |
| 3 | 3912.25 | 3918.27 | 3925.33 | 3911.34 | 3917.99 |
| 4 | 3913.92 | 3911.22 | 3922.66 | 3913.92 | 3910.15 |
| SD | 3.38 | 5.89 | 8.45 | 5.78 | 3.84 |
| 排序 | 5 | 2 | 1 | 3 | 4 |
图5
图5
IMMBO算法中的5个参数在4个水平变化趋势图
Fig.5
Trend of 5 parameters in IMMBO algorithm at 4 levels
3.3 算法各部分有效性测试
通过测试IMMBO的4个变体分别说明算法各部分的有效性.选择32个自适应算例进行测试,即Ta算例(Ta32,Ta34, …, Ta46),自适应考虑4种准备时间且每个阶段3台机器情况.IMMBO的4个变体分别为:去掉领飞鸟邻域搜索策略中的DC(IMMBO_NDC)、 去掉子种群交互机制的DWOA算法(IMMBO_NDWOA)、 去掉LS的算法(IMMBO_NLS)和去掉种群多样化控制机制(IMMBO_NR).表4中所列出的值表示选择不同准备时间时,每个变体独立运行5次测试8个算例(8×5=40)的Cmax平均值,表达式为
式中:
表4 IMMBO算法4个变体测试P3情况均值响应表
Tab.4
| 算法 | SSD10_ P3_50 | SSD50_ P3_50 | SSD100_ P3_50 | SSD125_ P3_50 |
|---|---|---|---|---|
| IMMBO_NDC | 1511.98 | 1994.43 | 2584.83 | 2871.30 |
| IMMBO_NDWOA | 1502.53 | 1973.93 | 2553.50 | 2848.08 |
| IMMBO_NLS | 1495.90 | 1965.15 | 2536.13 | 2824.58 |
| IMMBO_NR | 1511.20 | 1992.33 | 2581.05 | 2875.90 |
表4的同一组算例中,CAVG越大,说明去掉的对应算子对优化结果影响越大.可知,邻域搜索中的DC和种群多样化控制机制对算法优化效果影响最大,子种群交互机制对算法的影响次之,LS对算法的影响最小.
3.4 算法性能测试
表5 IMMBO/IMBO/DABC/ILSMRLS算法针对P13和P3算例的测试结果对比
Tab.5
| 算法 | P13 | P3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| SSD10_ P13_50 | SSD50_ P13_50 | SSD100_ P13_50 | SSD125_ P13_50 | SSD10_ P3_50 | SSD50_ P3_50 | SSD100_ P3_50 | SSD125_ P3_50 | ||
| ILSMRLS | 2860.13 | 3887.24 | 5058.04 | 5605.45 | 1163.29 | 1616.35 | 2125.87 | 2389.60 | |
| IMBO | 2891.37 | 3882.24 | 5094.32 | 5646.12 | 1178.13 | 1611.34 | 2124.73 | 2390.25 | |
| DABC | 2857.31 | 3981.69 | 5082.48 | 5627.08 | 1173.28 | 1607.95 | 2113.76 | 2354.56 | |
| IMMBO | 2834.60 | 3856.52 | 5000.99 | 5526.81 | 1110.60 | 1498.79 | 1955.79 | 2170.61 | |
表6 4个算法测试8个自适应算例的运行时间对比
Tab.6
| 算例 | 算法 | P3 | |||
|---|---|---|---|---|---|
| SSD10_P3_50 | SSD50_P3_50 | SSD100_P3_50 | SSD125_P3_50 | ||
| Ta32 | ILSMRLS | 2033.51 | 1995.49 | 2015.03 | 1920.50 |
| IMBO | 1093.25 | 1099.30 | 1097.90 | 1099.67 | |
| DABC | 108.93 | 108.25 | 108.34 | 108.14 | |
| IMMBO | 3173.05 | 3134.05 | 3148.59 | 3132.99 | |
| Ta34 | ILSMRLS | 2102.98 | 1911.52 | 2009.56 | 2056.72 |
| IMBO | 1086.26 | 1097.10 | 1095.33 | 1089.54 | |
| DABC | 109.96 | 107.98 | 108.21 | 107.21 | |
| IMMBO | 3160.43 | 3143.98 | 3147.07 | 3129.43 | |
图6
图6
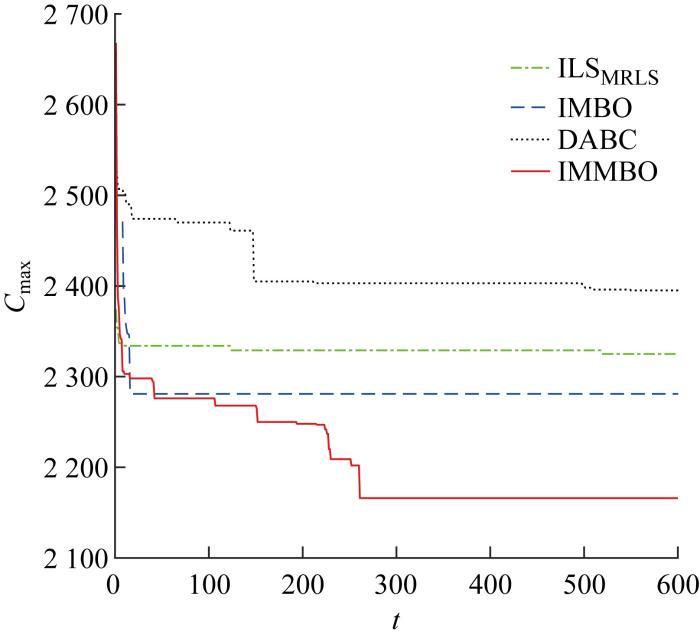
算例Ta56中SSD125_P3_50的4个算法收敛曲线图
Fig.6
Convergence of 4 algorithms for case SSD125_P3_50 of Ta56
图7
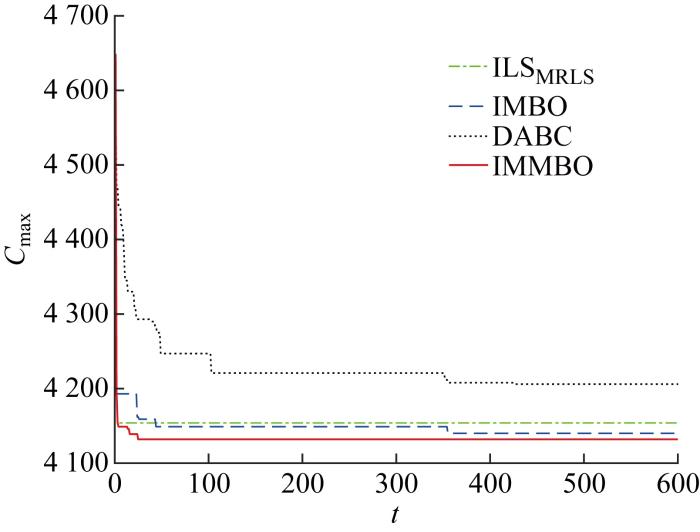
图7
算例Ta60中SSD50_P13_50的4个算法收敛曲线图
Fig.7
Convergence of 4 algorithms for case SSD50_P13_50 of Ta60
4 结语
针对有较强工业背景的HFS-SDST问题,提出IMMBO算法,优化调度目标是找到使最大完成时间最短的工件在第1阶段机器上的加工顺序,即使Cmax最小的调度解.首先,采用MNEH初始化种群,并将其随机分配到各子种群,子种群规模为3,由1个领飞鸟和2个跟飞鸟组成.然后采用多种群候鸟迁徙算法的各子种群独立并行搜索和 DWOA算法实现子种群信息交互,同时加入LS和种群多样化控制策略平衡算法的探索和开发能力.为了使算法在最佳状态下求解HFS-SDST问题,针对IMMBO算法进行参数调整和算法各部分的性能测试,为了验证算法的有效性,与ILSMRLS、IMBO和DABC算法进行比较.结果表明,IMMBO的优化效果优于其他算法,且在进化前期所提算法有较快的收敛速度,后期能够跳出局部最优.
参考文献
An immune algorithm approach to hybrid flow shops scheduling with sequence-dependent setup times
[J].DOI:10.1016/j.amc.2005.11.136 URL [本文引用: 3]
混合流水车间调度问题研究综述
[J].
DOI:10.3969/j.issn.1004-132X.2020.23.004
[本文引用: 2]

混合流水车间在流水车间的基础上,在所有或部分阶段引入多台可选择的并行机器,提高了车间的生产能力和柔性,是车间调度领域的研究热点之一。按阶段数和机器特征对混合流水车间调度方法进行了综述,系统总结了实际工程背景下相关扩展问题的研究现状,并指出了当前研究中存在的问题和可能的解决途径。结合运筹学的发展趋势,对混合流水车间调度在新兴领域中的应用前景进行了探讨。最后,指出了未来若干可能的研究方向。
Review on hybrid flow shop scheduling problems
[J].
DOI:10.3969/j.issn.1004-132X.2020.23.004
[本文引用: 2]

Hybrid flow shop scheduling problems (HFSP), one of popular research topics in the field of shop scheduling, several alternative parallel machines in all or part of stages of the flow-shop were introduced, and production capacity and flexibility of the shop were improved. Hybrid flow-shop scheduling methods were reviewed according to the number of stages and machine characteristics herein. Related extension problems in background of practical engineering were systematically summarized, and the existing problems and possible solutions were pointed out. Combined with development trend of operations research, application prospect of HFSP in emerging fields was discussed. Finally, some possible research directions in future were pointed out.
Enhanced migrating birds optimization algorithm for the permutation flow shop problem with sequence dependent setup times
[J].DOI:10.1016/j.ejor.2017.06.027 URL [本文引用: 3]
时间约束混合流水车间调度问题综述
[J].
A survey on time constrained hybrid flow shop scheduling problems
[J].
Scheduling hybrid flowshops with sequence dependent setup times to minimize makespan and maximum tardiness
[J].DOI:10.1007/s00170-008-1569-3 URL [本文引用: 1]
Heuristic algorithms for scheduling hybrid flow shops with machine blocking and setup times
[J].DOI:10.1007/s40430-017-0921-7 URL [本文引用: 1]
Iterated greedy algorithms enhanced by hyper-heuristic based learning for hybrid flexible flowshop scheduling problem with sequence dependent setup times: A case study at a manufacturing plant
[J].DOI:10.1016/j.cor.2020.105044 URL [本文引用: 1]
考虑能耗和准时的混合流水线多目标调度
[J].
Multi-objective hybrid flow-shop scheduling problem considering energy consumption and on-time delivery
[J].
An agent-based genetic algorithm for hybrid flowshops with sequence dependent setup times to minimise makespan
[J].DOI:10.1016/j.eswa.2012.01.158 URL [本文引用: 1]
Effective metaheuristics for scheduling a hybrid flowshop with sequence-dependent setup times
[J].DOI:10.1016/j.amc.2017.01.004 URL [本文引用: 5]
A Pareto-based adaptive variable neighborhood search for biobjective hybrid flow shop scheduling problem with sequence-dependent setup time
[J].
Scheduling hybrid flowshop with sequence-dependent setup times and due windows to minimize total weighted earliness and tardiness
[J].DOI:10.1016/j.cie.2019.06.057 URL [本文引用: 3]
Migrating birds optimization: a new metaheuristic approach and its performance on quadratic assignment problem
[J].DOI:10.1016/j.ins.2012.06.032 URL [本文引用: 1]
An improved migrating birds optimisation for a hybrid flowshop scheduling with total flowtime minimisation
[J].DOI:10.1016/j.ins.2014.02.152 URL [本文引用: 2]
An improved migrating birds optimization algorithm for a hybrid flow shop scheduling within steel plants
[J].
DOI:10.3390/math8101661
URL
[本文引用: 1]

Steelmaking and the continuous-casting (SCC) scheduling problem is a realistic hybrid flow shop scheduling problem with continuous-casting production at the last stage. This study considers the SCC scheduling problem with diverse products, which is a vital and difficult problem in steel plants. To tackle this problem, this study first presents the mixed-integer linear programming (MILP) model to minimize the objective of makespan. Then, an improved migrating birds optimization algorithm (IMBO) is proposed to tackle this considered NP-hard problem. In the proposed IMBO, several improvements are employed to achieve the proper balance between exploration and exploitation. Specifically, a two-level decoding procedure is designed to achieve feasible solutions; the simulated annealing-based acceptance criterion is employed to ensure the diversity of the population and help the algorithm to escape from being trapped in local optima; a competitive mechanism is developed to emphasize exploitation capacity by searching around the most promising solution space. The computational experiments demonstrate that the proposed IMBO obtains competing performance and it outperforms seven other implemented algorithms in the comparative study.
An improved migrating birds optimization for an integrated lot-streaming flow shop scheduling problem
[J].DOI:10.1016/j.swevo.2017.06.003 URL [本文引用: 1]
基于改进候鸟迁徙优化的多目标批量流混合流水车间调度
[J].
A modified migrating birds optimization for multi-objective lot streaming hybrid flowshop scheduling
[J].
A hybrid metaheuristic algorithm for a parallel machine scheduling problem with dependent setup times
[J].DOI:10.1016/j.cie.2019.03.051 URL [本文引用: 1]
Improved multipopulation discrete differential evolution algorithm for the scheduling of multipurpose batch plants
[J].DOI:10.1021/acs.iecr.0c06041 URL [本文引用: 1]
A shuffled multi-swarm micro-migrating birds optimizer for a multi-resource-constrained flexible job shop scheduling problem
[J].DOI:10.1016/j.ins.2016.08.046 URL [本文引用: 1]
PSO-based improved multi-flocks migrating birds optimization (IMFMBO) algorithm for solution of discrete problems
[J].DOI:10.1007/s00500-018-3199-5 [本文引用: 1]
A simple and effective iterated greedy algorithm for the permutation flowshop scheduling problem
[J].DOI:10.1016/j.ejor.2005.12.009 URL [本文引用: 1]
The whale optimization algorithm
[J].DOI:10.1016/j.advengsoft.2016.01.008 URL [本文引用: 2]
Synthetic and real benchmarks for complex flow-shops problems
[R].