基于周向应变分析的重载轮胎垂向力估计算法

doi:10.16183/j.cnki.jsjtu.2022.249

基于周向应变分析的重载轮胎垂向力估计算法

刘钇汛, 刘志浩^,, 高钦和, 黄通, 马栋

火箭军工程大学导弹学院,西安 710025

Vertical Force Estimation of Heavy-Loaded Radial Tire Based on Circumferential Strain Analysis

LIU Yixun, LIU Zhihao^,, GAO Qinhe, HUANG Tong, MA Dong

School of Missile Engineering, Rocket Force University of Engineering, Xi’an 710025, China

通讯作者: 刘志浩,副教授;E-mail:liuzh_epgc@163.com.

责任编辑: 王一凡

收稿日期: 2022-07-1 修回日期: 2022-09-20 接受日期: 2022-09-29

基金资助:

国家自然科学基金资助项目(51905541)
装发基础研究项目(514010502-302)
陕西省自然科学基础研究计划(2020JQ487)
陕西省高校科协青年人才托举计划(20190412)

Received: 2022-07-1 Revised: 2022-09-20 Accepted: 2022-09-29

作者简介 About authors

刘钇汛(1997-),硕士生,从事智能轮胎信息感知研究.

摘要

为实现对轮胎垂向力的量化估计,开展了基于周向胎内应变分析的重载轮胎垂向力估计算法研究.建立16.00R20重载轮胎有限元模型,通过轮胎加载实验和模态振动实验对比发现模型垂向刚度误差和振动频率误差分别在7.79%和5.49%以内,验证了模型的有效性;利用有限元方法研究了垂向力对轮胎接地特性和内衬层周向应变的影响规律,根据周向应变曲线特征分析了周向应变与接地角的关系,提出并验证了轮胎接地角表征指标,3个表征指标误差均小于8%;以接地角和接地长度作为辨识特征,结合灰狼优化算法和支持向量回归机建立垂向力估计模型,通过有限元仿真对比验证估计精度.结果表明:结合应变曲线零阶、一阶、二阶导数特征点间距角的表征指标能较准确估算接地角;基于灰狼支持向量回归机的垂向力估计算法估计效果良好,估计值与有限元仿真值误差在1.8%以内,能够准确地估算轮胎垂向力.

关键词： 有限元模型; 周向应变; 垂向力; 支持向量回归机

Abstract

In order to realize the quantitative estimation of tire vertical force, the algorithm of heavy-loaded tire vertical force estimation based on circumferential strain analysis is studied. A finite element analysis model of 16.00R20 tire is established. A comparison of tire loading test and modal vibration test indicates that the vertical stiffness error and vibration frequency error of the model are less than 7.79% and 5.49% respectively, which verifies the validity of the model. Using the finite element method, the influence of vertical force on tire grounding characteristics and circumferential strain of inner liner is studied. The characterization index of tire contact angle is proposed and verified by circumferential strain analysis, and the errors of the three indexes are all less than 8%. Taking the grounding angle and grounding length as identification features, the vertical force estimation model is established by combining grey wolf optimization (GWO) and the support vector regression (SVR), and the estimation accuracy is verified by finite element simulation. The results indicate that the characterization index in combination with the of characteristic point spacing angle of zero-order, first-order and second-order derivative of strain curve can accurately estimate tire contact angle. The error between the estimated value of the vertical force estimation algorithm based on GWO-SVR and the finite element simulation value is less than 1.8%.

Keywords： finite element analysis model; circumferential strain; vertical force; support vector regression (SVR)

PDF (14550KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘钇汛, 刘志浩, 高钦和, 黄通, 马栋. 基于周向应变分析的重载轮胎垂向力估计算法[J]. 上海交通大学学报, 2023, 57(10): 1273-1281 doi:10.16183/j.cnki.jsjtu.2022.249

LIU Yixun, LIU Zhihao, GAO Qinhe, HUANG Tong, MA Dong. Vertical Force Estimation of Heavy-Loaded Radial Tire Based on Circumferential Strain Analysis[J]. Journal of Shanghai Jiaotong University, 2023, 57(10): 1273-1281 doi:10.16183/j.cnki.jsjtu.2022.249

特种车辆行驶过程中,轮胎是整车与路面接触的唯一部件.轮胎与地面接触面产生车辆运动所需的力与力矩,且轮胎-路面接触面内存在复杂三维速度场^[1].轮胎与路面的相互作用信息对改进车辆的平顺性^[2]、操纵稳定性^[3]、动力性^[4]、制动性^[5]等性能指标有着重大参考作用.轮胎垂向力影响着车辆垂向振动特性,对车辆平顺性的控制和车辆参数估计有重要意义.

轮胎力信息对车辆控制系统至关重要,但车辆行驶中轮胎力动态测量受到技术和成本的限制很难实现.先前国内外学者建立了多种车辆动力学模型估算轮胎力,例如解析模型中被广泛应用的LuGre模型和Brush轮胎模型^[6-7],经验模型中的Rill模型、Burckhardt轮胎模型^[8-9]等.但由于经验模型无法描述动态特性和非线性特征,解析模型存在影响因素表征不够完善、使用范围限制较大等缺陷,仅依靠车辆动力学模型难以完成对轮胎力的实时估计.

随着传感器技术的巨大改进和进步,结合传感技术的智能轮胎为轮胎动态信息的感知获取提供了新思路,利用传感器测量实际的轮胎动态数据,再通过算法分析进行轮胎状态和参数的估计.近些年来,一些学者对轮胎垂向力的估计算法进行了相关研究.赵健等^[10]设计了三轴加速度测试微机电系统(MEMS),通过对加速度信号特征的分析提取,利用反向传播(BP)神经网络建立了垂向力估计算法.王国林等^[11]利用环模型分析了接触角与垂向力的关系,结合内衬层加速度数据对垂向力进行估计.梁冠群等^[12]等利用加速度信号估计接地长度,并通过多项式拟合研究垂向力和接地长度及胎压的关系来估测轮胎垂向力.加速度传感器轻巧价廉、结构紧凑,被广泛应用于智能轮胎中,但加速度噪声信号干扰大、加速度信号种类冗杂,特征信息提取较为困难.而应变传感器同样具有轻巧、紧凑、价廉的优点,且信号更单一纯粹,随着柔性传感技术的发展,应变传感器在智能轮胎中的应用获得了更大的空间.

1 重载轮胎有限元模型

随着计算机技术的飞速发展,有限元分析技术成为轮胎结构力学性能设计和分析的重要手段.利用计算机的技术优势能精确描述各种复杂工况下轮胎的形变、受力,准确表达轮胎的力学特性.

1.1 有限元模型的建立

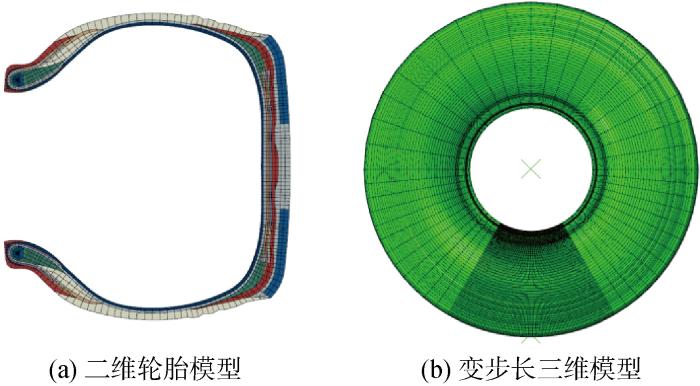
轮胎有限元模型如图1所示.利用AutoCAD软件完成重载轮胎二维结构模型的绘制和建立后,选用HyperMesh软件对轮胎的二维结构模型进行网格划分,如图1(a)所示,完成轮胎二维有限元建模的其余前处理步骤^[13].再参照中心参考点,通过inp文件命令编辑将轮胎二维有限元模型旋转为轮胎三维模型.考虑到轮胎不同部位在运行过程中的应力分布和应变程度存在较大梯度,对轮胎分析结果影响也有较大差异,若旋转步长采用单一尺寸,能够以恒定的采样频率获取节点信号,一定程度上提高了模型的计算精度,且避免了步长变化导致的应力突变.在有限元仿真中,网格越精细,仿真精度越高,但却增加了计算量、资源消耗和降低了收敛率.由于轮胎应变的主要变化区域是在接地区前后,所以对于非接地区的形变与应变的精度要求不高.由二维模型旋转生成三维模型时,采用变旋转步长方法,如图1(b)所示,仅对接地区域附近进行网格细化.在减少计算成本、节省资源的同时,更真实地模拟轮胎接地区的实际行为,提高了接地区应变信号的精度.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 轮胎有限元模型

Fig.1 Finite element model of tire

1.2 模型验证

轮胎垂向刚度是表征轮胎特性的重要参数,对车辆的承载能力和平顺性有着重要影响.而轮胎的接地印记特性直接影响轮胎的使用寿命、磨损状况和轮胎力特性,对车辆的安全性也有重要影响.

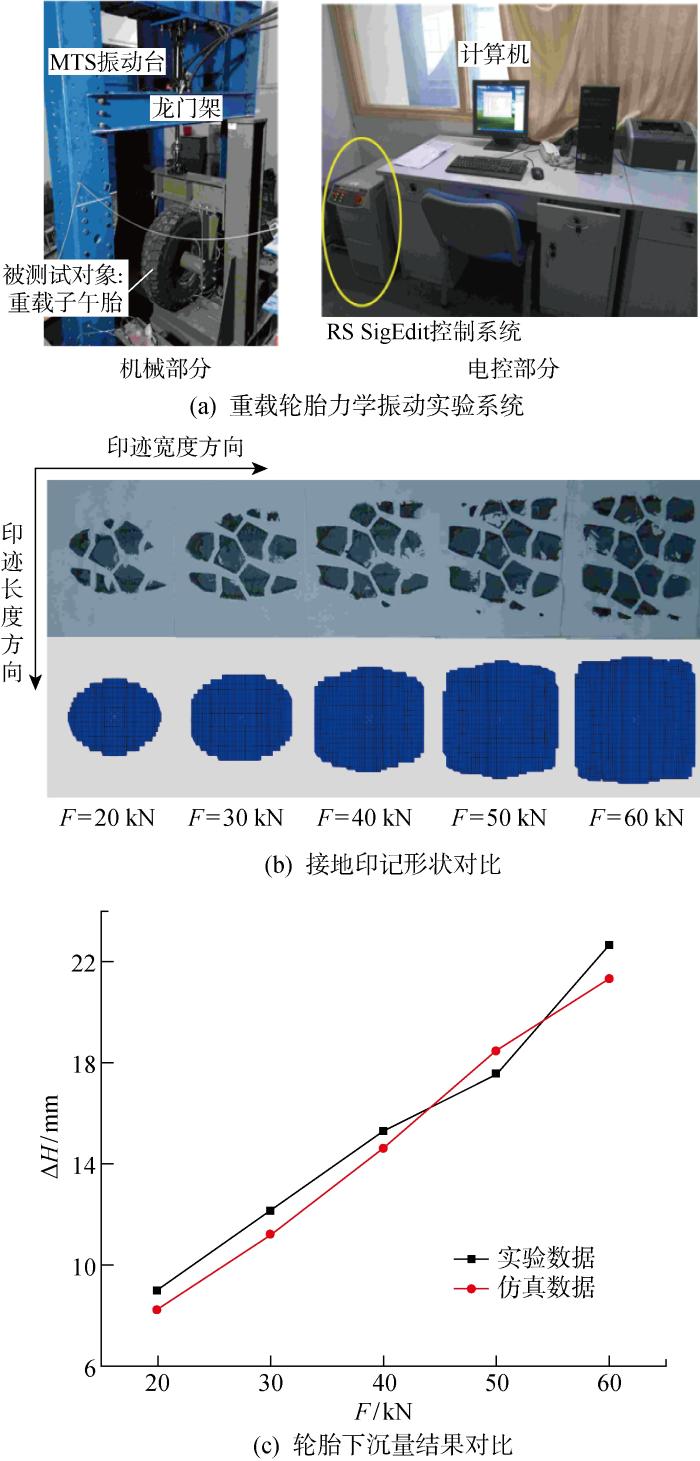
利用重载轮胎力学振动实验系统进行重载轮胎加载实验,如图2所示,获取重载轮胎不同静载荷下接地印记形状和轮胎下沉量,实验系统如图2(a)所示.对比有限元仿真结果进行接地印记特性和垂向刚度验证,结果如图2(b)、2(c)所示.图中:F为加载力;ΔH为下沉量.由图可知,各载荷下实验与仿真的轮胎接地印记形状均对应相似;轮胎下沉量随载荷增大,变化趋势一致,误差最大为7.79%.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 重载轮胎加载实验验证

Fig.2 Verification of tire loading experiment

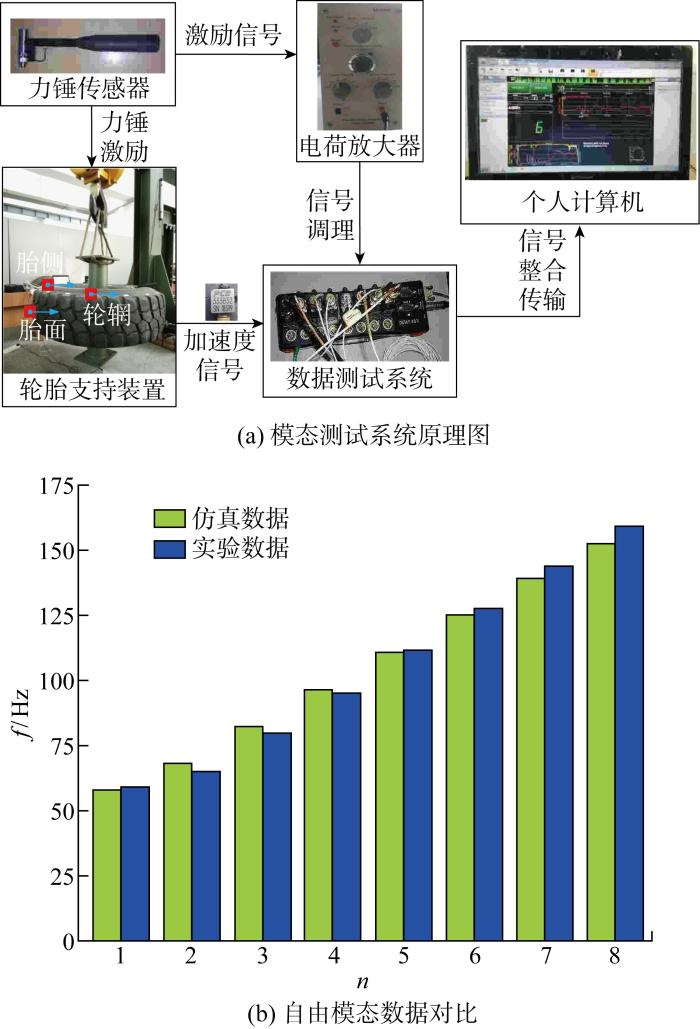
轮胎的模态参数可以表征其振动特性,与轮胎的充气压力和约束条件有直接关系.本文搭建重载轮胎模态测试系统如图3所示.图中:f为频率;n为阶次.模态测试系统包括:轮胎支撑装置、力锤及电荷放大器、数据测试系统和个人计算机.利用模态测试系统对轮辋自由状态下的轮胎进行力锤锤击实验,提取了轮胎前8阶径向振动模态振型.对比实验测试模态结果和有限元仿真的解析模态结果,发现两者振型顺序一致,同振型对应的特征频率误差最大为5.49%.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 重载轮胎模态实验验证

Fig.3 Verification of tire modal experiment

上述实验结果表明:所建轮胎有限元模型的垂向刚度和模态参数同实胎具有较好的一致性,能够可靠反映轮胎的真实力学特性,模型的精度和真实性满足后续研究的条件.

2 轮胎垂向力与周向应变的关系

车辆运行过程中,只有轮胎胎面与地面是直接接触的,在胎面上安装传感器获取的信号能最直观地反映轮胎的形变与受力.但胎面上的传感器信号对外界干扰因素响应较大,信号曲线特征杂乱,且传感器安装难度较大.目前多数学者选择将传感器安装在内衬层上,王国林等^[14]采用基于方差的全局灵敏度分析法研究了内衬层轮胎力敏感区域,其中胎冠区对于周向应变的响应最为灵敏.考虑到静载和直线滚动下轮胎的受力和形变关于胎面中心线对称,选择胎面中心点作为应变传感器安装点.

2.1 重载轮胎静载接地特性分析

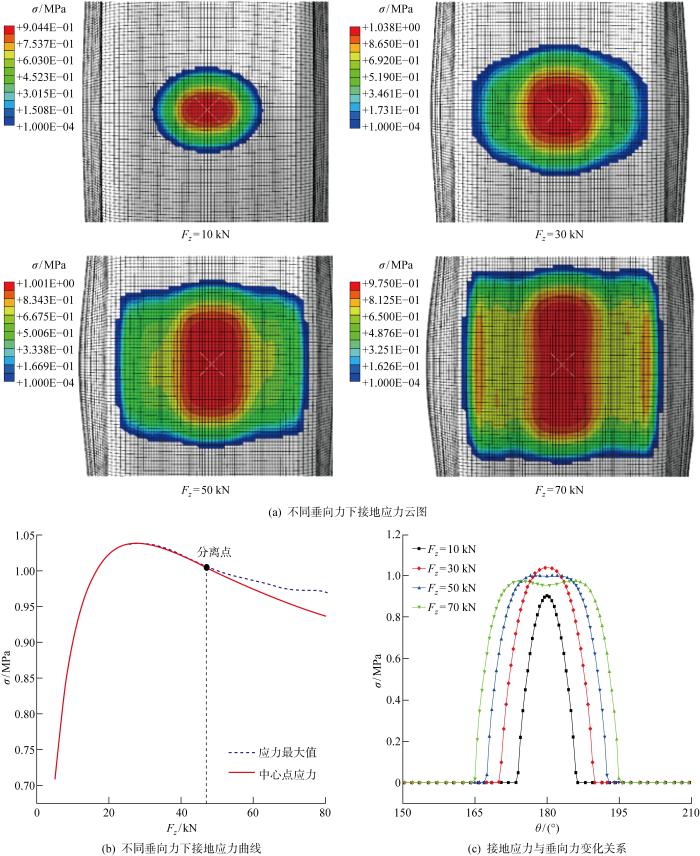
利用轮胎有限元模型对不同垂向力F_z下的静载工况进行仿真,对轮胎接地胎面中心线接地应力σ进行提取分析,结果如图4所示.图中:θ为测量点位与穿过有限元模型中心的横轴方向之间的角度.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 静载荷对接地特性的影响规律

Fig.4 Effect of static load on tire grounding characteristics

从图4可以看出:随垂向力增大,接地印记形状从椭圆形向矩形转变,轮胎接地印记长度持续增加,接地宽度在增长至接近胎面宽度后基本不再变化;接地区中心点接地应力和接地应力最大值均先快速增大后缓慢减小,F_z=28 kN时接地应力达到最大值;当F_z>47 kN时,接地应力最大值和中心点接地应力开始出现显著差值,接地应力曲线由上凸抛物线变为马鞍形,接地应力最大值点由中心点向两侧偏移.

通过接地应力曲线提取轮胎前后接地角ϕ_f和ϕ_r,结合接地长度计算公式求解各垂向力下的接地长度:

(1)L=R(sin ϕ_f+sin ϕ_r)

式中:R为轮胎充气后自由状态半径;静载状态前后接地角相等,ϕ_f=ϕ_r.

与有限元仿真值进行对比,结果如图5所示.接地长度的公式计算结果与仿真结果误差最大为1.3%,一致性较高;随着垂向力从5 kN增大到80 kN,接地长度和接地角不断增大,但增长幅度不断减小.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 接地参数与垂向力关系

Fig.5 Tire grounding parameters versus vertical force

2.2 重载轮胎静载周向应变分析

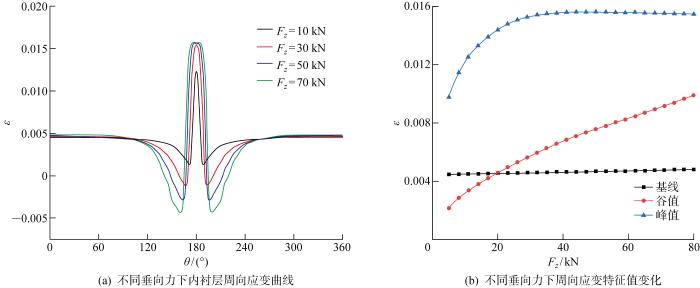
通过有限元仿真对0.8 MPa标准胎压、不同静载荷工况轮胎的内衬层周向应变曲线进行仿真分析,结果如图6所示.图中:ε为周向应变.可以看出:垂向力由5 kN增大到80 kN过程中,由于非接地区的作用力基本不变,导致周向应变曲线基线值无明显变化;随垂向力增大,曲线谷值和谷值间距角均呈现降幅增长.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 垂向力对周向应变的影响规律

Fig.6 Effect of vertical force on circumferential strain

结合图4(c)和图6(b),发现曲线峰值随垂向力变化趋势与接地应力变化趋势相似,先快速增大到最大值后再缓慢减小.垂向力从5 kN增大到28 kN过程中,应变曲线与接地应力曲线均处于快速增长状态;垂向力在28 kN到47 kN范围内增长时,接地应力随垂向力增大开始减小,应变曲线峰值以极小幅度增长;当垂向力超过47 kN时,应变峰值开始缓慢减小,接地中心附近的应变曲线也出现马鞍形;在各程度垂向力下,接地区范围的轮胎内衬层周向应变曲线与接地应力曲线形状相似度都极高.

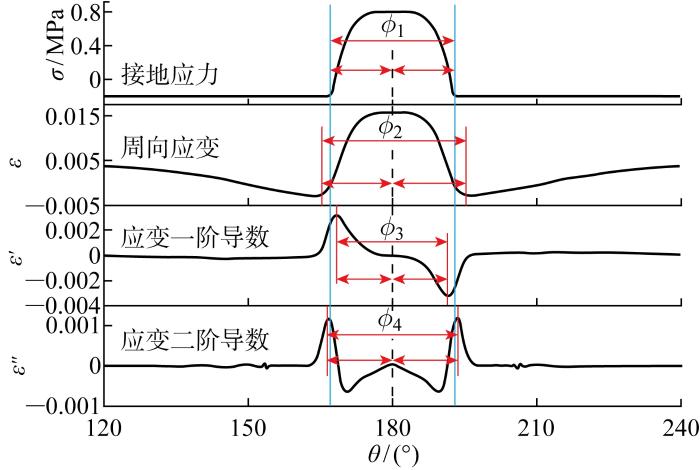
2.3 基于内衬层周向应变的接地角估计

通过上述分析可以发现,轮胎内衬层周向应变曲线的相邻谷值的间距角度、轮胎接地角、接地印记长度随垂向力均呈正相关,且三者曲线趋势相似.本文认为,轮胎接地角与周向应变曲线谷值间距角密切相关,可通过周向应变曲线特征参量表征轮胎接地角.

提取0.8 MPa标准压力、静载荷下的模型有限元仿真计算结果,如图7所示.图中:ϕ₁为实际接地角;ϕ₂为周向应变零阶导数曲线特征点间距角;ϕ₃为周向应变一阶导数曲线特征点间距角;ϕ₄为周向应变二阶导数曲线特征点间距角.将接地角与周向应变零阶、一阶、二阶导数曲线特征点间距角进行对比,不同垂向力下的应变曲线特征点间距角结果如表1所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 内衬层周向应变曲线特征点角度差与接地角对比图

Fig.7 Comparison of characteristic point angle difference and contact angle of circumferential strain curve of tire inner liner

表1 不同垂向力下应变曲线特征点间距角

Tab.1 Spacing angle of characteristic points of strain curve at different vertical forces

F_z/kN	ϕ₁/(°)	ϕ₂/(°)	ϕ₃/(°)	ϕ₄/(°)
10	13	17	11	13
20	17	22	14	18
30	20	26	17	21
40	23	29	20	24
50	26	32	23	27
60	28	35	26	29
70	31	38	28	32

新窗口打开| 下载CSV

由表1可见,周向应变曲线谷值间距角和应变二阶导数峰值间距角均大于接地角,应变一阶曲线峰谷值间距角小于接地角,且随垂向力增大,误差角度越大.单靠一类应变曲线难以准确表征接地角,考虑选用多类间距角均值作为接地角表征指标.由于接地角夹在应变零阶、二阶与一阶特征点间距角之间,提出均值表征指标C_A1、C_A2、C_A3,与接地角误差分别为δ₁、δ₂、δ₃,则有:

(2)

\begin{array}{l} C_{A 1} = \frac{ϕ_{2} + ϕ_{3}}{2}, δ_{1} = \frac{| C_{A 1} - ϕ_{1} |}{2} \\ C_{A 2} = \frac{ϕ_{3} + ϕ_{4}}{2}, δ_{2} = \frac{| C_{A 2} - ϕ_{1} |}{2} \\ C_{A 3} = \frac{ϕ_{2} + ϕ_{3} + ϕ_{4}}{2}, δ_{3} = \frac{| C_{A 3} - ϕ_{1} |}{2} \end{array}\}

不同表征指标误差结果如表2所示.由表2可见,C_A1、C_A2、C_A3对接地角均有较好的表征效果,C_A1和C_A3在不同垂向力作用下,误差值较为稳定,但基本在5%~7%范围内;C_A2在大载荷下误差值能维持在4%内,但在小载荷下误差值偏大.造成C_A2误差变化的原因主要是小载荷下,接地角和应变一阶导数特征角较小,模型网格精度对角度影响误差被放大.16.0020重载轮胎的标准载荷为 63700 N 大载荷,所以C_A2更适合作为接地角的表征指标.

表2 不同表征指标误差结果

Tab.2 Error results of different characterization indexes

F_z/kN	δ₁/%	δ₂/%	δ₃/%
10	7.69	7.69	5.12
20	5.88	6.67	5.88
30	7.50	5.00	6.67
40	6.52	4.34	5.79
50	5.77	3.85	5.12
60	8.93	1.78	7.14
70	6.45	3.22	5.38

新窗口打开| 下载CSV

3 垂向力估计模型

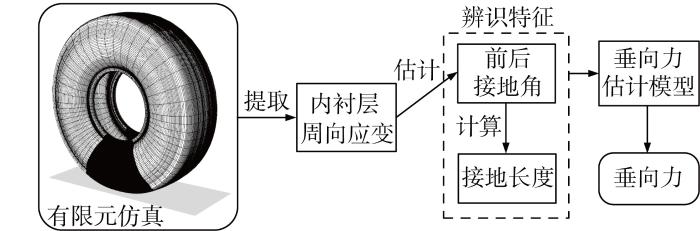
通过上述分析发现,垂向力与接地角之间关系密切,且已有学者通过柔性环模型建立了接地角与垂向力的关系方程.但通过数学方程计算垂向力所需轮胎参数较多、公式较为复杂,且公式本身存在误差和参数获取过程的误差,会造成垂向力估计精度下降.采用建立黑盒系统的方法,在确立接地角、接地长度与垂向力的输入输出关系后,通过有限元仿真获取数据集,建立估计模型对垂向力进行预测,垂向力估计流程图如图8所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 垂向力估计流程图

Fig.8 Flow chart of vertical force estimation

3.1 基于灰狼支持向量回归机的垂向力估计模型

估计模型所需的大量数据集在实际获取上存在困难,而支持向量回归机可在小样本数据集下取得良好性能,且具有较好鲁棒性、泛化能力优秀等优点^[15-16].惩罚系数C是对误差的容忍度,核函数参数γ决定模型的泛化性,支持向量机的精度主要由这两个参数决定.

GWO算法是Mirjalili等^[17]受灰狼群捕猎行为提出的优化搜索算法,具有良好的收敛性能、参数少、易实现等优点.GWO算法优化过程包括主要狼群等级分层、搜索包围猎物和狩猎攻击猎物.

(1) 狼群等级分层.在搜索空间随机生成狼群后,将狼群中适应度最好的3匹灰狼依次标记为α、β和δ,余下的均划分为ω,每次迭代后重复分级过程.

(2) 搜索包围猎物.灰狼在攻击猎物前先对猎物的位置进行确定,通过协同系数向量μ和B、随机向量r₁和r₂调整对猎物的搜索模式和搜索方向.|μ|>1时,狼群外散进行全局搜索;|μ|<1时,狼群对某区域进行局部搜索.

(3)D=|BX_p(t)-X(t)|

(4)X(t+1)=X_p(t)-μD

(5)μ=(2a|r₂|-a)r₂

(6)B=2r₁

式中:D为当前狼与猎物之间的距离;X_p(t)为第t代猎物位置向量;X(t)为第t代当前狼位置向量;整个迭代过程中a由2线性降到0;r₁和r₂为[0,1]中的随机向量.

(3) 狩猎.灰狼群在迭代后,α、β和δ3匹狼与猎物距离最近,3匹狼利用自身与猎物间的距离联合指导其他ω狼调整位置围剿猎物.

(7)D_k=|C_iX_k(t)-X(t)|

(8)X_i=X_k-μ_iD_k

(9)X_p(t+1)=

\frac{X_{1} + X_{2} + X_{3}}{3}

式中:k=α,β,δ;i=1,2,3;X_p(t+1)为第t+1代猎物位置向量;X_i定义了ω狼朝高等级狼前进的方向和步长;X_p(t+1)定义了ω狼的最终位置.

选用支持向量回归机建立轮胎垂向力估计模型,利用灰狼算法实现对SVR参数C和γ进行寻优,以实现对轮胎垂向力的预测.

3.2 特征集获取与模型训练

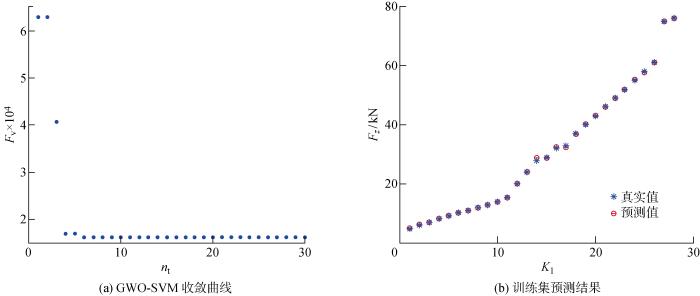
根据垂向力与接地角、接地长度的关系,将接地角ϕ、接地长度L作为估计模型的特征参数.通过有限元对轮胎模型进行5 kN到80 kN静载工况的仿真计算,提取内衬层周向应变,结合接地角表征指标C_A₂和式(1)求解接地角和接地长度.总共采集了56个样本,选取28个作为训练集,用于垂向力估计模型的训练,其余的作为测试集来检验模型的训练效能.基于灰狼算法对支持向量机参数C、γ寻优过程的适应度变化曲线和训练集预测结果如图9所示.图中:F_v为适应度;n_t为迭代次数;K₁为训练集样本编号.可以看出,适应度迅速下降并稳定在了0.000 16附近,收敛性良好,能够较好获取参数最优解;模型训练集均方根误差为 0.258 7 kN,平均绝对误差为1.06%.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 模型训练结果

Fig.9 Results of model training

3.3 垂向力预测结果

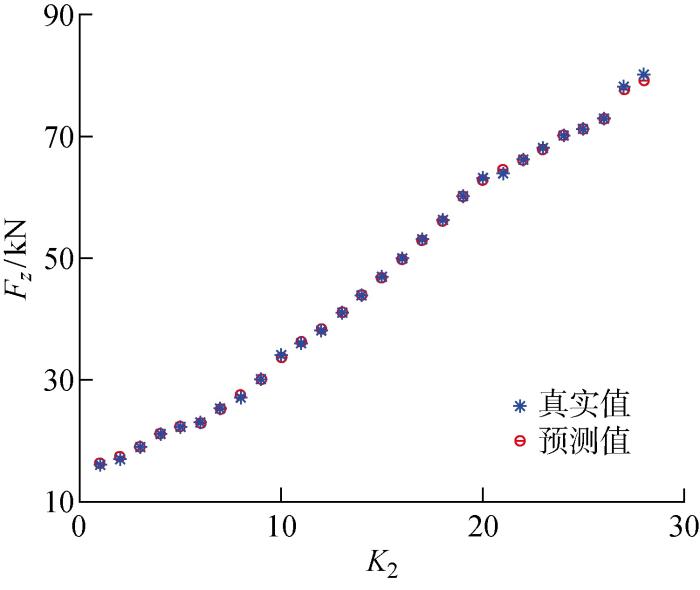
模型测试结果如图10所示.图中:K₂为测试集样本编号.测试集均方根误差为 0.289 4 kN,最大绝对误差为1.79%,决定系数达到99.985%,具有良好的估计精度.可以认为本文所提出的基于周向应变曲线获取接地参数进行垂向力估计的方法是可行的.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 垂向力估测结果

Fig.10 Estimation result of vertical force

4 结语

建立了16.00R20重载轮胎有限元模型,通过加载实验和模态实验对模型进行了垂向刚度和振动特性的双重验证;利用有限元仿真分析了载荷对轮胎接地特性和内衬层周向应变曲线的影响;提出了接地角均值表征指标,对比有限元仿真结果验证了指标可靠性;以接地角、接地长度估算值作为辨识特征,结合灰狼优化算法和支持向量回归机建立了垂向力估计模型.结果表明:接地角、接地长度随垂向力增大降幅增长;周向应变曲线的极值点间距对垂向力变化响应较敏感,垂向力越大,间距越大;采用周向应变零阶、一阶、二阶导数特征点间距角均值作为轮胎接地角表征指标的估计误差均在8%以内,用一阶与二阶间距角均值作为表征指标效果最好;以轮胎接地角和接地长度作为支持向量机的输入特征的垂向力估计模型估测垂向力误差在1.8%以内,能对垂向力进行准确估计.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

危银涛, 沈筱亮.

轮胎稳态运动学与六分力预报I: 理论与方法[J]

机械工程学报, 2012, 48(15): 65-74.

F_z/kN	ϕ₁/(°)	ϕ₂/(°)	ϕ₃/(°)	ϕ₄/(°)
10	13	17	11	13
20	17	22	14	18
30	20	26	17	21
40	23	29	20	24
50	26	32	23	27
60	28	35	26	29
70	31	38	28	32

F_z/kN	ϕ₁/(°)	ϕ₂/(°)	ϕ₃/(°)	ϕ₄/(°)
10	13	17	11	13
20	17	22	14	18
30	20	26	17	21
40	23	29	20	24
50	26	32	23	27
60	28	35	26	29
70	31	38	28	32