伴热分为恒壁温和恒热流两种加热方式,电加热圆管为恒热流加热.恒壁温加热时构件的壁面温度保持恒定,而恒热流加热是以恒定的热流量输入,热量损失小于输入热流量,壁面温度持续升高.受加热方式的影响,对流换热效果也存在一定差异.目前,圆管的对流换热研究主要集中在恒壁温加热方式.文献[4]采用数值模拟研究了二维等温圆管的强制对流,结果表明高雷诺数(Re)范围内传热速率有明显提高.周柏男[5]考虑了数值仿真过程中有限边界对圆管换热产生的影响,提出了不同雷诺数范围内合适的数值模拟方法.Ikhtiar等[6]采用数值模拟研究了二维稳态旋转圆柱的强制对流换热,发现涡脱区域的努塞尔数随风速增大而加大,涡抑制区域的努塞尔数随风速增大而减小.Wan等[7]采用大涡模拟(VLES)、雷诺数平均法和延迟分离涡方法研究了圆柱的对流换热,发现VLES方法在模拟圆柱传热方面优于另外两种方法.李晓辰[8]采用实验和数值模拟研究了低温海水外掠圆管的对流换热,发现圆管对流换热系数随圆管直径增大而加大,且在低雷诺数时,管径对对流换热的影响更加显著,并建立了层流范围内对流换热系数的实验关联式.
极地海洋工程装备的防寒措施通常采用恒热流电加热方式,圆管结构的对流换热在极地复杂环境条件下变化规律不明确,仅仅依据各国船级社的相关规范[11]建议值,极易造成加热量的严重浪费.因此,亟需建立圆管构件的对流换热系数预测模型,为极地海洋工程装备防寒设计提供参考.本文通过数值仿真研究了在温度为-40~0 ℃、风速为 0~40 m/s的条件下,圆管结构的对流换热系数随温度和风速的变化规律,建立了不同温度范围的对流换热系数预测模型.同时,在低温实验室进行了圆管结构对流换热的模型实验,验证了数值模拟的可靠性和对流换热系数预测模型的适用性.
1 电加热圆管对流换热实验
为实现圆管构件在不同风速、温度条件下对流换热系数的准确测定,本文依据牛顿冷却公式,搭建了圆管对流换热系数测定的实验平台.低温实验室可控调节最低温度为-50 ℃,最大风速为 15 m/s,基本可以模拟极地的低温环境.
1.1 实验原理
根据牛顿冷却公式可知,空气横掠圆管损失的热量为
由此可得:
式中:h为圆管对流换热系数; A为圆管换热面积且A=πdl,d为圆管外径,l为圆管长度,Tw和Tf分别为圆管表面和空气的平均温度.
圆管采用电伴热的恒热流加热方式,当圆管表面温度Tw稳定时,可以认为对流换热消耗的热量与实验时电加热输入的热量一致.由式(2)可以计算得到不同风速、温度下圆管构件的对流换热系数.
1.2 实验系统
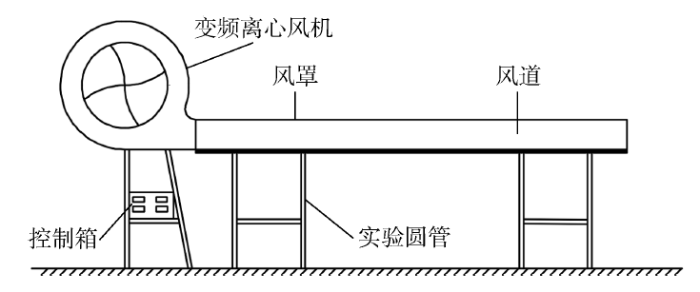
在低温实验室搭建圆管对流换热系数测定试验平台如图1所示.通过控制箱调节变频风机的风速,风道内的风速均匀稳定,能很好地满足实验要求.圆管试件通过隔热效果较好的木材放置在风道内的支撑架上,保证流体经过圆管的均匀性.
图1
图1
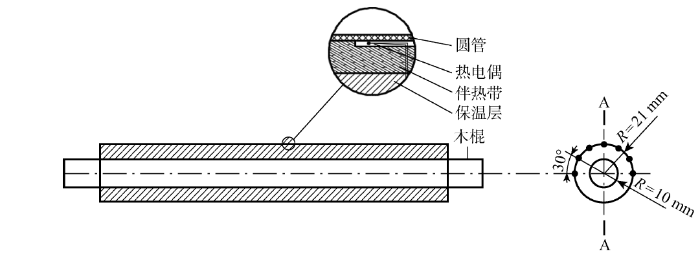
对流换热系数测定实验装置示意图
Fig.1
Experimental device for measuring convective heat transfer coefficient
图2
表1 实验测量装置仪器
Tab.1
| 实验测量装置 | 测量范围 | 精度 |
|---|---|---|
| 温度采集仪1台 | -99~999 ℃ | |
| K型温度热电偶7个测管温,2个测风温 | -50~220 ℃ | 1% |
| NK1000高精度风速仪1台 | 0.6~60 m/s | 3% |
2 电加热圆管对流换热数值仿真
本文通过Fluent有限元分析软件,采用二维建模,根据电加热圆管对流换热实验情况建立物理模型.由于圆管形状不规则,所以采用非结构网格划分,考虑圆管附近以及后部流场变化剧烈,将圆管附近网格进行加密处理,网格总数为 107 583.流体域的进出口分别为速度入口和压力出口.考虑伴热带进行均匀加热,将壁面设置为非滑移边界条件,热边界条件设置为固定热流量,其大小为 1 801.86 W/m2.空气横掠圆管时会产生脱体绕流,考虑边界层受到脱体绕流的影响,数值模拟选择k-ε湍流模型,同时进行非稳态计算.数值分析中,风速为0~40 m/s,温度为 -40~0 ℃.
2.1 仿真结果分析
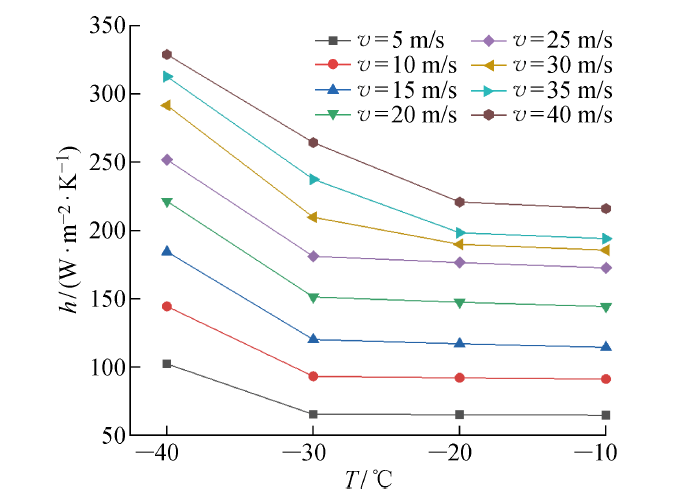
加热圆管对流换热系数随风速和温度的变化如图3和4所示.图中:v为风速;T为温度.由图3可知,增大风速和降低温度都会提高圆管的对流换热系数;当温度在-30~-20 ℃ 内且风速大于 25 m/s,以及当温度低于-30 ℃ 时,风速对圆管对流换热系数影响增大.由图4可知,温差一定时,不同风速下的对流换热系数增幅不同.当温度在-30~-20 ℃ 内且风速大于 25 m/s,以及温度低于-30 ℃ 时,对流换热系数随温度变化的曲线斜率变大,说明该环境条件下,温度对圆管的对流换热系数影响加大. 风速大于 25 m/s 时,绕流脱体的起点后移,脱体区域的扰动强化换热效果减弱,因此,-10 ℃ 和-20 ℃ 时的对流换热系数随风速的变化率减小;而在温度低于-20 ℃时,空气黏性的降低较大地增强了对流换热,在一定程度上抵消了风速引起的换热影响.
图3
图3
不同温度下对流换热系数随风速变化
Fig.3
Convective heat transfer coefficient versus wind speed at different temperatures
图4
图4
不同风速下对流换热系数随温度变化
Fig.4
Convective heat transfer coefficient versus temperature at different wind speeds
2.2 对流换热系数预测模型
表2 对流换热系数仿真分析结果
Tab.2
| T/℃ | v/ (m·s-1) | T对h增幅 影响/% | v对h增幅 影响/% |
|---|---|---|---|
| (-20,0] | <25 | 1.7 | 21.2 |
| >25 | 2.2 | 7.8 | |
| (-30,-20] | <25 | 1.9 | 22.4 |
| >25 | 1.7 | 13.5 | |
| [-40,-30] | <25 | 43.2 | 23.6 |
| >25 | 31.7 | 9.4 |
(1) -20 ℃<T≤0 ℃条件下,风速小于25 m/s时,温度降低10 ℃,对流换热系数增大1.7%;风速增大5 m/s,对流换热系数增大21.2%.风速大于25 m/s时,温度每降低10 ℃,对流换热系数随之增大2.2%;风速每增加5 m/s,对流换热系数随之增大7.8%.
(2) -30 ℃<T≤-20 ℃条件下,当风速小于25 m/s 时,温度每降低10 ℃,对流换热系数增随之大1.9%;风速每增加5 m/s,对流换热系数随之增大22.4%.风速大于25 m/s时,温度每降低10 ℃,对流换热系数随之增大1.7%;风速每增加 5 m/s,对流换热系数随之增大13.5%.
(3) -40 ℃≤T≤-30 ℃条件下,当风速小于25 m/s 时,对流换热系数随温度降低10 ℃而增大43.2%;风速每增加5 m/s,对流换热系数随之增大23.6%.风速大于25 m/s时,温度降低10 ℃,对流换热系数增大31.7%;风速每增加5 m/s,对流换热系数随之增大9.4%.当温度高于-30 ℃时,风速是影响圆管对流换热的主要因素;当温度低于-30 ℃ 时,温度对圆管对流换热的影响显著性增大,风速的影响基本保持不变.
因此,对流换热系数预测模型应充分考虑不同温度、风速的影响.
风速和温度是影响圆管对流换热的主要因素,受温度影响的相关参数变化范围如表3所示.表中:Pr为普朗特数;λ为导热系数.
表3 普朗特数和导热系数的范围
Tab.3
| T/℃ | Pr | λ/(W·m-1·K-1) |
|---|---|---|
| (-30,0] | [0.707,0.723) | [0.022 0, 0.023 6] |
| [-40,-30] | [0.723,0.728] | [0.021 2,0.022 0) |
受温度影响的相关参数变化范围较小,在电加热圆管对流换热数值分析拟合过程中将普朗特数Pr、导热系数λ看作常数.-30 ℃<T≤0 ℃时,Pr为0.715,λ为 0.022 8;-40 ℃≤T≤-30 ℃ 时,Pr为0.726,λ为 0.021 6.对流换热系数在不同温度范围内的数学预测模型可表示为
式中:C1=0.490;m1=0.659;n2=3.141;C2=0.191;m2=0.599;n2=1.680.
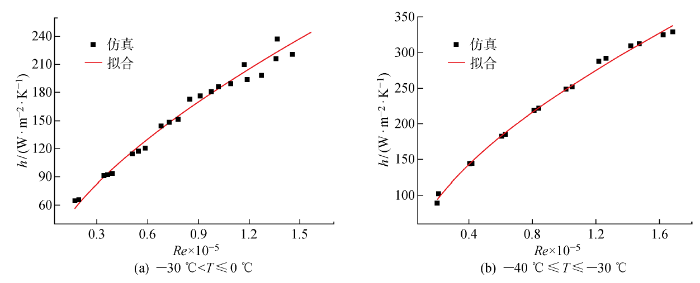
基于式(3),对数值仿真数据进行拟合,结果如图5所示.拟合的统计学结果中决定系数R2分别为98.0%和99.6%,拟合结果可靠度较高.
图5
图5
对流换热系数数值分析拟合结果
Fig.5
Fitted measured data of convective heat transfer coefficients
3 对流换热实验验证
在低温实验室建立了圆管构件电伴热对流换热的实验平台,实现了圆管结构件在不同风速、温度条件下对流换热系数的测定.实验温度控制范围为 -5~-50 ℃;风速为4~13.7 m/s.实验的圆管构件为极地工程装备上部设施扶手的真实构件,尺寸参数为外径0.042 m、内径0.020 m、长0.251 m.
3.1 实验与仿真结果对比分析
在低温实验室进行了24组对流换热实验,实验工况及相应的结果如表4所示.表中:hmea为实测对流换热系数.
表4 实验工况及结果
Tab.4
| 试验编号 | T/℃ | v/(m·s-1) | hmea/(W·m-2·K-1)) |
|---|---|---|---|
| 1 | -5.0 | 4.9 | 60.2 |
| 2 | -5.1 | 8.8 | 78.3 |
| 3 | -4.7 | 13.7 | 101.2 |
| 4 | -10.0 | 5.0 | 60.4 |
| 5 | -10.0 | 8.6 | 77.6 |
| 6 | -10.0 | 13.1 | 98.7 |
| 7 | -15.0 | 5.1 | 61.2 |
| 8 | -14.8 | 9.3 | 79.1 |
| 9 | -14.8 | 13.3 | 99.8 |
| 10 | -20.0 | 5.1 | 61.7 |
| 11 | -19.9 | 9.3 | 78.7 |
| 12 | -19.4 | 13.1 | 97.4 |
| 13 | -25.0 | 4.9 | 59.8 |
| 14 | -25.1 | 8.7 | 78.3 |
| 15 | -24.3 | 12.5 | 98.5 |
| 16 | -30.0 | 4.8 | 60.1 |
| 17 | -29.9 | 8.4 | 76.9 |
| 18 | -29.3 | 12.1 | 97.8 |
| 19 | -34.9 | 4.9 | 94.5 |
| 20 | -35.0 | 8.3 | 117.7 |
| 21 | -34.3 | 11.2 | 129.7 |
| 22 | -39.6 | 4.1 | 87.4 |
| 23 | -39.7 | 7.6 | 112.3 |
| 24 | -40.3 | 11.2 | 127.5 |
对流换热系数的实测值误差主要包含两方面:① 实验测量的圆管温度呈周期性波动,测量温度的K型热电偶精度为1%;② 在处理实验数据时,为减小实验测量误差,每组实验工况进行3次;考虑绕流脱体的影响,数据处理时取每个测点平均值作为圆管总体的平均换热系数.
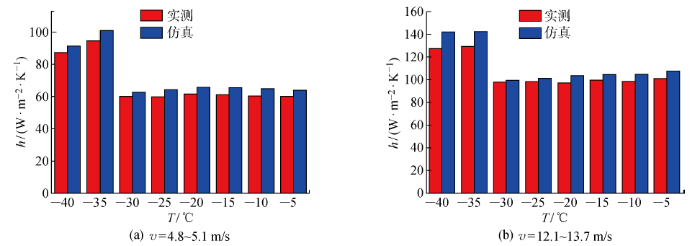
为明确温度对圆管构件对流换热的影响,选取风速大小较接近的实验工况对比分析,其结果如图6所示.由图可知,电加热圆管的对流换热仿真结果与实测结果接近,平均误差为7.5%,验证了数值计算模型的正确性;当温度高于-30 ℃ 并且风速一定时,温度对圆管的对流换热系数影响较小;当温度低于-30 ℃ 时,接近风速工况下的对流换热系数显著增大,表明温度对圆管的对流换热影响增大.
图6
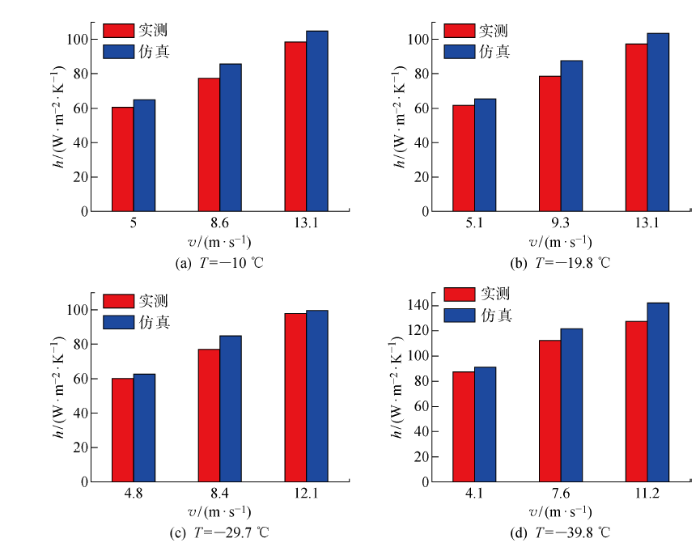
选取温度接近的实验工况下对流换热系数的对比分析,结果如图7所示.由图可知:① 实测结果与仿真结果接近,平均误差为7.3%;② 由于实验过程中风速在较小的范围内波动(通常略低于数值模拟设置的风速),加热圆管过程中存在一定量的热量损失,所以造成实测结果偏小;③ 当温度一定时,圆管的对流换热系数随风速增大而增加.
图7
3.2 对流换热系数预测模型的验证分析
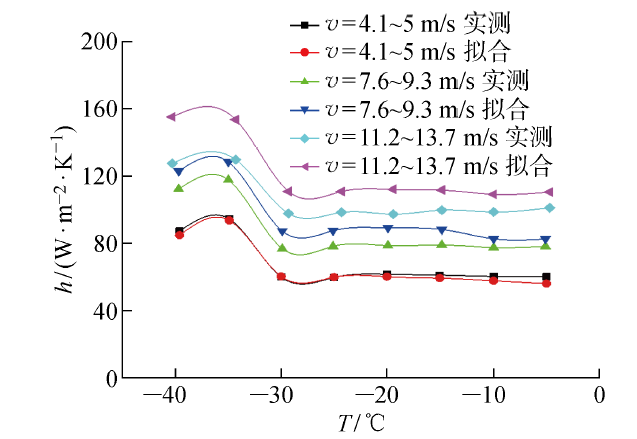
电加热圆管对流换热系数预测模型与实测结果对比如图8所示.当风速在4.1~5.1 m/s内,对流换热系数实测结果与拟合结果比较接近,平均误差为2.6%;当风速在7.6~9.3 m/s内,对流换热系数实测结果大于拟合结果,平均误差为10.1%;当风速在11.2~13.7 m/s内,对流换热系数实测结果大于拟合结果,平均误差为14.1%.综上所述,拟合结果与实测结果误差较小,电加热圆管构件的对流换热系数预测模型可以为极地海洋工程装备防寒设计提供一定的参考.
图8
4 结论
本文通过Fluent有限元软件,数值模拟研究了温度-40~0 ℃、风速0~40 m/s内电加热圆管的对流换热系数变化情况,仿真结果表明:① 增大风速和降低温度都会使圆管的对流换热系数增大;② 当温度低于-30 ℃ 时,温度对圆管的对流换热系数影响增大;③ 当风速大于 25 m/s且温度降低至-20 ℃ 以下时,温度对圆管的对流换热系数影响增大;④ 基于仿真数据建立了圆管的对流换热系数预测模型.
在低温实验室,搭建了面向极地海洋工程装备电加热圆管构件对流换热实验平台,研究了温度-40~0 ℃、风速0~13.7 m/s内电加热圆管的对流换热系数变化情况.实验结果表明:①仿真结果与实测结果比较接近,验证了数值模拟的合理性;②当温度低于-30 ℃时,温度对圆管化热影响增大,与仿真结果一致;③验证了基于仿真建立的对流换热系数预测模型在一定风速范围内的适用性,预测模型误差较小,满足工程要求.
极地海洋工程装备上部设施构件繁多,本文仅对电加热圆管构件的对流换热影响进行了分析,其他构件(例如平板等规则构件、踏步等非规则构件等)还需要进一步开展研究.
参考文献
基于Fluent和FENSAP-ICE的极区海洋平台甲板结构结冰数值模拟
[J].
DOI:10.13679/j.jdyj.20190033
[本文引用: 1]

极区自然资源丰富却气候恶劣, 海洋平台在此地区作业时甲板表面极易出现结冰现象。针对极区海洋平台甲板结构结冰问题, 采用Fluent与FENSAP-ICE软件相结合的方法, 分析在过冷雾和过冷雨条件下, 距海面高度和结构特征长度对甲板结构结冰的影响。结果表明: 当特征风速为5 m·s<sup>–1</sup>、6 m·s<sup>–1</sup>和7 m·s<sup>–1</sup>时, 在风速不变的条件下, 随着距海面高度由2 m增加到20 m, 结构表面的平均结冰厚度均逐渐增加且结构表面的结冰相对增长率逐渐减小; 在特征风速为5m·s<sup>–1</sup>条件下, 在距海面高度为20 m和80 m处, 随着结构特征长度由1 m增加到30 m时, 结构表面的平均结冰厚度均逐渐减小且减少程度逐渐减缓。
Numerical simulations of deck structure icing on polar offshore platforms based on fluent and fensap-ice
[J].
DOI:10.13679/j.jdyj.20190033
[本文引用: 1]

<p>The polar region is rich in natural resources, but the climate is harsh. The deck surface of offshore platforms in this region is prone to icing, which is dangerous. To investigate factors affecting the icing of deck structures on polar marine platforms, a combination of the software programs Fluent and FENSAP-ICE was used to analyze the influence of sea surface height and structure length on deck icing under conditions of supercooled fog and rain. The results showed that when Characteristic wind speeds were 5 m·s<sup>–1</sup>, 6 m·s<sup>–1</sup> and 7 m·s<sup>–1</sup>, average ice thickness on the structure surface increased gradually with height from 2 m to 20 m and the relative growth rate of ice on the structure surface decreased gradually. Additionally, when Characteristic wind speed was 5 m·s<sup>–1</sup> at altitudes of 20 m and 80 m above sea level, the length of the structure increased from 1 m to 30 m, and average ice thickness on the structure surface and degree of reduction decreased.</p>
船舶防冻除冰技术现状与发展
[J].
Present situation and development of de-icing and prevent frostbite technology of ships
[J].
Heat transfer from a heated non-rotating cylinder performing circular motion in a uniform stream
[J].DOI:10.1016/j.ijheatmasstransfer.2017.04.097 URL [本文引用: 1]
Free stream flow and forced convection heat transfer around a rotating circular cylinder subjected to a single gust impulse
[J].DOI:10.1016/j.ijheatmasstransfer.2016.04.045 URL [本文引用: 1]
Very Large Eddy Simulation of turbulent flow and heat transfer for single cylinder and cylindrical pin matrix
[J].DOI:10.1016/j.applthermaleng.2020.114972 URL [本文引用: 1]
A correlating equation for forced convection from gases and liquids to a circular cylinder in crossflow
[J].DOI:10.1115/1.3450685 URL [本文引用: 1]
Unsteady computation of flow field and convective heat transfer over tandem cylinders at subcritical Reynolds numbers
[J].DOI:10.1007/s12206-017-0223-0 URL [本文引用: 1]