降雨是导致滑坡的主要原因之一,其致灾机理一直都备受关注.尤其是在土质边坡中,雨水入渗使土体湿润锋不断下移,土体性质会发生改变,导致边坡发生浅层滑动破坏[1],其滑动面一般出现在湿润锋所在界面.因此,研究降雨作用下湿润锋迁移规律对于边坡防治具有重要意义.
目前,许多学者已对GA模型进行了相应的改进研究.Chen等[5]扩展了传统GA模型,分析了边坡角度对降雨入渗的影响;李宁等[6]在GA模型中考虑坡角和非饱和土特性的影响,建立了相应的浅层滑坡失稳模型,应用范围较广.另外,汪丁建等[7]考虑了饱和区内雨水渗流的影响,对GA模型进行修正,但并未考虑初始含水率分布的影响;Liu等[8]在GA模型中,假定坡体的初始含水率呈线性分布,适用范围有限;张洁等[9]通过基质吸力来确定坡体的初始含水率分布情况,并建立了相应的降雨入渗模型,过程较为复杂;文献[10-11]研究了坡体初始含水率为指数形式的浅层滑坡非积水降雨入渗模型,简化了计算过程,适用工况较窄;王千等[12]推导了初始含水率为任意分布下的GA模型,但未考虑降雨过程中的各阶段变化.另外,文献[13⇓-15]将气压力引入GA模型中,建立了相应的滑坡延时效应模型和稳定性分析模型,但均未考虑渗透力等的影响.
针对以上问题,本文在前人已有研究的基础上,综合考虑了土体初始含水率的非均匀性、饱和带渗流和气压作用等多种条件,对GA模型进行改进,并推导了相应的边坡稳定性系数表达式,使模型尽可能反映天然状况下的降雨入渗情况,扩大模型的适用性,为边坡防治提供理论支持.
1 GA入渗模型的改进
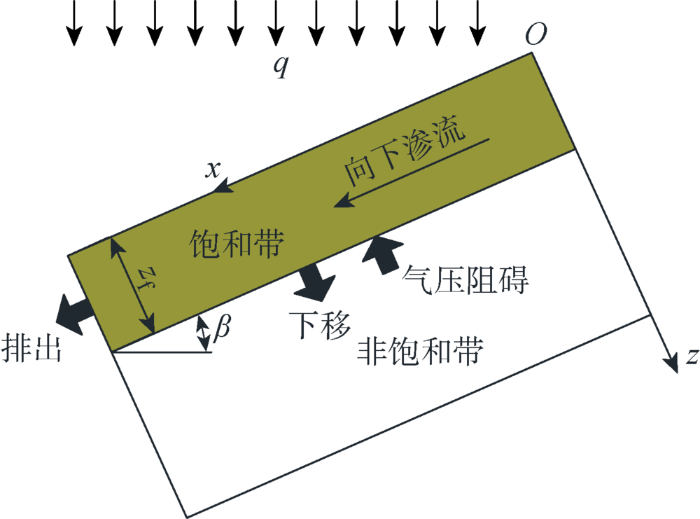
研究表明,在强降雨条件下,边坡表层土体会先形成饱和带,后饱和带不断向坡体内部移动,如图1所示,图中zf为湿润锋深度.假设有一个倾角为β的边坡,降雨强度为q且在数值上远大于土体饱和渗透系数,土体中存在一条显著的湿润锋,将土体划分为饱和带与非饱和带两个区域,湿润锋平行于坡表向边坡内部迁移.
图1
将降雨过程概括为3个部分:一是雨水渗入,使饱和带范围不断扩大;二是受边坡几何条件的影响,部分雨水会在饱和带内向坡下渗流,排出分析坡体段进入下段坡体(见图1),并产生一定渗透力;三是饱和带不断下移的过程中,会不断压缩下部气体,产生的气压对雨水入渗起阻碍作用.
文献[2]提出的GA模型主要研究土壤在薄层积水时的入渗问题,该模型形式简单,参数物理意义明确,应用广泛,被称为活塞(或打气筒)模型,其表达式为
式中:i为入渗速率;Ks为饱和渗透系数;sf为湿润锋处基质吸力;H为地表积水深度.
式(1)为地表水平假设条件下的GA模型,对于边坡而言,由于入渗界面与水平面有一定夹角,相应地,模型需要修正.Chen等[5]根据边坡降雨入渗的特点,将式(1)修正为
式中:因边坡倾斜,假定积水很薄,即H=0.
另外,在强降雨条件下,边坡表层土体会很快饱和,使边坡形成封闭环境并不断压缩内部气体产生气压Ha,阻碍雨水入渗,因此,可将式(2)修正为[13]
式中:Ha为气体压力头(超过大气压力部分).
因湿润峰以上为饱和土体,对于均质土,由上述模型和水量平衡原理,进一步可得总入渗量与湿润锋深度的关系为
式中:I为总入渗量;θi和θs分别为土体初始含水率和饱和含水率.
式中:Hc≈(1.00~1.21)hd,hd为进气水头值,即饱和土壤脱水过程中开始进入空气时的吸力值.为简化计算,Hc取平均值1.105hd.
同时,在降雨过程中,湿润锋以上土体很难达到完全饱和,因此在分析时将降雨入渗时,将含水率达到90%以上的区域定义为饱和区[18],则有
式中:θw为饱和区域含水率.
在天然状态下,土体边坡初始含水率θi并不是随深度均匀分布,而是从坡面到地下水位面呈现逐渐增大的趋势.依据文献[12]计算结果,可用多项式函数来描述土体初始含水率分布规律:
式中:θ(zf)为垂直于坡面以下zf处的土体含水率;Aj (j=0,1,…,n,n为整数)为拟合参数.
需要注意的是,在降雨初期,边坡表层没有饱和,尚未形成湿润锋,而式(3)只适用于湿润锋形成后的积水入渗.因此,必须分阶段研究降雨入渗过程.
湿润锋形成前,边坡处于非饱和状态,雨水全部渗入土体,但此时孔隙通道未全部封闭,边坡内外气压相互连通,即Ha=0.随着降雨的不断进行,在某临界时刻tp,湿润锋开始形成,此时入渗速率i(t)=qcosβ,代入式(3)有
相应的临界降雨入渗量Ip为
式中:zp为临界湿润锋深度.
对式(8)和(9)两个方程化简求解可得zp和 Ip为
则临界时刻:
结合式(1)~(12),当降雨时间t≤tp时,入渗深度与降雨时间的关系为
式中:C为常数.
代入初始条件,当t=0时,zf=0,则C=0.所以有
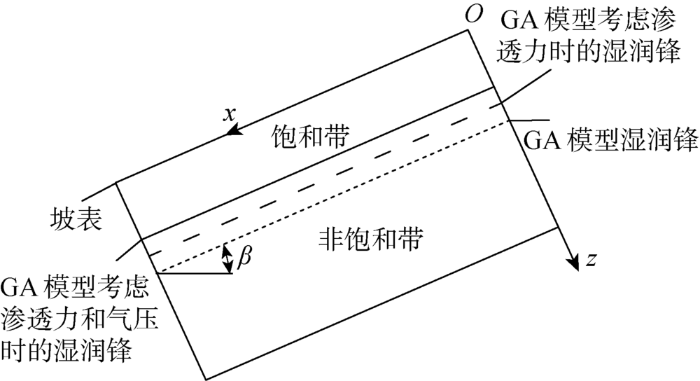
当湿润锋形成以后,受边坡几何条件的影响,部分雨水会沿着饱和带平行于湿润锋方向排出坡底土体,减少入渗总量.同时,由于饱和带的挤压作用,边坡内部会产生气压,阻止降雨入渗,所以,在分析斜坡降雨入渗过程时,应考虑饱和带渗流和气压阻碍的影响.图2所示为考虑不同因素影响时GA模型湿润锋位置的比较.可知,当考虑渗透力和气压作用时,湿润锋迁移速率明显更慢,但更符合实际情况.
图2
图2
考虑不同因素影响时的GA模型湿润锋比较
Fig.2
Comparison of GA models considering different factors
入渗总量对时间的导数即为降雨入渗速率,对式(4)求导并代入式(3),整理可得湿润锋迁移速率为
另外,部分雨水会沿着饱和带区域向左下边界渗流排出,湿润锋迁移速率相应减小,此时,由达西定律[7],饱和带内有
式中:L为斜坡沿坡面方向长度.
因此,湿润锋相对减小速率为
式(15)与式(17)之差即为湿润锋实际迁移速率:
则饱和带形成后入渗速率为
结合式(15)~(19),当t>tp时,湿润锋形成后入渗深度与降雨时间的关系为
当t=tp时,zf=zp,可得:
所以有
式(14)和(22)即为边坡入渗深度与降雨持续时间的动态变化规律.
2 边坡稳定性分析
有研究表明,降雨会使土体基质吸力、黏聚力和内摩擦角减小,导致边坡抗滑力降低,而饱和带渗流产生的渗透力和雨水入渗导致的自重增加会使边坡下滑力增大,加剧边坡破坏进程,同时土体内部的气压会阻碍湿润锋的扩展,在一定程度上能增加边坡的稳定性.因此,边坡稳定性分析需综合考虑各种因素的影响,是一个非常复杂的问题.
在土质边坡中滑动面往往出现在湿润锋处或不同类型土层的分界面处,本文假定边坡为均质土体,在湿润锋处发生平面滑动,通过应用较广的非饱和土Mohr-Coulomb破坏准则和极限平衡法来计算边坡稳定性系数Fs,即为湿润锋处抗滑力τf与下滑力τm的比值[14]:
式中:c'和φ'分别为土的有效黏聚力和内摩擦角;φb为抗剪强度随基质吸力变化的吸力摩擦角;σn为湿润锋上部正应力;pa为湿润锋下部土体总的气压力;γw为水的重度;ψ为基质吸力,因湿润锋上部饱和,假设为0.
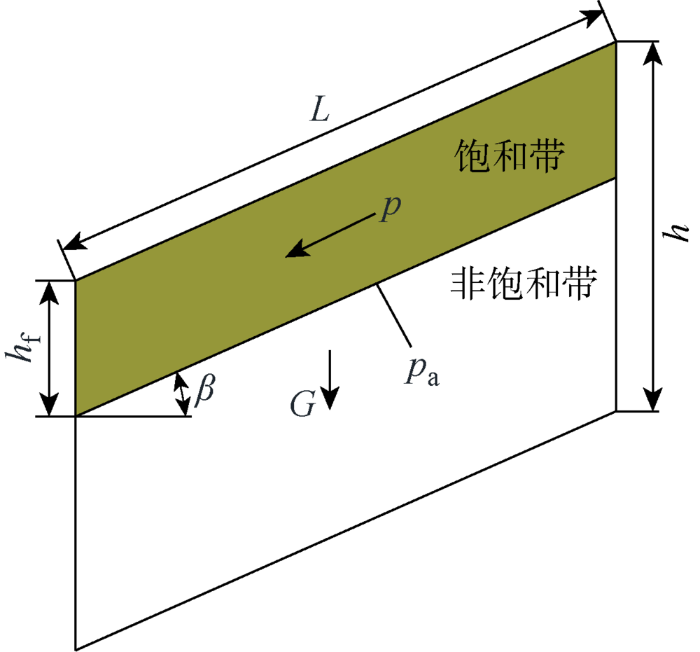
取一单位宽度的简化边坡进行分析,假设滑动面平行坡表,其几何形状如图3所示.图中:h为边坡高度;L为坡长;hf为饱和带竖向高度,hf=zf/cosβ.边坡受饱和带重力G、渗透力p和气压力pa等共同作用.因其潜在滑动面为湿润峰所在平面,所以土体的强度参数取饱和状态下的强度参数,取湿润峰以上土体为研究对象.
图3
湿润锋以上土体重力为
式中:γs为土体饱和重度.
正应力σn为
式中:uw为孔隙水压.
总的气压力pa为
式中:ua为孔隙气压.
由饱和带渗流产生的渗透力为
则下滑力τm为
将式(24)~(28)代入式(23),得到:
式(29)即为强降雨条件下边坡稳定性系数表达式,当Fs>1时,边坡安全;当Fs<1时,边坡失稳.该方程综合考虑了降雨过程中土体强度、渗透力和气压力的影响,更符合工程实际.
3 结果分析与验证
3.1 降雨入渗模型对比
为对本文提出的方法进行分析验证,将改进模型计算所得结果与其他模型结果进行比较.算例选自文献[11]中的计算模型,边坡高10 m,宽20 m,坡度为30°,降雨强度q=50.8 mm/h.土体参数取θs=0.42,hd=0.14,Ks=6.88×10-6 m/s,c'=5.7 kPa,φ'=29.7°,γs=18.08 kN/m3,sf=30 cm.
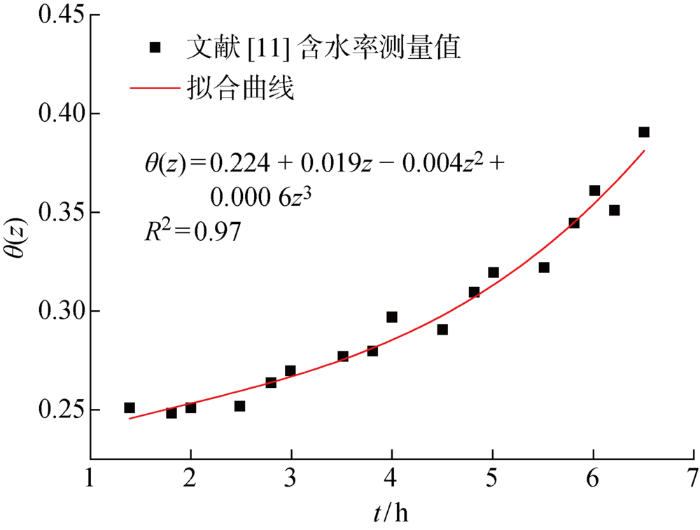
首先需确定土体初始含水率分布规律,将文献中测量结果按照式(7)进行非线性拟合,拟合结果如图4所示.拟合精度R2=0.97,效果较好,据此可获得初始含水率θ(z)随深度z变化的函数关系.
图4
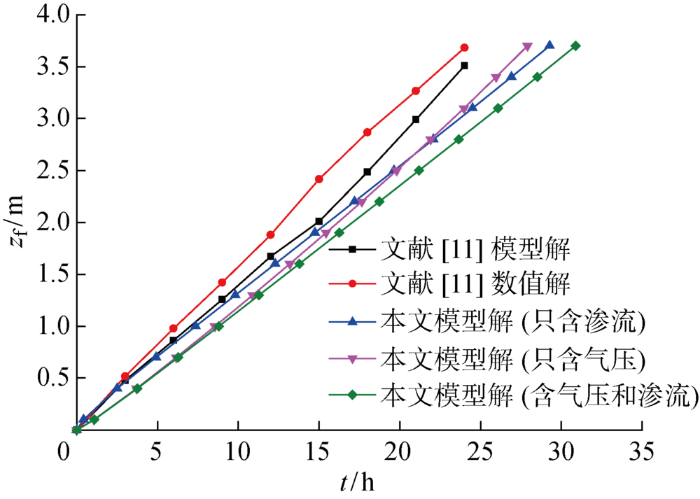
在此基础上,分别用本文改进模型与文献[11]中模型和数值模拟结果来研究湿润锋的变化规律,此处取坡表到湿润锋的法向距离作为湿润锋的迁移深度,结果如图5所示.由图可知,本文改进的GA模型计算结果与文献[11]中两种计算结果具有较好的一致性,湿润锋深度均随时间呈线性增长趋势.由图可知,按文献[11]方法计算出的相同时间内入渗深度略大于本文改进模型计算的入渗深度,这是因为其没有考虑饱和带渗流和气压阻滞的结果.并且,气压前期基本无作用,原因是湿润锋形成前,孔隙通道未封闭,无气压产生;同时,本文改进模型中只考虑气压和只考虑渗流的湿润锋深度最终计算结果相近,说明两者对降雨入渗的阻碍程度大致相同.因此,当渗流和气压共同作用时,最终计算结果明显低于前两者,但更符合工程实际.
图5
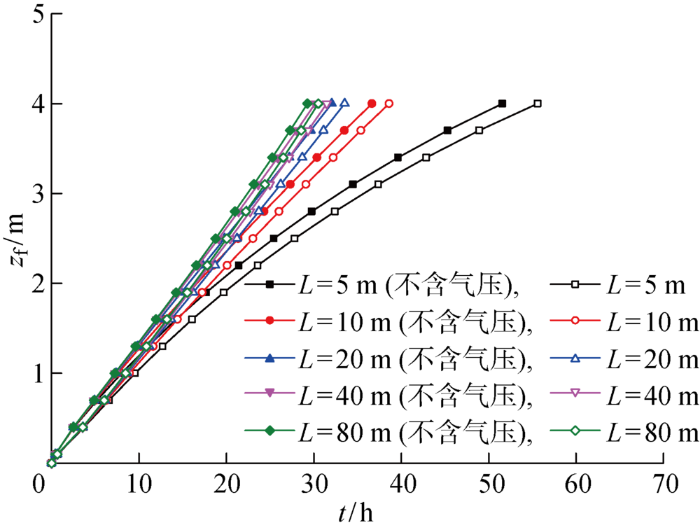
图6
图6
坡长对湿润锋深度的影响规律
Fig.6
Influence of slope length on the depth of wetting front
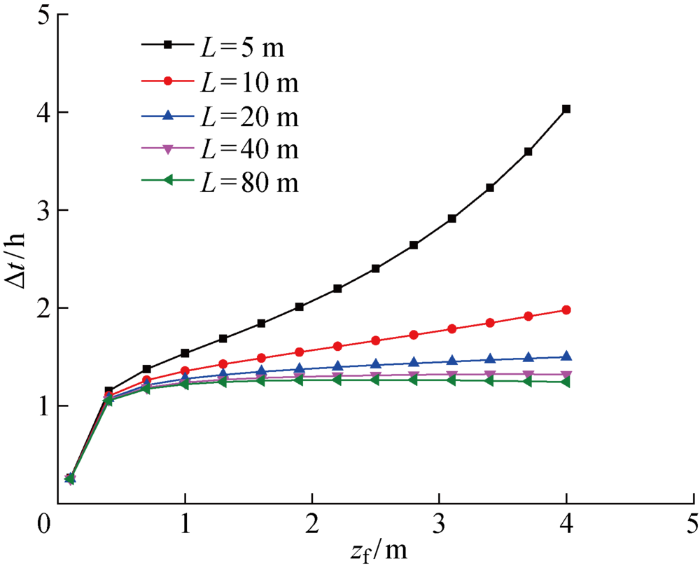
边坡降雨入渗的尺寸效应还表现在另一方面,图7所示为不同坡长下湿润锋深度与是否考虑气压时时间差Δt的变化规律.由图可知,随着湿润锋深度的增加,时间差也相应增加,但当坡长较小时,时间差增加趋势更明显,即达到相同的湿润锋深度,考虑气压作用时所需的时间越长,当坡长增大到一定程度后,时间差的变化就不明显.其原因是坡长越小,随着雨水的持续入渗,湿润锋下部空气活动程度越剧烈,对雨水的阻滞作用越明显,相当于一个针筒活塞,越向下受到的阻力越大,同样推力的情况下推进相同距离所需的时间也越长.
图7
3.2 稳定性评价对比
同样以上述模型来研究边坡稳定性系数随降雨时间的变化规律,取坡长L=80 m,倾角β=30°,并考虑不同因素进行对比,图8所示为计算结果.
图8
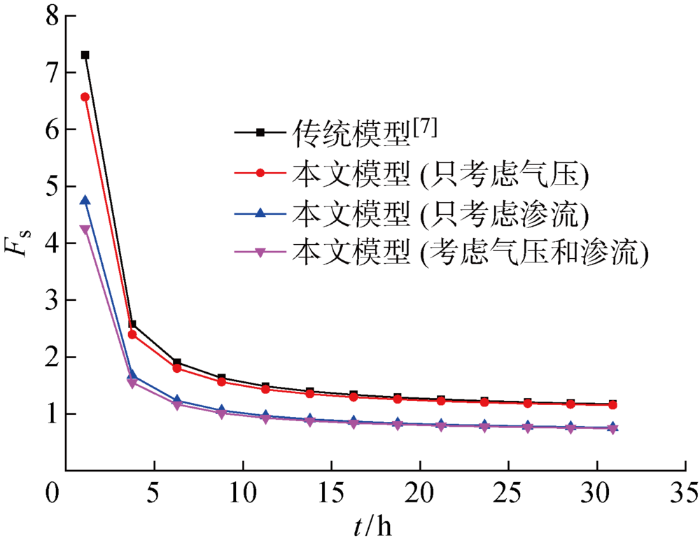
图8
考虑不同因素时稳定性系数随降雨时间的变化规律
Fig.8
Stability coefficient versus rainfall time considering different factors
由图可知,降雨初期稳定性快速下降,后期逐渐平缓.当只考虑气压时,计算所得稳定性系数相对较大,只略低于传统模型结果,边坡始终处于稳定状态.当只考虑渗透力时,稳定性下降速率明显较只考虑气压时快,约10 h时边坡失稳.当综合考虑渗透力和气压的作用,稳定性下降最快,但整体只略低于只考虑渗透力的结果,且主要发生在降雨初期,后期稳定性下降速率基本平缓,与前者大致相同,约8 h时边坡失稳.
对比分析可知,在边坡稳定性分析中,渗透力比气压的影响更大.气压作用在降雨初期比较明显,原因是随着湿润锋的不断扩展,由式(27)可知渗透力逐渐增大,而气压却基本保持不变,所以后期渗透力影响占比越来越大,气压影响越来越小.
4 结论
(1) 在经典GA模型的基础上,推导了初始含水率在天然非均匀分布条件下,考虑饱和带渗流和气压作用的边坡降雨入渗模型,较之传统模型具有更广的工程应用范围和普遍意义,结果与数值模拟具有较好的一致性.
(2) 降雨入渗受边坡的尺寸影响明显.一方面,由于饱和带渗流的影响,湿润锋迁移速率随着坡长的增大而增大,随着坡长的增大,渗流影响作用逐渐减小,迁移速率基本保持不变;另一方面,当考虑气压作用时,坡长越小,达到相同的湿润锋深度,所需的时间越长,当坡长增大到一定程度后,迁移速率基本保持不变,时间差别也不明显.
(3) 降雨初期,边坡稳定性下降较快,后期逐渐平缓.渗透力比气压对边坡稳定性的影响更大,气压作用在降雨初期比较明显,后期随着湿润锋的不断扩展,渗透力逐渐增大,而气压却基本保持不变,因此渗透力影响占比越来越大,气压影响越来越小.
参考文献
Instability of unsaturated soil slopes due to infiltration
[J].
Studies on soil physics. Part 1: The flow of air and water through soils
[J].
Modeling infiltration during a steady rain
[J].DOI:10.1029/WR009i002p00384 URL [本文引用: 1]
A simple method to analyze infiltration into unsaturated soil slopes
[J].DOI:10.1016/j.compgeo.2007.04.002 URL [本文引用: 1]
Green-Ampt infiltration model for sloping surfaces
[J].
降雨诱发浅层滑坡稳定性的计算模型研究
[J].
Research on calculation model for stability evaluation of rainfall-induced shallow landslides
[J].
强降雨作用下堆积层滑坡稳定性分析
[J].
Stability analysis of colluvial landslide due to heavy rainfall
[J].
Infiltration regulation and stability analysis of soil slope under sustained and small intensity rainfall
[J].DOI:10.1007/s11771-013-1764-8 URL [本文引用: 1]
适用于斜坡降雨入渗分析的修正Green-Ampt模型
[J].
Modified Green-Ampt model for analyzing rainfall infiltration in slopes
[J].
基于指数型的浅层滑坡非积水降雨入渗模型研究
[J].
Exponential model of rainfall infiltration of shallow landslides for non-ponding conditions
[J].
基于改进Green-Ampt模型的花岗岩残积土边坡降雨入渗规律研究
[J].
Research on rainfall infiltration law of granite residual soil slope based on improved Green-Ampt model
[J].
预测湿润锋进程的新方法
[J].
A new method for predicting the progress of the wet front
[J].
强降雨条件下气压对滑坡延时效应研究
[J].
Research on delayed effect of landslides caused by air pressure under heavy rainfall
[J].
大降雨条件下气压力对边坡稳定的影响研究
[J].
Research on effect of closed air pressure on slope stability under intense rainfall
[J].
Air entrapment effects on infiltration rate and flow instability
[J].DOI:10.1029/97WR02804 URL [本文引用: 1]
Effects of air compression and counterflow on infiltration into soils
[J].
An analysis of storm-induced landslides in colluvial soils overlying mudrock sequences, southeastern Ohio, USA
[J].DOI:10.1016/j.enggeo.2005.01.001 URL [本文引用: 1]