一种并网逆变器直流电容容值辨识方法

doi:10.16183/j.cnki.jsjtu.2021.515

一种并网逆变器直流电容容值辨识方法

朱城昊¹, 王晗¹, 孙国歧², 魏晓宾², 王富文³, 蔡旭^,¹

1.上海交通大学电力传输与功率变换控制教育部重点实验室, 上海 200240

2.山东德佑电气股份有限公司, 山东淄博 255035

3.陕西鲁能靖边风力发电有限责任公司,西安 718500

An Identification Method for DC-Link Capacitor Capacitance of Grid Connected Inverter

ZHU Chenghao¹, WANG Han¹, SUN Guoqi², WEI Xiaobin², WANG Fuwen³, CAI Xu^,¹

1. Key Laboratory of Control of Power Transmission and Conversion of the Ministry of Education, Shanghai Jiao Tong University, Shanghai 200240

2. Shandong Deyou Electric Co., Ltd., Zibo 255035, Shandong, China

3. Shaanxi Luneng Jingbian Wind Power Co., Ltd., Xi’an 718500, China

通讯作者: 蔡旭,男,教授,博士生导师;E-mail:xucai@sjtu.edu.cn.

责任编辑: 陈晓燕

收稿日期: 2021-12-15

基金资助:

山东省重点研发计划(重大科技创新工程)(2019JZZY020804)

Received: 2021-12-15

作者简介 About authors

朱城昊(1994-),男,内蒙古自治区赤峰市人,硕士生,从事风电变流器故障诊断研究.

摘要

直流电容是并网逆变器中最易老化失效的器件之一,对其进行容值参数辨识可以及时发现并更换老化电容,有利于提高系统可靠性.提出一种基于预充电电路的并网逆变器直流电容容值辨识方法,通过分析预充电过程中电容容值与充电电流、电压的数值关系,结合历史运行数据,构建电容状态特征向量集合.利用该集合训练支持向量回归(SVR)模型,建立状态值与容值的回归预测关系,并采用粒子群优化(PSO)算法对模型进行优化,优化后的模型可用于直流电容容值辨识.仿真和实验结果表明,所提方法可对并网逆变器直流电容进行容值辨识,辨识误差小于0.95%.该方法无需增加硬件电路且不改变控制算法,具有一定的实用价值.

关键词： 并网逆变器; 直流电容; 容值辨识; 预充电电路; 支持向量回归

Abstract

DC-link for the capacitor is one of the most vulnerable components of the grid connected converter, whose capacitance identification will help to improve the system reliability by finding and replacing the aging capacitor in time. An identification method for the DC-link capacitor capacitance of the grid connected inverter based on pre-charging circuit is proposed. By analyzing the relationship between the capacitance and the charging current, charging voltage during pre-charging process, and combining the historical operating data, the set of capacitance state feature vector is built. The support vector regression (SVR) model is trained and the regression prediction relationship between the state value and the capacitance is set. The model is optimized by using the particle swarm optimization (PSO) algorithm, which can be used for capacitance identification of the DC-link capacitor. Simulation and experiments results show that the proposed method can implement the accurate capacitance identification of the DC-link capacitor of the grid connected inverter, with an identification error of less than 0.95%. This method does not need to add hardware circuit and change the control algorithm, and has a certain practical value.

Keywords： grid connected inverter; DC-link capacitor; capacitance identification; pre-charging circuit; support vector regression (SVR)

PDF (5050KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

朱城昊, 王晗, 孙国歧, 魏晓宾, 王富文, 蔡旭. 一种并网逆变器直流电容容值辨识方法[J]. 上海交通大学学报, 2022, 56(6): 693-700 doi:10.16183/j.cnki.jsjtu.2021.515

ZHU Chenghao, WANG Han, SUN Guoqi, WEI Xiaobin, WANG Fuwen, CAI Xu. An Identification Method for DC-Link Capacitor Capacitance of Grid Connected Inverter[J]. Journal of Shanghai Jiaotong University, 2022, 56(6): 693-700 doi:10.16183/j.cnki.jsjtu.2021.515

随着“30·60碳达峰、碳中和”构想的提出与实施,以光伏、风电为代表的新能源发电机组大量接入电网^[1].作为连接新能源与电网的关键设备,并网逆变器扮演着越来越重要的角色,然而以直流电容故障为主的核心器件故障导致其往往不能长期健康、稳定运行^[2-3].直流电容故障主要是由于其材料老化导致的性能衰退,进而引起突发性故障,破坏逆变器正常运行.因此,对直流电容进行参数辨识,及时发现并更换老化电容,对并网逆变器稳定、可靠和经济运行具有重要意义.

针对逆变器直流电容的参数辨识,国内外研究主要集中于离线辨识法、准在线辨识法以及在线辨识法.离线辨识法指在并网逆变器停机时,拆解直流电容,并利用LCR测量仪或设计硬件电路进行性能参数测量^[4⇓-6].由于该类方法需要拆解电容,工业应用中往往难以操作,实用性较低.在线辨识法可在并网逆变器工作时进行参数辨识,如文献[7]利用高精度传感器采集中频段电容的纹波电压和纹波电流,用于估计电容性能参数.文献[8]通过在直流电容上注入特定频率的电流激励信号,利用电容响应的交流电压信号进行电容参数的计算.该类在线识别方法通常需要改变逆变器控制算法,注入特定频率信号,或安装高精度传感器测量直流电容的纹波,对已投产使用的并网逆变器而言,可行性较低.

考虑到电容老化进程十分缓慢,通常失效时间以年为单位,部分专家学者提出了针对直流电容的准在线参数辨识方法.该类方法应用于逆变器启动、停机以及负载瞬态变化过程,其监测周期远小于电容的老化失效周期,充分满足参数辨识的频率要求,且该类方法具有实现简单、成本低、对逆变器工作状态无干扰等优点,成为当下直流电容参数辨识技术的研究热点^[9].文献[10]利用逆变器的卸荷电路,通过采集卸荷过程中的电容电压放电曲线,结合电路数学模型,完成容值估计.该方法辨识精度较高,但需要增加硬件电路,不利于系统整体可靠性设计.文献[11]通过分析负载变化时直流电压的变化轨迹与电容性能参数变化之间的关系,实现了铝电解电容参数辨识.该方法无需增加硬件,但辨识精度较低,无法满足薄膜电容的高精度参数识别要求,而薄膜电容为目前逆变器采用的主流电容选型.

基于上述分析,本文提出一种基于预充电电路的并网逆变器直流电容准在线容值辨识方法,无需增加硬件电路和改变控制算法,即可实现对薄膜电容的参数辨识.首先分析预充电过程中网侧电流与直流侧电压的数学关系,结合逆变器拓扑结构,确定容值辨识的数值表达式.结合历史运行数据,构建电容状态特征向量集合,用于训练支持向量回归(Support Vector Regression, SVR)模型,建立状态特征值和容值的回归预测关系;利用粒子群优化 (Particle Swarm Optimization, PSO) 算法优化SVR回归模型参数,避免陷入局部最优,提升预测精度;优化后的模型可用于直流电容容值辨识;通过仿真和实验对所述方法的有效性进行验证.

1 电容特性与预充电电路

应用于并网逆变器的直流电容主要有两种,分别为铝电解电容(Aluminum Electrolytic Capacitance, AEC)和金属薄膜电容(Metallized Film Capacitance, MFC)^[12].铝电解电容具有能量密度高、成本低的优点,但可靠性较差,多用于低纹波电流的应用场合;金属薄膜电容耐压高、耐受纹波电流大,且串联等效电阻相比铝电解电容而言较小.随着其成本逐渐降低,被越来越多地应用在并网逆变器中^[13].图1所示为薄膜电容简化等效电路图,图中C_e代表薄膜电容器等效电容;ESR代表等效串联电阻;ESL代表等效串联电感.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 电容器简化等效电路图

Fig.1 Simplified equivalent circuit of capacitor

薄膜电容的ESR和ESL通常很小,可忽略其影响^[14],且工业领域对薄膜电容的失效评价标准为容值降至标称值的95%时,即可认为失效^[13].因此,本文将薄膜电容器等效电容C_e作为辨识目标进行研究,但所提方法不仅仅适用于薄膜电容器,还能够适应于包含电解电容器在内的多种类型电容器的参数辨识.

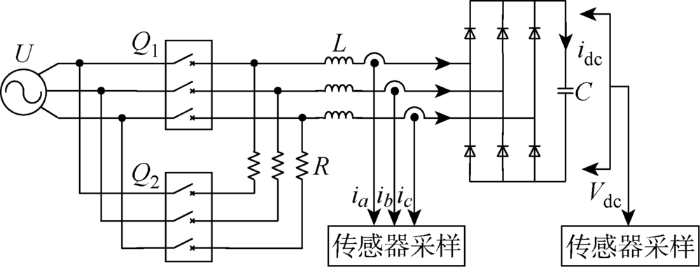
根据变流器安全运行规范,启动前,直流电容应处于完全放电状态,电容和电压接近为0,此时如果直接将逆变器接入电网,电网线电压作用于直流电容会产生强大的冲击电流,该冲击电流大小远远超过功率模块和直流电容等器件能承受的最大电流,造成不可逆损伤,减少器件寿命,严重情况下甚至会烧毁器件.因此,并网逆变器通常会配备预充电系统.图2所示为目前主流的并网逆变器预充电电路,图中:U代表电网等效电源;Q₁代表网侧变流器与电网连接的断路器;Q₂代表预充电电路断路器;L代表滤波器电感;R代表预充电电阻,用于限流,防止冲击电流过大;i_dc代表直流电流;C代表直流电容; V_dc代表直流电压;i_a、i_b、i_c代表交流侧单相电流.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 风电变流器预充电电路图

Fig.2 Pre-charging circuit of wind power converter

预充电过程操作如下:在逆变器启动前,先闭合Q₂,电网通过预充电电阻连接变流器,此时三相六桥臂绝缘栅双极晶体管(Insulated Gate Bipolar Transistor,IGBT)模块为关断状态,而反并联二极管可导通,因此逆变器等效运行于三相不控整流模式.电网通过预充电电阻对直流电容进行充电,待直流电压达到额定工作电压的80%左右时,即可断开Q₂断路器,切断预充电电阻,闭合Q₁断路器,由电网直接连接逆变器,完成启动过程.

2 辨识原理与方法

2.1 直流电容容值辨识原理

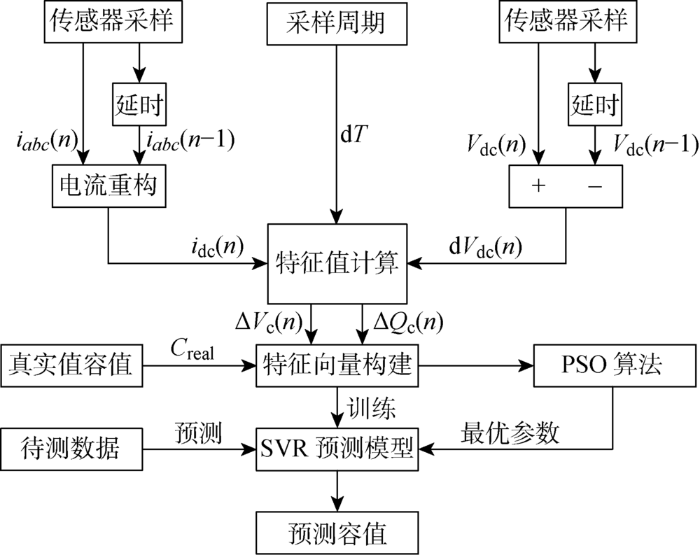
图3所示为直流电容容值辨识流程图,图中:i_abc代表交流侧三相电流;n代表采样次序;T代表系统时间;ΔV_c(n) 代表电容电压变化值;ΔQ_c代表电容电荷变化量;C_real代表电容真实值.具体实现步骤如下.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 电容容值辨识流程图

Fig.3 Flow chart of capacitance identification of capacitor

(1) 数据获取.对预充电过程中的网侧电流信号和直流电压信号采样,根据电路拓扑结构,对直流电流信号重构,并确定容值表达式,将采集的电气信号数据储存,用于后续特征向量构建和数据库扩充.

(2) 特征向量构建.根据容值表达式,确定电容状态特征值,用于表征直流电容状态,即老化程度.将该特征值与电容真实容值组成特征向量.根据历史运行数据,获得多组特征向量,用于后续SVR模型训练以及数据库扩充.

(3) SVR模型训练.SVR模型用于建立特征值与容值的回归预测关系,将多组特征向量用于SVR回归模型训练,训练参数通过PSO算法进行优化选取.完成训练的SVR模型可以对电容容值进行辨识,从而实现电容器失效判断.

2.2 特征向量构建

本文基于数据驱动的方法,因此需选择合适的电容状态特征值反映电容老化状态.根据预充电过程中的容值表达式,选择与容值直接相关的电气量作为特征值,可以最大程度反映容值的变化情况.首先推导预充电过程中的直流电容容值表达式.

变流器预充电过程中,负载端为开路模式,直流电流即为电容电流,因此直流侧电压、电流和DC-Link电容值的关系为

(1)i_c=i_dc=C

\frac{d V_{c}}{d t}

式中:V_c为电容电压;t为电容器充电放电时间.对上式进行整理,可以得到容值表达式:

(2)C=

\frac{i_{d c} d t}{d V_{c}}

\frac{Δ Q_{c}}{Δ V_{c}}

根据前文分析,电容电压可表示为

(3)V_c≈V_dc-V_ESR=V_dc-i_dcR_ESR

式中:V_ESR为ESR两端电压;R_ESR为ESR的电阻值.假设ΔV_c(n)表示第n个采样周期内的电容电压变化值,其离散表达式为

(4)ΔV_c(n)=V_c(n)-V_c(n-1)=V_dc(n)-V_dc(n-1)-(i_dc(n)-i_dc(n-1))R_ESR

由于直流电流在一个采样周期内的变化值(i_dc(n)-i_dc(n-1))和直流电容的ESR值都很小,可忽略两者的乘积项,ΔV_c(n)近似等于直流侧电压的变化值ΔV_dc(n),即

(5)ΔV_c(n)≈V_dc(n)-V_dc(n-1)=ΔV_dc(n)

根据式(2),计算ΔQ_c需要确定直流电流信号i_dc.出于经济性的考虑,风电变流器等并网逆变器的直流侧通常不会配置电流传感器,因此本文利用交流三相电流数据i_abc或两相电流数据i_ab对i_dc进行重构,从而间接获取i_dc.

设定电流从电网流向变流器为正方向,根据基尔霍夫电流定律:

(6)i_a+i_b+i_c=0

除去三相电流均为0的极端情况,i_a、i_b和i_c中应有一相或两相电流为正向,而该正向电流通过上桥臂二极管流入直流侧,形成i_dc, 只需监测i_a、i_b及i_c中的正向电流值,然后对其求代数和,即可获得直流电流,从而实现对直流电流的重构.

本文提出一种改进的直流侧电流计算方法.根据上述分析,三相电流中一定存在某一相的电流流向与另外两相电流流向不同,假设a相电流为正向,b、c相电流为负向或0,那么直流电流即等于i_a.结合式(6),可知:

(7)i_dc=i_a=-i_b-i_c=

|i_{b}|

|i_{c}|

对上例进行归纳和总结,可得任意运行情况下直流电流的重构表达式:

(8)i_dc=

\frac{|i_{a}| + |i_{b}| + |i_{c}|}{2}

部分并网逆变器交流侧只配置两相电流传感器,结合式(6)与 (8),得到两相电流重构的直流电流表达式:

(9)i_dc=

\frac{|i_{a}| + |i_{b}| + |i_{a} + i_{b}|}{2}

综上,通过计算直流电流在一个周期内的积分,可得到ΔQ_c:

(10)ΔQ_c(n)=

\int_{(n - 1) T}^{n T}

i_dcdt

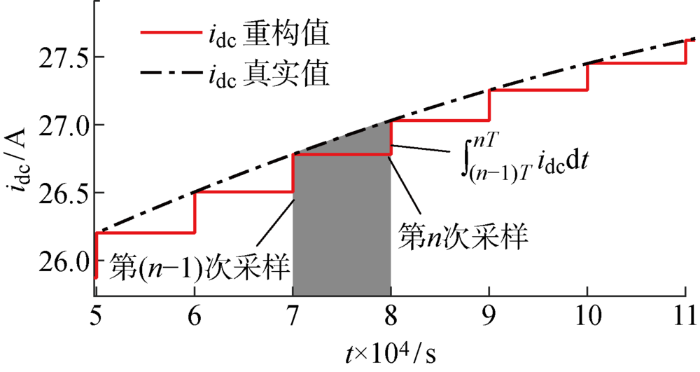
图4所示为第n个采样周期的直流重构电流采样过程.电流对采样周期的积分值对应于图中的黑色阴影面积,由于采样的离散性,无法直接进行积分计算.考虑到在足够小的采样周期内,直流电流近似线性变化,因此可将阴影面积近似为直角梯形,利用直角梯形面积公式对ΔQ_c进行计算:

(11)ΔQ_c=

\int_{(n - 1) T}^{T}

i_dcdt≈

\frac{(i_{d c} (n) + i_{d c} (n - 1)) T}{2}

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 直流重构电流采样图

Fig.4 Sampling process of DC reconstructed current

结合式(2)、(5)及(11),第n个采样周期内电容值的计算表达式如下:

(12)C(n)≈

\frac{((i_{d c} (n) + i_{d c} (n - 1)) T}{2 (V_{d c} (n) - V_{d c} (n - 1))}

由式(12)可知,C可由传感器采集的电流、电压数据直接计算得到.但受传感器测量误差以及噪声干扰等因素影响,直接计算容值存在较大误差.为克服该问题,选择ΔQ_c和ΔV_c作为电容状态特征值,利用SVR算法强大的回归预测能力,建立特征值(ΔQ_c, ΔV_c)对C的回归预测模型,实现容值参数高精度辨识,有效地降低辨识误差.

2.3 改进的SVR预测算法

SVR预测算法是一种基于统计学习理论提出的机器学习算法,通过对历史数据集进行训练学习,从而估计系统输入量与输出量之间的映射关系^[15].由于SVR在小样本回归问题中的良好表现,采用该算法建立电容状态特征值(ΔQ_c, ΔV_c)与直流电容容值C之间的回归模型,用于容值辨识,流程如下.

根据并网逆变器历史运行数据,建立电容状态特征值集合{ΔQ_c_{_i}, ΔV_c_{_i}, C_i, i=1, 2, …, m},其中m为样本个数,(ΔQ_c_{_i}, ΔV_c_{_i})∈R为第i个训练样本的输入向量,C_i∈R为对应输出值.通过非线性映射函数Φ(x)将数据集映射到高维特征空间:

(13)f(ΔQ_c_{_i}, ΔV _c_{_i})=ωΦ(ΔQ_c_{_i}, ΔV _c_{_i})+b

式中:w为权重参数;b为偏置参数;Φ(x)选择高斯核函数:

(14)Φ(x)→K(x, x')=

e^{- \frac{‖ x - x' ‖^{2}}{2 σ^{2}}}

式中:x为空间中某一点;x'为高斯核函数中心点;σ²为核函数参数.通过引入松弛变量ξ和ξ^*,回归预测即转化为求解如下目标方程:

(15)min

\frac{1}{2}

‖ω‖²+C_T

\overset{n}{\sum_{i = 1}}

(ξ_i+

ξ_{i}^{*}

)

s.t. C_i-ωΦ(x)-b≤ε+ξ_i

-C_i+ωΦ(x)+b≤ε+ $ξ_{i}^{*}$

ξ_i, $ξ_{i}^{*}$ ≥0, i=1, 2, …, n

式中:C_T为惩罚因子;ε为不敏感损失函数.

SVR回归模型的优劣由其C_T和σ²决定.C_T代表模型对误差的容忍度,其值越高说明对误差的容忍度越低,容易出现过拟合,其值过低则导致模型预测精度不足; σ²决定了模型的学习能力和预测准确度.通常两个参数的选取采用网格搜索法,以遍历的方式进行参数寻优,效率低、耗时长且难以确定最优参数.因此本文改用PSO算法对C_T和σ²参数进行寻优.

PSO算法利用群体中个体间的协作和信息共享来寻找最优解,对比其他优化算法,其核心优势是实现简单、待调参数少、寻优能力强^[16].针对SVR回归模型,将每组参数(C_T, σ²)设置为PSO中的粒子, 选取均方差E作为目标函数,其表达形式如下:

(16)E=

\overset{n}{\sum_{i = 1}}

(

{\hat{y}}_{i}

-y_i)²

式中: ${\hat{y}}_{i}$ 和y_i分别为第i个样本的预测值和真实值.

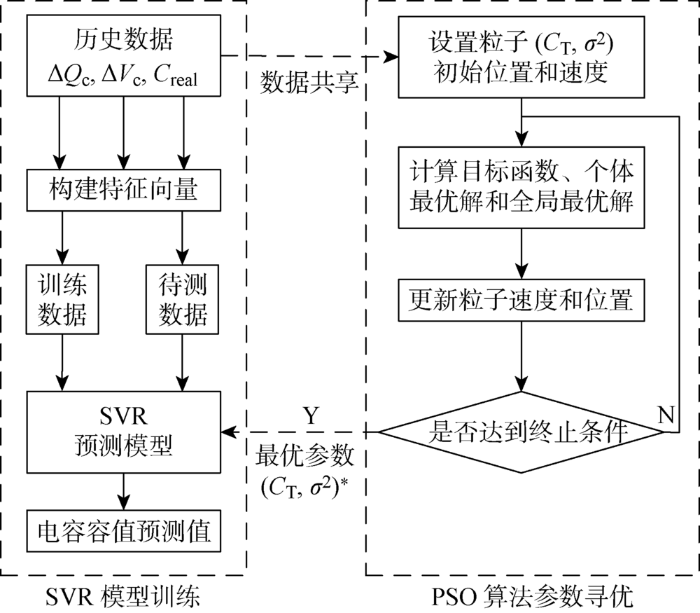
利用改进的SVR回归模型对容值进行预测辨识,流程如图5所示.在模型训练阶段,将历史数据中包含噪声和干扰的信号量ΔQ_c与ΔV_c作为电容状态特征值,将与之对应的C_real作为电容状态参数,三者组成特征向量[ΔQ_c ΔV_cC_real].根据历史数据可以获得多组特征向量,将其分为训练数据集和待测数据集,前者用于SVR模型训练,后者用于模型准确度检验.利用PSO算法对模型参数进行全局寻优,根据历史数据设置粒子初始位置和速度,每次循环计算一次粒子的目标函数、个体的最优解和全局最优解,根据计算结果,更新粒子的速度和位置,然后判断是否达到终止循环的条件.循环结束时,将当前计算得到的全局最优解, 即最优参数(C_T, σ²)^*

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 基于改进SVR算法的容值辨识流程图

Fig.5 Flow chart of capacitance identification based on improved SVR algorithm

传回SVR模型,用于模型训练.最终通过优化训练得到的SVR预测模型用于逆变器直流电容容值辨识.

3 仿真验证

基于MATLAB/SIMULINK平台,搭建图2所示仿真模型,系统参数如下:逆变器额定功率 1.5 MW,交流侧额定电压690 V,变流器采用单L滤波器,滤波电感250 μH,预充电电阻20 Ω,传感器采样频率为10 kHz.

实验方案如下:单次仿真为一个完整的并网逆变器直流电容预充电过程,采样数据为交流侧三相电流i_abc以及直流电压V_dc,为模拟真实场景,对采样数据添加不同信噪比的高斯白噪声.由于并网逆变器电流传感器精度较差(大于0.5%),而预充电开始时,充电电流较大,可以有效减少电流传感器精度导致的误差影响.同时,为去除冗余数据,提升计算速度,单次仿真数据采样区间设置为充电过程中直流电压由0升至5%额定值.根据式(5),计算获得直流电压数据集 $\{Δ V_{d c} (k), k = 1,2, \dots, n\}$ ,用作SVR预测模型的输入变量x₁;根据式(8),利用三相电流数据进行直流电流重构,计算得到电荷量变化数据集 $\{Δ Q_{c} (k), k = 1,2, \dots, n\}$ ,作为SVR预测模型的输入变量x₂;每次仿真采用的C_real作为输出变量y.综上,以[x₁x₂y ]作为SVR算法的特征向量,用于模型训练和学习.

为获得由足够多特征向量组成的数据集,共进行10组仿真,每组仿真采用不同的直流电容容值,模拟电容不同老化状态.每次仿真可以获得199组数据.随机选择10组仿真数据中的7组用于SVR预测模型训练,剩余的数据用于模型准确度测试.

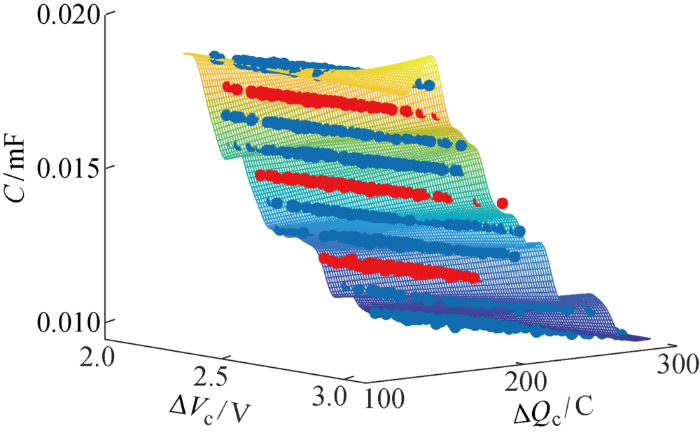
基于Python平台Tensorflow框架,编写PSO算法优化的SVR训练模型.将随机选择的7组共1397个数据用于SVR模型训练,得到回归预测函数y=f(x₁, x₂),如图6所示.剩余的3组597个数据用于模型准确度检验,其中蓝色点代表训练数据,红色点代表测试数据,曲面代表拟合函数.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 仿真数据与拟合曲面图

Fig.6 Diagram of simulation data and fit surface

为验证预测模型对噪声和干扰的抑制能力,分别在原始采样信号中添加信噪比为20、15及10 dB的高斯白噪声,采用平均绝对百分比误差(MAPE)、均方根误差(MSE)和相关系数R'对获得的拟合函数进行拟合效果评估.R'越接近1,实际值和预测值的相关度越高,模型预测的准确度越高;MSE和MAPE越小,表明实际值与预测值越接近,模型拟合性能越好.基于训练数据集和待测数据集的MSE、R'及MAPE如表1所示.

表1 SVR模型评估

Tab.1 Performance evaluation of SVR model

信噪比/dB	数据集类型	MSE	R'	MAPE
20	训练	7.2278×10^-6	0.9948	0.1761
	待测	5.1128×10^-7	0.9989	0.0444
15	训练	7.4148×10^-6	0.9945	0.1760
	待测	8.3376×10^-7	0.9982	0.0584
10	训练	7.4364×10^-6	0.9943	0.1754
	待测	1.0387×10^-6	0.9978	0.0654

新窗口打开| 下载CSV

根据表中评估参数,当信噪比为20 dB时,预测模型具有良好的拟合能力和预测能力,当信噪比逐渐减少时,预测模型的在拟合能力和预测能力方面有所下降,不过仍处于较高水平.因此,该SVR预测模型具备一定的抑制噪声和干扰的能力,且能实现较高精度的电容容值预测和辨识.

4 实验验证

为进一步验证所提方法的有效性,搭建5 kW风电变流器预充电实验平台,如图7所示,其中包含MWINV5R022变流器、Myway控制器以及上位机系统等.变流器主电路参数如下:电网侧三相线电压幅值为110 V;预充电电阻为10 Ω;滤波电感为 8 mH,传感器采样频率设置为10 kHz.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 风电变流器预充电实验平台

Fig.7 Pre-charging experiment platform of wind power converter

实验方案如下:共进行7组并网逆变器直流电容预充电实验,每组采用不同的直流电容容值,对应电容老化过程中的7种状态.采集三相交流电流以及直流电压数据,对直流电流进行重构,重构算法嵌入Myway控制器控制算法中.同仿真实验,计算获得SVR预测模型的输入变量x₁和x₂,真实容值作为输出变量y;将实验获得的多组特征向量[x₁x₂y]输入SVR算法中进行训练和预测.为测试模型准确度,本文将7次实验分成6次训练实验和1次测试实验.

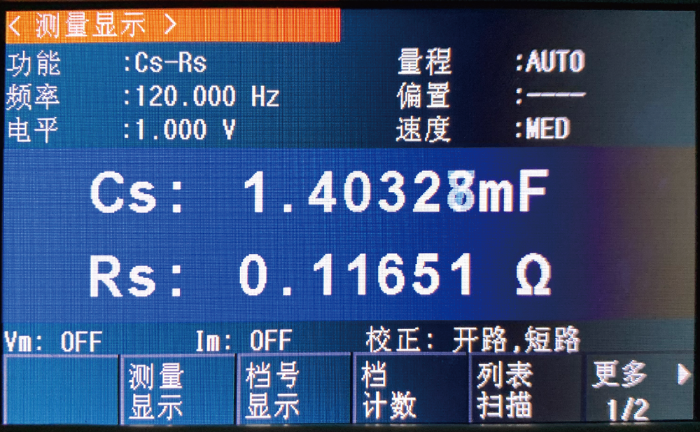
利用LCR分析仪(型号为TH2830)测量的直流电容容值作为基准值,测量室温为23.5 ℃,频率为120 Hz.图8所示为容值测量结果示意图.受条件限制,无法对电容进行真实老化实验,因此本文采用将多个电容并联在直流侧,逐次实验断开一个电容,从而模拟电容老化过程中的容值衰退现象.对全部7次实验直流侧容值进行测量,测量结果如表2所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 容值测量结果示意图

Fig.8 Schematic diagram of capacitance measurement results

表2 直流侧容值

Tab.2 C values at DC side

实验组号	C/mF
1	1.15040
2	1.19154
3	1.23243
4	1.27497
5	1.31783
6	1.36036
7	1.40328

新窗口打开| 下载CSV

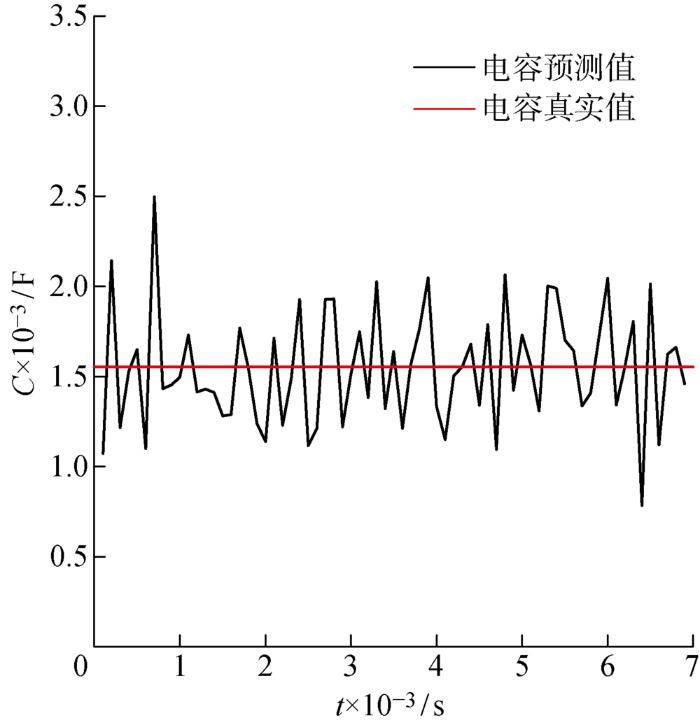
以7次实验得到的实验数据作为特征向量,将第5组作为测试组,其他6组作为训练组,进行SVR模型训练和预测,获得如图9所示的预测结果.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 电容值预测结果

Fig.9 Prediction result of capacitance

如图9所示,受传感器采样误差、噪声干扰等影响,每个采样周期预测的电容值存在较大波动,因此采用平均值滤波法,将预测得到的多个电容容值计算平均值,作为最终预测值.为验证所提方法的可靠性,避免偶然误差,将7组实验中的每组实验依次作为测试组,分别利用传统的SVR算法和改进的SVR算法,进行7次测试实验.图10所示为实验最终容值预测值与真实值对比情况.

图10

新窗口打开| 下载原图ZIP| 生成PPT

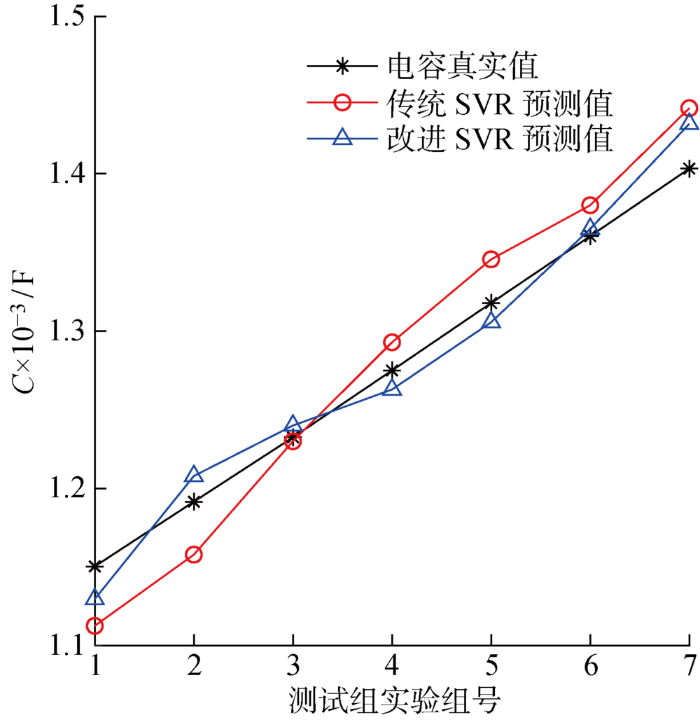
图10 电容预测值与真实值对比图

Fig.10 Comparison of prediction value and real value of capacitance

根据图10,对比传统的SVR算法,改进后的SVR算法对电容值预测更加接近真实值,预测精度更高,效果更好,验证了本文所提改进的SVR算法在直流电容容值辨识方面具有更优异的性能.

表3所示为7次实验中基于改进的SVR算法对电容值预测的结果以及预测误差.根据表中数据,容值预测值较为接近真实值,但受限于传感器采样误差、噪声干扰等,最大预测误差大于仿真获得的结果,但仍小于0.95%,可以满足并网逆变器直流电容容值辨识的要求.

表3 电容预测值与误差

Tab.3 Prediction values of capacitance and its error

测试组号	电容真实值/mF	电容预测值/mF	误差/%
1	1.15040	1.1196	0.938
2	1.19154	1.2029	0.950
3	1.23243	1.2399	0.609
4	1.27497	1.2629	0.950
5	1.31783	1.3056	0.927
6	1.36036	1.3650	0.340
7	1.40328	1.4117	0.601

新窗口打开| 下载CSV

5 结论

本文提出一种基于预充电电路的并网逆变器直流电容容值辨识方法,通过PSO优化的SVR算法对预充电过程中的电容状态特征值进行训练学习,建立其与电容容值的回归关系,进而利用SVR模型实现容值辨识.仿真和实验结果验证了所提方法的有效性,具体优势如下:

(1) 无需增加硬件电路.仅利用并网逆变器配置的交流侧电流传感器以及直流侧电压传感器即可实现电容值的辨识.

(2) 无需改变逆变器控制算法.仅利用并网逆变器预充电过程的采样数据,即可实现电容值的辨识,不影响逆变器的正常运行.

(3) 辨识精度高.采用回归预测算法可有效降低噪声和干扰信号的影响,采用低精度传感器,即可满足对薄膜电容容值的辨识精度.

(4) 方法可移植性强.基于AC-DC-AC变换器的风电变流器、三相电机驱动器等电路均需配置有直流电容的预充电电路,因此该方法非常方便移植于上述应用电路中.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

蔡旭, 杨仁炘, 周剑桥, 等.

海上风电直流送出与并网技术综述

[J]. 电力系统自动化, 2021, 45(21): 2-22.

[本文引用: 1]

CAI

, YANG

Renxin

, ZHOU

Jianqiao

, et al.

Review on offshore wind power integration via DC transmission

[J]. Automation of Electric Power Systems, 2021, 45(21): 2-22.

[本文引用: 1]

[2]

YANG

S Y

, BRYANT

, MAWBY

, et al.

An industry-based survey of reliability in power electronic converters

[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1441-1451.

DOI:10.1109/TIA.2011.2124436 URL [本文引用: 1]

[3]

FISCHER

, STALIN

, RAMBERG

, et al.

Field-experience based root-cause analysis of power-converter failure in wind turbines

[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2481-2492.

DOI:10.1109/TPEL.2014.2361733 URL [本文引用: 1]

[4]

BRUNSON

, EMPRINGHAM

, DE

LILLO L

, et al.

Open-circuit fault detection and diagnosis in matrix converters

[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2840-2847.

DOI:10.1109/TPEL.2014.2364152 URL [本文引用: 1]

[5]

AMARAL

A M R

, CARDOSO

A J M

A simple offline technique for evaluating the condition of aluminum-electrolytic-capacitors

[J]. IEEE Transactions on Industrial Electronics, 2009, 56(8): 3230-3237.

DOI:10.1109/TIE.2009.2022077 URL [本文引用: 1]

[6]

AMARAL

A M R

, CARDOSO

A J M

Using a sinosoidal PWM to estimate the ESR of aluminum electrolytic capacitors

[C]∥2009 International Conference on Power Engineering, Energy and Electrical Drives. Lisbon, Portugal: IEEE, 2009: 691-696.

[本文引用: 1]

[7]

VOGELSBERGER

M A

, WIESINGER

, ERTL

Life-cycle monitoring and voltage-managing unit for DC-link electrolytic capacitors in PWM converters

[J]. IEEE Transactions on Power Electronics, 2011, 26(2): 493-503.

DOI:10.1109/TPEL.2010.2059713 URL [本文引用: 1]

[8]

X S

, NGUYEN

T H

, LEE

D C

, et al.

Capacitance estimation of DC-link capacitors for single-phase PWM converters

[C]∥2009 IEEE 6th International Power Electronics and Motion Control Conference. Wuhan, Hubei, China: IEEE, 2009: 1656-1661.

[本文引用: 1]

[9]

ZHAO

Z Y

, DAVARI

, LU

W G

, et al.

An overview of condition monitoring techniques for capacitors in DC-link applications

[J]. IEEE Transactions on Power Electronics, 2020, 36(4): 3692-3716.

DOI:10.1109/TPEL.2020.3023469 URL [本文引用: 1]

[10]

, DU

A VEN condition monitoring method of DC-link capacitors for power converters

[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1296-1306.

DOI:10.1109/TIE.2018.2835393 URL [本文引用: 1]

[11]

ZHAO

Z Y

, LU

W G

, DAVARI

, et al.

An online parameters monitoring method for output capacitor of buck converter based on large-signal load transient trajectory analysis

[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(4): 4004-4015.

DOI:10.1109/JESTPE.2020.2964068 URL [本文引用: 1]

[12]

WANG

, BLAABJERG

Reliability of capacitors for DC-link applications in power electronic converters—An overview

[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3569-3578.

DOI:10.1109/TIA.2014.2308357 URL [本文引用: 1]

[13]

姚芳, 王槟, 唐圣学, 等.

DC-link电容器在线状态监测方法综述

[J]. 电力自动化设备, 2019, 39(11): 188-197.

[本文引用: 2]

YAO

Fang

, WANG

Bing

, TANG

Shengxue

, et al.

Review of online condition monitoring methods for DC-link capacitor

[J]. Electric Power Automation Equipment, 2019, 39(11): 188-197.

[本文引用: 2]

[14]

吴宇.

三相变流器中直流母线电容的状态监测技术研究[D]. 重庆: 重庆大学, 2016.

[本文引用: 1]

Study on condition monitoring technique of DC-link capacitors in three-phase AC/DC/AC PWM power converters[D]. Chongqing: Chongqing University, 2016.

[本文引用: 1]

[15]

ABO-KHALIL

A G

, LEE

D C

DC-link capacitance estimation in AC/DC/AC PWM converters using voltage injection

[J]. IEEE Transactions on Industry Applications, 2008, 44(5): 1631-1637.

DOI:10.1109/TIA.2008.2002181 URL [本文引用: 1]

[16]

, AN

, QIAO

X D

, et al.

Multi-output least-squares support vector regression machines

[J]. Pa-ttern Recognition Letters, 2013, 34(9): 1078-1084.

[本文引用: 1]

海上风电直流送出与并网技术综述

2021

... 随着“30·60碳达峰、碳中和”构想的提出与实施,以光伏、风电为代表的新能源发电机组大量接入电网^[1].作为连接新能源与电网的关键设备,并网逆变器扮演着越来越重要的角色,然而以直流电容故障为主的核心器件故障导致其往往不能长期健康、稳定运行^[2-3].直流电容故障主要是由于其材料老化导致的性能衰退,进而引起突发性故障,破坏逆变器正常运行.因此,对直流电容进行参数辨识,及时发现并更换老化电容,对并网逆变器稳定、可靠和经济运行具有重要意义. ...

海上风电直流送出与并网技术综述

2021

An industry-based survey of reliability in power electronic converters

2011

Field-experience based root-cause analysis of power-converter failure in wind turbines

2015

Open-circuit fault detection and diagnosis in matrix converters

2015

... 针对逆变器直流电容的参数辨识,国内外研究主要集中于离线辨识法、准在线辨识法以及在线辨识法.离线辨识法指在并网逆变器停机时,拆解直流电容,并利用LCR测量仪或设计硬件电路进行性能参数测量^[4⇓-6].由于该类方法需要拆解电容,工业应用中往往难以操作,实用性较低.在线辨识法可在并网逆变器工作时进行参数辨识,如文献[7]利用高精度传感器采集中频段电容的纹波电压和纹波电流,用于估计电容性能参数.文献[8]通过在直流电容上注入特定频率的电流激励信号,利用电容响应的交流电压信号进行电容参数的计算.该类在线识别方法通常需要改变逆变器控制算法,注入特定频率信号,或安装高精度传感器测量直流电容的纹波,对已投产使用的并网逆变器而言,可行性较低. ...

A simple offline technique for evaluating the condition of aluminum-electrolytic-capacitors

2009

Using a sinosoidal PWM to estimate the ESR of aluminum electrolytic capacitors

2009

Life-cycle monitoring and voltage-managing unit for DC-link electrolytic capacitors in PWM converters

2011

Capacitance estimation of DC-link capacitors for single-phase PWM converters

2009

An overview of condition monitoring techniques for capacitors in DC-link applications

2020

... 考虑到电容老化进程十分缓慢,通常失效时间以年为单位,部分专家学者提出了针对直流电容的准在线参数辨识方法.该类方法应用于逆变器启动、停机以及负载瞬态变化过程,其监测周期远小于电容的老化失效周期,充分满足参数辨识的频率要求,且该类方法具有实现简单、成本低、对逆变器工作状态无干扰等优点,成为当下直流电容参数辨识技术的研究热点^[9].文献[10]利用逆变器的卸荷电路,通过采集卸荷过程中的电容电压放电曲线,结合电路数学模型,完成容值估计.该方法辨识精度较高,但需要增加硬件电路,不利于系统整体可靠性设计.文献[11]通过分析负载变化时直流电压的变化轨迹与电容性能参数变化之间的关系,实现了铝电解电容参数辨识.该方法无需增加硬件,但辨识精度较低,无法满足薄膜电容的高精度参数识别要求,而薄膜电容为目前逆变器采用的主流电容选型. ...

A VEN condition monitoring method of DC-link capacitors for power converters

2019

An online parameters monitoring method for output capacitor of buck converter based on large-signal load transient trajectory analysis

2021

Reliability of capacitors for DC-link applications in power electronic converters—An overview

2014

... 应用于并网逆变器的直流电容主要有两种,分别为铝电解电容(Aluminum Electrolytic Capacitance, AEC)和金属薄膜电容(Metallized Film Capacitance, MFC)^[12].铝电解电容具有能量密度高、成本低的优点,但可靠性较差,多用于低纹波电流的应用场合;金属薄膜电容耐压高、耐受纹波电流大,且串联等效电阻相比铝电解电容而言较小.随着其成本逐渐降低,被越来越多地应用在并网逆变器中^[13].图1所示为薄膜电容简化等效电路图,图中C_e代表薄膜电容器等效电容;ESR代表等效串联电阻;ESL代表等效串联电感. ...

DC-link电容器在线状态监测方法综述

2019

... 薄膜电容的ESR和ESL通常很小,可忽略其影响^[14],且工业领域对薄膜电容的失效评价标准为容值降至标称值的95%时,即可认为失效^[13].因此,本文将薄膜电容器等效电容C_e作为辨识目标进行研究,但所提方法不仅仅适用于薄膜电容器,还能够适应于包含电解电容器在内的多种类型电容器的参数辨识. ...

DC-link电容器在线状态监测方法综述

2019

2016

DC-link capacitance estimation in AC/DC/AC PWM converters using voltage injection

2008

... SVR预测算法是一种基于统计学习理论提出的机器学习算法,通过对历史数据集进行训练学习,从而估计系统输入量与输出量之间的映射关系^[15].由于SVR在小样本回归问题中的良好表现,采用该算法建立电容状态特征值(ΔQ_c, ΔV_c)与直流电容容值C之间的回归模型,用于容值辨识,流程如下. ...

Multi-output least-squares support vector regression machines

2013

... PSO算法利用群体中个体间的协作和信息共享来寻找最优解,对比其他优化算法,其核心优势是实现简单、待调参数少、寻优能力强^[16].针对SVR回归模型,将每组参数(C_T, σ²)设置为PSO中的粒子, 选取均方差E作为目标函数,其表达形式如下: ...

〈

〉