地铁运行的线速度并非恒定不变,列车在车站附近具有一个减速-停站-加速的过程.地铁进出站时的变速运动不仅会产生水平应力,还会引起变频循环荷载,从而给地基土的变形产生一定的影响.
国内外针对地铁变速移动的振动问题的研究有:Michaltsos理论[1]分析了单双轴变速荷载作用下简支梁的动力响应.卢正等[2]采用半解析方法求得变速移动荷载下黏弹性地基板的振动响应.张楠等[3]采用车辆结构耦合的方法研究了制动力作用下的结构动力响应.张谦等[4]对进站时引起的柱面纵向振动和振源特性进行解析分析,得到了列车在进站方向上振动响应的变化规律.He[5]使用数值模拟的方式对不同加减速下移动地铁轨道振动进行了模拟.张谦等[6]使用柱面波解析法研究出、进站两种情况的波动差异,并分析了地铁列车运行加速度和速度、土层模量、隧道尺寸及埋深等因素对振动反应的影响.陈文化等[7]采用解析法分析了地铁进、出站时引起土层振动差异性和空间振动特性.可以看出,针对地铁变速移动的振动问题大多采用解析或数值模拟的方法对轨道或地基动力响应进行研究,而对地铁站附近地基土累积应变的研究相对较少.
地铁站附近区域也是地铁工程防治的重点,研究地铁站附近的地基土的累积塑性变形特性有助于对该区域内轨道基础变形的控制,确保地铁运行安全[8].为此,本文通过对土体进行倾斜削样并配合使用GDS动三轴(型号DNYTTS, GDS仪器设备有限公司)进行不排水动力测试的方法来模拟地铁进出站荷载,对不同进出站距离、进出站加速度、动应力幅值及固结围压对南京饱及软黏土累积塑性变形的影响进行研究.
1 荷载工况
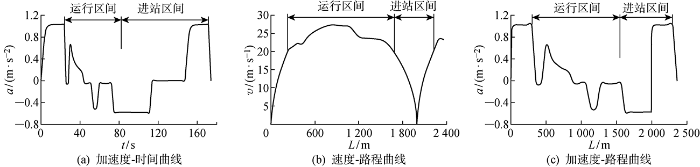
以长江三角洲地区地铁运行为研究对象,南京地铁3#线运行特征如图1所示.图中: a为地铁列车进出站加速度;v为地铁列车进出站速度;T为地铁列车运行时间;L为地铁运行里程.
图1
地铁列车在一个站间的运行状态主要有“恒定加速-惰行-变力矩牵引-小级位制动-惰行-制动-停车”7个阶段.国内普遍地铁出站加速度为0.83~1.03 m/s2,进站减速度为0.50~0.60 m/s2 [6].列车在临近地铁站的区域,列车大致处于一个恒定的加速或恒定减速的过程.可以将这个稳定加减速运行过程所影响到的区域称为地铁进出站区间.
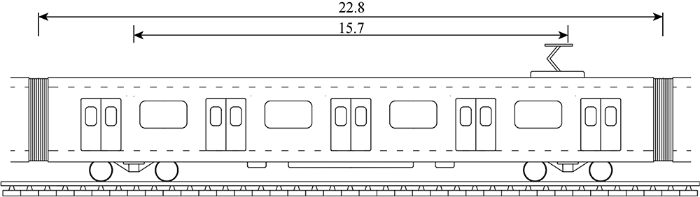
国产地铁主要有3种型号,南京地铁以国产地铁C型车为主,6节车厢编成一趟班组,其列车尺寸如图2所示.地铁列车每次进出站时,不仅会因其自身的12组车轮挤压枕木从而引发相同次数的变频竖向循环荷载, 还会因其自身的加速度给土体施加水平切应力.将土体经历一趟列车进出站所产生的规律性的变频循环荷载定义为经历1次进出站振动循环.
图2
2 试验
2.1 试验材料
使用南京市原状饱和粉质黏土进行试验,该土层为河漫滩相沉积,是一种含水率高、压缩性高、孔隙率大、强度低、灵敏度高的饱和软黏土土层.试验所用的原状软黏土取样于南京市鼓楼区上元门地铁站附近,取样深度为10 m,采用钻孔取样的方式进行.钻孔采用XY-1型百米油压钻机进行施工,110 mm 钻具钻进,软黏土层设置井管护壁,护臂管管径110 mm,长度3.0~5.0 m.饱和软黏土使用直径85 mm的薄壁取土器通过静压的方法进行取样.原状饱和软黏土的岩土工程性质如表1所示.
表1 饱和软黏土的岩土工程性质
Tab.1
| 重度/ (kN·m-3) | 含水率/ % | 孔隙比 | 压缩系数/ MPa-1 | 内摩擦 角/(°) | 黏聚力/ kPa | 渗透系数×106/(m·s-1) | 液限/% | 塑限/% | 动泊 松比 | 波速/(m·s-1) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 水平 | 竖直 | 压缩 | 剪切 | ||||||||||
| 18.4 | 35.9 | 1.04 | 0.63 | 7.6 | 14.0 | 5.09 | 3.61 | 36.1 | 21.6 | 0.439 | 360 | 120 | |
2.2 试验方案
动三轴的试验研究[9]大多使土样在竖直方向上进行受荷振动,这种土体的受荷形式不能有效地模拟地铁进出站加速度产生的水平切应力.根据荷载工况对土体进行倾斜切削制样,试验时可以通过对试样主应力的控制,以等效土体竖直方向上的压应力与水平方向上的切应力,从而有效地模拟土体在地铁进出站荷载下的应力状态.试验通过对土体进行倾斜削样,并配合使用GDS动三轴系统进行不排水动力测试以模拟地铁进出站荷载工况.地铁运动引发竖向应力幅值σd与水平切应力τd应满足:
式中:g为重力加速度.
式中:x为列车车头距停站点的距离;t为出站区间地铁开出运行时间或进站区间地铁距停站还需的时间差.
如图2所示,每一节车厢前后都对称分布着两个列车车轮组.一趟列车的荷载曲线可分解为3种类型的正弦式荷载的重复叠加曲线:① 第1节/最后一节车厢不连续车轮组的荷载类型;② 同一节车厢前后两轮组之间的荷载类型;③ 前一节车厢后轮组与后一节车厢前轮组之间的荷载类型.根据车厢的尺寸,可以计算得到该点在相应荷载区间内的相对位置x':
式中:x0为该点距停站点的距离;lm为同一节车厢前后两组车轮之间的间距,对于国产C型车,lm=15.7 m;lb为同一节车厢前后两组车轮之间的间距,国产C型车lb=7.1 m.
倘若某时刻该点处于同一车厢前后2组车轮之间,荷载曲线模拟为
式中:σ为某时刻的列车荷载动应力值;σc为地铁荷载的附加动应力基准值.
若某时刻该点处于前一节车厢后轮组与后一节车厢前车轮组之间时,荷载曲线模拟为
式中:
此外,列车头节车厢与最后一节车厢不具有相邻节车厢,荷载曲线模拟为
式中:la为列车驶入或离开的影响区间长度,本文近似采用la=lm来模拟.
动三轴试验控制地铁荷载影响的轴压增量Δσ1、围压增量Δσ3及试样的斜削角度θ(见图3)应满足:
图3
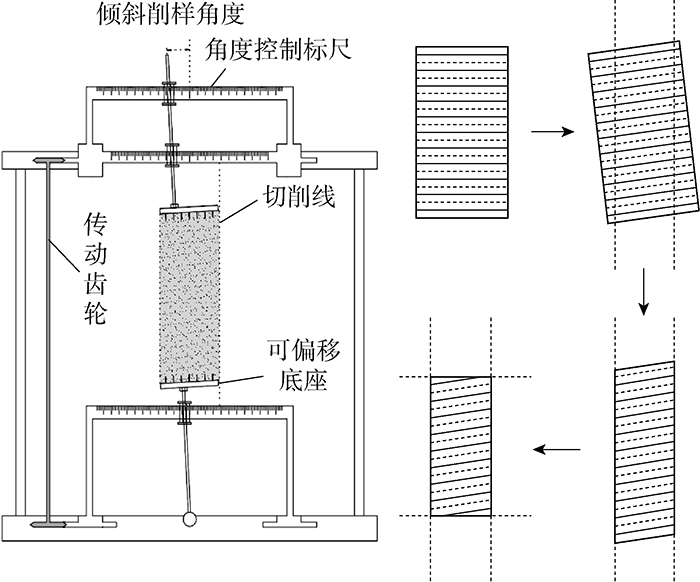
制样时使用倾斜削样装置严格控制倾斜角度,削样装置、削样操作示意如图4所示.
图4
南京市隧道的埋深为10~15 m,地下水的埋深为 0.5 ~1.2 m,地铁荷载竖向应力基准值大约为 30 kPa,竖向荷载的应力幅值为10~20 kPa[10].由于进出站加速度相较于重力加速度要小得多,这就使得地铁列车荷载引起附加应力的Δσ3<1%Δσ1.试验忽略对地铁列车荷载引起的附加围压应力Δσ3的控制,采用单向激振等压固结的方式进行试验.本文选取围压250 kPa、反压125 kPa、列车荷载竖向应力基准值30 kPa、列车荷载竖向应力幅值15 kPa的工况为基准试验组,设计试验方案对距地铁站距离
表2 软黏土累积变形试验方案
Tab.2
| 试样编号 | 固结围压/kPa | 进出站加速度/(m·s-2) | 列车竖向动应力/kPa | 进出站距离/m | 试验加载动应力/kPa | 削样角度/(°) |
|---|---|---|---|---|---|---|
| A1 | 125 | -0.50 | 30±15 | +50 | 30.08±15.04 | 2.91 |
| A2 | 125 | -0.50 | 30±15 | +150 | 30.08±15.04 | 2.91 |
| A3 | 125 | -0.50 | 30±15 | +250 | 30.08±15.04 | 2.91 |
| A4 | 125 | -0.55 | 30±15 | +50 | 30.09±15.05 | 3.20 |
| A5 | 125 | -0.55 | 30±15 | +150 | 30.09±15.05 | 3.20 |
| A6 | 125 | -0.55 | 30±15 | +250 | 30.09±15.05 | 3.20 |
| A7 | 125 | -0.60 | 30±15 | +50 | 30.11±15.06 | 3.49 |
| A8 | 125 | -0.60 | 30±15 | +150 | 30.11±15.06 | 3.49 |
| A9 | 125 | -0.60 | 30±15 | +250 | 30.11±15.06 | 3.49 |
| A10 | 100 | -0.55 | 30±10 | +50 | 30.09±10.03 | 3.20 |
| A11 | 100 | -0.55 | 30±10 | +150 | 30.09±10.03 | 3.20 |
| A12 | 100 | -0.55 | 30±10 | +250 | 30.09±10.03 | 3.20 |
| A13 | 150 | -0.55 | 30±20 | +50 | 30.09±20.06 | 3.20 |
| A14 | 150 | -0.55 | 30±20 | +150 | 30.09±20.06 | 3.20 |
| A15 | 150 | -0.55 | 30±20 | +250 | 30.09±20.06 | 3.20 |
| A16 | 100 | -0.55 | 30±15 | +50 | 30.09±15.05 | 3.20 |
| A17 | 100 | -0.55 | 30±15 | +150 | 30.09±15.05 | 3.20 |
| A18 | 100 | -0.55 | 30±15 | +250 | 30.09±15.05 | 3.20 |
| A19 | 150 | -0.55 | 30±15 | +50 | 30.09±15.05 | 3.20 |
| A20 | 150 | -0.55 | 30±15 | +150 | 30.09±15.05 | 3.20 |
| A21 | 150 | -0.55 | 30±15 | +250 | 30.09±15.05 | 3.20 |
| B1 | 125 | +0.85 | 30±15 | +50 | 30.22±15.11 | 4.92 |
| B2 | 125 | +0.85 | 30±15 | +150 | 30.22±15.11 | 4.92 |
| B3 | 125 | +0.85 | 30±15 | +250 | 30.22±15.11 | 4.92 |
| B4 | 125 | +0.90 | 30±15 | +50 | 30.25±15.13 | 5.20 |
| B5 | 125 | +0.90 | 30±15 | +150 | 30.25±15.13 | 5.20 |
| B6 | 125 | +0.90 | 30±15 | +250 | 30.25±15.13 | 5.20 |
| B7 | 125 | +0.95 | 30±15 | +50 | 30.28±15.14 | 5.49 |
| B8 | 125 | +0.95 | 30±15 | +150 | 30.28±15.14 | 5.49 |
| B9 | 125 | +0.95 | 30±15 | +250 | 30.28±15.14 | 5.49 |
| B10 | 125 | +1.00 | 30±15 | +50 | 30.31±15.15 | 5.77 |
| B11 | 125 | +1.00 | 30±15 | +150 | 30.31±15.15 | 5.77 |
| B12 | 125 | +1.00 | 30±15 | +250 | 30.31±15.15 | 5.77 |
| B13 | 100 | +0.90 | 30±10 | +50 | 30.25±10.08 | 5.20 |
| B14 | 100 | +0.90 | 30±10 | +150 | 30.25±10.08 | 5.20 |
| B15 | 100 | +0.90 | 30±10 | +250 | 30.25±10.08 | 5.20 |
| B16 | 150 | +0.90 | 30±20 | +50 | 30.25±20.17 | 5.20 |
| B17 | 150 | +0.90 | 30±20 | +150 | 30.25±20.17 | 5.20 |
| B18 | 150 | +0.90 | 30±20 | +250 | 30.25±20.17 | 5.20 |
| B19 | 100 | +0.90 | 30±15 | +50 | 30.25±15.13 | 5.20 |
| B20 | 100 | +0.90 | 30±15 | +150 | 30.25±15.13 | 5.20 |
| B21 | 100 | +0.90 | 30±15 | +250 | 30.25±15.13 | 5.20 |
| B22 | 150 | +0.90 | 30±15 | +50 | 30.25±15.13 | 5.20 |
| B23 | 150 | +0.90 | 30±15 | +150 | 30.25±15.13 | 5.20 |
| B24 | 150 | +0.90 | 30±15 | +250 | 30.25±15.13 | 5.20 |
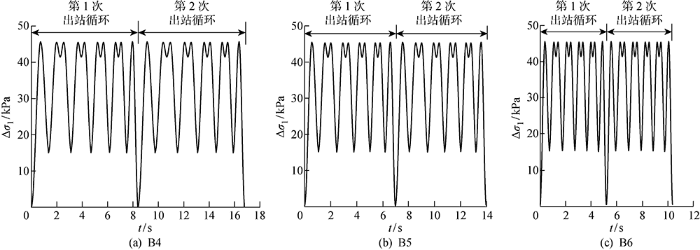
以B4~B6为例,其动三轴轴向附加应力时程曲线如图5所示.
图5
最后采用差分的方法将一趟列车的模拟荷载差分成0.01 s间隔的数据集.并将一趟列车的所有差分结果作为一组荷载振动输入动三轴的自定义荷载模块,从而完成对变频荷载的控制.
2.3 试验过程
3 试验结果
3.1 进出站距离对累积塑性变形的影响
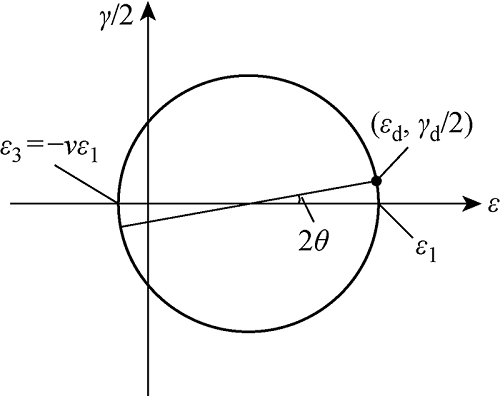
进出站区间内不同位置地铁运行速度不同,这使得软黏土受到的振动荷载形式不同,从而进一步影响土体的变形特性.通过动三轴试验结果,可以还原出地铁进出站荷载下引发的土体竖向应变和切应变示意图(见图6,图中ε3为最小应变;γd为地铁进出站荷载下在水平面上的切应变):
式中:
图6
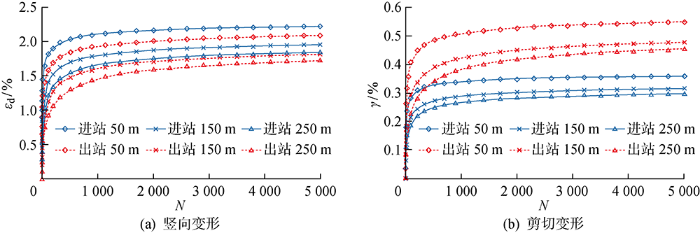
图7(a)所示为不同进出站距离下软黏土累积塑性竖向变形与进出站次数(N)的关系曲线,图7(b)所示为不同进出站距离下软黏土累积塑性剪切变形与进出站次数的关系曲线.由图7可知,不同进出站距离,地铁进出站荷载下软黏土累积塑性应变曲线特征都大致相同,应变曲线大致可划分为3个发展阶段:① 初始阶段.应变爆发式增长,在短时间内便产生了较多的塑性应变累积;② 中期阶段.塑性应变增长速率随进出站振动循环次数的增多而降低;③ 稳定阶段.当进出站振动循环次数到达600~1200 次时,土体进入应变稳定阶段,该阶段土体累积塑性应变变化较小.同时,距地铁站越近,土体进入逐渐稳定阶段所经历的进出站次数越少.进站区间的土体能更早进入逐渐稳定阶段,特别是切应变的发展.这说明,进出站区间内的土体,不论是竖向应变还是剪切变形在地铁运行初期增长速率最大.地铁运行初期是工程地质灾害防治的重点.随着振动荷载的不断施加,土体逐渐趋于密实,应变速率减小.
图7
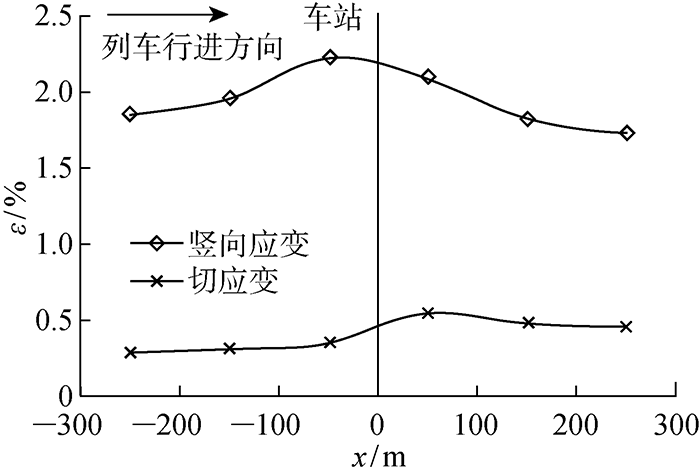
图8
产生上述现象的原因是:距离地铁站越近,地铁平均运行速度越慢,运行速度慢的列车全车经过某点所需的时间更长.这就使得相同条件下距地铁站更近的列车荷载对土体产生的冲量更大.冲量大的工况土体应变速率更快,也就造成了土体前期变形发展地更迅猛.同时,对于软黏土这种黏塑性材料来说,冲量可以致使塑性变形增大.另外,地铁运行至距地铁站40~70 m时,其产生的低频振动恰巧与软黏土自身固有频率(1.3 ~1.4 Hz)相吻合[12],列车荷载与土体会产生微小的共振.共振效应在一定程度上加剧了距地铁站50 m左右的土体变形.综合以上原因,最终产生了距地铁站近的土体累积塑性变形量较大的现象.
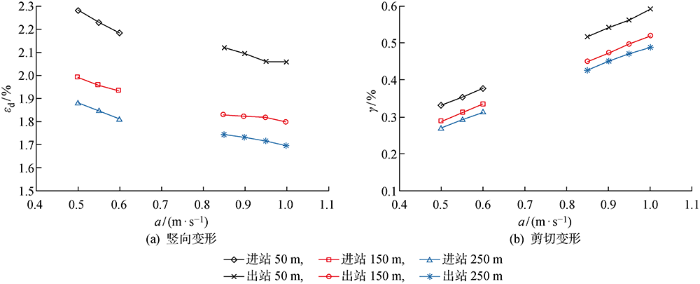
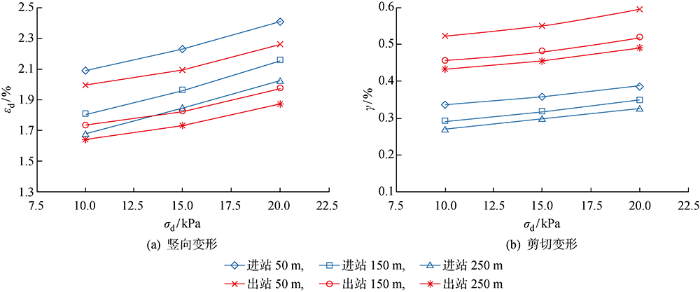
3.2 进出站加速度对累积塑性变形的影响
图9
产生上述现象的原因是:地铁进出站加速度越大,相同位置地铁运行速度越快.高速运行的列车所产生的高频振动使得土体竖向变形更大.对于土体剪切应变来说,地铁加减速所产生的切应力对其影响更直接、影响程度更深.试验结果也表明土体的剪切变形与地铁加速度基本具有正相关关系.
3.3 动应力幅值对累积塑性变形的影响
图10
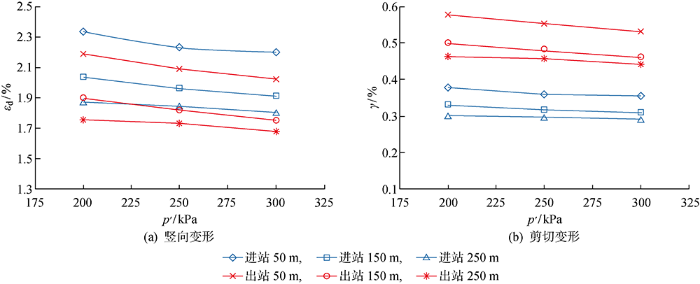
3.4 围压对累积变形的影响
不同固结围压下软黏土在 5000 次进出站变频荷载循环作用下的累积塑性竖向应变、切应变如图11所示.结果表明,土体固结围压越大,土体的累积塑性竖向变形越小,剪切变形也越小.固结应力大的土体抵抗变形的能力强.
图11
4 累积塑性应变模型
双曲指数模型[13]是一种针对长江三角洲地区软黏土在循环荷载下长期变形的预测模型,其累积塑性应变与循环次数的关系为
式中:εp为累积塑性应变;
表3 数据模型拟合结果
Tab.3
| 试样编号 | 竖向应变 | 切应变 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| a | b | c | 相关系数 | a | b | c | 相关系数 | ||
| A2 | 1.729 | 0.462 | 0.441 | 0.996 | 17.739 | 3.252 | 0.491 | 0.990 | |
| A4 | 0.964 | 0.424 | 0.432 | 0.996 | 5.979 | 2.628 | 0.432 | 0.996 | |
| A5 | 2.026 | 0.467 | 0.452 | 0.990 | 12.566 | 2.897 | 0.452 | 0.996 | |
| A6 | 3.497 | 0.492 | 0.502 | 0.997 | 21.688 | 3.053 | 0.502 | 0.992 | |
| A8 | 2.606 | 0.478 | 0.491 | 0.997 | 9.848 | 2.631 | 0.441 | 0.988 | |
| A11 | 2.659 | 0.488 | 0.434 | 0.994 | 16.489 | 3.025 | 0.434 | 0.996 | |
| A14 | 1.551 | 0.436 | 0.472 | 0.992 | 10.024 | 2.754 | 0.496 | 0.989 | |
| A17 | 1.922 | 0.451 | 0.452 | 0.994 | 11.922 | 2.799 | 0.452 | 0.990 | |
| A20 | 2.543 | 0.482 | 0.484 | 0.997 | 15.775 | 2.987 | 0.484 | 0.992 | |
| B2 | 3.403 | 0.487 | 0.476 | 0.988 | 13.688 | 1.960 | 0.476 | 0.996 | |
| B4 | 1.307 | 0.434 | 0.400 | 0.995 | 4.970 | 1.651 | 0.400 | 0.988 | |
| B5 | 3.943 | 0.489 | 0.492 | 0.989 | 14.988 | 1.858 | 0.492 | 0.987 | |
| B6 | 8.131 | 0.502 | 0.551 | 0.987 | 30.898 | 1.908 | 0.550 | 0.987 | |
| B8 | 4.182 | 0.491 | 0.500 | 0.993 | 15.067 | 1.768 | 0.500 | 0.990 | |
| B11 | 5.312 | 0.493 | 0.520 | 0.990 | 18.194 | 1.689 | 0.520 | 0.990 | |
| B14 | 4.079 | 0.499 | 0.464 | 0.990 | 15.506 | 1.897 | 0.464 | 0.994 | |
| B17 | 3.327 | 0.468 | 0.520 | 0.993 | 12.647 | 1.780 | 0.520 | 0.989 | |
| B20 | 3.515 | 0.481 | 0.510 | 0.996 | 13.362 | 1.828 | 0.510 | 0.990 | |
| B23 | 3.764 | 0.496 | 0.461 | 0.987 | 14.307 | 1.886 | 0.461 | 0.989 | |
5 结论
本文通过倾斜制样并使用动三轴对进出站作用下软黏土的累积塑性变形特性进行研究,得到如下结论:
(1) 进出站变频荷载循环作用下软黏土累积塑性应变曲线可大致划分为爆发增长-较快增长-逐渐稳定3个阶段.地铁运营初期土体形变速率较高,是工程地质灾害防治的重点.
(2) 距地铁站越近,土体进入逐渐稳定阶段所需的进出站次数越少,土体竖向沉降越大,剪切变形越小.距地铁站远的区域土体快速增长阶段持续的时间长,距地铁站近的区域土体最终沉降量大.
(3) 进出站区间内地铁加(减)速度值越大,土体竖向变形越小、剪切变形越大.进站区间土体沉降变形、出站区间土体水平位移更为明显.
(4) 地铁荷载动应力幅值越大,土体的累积塑性变形越大.
(5) 进出站区间内土体的固结应力越大,其抵抗荷载变形的能力越强.
参考文献
Dynamic behaviour of a single-span beam subjected to loads moving with variable speeds
[J].DOI:10.1006/jsvi.2002.5141 URL [本文引用: 1]
黏弹性地基板在矩形变速荷载作用下的振动分析
[J].
Vibration analysis of a plate on viscoelastic foundation under moving rectangular loads with variable speeds
[J].
制动力作用下车辆-车站结构耦合系统分析
[J].
Analysis method for a vehicle structure coupled system under braking force
[J].
地铁列车进站引起场地柱面纵向振动
[J].
Cylindrical longitudinal vibration while metro train arriving at station
[J].
Vertical dynamics of a single-span beam subjected to moving mass-suspended payload system with variable speeds
[J].DOI:10.1016/j.jsv.2017.12.030 URL [本文引用: 1]
地铁列车出、进站加、减速的轴向激励引起出平面振动
[J].
Out-of-plane vibration induced by axial excitation while a metro train arriving at or leaving a station
[J].
地铁列车进出站时土层空间振动特性分析
[J].
Space vibration of subsoil during metro train arriving at or leaving station
[J].
上海地层长期变形特性及其对基础设施的影响
[J].
Long-term deformation characteristics of Shanghai soil layer and its influence on infrastructure
[J].
基于加速度响应的轨道监测研究
[J].
Track monitoring based on locomotive acceleration response
[J].
地铁振动荷载作用下隧道周围饱和软黏土动力响应研究
[J].
Dynamic response of saturated soft clay around a subway tunnel under vibration load
[J].
冻融饱和粉砂动力性能试验
[J].
Experimental study on dynamic cumulative axial strain performance of artificial frost-thawed saturated silty sand
[J].
地铁荷载下饱和软黏土累积变形特性
[J].
Accumulative deformation characteristics of saturated soft clay under subway loading in Shanghai
[J].