柔性控制器MMC子模块最优冗余数量双重协同优化方法

doi:10.16183/j.cnki.jsjtu.2021.444

柔性控制器MMC子模块最优冗余数量双重协同优化方法

马洲俊¹, 王勇¹, 王杰^,², 陈少宇²

1.国网江苏省电力有限公司南京供电分公司, 南京 210019

2.上海交通大学电力传输与功率变换控制教育部重点实验室, 上海 200240

A Dual Cooperative Optimization for Optimal Redundancy Quantity of MMC Submodules of Flexible Controller

MA Zhoujun¹, WANG Yong¹, WANG Jie^,², CHEN Shaoyu²

1. State Grid Jiangsu Electric Power Co., Ltd., Nanjing 210019, China

2. Key Laboratory of Control of Power Transmission and Conversion of the Ministry of Education, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 王杰,男,博士生,电话(Tel.):15805694830;E-mail:jiewangee@sjtu.edu.cn.

责任编辑: 孙伟

收稿日期: 2021-11-4

基金资助:

国网江苏省电力有限公司科技项目(J2019063)

Received: 2021-11-4

作者简介 About authors

马洲俊(1986-),男,江苏省南京市人,博士,高级工程师,从事电网规划及调控运行研究.

摘要

柔性直流系统中模块化多电平换流器(MMC)的子模块故障影响系统正常运行,可靠性和经济性的相互制约是MMC冗余数量配置优化的关键问题之一.对此,建立含冗余子模块MMC可靠性和经济性数学模型的多目标优化函数,提出一种柔性控制器子模块冗余数量双重协同优化方法.该方法结合权重系数和NSGAII多目标优化算法的优势,在冗余数量取相同选择偏好下,计算得到两者优化结果的交集.以南京某柔性台区直流工程为例,在MATLAB中搭建模型,仿真结果表明所提方法在满足柔性直流系统可靠性的同时,能够显著提高经济性,为实际柔性直流工程中MMC冗余子模块数量配置提供思路.

关键词： 模块化多电平换流器; 冗余子模块; NSGAII多目标优化; 权重系数; 冗余数量优化

Abstract

The failure of modular multilevel converter (MMC) submodules in the flexible direct current (DC) system affects the normal operation of the system, and the mutual restriction of reliability and economy is one of the key issues of MMC redundancy configuration optimization. A multi-objective optimization function of MMC reliability and economy mathematical model with redundant submodules was established. Based on the weight coefficient and NSGAII multi-objective optimization methods, a dual collaborative optimization for redundancy quantity of flexible controller was proposed. Combining the advantages of the two methods, the intersection of the two optimization results was calculated under the same redundancy quantity selection preference. A model based on a DC project in a flexible station area of Nanjing was built in MATLAB. The simulation results prove that the proposed method can not only meet the reliability of the flexible DC system, but also significantly improve the economy. It provides ideas for redundancy quantity of MMC submodules in the actual flexible DC project.

Keywords： modular multilevel converter (MMC); redundant submodule; NSGAII multi-objective optimization; weight coefficient; redundancy quantity optimization

PDF (0KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

马洲俊, 王勇, 王杰, 陈少宇. 柔性控制器MMC子模块最优冗余数量双重协同优化方法[J]. 上海交通大学学报（自然版）, 2022, 56(3): 325-332 doi:10.16183/j.cnki.jsjtu.2021.444

MA Zhoujun, WANG Yong, WANG Jie, CHEN Shaoyu. A Dual Cooperative Optimization for Optimal Redundancy Quantity of MMC Submodules of Flexible Controller[J]. Journal of shanghai Jiaotong University, 2022, 56(3): 325-332 doi:10.16183/j.cnki.jsjtu.2021.444

模块化多电平换流器(Modular Multilevel Converter,MMC)具有扩展性好和波形质量优等优点,在柔性直流输配电系统中应用广泛^[1,2].目前,柔性控制器的主流拓扑结构采用功率子模块级联的MMC结构^[3,4,5].与两电平电压源换流器(Voltage Source Converter,VSC)相比,级联MMC结构具有输出电平高波形质量好、谐波含量低、易于冗余模块化设计和可节省交流滤波器的投资成本等优点^[6,7,8,9].现阶段国内外已有较多基于MMC换流器的柔性直流系统正处于规划和设计中,我国已有多个柔性直流示范工程,例如舟山多端互联^[10,11]、厦门双端互联和广东三端互联等^[12,13].

高电压等级和高功率密度是未来MMC直流系统的发展趋势.MMC常采用子模块级联形式^[14,15,16],由于子模块数量较多,任一子模块故障,均会影响换流器的正常运行,导致MMC退出运行,柔性直流系统供电中断^[17].为提高MMC的运行可靠性和故障处理能力^[18],一般配置一定数量的冗余子模块,用于替代故障子模块.随着模块化多电平换流器型高压直流输电(MMC-HVDC)系统向高电压和大容量方向发展,MMC的子模块数量也将不断增多.冗余子模块数量越多,MMC的可靠性越高,但冗余成本也越高,经济性显著降低;而冗余子模块数量过少,MMC的可靠性得不到保证^[19].因此,运行可靠性和冗余经济性的相互制约是冗余数量配置优化的关键问题之一.

目前,已有MMC运行可靠性和冗余数量优化的相关研究.王宝安等^[19]通过换流阀的可靠度函数计算,分析MMC运行可靠性;许建中等^[20]通过计算MMC的阀损耗,设计出换流阀损耗最小的优化方法;王秀丽等^[21]设计出MMC可靠性数学模型,提出MMC最优冗余子模块优化方法.黄守道等^[22]考虑元件损耗对MMC寿命影响,基于半马尔可夫(Semi-Markov)方法建立MMC的数学模型.李辉等^[23]考虑MMC运行工况,基于故障树分析方法,详细分析MMC薄弱环可靠性.全少理等^[24]以柔性多状态开关为例,结合故障树和Markov过程得到MMC的状态转移矩阵,并提出基于贝叶斯网络的可靠性建模方法.朱晋等^[25]基于故障树模型计算不同功率器件拓扑结构的可靠度,通过衡量可靠性贡献度,优化冗余设计.Xu等^[26]对混合结构的MMC子模块进行可靠性建模,得到具有一定故障穿越能力的各种拓扑子模块的最优配置.但上述研究并未涉及MMC的冗余经济性.在保障可靠性的基础上,MMC的冗余设计应尽量提高配置经济性以减少成本.因此,在设计MMC子模块最优冗余配置数量时,需要综合考虑两者因素.

本文考虑冗余经济性和供电可靠性等因素,建立含冗余子模块MMC的可靠性和经济性数学模型的多目标优化函数.基于权重系数和NSGAII算法多目标优化的柔性控制器子模块冗余数量双重协同优化方法,优化冗余子模块数量.所配置的冗余子模块数量可以同时使系统的可靠性和冗余经济性达到最优效果.

1 三相MMC拓扑结构和特点

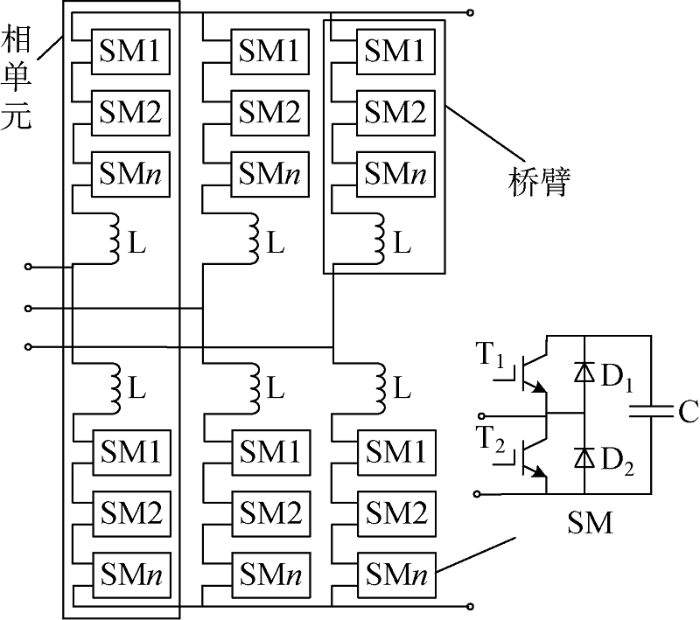
图1为三相MMC与子模块结构图.其中, SMi(i=1, 2, …, n) 为子模块,L为电感器,C为电容器,T₁和T₂为绝缘栅双极型晶体管,D₁和D₂为二极管.正常运行时,控制系统利用“子模块电容均压策略”控制各子模块的投入或切除状态,当任一子模块发生故障时,换流器将无法正常运行,因此需要增设一定数量的冗余子模块.当子模块发生故障时,可用冗余子模块替代故障子模块,当故障子模块数量小于冗余子模块数量时,可以保证MMC柔性直流系统正常运行.冗余子模块数量影响运行可靠性和冗余经济性,因此需要研究兼顾运行可靠性和冗余经济性多目标的冗余子模块数量优化方法.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 三相MMC与子模块结构图

Fig.1 Structure of three phase MMC and submodules

2 冗余子模块MMC的可靠性和经济性数学模型

冗余优化目标考虑MMC系统的可靠性、期望替代率和冗余数量经济函数共3个因素,建立子模块MMC的可靠性和经济性数学模型.

2.1 MMC系统可靠性

子模块可靠性为该子模块不出现故障的概率,由其所组成的器件可靠性共同决定.单独子模块的可靠性为

(1)R_SM≥

R_{I}^{2} R_{D}^{2}

R_C

式中:R_I、R_D和R_C分别为绝缘栅双极型晶体管、二极管和电容的可靠性.则该子模块的故障概率为 1-R_SM.设每相每桥臂配置的子模块冗余数为N₀,有i个子模块出现故障的概率为

(2)P(i)≥

C_{N + N_{0}}^{i}

(1-R_SM)ⁱ

R_{SM}^{N + N_{0} - i}

式中: $C_{N + N_{0}}^{i}$ = $\frac{(N + N_{0})!}{i! (N + N_{0} - i)!}$ N为每相每桥臂子原有子模块数.A相上桥臂的可靠性为不超过N₀个SM故障的概率:

(3)R_A=

\overset{N_{0}}{\sum_{i = 1}} C_{N + N_{0}}^{i}

(1-R_SM)ⁱ

R_{SM}^{N + N_{0} - i}

三相MMC系统共有6个桥臂,每个桥臂均含有N₀个冗余子模块.由于每个桥臂故障是相互独立事件,所以三相MMC的可靠性为

(4) R_MMC=

{(\overset{N_{0}}{\sum_{i = 0}} C_{N + N_{0}}^{i} (1 - R_{SM})^{i} R_{SM}^{N + N_{0} - i})}^{6}

2.2 冗余子模块期望替代率

定义冗余子模块替代故障子模块数量的期望值为期望替代数量,则A相上桥臂冗余子模块期望替代数量为

(5)Q_A=

\overset{N_{0}}{\sum_{i = 0}}

C_{N + N_{0}}^{i}

(1-R_SM)ⁱ

R_{SM}^{N + N_{0} - i}

\overset{N_{0}}{\sum_{i = 0}}

iP(i)

三相MMC系统的冗余子模块期望替代数量为

(6)Q_MMC=6

\overset{N_{0}}{\sum_{i = 0}}

C_{N + N_{0}}^{i}

(1-R_SM)ⁱ

R_{SM}^{N + N_{0} - i}

定义冗余子模块期望替代数量与实际冗余子模块配置总数量的比值为冗余子模块期望替代率:

(7)E_MMC=

\frac{Q_{MMC}}{6 N_{0}}

\frac{1}{N_{0}} \overset{N_{0}}{\sum_{i = 0}}

C_{N + N_{0}}^{i}

(1-R_SM)ⁱ

R_{SM}^{N + N_{0} - i}

2.3 冗余数量经济函数

经济优化目标为冗余子模块数量尽量取小,即

(8)C(N₀)=min(N₀)

为便于多目标优化问题的统一求解,将其取值范围限制在[0,1]之间,并将最小值问题转化为最大值问题,以实现R_MMC、E_MMC和冗余数量经济函数(C_MMC)取值均在[0,1]之间,且目标函数使三者均可达到最大理想值.转化公式为

(9)C(N₀)=max

(\frac{N - N_{0}}{N})

其中:

(10)C_MMC=

\frac{N - N_{0}}{N}

3 基于权重系数和NSGAII算法的柔性控制器子模块冗余数量双重协同优化方法

3.1 多目标优化函数

多目标优化函数使得系统可靠性、期望替代率和冗余数量经济函数3个子目标同时达到最优,其优化函数分别为

(11)

\begin{array}{l} R (N_{0}) = \\ \max ((\overset{N_{0}}{\sum_{i = 0}} C_{N + N_{0}}^{i} (1 - R_{SM})^{i} R_{SM}^{N + N_{0} - i})^{6}) \\ E (N_{0}) = \\ \max (\frac{1}{N_{0}} \overset{N_{0}}{\sum_{i = 0}} i C_{N + N_{0}}^{i} (1 - R_{SM})^{i} R_{SM}^{N + N_{0} - i}) \\ C (N_{0}) = \max (\frac{N - N_{0}}{N}) \end{array}\}

多目标优化应尽量满足3个子目标的期望结果.

3.2 约束条件

3个约束条件如下:

(12)s.t. R_MMC≥0.95

(13)

\begin{array}{l} N_{0} \leq 0.5 N \\ C_{MMC} \geq 0.5 \end{array}\}

(14) E_MMC≥0.1

3.3 双重协同优化方法

权重系数法利用权重系数将多个目标函数融合在一个综合目标函数中,有利于探寻综合目标函数与冗余数量的关系.该方法直观、方便,可以高效解决复杂的多目标函数优化问题.为求解3个目标的共同优化结果,引入权值系数μ₁、μ₂和μ₃,将3个目标函数统一为一个目标函数,表示为

(15)MOF(N₀)=max(μ₁R_MMC+μ₂E_MMC+μ₃C_MMC)

根据优化目标更偏重可靠性还是经济性而确定权重系数.若优化目标对可靠性的要求较低,满足系统所需可靠性的前提下,尽量减少冗余配置数量,提高冗余期望替代率和经济性,则表示可靠性的系数 μ₁可适当减小,表示经济性的系数μ₂和μ₃可适当增大.若优化目标对可靠性的要求较高,则μ₁应取更大值,μ₂和μ₃ 取值相对减小.

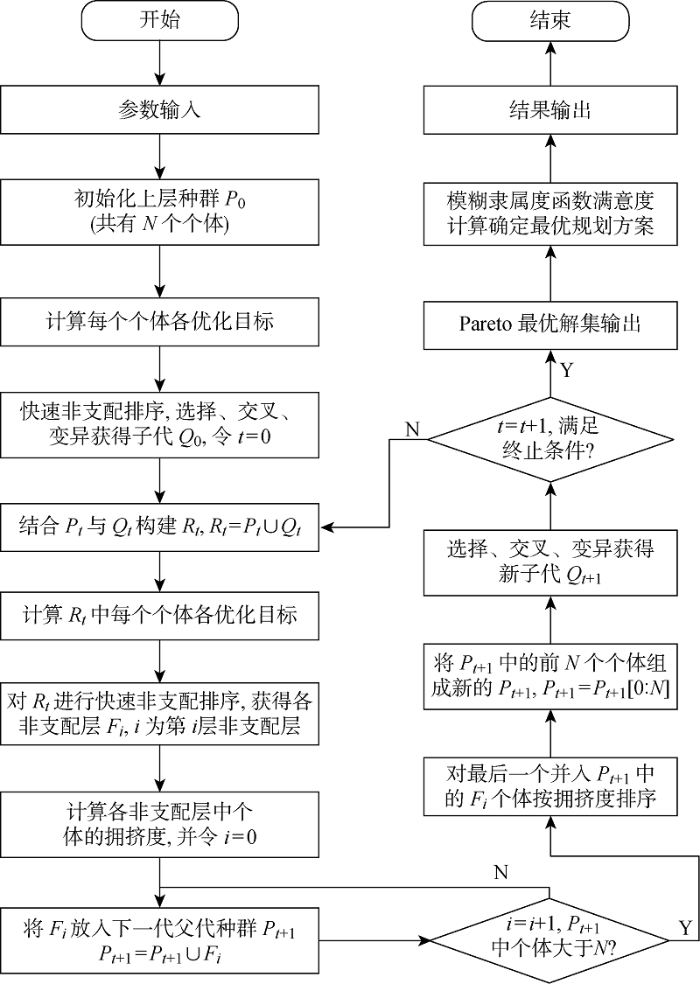
NSGAII算法适合应用于复杂多目标优化问题,能够实现快速准确的搜索性能,减小时间复杂度,提升排序速度和性能.其流程如图2所示,包括初始种群的设定、拥挤度排序和遗传算法等过程.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 NSGAII多目标优化算法流程图

Fig.2 Flow chart of NSGAII multi-objective optimization algorithm

NSGAII算法是基于Pareto最优解的多目标优化算法,其核心为得到规划方案Pareto非支配解集,并从非支配解集中选择最优规划方案.收敛判定条件为使优化结果收敛到非劣最优目标域.该算法在求解时无需确定各优化目标的权重,因此能够避免主观性对优化过程的干扰.NSGAII算法的输出结果为一个最优解集,且解集中的每一个解均为互不支配的Pareto非劣解.

根据上述双重算法,协同计算MMC冗余子模块数量,利用权重系数法引入 μ₁、μ₂和μ₃, 将3个目标函数统一为一个目标进行求解,根据选择偏好设定权值系数大小.利用NSGAII算法可以直接获得Pareto非劣最优解集.在不同选择偏好下,利用非劣最优解集中获得的期望最优解,可以得到不同最优冗余配置数量的优化结果.将两种方法结合,取优化结果交集,可以有效改善人为主观因素对冗余配置结果的影响.

4 仿真验证

以南京某柔性台区MMC直流工程为例,利用MATLAB搭建模型.柔性台区的直流工程以背靠背MMC控制器拓扑为基础,系统参数如表1所示.优化设计MMC子模块冗余数量,以验证所提策略的有效性.其中,N=20,R_SM=0.97,N₀取[0,10]的整数值,则求解最大值的优化函数为

表1 算例参数

Tab.1 Parameters of examples

系统参数	取值
PCC额定电压	10 kV
交流侧等效电感(p.u.)	0.018
交流侧等效电阻(p.u.)	0.006
桥臂电感(p.u.)	0.0025
控制器额定容量	2 MV·A
PCC额定频率	50 Hz

新窗口打开| 下载CSV

(16)

\begin{array}{l} R_{MMC} (N_{0}) = \\ {(\overset{N_{0}}{\sum_{i = 0}} C_{20 + N_{0}}^{i} \times 0 . 03^{i} \times 0 . 97^{20 + N_{0} - i})}^{6} \\ E_{MMC} (N_{0}) = \\ \frac{1}{N_{0}} \overset{N_{0}}{\sum_{i = 0}} (i C_{20 + N_{0}}^{i} \times 0 . 03^{i} \times 0 . 97^{20 + N_{0} - i}) \\ C_{MMC} (N_{0}) = \frac{20 - N_{0}}{20} \end{array}\}

综合考虑R_MMC、E_MMC和C_MMC,其不同取值下的MOF如表2所示.在权值系数(μ₁,μ₂,μ₃)分别取 (0.5,0.2,0.3)、(0.6,0.1,0.3)、(0.7,0.1,0.2)和(0.8,0.1,0.1)时,得到不同权重下的仿真结果,如表3所示.

表2 最优冗余优化结果

Tab.2 Optimization results of optimal redundancy

N₀	R_MMC	E_MMC	C_MMC	满足约束	MOF
0	0.02585878	0	1.00	否	0.315515
1	0.43383842	0.34259043	0.95	否	0.579562
2	0.84775460	0.28712341	0.90	否	0.807365
3	0.97306173	0.22375505	0.85	是	0.861213
4	0.99616279	0.17918262	0.80	是	0.855616
5	0.99952667	0.14990391	0.75	是	0.839706
6	0.99994782	0.12998974	0.70	是	0.822968
7	0.99999476	0.11571327	0.65	是	0.806568
8	0.99999951	0.10499990	0.60	是	0.790500
9	0.99999996	0.09666665	0.55	否	0.774667
10	1.00000000	0.08999999	0.50	否	0.759000

新窗口打开| 下载CSV

表3 不同权重下的优化结果

Tab.3 Optimization results at different weights

N₀	满足约束	MOF
N₀	满足约束	(0.5,0.2, 0.3)	(0.6,0.1, 0.3)	(0.7,0.1, 0.2)	(0.8,0.1, 0.1)
0	否	0.3129290	0.315515	0.218101	0.120687
1	否	0.5704372	0.579562	0.527946	0.476330
2	否	0.7513019	0.807365	0.802141	0.796916
3	是	0.7862818	0.861213	0.873519	0.885825
4	是	0.7739179	0.855616	0.875232	0.894848
5	是	0.7547441	0.839706	0.864659	0.889612
6	是	0.7359718	0.822968	0.852962	0.882957
7	是	0.7181400	0.806568	0.841568	0.876567
8	是	0.7009997	0.790500	0.830500	0.870500
9	否	0.7293333	0.774667	0.819667	0.864667
10	否	0.7180000	0.759000	0.809000	0.859000

新窗口打开| 下载CSV

表2中,MOF在 N₀=3时取得最大值,即最优冗余子模块配置数为3.当N₀=3时,μ₁达到较高值,可靠性满足系统要求,且冗余子模块可以得到充分有效利用;同时满足冗余子模块数尽可能小,可以有效降低成本.随着N₀ 增大,可知:

(1) R_MMC单调递增.当N₀从0增大至3时,R_MMC急剧增大;当N₀=3时,R_MMC取得较高值约为0.973;当N₀=4时,R_MMC≈0.996,此时可靠性很高,故障概率几乎为0;当N₀>4时,R_MMC几乎保持不变,此时再增大冗余数量不会显著增益可靠性.因此,N₀=3,4较佳.

(2) E_MMC先增大后减小.当N₀在[1, 4]之间取值时,冗余子模块能够得到更充分有效地利用.因此,N₀在[1, 4]之间取值较佳.

(3) C_MMC单调递减.N₀取值不宜过大,否则经济性不佳.

(4) MOF先增大后减小.当N₀=3时,MOF取得最大值.因此,在该权值分配下,N₀=3最佳.

表3中,若优化目标对可靠性要求较低,在满足系统所需可靠性的前提下,应尽量减少冗余配置数量,提高冗余期望替代率和经济性, 则μ₁可取较小值,如(μ₁,μ₂,μ₃)分别取(0.5,0.2,0.3)和(0.6,0.1,0.3),此时取N₀=3最佳.若优化目标对可靠性要求较高,则μ₁要取较大值,如(μ₁,μ₂,μ₃)分别取(0.7,0.1,0.2)和(0.8,0.1,0.1),此时取N₀=4最佳.此外,不同权重分配下优化结果可能不同.优化目标对系统可靠性的要求越高,则μ₁取值越大,μ₂和μ₃取值相对减小,最佳冗余子模块配置数可能会增大;当优化目标对可靠性要求较低,更关注经济性因素时,μ₁取值可相应减小,μ₂和μ₃取值相对增大,最佳冗余子模块配置数可能会减小.因此,权值系数μ₁、μ₂和μ₃ 的取值十分依赖于优化目标更偏重可靠性还是经济性.

为方便得到Pareto非劣解集,需要将式(16)统一转化为最小值问题:

(17)

\begin{array}{l} F (N_{0}) = \min (1 - (\overset{N_{0}}{\sum_{i = 0}} C_{20 + N_{0}}^{i} \times \\ 0 . 03^{i} \times 0 . 97^{20 + N_{0} - i})^{6}) \\ C (N_{0}) = \min (N_{0}) \end{array}\}

式中:F(N₀)为故障概率函数.式(17)将式(16)的R_MMC最高转换为F(N₀)最低,E_MMC和C_MMC最大转换为C(N₀)最小问题.转化为最小值问题后更方便NSGAII算法的求解.

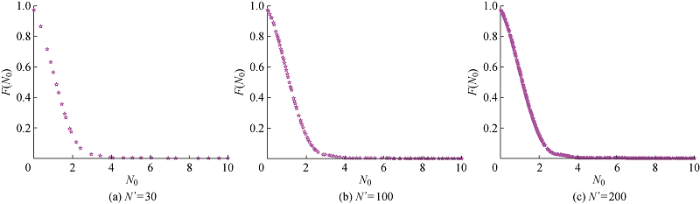
当目标数量种群较大时,利用NSGAII算法无法处理离散化数据,因此需要将式(17)连续化处理,采用最小二乘法拟合函数进行分段线性化拟合 F(N₀).不同目标数量种群时,利用NSGAII算法求解式(17)的非劣最优目标域如图3所示.其中,非劣最优目标域由N'个目标解集构成,解集中的每个个体均为Pareto非劣解.可知,非劣解集的变化轨迹大致为反比例函数曲线,表明优化目标1(故障概率最低)与优化目标2(冗余数量最小)相互冲突,降低故障概率的同时,冗余数量随之增加.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 不同目标数量种群的Pareto非劣最优目标域

Fig.3 Pareto non-inferior optimal target regions of different target populations

在实际冗余配置中,需要按照系统可靠性最低的要求进行配置,一般要求可靠性不低于一定值时,冗余数量尽量取较小值.根据图3可知,若要求 3%≤F(N₀)<5%,则N₀=3最佳;若要求 0.3%≤F(N₀)<3%,则N₀=4最佳;若要求F(N₀)<0.3%,则N₀=5 最佳.

综上,权重系数法易受权重系数分配影响,优化结果直观清晰但受人为主观因素影响;NSGAII算法可以在不受人为主观因素影响下直接得到一组非劣解集,并根据系统可靠性要求配置最优冗余数量,但其结果并不直观清晰.所提双重协同优化方法最优性结合了权重系数法和NSGAII算法的优势.协同优化结果表明,对于额定子模块数量为20的MMC,更注重经济性,则N₀=3;更注重可靠性,则N₀=4.协同优化能够实现冗余子模块数量的最优配置,在满足柔性直流系统可靠性前提下,最大程度提高系统经济性.此外,冗余子模块数受子模块总数影响.当子模块总数更多时,则需要配置更多的冗余子模块,运行可靠性才可以满足要求.而所提双重协同优化方法并不受制于子模块数量,能够在子模块总数不同时计算最优冗余配置.

5 结语

本文设计了基于权重系数和NSGAII算法的柔性控制器子模块冗余数量双重协同优化方法.综合考虑可靠性、期望替代率和冗余数量经济性,并通过建立含权重系数的综合目标函数和约束条件,得到最优冗余子模块数目设计算法.引入权值系数μ₁、μ₂和μ₃,将3个目标函数统一为一个目标进行求解;在不同权重下,得到不同最优冗余配置数量的优化结果.引入NSGAII多目标优化算法,可以直接得到Pareto非劣最优解集,并从非劣最优解集中得到期望的最优解.取相同选择偏好下双重优化结果的交集,能够有效避免主观人为因素的影响.协同优化所得结论表明,对于额定子模块数量为20的MMC,最优冗余子模块数量取3或4.N₀=3在保证系统基本可靠性的前提下更注重经济性;N₀=4则更适用于对系统可靠性要求更高的场合.所提方法适用于不同电压等级和容量的柔性直流输配电系统MMC冗余子模块配置设计,在满足系统可靠性的前提下,可以最大程度提高系统经济性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

FLOURENTZOU

, AGELIDIS V

, DEMETRIADES G

VSC-based HVDC power transmission systems: An overview

[J]. IEEE Transactions on Power Electronics, 2009, 24(3):592-602.

DOI:10.1109/TPEL.2008.2008441 URL [本文引用: 1]

[2]

HARNEFORS

, ANTONOPOULOS

, NORRGA

, et al.

Dynamic analysis of modular multilevel converters

[J]. IEEE Transactions on Industrial Electronics, 2013, 60(7):2526-2537.

DOI:10.1109/TIE.2012.2194974 URL [本文引用: 1]

[3]

HAGIWARA

, AKAGI

Control and experiment of pulsewidth-modulated modular multilevel converters

[J]. IEEE Transactions on Power Electronics, 2009, 24(7):1737-1746.

DOI:10.1109/TPEL.2009.2014236 URL [本文引用: 1]

[4]

宋平岗, 李云丰, 王立娜.

无锁相环模块化多电平换流器直接功率控制器设计

[J]. 高电压技术, 2014, 40(11):3500-3505.