开挖引起的隧道位移动态多目标优化反演预测

图1 Pareto解在二维目标函数空间上的分布及映射

Fig.1 Distribution and mapping of Pareto solutions on two-dimensional objective functions space

1.2 Kriging代理模型

代理模型常被用来在工程优化中近似计算昂贵的数值模型.常用的代理模型包括Kriging模型、多项式响应面及径向基函数等^[7],其中Kriging插值模型具有良好的非线性拟合能力,近似精度较高,基于Kriging的加点准则应用也较为广泛.

采用Kriging方法对数值模型进行近似,假设对于设计变量未知点x,其对应的函数响应值 y(x) 可表示为随机函数:

(2)

\begin{matrix} Y (x) = \overset{J}{\sum_{j = 1}} β_{j} f_{j} (x) + Z (x) \end{matrix}

式中: $f_{j} (x)$ 为多项式基函数; $β_{j}$ 为多项式回归系数;J为多项式的项数;Z(x)是均值为0、方差为 $σ_{s}^{2}$ 的随机过程函数.不同试验设计点之间的协方差可表示为

(3)

\begin{matrix} C o v [Z (x), Z (x^{*})] = σ_{s}^{2} R (θ, x, x^{*}) \end{matrix}

式中: $R (θ, x, x^{*}) 为与距离有关的相关函数; θ$ 为函数的宽度控制参数.Kriging插值的公式推导过程和实现见文献[15].

1.3 动态多目标优化

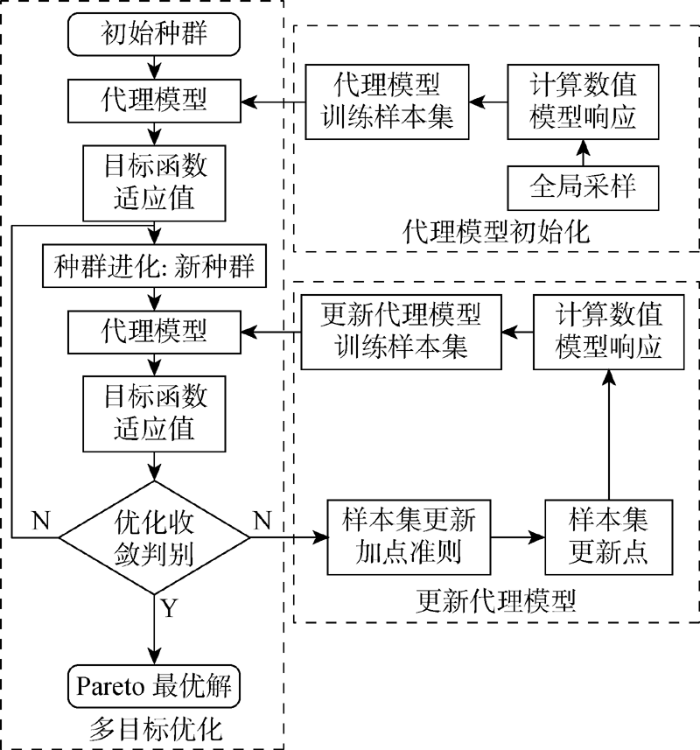
动态优化是在优化进程中不断更新代理模型的优化方法,可分为动态单目标和多目标优化.动态多目标优化的框架如图2所示.

图2

图2 动态多目标代理模型优化框架

Fig.2 Framework of dynamic multi-objective optimization using surrogate models

步骤1 基于全局抽样方法抽取一定数目的初始样本集,调用数值模型计算模型响应,训练初始代理模型.

步骤2 构建多目标优化函数,融合监测数据,调用代理模型计算目标函数适应值.

步骤3 基于多目标优化算法寻找目标函数的最优解.

步骤4 基于相应的加点准则,得到最优的样本点并更新样本集,详见1.4节.

步骤5 调用数值模型计算新样本点的模型响应,更新代理模型.

步骤6 判别优化过程的收敛准则,当满足收敛准则时,停止优化并输出Pareto最优解,否则,重复步骤2~5.

1.4 基于距离的自适应加点准则

为减少优化过程中数值模型的计算次数,DMO-AIC方法在基于距离的加点准则^[13]中加入了收敛判别策略,使得算法可以在种群陷入多样性寻优空间时停止更新代理模型,提升了多目标优化方法的计算效益及其对于工程优化的适用性.DMO-AIC的自适应加点准则包含3个策略:样本产生、收敛判别及样本选取.

策略1 采用多目标粒子群(Multi-Objective Particle Swarm Optimization, MOPSO)算法^[16]优化过程中每一代的当前非支配解作为候选样本集.当前非支配解由上一代解以及种群中其他粒子在经过局部飞行和全局变异两种机制后演化而来,兼具较强的局部搜索和全局搜索能力.MOPSO算法详见文献[16],本文将重点介绍基于距离的收敛判别策略和样本选取策略.

策略2 首先,定义某一代种群的非支配解粒子在目标空间的平均相邻距离:

(4)

\begin{matrix} \bar{d} = \frac{1}{n - 1} \overset{n}{\sum_{i = 2}} ‖ f (x_{i}) - f (x_{i - 1}) ‖ \end{matrix}

式中:n为种群中的粒子总数; $f (x_{i})$ 为排序后的第i个非支配解粒子在目标空间的函数值.

为了评价当前非支配解与上一代非支配解相比的进化效果,定义当前非支配解和上一代非支配解之间的最小距离为 $d^{*}, 则前非支配解中第 i 个粒子 x_{i}^{g}$ 的最小距离为

(5)

\begin{matrix} d_{i}^{*} = \underset{x^{g - 1} \in Ω_{g - 1}^{d}}{m i n} ‖ f (x_{i}^{g}) - f (x^{g - 1}) ‖ \end{matrix}

式中: g为当前非支配解的序号,表示迭代次数; $f (x_{i}^{g}) 为 x_{i}^{g}$ 的函数值; $f (x^{g - 1})$ 为上一代非支配解 $x^{g - 1}$ 的函数值; $Ω_{g - 1}^{d}$ 为上一代非支配解的可行域. $d_{i}^{*} 越大,$ 表示该粒子的优化效果越好.根据 $d^{*} 和 \bar{d},$ 提出了如下加点准则的收敛判别式

(6)

\begin{array}{l} \begin{matrix} α = m i n \{\frac{\underset{x^{g} \in Ω_{g}^{d}}{m a x} d^{*} (x^{g})}{ω {\bar{d}}^{g - 1}}, 1\} \end{matrix} \end{array}

(7)

ω = (1 - ω_{0}) {(g / G)}^{\frac{1}{2}} + ω_{0}

式中: α为一个距离比率; $\underset{x^{g} \in Ω_{g}^{d}}{m a x} d^{*} (x^{g})$ 为目标空间中当前非支配解粒子距上一代非支配解的最小距离的最大值; $ω {\bar{d}}^{g - 1}$ 为目标空间中上一代非支配解的平均相邻距离折减值,ω为跟迭代次数相关的折减系数;G为最大迭代次数; $ω_{0}$ 为折减系数初始值.

根据式(6),当α=1时,认为当前非支配解与上一代非支配解相比的进化效果能够满足预期,则根据一定的选点策略从当前的候选支配解选取新的代理模型训练样本点.当α<1时,则认为当前的候选非支配解中没有能够满足更新预期的粒子.

策略3 为了从当前非支配集中选出一个最优粒子,采用两种寻优机制^[13]:① 使样本更新点与上一代非支配解在目标空间的最小距离 $d^{*}$ 最大,即选取 $d_{m a x}^{*}$ 为样本更新点,如图3所示;② 使样本更新点与上一代非支配解在参数空间的最小距离 $d^{Ω}$ 最大.样本更新点与上一代非支配解在目标空间的最小距离 $d^{*}$ 可参照式(5)求得.类似地,当前非支配解中第i个粒子 $x_{i}^{g}$ 的最小距离可用下式计算:

(8)

\begin{matrix} {d^{Ω}}_{i} = \underset{x^{g - 1} \in Ω_{g - 1}^{d}}{m i n}‖ x_{i}^{g} - x^{g - 1} ‖ \end{matrix}

图3

图3 最优样本更新点在目标函数空间中的位置

Fig.3 Location of best new sample point on objective function space

为综合考虑两种寻优机制,定义一个相对参数空间最小距离D^Ω,则第i个粒子的相对参数空间最小距离为

(9)

{D^{Ω}}_{i} = \frac{{d^{Ω}}_{i} - m i n {d^{Ω}}_{i}}{m a x {d^{Ω}}_{i} - m i n {d^{Ω}}_{i}}, i = 1, 2, \dots, n

再定义一个相对目标空间最小距离 $D^{*}, 则第 i$ 个粒子的相对参数空间最小距离为

(10)

D_{i}^{*} = \frac{d_{i}^{*} - m i n d_{i}^{*}}{m a x d_{i}^{*} - m i n d_{i}^{*}}, i = 1, 2, \dots, n

基于式(4)和(5),被选取为代理模型新样本点的粒子将使得一个距离因子W^D最大,如下:

(11)

\begin{matrix} W^{D} = c_{1} D^{Ω} + c_{2} D^{*} \end{matrix}

式中: $c_{1} 和 c_{2}$ 为两个权重系数,满足 $c_{1} + c_{2} = 1 .$ 本文采用等权分配,即 $c_{1} = c_{2} = 0.5 .$

2 DMO-AIC计算效益

为验证所提自适应加点准则的计算效益,用两个常用的已知最优解的多目标优化函数对DMO-AIC进行测试,并与无收敛判别策略的加点方法(简称DMO)的测试结果进行对比.

2.1 测试函数

测试函数ZDT2:

(12)

\begin{array}{l} \begin{matrix} m i n \{\begin{array}{l} f_{1} (x) = x_{1} \\ f_{2} (x) = g (x) [1 - (x_{1} / g {(x))}^{2}] \\ g (x) = 1 + 9 \overset{n}{\sum_{i = 2}} x_{i} / (n - 1) \end{array} \end{matrix} \\ s . t . 0 \leq x_{i} \leq 1, i = 1, 2, \dots, n \end{array}

ZDT2真实最优解集为

(13)

\begin{array}{l} \begin{matrix} {x = [x_{1} x_{2} \dots x_{n}]^{T} | x_{1} \in [0, 1], \end{matrix} \\ x_{i} = 0, i = 2, 3, \dots, n} \end{array}

测试函数FON:

(14)

\begin{array}{l} m i n \{\begin{array}{l} f_{1} (x) = 1 - e x p [- \overset{n}{\sum_{i = 1}} {(x_{i} - \frac{1}{\sqrt{n}})}^{2}] \\ f_{2} (x) = 1 - e x p [- \overset{n}{\sum_{i = 1}} {(x_{i} + \frac{1}{\sqrt{n}})}^{2}] \end{array} \\ s . t . - 4 \leq x_{i} \leq 4, i = 1, 2, \dots, n \end{array}

FON真实最优解集为

(15)

\begin{array}{l} {x = [x_{1} x_{2} \dots x_{n}]^{T} | x_{1} = x_{2} = \dots = \\ x_{i} \in [- \frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}], i = 1, 2, \dots, n} \end{array}

基于已知最优解,可以引入两个距离指标^[17]对所得的优化解集进行收敛性和多样性的评价.其中,收敛性指的是优化得到的解与真实Pareto前沿的靠近程度,可通过优化解与Pareto前沿的样本点的最小距离D^G来评价,计算如下:

(16)

\begin{matrix} D^{G} = \frac{1}{n} \overset{n}{\sum_{i = 1}} d_{i} \end{matrix}

式中:d_i为优化解中第i个个体与真实Pareto解集样本之间的最小目标空间距离.多样性是指优化解的分布均匀性,多样性评价指标为

(17)

\begin{matrix} Δ = \frac{d_{f} + d_{s} + \overset{n - 1}{\sum_{i = 1}} |d_{i} - \bar{d}|}{d_{f} + d_{s} + (n - 1) \bar{d}} \end{matrix}

式中:d_f和d_s为优化解的两端个体与真实Pareto解集样本之间的最小目标空间距离.

2.2 测试结果

对两个测试函数的主要优化参数设置如表1所示.Kriging代理模型的基函数和相关函数分别采用二项式函数和高斯指数函数.

表1 两个测试函数的优化参数设置

Tab.1 Parameter settings for optimization of two test functions

测试函数	优化方法	输入参数维度	种群规模	初始代理模型训练样本数	最大迭代次数	折减系数初始值
ZDT2	DMO-AIC	8	50	50	100	0.5
	DMO	8	50	50	100	0.5
FON	DMO-AIC	6	100	100	300	0.5
	DMO	6	100	100	300	0.5

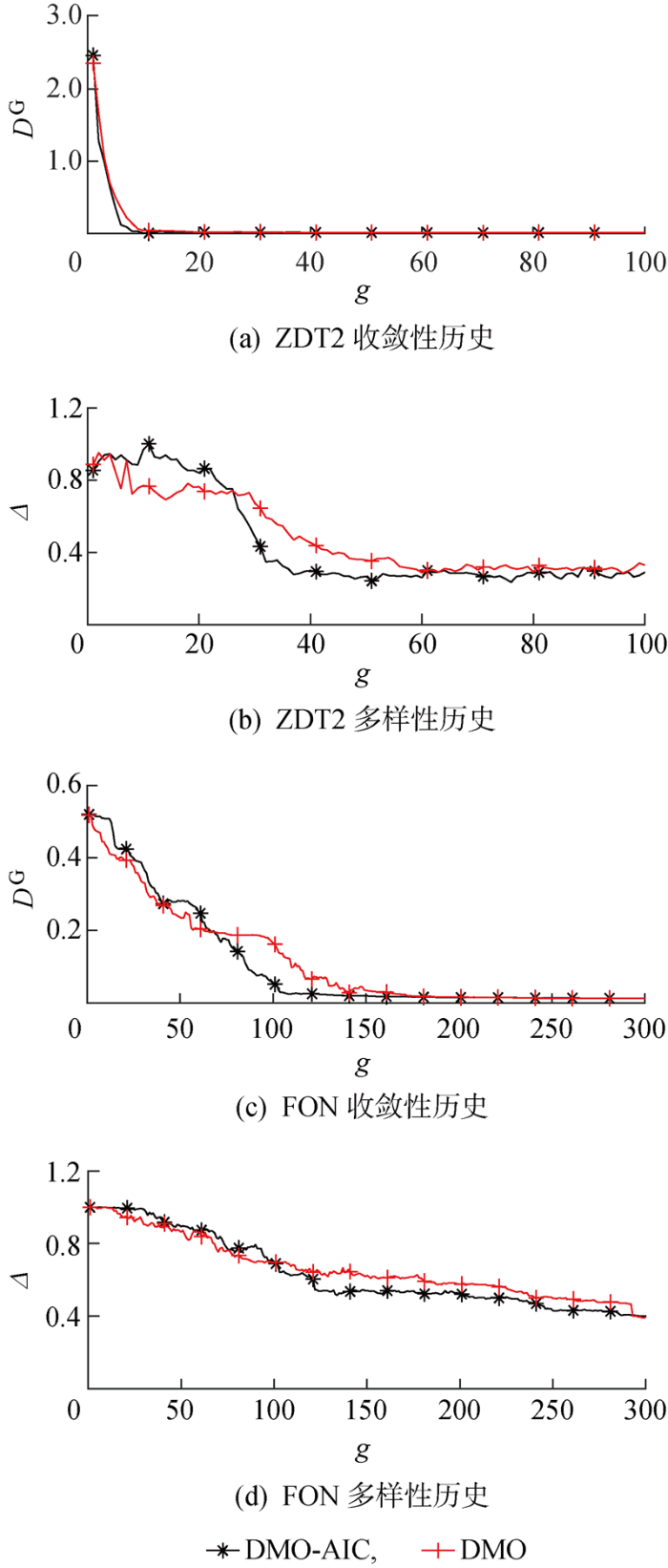
为避免优化过程的偶然性,对每个测试函数进行3次优化计算并取其平均值.图4所示为两个测试函数的优化历史.使用DMO-AIC和DMO的收敛性、多样性寻优速度都表现较快.相比收敛性,优化解的多样性寻优需要更多的计算时间,通常在种群收敛性稳定后其多样性才能趋于稳定.

图4

图4 使用DMO-AIC和DMO的优化历史比较

Fig.4 Comparison of optimization histories by using DMO-AIC and DMO

表2所示为两个测试函数优化结果的关键评价指标.可以看到,使用DMO-AIC方法和使用DMO方法的最终收敛性、多样性结果接近,且都能满足计算精度要求.

表2 DMO-AIC和DMO的优化质量比较

Tab.2 Comparison of optimization quality of DMO-AIC and DMO

测试函数	优化方法	D^G	Δ	新增样本数
ZDT2	DMO-AIC	8.60×10^-3	0.29	30
	DMO	8.30×10^-3	0.33	93
FON	DMO-AIC	1.23×10^-2	0.40	97
	DMO	1.22×10^-2	0.39	214

结合表2和图4的计算结果可以发现,相比DMO,DMO-AIC寻优性能和收敛速度相近,但是使用DMO-AIC方法所需要的样本更新点平均数是30和97,而使用DMO所需要的样本更新点平均数是93和214,说明DOM-AIC的自适应加点准则能够在优化过程的多样性寻优阶段判断、筛选无效(进化效果差)的新样本点,从而提高计算效率.这种自适应加点准则在面对最优解未知的昂贵数值模型优化问题时,能够保证充分的寻优时间(较大迭代次数),同时避免了数值模型的无效调用,有利于动态多目标优化方法在工程实践中的应用.

3 多目标响应更新

3.1 虚拟数值模型

利用虚拟数值模型来验证DMO-AIC对基坑开挖-既有隧道中多目标响应的更新和预测能力,在虚拟模型的模型响应值中加入合理的人工误差后,可认为最优解存在于模型参数真实值附近^[18].同时该算例仅考虑单层土,输入参数较少,能较快寻优到其最优解.

虚拟模型如图5所示,整体宽30 m,深25 m.基坑采取一步开挖,宽5 m,深6 m,有限元模型采用对称设置.地连墙和顶管隧道结构采用梁单元模拟,均假设为弹性材料,弹性模量分别为20和30 GPa,泊松比均为0.2,墙体厚度为 0.6 m,管壁厚度为0.3 m,隧道内径为3 m. 地连墙以及隧道和土体之间采用绑定接触.支撑结构采用弹簧单元模拟,弹簧刚度上下分别设为12 和 50 MN/m.土体的重度为18 kN/m³,水平土压力系数K₀=0.5.土体参数设置采用修正剑桥模型,参数取值如表3所示.数值模型边界约束水平位移,底部同时约束水平和竖向位移.

图5

图5 虚拟数值模型的土层及结构示意图(m)

Fig.5 Schematic of soil layer and structure of virtual numerical model (m)

表3 土体修正剑桥模型参数

Tab.3 Soil parameters of modified Cam clay model

土层	临界状态应力比M	回弹参数κ	泊松比ν	压缩参数λ	起始孔隙比e₀
软黏土	1.20 (0.80~1.40)	0.020 (0.007~0.040)	0.30 (0.25~0.35)	0.20	2.0

文献[19]指出相对敏感度较高的修正剑桥模型的土体参数包括临界状态应力比M、回弹参数κ和泊松比ν.因此对土体的M,κ,ν这3个参数进行反演分析,其参数寻优范围见表3括号内取值.

数值模型的参数优化需要对模型计算值和监测值进行融合,采用一个基于最小二乘法的目标函数对每个监测点的计算误差进行等权分配,并采用多个目标函数分别融合地连墙的侧移和隧道位移数据.目标函数值可根据下式计算:

(18)

\begin{matrix} f (X) = \sqrt{\frac{1}{N} \overset{N}{\sum_{m = 1}} (\frac{D_{m} - U_{m}}{D_{m}})} \end{matrix}

式中:x为待优化的参数向量;N为该目标函数所利用的监测点个数;

D_{m} 、 U_{m}

分别为第m个监测点的监测值和模型计算值.虚拟监测值通过在基于参数真实值计算得到的模型响应值中加入人工的高斯随机误差^[18]来模拟,高斯随机误差e由仪器系统误差ε和高斯观测误差δ两部分组成:

(19)

\begin{matrix} e = ε + δ \end{matrix}

式中: ε服从均值为0,标准差为 $ξ U^{*}$ 的正态分布,ξ为系统误差系数,本文取0.01, $U^{*}$ 为模型计算值;δ的均值为0,其标准差 $σ_{δ}$ 取决于仪器精度,取仪器精度为±0.1 mm时,按95%的置信区间设置 $σ_{δ}$ 为0.05.

3.2 多目标响应更新结果

为实现基坑开挖-隧道工程的多目标响应更新,基于式(17),建立两个目标函数f₁和f₂,分别融合了地连墙和隧道的位移数据.优化过程的种群规模设为50,初始代理模型训练样本数为16,最大迭代次数为100,折减系数初始值为0.5.

为避免优化的偶然性,共进行3次优化计算,代理模型更新平均增加样本数约为12.图6给出了其中一次优化计算得到的Pareto最优解,解呈现凹的形态,且其在目标函数空间上的最大适应值在5%左右,误差较小,说明多目标函数之间的“权衡”较好^[20],因此将最优解集的每个粒子都输入到数值模型中计算模型响应再取其平均值作为位移更新的结果.

图6

图6 虚拟案例的Pareto最优解

Fig.6 Pareto optimal solutions of virtual case

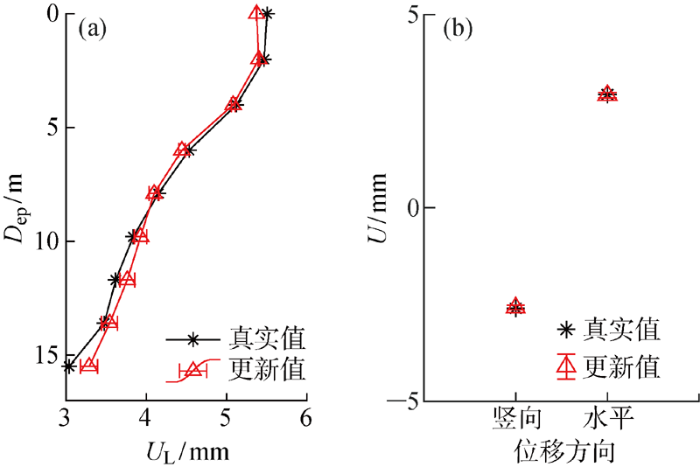
图7(a)和7(b)分别给出了基于3组Pareto最优解计算得到的地连墙侧向位移U_L、隧道位移U的更新均值和误差条,图中D_ep为地连墙的测点深度.可以看到地连墙和隧道的位移更新平均值与模拟监测值都吻合很好,且其误差条较窄,表明使用图6中的全部最优解能够对多目标响应同时进行准确更新.

图7

图7 地连墙及隧道位移的更新均值和误差条

Fig.7 Updated mean value and error bar of wall deflection and tunnel displacement

表4所示为3组Pareto最优解得到的土体参数更新结果.更新后的土体参数均值与真实值基本一致,且更新后的土体参数标准差较小,说明Pareto最优解在参数空间中唯一存在于参数真实值附近.

表4 更新后的虚拟案例土体参数

Tab.4 Updated soil parameters of virtual case

指标	M	κ	ν
真实值	1.20	0.020	0.30
更新参数平均值	1.40	0.020	0.31
更新参数标准差	2.9×10^-3	5.0×10^-4	2.3×10^-3

4 上海外滩596基坑工程

4.1 工程概况

上海外滩596基坑^[21]整体分为S1-A区、S1-B区及S2-A区、S2-B区,工程具体开挖步及时间进度如表5所示.采用Abaqus 2018软件对基坑开挖过程进行模拟,二维数值模型如图8所示,土体采用莫尔-库仑模型,各土层参数如表6所示.地连墙和隧道衬砌结构采用梁单元模拟,假设为弹性材料,弹性模量分别为20和30 GPa,泊松比均为0.2,墙体等效厚度为0.8 m,衬砌结构厚度为0.3 m,隧道内径为6 m.文献[21]中未介绍支撑参数,而本算例目的为预测和更新下卧隧道的竖向位移,不预测基坑挡墙侧移,故支撑结构由等效位移约束替代模拟^[22-23],在挡墙上施加监测所得侧移值^[21].模型两端施加水平方向位移约束,底部同时施加水平和竖直方向位移.

表5 上海外滩596基坑的开挖进程

Tab.5 Excavation stages of Shanghai Bund 596 project

步骤	进度	周期/d	步骤	开挖进度	周期/d
1	S2-A开挖至-1.7 m	1	12	S2-B开挖至-4.8 m	2
2	S1-A开挖至-1.7 m	24	13	S2-B开挖至-7.65 m	2
3	S2-A开挖至-6.0 m	2	14	S2-B开挖至-10.5 m	4
4	S2-A 开挖至-10.1 m	14	15	S2-B开挖至-14.25 m	2
5	S1-A 开挖至-5.9 m	10	16	S2-B开挖至坑底	9
6	S2-A开挖-13.85 m	3	17	S1-B开挖至-1.7 m	3
7	S1-A开挖至-9.9 m	12	18	S1-B开挖至-4.8 m	1
8	S2-A开挖至坑底	13	19	S1-B开挖至-7.5 m	1
9	S1-A开挖-13.7 m	8	20	S1-B开挖至-10.2 m	2
10	S1-A开挖至坑底	6	21	S1-B开挖至-14.0 m	3
11	S2-B开挖至-1.7 m	5	22	S1-B开挖至坑底	3

图8

图8 上海外滩596项目的有限元模型(m)

Fig.8 FE model of Shanghai Bund 596 project (m)

表6 土体莫尔-库仑模型参数

Tab.6 Soil parameters of Mohr-Coulomb model

土层	土质	厚度/m	重度γ/(kg·m^-3)	卸荷模量E_u/MPa	泊松比ν	黏聚力c'/kPa	摩擦角φ'/(°)
1	水泥搅拌桩	0~22, 0~28	22.0	180.0	0.40	50.0	40.0
2	淤泥质黏土	0~10	18.5	18.0(10~50)	0.28	7.0	27.6
3	粉质黏土	10~29	17.5	28.5(15~90)	0.31	15.0(0.22~0.40)	29.5(17~35)
4	杂填土	29~39	18.0	25.2	0.28	10.4	22.0
5	江滩土	39~49	19.3	40.3(30~150)	0.27	5.0	30.4
6	砂质粉土	49~64	18.8	74.8(50~180)	0.27	5.0	33.4
7	粉砂层	64~80	20.2	94.3(60~220)	0.27	4.0	34.3

注:土体的卸荷模量E_u取自文献[24],其余土体参数取自文献[25-26]对上海典型软土的统计量;括号内数值表示该参数的寻优范围,详见 4.3节;0~22 m和0~28 m为水泥搅拌桩土层的两种不同加固深度.

4.2 时间效应

文献[2]基于上海软土基坑开挖引起的下方隧道位移实测资料,提出了如下时间效应修正系数:

(20)

\begin{matrix} {ε^{T}}_{p q} = 1 - α_{1} e^{- β t_{p q}} \end{matrix}

式中: ${ε^{T}}_{p q}$ 为施工到第q个开挖步时对应于第p个开挖步的时间效应修正系数, $p = 1, 2, \dots, q; α_{1} 和 β$ 为两个回归参数,初始值分别为0.462和0.012; $t_{p q}$ 为施工到第q个开挖步时对应于第p个开挖步的作用时间.根据表5,可计算得开挖卸荷作用的时间矩阵为

(21)

\begin{matrix} t = 24 {[\begin{array}{l} 1 & 25 & 27 & \dots & 130 \\ 0 & 24 & 26 & \dots & 129 \\ 0 & 0 & 2 & \dots & 105 \\ ︙ & ︙ & ︙ & ⋱ & ︙ \\ 0 & 0 & 0 & \dots & 3 \end{array}]}_{22 \times 22} \end{matrix}

基于式(20)和式(21),可得到隧道在不同开挖步时的累积位移:

(22)

\begin{matrix} {U^{C}}_{q} = \overset{q}{\sum_{p = 1}} {ε^{T}}_{p q} Δ U_{p}^{F E M} = \overset{q}{\sum_{p = 1}} Δ U_{p q}^{F E M'} \end{matrix}

式中: ${U^{C}}_{q}$ 为第q个开挖步时的累积位移; $Δ U_{p}^{F E M}$ 为第p个开挖步产生的阶段位移; $Δ U_{p q}^{{F E M}^{'}}$ 为其对应的经过时间效应系数 ${ε^{T}}_{p q}$ 修正后的阶段位移.

图9所示为基于土体参数及时间效应参数初始值计算得到的隧道竖向位移(U_V),图中E^S为开挖步,初始计算值与监测值有显著偏差,说明本文依据同类软土基坑的文献资料所决定的土体参数可靠性较低,且可推测隧道的实际位移相比计算值较为滞后.但位移计算值和监测值在不同的开挖区域施工时都有着相似的发展趋势,说明了有限元模型的合理性.

图9

图9 使用模型参数初始值计算得到的隧道竖向位移

Fig.9 Tunnel vertical displacement calculated by using initial values of model parameters

4.3 优化参数设置

实例计算中,采用DMO-AIC方法预测更新下卧隧道的竖向位移.考虑深厚土层的开挖对下卧隧道的影响较大,隧道位移可能随之快速发展,有必要对近期的隧道位移监测数据重点关注,因此多目标优化函数向量可设为 $F (X) = [f_{1} (X) f_{2} {(X)]}^{T}, 其中 f_{1} (X) 、 f_{2} (X)$ 分别为融合了全部开挖步数据和近期开挖步数据的目标函数.多目标优化函数所融合的监测数据构成如表7所示.

表7 两次更新计划所融合的监测数据

Tab.7 Monitoring data merged from two update schemes

更新计划	开挖阶段	f₁所融合数据	f₂所融合数据
I	S2-B	开挖步5~14	开挖步10~14
II	S1-B	开挖步5~17	开挖步17

注:在基坑开挖初期,即开挖步1~4时,隧道因前期降水发生了沉降,故前几个开挖步的监测数据不在本模型考虑范围内.

为识别关键的影响参数,降低未知参数维度,对上海外滩596基坑有限元模型进行参数敏感性分析,计算公式^[19]如下:

(23)

\begin{matrix} S_{p q} = \frac{Δ U_{p} / Δ x_{q}}{U_{p} / x_{q}} \end{matrix}

式中: $S_{p q}$ 为第p个开挖步的隧道位移对应于第q个输入参数的相对敏感性系数; $U_{p}$ 为第p个开挖步的隧道位移值; $Δ U_{p}$ 为第p个开挖步的隧道位移差值; $x_{q}$ 为第q个参数的输入值; $Δ x_{q} 为第 q$ 个参数的差值.

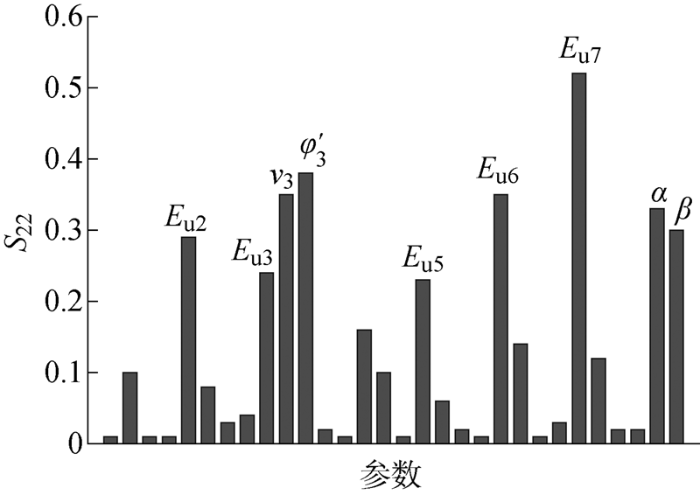
图10所示为所有土体参数以及时间效应参数的敏感性分析结果.相对高敏感度的9个输入参数包括E_u2,E_u3,ν₃,φ'₃,E_u5,E_u6,E_u7,α₁和β.取这9个参数为目标参数进行更新,其中土体参数寻优范围如表6括号内所示,α₁的范围为0.2~0.9,β的范围为(9.00~150.00)×10^-4.高敏感性参数中包含7个土体参数,根据这个7个土体参数的寻优空间进行拉丁超立方全局采样,初始代理模型训练样本数为50.优化过程中的种群规模为100,最大迭代次数为200,折减系数初始值为0.5.为避免优化的偶然性,每个更新计划计算3次.

图10

图10 土体参数及时间效应参数的敏感度

Fig.10 Sensitivity of soil parameters and time effect parameters

4.4 位移预测更新

相比单目标优化得到的唯一“最优解粒子”,多目标优化得到的最优解集能体现出多目标函数之间的“权衡”.为了避免工程案例的多目标最优解两端延伸过广,采用一个误差限制对最优解进行二次择优,该误差限制代表了决策者对各个目标函数的容许误差.

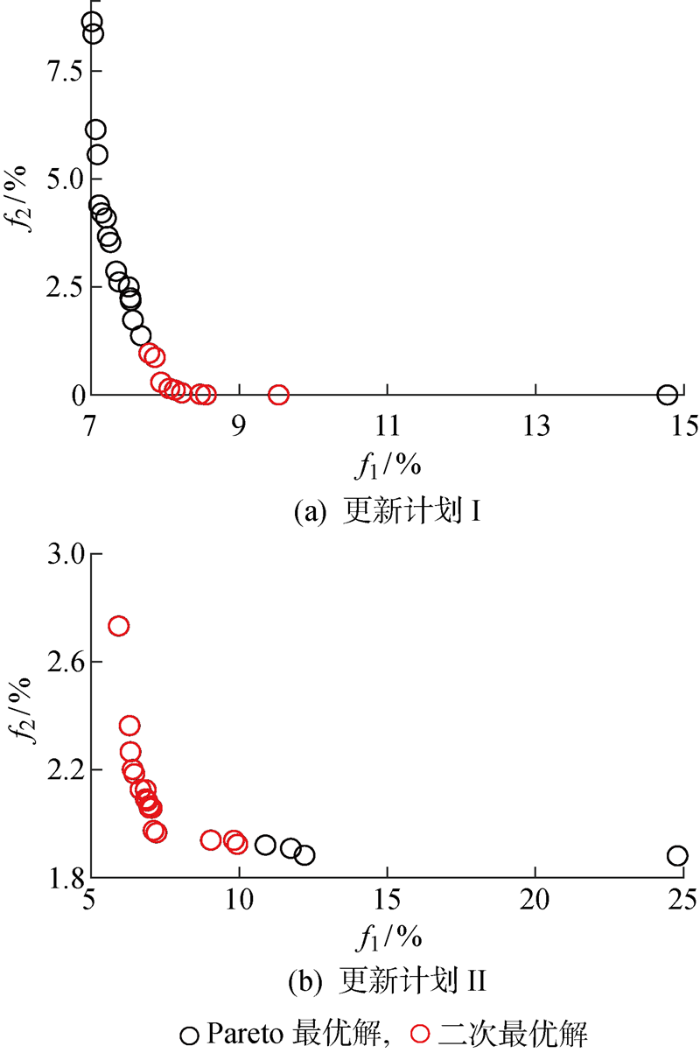
图11(a)和11(b)分别给出了两次更新计划I、II得到的Pareto解集.黑色粒子是优化计算得到的Pareto解,红色粒子表示对目标函数设置一定的“误差限制”后得到的二次择优解.解呈现出凹的形态,说明多目标函数间的“权衡”较好.但粒子在Pareto前沿上的分布比较不均匀,解的多样性较差,且由于工程案例最优解的未知性,端部粒子在目标函数f₁上的误差值较大,为了提升预测准确度,有必要对目标函数设置一定的“误差限制”来对Pareto解集进行二次择优.本文案例中的“误差限制”可以设置为f₁≤10%且f₂尽可能小.

图11

图11 两次更新计划下使用DMO-AIC得到的Pareto解集

Fig.11 Pareto solutions of DMO-AIC in two updated schemes

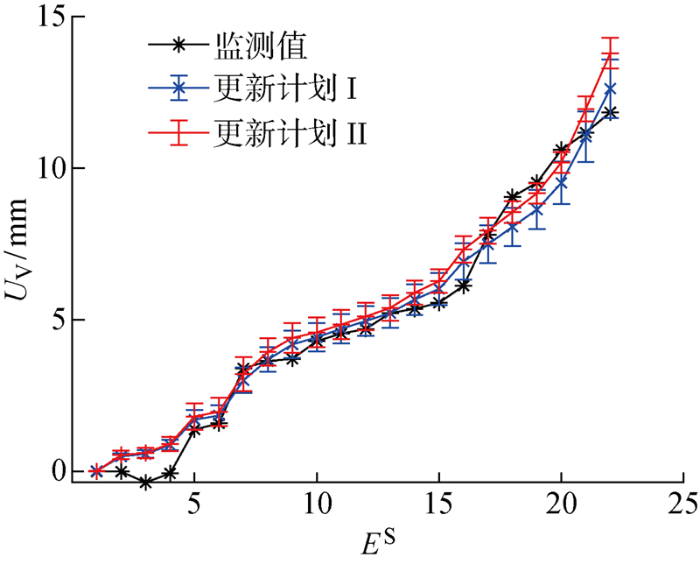
图12所示为在两次更新计划下使用DMO-AIC方法的二次择优解计算得到的隧道位移预测均值和误差,可以看出,两次更新中后续开挖步的位移预测值与监测值都很接近.具体来说,更新计划 I 对近期开挖步10~14的监测数据赋予了较高权重,其对后续开挖步15~17的隧道位移预测值比更新计划 II 的计算值更为准确;而更新计划 II 对开挖步17的监测数据赋予了较高权重,其对后续开挖步18~20的隧道位移预测准确度高于更新计划 I,说明近期监测数据更能反映隧道位移的发展趋势.当隧道位移在某些开挖步突然快速发展时,需要及时融合近期的监测数据并更新预测.

图12

图12 使用DMO-AIC的二次择优解计算得到的隧道竖向位移更新值

Fig.12 Updated tunnel vertical displacement calculated by using selected optimal solutions of DMO-AIC

图13所示为在更新计划 II 下使用DMO-AIC和DMO方法对隧道位移的预测准确度,图中T^a为所有开挖步完成后的后续施工时间.可以看出,二者对后续开挖步18~20的隧道位移预测误差接近且都较小.更新后的时间效应表明,隧道位移在开挖至坑底后的3个月内将会快速发展,其位移最大值为 25 mm 左右,远远大于开挖至基底时的12 mm监测值,说明如果基坑被暂停施工足够长时间,隧道位移将会有持续的较大发展,应及时进行后序的施工步骤.

图13

图13 更新计划 II 下DMO-AIC、DMO的预测精度比较

Fig.13 Comparison of prediction accuracy of DMO-AIC and DMO in Scheme II

表8所示为使用DMO-AIC和DMO方法对上海596基坑案例的计算效率.使用DMO-AIC所需的平均样本更新点个数为11和12个,使用DMO所需的平均样本更新点为72和79个,说明以最大迭代次数作为工程优化问题的收敛判别条件时,使用DMO-AIC方法能很好地避免产生过多的无效代理模型样本更新点,大大提高寻优的计算效率.

表8 使用DMO-AIC和DMO时两次更新计划的计算效率

Tab.8 Calculation efficiency of two updated schemes by using DMO-AIC and DMO

更新计划	优化方法	初始样本点	平均增加样本更新点
I	DMO-AIC	50	11
	DMO	50	72
II	DMO-AIC	50	12
	DMO	50	79

DOI:10.1016/j.engappai.2018.11.002 URL [本文引用: 1]

5 结论

为提高工程优化中的动态代理模型方法的计算效率,提出一种基于自适应加点准则的动态多目标优化方法(DMO-AIC),将其应用于上海外滩596基坑案例中,成功预测了基坑开挖引起的既有隧道位移,具体结论包括:

(1) 在两个多目标测试函数以及上海外滩596基坑案例的计算结果中,DMO-AIC和DMO方法都具有较高的计算精度,但DMO-AIC所需的样本更新点平均数分别仅为DMO的31%、45%和15%,有效避免了优化进程中原模型的无效调用.DMO-AIC的计算效率提升对于复杂工程优化问题具有重要意义.

(2) 虚拟基坑案例计算结果表明,最优解在目标函数空间上的误差值较小,表明最优解能较好满足多目标函数之间的“权衡”,此时使用所有最优解粒子能够对基坑开挖中的多目标响应同时进行准确更新.

(3) 以上海外滩596基坑为例,利用DMO-AIC方法分步融合了监测数据,成功准确预测了后续开挖步的邻近隧道竖向位移.其中,近期监测数据更能反映隧道位移的发展趋势,应对新的监测数据及时进行融合并赋予更高的权重.

(4) 上海外滩596基坑的更新后参数表明,隧道位移在开挖至坑底后的3个月内将会快速发展,最大值为25 mm,远大于开挖至基底时的12 mm监测值,说明该隧道位移的时间效应显著,在开挖至基底后应及时进行后序的施工步骤.所提时间效应修正模型及反演方法可为同类软土基坑开挖实践提供参考.

(5) 实际工程案例的Pareto最优解在目标函数空间上可能分布过广,通过对目标函数设置一定的“误差限制”可以对Pareto最优解二次择优,从而提升解的预测准确度.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

JIN

Y F

, YIN

Z Y

, ZHOU

W H

, et al.

Multi-objective optimization-based updating of predictions during excavation

[J]. Engineering Applications of Artificial Intelligence, 2019, 78: 102-123.

[2]

吉茂杰, 刘国彬.

开挖卸荷引起地铁隧道位移预测方法

[J]. 同济大学学报(自然科学版), 2001, 29(5): 531-535.

Maojie

, LIU

Guobin

Prediction method of displacement of subway tunnel due to excavation

[J]. Journal of Tongji University (Natural Science), 2001, 29(5): 531-535.

DOI:10.1016/j.enggeo.2020.105753 URL [本文引用: 1]

[3]

TAO

Y Q

, SUN

H L

, CAI

Y Q

Predicting soil settlement with quantified uncertainties by using ensemble Kalman filtering

[J]. Engineering Geology, 2020, 276: 105753.

[4]

郑栋, 黄劲松, 李典庆.

基于多源信息融合的路堤沉降预测方法

[J]. 岩土力学, 2019, 40(2): 709-719.

ZHENG

Dong

, HUANG

Jinsong

, LI

Dianqing

An approach for predicting embankment settlement by integrating multi-source information

[J]. Rock and Soil Mechanics, 2019, 40(2): 709-719.

[5]

蒋水华, 刘源, 张小波, 等.

有限数据条件下空间变异岩土力学参数随机反演分析及比较

[J]. 岩石力学与工程学报, 2020, 39(6): 1265-1276.

JIANG

Shuihua

, LIU

Yuan

, ZHANG

Xiaobo

, et al.

Stochastic back analysis and comparison of spatially varying geotechnical mechanical parameters based on limited data

[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(6): 1265-1276.

DOI:10.1016/j.enggeo.2018.03.019 URL [本文引用: 1]

[6]

SUN

, JIANG

Q H

, YIN

, et al.

A back-analysis method using an intelligent multi-objective optimization for predicting slope deformation induced by excavation

[J]. Engineering Geology, 2018, 239: 214-228.

[7]

BOOKER

A J

, DENNIS

J E

, FRANK

P D

, et al.

A rigorous framework for optimization of expensive functions by surrogates

[J]. Structural Optimization, 1999, 17(1): 1-13.

DOI:10.1007/BF01197708 URL [本文引用: 2]

[8]

张扬, 张维刚, 马桃, 等.

基于全局敏感性分析和动态代理模型的复杂非线性系统优化设计方法

[J]. 机械工程学报, 2015, 51(4): 126-131.

DOI:10.3901/JME.2015.04.126 [本文引用: 1]

针对复杂非线性系统多参数优化设计不仅计算工作量大，而且难以获得理论上最优解的问题，提出将全局敏感性分析和动态代理模型技术相结合的多参数多目标优化策略。通过基于方差的Sobol全局敏感性分析精简系统模型，确定敏感参数，并构造基于敏感参数的多目标代理模型，采用NSGA-II遗传优化算法得到当代最优解。优化过程中，代理模型和搜索空间不断更新，最优解附近的精度不断提高，直到满足优化迭代的收敛准则。将本方法应用于某汽车乘员约束系统的概念优化设计中，乘员的头部损伤指标(Head injury criterion, HIC)、胸部3 ms伤害指标C3ms和胸部压缩量D分别降低了11.3%、11.8%和9.4%，优化结果和最优解附近的精度都优于静态代理模型与NSGA-II遗传优化算法，取得明显的优化效果，证明了研究方法的有效性。

ZHANG

Yang

, ZHANG

Weigang

, MA

Tao

, et al.

Optimization design method of non-linear complex system based on global sensitivity analysis and dynamic metamodel

[J]. Journal of Mechanical Engineering, 2015, 51(4): 126-131.

DOI:10.3901/JME.2015.04.126 [本文引用: 1]

Multi-parameter optimization design of complex nonlinear system with high nonlinearity involves huge computer, and the optimal solution in theory is also difficult to obtain. A new method is proposed that combines the global sensitivity analysis with dynamic metamodel. By using the variance-based Sobol global sensitivity analysis method, the complex system model is simplified, and the sensitivity parameters are defined to construct the multi-objective metamodel, which is solved by using the genetic optimization algorithm of NSGA-II to obtain the contemporary optimal solution. In the process of optimization, the metamodel and the searching space are continually updated, and the accuracy of the solutions in the optimal zone is improved gradually till the optimization iterations terminate with the convergence criteria satisfied. This method is used to concept optimization design of a vehicle occupant restraint system and good results are achieved with the head injury criterion(HIC), chest acceleration C3ms and chest deflection D reduced by 11.3%, 11.8% and 9.4% respectively. The optimization results and the precision of the near optimal solution is better than that of static metamodel and the NSGA-II genetic optimization algorithm, which has proved the validity of the proposed new method.

[9]

ZHOU

, LI

D Q

, XIAO

, et al.

Response surface guided adaptive slope reliability analysis in spatially varying soils

[J]. Computers and Geotechnics, 2021, 132: 103966.

DOI:10.1016/j.compgeo.2020.103966 URL [本文引用: 1]

[10]

LIU

, HAN

Z H

, SONG

W P

Comparison of infill sampling criteria in kriging-based aerodynamic optimization

[C]//28th congress of the international council of the aeronautical sciences. Brisbane, Australia: ICAS, 2012: 23-28.

[11]

BISCHL

, WESSING

, BAUER

, et al.

MOI-MBO: Multiobjective infill for parallel model-based optimization[M]. Cham: Springer International Publishing, 2014, 173-186.

[12]

WAGNER

, TRAUTMANN

, MARTÍ

A taxonomy of online stopping criteria for multi-objective evolutionary algorithms

[C]//International Conference on Evolutionary Multi-Criterion Optimization. Berlin, Heidelberg: Springer, 2011.

DOI:10.1016/j.jocs.2016.05.013 URL [本文引用: 3]

[13]

REGIS

R G

Multi-objective constrained black-box optimization using radial basis function surrogates

[J]. Journal of Computational Science, 2016, 16: 140-155.

[14]

WAGNER

, EMMERICH

, DEUTZ

, et al.

On expected-improvement criteria for model-based multi-objective optimization

[C]//International Conference on Parallel Problem Solving from Nature. Berlin, Heidelberg: Springer, 2010.

DOI:10.1109/TEVC.2004.826067 URL [本文引用: 2]

[15]

LOPHAVEN

, NIELSEN

H B

, SØNDERGAARD

DACE: A Matlab kriging toolbox[M]. Copenhagen: The Technical University of Denmark, 2002.

[16]

COELLO

C A C

, PULIDO

G T

, LECHUGA

M S

Handling multiple objectives with particle swarm optimization

[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 256-279.

[17]

刘若辰, 李建霞, 刘静, 等.

动态多目标优化研究综述

[J]. 计算机学报, 2020, 43(7): 1246-1278.

LIU

Ruochen

, LI

Jianxia

, LIU

Jing

, et al.

A survey on dynamic multi-objective optimization

[J]. Chinese Journal of Computers, 2020, 43(7): 1246-1278.

DOI:10.1002/nag.614 URL [本文引用: 2]

[18]

LEVASSEUR

, MALÉCOT

, BOULON

, et al.

Soil parameter identification using a genetic algorithm

[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32(2): 189-213.

[19]

ZHAO

B D

, ZHANG

L L

, JENG

D S

, et al.

Inverse analysis of deep excavation using differential evolution algorithm

[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(2): 115-134.

DOI:10.1002/nag.2287 URL [本文引用: 2]

[20]

SCHULTE

D O

, ARNOLD

, GEIGER

, et al.

Multi-objective optimization under uncertainty of geothermal reservoirs using experimental design-based proxy models

[J]. Geothermics, 2020, 86: 101792.

DOI:10.1016/j.geothermics.2019.101792 URL [本文引用: 1]

[21]

徐中华, 宗露丹, 沈健, 等.

邻近地铁隧道的软土深基坑变形实测分析

[J]. 岩土工程学报, 2019, 41 (Sup.1): 41-44.

Zhonghua

, ZONG

Ludan

, SHEN

Jian

, et al.

Deformation of a deep excavation adjacent to metro tunnels in soft soils

[J]. Chinese Journal of Geotechnical Engineering, 2019, 41 (Sup.1): 41-44.

[22]

ADDENBROOKE

T I

A flexibility number for the displacement controlled design of multi propped retaining walls

[J]. Ground Engineering, 1994, 27(7): 41-45.

DOI:10.1061/(ASCE)1090-0241(2000)126:8(718) URL [本文引用: 1]

[23]

ADDENBROOKE

T I

, POTTS

D M

, DABEE

Displacement flexibility number for multipropped retaining

[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(8): 718-726.

[24]

刘国彬, 侯学渊.

软土的卸荷模量

[J]. 岩土工程学报, 1996, 18(6): 18-23.

LIU

Guobin

, HOU

Xueyuan

Unloading modulus of the Shanghai soft clay

[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(6): 18-23.

[25]

刘溢, 李镜培, 陈伟.

被动区深层搅拌桩加固对超大深基坑变形的影响

[J]. 岩土工程学报, 2012, 34 (Sup.1): 465-469.

LIU

, LI

Jingpei

, CHEN

Wei

Effect of reinforcement of deep mixing piles on deformation of ultra-deep excavations in passive zone

[J]. Chinese Journal of Geotechnical Engineering, 2012, 34 (Sup.1): 465-469.

[26]

徐中华.

上海地区支护结构与主体地下结构相结合的深基坑变形性状研究[D]. 上海: 上海交通大学, 2007.

Zhonghua

Deformation behavior of deep excavations supported by permanent structure in Shanghai soft deposit[D]. Shanghai: Shanghai Jiao Tong University, 2007.