上海交通大学学报

上海交通大学学报 >

2023 , Vol. 57 >Issue 12: 1531 - 1542

DOI: https://doi.org/10.16183/j.cnki.jsjtu.2022.180

新型电力系统与综合能源

基于时空协方差函数的风能场景生成方法与应用

展开
  • 上海交通大学 机械与动力工程学院, 上海 200240
彭星皓(1998-),硕士生,研究方向为数据驱动的能源系统预测.

收稿日期: 2022-05-24

  修回日期: 2022-07-19

  录用日期: 2022-09-15

  网络出版日期: 2023-04-26

基金资助

国家自然科学基金面上项目(72072114)

收起

Wind Power Scenario Generation Method and Application Based on Spatiotemporal Covariance Function

Expand
  • School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

Received date: 2022-05-24

  Revised date: 2022-07-19

  Accepted date: 2022-09-15

  Online published: 2023-04-26

Fold

摘要

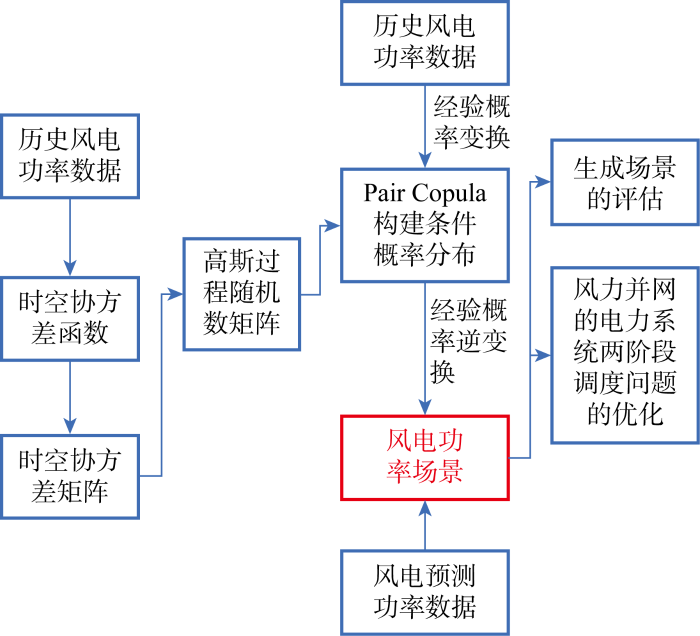
与传统发电不同,风力发电具有较大的随机性与时空相关性.在风力发电并网的电力系统优化调度问题中,保障电力调度在不同风力发电功率场景中的最优执行是决策问题的关键点,因此高质量的风能场景生成非常重要.基于高斯随机过程和时空协方差函数表征风力发电站输出功率的时空相关性,由Pair Copula模型建立联合概率分布,通过经验概率逆变换方法实现具体场景.评估生成场景的多种指标,验证生成场景的优越性.基于修改的IEEE 6总线系统建立电力系统机组组合的混合整数规划模型,求解不同场景下的问题,验证场景生成方法在风力发电并网调度问题中所具有的经济性和可行性.

关键词： 风力发电; 场景生成; 时空协方差函数; Copula函数; 经济调度

本文引用格式

彭星皓, 李艳婷 . 基于时空协方差函数的风能场景生成方法与应用[J]. 上海交通大学学报, 2023 , 57(12) : 1531 -1542 . DOI: 10.16183/j.cnki.jsjtu.2022.180

Abstract

Wind power generation is different from traditional power generation in which wind power output is highly stochastic and spatio-temporally dependent. In the optimal scheduling problem of wind power grid-connected power system, ensuring the optimal execution of power scheduling in different wind power scenarios is the key of the decision-making problem. Therefore, high quality wind power scenario generation is of great importance. The spatiotemporal correlation of the output power of wind power plants are characterized based on Gaussian stochastic process and spatiotemporal covariance function, and the joint probability distribution is established by the Pair Copula model, and specific scenarios are implemented by the method of empirical probability inverse transformation. A variety of scene metrics of the generated scene are generated, which verifies the superiority of the generated scene. Finally, based on the modified IEEE 6-bus system, a mixed integer programming model for the unit output of the power system is established to solve the problems in different scenarios and verify the economic advantages of the scenario generation method in the dispatching problem of wind power grid connection.

Key words： wind power generation; scenario generation; spatiotemporal covariance function; Copula function; economic dispatch

参考文献

[1] GWEC. GWEC global wind report 2022[EB/OL]. (2022-04-04)[2022-04-04]. https://gwec.net/global-wind-report-2022.
[2] CHEN P Y, PEDERSEN T, BAK-JENSEN B, et al. ARIMA-based time series model of stochastic wind power generation[J]. IEEE Transactions on Power Systems, 2010, 25(2): 667-676.
[3] DíAZ G, GóMEZ-ALEIXANDRE J, COTO J. Wind power scenario generation through state-space specifications for uncertainty analysis of wind power plants[J]. Applied Energy, 2016, 162: 21-30.
[4] 董骁翀, 孙英云, 蒲天骄. 基于条件生成对抗网络的可再生能源日前场景生成方法[J]. 中国电机工程学报, 2020, 40(17): 5527-5536.
[4] DONG Xiaochong, SUN Yingyun, PU Tianjiao. Day-ahead scenario generation of renewable energy based on conditional GAN[J]. Proceedings of the CSEE, 2020, 40(17): 5527-5536.
[5] 肖白, 于龙泽, 刘洪波, 等. 基于生成虚拟净负荷的多能源电力系统日前优化调度[J]. 中国电机工程学报, 2021, 41(21): 7237-7249.
[5] XIAO Bai, YU Longze, LIU Hongbo, et al. Day ahead optimal dispatch of multi-energy power system based on generating virtual net load[J]. Proceedings of the CSEE, 2021, 41(21): 7237-7249.
[6] CHEN Y Z, WANG Y S, KIRSCHEN D, et al. Model-free renewable scenario generation using generative adversarial networks[C]// 2019 IEEE Power & Energy Society General Meeting. Atlanta, USA: IEEE, 2019: 1.
[7] ZHANG Y F, AI Q, XIAO F, et al. Typical wind power scenario generation for multiple wind farms using conditional improved Wasserstein generative adversarial network[J]. International Journal of Electrical Power & Energy Systems, 2020, 114: 105388.
[8] PINSON P, MADSEN H, NIELSEN H A, et al. From probabilistic forecasts to statistical scenarios of short-term wind power production[J]. Wind Energy, 2009, 12(1): 51-62.
[9] 唐锦, 张书怡, 吴秋伟, 等. 基于Copula函数与等概率逆变换的风电出力场景生成方法[J]. 电力工程技术, 2021, 40(6): 86-94.
[9] TANG Jin, ZHANG Shuyi, WU Qiuwei, et al. Wind power output scenario generation method based on Copula function and equal probability inverse transformation[J]. Electric Power Engineering Technology, 2021, 40(6): 86-94.
[10] CAI D F, SHI D Y, CHEN J F. Probabilistic load flow computation with polynomial normal transformation and Latin hypercube sampling[J]. IET Generation, Transmission & Distribution, 2013, 7(5): 474-482.
[11] PAPAEFTHYMIOU G, KLOCKL B. MCMC for wind power simulation[J]. IEEE Transactions on Energy Conversion, 2008, 23(1): 234-240.
[12] 赵鉴, 袁渤巽, 于浩, 等. 基于风光不确定性和相关性的场景生成[J]. 能源与节能, 2021(8): 8-12.
[12] ZHAO Jian, YUAN Boxun, YU Hao, et al. Scene generation based on uncertainty and correlation of wind and photovoltaic power[J]. Energy and Energy Conservation, 2021(8): 8-12.
[13] LI J H, ZHU D L. Combination of moment-matching, Cholesky and clustering methods to approximate discrete probability distribution of multiple wind farms[J]. IET Renewable Power Generation, 2016, 10(9): 1450-1458.
[14] LI B H, SEDZRO K, FANG X, et al. A clustering-based scenario generation framework for power market simulation with wind integration[J]. Journal of Renewable and Sustainable Energy, 2020, 12(3): 036301.
[15] WANG Z, WANG W S, LIU C, et al. Forecasted scenarios of regional wind farms based on regular vine copulas[J]. Journal of Modern Power Systems and Clean Energy, 2019, 8(1): 77-85.
[16] MA X Y, SUN Y Z, FANG H L. Scenario generation of wind power based on statistical uncertainty and variability[J]. IEEE Transactions on Sustainable Energy, 2013, 4(4): 894-904.
[17] TAN J, WU Q W, ZHANG M L, et al. Wind power scenario generation with non-separable spatio-temporal covariance function and fluctuation-based clustering[J]. International Journal of Electrical Power & Energy Systems, 2021, 130: 106955.
[18] DENG J C, LI H R, HU J X, et al. A new wind speed scenario generation method based on spatiotemporal dependency structure[J]. Renewable Energy, 2021, 163: 1951-1962.
[19] DRAXL C, CLIFTON A, HODGE B M, et al. The wind integration national dataset (WIND) toolkit[J]. Applied Energy, 2015, 151: 355-366.
[20] GNEITING T. Nonseparable, stationary covariance functions for space-time data[J]. Journal of the American Statistical Association, 2002, 97(458): 590-600.
[21] ABDI H. The Kendall rank correlation coefficient[C]// SALKIND N J. Encyclopedia of Measurement and Statistics. California, USA: Sage, 2006: 508-510.
[22] SKLAR A. Random variables, joint distribution functions, and copulas[J]. Kybernetika, 1973, 9(6): 449-460.
[23] SAMPSON P D, GUTTORP P. Nonparametric estimation of nonstationary spatial covariance structure[J]. Journal of the American Statistical Association, 1992, 87(417): 108-119.
[24] KRUSKAL J B, WISH M. Multidimensional scaling[M]. London: Sage, 1978.
[25] VILLANUEVA D, FEIJóO A. Wind power distributions: A review of their applications[J]. Renewable and Sustainable Energy Reviews, 2010, 14(5): 1490-1495.
[26] HERSBACH H. Decomposition of the continuous ranked probability score for ensemble prediction systems[J]. Weather and Forecasting, 2000, 15(5): 559-570.
[27] SCHEUERER M, HAMILL T M. Variogram-based proper scoring rules for probabilistic forecasts of multivariate quantities[J]. Monthly Weather Review, 2015, 143(4): 1321-1334.
[28] HOLTTINEN H, TUOHY A, MILLIGAN M, et al. The flexibility workout: Managing variable resources and assessing the need for power system modification[J]. IEEE Power and Energy Magazine, 2013, 11(6): 53-62.
[29] 江婷, 邓晖, 陆承宇, 等. 电能量和旋转备用市场下电-热综合能源系统低碳优化运行[J]. 上海交通大学学报, 2021, 55(12): 1650-1662.
[29] JIANG Ting, DENG Hui, LU Chengyu, et al. Low-carbon optimal operation of an integrated electricity-heat energy system in electric energy and spinning reserve market[J]. Journal of Shanghai Jiao Tong University, 2021, 55(12): 1650-1662.
[30] LIU F, BIE Z H, LIU S Y, et al. Day-ahead optimal dispatch for wind integrated power system considering zonal reserve requirements[J]. Applied Energy, 2017, 188: 399-408.
[31] NASROLAHPOUR E, KAZEMPOUR J, ZAREIPOUR H, et al. A bilevel model for participation of a storage system in energy and reserve markets[J]. IEEE Transactions on Sustainable Energy, 2018, 9(2): 582-598.
[32] ZHANG M L, AI X M, FANG J K, et al. A systematic approach for the joint dispatch of energy and reserve incorporating demand response[J]. Applied Energy, 2018, 230: 1279-1291.
Options
文章导航

/

〈 〉