基于统一强度理论的螺纹桩承载力计算方法

doi:10.16183/j.cnki.jsjtu.2021.077

基于统一强度理论的螺纹桩承载力计算方法

马甲宽^a, 罗丽娟^,^a^,^b, 任翔^a, 时航^a, 尹怡墨^a

a.长安大学建筑工程学院,西安 710064

b.长安大学地下结构与工程研究所,西安 710064

Calculation Method of Bearing Capacity of Screw Pile Based on Unified Strength Theory

MA Jiakuan^a, LUO Lijuan^,^a^,^b, REN Xiang^a, SHI Hang^a, YIN Yimo^a

a. School of Civil Engineering, Chang’an University, Xi’an 710064, China

b. Institute of Underground Structure and Engineering, Chang’an University, Xi’an 710064, China

通讯作者: 罗丽娟,女,副教授,电话(Tel.): 029-82339235;E-mail:luojuan@chd.edu.cn.

责任编辑: 陈晓燕

收稿日期: 2021-03-10

基金资助:

国家自然科学基金(42077248)
国家自然科学基金(41877285)
中央高校基本科研业务费(300102289201)

Received: 2021-03-10

作者简介 About authors

马甲宽(1993-),男,河南省濮阳市人,博士生,主要从事桩基础工程方面研究.

摘要

基于统一强度理论及太沙基极限平衡原理推导了螺纹桩极限承载力,提出了螺纹桩螺牙单独承载破坏与圆柱形剪切破坏两种模式下临界螺距的确定方法和极限承载力计算方法,讨论了统一强度理论参数b与螺纹桩关键参数对极限承载力的影响.结果表明:螺纹桩的极限承载力是同外径圆桩的1.5~2倍,螺牙提供的极限承载力主要由土体黏聚力、内摩擦角及埋深决定.当b从0增加到1时,螺纹桩极限承载力理论计算值增幅约48%,考虑中主应力对土体强度的影响会使得螺纹桩承载力理论计算结果更加准确.螺纹桩的参数中,螺牙高度b_h对其极限承载力影响最大,而螺牙厚度t对承载力基本无影响.设计螺纹桩时可适当增加螺牙高度,以提高螺纹桩极限承载力.

关键词： 螺纹桩; 统一强度理论; 现场监测; 太沙基极限平衡原理; 临界螺距

Abstract

Based on the unified strength theory and the Terzaghi limit equilibrium theory, the ultimate bearing capacity of screw pile has been deduced. The method to determine the critical pitch and calculate the ultimate bearing capacity of the screw pile in two failure modes including the independent bearing failure mode and the cylinder shear failure mode has been proposed. The influence of the unified strength theoretical parameter b and the key parameters of concrete screw pile on the ultimate bearing capacity has been analyzed. The results show that the ultimate bearing capacity of the screw pile is 1.5—2 times that of the round pile with the same outer diameter. The ultimate bearing capacity of the screw teeth is mainly determined by the cohesion, the internal friction angle, and the buried depth of the soil. As b increases from 0 to 1, the theoretical value of the ultimate bearing capacity of the screw pile increases by nearly 48%. As the influence of the medium principal stress on the soil strength is considered, the theoretical calculation results of the bearing capacity of the concrete screw pile will be more accurate. Of the parameters of the concrete screw pile, the screw height b_h has the greatest influence on the ultimate bearing capacity, while the screw thickness t has little influence on the bearing capacity. When designing threaded pile, the height of screw can be increased to some extent to improve the ultimate bearing capacity of the screw pile.

Keywords： screw pile; unified strength theory; field monitoring; Terzaghi limit equilibrium principle; critical screw pitch

PDF (1180KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

马甲宽, 罗丽娟, 任翔, 时航, 尹怡墨. 基于统一强度理论的螺纹桩承载力计算方法[J]. 上海交通大学学报, 2022, 56(6): 754-763 doi:10.16183/j.cnki.jsjtu.2021.077

MA Jiakuan, LUO Lijuan, REN Xiang, SHI Hang, YIN Yimo. Calculation Method of Bearing Capacity of Screw Pile Based on Unified Strength Theory[J]. Journal of Shanghai Jiaotong University, 2022, 56(6): 754-763 doi:10.16183/j.cnki.jsjtu.2021.077

螺纹桩是一种由桩芯和连续螺牙组成的异形截面桩,因形似螺丝钉而得名.其前身包括螺旋钢桩(螺牙为分离式,一般为1~3片)、预制螺纹桩、Atlas 桩等,最初由吴敏等^[1]借鉴国外相关桩型设计而成,具有良好的承载性能.

近年来,螺纹桩凭借其承载力高、沉降较小、施工效率高、经济环保等优点在房建及交通工程基础设施建设领域中得以广泛使用^[2⇓-4].然而,目前关于螺纹桩承载机理的研究却主要集中在数值模拟、模型试验及现场试验等方面,倾向于从宏观角度分析螺纹桩承载机理.李成巍等^[5]通过模型试验和数值分析,研究了螺纹桩的竖向承载机理,发现影响螺纹桩竖向承载力的关键因素为土体抗剪强度指标、螺距及螺牙高度.王国才等^[6]通过Abaqus对螺纹桩竖向承载特性及影响因素进行研究,发现螺纹桩极限承载力随S_p/D(S_p为螺距,D为外径)先增大后减小,并在S_p/D处于0.5~2时达到最大值.孟振等^[7]通过室内模型试验对比分析发现在相同条件下,螺纹桩的极限承载力约是普通桩极限承载能力的1~4倍,而蒋鹏程^[8]发现螺纹桩极限承载力比普通桩单桩提高了67%.

在螺纹桩极限承载力计算方面,常规方法仍以混凝土圆桩承载力计算方法为基础进行适当修正,主要包括将螺纹桩极限侧摩阻力乘以一定放大系数、将桩土极限侧摩阻力替换为土体抗剪强度或者将螺纹桩简化为多支点的摩擦端承桩等^[9⇓-11].这类方法忽略了螺牙与桩间土的局部相互作用,承载机制不清的同时阻碍了计算精度的提高,易造成工程实践浪费或安全隐患.因此,若要实现螺纹桩承载力的准确计算,必然要明确螺牙与桩间土的相互作用规律,尝试基于解析手段揭示螺纹桩的承载机理.

综合当前国外螺纹桩破坏机制的研究成果可以发现,关于螺纹桩破坏机制的研究尚不多见,且主要集中于螺纹桩的前身螺旋钢桩.有关螺旋钢桩的研究最早开始于20世纪60年代,已提出了多种破坏模型:叶片支撑破坏模型^[12]、圆柱破坏模型^[13-14]、单层叶片对数滑裂面破坏模型等.然而,螺纹桩在构造特点上与螺旋钢桩具有较大差异,相关理论的普适性尚有待商榷.国内关于螺纹桩破坏机制的研究处于起步阶段,目前关于这方面的报道为数不多.董天文等^[15]认为桩受荷载后桩顶处螺牙下方地基出现压密区,继而压密区向外挤出产生滑裂面,最终形成梨形滑裂面破坏区,螺牙端阻力达到极限;继续加载则螺牙间土柱被剪切破坏,下级螺牙开始承载,直至整个桩体发生破坏.孟振^[16]提出极限荷载下螺纹桩的两种破坏模式,即“单独承载破坏”与“圆柱形剪切破坏”,并分别讨论了两种模式下的承载力计算方法及破坏模式的判别方法.

然而,上述理论计算方法采用的屈服准则一般为单切应力屈服准则——Mohr-Coulomb(M-C)屈服准则,忽略了中主应力σ₂对土体屈服与破坏的影响.既有研究表明,σ₂往往对材料的强度起到提升作用^{[17⇓⇓⇓-21]},而M-C屈服准则推导的地基承载力显然不能反映地基实际情况,结果偏于保守,具有一定不足.

鉴于此,本文拟基于双剪统一强度理论,以太沙基极限平衡理论为基础提出螺纹桩的承载力计算公式,通过工程实例验证计算公式的准确性及适用性,进而讨论了统一强度理论参数b(该参数反映了中间主切应力对材料屈服的影响)及螺纹桩关键参数对螺纹桩承载力的影响,以期进一步完善螺纹桩承载理论体系.

1 双剪统一强度理论的M-C表述

双剪统一强度理论数学表达式为

(1)

\begin{array}{l} F = σ_{1} - \frac{α}{1 + b} (b σ_{2} + σ_{3}) = σ_{t}, \\ 当 σ_{2} \leq \frac{σ_{1} + α σ_{3}}{1 + α} \\ F = \frac{1}{1 + b} (σ_{1} + b σ_{2}) - α σ_{3} = σ_{t}, \\ 当 σ_{2} > \frac{σ_{1} + α σ_{3}}{1 + α} \end{array}\}

式中:F为屈服函数;σ₁为大主应力;σ₃为小主应力;b值反映了中间主切应力τ₁₂= $\frac{σ_{1} - σ_{2}}{2}$ 或τ₂₃= $\frac{σ_{2} - σ_{3}}{2}$ 对材料屈服或破坏的影响,0≤b≤1;α=σ_t/σ_c,其中σ_t为材料抗拉强度,σ_c为材料抗压强度.

根据既有研究^[19],当采用土体黏聚力c与内摩擦角φ作为基本参数时,可转换为M-C屈服准则形式:

τ_f=c_t+σtan φ_t

其中:σ、τ_f分别为屈服面上正应力与切应力;c_t、φ_t分别为统一黏聚力与统一内摩擦角.

该准则具有与M-C屈服准则同样的表达形式,却可以合理考虑中主应力σ₂效应.极限平衡状态时计算表达式为

(2)

\begin{array}{l} φ_{t} = a r c s i n [\frac{2 (1 + b) s i n φ}{2 + b (1 + s i n φ)}] \\ c_{t} = \frac{2 (1 + b) c c o s φ}{[2 + b (1 + s i n φ)] c o s φ_{t}} \end{array}\}

2 螺纹桩承载力推导

2.1 极限平衡理论及假定

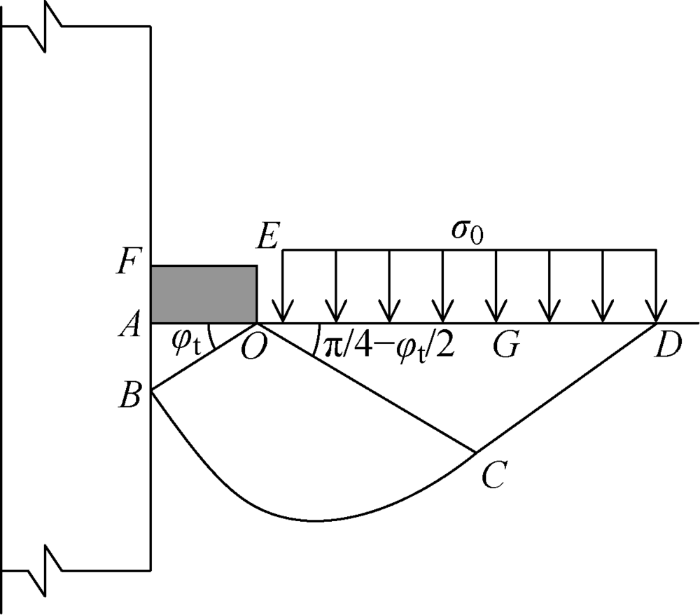
对于单独承载破坏模式的螺纹桩,根据太沙基地基极限承载力计算方法,螺牙下土体分为3个区域,如图1所示.图中:OA面为螺牙底部;EF面为螺牙顶部;π/4-φ_t/2为朗肯被动状态区OC面与水平面OD的夹角;σ₀为OD面上的均布压力.3个区域包括弹性压密区OAB、辐射向剪切区OBC、朗肯被动状态区OCD,BC曲线为对数螺旋曲线,形式为R=R₀ $e^{θ t a n φ_{t}}$ ,其中R为旋转半径,R₀为初始半径,θ为旋转角.本文在推导螺牙极限承载力时,基于太沙基极限平衡原理的假定,同时结合工程实际对计算模型进行了一定的简化,作出如下假定:

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 螺牙受力示意图

Fig.1 Force diagram of screw teeth

(1) 考虑到实际工程中灌注桩与土体的摩擦及咬合作用,假定螺牙下底面完全粗糙,压密区与螺牙下底部夹角为φ_t,螺旋线中心为O点,同时假定计算由滑动区自重引起的承载力时螺旋中心线也是O点.

(2) 假定承载极限时OE面正应力为 σ_h=Kγh,其中K为静止土压力系数,γ为土体重度,h为埋深;切应力τ_h=σ_htan δ,δ为桩土界面摩擦角,取0.65 ${φ_{t}}^{[16]}$ ,EF面上土体与螺牙分离,二者相互作用为0.

(3) 假定OD边上竖向力均匀分布且仅考虑土体自重,即σ₀=γh.

上述3个假定中,实际上OE面上的侧摩阻力略大于σ_htanδ,这里主要忽略了极限承载状态下桩土界面间残余黏结力,考虑到该值与侧摩阻力相比较小,故而未计入.此外,OD面上竖向应力取γh时忽略了土体之间抗剪强度提供的竖向应力,小于实际值,然而该面上的竖向应力分布形式及数值的选取一直未得到精确解答.本文参考太沙基推导地基极限承载力时所作假设,假定OD面上的竖向压力为均匀分布,其值取γh.

2.2 螺牙极限承载力计算

根据太沙基研究成果,从实际工程要求的精度出发,计算基础极限承载力时可将其分为3种原因引起的极限承载力的总和^[22]:① 土体无质量,有黏聚力和内摩擦角,无超载,即γ=0,c_t≠0,φ_t≠0,h=0;② 土体无质量,无黏聚力,有内摩擦角,有超载,即γ=0,c_t=0,φ_t≠0,h≠0;③ 土体有质量,无黏聚力,有内摩擦角,无超载,即γ≠0,c_t=0,φ_t≠0,h≠0.本文将前两种原因归为一类进行计算.

2.2.1 由埋深、黏聚力、摩擦角产生的承载力

(1) OB面上的应力.

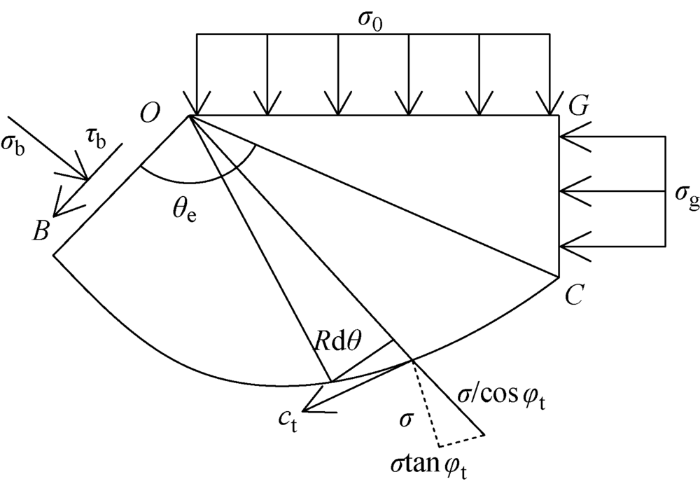
对于螺旋过渡区(OBC区域),BC滑动面上土体正应力σ与切应力τ之间关系为τ=σtanφ_t+c_t,其中正应力σ与其产生的摩阻力σtanφ_t的合力与滑面法向夹角为φ_t,即指向螺旋线的中心O,如图2所示.图中:θ_e为螺旋曲线的最大旋转角;R为螺旋曲线的旋转半径;σ_b、τ_b分别是OB面上的正应力、切应力;σ_g为CG面上的正应力;指数螺旋线的方程为

R=R₀ $e^{θ t a n φ_{t}}$

σ_g=σ₀tan²( $\frac{π}{4}$ + $\frac{φ_{t}}{2}$ )+2ctan( $\frac{π}{4}$ + $\frac{φ_{t}}{2}$ )

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 滑动区受力示意图

Fig.2 Force diagram of sliding region

滑动面上取微段ds_h对O点求力矩,则dM=c_tds_hcosφ_tR=c_tR²dθ,其中s_h为滑动面BC长度,M为弯矩.由O点力矩之和为0可得(不计入滑动区重力):

(3)

\begin{array}{l} M_{O} = σ_{0} \frac{R_{0}^{2} e^{2} θ_{e} t a n φ_{t}}{2} c o s^{2} θ_{A} + \\ σ_{g} \frac{R_{0}^{2} e^{2} θ_{e} t a n φ_{t}}{2} \\ s i n^{2} θ_{A} + c_{t} R_{0}^{2} \int_{0}^{θ_{e}} e^{2 θ t a n φ_{t}} d θ - \frac{σ_{b} R_{0}^{2}}{2} = 0 \end{array}\}

式中:M_O为O点合力矩;θ_A= $(\frac{π}{4} - \frac{φ_{t}}{2})$ ;θ_B= $(\frac{π}{4} + \frac{φ_{t}}{2})$ .

由式(3)解得:

(4)σ_b=λ₁

(c o s^{2} θ_{A} + t a n^{2} θ_{B} s i n^{2} θ_{A})

σ₀+

(2 λ_{1} t a n θ_{B} s i n^{2} θ_{A} + \frac{λ_{1} - 1}{t a n φ_{t}})

c_t

(5)τ_b= σ _btanφ_t+c_t

式中:θ_e=π-φ_t- $(\frac{π}{4} - \frac{φ_{t}}{2})$ = $\frac{3 π}{4}$ - $\frac{φ_{t}}{2}$ ;λ₁= $e^{2 θ_{e} t a n φ_{t}}$ .

(2) OA面上应力.

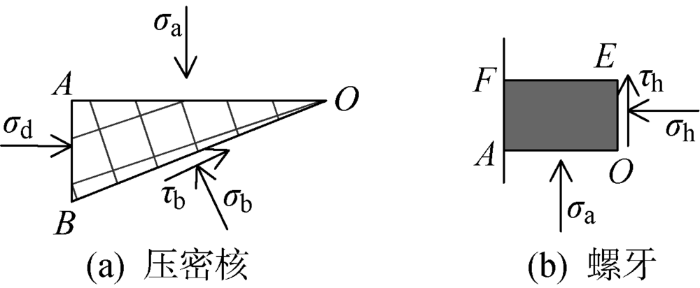
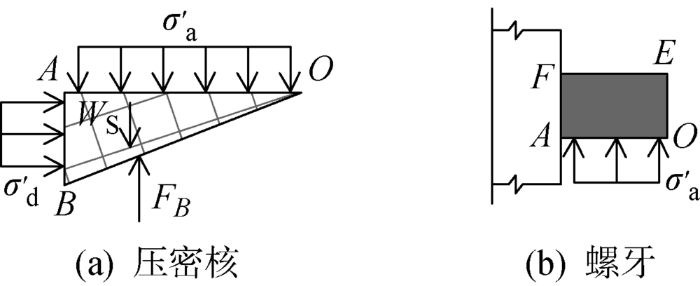
对于弹性压密区,假定螺牙达到极限承载力时,AB面上只有正应力,而无切应力,如图3(a)所示.图中:σ_a为螺牙底面与土体之间的法向应力;σ_d为表面与压密核之间的法向应力.则由y方向力系平衡关系可得:

(6)∑F_y=τ_bR₀sinφ_t+σ_bR₀cosφ_t-σ_aR₀cosφ_t=0

式中:∑F_y为y方向的合力.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 压密核及螺牙受力

Fig.3 Stress of compacting core and screw teeth

解得:

(7)σ_a=σ_b+τ_btanφ_t

(3) 螺牙竖向应力.

对螺牙受力分析,假定螺纹桩在达到极限承载力时,EF面与土体脱空,二者之间无相互作用,此时螺牙上受到的竖向力除σ_a之外,还包括τ_h,如图3(b)所示.因此螺牙上平均竖向应力q₁为

(8)q₁=σ_a+

\frac{σ_{h} t a n δ t}{b_{h}}

=N_cc_t+N_qσ₀

N_q=λ₁ $(c o s^{2} θ_{A} + t a n^{2} θ_{B} s i n^{2} θ_{A})$ ×(1+tan²φ_t)+ $\frac{K t t a n δ}{b_{h}}$

N_c= $(2 λ_{1} t a n θ_{B} s i n^{2} θ_{A} + \frac{λ_{1} - 1}{t a n φ_{t}})$ ×(1+tan²φ_t)+tanφ_t

式中:t为螺牙厚度;b_h为螺牙高度;N_c为与黏聚力相关的承载力系数;N_q为与埋深相关的承载力系数.

2.2.2 由滑动区自重产生的极限承载力

(1) OBCG块受力.

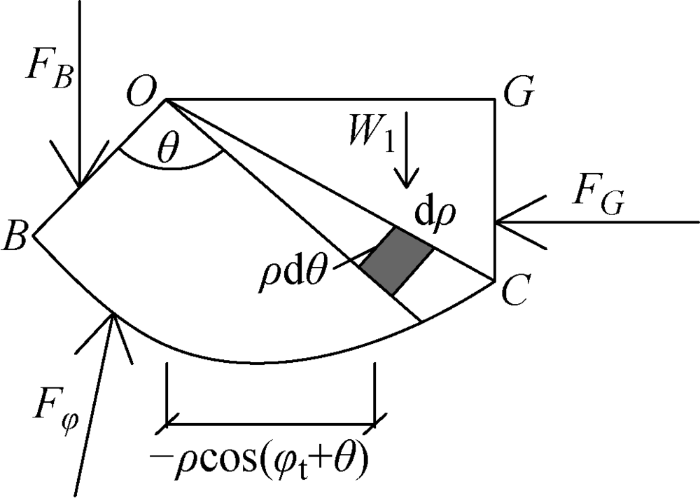
CG面上的侧向压力呈三角分布,切应力为0,则其合力作用于距离C点CG/3处,OBCG块体受力如图4所示.而OB面上反力F_B作用于距离O点2OB/3处,并且与OB面法向夹角为φ_t,其方向为竖直向下.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 自重引起的OBCG块受力

Fig.4 Force on OBCG caused by dead weight

对于OBC区域,BC面上反力F_φ正指向O点,对O点取矩为0.同时,取面积微元dA,该微元土体到O点的水平距离为l,假定微元位于O点左侧时l为负,右侧为正,则l=-ρcos(φ_t+θ),微元重力对O点力矩为

dM=γdAl=-γρdρdθρcos(φ_t+θ)

式中:ρ为面积微元到O点的距离.由O点力矩为0可得:

(9)M_O=F_G

\frac{2 C G}{3}

-γ

\int_{0}^{R} \int_{0}^{θ_{e}}

ρ²cos(φ_t+θ)dρdθ+W₁

\frac{2 O G}{3}

-F_Bcosφ_t

\frac{2 O B}{3}

式中:F_G为OB面上的合力;W₁为OCG土块的自重.

解得:

(10)F_B=γ

R_{0}^{2}

(

e^{3 θ_{e} t a n φ}

sin³θ_Atan²θ_B-λ₂+

e^{3 θ_{e} t a n φ}

sinθ_Acos²θ_A)/2cosφ_t

λ₂= $\frac{e^{3 θ_{e} t a n φ_{t}} (c o s θ_{B} - 3 t a n φ_{t} s i n θ_{B}) - 4 s i n φ_{t}}{1 + 9 t a n^{2} φ_{t}}$

(2) OAB块受力.

OAB块受力如图5(a)所示,图中:σ'_a为OA面上的法向应力;σ'_d 为AB面上的法向应力.根据y方向力系平衡得:

(11)∑F_y=F_B-σ'_aR₀cosφ_t-W_S=0

W_S= $\frac{γ R_{0}^{2} s i n 2 φ_{t}}{4}$

式中: W_S为压密核自重.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 自重作用下压密核及螺牙受力

Fig.5 Stress of compression core and screw teeth under dead weight

解得:

(12)σ'_a=

\frac{F_{B} - W_{S}}{R_{0} c o s φ_{t}}

即由土体自重引起的螺牙上平均竖向应力为

(13)q'₁=σ'_a=

\frac{1}{2}

γN_γ

N_γ=R₀( $e^{3 θ_{e} t a n φ_{t}}$ sin³θ_Atan²θ_B-λ₂+ $e^{3 θ_{e} t a n φ_{t}}$ sinθ_Acos²θ_A-sinφ_tcos²φ_t)/cos²φ_t

式中:N_γ为与土体重度相关的承载力系数.

综上,螺牙达到极限承载阶段时所受的竖向压力为

(14)q_ul=q₁+q'₁=N_cc+N_qσ_h+

\frac{1}{2}

N_γγ

2.3 螺纹桩极限承载力计算

2.3.1 螺距大于临界螺距

若上下螺牙塑性区不相互影响,二者之间的距离必然要大于某一数值,将其命名为临界螺距H_cr.根据Rao等^[23-24]的研究,若螺旋钢桩(螺纹桩前身)达到极限承载力时产生圆柱形剪切破坏,S_p/D的值需小于3,考虑到螺旋钢桩外径D一般为其内径d的数倍,因此S_p/D的值实际由叶片的螺距S_p与悬臂端长度(对应于螺纹桩的螺牙高度b_h)的比值来决定.因此,确定混凝土螺纹桩临界螺距时,需对上述方法进行一定的修正.结合《螺纹桩技术规程》^[25],本文建议当S_p与b_h的比值S_p/b_h<6时,计算螺纹桩极限承载力采用圆柱形剪切破坏模型;当螺距S_p/b_h>6且S_p>D时,采用单独承载破坏模型,即此时S_p>H_cr.

当S_p>H_cr时,螺纹桩承载力由螺牙承载力、桩芯侧摩阻力、桩底承载力3部分组成.

(1) 螺牙承载力Q_ul1.

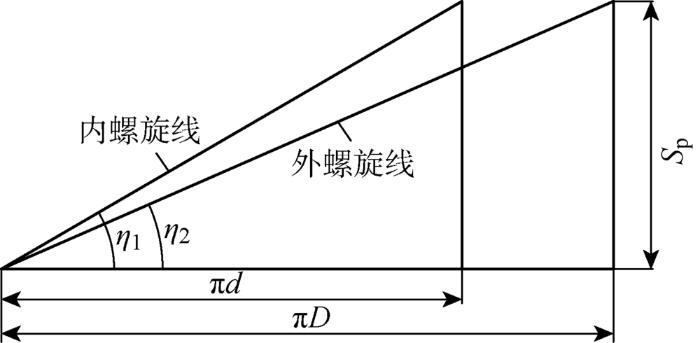
将一个螺距内螺纹分别沿内周与外周展开,如图6所示.内周与外周的倾角分别为η₁、η₂,则 tanη₁= $\frac{S_{p}}{π d}$ ,tanη₂= $\frac{S_{p}}{π D}$ .

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 内外螺旋线倾角

Fig.6 Inclination of inner and outer helical line

dz高度内,螺牙竖向投影面积为

dA= $\frac{b_{h}}{2} (\frac{1}{s i n η_{1}} + \frac{1}{s i n η_{2}})$ dz

式中:z为埋深.

假定螺纹桩穿过n层土体,第i层土体厚度为h_i,内摩擦角及黏聚力分别为φ_t_i、c_t_i,重度为γ_i,则螺牙产生的竖向承载力之和为

(15)Q_ul1=

\overset{n}{\sum_{i = 1}} \int_{z_{i - 1}}^{z_{i}}

λ₃b_h(N_q_iσ₀+N_c_ic_t_i+

\frac{1}{2}

N_γγ_i)dz=λ₃b_h

\overset{n}{\sum_{i = 1}}

{N_q_ih_i[

(\overset{i - 1}{\sum_{j = 1}} γ_{j} h_{j})

\frac{γ_{i} h_{i}}{2}

]+N_c_ic_t_ih_i+

\frac{1}{2}

N_γγ_ih_i}

λ₃= $\frac{1}{2} (\frac{1}{s i n η_{1}} + \frac{1}{s i n η_{2}})$

式中:i、j分别为土层编号;h_j为第j层土体厚度;γ_j为第j层土体重度;N_q_i、N_c_i、N_γ_i为第i层土体承载系数.

(2) 桩芯侧摩阻力.

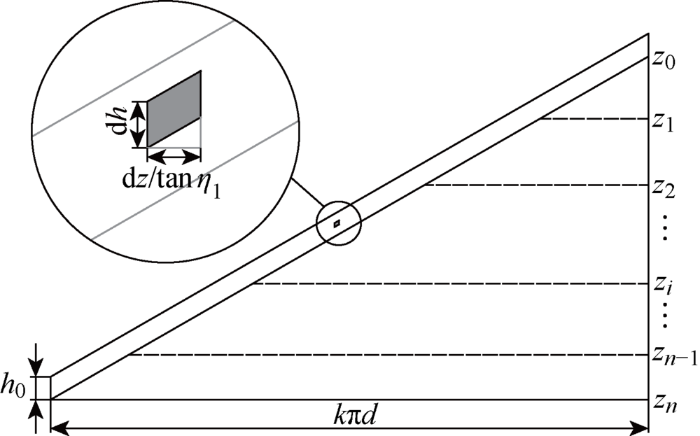
螺牙下土体受力状态复杂,压密核附近的竖向承载力主要由螺牙提供,本文在计算桩芯侧摩阻力时不计入压密区的摩阻力,上下螺牙间有效桩芯摩擦高度h₀为

(16)h₀=S_p-t-h_max

式中:h_max为螺牙下侧滑动边界与O点的最大竖向距离.

螺旋线边界上任意一点与O点的竖向距离为

(17)h_v=R₀

e^{θ t a n φ_{t}}

sin(φ_t+θ), φ_t+θ⊂(0,π)

对h_v求θ的导数,令其等于0,得:

(18)

\frac{d h_{v}}{d θ}

=R₀

e^{θ t a n φ_{t}} [c o s (φ_{t} + θ) t a n φ_{t} s i n (φ_{t} + θ)]

解得θ= $\frac{π}{2}$ .

因此:

(19)h_max=R₀

e^{\frac{π}{2} t a n φ_{t}}

cosφ_t

螺纹桩桩芯有效摩擦区展开后如图7所示,图中z_i (i=0,1,…,n)为第i层土体底部埋深,k为螺牙旋转周数.取微元面积dA,则dA=dhdz/tanη₁,考虑到埋深z远大于h₀,忽略h₀土体高度引起的侧摩阻力,故而微元面上的极限摩阻力为

dQ₂=K_ip(z)tanδdh $\frac{d z}{t a n η_{1}}$

式中:Q₂为桩芯侧摩阻力;K_i为第i层土体静止土压力系数;p(z)为埋深z处的土体自重应力.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 桩芯侧摩阻区展开图

Fig.7 Expansion diagram of inner pile side friction zone

桩芯极限侧摩阻力为

(20)Q_ul2=

\overset{n}{\sum_{i = 1}} \int_{z_{i - 1}}^{z_{i}} \int_{0}^{h_{0}}

K_ip(z)tanδdh

\frac{d z}{t a n η_{1}}

\frac{\overset{n}{\sum_{i = 1}} t a n δ_{i} h_{0} K_{i} h_{i} [(\overset{i - 1}{\sum_{j = 1}} γ_{j} h_{j}) + \frac{γ_{i} h_{i}}{2}]}{t a n η_{1}}

(3) 桩端承载力.

计算桩端承载力时,桩端面积按桩芯底面积A_p来计算,即A_p=πd²/4,根据《建筑桩基技术规范》^[26],极限端阻力标准值为

(21)Q_ul3= q_pkA_p

式中:q_pk为端阻力标准值.

综上,螺距大于临界螺距的螺纹桩极限承载力计算公式如下:

(22)Q_ult=Q_ul1+Q_ul2+Q_ul3=λ₃b_h

\overset{n}{\sum_{i = 1}}

{N_q_ih_i

[(\overset{i - 1}{\sum_{j = 1}} γ_{j} h_{j}) + \frac{γ_{i} h_{i}}{2}]

+N_c_ic_t_ih_i+

\frac{1}{2}

N_γγ_ih_i}+

\frac{1}{t a n η_{1}}

\overset{n}{\sum_{i = 1}}

tanδ_ih₀K_ih_i

[(\overset{i - 1}{\sum_{j = 1}} γ_{j} h_{j}) + \frac{γ_{i} h_{i}}{2}]

+ q_pkA_p

2.3.2 螺距小于临界螺距

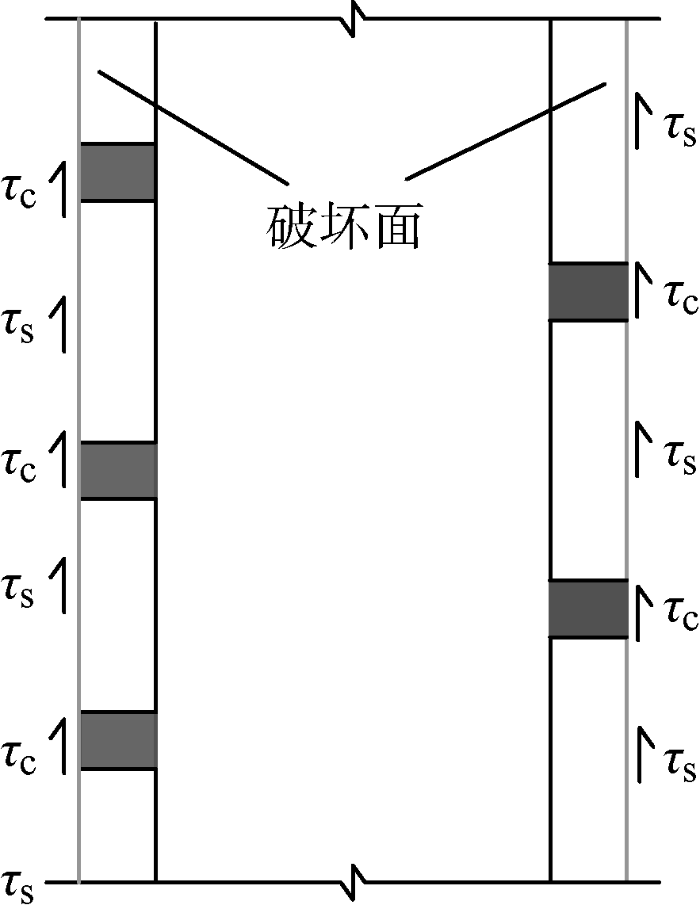
当S_p≤H_cr时,上下螺牙之间作用交叉明显,太沙基极限平衡理论不再适用于螺纹桩极限承载力的计算.根据既有研究^[16,24]及《螺纹桩技术规程》^[25],螺纹桩达到极限荷载时沿桩体外径呈圆柱形剪切破坏,如图8所示,图中τ_c、τ_s分别为圆柱剪切面上不同位置的极限切应力.此时螺纹桩的极限承载力计算方法如下:

(23)Q_ult=Q'_ul1+Q'_ul2+Q'_ul3=

\overset{n}{\sum_{i = 1}} \int_{z_{i - 1}}^{z_{i}} \int_{0}^{h_{a}}

(c_t_i+K_ip(z)tanφ_t_i)dh

\frac{d z}{t a n η_{2}}

\overset{n}{\sum_{i = 1}} \int_{z_{i - 1}}^{z_{i}} \int_{0}^{t}

K_ip(z)tanδ_idh

\frac{d z}{t a n η_{2}}

+q_pkA'_p=

\overset{n}{\sum_{i = 1}} \frac{c_{t i} h_{i} h_{a}}{t a n η_{2}}

\overset{n}{\sum_{i = 1}} \frac{K_{i} h_{i} (t a n φ_{t i} h_{a} + t a n δ_{i} t) [(\overset{i - 1}{\sum_{j = 1}} γ_{j} h_{j}) + \frac{γ_{i} h_{i}}{2}]}{t a n η_{2}}

+q_pkA'_p

式中:Q'_ul1、Q'_ul2及Q'_ul3分别为桩侧土体摩阻力、螺牙摩阻力以及桩端承载力;h_a=S_p-t;A'_p为按外径D计算的桩端面积.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 螺纹桩圆柱形剪切破坏模型

Fig.8 Cylindrical shear failure model of screw pile

3 实例验证及参数讨论

某工地现场试验^[2]的桩型中,灌注螺纹桩的内径为400 mm、外径为560 mm、螺齿宽为80 mm、螺距为700 mm、桩长为8 m、宽厚比为1,干作业钻孔桩.现场试验场地工程地质条件如表1所示,所在土层为粉质黏土,土体重度平均为19 kN/m³.

表1 土体物理指标

Tab.1 Physical indexes of soil

层号	层厚/m	液性指数	φ/(°)	c/kPa
1	2.25	0.14	13.0	35.4
2	3.80	0.51	19.4	25.9
3	2.00	0.35	16.0	36.4
4	5.05	0.51	11.4	23.6

新窗口打开| 下载CSV

螺纹桩参数S_p/b_h>6且S_p>D,采用式(22)对螺纹桩承载力进行计算,螺纹桩极限端阻力标准值根据《建筑桩基技术规范》^[26]取 1000 kPa.当b取0时(即按M-C屈服准则计算),螺纹桩承载力计算结果如表2所示.

表2 螺纹桩承载力理论推导值

Tab.2 Theoretical bearing capacity of screw pile

极限承载力	分项	分项承载力/kN	分项占比/%	总占比/%
Q_ul1	黏聚力	571.5	45.1	85.8
	埋深	685.1	54.2	-
	滑块自重	9.4	0.7	-
Q_ul2	-	83.6	-	5.7
Q_ul3	-	125.7	-	8.5
Q_ult	-	1475.3	-	100

新窗口打开| 下载CSV

可以发现,螺纹桩极限承载力理论值为 1475.3 kN,螺牙提供的承载力达到了螺纹桩极限承载力的85%左右,而同外径混凝土圆桩极限承载力约为 1100 kN,侧摩阻力占总承载力的77%.可以看出,螺牙的存在不但改变了桩体的承载特性,而且大大提高了承载力.同时发现,螺牙提供的极限承载力主要由土体c、φ及桩体埋深决定,而滑块自重(非土体自重)引起的承载力仅占螺牙承载力的1%左右,因此忽略滑块自重对滑动面的影响,假定对数螺旋线的中点为O点是合理的.

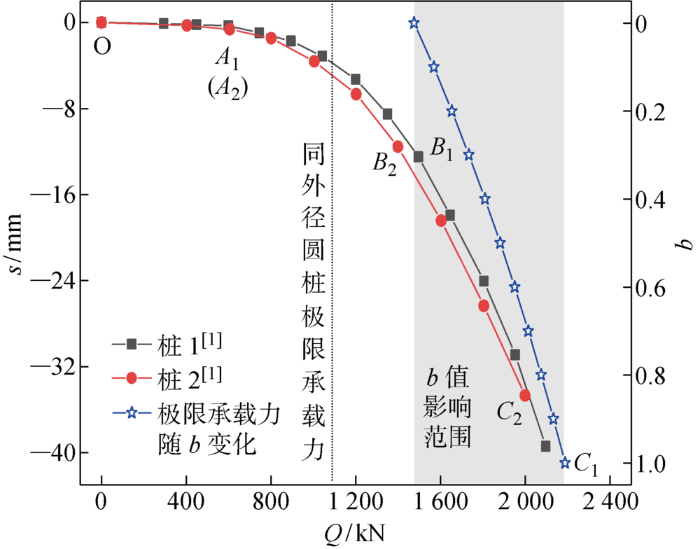
图9所示为螺纹桩承载力现场实测与理论值对比图,图中Q为桩所受荷载,s为桩体沉降.可以发现,螺纹桩沉降曲线可以分为3个阶段:直线增加段OA(包括OA₁与OA₂,下同)、过渡段AB及迅速沉降段BC,本文推导的极限承载力下限值正好位于过渡段与迅速沉降段的过渡点B点附近.根据《建筑基桩检测技术规范》^[27]规定,对于缓变型Q-s曲线,取沉降值达到40 mm时对应的荷载为极限承载力,对于陡降型Q-s曲线,取拐点处荷载为极限承载力.本文中螺纹桩Q-s曲线属于二者之间的过渡型,在判定极限承载力时徐春华等^[2]选择沉降40 mm时的荷载为极限承载力,分别为 2000 kN及 2100 kN,但是考虑到过渡点B以后桩沉降速率明显过大,对工程的安全性极为不利.因此,本文认为选取B点或者B点与40 mm之间的某个点对应的荷载为极限承载力更为合适,即螺纹桩极限承载力在 1500~2000 kN之间.从图9中b可以看出,当b从0增大到1时,本文方法推导的螺纹桩极限承载力从 1475 kN增加到了 2187 kN,增幅约48%,说明极限承载力随着b的增大而显著提高,计算过程中考虑该值的影响能更好发挥土体的承载潜能.当b值取值合适时,本文方法计算结果与螺纹桩实际极限承载力将更加接近.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 现场实测与理论值对比

Fig.9 Comparison of field measurements and theoretical values

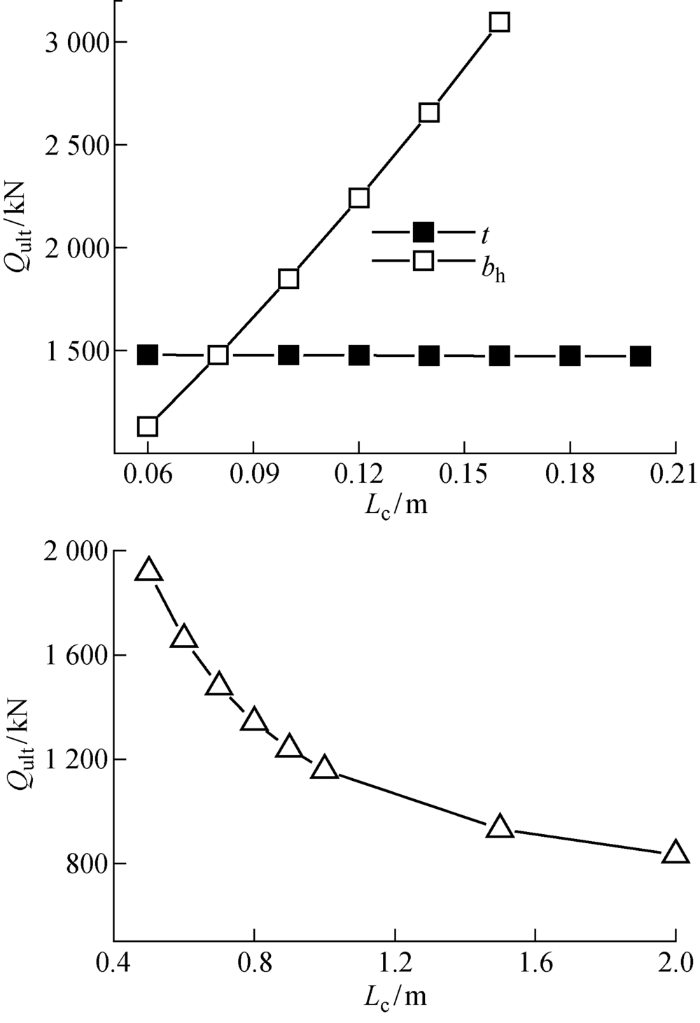
从前文推导中可以发现,除桩径等常规参数外,影响螺纹桩承载力的主要参数包括b_h、t及S_p.图10所示为螺纹桩在b=0时满足单独承载破坏条件下极限承载力随其关键参数的变化曲线,图中L_c为参数尺寸.可以发现,b_h对螺纹桩承载力影响最为明显,当b_h从0.06 m增加到0.15 m时,螺纹桩承载力随之增加了约2倍,从 1129 kN增加到了 3096 kN,即较小螺牙高度的增加即可带来明显的承载力提升.然而,考虑到当螺牙高度较大时,螺牙悬臂端过长,容易产生冲剪破坏,而且螺牙下土体塑性区的发展受到限制,当螺牙高度超过到某一数值时,反而可能造成螺纹桩承载能力下降,这也是设计人员在螺纹桩设计过程中需注意的问题.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 极限承载力随螺纹桩参数变化

Fig.10 Variation of ultimate bearing capacity with the parameters of screw pile

同时可以看出,螺牙厚度t对螺纹桩承载力几乎没有明显影响,这是因为螺纹桩的承载力主要由螺牙下土体提供,而螺牙侧面面积较小,提供的承载力有限,故在螺纹桩设计过程中,在满足螺牙抗剪强度的前提下,可适当减小螺牙厚度,为螺牙间土体提供更多的塑性变形空间.当螺牙满足单独承载破坏条件时,随着螺距的增加,螺纹桩承载力先迅速降低.这是因为当螺距增加的时候,与螺旋线倾角相关的系数λ₃非线性降低,进而使得螺牙受力总面积迅速减小,极限承载力锐减.之后当螺距增加到一定范围时,承载力下降趋于平缓,这时螺牙提供的承载力仅占桩体的总承载力的一小部分,螺纹桩朝着混凝土圆桩的方向“退化”.因此,在保证螺牙下土体塑性区能充分发展的前提下,若要提高螺纹桩承载力,可适当减小螺距,使得螺牙下土体尽可能多的产生塑性破坏.

4 结论

针对螺纹桩承载机理不清、既有极限承载力计算不准确等问题,基于统一强度理论与太沙基极限平衡理论,推导了螺纹桩极限承载力计算公式,提出了螺纹桩不同模式下临界螺距的确定方法和极限承载力计算方法,并讨论了螺纹桩各参数对其承载力的影响,得出以下结论:

(1) 螺纹桩极限桩承载力是同外径圆桩的 1.5~2倍,螺牙提供的承载力主要由土体黏聚力c、内摩擦角φ及埋深决定,滑块自重贡献的承载力相对较小.

(2) 统一强度理论参数b从0增加到1时,螺纹桩极限承载力理论值约增大48%,b取值合适时可以更准确地预测螺纹桩实际承载力,具有较好经济性、合理性.

(3) 螺纹桩关键参数中,螺牙高度b_h对其极限承载力影响最大,二者基本呈线性相关,而螺牙厚度t对承载力基本不产生影响.

(4) 在保证螺牙抗剪满足要求时,可适当增加螺牙高度,减小螺距,使得螺纹桩桩侧土体最大限度进入塑性变形,以提高螺纹桩极限承载力.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

吴敏, 李波扬.

全螺旋灌注桩-螺纹桩竖向承载力初探

[J]. 武汉大学学报(工学版), 2002, 35(5): 109-112.