同步实施的相邻基坑相互作用机理

doi:10.16183/j.cnki.jsjtu.2021.149

同步实施的相邻基坑相互作用机理

杨其润¹, 李明广¹, 陈锦剑^,¹, 吴航²

1.上海交通大学土木工程系; 上海市公共建筑和基础设施数字化运维重点实验室, 上海 200240

2.上海市城市建设设计研究总院(集团)有限公司, 上海 200125

Interaction Mechanisms of Synchronously Performed Adjacent Excavations

YANG Qirun¹, LI Mingguang¹, CHEN Jinjian^,¹, WU Hang²

1. Department of Civil Engineering; Shanghai Key Laboratory for Digital Maintenance of Buildings and Infrastructure, Shanghai Jiao Tong University, Shanghai 200240, China

2. Shanghai Urban Construction Design and Research Institute (Group) Co., Ltd., Shanghai 200125, China

通讯作者: 陈锦剑,男,教授,博士生导师;E-mail:chenjj29@sjtu.edu.cn.

责任编辑: 陈晓燕

收稿日期: 2021-05-8

基金资助:

国家自然科学基金(41727802)
国家自然科学基金(41977216)
上海市优秀学术带头人计划(20XD1422100)

Received: 2021-05-8

作者简介 About authors

杨其润(1997-),男,山东省枣庄市人,硕士生,从事基坑工程方面的研究.

摘要

采用数值方法建立基于小硬变硬化(HSS)本构模型的相邻基坑模型,将其与单个基坑模型和不考虑墙土摩擦的相邻基坑模型进行对比分析,得到了同步实施的相邻基坑的受力变形特性,揭示相邻基坑相互作用机理.结果表明:坑间土体中存在两种土拱效应,一种是由墙体不均匀变形引起的土拱效应,另一种是由墙土摩擦引起的土拱效应,两者共同影响作用在围护墙上的土压力.随着基坑间距的减小,前者减弱,导致开挖面附近土体向被支撑土体的土压力转移减弱;后者增强,导致作用在相邻围护墙上的土压力减小.在两者的作用下,随着基坑间距的减小,作用在相邻墙体上的土压力先由R型分布向线性分布发展,再向R型分布发展,非相邻墙体水平位移最大值增大,相邻墙体水平位移最大值先增大后减小.

关键词： 相邻基坑; 土拱效应; 土压力; 墙体变形

Abstract

An adjacent excavation model based on the hardening soil-small strain (HSS) constitutive model was established by using the numerical method, which was compared with the single excavation model and the adjacent excavation model without considering the wall-soil friction. The stress deformation characteristics of adjacent excavation implemented simultaneously were obtained, and the interaction mechanism of adjacent excavations were revealed. The results show that two kinds of arching effects exist in the confined soil. One is the arching effect caused by uneven deformation of walls, and the other is the arching effect caused by the wall-soil friction, both of which affect the lateral earth pressure acting on the retaining walls. With the decrease of the excavation spacing, the former is weakened, resulting in the weakening of the transfer of lateral earth pressure between the soil near the excavation face to bracing soil, while the latter is enhanced, leading to the decrease of magnitude of the lateral earth pressure acting on adjacent retaining walls. Under the action of the arching effects, the curve of lateral earth pressure develops from an R-shaped distribution to a linear distribution and then returns to an R-shaped distribution with the decrease of the spacing. The maximum horizontal displacement of non-adjacent walls increases, and the maximum horizontal displacement of adjacent walls increases primarily and then decreases.

Keywords： adjacent excavations; arching effect; earth pressure; wall deformation

PDF (1386KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨其润, 李明广, 陈锦剑, 吴航. 同步实施的相邻基坑相互作用机理[J]. 上海交通大学学报, 2022, 56(6): 722-729 doi:10.16183/j.cnki.jsjtu.2021.149

YANG Qirun, LI Mingguang, CHEN Jinjian, WU Hang. Interaction Mechanisms of Synchronously Performed Adjacent Excavations[J]. Journal of Shanghai Jiaotong University, 2022, 56(6): 722-729 doi:10.16183/j.cnki.jsjtu.2021.149

随着我国城市化进程的不断加快和地下空间的大规模开发利用,基坑工程作为城市建设的重要手段,数量越来越多,面积越来越大,施工越来越复杂.一方面,由于基坑数量增多,城市用地紧张,许多基坑不得不与其他基坑相邻;另一方面,为了减小超大基坑的变形及其对周围环境的影响,需要将超大基坑划分为相邻基坑进行施工.因此,相邻基坑工程日益增多.许多相邻基坑工程往往采用同步实施的施工方法,从而加快建设进程,而同步实施的相邻基坑的受力变形特性与单个基坑存在较大差异,这一问题引起了学者们的广泛关注.

理论研究方面,岳树桥等^[1]采用薄层单元法,推导了相邻基坑间有限宽度土体的主动土压力计算公式.陈小雨等^[2]根据极限平衡理论,得到了相邻基坑相互影响的临界间距表达式.现场实测方面,Zeng等^[3]根据监测数据,对相邻基坑的围护墙水平位移、墙顶垂直位移及地表沉降等变形特性进行了研究.李成巍等^[4]则提出了相邻基坑同步实施的总体思路和技术措施,并通过实测数据验证了方法的可行性和有效性.数值分析方面,李明广^[5]重点关注开挖方式和基坑间距等因素对相邻基坑的影响.叶建峰等^[6]对相邻基坑的失效机理和破坏模式进行了分析.尽管许多学者从多种角度对同步实施的相邻基坑展开了研究,但相邻基坑的相互作用机理尚不清晰,阻碍了工程实践的发展.

本文采用数值方法,首先通过工程实例对计算方法进行验证,在此基础上建立起基于小硬变硬化(HSS)本构模型的相邻基坑理想模型,通过对比单个基坑模型和不考虑墙土摩擦的相邻基坑模型,得到了同步实施的相邻基坑的受力变形特性.基于土拱效应原理,揭示了相邻基坑相互作用机理,并研究了基坑间距对基坑受力变形的影响规律.

1 计算方法验证

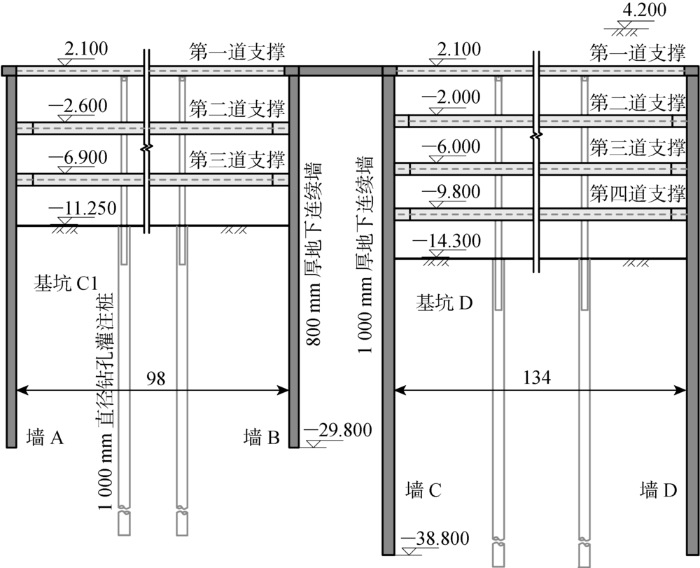
1.1 工程概况

在上海世界博览会B片区地下空间工程中,基坑C1和基坑D被一条道路分隔而形成相邻基坑,剖面如图1所示.基坑C1的开挖深度H为15.45 m,其地下连续墙长31.9 m,厚0.8 m;基坑D的开挖深度为18.50 m,其地下连续墙长40.9 m,厚1 m.基坑C1和基坑D分别设置3道和4道钢筋混凝土支撑,并分4层和5层开挖.两基坑几乎同步实施,并在基坑开挖前中间道路的施工已完成.Zeng等^[3]对该工程进行了详细报道,本文不再赘述.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 相邻基坑剖面图(m)

Fig.1 Profile of adjacent excavations (m)

1.2 数值模拟

基坑形状较为规则且实测数据表明可以将该基坑简化为平面应变模型^[3],因此本文采用有限元软件Plaxis 2D进行数值模拟.考虑土体的小应变特性可以较好地模拟基坑开挖引起的墙体变形和地表沉降^[7-8],故本构模型采用先进的HSS模型,从而更好地模拟墙土相互作用,并且研究土拱效应.根据地勘报告,结合张娇^[9]总结的上海典型土层HSS模型参数的取值方法确定土层的HSS模型参数,如表1所示.表中,E_s为压缩模量, $E_{o e d}^{r e f}$ 为固结试验的参考切线模量, $E_{50}^{r e f}$ 为三轴排水剪切试验的参考割线模量, $E_{u r}^{r e f}$ 为三轴排水剪切试验的参考卸载再加载模量, $G_{0}^{r e f}$ 为小应变刚度试验的参考初始模量,γ_0.7为割线切变模量衰减到初始切变模量70%时所对应的切应变,c'为有效黏聚力,φ'为有效内摩擦角,ψ为剪胀角,m为幂指数,R_f为破坏比.

表1 HSS模型参数

Tab.1 Soil parameters for HSS model

土层编号	厚度/m	E_s/MPa	$E_{o e d}^{r e f}$ /MPa	$E_{50}^{r e f}$ /MPa	$E_{u r}^{r e f}$ /MPa	$G_{0}^{r e f}$ /Pa	γ_0.7×10⁴	c'/kPa	φ'/(°)	ψ/(°)	m	R_f
①	3.9	4.26	3.83	4.60	30.67	122.69	2.7	1	30	0	0.8	0.6
③	5.1	4.72	4.25	5.10	33.98	135.94	2.7	3	28	0	0.8	0.6
④	8.4	2.44	2.20	2.64	17.57	70.27	2.7	4	25	0	0.8	0.6
⑤_2-1	8.2	10.22	9.20	11.04	55.19	220.75	2.7	5	30	0	0.8	0.9
⑤_2-2	11.9	6.21	5.59	6.71	33.53	134.14	2.7	5	30	0	0.8	0.9
⑤_2-3	8	9.31	8.38	10.06	50.27	201.10	2.7	5	30	0	0.8	0.9
⑤_2-3t	8.9	5.28	4.75	5.70	28.51	114.05	2.7	5	30	0	0.8	0.9
⑦	9.8	14.31	12.88	15.46	90.15	360.61	2.7	6	32	2	0.5	0.9
⑨	35.8	12.74	11.47	13.76	80.26	321.05	2.7	6	32	2	0.5	0.9

新窗口打开| 下载CSV

为了消除边界对基坑的影响,墙A至模型左侧边界的距离和墙D至模型右侧边界的距离均超过5倍开挖深度.围护墙和道路板采用板单元模拟.混凝土支撑采用点对点锚杆模拟.在Plaxis 2D中点对点锚杆无重度,所以未模拟立柱.钻孔灌注桩采用嵌入式梁单元模拟.混凝土的弹性模量取25 GPa,泊松比取0.2.为考虑汽车荷载、材料堆积荷载等因素的影响,在两基坑中间和基坑D右侧施加20 kPa的竖向荷载.

根据实际施工过程确定施工步:首先开挖基坑C1的第1层土,再开挖基坑D的第1层土,之后依次同步开挖两基坑的第2、第3、第4层土.由于基坑C1和基坑D为基坑群中的两个子基坑,两基坑在其第4层土开挖结束后受到了周围基坑开挖的显著影响,故本文不考虑基坑D第5层土的开挖.

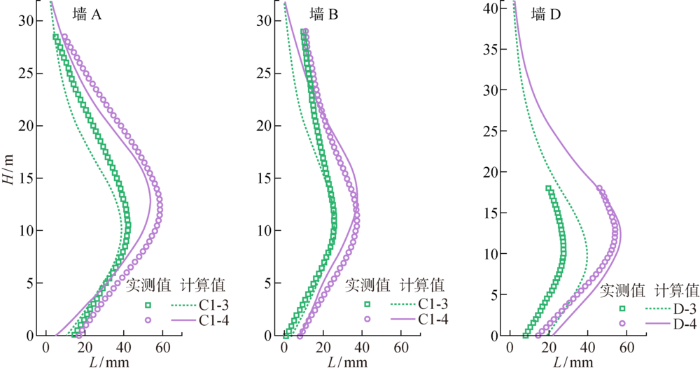
1.3 结果验证

图2所示为分别位于墙A、墙B和墙D上的3个测点的实测数据与相应数值模拟结果的对比,图中L为水平位移,C1-3表示基坑C1开挖第3层土,其余类似.由图2可以看出,数值模拟结果与实测数据整体吻合较好,验证了本文建模方法和模型参数的合理性和准确性.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 实测数据与数值模拟结果的对比

Fig.2 Comparison of measured results and numerical simulated results

2 理想模型及其变形特性

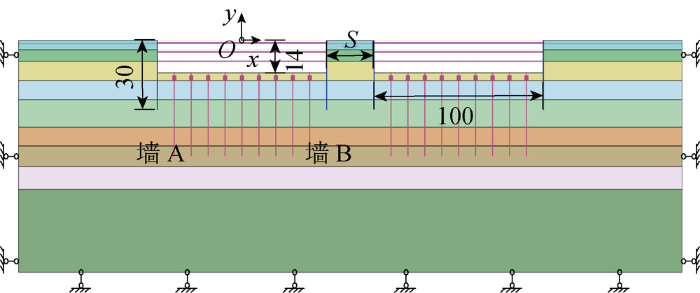
根据实际工程建立的数值模型存在许多干扰因素,因此本文以上述模型为基础,通过适当调整参数建立如图3所示的理想模型.在该模型中,两侧边界为法向约束,底部边界为全约束.左右两基坑完全相同,宽度为100 m,开挖深度H为14 m.分4层同步开挖,每层分别开挖2、4、4及4 m.设置3道支撑,3道支撑所在深度分别为1、5及9 m.围护墙深度均为30 m,厚度均为0.8 m,非相邻围护墙称为墙A,相邻围护墙称为墙B,基坑间距记为S.为了研究相邻基坑相互影响机理,本文还建立了单独开挖的基坑模型,并且通过控制围护墙界面单元摩擦角为0°,建立了不考虑墙土摩擦的基坑模型.后文中若无特别说明,分析均针对考虑墙土摩擦的情况.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 相邻基坑理想模型 (m)

Fig.3 Hypothetical models of adjacent excavations (m)

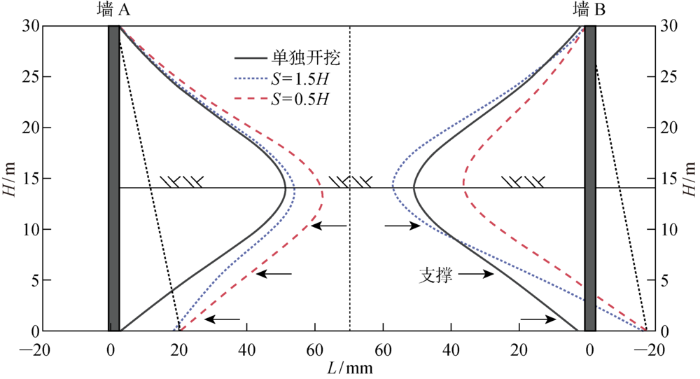
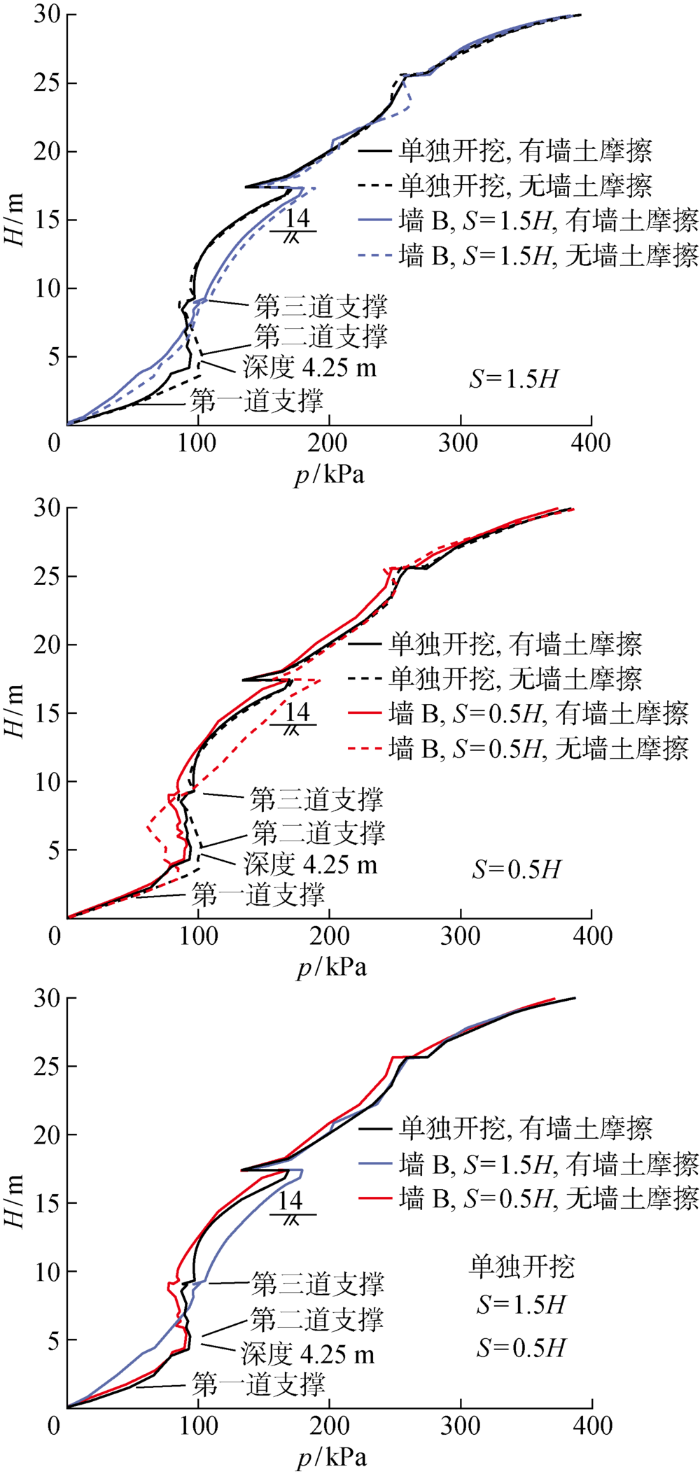
Zhang等^[10]认为同步实施的相邻基坑不存在相互影响的临界间距约为1.7H,陈小雨等^[2]则认为土压力的临界间距约为2H,墙体变形的临界间距约为3H.基于此,本文选取单独开挖、S=1.5H和S=0.5H 共3个代表工况分析基坑的受力变形特性.图4所示为开挖至坑底时围护墙的水平位移,规定向基坑内的变形为正,向基坑外的变形为负.当S=1.5H时,墙A和墙B的水平位移最大值均大于单独开挖时的水平位移最大值,墙A顶部向基坑内移动,墙B顶部向基坑外移动,从基坑变形的角度看,两基坑向中间倾斜.当S=0.5H时,墙A的水平位移最大值进一步增大,而墙B的水平位移最大值减小,并且小于单独开挖时的水平位移最大值,两墙的墙顶位移与S=1.5H时的墙顶位移大致相同.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 围护墙水平位移

Fig.4 Horizontal displacement of lateral walls

3 相邻基坑相互作用机理

3.1 土压力分布

图5所示为3个代表工况下围护墙所受土压力p的分布图.由图5(a)可知,在考虑墙土摩擦的情况下,单独开挖时,围护墙所受土压力呈R型分布.当S=1.5H时,与单独开挖相比,墙B上部所受土压力减小,开挖面附近所受土压力增大,土压力分布由R型分布向线性分布发展.在不考虑墙土摩擦的情况下,单独开挖和S=1.5H时的土压力均大于相应的考虑墙土摩擦时的土压力.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 单独开挖,S=1.5H及S=0.5H时围护墙所受土压力分布

Fig.5 Distribution of lateral earth pressure against walls for independent excavation, S=1.5H and S=0.5H

由图5(b)可知,当S=0.5H时,在考虑墙土摩擦的情况下,土压力并没有进一步向线性分布发展,而是回到R型分布.在不考虑墙土摩擦的情况下,墙B上部所受土压力减小,开挖面附近所受土压力增大.

图5(c)为在考虑墙土摩擦时单独开挖、S=1.5H和S=0.5H的土压力对比.可见,随着基坑间距的减小,土压力分布先由R型分布向线性分布发展,再回到R型分布.

3.2 土拱效应对土压力的影响

土拱效应是影响土压力大小和分布的重要因素.文献[11]认为土拱效应是土工试验中最普遍的现象之一.基坑围护墙后也存在土拱效应.当围护墙由静止状态向主动极限状态发展时,墙后土体相对于围护墙和滑裂面向下运动,墙土摩擦角和土体内摩擦角的发挥导致应力重分布^{[12⇓⇓-15]}.此外,Hashash等^[16]发现,对于设置内支撑的柔性围护结构,墙体的不均匀变形和围护墙侧向刚度的变化,被支撑土体和其下方土体之间也存在土拱效应,支撑下方土体的部分应力会转移至被支撑土体.因此,单独开挖时围护墙所受土压力呈R型分布.对于围护结构为柔性的相邻基坑,在坑间土体中会出现两种土拱效应的叠加.

当S=1.5H时,与单独开挖相比,作用在墙B上的土体宽度减小,导致土层之间的摩擦力减小,由墙体不均匀变形引起的土拱效应减弱,被支撑土体和开挖面附近土体之间的土压力转移减弱,所以土压力趋近于呈线性分布.在考虑墙土摩擦的情况下,土体中的部分应力向墙体转移,因此单独开挖和S=1.5H时的土压力均小于相应的不考虑墙土摩擦时的土压力.

当S=0.5H时,土体宽度进一步减小,由墙体不均匀变形引起的土拱效应进一步减弱,墙B上部向坑外的位移对土压力的影响越来越大,因此墙B上部所受土压力并未减小,反而因承受被动土压力而增大.在考虑墙土摩擦的情况下,由于基坑间距减小,坑间地表沉降增大,由墙土摩擦引起的土拱效应增强,所以开挖面附近墙B所受土压力减小,而当不考虑墙土摩擦时,墙B在开挖面附近所受的土压力增大.

3.3 主应力旋转

对于由墙土摩擦引起的土拱效应,Handy^[17]提出了小主应力拱迹线理论,墙后土体的应力状态可用图6(a)所示的莫尔圆表示.图中,σ₁为大主应力,σ₃为小主应力,τ为切应力,σ_h为水平正应力,σ_v为竖向正应力,δ为墙土摩擦角,θ为大主应力与水平方向的夹角.由此可知小主应力迹线为一条向下弯曲的曲线.对于由墙体不均匀变形引起的土拱效应,根据Handy^[17]的小主应力拱迹线理论,最后一道支撑处土体的应力状态可用图6(b)所示的莫尔圆表示.图中,γ为土体内摩擦角,ε为小主应力与竖直方向的夹角.由此可知大主应力迹线为一条凸向坑外稳定土体的曲线.因此,主应力旋转角能够直接反映土拱效应的变化.在最后一道支撑附近,上下土层之间发生土压力转移,主应力旋转明显,因此选择9 m深度处观察坑间土体主应力旋转角的变化,如图7所示.图中,D为点到墙B的距离,λ为主应力旋转角,规定主应力顺时针旋转为正,逆时针旋转为负.由于主应力旋转角成中心对称,所以只取D=(0~0.5)S进行分析.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 主应力迹线和莫尔圆

Fig.6 Major principal stress traces and Mohr’s circles

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 坑间土体9 m深处主应力旋转角

Fig.7 Rotation angles of principal stress in confined soil at a depth of 9 m

在考虑墙土摩擦的情况下,当S=1.5H时,紧靠墙B处墙土摩擦导致主应力顺时针旋转,主应力旋转角为正值;随着D的增大,墙土摩擦作用减弱,土层之间的摩擦作用导致主应力逆时针旋转,因此在0.1S范围内,主应力旋转角强烈变化,由正值变为负值;在0.1S~0.5S范围内,随着D的进一步增大,上下土层之间的摩擦作用逐渐减弱,主应力旋转角逐渐减小为0°.S=0.5H时,由墙土摩擦引起的土拱效应较强,主应力旋转角主要为正值且大致成线性变化.不考虑墙土摩擦的情况下, S=1.5H和S=0.5H时,紧靠墙B处主应力旋转角明显减小,而S=0.5H时主应力旋转角依然为正,可能是因为受上部土体大主应力为水平方向(90°)的影响.

4 基坑间距影响分析

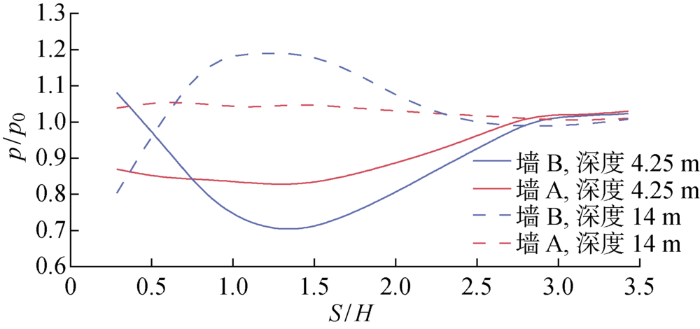
建立多个不同间距的相邻基坑模型,研究基坑间距对基坑受力变形的影响.4.25 m位于第一道支撑和第二道支撑之间且靠近第二道支撑(见图5),14 m 为最终开挖面所在的深度.取两处作为典型深度研究墙A和墙B所受土压力随间距的变化,如图8所示,图中p₀为单独开挖时的土压力.可知,随着基坑间距的减小,墙B在4.25 m深度处所受的土压力先减小后增大,在 14 m 深度处所受的土压力先增大后减小.由墙体不均匀变形引起的土拱效应的减弱和由墙土摩擦引起的土拱效应的增强导致了墙B在两典型深度处所受土压力的变化.随着基坑间距的减小,墙A在4.25 m深度处所受的土压力略有增大,在14 m深度处所受的土压力先减小后略有增大,墙A所受土压力的变化则是两墙变形协调的结果.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 典型深度处土压力随基坑间距的变化

Fig.8 Variation of lateral earth pressure with spacings at typical depths

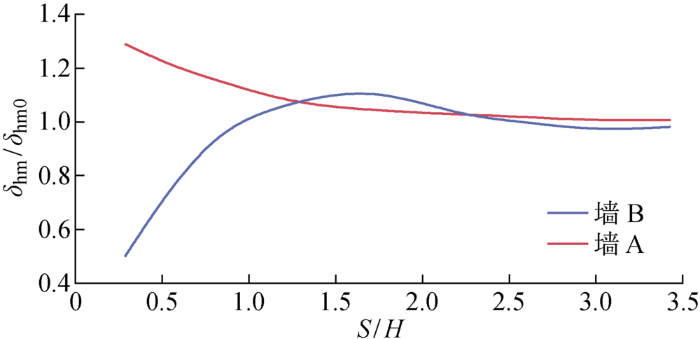
图9所示为水平位移最大值随间距的变化,图中δ_hm为不同间距下的水平位移最大值,δ_hm0为单独开挖时的水平位移最大值.可知,随着基坑间距减小,墙B的水平位移最大值先增大后减小,墙A的水平位移最大值不断增大.两墙水平位移最大值的变化规律与其在14 m深度处所受土压力的变化规律基本一致.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 水平位移最大值随基坑间距的变化

Fig.9 Variation of maximum horizontal displacement with excavation spacings

可将变化曲线大致划分为3部分:当S≥2.5H时,墙A和墙B水平位移最大值基本不变;当1.0H≤S<2.5H时,两墙水平位移最大值均大于单独开挖时的水平位移最大值,但变化量较小;当S<1.0H时,水平位移最大值发生显著变化,并且与单独开挖相比,墙A水平位移最大值增大,墙B水平位移最大值减小.

5 结论

本文依托实际工程,采用数值模拟的方法,得到了同步实施的相邻基坑的受力变形特性,揭示了相邻基坑相互作用机理,研究了基坑间距对基坑受力变形的影响规律,得出以下主要结论.

(1) 坑间土体中存在两种土拱效应,一种是由墙体不均匀变形引起的土拱效应,另一种是由墙土摩擦引起的土拱效应,两者共同影响作用在围护墙上的土压力.随着基坑间距的减小,由墙体不均匀变形引起的土拱效应减弱,导致开挖面附近土体向被支撑土体的土压力转移减弱.由墙土摩擦引起的土拱效应增强,导致作用在相邻围护墙上的土压力减小.

(2) 在两种土拱效应的作用下,随着基坑间距的减小,作用在相邻墙体上的土压力先由R型分布向线性分布发展,再向R型分布发展.非相邻墙体水平位移最大值增大,相邻墙体水平位移最大值先增大后减小,两基坑向中间倾斜.

(3) 水平位移最大值随基坑间距的变化可以分为3部分:当S≥2.5H时,相邻和非相邻墙体的水平位移最大值基本不变;当1.0H≤S<2.5H时,与单独开挖相比,两墙水平位移最大值均增大,但变化量较小;当S<1.0H时,水平位移最大值发生显著变化,并且与单独开挖相比,非相邻墙体水平位移最大值增大,相邻墙体水平位移最大值减小.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

岳树桥, 左人宇, 陆钊.

相邻基坑有限宽度土条主动土压力的计算

[J]. 岩土力学, 2016, 37(7): 2063-2069.

[本文引用: 1]

YUE

Shuqiao

, ZUO

Renyu

, LU

Zhao

A method for calculating active earth pressure of soil piece with a finite width between adjacent foundation pits

[J]. Rock and Soil Mechanics, 2016, 37(7): 2063-2069.

[本文引用: 1]

[2]

陈小雨, 袁静, 胡敏云, 等.

相邻深大基坑安全距离理论分析与数值模拟

[J]. 地下空间与工程学报, 2019, 15(5): 1557-1564.

[本文引用: 2]

CHEN

Xiaoyu

, YUAN

Jing

, HU

Minyun

, et al.

Theoretical analysis and numerical simulation of safe distance of adjacent deep foundation pits

[J]. Chinese Journal of Underground Space and Engineering, 2019, 15(5): 1557-1564.

[本文引用: 2]

[3]

ZENG

F Y

, ZHANG

Z J

, WANG

J H

, et al.

Observed performance of two adjacent and concurrently excavated deep foundation pits in soft clay

[J]. Journal of Performance of Constructed Facilities, 2018, 32(4): 04018040.

DOI:10.1061/(ASCE)CF.1943-5509.0001184 URL [本文引用: 3]

[4]

李成巍, 李伟, 梁志荣.

软土地区隧道两侧深基坑同步施工设计与分析

[J]. 地下空间与工程学报, 2018, 14(Sup.1): 193-199.

[本文引用: 1]

Chengwei

, LI

Wei

, LIANG

Zhirong

Design and analysis on synchronous construction of deep foundation pit on both sides of tunnels in soft soils

[J]. Chinese Journal of Underground Space and Engineering, 2018, 14(Sup.1): 193-199.

[本文引用: 1]

[5]

李明广.

基坑群中相邻围护结构受力变形特性研究[D]. 上海: 上海交通大学, 2016.

[本文引用: 1]

Mingguang

Deformation behavior of adjacent retaining walls in group excavation[D]. Shanghai: Shanghai Jiao Tong University, 2016.

[本文引用: 1]

[6]

叶建峰, 林海, 颜桂云.

相邻双基坑开挖失效机理及破坏模式分析

[J]. 工业建筑, 2017, 47(2): 105-112.

[本文引用: 1]

Jianfeng

, LIN

Hai

, YAN

Guiyun

Analysis on failure mechanism and failure mode of adjacent twin excavations

[J]. Industrial Construction, 2017, 47(2): 105-112.

[本文引用: 1]

[7]

C W W

, ZHENG

, NI

J J

, et al.

Use of unsaturated small-strain soil stiffness to the design of wall deflection and ground movement adjacent to deep excavation

[J]. Computers and Geotechnics, 2020, 119: 103375.

DOI:10.1016/j.compgeo.2019.103375 URL [本文引用: 1]

[8]

LIKITLERSUANG

, SURARAK

, WANATOWSKI

, et al.

Finite element analysis of a deep excavation: A case study from the Bangkok MRT

[J]. Soils and Foundations, 2013, 53(5): 756-773.

DOI:10.1016/j.sandf.2013.08.013 URL [本文引用: 1]

[9]

张娇.

上海软土小应变特性及其在基坑工程中的应用[D]. 上海: 同济大学, 2017.

[本文引用: 1]

ZHANG

Jiao

Small strain stiffness properties of Shanghai soft soils and application in deep excavations[D]. Shanghai: Tongji University, 2017.

[本文引用: 1]

[10]

ZHANG

Z J

, LI

M G

, CHEN

J J

, et al.

Innovative construction method for oversized excavations with bipartition walls

[J]. Journal of Construction Engineering and Management, 2017, 143(8): 04017056.

DOI:10.1061/(ASCE)CO.1943-7862.0001357 URL [本文引用: 1]

[11]

KARL

Theoretical Soil Mechanics

[M]. Hoboken, NJ, USA: John Wiley & Sons, Inc., 1943.

[本文引用: 1]

[12]

PATEL

, DEB

Study of active earth pressure behind a vertical retaining wall subjected to rotation about the base

[J]. International Journal of Geomechanics, 2020, 20(4): 04020028.

DOI:10.1061/(ASCE)GM.1943-5622.0001639 URL [本文引用: 1]

[13]

CHEN

J J

, LI

M G

, WANG

J H

Active earth pressure against rigid retaining walls subjected to confined cohesionless soil

[J]. International Journal of Geomechanics, 2017, 17(6): 06016041.

DOI:10.1061/(ASCE)GM.1943-5622.0000855 URL [本文引用: 1]

[14]

M G

, CHEN

J J

, WANG

J H

Arching effect on lateral pressure of confined granular material: Numerical and theoretical analysis

[J]. Granular Matter, 2017, 19(2): 1-11.

DOI:10.1007/s10035-016-0682-5 URL [本文引用: 1]

[15]

RAO

P P

, CHEN

Q S

, ZHOU

Y T

, et al.

Determination of active earth pressure on rigid retaining wall considering arching effect in cohesive backfill soil

[J]. International Journal of Geomechanics, 2016, 16(3): 04015082.

DOI:10.1061/(ASCE)GM.1943-5622.0000589 URL [本文引用: 1]

[16]

HASHASH

Y M A

, WHITTLE

A J

Mechanisms of load transfer and arching for braced excavations in clay

[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(3): 187-197.

DOI:10.1061/(ASCE)1090-0241(2002)128:3(187) URL [本文引用: 1]

[17]

HANDY

R L

The arch in soil arching

[J]. Journal of Geotechnical Engineering, 1985, 111(3): 302-318.

DOI:10.1061/(ASCE)0733-9410(1985)111:3(302) URL [本文引用: 2]

相邻基坑有限宽度土条主动土压力的计算

2016

... 理论研究方面,岳树桥等^[1]采用薄层单元法,推导了相邻基坑间有限宽度土体的主动土压力计算公式.陈小雨等^[2]根据极限平衡理论,得到了相邻基坑相互影响的临界间距表达式.现场实测方面,Zeng等^[3]根据监测数据,对相邻基坑的围护墙水平位移、墙顶垂直位移及地表沉降等变形特性进行了研究.李成巍等^[4]则提出了相邻基坑同步实施的总体思路和技术措施,并通过实测数据验证了方法的可行性和有效性.数值分析方面,李明广^[5]重点关注开挖方式和基坑间距等因素对相邻基坑的影响.叶建峰等^[6]对相邻基坑的失效机理和破坏模式进行了分析.尽管许多学者从多种角度对同步实施的相邻基坑展开了研究,但相邻基坑的相互作用机理尚不清晰,阻碍了工程实践的发展. ...

相邻基坑有限宽度土条主动土压力的计算

2016

相邻深大基坑安全距离理论分析与数值模拟

2019

... Zhang等^[10]认为同步实施的相邻基坑不存在相互影响的临界间距约为1.7H,陈小雨等^[2]则认为土压力的临界间距约为2H,墙体变形的临界间距约为3H.基于此,本文选取单独开挖、S=1.5H和S=0.5H 共3个代表工况分析基坑的受力变形特性.图4所示为开挖至坑底时围护墙的水平位移,规定向基坑内的变形为正,向基坑外的变形为负.当S=1.5H时,墙A和墙B的水平位移最大值均大于单独开挖时的水平位移最大值,墙A顶部向基坑内移动,墙B顶部向基坑外移动,从基坑变形的角度看,两基坑向中间倾斜.当S=0.5H时,墙A的水平位移最大值进一步增大,而墙B的水平位移最大值减小,并且小于单独开挖时的水平位移最大值,两墙的墙顶位移与S=1.5H时的墙顶位移大致相同. ...

相邻深大基坑安全距离理论分析与数值模拟

2019

Observed performance of two adjacent and concurrently excavated deep foundation pits in soft clay

2018

... 在上海世界博览会B片区地下空间工程中,基坑C1和基坑D被一条道路分隔而形成相邻基坑,剖面如图1所示.基坑C1的开挖深度H为15.45 m,其地下连续墙长31.9 m,厚0.8 m;基坑D的开挖深度为18.50 m,其地下连续墙长40.9 m,厚1 m.基坑C1和基坑D分别设置3道和4道钢筋混凝土支撑,并分4层和5层开挖.两基坑几乎同步实施,并在基坑开挖前中间道路的施工已完成.Zeng等^[3]对该工程进行了详细报道,本文不再赘述. ...

... 基坑形状较为规则且实测数据表明可以将该基坑简化为平面应变模型^[3],因此本文采用有限元软件Plaxis 2D进行数值模拟.考虑土体的小应变特性可以较好地模拟基坑开挖引起的墙体变形和地表沉降^[7-8],故本构模型采用先进的HSS模型,从而更好地模拟墙土相互作用,并且研究土拱效应.根据地勘报告,结合张娇^[9]总结的上海典型土层HSS模型参数的取值方法确定土层的HSS模型参数,如表1所示.表中,E_s为压缩模量,

E_{o e d}^{r e f}

为固结试验的参考切线模量,

E_{50}^{r e f}

为三轴排水剪切试验的参考割线模量,

E_{u r}^{r e f}

为三轴排水剪切试验的参考卸载再加载模量,

G_{0}^{r e f}

为小应变刚度试验的参考初始模量,γ_0.7为割线切变模量衰减到初始切变模量70%时所对应的切应变,c'为有效黏聚力,φ'为有效内摩擦角,ψ为剪胀角,m为幂指数,R_f为破坏比. ...

软土地区隧道两侧深基坑同步施工设计与分析

2018

软土地区隧道两侧深基坑同步施工设计与分析

2018

2016

相邻双基坑开挖失效机理及破坏模式分析

2017

相邻双基坑开挖失效机理及破坏模式分析

2017

Use of unsaturated small-strain soil stiffness to the design of wall deflection and ground movement adjacent to deep excavation

2020

E_{o e d}^{r e f}

为固结试验的参考切线模量,

E_{50}^{r e f}

为三轴排水剪切试验的参考割线模量,

E_{u r}^{r e f}

为三轴排水剪切试验的参考卸载再加载模量,

G_{0}^{r e f}

Finite element analysis of a deep excavation: A case study from the Bangkok MRT

2013

E_{o e d}^{r e f}

为固结试验的参考切线模量,

E_{50}^{r e f}

为三轴排水剪切试验的参考割线模量,

E_{u r}^{r e f}

为三轴排水剪切试验的参考卸载再加载模量,

G_{0}^{r e f}

2017

E_{o e d}^{r e f}

为固结试验的参考切线模量,

E_{50}^{r e f}

为三轴排水剪切试验的参考割线模量,

E_{u r}^{r e f}

为三轴排水剪切试验的参考卸载再加载模量,

G_{0}^{r e f}

2017

E_{o e d}^{r e f}

为固结试验的参考切线模量,

E_{50}^{r e f}

为三轴排水剪切试验的参考割线模量,

E_{u r}^{r e f}

为三轴排水剪切试验的参考卸载再加载模量,

G_{0}^{r e f}

Innovative construction method for oversized excavations with bipartition walls

2017

Theoretical Soil Mechanics

1943

... 土拱效应是影响土压力大小和分布的重要因素.文献[11]认为土拱效应是土工试验中最普遍的现象之一.基坑围护墙后也存在土拱效应.当围护墙由静止状态向主动极限状态发展时,墙后土体相对于围护墙和滑裂面向下运动,墙土摩擦角和土体内摩擦角的发挥导致应力重分布^{[12⇓⇓-15]}.此外,Hashash等^[16]发现,对于设置内支撑的柔性围护结构,墙体的不均匀变形和围护墙侧向刚度的变化,被支撑土体和其下方土体之间也存在土拱效应,支撑下方土体的部分应力会转移至被支撑土体.因此,单独开挖时围护墙所受土压力呈R型分布.对于围护结构为柔性的相邻基坑,在坑间土体中会出现两种土拱效应的叠加. ...

Study of active earth pressure behind a vertical retaining wall subjected to rotation about the base

2020

Active earth pressure against rigid retaining walls subjected to confined cohesionless soil

2017

Arching effect on lateral pressure of confined granular material: Numerical and theoretical analysis

2017

Determination of active earth pressure on rigid retaining wall considering arching effect in cohesive backfill soil

2016

Mechanisms of load transfer and arching for braced excavations in clay

2002

The arch in soil arching

1985

... 对于由墙土摩擦引起的土拱效应,Handy^[17]提出了小主应力拱迹线理论,墙后土体的应力状态可用图6(a)所示的莫尔圆表示.图中,σ₁为大主应力,σ₃为小主应力,τ为切应力,σ_h为水平正应力,σ_v为竖向正应力,δ为墙土摩擦角,θ为大主应力与水平方向的夹角.由此可知小主应力迹线为一条向下弯曲的曲线.对于由墙体不均匀变形引起的土拱效应,根据Handy^[17]的小主应力拱迹线理论,最后一道支撑处土体的应力状态可用图6(b)所示的莫尔圆表示.图中,γ为土体内摩擦角,ε为小主应力与竖直方向的夹角.由此可知大主应力迹线为一条凸向坑外稳定土体的曲线.因此,主应力旋转角能够直接反映土拱效应的变化.在最后一道支撑附近,上下土层之间发生土压力转移,主应力旋转明显,因此选择9 m深度处观察坑间土体主应力旋转角的变化,如图7所示.图中,D为点到墙B的距离,λ为主应力旋转角,规定主应力顺时针旋转为正,逆时针旋转为负.由于主应力旋转角成中心对称,所以只取D=(0~0.5)S进行分析. ...

... [17]的小主应力拱迹线理论,最后一道支撑处土体的应力状态可用图6(b)所示的莫尔圆表示.图中,γ为土体内摩擦角,ε为小主应力与竖直方向的夹角.由此可知大主应力迹线为一条凸向坑外稳定土体的曲线.因此,主应力旋转角能够直接反映土拱效应的变化.在最后一道支撑附近,上下土层之间发生土压力转移,主应力旋转明显,因此选择9 m深度处观察坑间土体主应力旋转角的变化,如图7所示.图中,D为点到墙B的距离,λ为主应力旋转角,规定主应力顺时针旋转为正,逆时针旋转为负.由于主应力旋转角成中心对称,所以只取D=(0~0.5)S进行分析. ...

〈

〉