成层广义Gibson地基中桩的水平动力响应

doi:10.16183/j.cnki.jsjtu.2020.382

成层广义Gibson地基中桩的水平动力响应

邱杰凯, 丁肇伟, 宋春雨^,, 陈龙珠

上海交通大学船舶海洋与建筑工程学院,上海 200240

Horizontal Dynamic Response of Pile Based on Layered Generalized Gibson Foundation

QIU Jiekai, DING Zhaowei, SONG Chunyu^,, CHEN Longzhu

School of Navy Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 宋春雨,女,讲师;E-mail:chysong@sjtu.edu.cn.

责任编辑: 陈晓燕

收稿日期: 2020-11-19

基金资助:

国家自然科学基金(51678361)

Received: 2020-11-19

作者简介 About authors

邱杰凯(1996-),男,四川省南充市人,硕士生,主要从事土与结构的动力相互作用.

摘要

为直接求解桩周土切变模量随深度线性变化情形下的单桩水平动力响应问题,基于成层广义Gibson地基,引入Adomian分解法,提出了一种求解非均质地基中桩水平动力响应的方法.相较于初参数法和传递矩阵法,该方法无需对非均质地基进行离散化处理.与数值方法相比,具有计算成本低、精度高和收敛速度快等优点.通过将本文方法和分层方法、均质地基解析方法、数值方法的计算结果进行对比,验证了本文方法的正确性和合理性.分析了桩底边界条件、地基土参数及桩身长细比对桩水平动力响应的影响.结果表明:在非均质地基中,桩土刚度比是影响桩水平动力响应的重要因素,随着地基土切变模量的增大,桩身水平位移幅值减小且分布趋于平缓.此外,相比于其他参数,土层泊松比和阻尼比对桩的水平动力响应影响较小.

关键词： 成层广义Gibson地基; 非均质地基; Adomian分解法; Novak薄层单元法; 水平动力响应

Abstract

In order to directly solve the horizontal dynamic response of a single pile under the condition that the shear modulus of the soil around the pile varies linearly with the depth, a method for solving the horizontal dynamic response of piles in nonhomogenous foundation is proposed based on the layered generalized Gibson foundation and the Adomian decomposition method. Compared with the initial parameter method and the transfer matrix method, the proposed method does not need to discretize the nonhomogeneous foundation. Compared with the numerical method, it has the advantages of low computational cost, high accuracy, and fast convergence speed. The correctness and rationality of this method are verified by comparing it with the calculation results of the layered method, the analytical method of homogeneous foundation, and the numerical method. The influence of boundary conditions on the pile bottom, soil parameters, and pile slenderness on the horizontal dynamic response of the pile is investigated. The result show that in nonhomogeneous foundation, the pile-soil elastic modulus ratio is an important factor affecting the horizontal dynamic response of pile. As the shear modulus of soil increases, the amplitude of horizontal displacement of the pile decreases, and the distribution tends to be gentle. In addition, compared with other parameters, Poisson’s ratio and damping ratio of soil have less influence on the horizontal dynamic response of pile.

Keywords： layered generalized Gibson foundation; nonhomogeneous foundation; Adomian decomposition method; Novak’s thin layer method; horizontal dynamic response

PDF (1931KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

邱杰凯, 丁肇伟, 宋春雨, 陈龙珠. 成层广义Gibson地基中桩的水平动力响应[J]. 上海交通大学学报（自然版）, 2022, 56(4): 431-442 doi:10.16183/j.cnki.jsjtu.2020.382

QIU Jiekai, DING Zhaowei, SONG Chunyu, CHEN Longzhu. Horizontal Dynamic Response of Pile Based on Layered Generalized Gibson Foundation[J]. Journal of shanghai Jiaotong University, 2022, 56(4): 431-442 doi:10.16183/j.cnki.jsjtu.2020.382

桩基础是建筑工程中最为常见的基础形式之一,已有数百年的发展历史,早期工程中对桩的研究主要集中在静力学问题,直到近几十年随着海上风机、核电站等新领域的出现,桩的水平动力问题研究开始完善起来^[1,2,3].以往的研究大多将桩周土视为均质土体,但由于天然土体的沉积作用,实际工程中理想的均质地基并不存在,地基土的切变模量往往是随深度连续变化^[4],该非均质性对桩的水平动力响应有较大影响.因此,采用更接近真实地基情况的地基模型研究桩-土的水平动力问题更具有实际工程意义和应用价值.

在桩的水平动力学理论研究中,关于桩周土非均质性的研究主要集中在土层的竖向自然分层非均质性^[5,6,7,8],对由于上覆土压力、土体自重等原因引起自然土层中土体切变模量随深度连续变化的非均质性研究较少.对于自然土层内的非均质性,一种思路是用多层均质地基近似非均质地基,多见于荷载作用下地基的变形和边坡稳定问题研究^[9,10,11].值得注意的是,采用有限元模拟非均质地基时,一般需要将不同深度单元的剪切刚度设置为与深度相关,这本质上也是一种分层^[12,13].用分层方法考虑地基土的竖向非均质性时,划分层数越多,结果越接近实际情况.文献[14]在群桩的动阻抗研究中基于初参数法和传递矩阵法,采用15层均质地基近似单层广义Gibson地基,得到了较好的近似结果.但传递矩阵等解析方法需进行大量的矩阵拼装和迭代,层数过多会给计算带来极大困难,难以得到问题的封闭解,即使采用有限元方法,在单元网格划分过细时往往也存在内存不足、计算耗时严重和修正误差过大的问题.因此,在非均质地基相关问题的研究中,相较于多层均质地基,采用连续地基形式显得更为简单合理.

Gibson首先应用解析法考虑了一种土体切变模量 $G$ 随地基深度z线性变化( $G (z) = kz, k$ 为土体切变模量随深度的变化率, $k > 0$ )的地基,该地基切变模量在地表处为 $0 (G (0) = 0),$ 被称为“Gibson地基”.当地基表面切变模量不为 $0 (G (z) = G (0) + kz, k > 0)$ 并且地基土不可压缩时,该地基被称为“广义Gibson地基”^[15].靳建明等^[16]针对成层Gibson地基,基于最小势能原理和土体弹塑性假定,研究了轴向荷载作用下单桩的非线性沉降响应.邹新军等^[17,18]首先将桩周土考虑为修正Gibson地基,根据剪切位移法和桩身荷载传递函数建立桩身位移控制方程,导出了桩周土体处于理想弹性和塑性受力状态时的桩身内力位移解答,由此求得不同桩顶竖向力和转矩组合与加载顺序下的桩身承载力及其包络线.此后,又基于双层修正广义Gibson地基,考虑土体切变模量和极限摩阻力的非线性变化及桩-土的相对滑移,提出了一种预测修正广义Gibson地基中单桩极限抗扭承载力的方法.

上述对各类Gibson地基中桩的特性研究都集中于静力学问题,而未涉及对动力学问题的研究.本文针对成层广义Gibson地基,基于Novak薄层单元法和Adomian微分分解法(ADM),得到了非均质土体内桩在各种边界条件下的水平动力响应近似解.Adomian方法能很好地解决特征方程法难以求解高阶变系数微分方程的问题,无需对非均质地基进行离散化,从而不用修正离散误差,相比于数值解法,具有计算成本低、精度高和收敛速度快等优点^[19,20],并且可通过符号运算来实现^[21].通过将本文方法与分层方法、均质地基解析方法、数值方法的计算结果进行对比,验证了本文方法的正确性和合理性.最后,结合具体算例分析了桩底边界条件、地基土参数及桩身长细比对桩水平动力响应的影响.

1 计算模型

桩土计算模型如图1所示,构建成层广义Gibson地基中单桩水平振动模型,设桩土连续紧密接触,桩为线弹性材料的圆截面桩,考虑桩周土由于历史沉积等原因引起的自然分层,设土层沿埋深方向自然分为 $J$ 层, $l_{j}$ 为第 $j$ 层土厚度, $z_{j}$ 为第 $j$ 层土体内的地基深度.各层土体的切变模量随深度线性增加,满足 $G_{sj} (z_{j}) = G_{sj} (0) + k_{j} z_{j}, k_{j} > 0, G_{sj} (z_{j}) 、 k_{j}$ 分别为第j层土体内的土体切变模量、土体切变模量随深度的变化率, $G_{sj} (0)$ 为第j层土体顶面的切变模量.图1中 $U_{j} (z_{j})$ 为第 $j$ 层土体中桩身水平位移复振幅, $d_{p}$ 为桩身直径, $l$ 为桩身总长度.桩头嵌入承台中,受水平简谐力 $Q_{0} e^{i ωt}$ ( $Q_{0}$ 为荷载幅值, $ω$ 为荷载激振频率, $t$ 为时间)作用,振动过程中桩顶部转角保持不变,其中.根据Novak薄层单元法^[22],忽略单元竖向位移,则第j层内桩的单元控制微分方程为

$\begin{array}{l} E_{p} I_{p} \frac{\partial^{4}}{\partial z_{j}^{4}} u_{j} (z_{j}, t) + ρ_{p} A_{p} \frac{\partial^{2}}{\partial t^{2}} u_{j} (z_{j}, t) + \\ k_{xj}^{*} (z_{j}) u_{j} (z_{j}, t) = 0 \end{array}$

(1)

$k_{xj}^{*} (z_{j}) = π G_{s j}^{*} (0) R_{j}^{*} (1 + k_{j} z_{j} / G_{s j} (0))$

(2)

$G_{s j}^{*} (z_{j}) = G_{s j} (z_{j}) (1 + 2 i β_{s j})$

(3)

$\begin{array}{l} R_{j}^{*} = s_{j}^{2} [4 K_{1} (q_{j}) K_{1} (s_{j}) + s_{j} K_{1} (q_{j}) K_{0} (s_{j}) + \\ q_{j} K_{0} (q_{j}) K_{1} (s_{j})] / [q_{j} K_{0} (q_{j}) K_{1} (s_{j}) + \\ s_{j} K_{1} (q_{j}) K_{0} (s_{j}) + q_{j} s_{j} K_{0} (q_{j}) K_{0} (s_{j})] \\ η_{s j} = \sqrt[]{2 (1 - v_{s j}) / (1 - 2 v_{s j})} \end{array}$

(4)

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 成层广义Gibson地基中单桩水平振动模型

Fig.1 Model of lateral vibration of a single pile in layered generalized Gibson foundation

式中:E_p、I_p、A_p、ρ_p分别为桩身弹性模量、截面惯性矩、截面积及密度; $u_{j} (z_{j}, t)$ 为桩身质点的水平位移; $k_{xj}^{*} (z_{j}) 、 G_{s j}^{*} (z_{j})$ 分别为第 $j$ 层内桩周土的复动阻抗、复切变模量; $η_{s j}$ 为第 $j$ 层土体压缩波波速与剪切波波速之比; $s_{j} = i a_{0 j} / (2 \sqrt[]{1 + 2 i β_{s j}})$ 和 $q_{j} = s_{j} / η_{s j}$ 为无量纲复参数, $a_{0 j} = ω d_{p} / V_{s j} (0)$ 为第 $j$ 层的无量纲频率, $V_{s j} (0) = \sqrt[]{G_{s j} (0) / ρ_{s j}}$ 为第 $j$ 层土体剪切波波速; $K_{0} 、 K_{1}$ 表示零阶、一阶第二类修正贝塞尔函数 $; ρ_{s j}, β_{s j}, v_{s j}$ 分别为第 $j$ 层内桩周土密度、阻尼比、泊松比.

2 基于成层Gibson地基和ADM的计算方法

假设桩身运动为简谐稳态振动,桩身位移可表达为

$\begin{matrix} u_{j} (z_{j}, t) = U_{j} (z_{j}) e^{i ωt} \end{matrix}$

(5)

将式(5)代入式(1),有:

$\begin{array}{l} \begin{matrix} \frac{d^{4}}{d z_{j}^{4}} U_{j} (z_{j}) - β_{1, j} U_{j} (z_{j}) = 0 \end{matrix} \\ z_{j} \in (0, l_{j}), j = 1,2, \dots, J \end{array}$

(6)

沿埋深各层有:

$\begin{matrix} β_{1, j} = \frac{ω^{2} ρ_{p} A_{p} - k_{xj}^{*} (z_{j})}{E_{p} I_{p}} \end{matrix}$

(7)

参考文献[23]中的Adomian分解法,桩水平动力位移复振幅可以分解为无穷级数形式:

$\begin{matrix} U_{j} (z_{j}) = \sum_{n = 0} U_{j}^{[n]} (z_{j}) \end{matrix}$

(8)

式中: $U_{j}^{[n]} (z_{j})$ 为无穷级数的第 $n$ 项, $n$ 为项数.假设线性算子 $L_{j} = \frac{d^{4}}{d z_{j}^{4}},$ 代入式(6)、(8)有:

$\begin{array}{l} L_{j}^{- 1} L_{j} [U_{j} (z_{j})] = U_{j} (z_{j}) - U_{j} (0) - \frac{d U_{j} (0)}{d z_{j}} z_{j} - \\ \frac{d^{2} U_{j} (0)}{d z_{j}^{2}} \frac{z_{j}^{2}}{2} - \frac{d^{3} U_{j} (0)}{d z_{j}^{3}} \frac{z_{j}^{3}}{6} \end{array}$

(9)

$\begin{array}{l} L_{j}^{- 1} L_{j} [U_{j} (z_{j})] = L_{j}^{- 1} [β_{1, j} U_{j} (z_{j})] = \\ L_{j}^{- 1} [β_{1, j} \sum_{n = 0} U_{j}^{[n]} (z_{j})] \end{array}$

(10)

将式(10)代入式(9),有:

$\begin{array}{l} U_{j} (z_{j}) = U_{j} (0) + \frac{d U_{j} (0)}{d z_{j}} z_{j} + \frac{d^{2} U_{j} (0)}{d z_{j}^{2}} \frac{z_{j}^{2}}{2} + \\ \frac{d^{3} U_{j} (0)}{d z_{j}^{3}} \frac{z_{j}^{3}}{6} + L_{j}^{- 1} [β_{1, j} \sum_{n = 0} U_{j}^{[n]} (z_{j})] \end{array}$

(11)

式(11)的近似解可用递推形式写出:

$\begin{array}{l} U_{j}^{[0]} (z_{j}) = U_{j} (0) + \frac{d U_{j} (0)}{d z_{j}} z_{j} + \\ \frac{d^{2} U_{j} (0)}{d z_{j}^{2}} \frac{z_{j}^{2}}{2} + \frac{d^{3} U_{j} (0)}{d z_{j}^{3}} \frac{z_{j}^{3}}{6} \\ j = 1,2, \dots, J \end{array}$

(12)

$\begin{array}{l} U_{j}^{[n]} (z_{j}) = L_{j}^{- 1} [β_{1, j} U_{j}^{[n - 1]} (z_{j})] \\ j = 1,2, \dots, J \end{array}$

(13)

$U_{j} (z_{j}) = \sum_{n = 0} U_{j}^{[n]} (z_{j}) j = 1,2, \dots, J$

(14)

式中: $N$ 为分解级数.当 $n > N$ 时, $U_{j}^{[N + 1]} (z_{j})$ 为一不影响计算精度的极小值.

对如图1所示的桩土相互作用模型,设桩顶边界条件为约束转角,桩底边界条件分别考虑自由、铰支和固定3种情况,结合桩身在土层交界面的连续性条件,具体边界条件如下:

(1) 桩顶边界条件.

$\begin{matrix} \begin{array}{l} \frac{d}{d z_{1}} U_{1} (0) = 0 \\ \frac{d^{3}}{d z_{1}^{3}} U_{1} (0) = \frac{Q_{0}}{E_{p} I_{p}} \end{array}\} \end{matrix}$

(15)

(2) 桩底边界条件.

(a) 桩底自由:

$\begin{matrix} \begin{array}{l} \frac{d^{2}}{d z_{J}^{2}} U_{J} (l_{J}) = 0 \\ \frac{d^{3}}{d z_{J}^{3}} U_{J} (l_{J}) = 0 \end{array}\} \end{matrix}$

(16)

(b) 桩底铰支:

$\begin{matrix} \begin{array}{l} U_{J} (l_{J}) = 0 \\ \frac{d^{2}}{d z_{J}^{2}} U_{J} (l_{J}) = 0 \end{array}\} \end{matrix}$

(17)

$\begin{matrix} \begin{array}{l} U_{J} (l_{J}) = 0 \\ \frac{d}{d z_{J}} U_{J} (l_{J}) = 0 \end{array}\} \end{matrix}$

(18)

(3) 桩身连续条件.

$U_{j} (0) = U_{j - 1} (l_{j - 1})$

(19)

$\frac{d}{d z_{j}} U_{j} (0) = \frac{d}{d z_{j - 1}} U_{j - 1} (l_{j - 1})$

(20)

$\frac{d^{2}}{d z_{j}^{2}} U_{j} (0) = \frac{d^{2}}{d z_{j - 1}^{2}} U_{j - 1} (l_{j - 1})$

(21)

$\frac{d^{3}}{d z_{j}^{3}} U_{j} (0) = \frac{d^{3}}{d z_{j - 1}^{3}} U_{j - 1} (l_{j - 1})$

(22)

将式(15)代入式(12)、(13),有:

$\begin{matrix} U_{1}^{[0]} (z_{1}) = U_{1} (0) + \frac{M_{0}}{E_{p} I_{p}} \frac{z_{1}^{2}}{2} + \frac{Q_{0}}{E_{p} I_{p}} \frac{z_{1}^{3}}{6} \end{matrix}$

(23)

$U_{1}^{[n]} (z_{1}) = L_{1}^{- 1} [β_{1,1} U_{1}^{[n - 1]} (z_{1})]$

(24)

式中:M₀为桩顶弯矩.

将式(19)~(22)代入式(12)、(13),有:

$\begin{array}{l} U_{j}^{[0]} (z_{j}) = U_{j - 1} (l_{j - 1}) + \frac{d U_{j - 1} (l_{j - 1})}{d z_{j - 1}} z_{j} + \\ \frac{d^{2} U_{j - 1} (l_{j - 1})}{d z_{j - 1}^{2}} \frac{z_{j}^{2}}{2} + \frac{d^{3} U_{j - 1} (l_{j - 1})}{d z_{j - 1}^{3}} \frac{z_{j}^{3}}{6} \end{array}$

(25)

$\begin{array}{l} U_{j}^{[n]} (z_{j}) = L_{j}^{- 1} [β_{1, j} U_{j}^{[n - 1]} (z_{j})] \\ j = 2,3, \dots, J \end{array}$

(26)

整理递推式(23)~ (26),代入式(16)~(18)中可得:

$\begin{matrix} [\begin{array}{l} λ_{11, i} & λ_{12, i} \\ λ_{21, i} & λ_{22, i} \end{array}] [\begin{array}{l} U_{1, i} (0) \\ M_{0, i} \end{array}] = [\begin{array}{l} μ_{1, i} \\ μ_{2, i} \end{array}] \end{matrix}$

(27)

式中: $i = 1,2, 3$ 分别对应自由、铰支、固定3种桩底边界条件; $λ_{11, i} 、 λ_{12, i} 、 λ_{21, i} 、 λ_{22, i} 、 μ_{1, i} 、 μ_{2, i}$ 均为由桩、土参数决定的定值.由此可得桩顶位移复振幅、弯矩如下:

$\begin{matrix} U_{1, i} (0) = \frac{λ_{22, i} μ_{1, i} - λ_{12, i} μ_{2, i}}{λ_{22, i} λ_{11, i} - λ_{12, i} λ_{21, i}} \end{matrix}$

(28)

$M_{0, i} = \frac{- λ_{21, i} μ_{1, i} + λ_{11, i} μ_{2, i}}{λ_{22, i} λ_{11, i} - λ_{12, i} λ_{21, i}}$

(29)

3 算例对比与参数分析

通过理论推导和数值计算,得到成层广义Gibson地基中桩的水平动力位移幅值 $|U_{j} (z_{j})|,$ 根据文献[24]将水平动力位移幅值进行无量纲化,可得:

$|{\bar{U}}_{j} (z_{j})| = E_{p} d_{p} |U_{j} (z_{j})| / (500 Q_{0})$

由于篇幅所限,只针对部分边界条件做详细讨论,后续分析如不作特殊说明,边界条件均为桩头约束转角、桩底自由的情况.首先,基于单层广义Gibson地基,分析了分解级数N对结果的影响,验证了本文方法的收敛性.通过和已有文献的对比,验证本文解的合理性和正确性.最后,基于双层广义Gibson地基,分析了桩底边界条件和桩土参数对桩水平动力响应的影响.

3.1 收敛性验证

基于单层广义Gibson地基验证分解级数N对桩顶和桩底位移幅值影响,桩、土参数取值分别取值如下:d_p=0.8 m, l/d_p=10, E_p/E_s1(0)=5000, ρ_p/ρ_s1=1.25, β_s1=5%, v_s1=0.4, a₀₁=0.5,E_s1是第一层土体表面弹性模量.土层切变模量变化率 k₁=G_s1(0),计算结果如表1所示.随着分解级数N的增加,桩顶、桩底水平振动位移响应幅值逐渐收敛,不妨取一个极小精度值10^-7,当N≥7时,有:

$\begin{array}{l} ε_{0} = ||\sum_{n = 1} {\bar{U}}_{1}^{[n]} (0)| - |\sum_{n = 1} {\bar{U}}_{1}^{[n]} (0)|| \leq 10^{- 7} \\ ε_{l} = ||\sum_{n = 1} {\bar{U}}_{1}^{[n]} (l)| - |\sum_{n = 1} {\bar{U}}_{1}^{[n]} (l)|| \leq 10^{- 7} \end{array}$

式中: $ε_{0} 、 ε_{l}$ 分别为桩顶、桩底位移幅值的相邻项误差绝对值.因此,本文后续计算如无特殊说明,分解级数 $N$ 均默认取为7.对任意给定精度,当 $N$ 足够大时,均可使得计算结果满足给定精度要求.

表1 桩端水平动力位移幅值与 $N$ 的关系

Tab.1 Horizontal displacement amplitude of pile tip versus $N$

N	$\|{\bar{U}}_{1} (0)\|$	$\|{\bar{U}}_{1} (l_{1})\|$
2	0.819792340	2.708522741
3	0.575465393	0.438747062
4	0.588914776	0.094956192
5	0.589908739	0.103157714
6	0.589898262	0.103125582
7	0.589898281	0.103125562
8	0.589898281	0.103125562
9	0.589898281	0.103125562
10	0.589898281	0.103125562
11	0.589898281	0.103125562
12	0.589898281	0.103125562

新窗口打开| 下载CSV

3.2 和已有文献对比

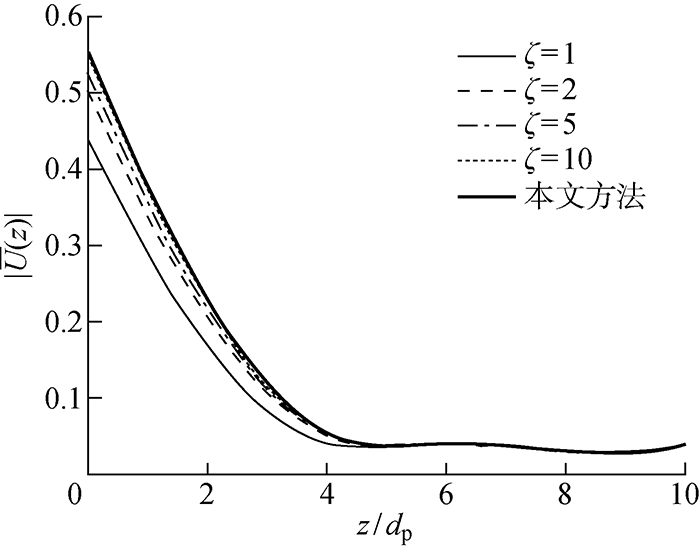
本节通过和已有文献对比,分别将本文方法的计算结果与分层方法^[14,25]、均质地基解析方法^[24]、数值方法^[12]的计算结果进行对比,从而验证本文解的正确性.首先,对单层广义Gibson地基中的桩-土水平动力问题用本文方法和分层方法进行计算比较,分层方法参考了文献[14]将广义Gibson地基近似为多层均质地基的思路,将单个自然非均质土层划分为ζ层均质土层,分层后的土层在各交界面处的位移、转角、弯矩和剪力均满足连续性条件,每个均质土层的剪切刚度取为层内均值,然后利用文献[25]的初参数法和传递矩阵法,得到单层广义Gibson地基内桩的水平动力位移响应.边界条件为桩头、桩底均自由,桩、土参数为:d_p=0.5 m, l/d_p=10, E_p/E_s1(0)=800, ρ_s1/ρ_p=0.7, β_s1=5%, v_s1=0.35, a₀₁=0.5, 土体模量随深度线性增加,底部模量是顶部的两倍.对比结果如图2所示,可以看到,随着划分层数的不断增加,采用分层方法的结果越来越接近实际的非均质情况,当划分层数足够大,可用多层均质地基近似代替非均质地基,但其计算量极大,耗时甚长,对于多层非均质地基处理起来较为困难,存在一定的局限性.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 本文方法与分层方法的结果的对比

Fig.2 Comparisons of results of the method proposed and those of layered method

令土层内的切变模量变化率k₁=0,则本文解退化为单层均质地基中桩的水平动力位移幅值解,将其与胡安峰等^[24]的解进行对比.参考文献[24]中参数,其中:d_p=0.3 m, l/d_p=10, E_p/E_s1(0)=5000, ρ_p/ρ_s1=1.25, β_s1=5%, v_s1=0.4, a₀₁=0.5.对比结果如图3所示,可以看到本文退化解与文献[24]的解吻合良好,进一步验证了本文解的合理性.

图3

新窗口打开| 下载原图ZIP| 生成PPT

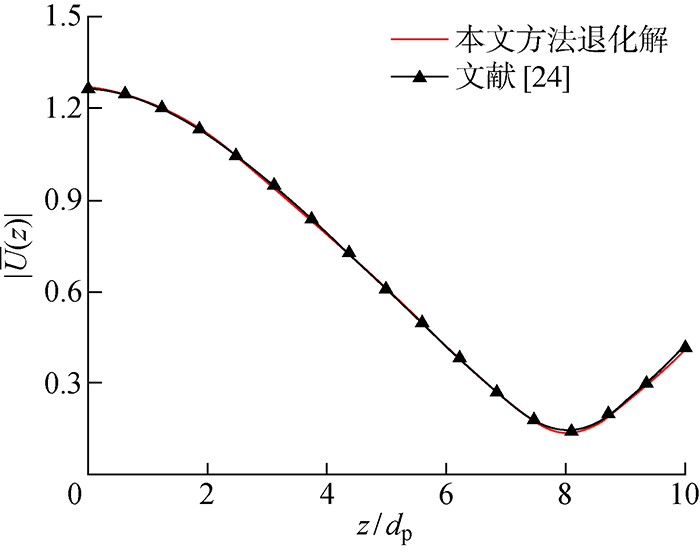
图3 本文退化解结果与均质地基中结果的对比

Fig.3 Comparisons of results of the degenerate solution proposed and those of homogeneous foundation

将本文解和基于有限元方法的数值计算结果^[12]、基于Novak相互作用模型的数值计算结果^[26]进行比较,参考文献[12]中的参数,桩、土参数取值为:d_p=0.5 m, l/d_p=15, E_p/E_s1(0)=800, ρ_s1/ρ_p=0.7, v_s1=0.4, Q₀=100 kN, 土体模量随深度线性增加,底部模量是顶部的2倍,计算得到桩顶部动阻抗为K_p=Q₀/U(0),对比结果如图4所示.随着荷载激振频率的增加,桩头动阻抗的实部和虚部也随之增大,增大到一定值时,动刚度略有下降,这与文献[12]、[16]得到的结果是一致的.

图4

新窗口打开| 下载原图ZIP| 生成PPT

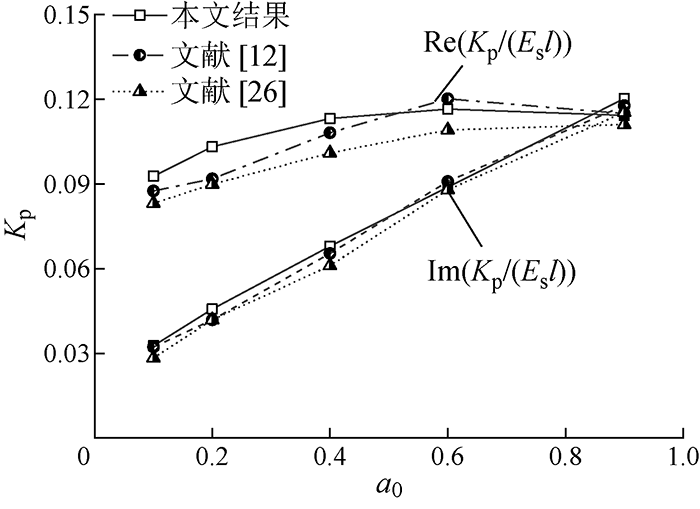
图4 本文结果与数值计算结果的对比

Fig.4 Comparisons of results of this paper and results of numerical calculation

3.3 参数分析

采用双层广义Gibson地基研究桩底边界条件、桩身参数 $(l / d)$ 和桩周土参数( $E_{s 1} (0) / E_{s 2} (0), a_{0}, ν_{s j}, β_{s j}$ 等)对桩水平动力响应的影响, $E_{s 2}$ 为第2层土体表面弹性模量.参考文献[27],设 $m_{1} = k_{1} / G_{s 1} (0), m_{2} = k_{2} / (G_{s 2} (0) - k_{2} l_{1}), m_{1} 、 m_{2}$ 将各层地基土切变模量随深度的变化率与对应的等效地表剪切刚度进行标定,当 $m_{1} = m_{2}$ 时能将多参数的问题的讨论简化为双参数问题,且广泛地近似实际地基情况,故后续均令 $m_{1} = m_{2} = m$ .设 $G_{s 1} (0) / (G_{s 2} (0) - k_{2} l_{1}) = λ, λ$ 用以区分上下土层的相对软硬情况,即上下土层切变模量比.如图5所示,保持上部土层刚度不变,则 $λ < 1$ 表示下部土层较硬; $λ > 1$ 表示下部土层较软; $λ = 1$ 时,退化为半空间单层Gibson地基情况;λ=0时,退化为下卧层为岩层的情况.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同λ下双层地基切变模量的变化

Fig.5 Variation of shear modulus of double-layers subgrade at different λ values

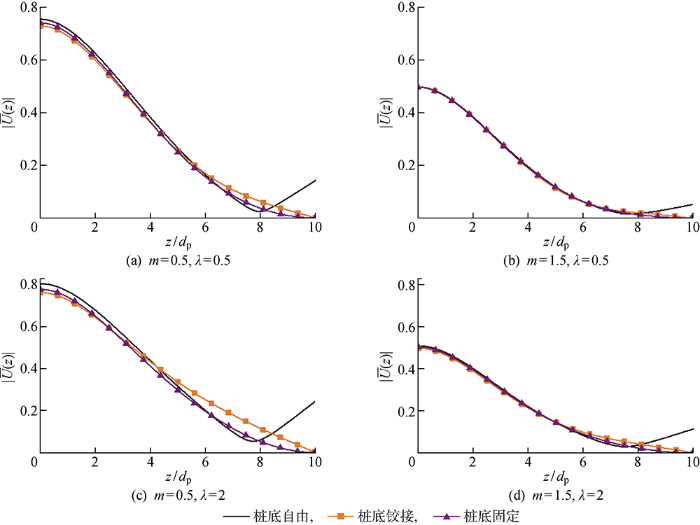
为研究在不同非均质条件下不同桩底条件对桩身水平动力位移幅值的影响,给出3种桩底边界条件下的桩水平动力位移幅值曲线,结果如图6所示.桩头均为约束转角边界条件,桩身直径d_p=0.8 m,上下土层切变模量比λ分别为0.5、2,m取为0.5、1.5.通常情况下,桩土刚度比都在 1000 甚至 10000 以上,为使结果具有代表性,桩土刚度比取为 5000.此外,如不作特殊说明,后续分析中采用的桩、土参数均为:l/d_p=10, l₁=l₂, ρ_p/ρ_s1=ρ_p/ρ_s2=1.25, β_s1=β_s2=5%, v_s1=v_s2=0.4, a₀₁=0.5.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 桩底边界条件对桩身水平位移幅值的影响

Fig.6 Influence of tip conditions on amplitude of horizontal displacement of pile

可见,桩底边界条件对桩身位移曲线的影响主要体现在桩底部的水平动力响应,3种边界条件对应的位移曲线差别明显.相比于下部土层较软(λ>1)的情况,下部土层较硬(λ<1)时位移曲线差别较小.图6反应了桩周土刚度变化对桩水平动力响应的影响.桩周土刚度越大,桩身水平动力位移幅值越小,不同边界条件对应的位移幅值曲线差别也愈小.

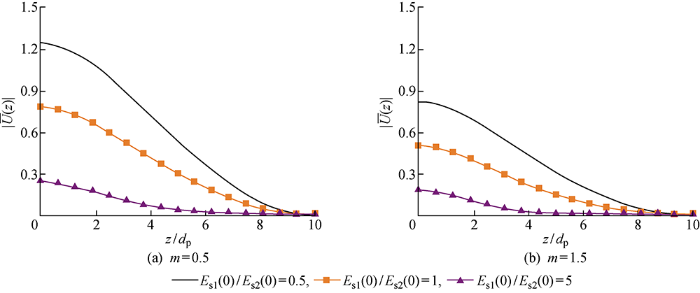
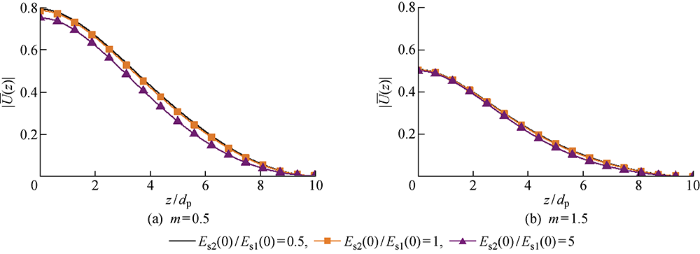
为研究上下土层土刚度比在不同非均质条件下对桩的影响,令m取为0.5、1.5,分两种情况进行讨论:① 保持桩土刚度比E_p/E_s2(0)=5000 不变,E_s1(0)/E_s2(0) 分别取为0.5、1、5,探讨上部土层性质对桩水平动力响应的影响,结果如图7所示.②保持桩土刚度比E_p/E_s1(0)=5000 不变,E_s2(0)/E_s1(0) 分别取为0.5、1、5,探讨下部土层性质对桩水平动力响应的影响,结果如图8所示.从图7、8中可以看出,表层土对桩的水平动力响应影响极为显著,随着上部土层刚度的增大,桩的水平动力位移幅值迅速减小,下部土层刚度变化对桩的水平动力响应影响和上部土层类似,但远不如上层土影响显著,图8(a)、8(b)表明,随着桩周土刚度增大,下部土层刚度对桩水平动力响应的影响愈小,表明E_p/E_s1(0)是影响桩水平动力响应的重要因素,下层土的桩土刚度比对桩的水平动力响应影响远不如上层土.可见在桩的水平动力响应中表层土起重要作用,桩的水平动力承载能力主要取决于上部土层性质.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 桩土刚度比E_p/E_s1(0)对桩身水平位移幅值的影响

Fig.7 Influence of E_p/E_s1(0) on amplitude of horizontal displacement of pile

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 桩土刚度比E_p/E_s2(0)对桩身水平位移幅值的影响

Fig.8 Influence of E_p/E_s2(0) on amplitude of horizontal displacement of pile

为研究不同荷载频率的影响,取无量纲荷载频率a₀₁为0.1、1.0,上、下土层切变模量比λ分别为0.5、2,其桩身水平动力位移幅值如图9所示.从图中可知,在土层软硬不同的情况下,保持其他条件不变,桩身水平位移响应均随无量纲频率a₀₁增大而减小,这是因为桩的惯性力与荷载作用方向相反,频率越高,惯性力越大,抵消的载荷越大,进而导致桩身水平位移响应减小.因此,低频简谐振动对桩的水平位移响应影响更显著,在设计水平动力受荷桩时,应尤其注意低频荷载的影响.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 λ不同时无量纲荷载频率对桩身水平位移幅值的影响

Fig.9 Influence of dimensionless load frequency on amplitude of horizontal displacement at different values of λ

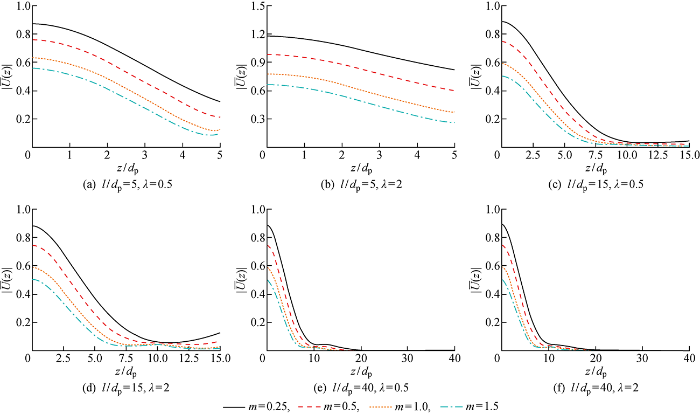
为研究桩身长细比的影响,取长细比分别为5、15、40,上下层切变模量比λ分别为0.5、2,结果如图10所示.从图中可知,中短桩的桩身长细比对桩的水平动力位移幅值影响较大,当长细比较小时(l/d_p=5),桩的相对刚度较大,可按刚性桩考虑, 桩身位移以平动和转动为主;当桩周土整体剪切刚度较大且下部土层较硬(λ<1)时,桩更容易发生转动位移,这在实际工程中需要引起注意,尤其当土体非均质性较为明显时;当下部土层较软(λ>1)时,随着长细比增加,桩周土土体复动阻抗增大,桩身水平位移幅值逐渐减小.当长细比增加到一定程度,桩的水平动力响应随深度减小,深度超过10倍桩径以后桩的水平动力响应很小且几乎无变化,下部土层表现出一定的嵌固效应.这与均质地基求解结果不同,这是因为均质地基未考虑桩周土刚度随深度增加,在桩的长细比较大时,底部依旧有较明显的动力响应^[24],这与实际是不相符的.随着长细比的进一步增大,由图10(e)、10(f)可知当桩长超过有效桩长时,桩深部的水平动力响应变得非常小,几乎可忽略不计,这与胡安峰等^[24]的临界长径比结论是一致的.图10(e)、10(f)中λ不同时,其桩身水平动力响应几乎一致,这是因为计算时图10(e)、10(f)中上部土层刚度是一致的,变化的仅是下部土层刚度,可以看到长桩的有效桩长小于上部土层厚度时,底部土层的软硬对长桩动力响应影响极小,这与前面探讨上下土层刚度影响得到的结论是一致的.因此,考虑长桩的水平动力承载能力时应更多关注有效桩长范围内的土层性质.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 λ不同时桩长细比对桩身水平位移幅值的影响

Fig.10 Influence of pile slenderness on amplitude of horizontal displacement at different values of λ

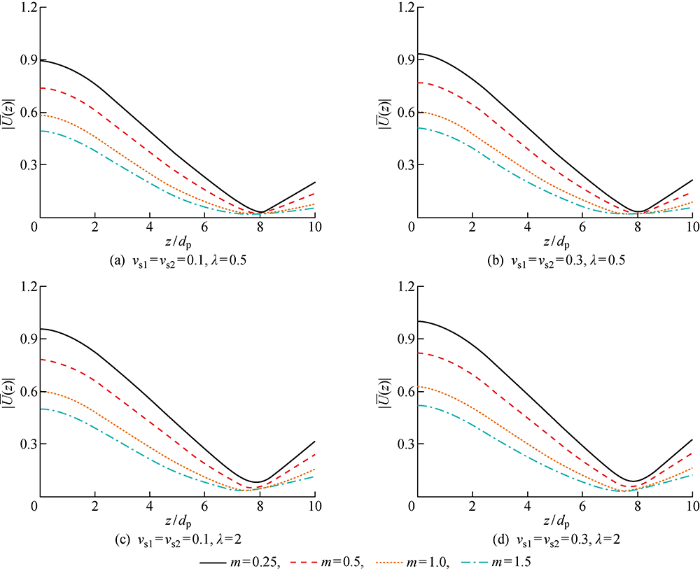
为分析土体泊松比的影响,分别取上、下土层的泊松比ν_s1、ν_s2为0.1、0.3,上、下层切变模量比λ分别为0.5、2,分析结果如图11所示.可以看出:随着土层泊松比增加,桩身水平动力位移幅值逐渐增大,这是因为泊松比跟桩周土刚度存在一定关系,泊松比增加,桩周土刚度减小,导致桩身水平动力位移幅值增加,这与实际工程是相符合的.值得指出的是,如果不考虑泊松比跟桩周土刚度的关系,直接定义桩周土剪切刚度取值而非采用地基土弹性模量换算,在理论分析中会出现随着泊松比增加,桩的水平动力位移幅值减小的情况.此外,可以看出土层泊松比的变化对桩上部的水平响应影响较大,土层泊松比对桩的位移中性点几乎无影响.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 λ不同时土体泊松比对桩身水平位移幅值的影响

Fig.11 Influence of Poisson's ratio of soil on amplitude of horizontal displacement of pile at different values of λ

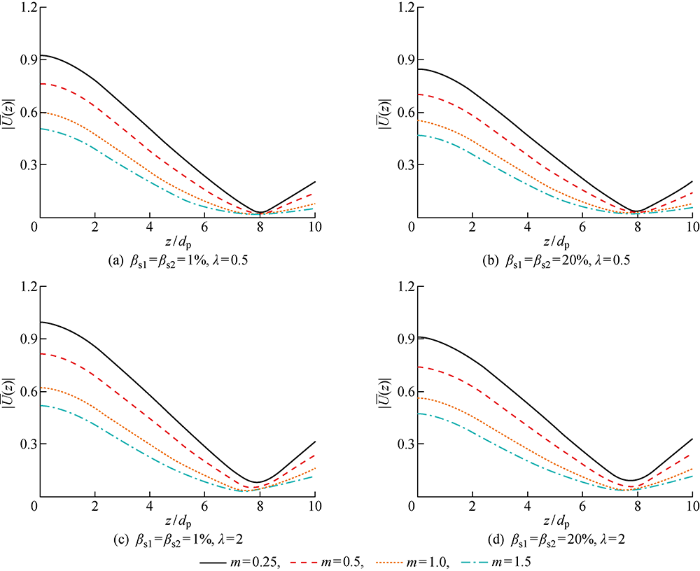
为分析土体阻尼比的影响,分别取上下土层阻尼比为0.01、0.2,分析结果如图12所示.m较小时,土体阻尼比的增加会导致桩身水平动力位移幅值减小,这是因为阻尼比增加,导致土体复动阻抗增大,桩身水平动力响应减小.与泊松比变化类似,土层阻尼比变化对桩的位移中性点几乎无影响, 阻尼比变化对桩顶部的水平动力位移幅值影响较大,因此,在实际工程中考虑桩的水平振动,需特别关注桩顶部的动力响应.综合来看,相比其他因素,土体泊松比和阻尼比对桩的水平动力响应影响较小.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 λ不同时土体阻尼比对桩身水平位移幅值的影响

Fig.12 Influence of damping ratio of soil on amplitude of horizontal displacement of pile at different values of λ

综合分析图4~10,可以看出切变模量随深度连续变化的非均质性对桩的水平动力位移幅值影响很大,即m越大,桩身水平动力位移幅值越小且分布趋于平缓,由物理意义可知,当地基模型退化为均质地基时(m=0),水平位移幅值达到最大.随着m逐渐增大,桩身位移中性点逐渐上移,上部土层承担更多荷载.故可以考虑在实际工程中可通过地基加固的方式来控制桩的水平振动幅值,避免桩产生过大位移.

分析上下土层软硬对桩的水平动力位移幅值影响,保持上部土层刚度不变,当下部土层较硬(λ<1)且m较小时,桩身水平动力位移幅值较下部土层较软(λ>1)时整体偏小,桩身位移中性点下移,下部土层承受更多的动力荷载并表现出一定的嵌固效应.需要指出的是,在上部土层剪切刚度相同情况下,下部土层剪切刚度变化对桩顶部水平动力响应影响程度跟地基土的非均质性有关,m较大时影响很小,当m较小时这种影响较为明显,这与工程实际是相符合的.

4 结论

本文基于Novak薄层单元法和Adomian分解方法,提出了一种计算竖向非均质地基中单桩水平振动的方法.与分层法相比,本方法对切变模量随深度连续变化的地基无需简化为多层均质地基求解,计算过程简单,收敛速度快,适用范围广,避免了数值方法的繁冗计算量,具有良好的收敛性和适用性.利用该计算方法详细分析了土体非均质性、上下土层软硬、桩土参数等对桩的水平振动响应影响,得到结论如下:

(1) 地基土切变模量的变化对桩的水平动力位移幅值影响很大,随着表征地基土非均质性的m值的增大,桩的水平动力位移幅值减小且分布趋于平缓,桩中性点上移,上部土层承受更多动力荷载.

(2) 双层地基中,当上部土层刚度保持一定时,下部土层较硬(λ<1)情况下的水平动力位移幅值小于下部土层较软(λ>1)情况下的位移幅值,桩位移中性点下移,下部土层承受更多的动力荷载并表现出一定的嵌固效应.其他条件保持不变时,随着荷载频率的增加,桩的水平动力响应幅值逐渐减小.在长细比较小时(l/d_p=5),桩的相对刚度较大,桩的位移以平动和转动为主.当下部土层较软时,随着长细比增加,桩周土土体复动阻抗增大,桩身水平位移幅值逐渐减小.当长细比增加到一定程度,桩的水平动力响应随深度减小,深度超过10倍桩径以后桩的水平动力响应很小且几乎无变化,下部土层表现出一定的嵌固效应.随着长细比进一步增大,当桩长超过有效桩长时,桩的水平动力响应变得非常小,几乎可忽略不计.当长桩的有效桩长小于上部土层厚度时,底部土层的软硬对长桩动力响应影响极小.因此,考虑长桩的水平动力承载能力时应更多关注有效桩长范围内的土层性质.

(3) 土性参数中,桩土相对刚度比是影响桩的水平动力响应的重要因素,下层土性质对桩水平动力响应的影响远小于表层土.因此,在设计水平动力受荷桩时,要尤其注意表层土的工程性质.

(4) 相比于其他参数,土层泊松比和阻尼比对桩的水平动力响应影响较小,且影响主要集中在桩顶部的动力响应.因此,在进行桩的水平动力分析时,需特别关注桩的顶部响应.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

ANOYATIS

, LAORA R

, LEMNITZER

Dynamic pile impedances for fixed-tip piles

[J]. Soil Dynamics and Earthquake Engineering, 2017, 97: 454-467.

DOI:10.1016/j.soildyn.2017.03.025 URL [本文引用: 1]

[2]

ANOYATIS

, LEMNITZER

Dynamic pile impedances for laterally-loaded piles using improved Tajimi and Winkler formulations

[J]. Soil Dynamics and Earthquake Engineering, 2017, 92: 279-297.

DOI:10.1016/j.soildyn.2016.09.020 URL [本文引用: 1]

[3]

KE W

, ZHANG

A closed-form solution for kinematic bending of end-bearing piles

[J]. Soil Dynamics and Earthquake Engineering, 2017, 103: 15-20.

DOI:10.1016/j.soildyn.2017.09.004 URL [本文引用: 1]

[4]

陈昌富, 汤宇, 梁冠亭.

剪切模量随深度呈指数函数增大地基中锚杆弹塑性分析

[J]. 中南大学学报(自然科学版), 2016, 47(3): 905-912.

[本文引用: 1]

CHEN

Changfu

, TANG

, LIANG

Guanting

Elastic-plastic analysis for bolts in ground with shear modulus increasing following an exponential function with depth

[J]. Journal of Central South University (Science and Technology), 2016, 47(3): 905-912.

[本文引用: 1]

[5]

, AI Z

Transient analysis of a fixed-head pile group in multi-layered transversely isotropic media due to horizontal loadings

[J]. Computers and Geotechnics, 2020, 127: 103772.

DOI:10.1016/j.compgeo.2020.103772 URL [本文引用: 1]

[6]

AI Z

, ZHAO Y

, YE

A coupling rational finite element-boundary element method for a laterally loaded pile in transversely isotropic poroelastic soils

[J]. Computers and Geotechnics, 2020, 117: 103227.

DOI:10.1016/j.compgeo.2019.103227 URL [本文引用: 1]

[7]

AI Z

, ZHAO Y

, CHENG Y

Time-dependent response of laterally loaded piles and pile groups embedded in transversely isotropic saturated viscoelastic soils

[J]. Computers and Geotechnics, 2020, 128: 103815.

DOI:10.1016/j.compgeo.2020.103815 URL [本文引用: 1]

[8]

熊辉, 江雅丰, 禹荣霞.

层状地基中基于Laplace变换的桩基横向振动阻抗计算

[J]. 岩土力学, 2018, 39(5): 1901-1907.

[本文引用: 1]

XIONG

Hui

, JIANG

Yafeng

, YU

Rongxia

Lateral vibration impedance of piles embedded in layered soil based on Laplace transform

[J]. Rock and Soil Mechanics, 2018, 39(5): 1901-1907.

[本文引用: 1]

[9]

陈云敏, 边学成.

高速铁路路基动力学研究进展

[J]. 土木工程学报, 2018, 51(6): 1-13.

[本文引用: 1]

CHEN

Yunmin

, BIAN

Xuecheng

The review of high-speed railway track foundation dynamics

[J]. China Civil Engineering Journal, 2018, 51(6): 1-13.

[本文引用: 1]

[10]

王路君, 朱斌, 文凯, 等.

层状路基路面体系温度应力和变形问题的位移函数解法

[J]. 岩石力学与工程学报, 2018, 37(7): 1691-1699.

[本文引用: 1]

WANG

Lujun

, ZHU

Bin

, WEN

Kai

, et al.

Displacement function method on thermal stress and thermal deformation problems for layered pavement structure

[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(7): 1691-1699.

[本文引用: 1]

[11]

DENG D

, LI

, ZHAO L

Stability analysis of a layered slope with failure mechanism of a composite slip surface

[J]. International Journal of Geomechanics, 2019, 19(6): 04019050.

DOI:10.1061/(ASCE)GM.1943-5622.0001417 URL [本文引用: 1]

[12]

SARKAR

, MAHESHWARI B

Effects of separation on the behavior of soil-pile interaction in liquefiable soils

[J]. International Journal of Geomechanics, 2012, 12(1): 1-13.

DOI:10.1061/(ASCE)GM.1943-5622.0000074 URL [本文引用: 5]

[13]

DI LAORA

, ROVITHIS

Kinematic bending of fixed-head piles in nonhomogeneous soil

[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015, 141(4): 04014126.

DOI:10.1061/(ASCE)GT.1943-5606.0001270 URL [本文引用: 1]

[14]

WANG

, ZHOU

, LIU W

Horizontal impedance of pile groups considering shear behavior of multilayered soils

[J]. Soils and Foundations, 2014, 54(5): 927-937.

DOI:10.1016/j.sandf.2014.09.001 URL [本文引用: 3]

[15]

AWOJOBI A

Estimation of the dynamic surface modulus of a generalized Gibson soil from the rocking frequency of rectangular foundations

[J]. Géotechnique, 1973, 23(1): 23-31.

DOI:10.1680/geot.1973.23.1.23 URL [本文引用: 1]

[16]

靳建明, 梁仕华.

成层Gibson地基中单桩沉降的非线性分析

[J]. 岩土力学, 2012, 33(6): 1857-1863.

[本文引用: 1]

JIN

Jianming

, LIANG

Shihua

Nonlinear analysis of settlement of axially loaded single pile in Gibson soil

[J]. Rock and Soil Mechanics, 2012, 33(6): 1857-1863.

[本文引用: 1]

[17]

邹新军, 夏尉桓, 王亚雄.

非均质地基中V-T联合受荷桩承载力分析

[J]. 中南大学学报(自然科学版), 2018, 49(10): 2553-2560.

[本文引用: 1]

ZOU

Xinjun

, XIA

Weihuan

, WANG

Yaxiong

Bearing capacity analysis of a single pile under combined V-T Loads in non-homogeneous subsoil

[J]. Journal of Central South University (Science and Technology), 2018, 49(10): 2553-2560.

[本文引用: 1]

[18]

ZOU X

, ZHAO L

, ZHOU

, et al.

Investigation of the torsional behaviour of circular piles in double-layered nonhomogeneous soil

[J]. Applied Ocean Research, 2020, 98: 102110.

DOI:10.1016/j.apor.2020.102110 URL [本文引用: 1]

[19]

KALIYAPPAN

, GRACE G

Solving nonlinear integral equations and nonlinear integro-differential equations using laplace adomian decomposition method through sagemath

[J]. International Journal of Advanced Research in Engineering and Technology, 2020, 11(6): 298-306.

[本文引用: 1]

[20]

TURKYILMAZOGLU

Accelerating the convergence of Adomian decomposition method (ADM)

[J]. Journal of Computational Science, 2019, 31: 54-59.

DOI:10.1016/j.jocs.2018.12.014 URL [本文引用: 1]

[21]

CHEN

, LU

An algorithm for Adomian decomposition method

[J]. Applied Mathematics and Computation, 2004, 159(1): 221-235.

DOI:10.1016/j.amc.2003.10.037 URL [本文引用: 1]

[22]

NOVAK

, ABOUL-ELLA

, NOGAMI

Dynamic soil reactions for plane strain case

[J]. Journal of the Engineering Mechanics Division, 1978, 104(4): 953-959.

DOI:10.1061/JMCEA3.0002392 URL [本文引用: 1]

[23]

丁肇伟, 宋春雨, 陈龙珠.

基于Pasternak地基模型和Adomian分解方法的扩底桩水平动力响应分析

[J]. 地震工程学报, 2019, 41(6): 1587-1596.

[本文引用: 1]

DING

Zhaowei

, SONG

Chunyu

, CHEN

Longzhu

Horizontal dynamic response of a belled pile based on the Pasternak foundation model and the Adomian decomposition method

[J]. China Earthquake Engineering Journal, 2019, 41(6): 1587-1596.

[本文引用: 1]

[24]

胡安峰, 谢康和, 肖志荣.

水平荷载下单桩动力反应分析

[J]. 浙江大学学报(工学版), 2003, 37(4): 420-425.

[本文引用: 7]

Anfeng

, XIE

Kanghe

, XIAO

Zhirong

Dynamic response analysis for a single pile subjected to lateral load ing

[J]. Journal of Zhejiang University (Engineering Science), 2003, 37(4): 420-425.

[本文引用: 7]

[25]

刘林超, 闫启方.

饱和土-管桩-刚性承台水平振动研究

[J]. 振动与冲击, 2019, 38(12): 126-132.

[本文引用: 2]

LIU

Linchao

, YAN

Qifang

A study on the lateral vibration of saturated soil-pipe pile-rigid platform

[J]. Journal of Vibration and Shock, 2019, 38(12): 126-132.

[本文引用: 2]

[26]

MAHESHWARI B

, WATANABE

Nonlinear dynamic behavior of pile foundations: Effects of separation at the soil-pile interface

[J]. Soils and Foundations, 2006, 46(4): 437-448.

DOI:10.3208/sandf.46.437 URL [本文引用: 1]

[27]

杜秦文, 王金昌, 朱向荣, 等.

双层广义Gibson地基轴对称问题求解

[J]. 岩土力学, 2007, 28(5): 933-938.

[本文引用: 1]

Qinwen

, WANG

Jinchang

, ZHU

Xiangrong

, et al.

Solutions for axisymmetric problems of double layers generalized Gibson subgrade

[J]. Rock and Soil Mechanics, 2007, 28(5): 933-938.

[本文引用: 1]

Dynamic pile impedances for fixed-tip piles

2017

... 桩基础是建筑工程中最为常见的基础形式之一,已有数百年的发展历史,早期工程中对桩的研究主要集中在静力学问题,直到近几十年随着海上风机、核电站等新领域的出现,桩的水平动力问题研究开始完善起来^[1,2,3].以往的研究大多将桩周土视为均质土体,但由于天然土体的沉积作用,实际工程中理想的均质地基并不存在,地基土的切变模量往往是随深度连续变化^[4],该非均质性对桩的水平动力响应有较大影响.因此,采用更接近真实地基情况的地基模型研究桩-土的水平动力问题更具有实际工程意义和应用价值. ...

Dynamic pile impedances for laterally-loaded piles using improved Tajimi and Winkler formulations

2017

A closed-form solution for kinematic bending of end-bearing piles

2017

剪切模量随深度呈指数函数增大地基中锚杆弹塑性分析

2016

剪切模量随深度呈指数函数增大地基中锚杆弹塑性分析

2016

Transient analysis of a fixed-head pile group in multi-layered transversely isotropic media due to horizontal loadings

2020

... 在桩的水平动力学理论研究中,关于桩周土非均质性的研究主要集中在土层的竖向自然分层非均质性^[5,6,7,8],对由于上覆土压力、土体自重等原因引起自然土层中土体切变模量随深度连续变化的非均质性研究较少.对于自然土层内的非均质性,一种思路是用多层均质地基近似非均质地基,多见于荷载作用下地基的变形和边坡稳定问题研究^[9,10,11].值得注意的是,采用有限元模拟非均质地基时,一般需要将不同深度单元的剪切刚度设置为与深度相关,这本质上也是一种分层^[12,13].用分层方法考虑地基土的竖向非均质性时,划分层数越多,结果越接近实际情况.文献[14]在群桩的动阻抗研究中基于初参数法和传递矩阵法,采用15层均质地基近似单层广义Gibson地基,得到了较好的近似结果.但传递矩阵等解析方法需进行大量的矩阵拼装和迭代,层数过多会给计算带来极大困难,难以得到问题的封闭解,即使采用有限元方法,在单元网格划分过细时往往也存在内存不足、计算耗时严重和修正误差过大的问题.因此,在非均质地基相关问题的研究中,相较于多层均质地基,采用连续地基形式显得更为简单合理. ...

A coupling rational finite element-boundary element method for a laterally loaded pile in transversely isotropic poroelastic soils

2020

Time-dependent response of laterally loaded piles and pile groups embedded in transversely isotropic saturated viscoelastic soils

2020

层状地基中基于Laplace变换的桩基横向振动阻抗计算

2018

层状地基中基于Laplace变换的桩基横向振动阻抗计算

2018

高速铁路路基动力学研究进展

2018

高速铁路路基动力学研究进展

2018

层状路基路面体系温度应力和变形问题的位移函数解法

2018

层状路基路面体系温度应力和变形问题的位移函数解法

2018

Stability analysis of a layered slope with failure mechanism of a composite slip surface

2019

Effects of separation on the behavior of soil-pile interaction in liquefiable soils

2012

... 本节通过和已有文献对比,分别将本文方法的计算结果与分层方法^[14,25]、均质地基解析方法^[24]、数值方法^[12]的计算结果进行对比,从而验证本文解的正确性.首先,对单层广义Gibson地基中的桩-土水平动力问题用本文方法和分层方法进行计算比较,分层方法参考了文献[14]将广义Gibson地基近似为多层均质地基的思路,将单个自然非均质土层划分为ζ层均质土层,分层后的土层在各交界面处的位移、转角、弯矩和剪力均满足连续性条件,每个均质土层的剪切刚度取为层内均值,然后利用文献[25]的初参数法和传递矩阵法,得到单层广义Gibson地基内桩的水平动力位移响应.边界条件为桩头、桩底均自由,桩、土参数为:d_p=0.5 m, l/d_p=10, E_p/E_s1(0)=800, ρ_s1/ρ_p=0.7, β_s1=5%, v_s1=0.35, a₀₁=0.5, 土体模量随深度线性增加,底部模量是顶部的两倍.对比结果如图2所示,可以看到,随着划分层数的不断增加,采用分层方法的结果越来越接近实际的非均质情况,当划分层数足够大,可用多层均质地基近似代替非均质地基,但其计算量极大,耗时甚长,对于多层非均质地基处理起来较为困难,存在一定的局限性. ...

... 将本文解和基于有限元方法的数值计算结果^[12]、基于Novak相互作用模型的数值计算结果^[26]进行比较,参考文献[12]中的参数,桩、土参数取值为:d_p=0.5 m, l/d_p=15, E_p/E_s1(0)=800, ρ_s1/ρ_p=0.7, v_s1=0.4, Q₀=100 kN, 土体模量随深度线性增加,底部模量是顶部的2倍,计算得到桩顶部动阻抗为K_p=Q₀/U(0),对比结果如图4所示.随着荷载激振频率的增加,桩头动阻抗的实部和虚部也随之增大,增大到一定值时,动刚度略有下降,这与文献[12]、[16]得到的结果是一致的. ...

... 进行比较,参考文献[12]中的参数,桩、土参数取值为:d_p=0.5 m, l/d_p=15, E_p/E_s1(0)=800, ρ_s1/ρ_p=0.7, v_s1=0.4, Q₀=100 kN, 土体模量随深度线性增加,底部模量是顶部的2倍,计算得到桩顶部动阻抗为K_p=Q₀/U(0),对比结果如图4所示.随着荷载激振频率的增加,桩头动阻抗的实部和虚部也随之增大,增大到一定值时,动刚度略有下降,这与文献[12]、[16]得到的结果是一致的. ...

... 所示.随着荷载激振频率的增加,桩头动阻抗的实部和虚部也随之增大,增大到一定值时,动刚度略有下降,这与文献[12]、[16]得到的结果是一致的. ...

Kinematic bending of fixed-head piles in nonhomogeneous soil

2015

Horizontal impedance of pile groups considering shear behavior of multilayered soils

2014

... 的计算结果进行对比,从而验证本文解的正确性.首先,对单层广义Gibson地基中的桩-土水平动力问题用本文方法和分层方法进行计算比较,分层方法参考了文献[14]将广义Gibson地基近似为多层均质地基的思路,将单个自然非均质土层划分为ζ层均质土层,分层后的土层在各交界面处的位移、转角、弯矩和剪力均满足连续性条件,每个均质土层的剪切刚度取为层内均值,然后利用文献[25]的初参数法和传递矩阵法,得到单层广义Gibson地基内桩的水平动力位移响应.边界条件为桩头、桩底均自由,桩、土参数为:d_p=0.5 m, l/d_p=10, E_p/E_s1(0)=800, ρ_s1/ρ_p=0.7, β_s1=5%, v_s1=0.35, a₀₁=0.5, 土体模量随深度线性增加,底部模量是顶部的两倍.对比结果如图2所示,可以看到,随着划分层数的不断增加,采用分层方法的结果越来越接近实际的非均质情况,当划分层数足够大,可用多层均质地基近似代替非均质地基,但其计算量极大,耗时甚长,对于多层非均质地基处理起来较为困难,存在一定的局限性. ...

Estimation of the dynamic surface modulus of a generalized Gibson soil from the rocking frequency of rectangular foundations

1973

... Gibson首先应用解析法考虑了一种土体切变模量

$G$

随地基深度z线性变化(

$G (z) = kz, k$

为土体切变模量随深度的变化率,

$k > 0$

)的地基,该地基切变模量在地表处为

$0 (G (0) = 0),$

被称为“Gibson地基”.当地基表面切变模量不为

$0 (G (z) = G (0) + kz, k > 0)$

并且地基土不可压缩时,该地基被称为“广义Gibson地基”^[15].靳建明等^[16]针对成层Gibson地基,基于最小势能原理和土体弹塑性假定,研究了轴向荷载作用下单桩的非线性沉降响应.邹新军等^[17,18]首先将桩周土考虑为修正Gibson地基,根据剪切位移法和桩身荷载传递函数建立桩身位移控制方程,导出了桩周土体处于理想弹性和塑性受力状态时的桩身内力位移解答,由此求得不同桩顶竖向力和转矩组合与加载顺序下的桩身承载力及其包络线.此后,又基于双层修正广义Gibson地基,考虑土体切变模量和极限摩阻力的非线性变化及桩-土的相对滑移,提出了一种预测修正广义Gibson地基中单桩极限抗扭承载力的方法. ...

成层Gibson地基中单桩沉降的非线性分析

2012

... Gibson首先应用解析法考虑了一种土体切变模量

$G$

随地基深度z线性变化(

$G (z) = kz, k$

为土体切变模量随深度的变化率,

$k > 0$

)的地基,该地基切变模量在地表处为

$0 (G (0) = 0),$

被称为“Gibson地基”.当地基表面切变模量不为

$0 (G (z) = G (0) + kz, k > 0)$

成层Gibson地基中单桩沉降的非线性分析

2012

... Gibson首先应用解析法考虑了一种土体切变模量

$G$

随地基深度z线性变化(

$G (z) = kz, k$

为土体切变模量随深度的变化率,

$k > 0$

)的地基,该地基切变模量在地表处为

$0 (G (0) = 0),$

被称为“Gibson地基”.当地基表面切变模量不为

$0 (G (z) = G (0) + kz, k > 0)$

非均质地基中V-T联合受荷桩承载力分析

2018

... Gibson首先应用解析法考虑了一种土体切变模量

$G$

随地基深度z线性变化(

$G (z) = kz, k$

为土体切变模量随深度的变化率,

$k > 0$

)的地基,该地基切变模量在地表处为

$0 (G (0) = 0),$

被称为“Gibson地基”.当地基表面切变模量不为

$0 (G (z) = G (0) + kz, k > 0)$

非均质地基中V-T联合受荷桩承载力分析

2018

... Gibson首先应用解析法考虑了一种土体切变模量

$G$

随地基深度z线性变化(

$G (z) = kz, k$

为土体切变模量随深度的变化率,

$k > 0$

)的地基,该地基切变模量在地表处为

$0 (G (0) = 0),$

被称为“Gibson地基”.当地基表面切变模量不为

$0 (G (z) = G (0) + kz, k > 0)$

Investigation of the torsional behaviour of circular piles in double-layered nonhomogeneous soil

2020

... Gibson首先应用解析法考虑了一种土体切变模量

$G$

随地基深度z线性变化(

$G (z) = kz, k$

为土体切变模量随深度的变化率,

$k > 0$

)的地基,该地基切变模量在地表处为

$0 (G (0) = 0),$

被称为“Gibson地基”.当地基表面切变模量不为

$0 (G (z) = G (0) + kz, k > 0)$

Solving nonlinear integral equations and nonlinear integro-differential equations using laplace adomian decomposition method through sagemath

2020

... 上述对各类Gibson地基中桩的特性研究都集中于静力学问题,而未涉及对动力学问题的研究.本文针对成层广义Gibson地基,基于Novak薄层单元法和Adomian微分分解法(ADM),得到了非均质土体内桩在各种边界条件下的水平动力响应近似解.Adomian方法能很好地解决特征方程法难以求解高阶变系数微分方程的问题,无需对非均质地基进行离散化,从而不用修正离散误差,相比于数值解法,具有计算成本低、精度高和收敛速度快等优点^[19,20],并且可通过符号运算来实现^[21].通过将本文方法与分层方法、均质地基解析方法、数值方法的计算结果进行对比,验证了本文方法的正确性和合理性.最后,结合具体算例分析了桩底边界条件、地基土参数及桩身长细比对桩水平动力响应的影响. ...

Accelerating the convergence of Adomian decomposition method (ADM)

2019

An algorithm for Adomian decomposition method

2004

Dynamic soil reactions for plane strain case

1978

... 桩土计算模型如图1所示,构建成层广义Gibson地基中单桩水平振动模型,设桩土连续紧密接触,桩为线弹性材料的圆截面桩,考虑桩周土由于历史沉积等原因引起的自然分层,设土层沿埋深方向自然分为

$J$

层,

$l_{j}$

为第

$j$

层土厚度,

$z_{j}$

为第

$j$

层土体内的地基深度.各层土体的切变模量随深度线性增加,满足

$G_{sj} (z_{j}) = G_{sj} (0) + k_{j} z_{j}, k_{j} > 0, G_{sj} (z_{j}) 、 k_{j}$

分别为第j层土体内的土体切变模量、土体切变模量随深度的变化率,

$G_{sj} (0)$

为第j层土体顶面的切变模量.图1中

$U_{j} (z_{j})$

为第

$j$

层土体中桩身水平位移复振幅,

$d_{p}$

为桩身直径,

$l$

为桩身总长度.桩头嵌入承台中,受水平简谐力

$Q_{0} e^{i ωt}$

(

$Q_{0}$

为荷载幅值,

$ω$

为荷载激振频率,

$t$

为时间)作用,振动过程中桩顶部转角保持不变,其中.根据Novak薄层单元法^[22],忽略单元竖向位移,则第j层内桩的单元控制微分方程为 ...

基于Pasternak地基模型和Adomian分解方法的扩底桩水平动力响应分析

2019

... 参考文献[23]中的Adomian分解法,桩水平动力位移复振幅可以分解为无穷级数形式: ...

基于Pasternak地基模型和Adomian分解方法的扩底桩水平动力响应分析

2019

... 参考文献[23]中的Adomian分解法,桩水平动力位移复振幅可以分解为无穷级数形式: ...

水平荷载下单桩动力反应分析

2003

... 通过理论推导和数值计算,得到成层广义Gibson地基中桩的水平动力位移幅值

$|U_{j} (z_{j})|,$

根据文献[24]将水平动力位移幅值进行无量纲化,可得: ...

... 令土层内的切变模量变化率k₁=0,则本文解退化为单层均质地基中桩的水平动力位移幅值解,将其与胡安峰等^[24]的解进行对比.参考文献[24]中参数,其中:d_p=0.3 m, l/d_p=10, E_p/E_s1(0)=5000, ρ_p/ρ_s1=1.25, β_s1=5%, v_s1=0.4, a₀₁=0.5.对比结果如图3所示,可以看到本文退化解与文献[24]的解吻合良好,进一步验证了本文解的合理性. ...

... 的解进行对比.参考文献[24]中参数,其中:d_p=0.3 m, l/d_p=10, E_p/E_s1(0)=5000, ρ_p/ρ_s1=1.25, β_s1=5%, v_s1=0.4, a₀₁=0.5.对比结果如图3所示,可以看到本文退化解与文献[24]的解吻合良好,进一步验证了本文解的合理性. ...

... 所示,可以看到本文退化解与文献[24]的解吻合良好,进一步验证了本文解的合理性. ...

... 为研究桩身长细比的影响,取长细比分别为5、15、40,上下层切变模量比λ分别为0.5、2,结果如图10所示.从图中可知,中短桩的桩身长细比对桩的水平动力位移幅值影响较大,当长细比较小时(l/d_p=5),桩的相对刚度较大,可按刚性桩考虑, 桩身位移以平动和转动为主;当桩周土整体剪切刚度较大且下部土层较硬(λ<1)时,桩更容易发生转动位移,这在实际工程中需要引起注意,尤其当土体非均质性较为明显时;当下部土层较软(λ>1)时,随着长细比增加,桩周土土体复动阻抗增大,桩身水平位移幅值逐渐减小.当长细比增加到一定程度,桩的水平动力响应随深度减小,深度超过10倍桩径以后桩的水平动力响应很小且几乎无变化,下部土层表现出一定的嵌固效应.这与均质地基求解结果不同,这是因为均质地基未考虑桩周土刚度随深度增加,在桩的长细比较大时,底部依旧有较明显的动力响应^[24],这与实际是不相符的.随着长细比的进一步增大,由图10(e)、10(f)可知当桩长超过有效桩长时,桩深部的水平动力响应变得非常小,几乎可忽略不计,这与胡安峰等^[24]的临界长径比结论是一致的.图10(e)、10(f)中λ不同时,其桩身水平动力响应几乎一致,这是因为计算时图10(e)、10(f)中上部土层刚度是一致的,变化的仅是下部土层刚度,可以看到长桩的有效桩长小于上部土层厚度时,底部土层的软硬对长桩动力响应影响极小,这与前面探讨上下土层刚度影响得到的结论是一致的.因此,考虑长桩的水平动力承载能力时应更多关注有效桩长范围内的土层性质. ...

... [24]的临界长径比结论是一致的.图10(e)、10(f)中λ不同时,其桩身水平动力响应几乎一致,这是因为计算时图10(e)、10(f)中上部土层刚度是一致的,变化的仅是下部土层刚度,可以看到长桩的有效桩长小于上部土层厚度时,底部土层的软硬对长桩动力响应影响极小,这与前面探讨上下土层刚度影响得到的结论是一致的.因此,考虑长桩的水平动力承载能力时应更多关注有效桩长范围内的土层性质. ...

水平荷载下单桩动力反应分析

2003

... 通过理论推导和数值计算,得到成层广义Gibson地基中桩的水平动力位移幅值

$|U_{j} (z_{j})|,$

根据文献[24]将水平动力位移幅值进行无量纲化,可得: ...

... 所示,可以看到本文退化解与文献[24]的解吻合良好,进一步验证了本文解的合理性. ...

饱和土-管桩-刚性承台水平振动研究

2019

... 层均质土层,分层后的土层在各交界面处的位移、转角、弯矩和剪力均满足连续性条件,每个均质土层的剪切刚度取为层内均值,然后利用文献[25]的初参数法和传递矩阵法,得到单层广义Gibson地基内桩的水平动力位移响应.边界条件为桩头、桩底均自由,桩、土参数为:d_p=0.5 m, l/d_p=10, E_p/E_s1(0)=800, ρ_s1/ρ_p=0.7, β_s1=5%, v_s1=0.35, a₀₁=0.5, 土体模量随深度线性增加,底部模量是顶部的两倍.对比结果如图2所示,可以看到,随着划分层数的不断增加,采用分层方法的结果越来越接近实际的非均质情况,当划分层数足够大,可用多层均质地基近似代替非均质地基,但其计算量极大,耗时甚长,对于多层非均质地基处理起来较为困难,存在一定的局限性. ...

饱和土-管桩-刚性承台水平振动研究

2019

Nonlinear dynamic behavior of pile foundations: Effects of separation at the soil-pile interface

2006

双层广义Gibson地基轴对称问题求解

2007

... 采用双层广义Gibson地基研究桩底边界条件、桩身参数

$(l / d)$

和桩周土参数(

$E_{s 1} (0) / E_{s 2} (0), a_{0}, ν_{s j}, β_{s j}$

等)对桩水平动力响应的影响,

$E_{s 2}$

为第2层土体表面弹性模量.参考文献[27],设

$m_{1} = k_{1} / G_{s 1} (0), m_{2} = k_{2} / (G_{s 2} (0) - k_{2} l_{1}), m_{1} 、 m_{2}$

将各层地基土切变模量随深度的变化率与对应的等效地表剪切刚度进行标定,当

$m_{1} = m_{2}$

时能将多参数的问题的讨论简化为双参数问题,且广泛地近似实际地基情况,故后续均令

$m_{1} = m_{2} = m$

.设

$G_{s 1} (0) / (G_{s 2} (0) - k_{2} l_{1}) = λ, λ$

用以区分上下土层的相对软硬情况,即上下土层切变模量比.如图5所示,保持上部土层刚度不变,则

$λ < 1$

表示下部土层较硬;

$λ > 1$

表示下部土层较软;

$λ = 1$

时,退化为半空间单层Gibson地基情况;λ=0时,退化为下卧层为岩层的情况. ...

双层广义Gibson地基轴对称问题求解

2007

... 采用双层广义Gibson地基研究桩底边界条件、桩身参数

$(l / d)$

和桩周土参数(

$E_{s 1} (0) / E_{s 2} (0), a_{0}, ν_{s j}, β_{s j}$

等)对桩水平动力响应的影响,

$E_{s 2}$

为第2层土体表面弹性模量.参考文献[27],设

$m_{1} = k_{1} / G_{s 1} (0), m_{2} = k_{2} / (G_{s 2} (0) - k_{2} l_{1}), m_{1} 、 m_{2}$

将各层地基土切变模量随深度的变化率与对应的等效地表剪切刚度进行标定,当

$m_{1} = m_{2}$

时能将多参数的问题的讨论简化为双参数问题,且广泛地近似实际地基情况,故后续均令

$m_{1} = m_{2} = m$

.设

$G_{s 1} (0) / (G_{s 2} (0) - k_{2} l_{1}) = λ, λ$

用以区分上下土层的相对软硬情况,即上下土层切变模量比.如图5所示,保持上部土层刚度不变,则

$λ < 1$

表示下部土层较硬;

$λ > 1$

表示下部土层较软;

$λ = 1$

时,退化为半空间单层Gibson地基情况;λ=0时,退化为下卧层为岩层的情况. ...

〈

〉