子通道程序对PSBT空泡分布实验计算的不确定性量化分析

doi:10.16183/j.cnki.jsjtu.2021.068

子通道程序对PSBT空泡分布实验计算的不确定性量化分析

张俊涛, 刘晓晶^,, 张滕飞, 柴翔

上海交通大学核科学与工程学院,上海 200240

Uncertainty Quantitative Analysis of Subchannel Code Calculation of PSBT Void Distribution Benchmark

ZHANG Juntao, LIU Xiaojing^,, ZHANG Tengfei, CHAI Xiang

School of Nuclear Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 刘晓晶,男,研究员,博士生导师,电话(Tel.):021-34207121;E-mail:xiaojingliu@sjtu.edu.cn.

责任编辑: 孙伟

收稿日期: 2021-03-3

基金资助:

国家自然科学基金(U20B2011)

Received: 2021-03-3

作者简介 About authors

张俊涛(1996-),男,河南省洛阳市人,硕士生,从事核反应堆热工水力研究.

摘要

为了评估子通道程序的准确性与可靠性,需要定量给出计算结果的不确定性.采用统计学上基于输入参数不确定性传递的方法进行不确定性分析,可以定量得到程序计算结果的不确定范围.在假设模型参数不确定性服从正态分布的基础上,采用统计学方法确定模型参数不确定性的分布以取代传统的专家判断.通过对压水堆子通道和棒束实验(PSBT)基准题空泡分布实验进行计算,分析子通道程序COBRA-IV 对实验结果的预测能力,同时得到满足容忍限的计算结果不确定性上下限.计算结果表明:评估得到的不确定带能较好地包络实验值;同时利用统计均值对模型进行标定后,可以得到比原模型更接近实验值的计算结果.

关键词： 不确定性量化; 子通道程序; 空泡份额

Abstract

In order to evaluate the accuracy and reliability of the subchannel code, it is necessary to quantitatively give the uncertainty of the calculation results. The uncertainty analysis is conducted by using the statistical method based on propagation of input uncertainties, and the uncertainty range of the subchannel code calculation results can be obtained quantitatively. Based on the assumption that the uncertainty of model parameters obeys normal distribution, the statistical method is used to determine the distribution of the uncertainty of model parameters to replace the traditional expert judgment. Through the calculation of the pressurized water reactor sub-channel and bundle tests (PSBT) benchmark, the ability of the subchannel code COBRA-IV to predict the experimental results is analyzed, and the uncertainty interval satisfying the tolerance limit of the calculation results is obtained. The results demonstrate that the experiment data is well enveloped by the obtained uncertainty bands and the model calibrated by the statistical mean value presents a good improvement of calculations.

Keywords： uncertainty quantification; subchannel code; void fraction

PDF (1810KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张俊涛, 刘晓晶, 张滕飞, 柴翔. 子通道程序对PSBT空泡分布实验计算的不确定性量化分析[J]. 上海交通大学学报, 2022, 56(10): 1420-1426 doi:10.16183/j.cnki.jsjtu.2021.068

ZHANG Juntao, LIU Xiaojing, ZHANG Tengfei, CHAI Xiang. Uncertainty Quantitative Analysis of Subchannel Code Calculation of PSBT Void Distribution Benchmark[J]. Journal of Shanghai Jiaotong University, 2022, 56(10): 1420-1426 doi:10.16183/j.cnki.jsjtu.2021.068

1989年美国发布管理导则RG 1.157^[1],允许在应急堆芯冷却系统分析中使用最佳估算程序.出于安全考虑,最佳估算程序必须与不确定性分析相结合,以判断计算与实际情况之间的差异.截至目前,国际上已有多种不同的不确定性分析方法,例如程序比例、适用性和不确定性分析方法(CSAU)^[2]、德国核安全中心方法(GRS)^[3]、基于精度外推的不确定性方法(UMAE)^[4]、先进统计学处理的不确定性方法(ASTRUM)^[5]等.这些不确定性分析方法大体可以分为两大类,一类是基于输入参数不确定性的传递,另一类是基于输出结果不确定性的外推^[6].基于输入参数不确定性传递的统计性方法的研究和应用相对更成熟和广泛,如在由经济合作与发展组织(OECD)发起的不确定性研究项目“最佳估算方法-不确定性和敏感性分析”阶段V中,14个参与者中有12个采用输入不确定性传递的方法^[7].

基于输入参数不确定性传递的方法需要知道输入参数的不确定性.然而,大多数热工水力程序都没有提供关于输入参数不确定性的足够信息,尤其是对于某些无法通过实验直接测量的输入模型参数,通常通过专家判断来进行量化.目前一些取代专家判断的评估方法被陆续提出,如比萨大学开发的基于快速傅里叶变换的方法(FFTBM)^[8],法国开发的输入参数经验确定方法(DIPE)^[8]和模型参数不确定性计算方法(CIRCÉ)^[9],韩国原子力研究院开发的通过数据同化进行模型标定方法(MCDA)^[10].李冬^[11]对CIRCÉ方法可评估参数有限和MCDA方法求解非线性问题耗时过长这两个缺点进行了改进;Xiong等^[12]开发了一种优化的最佳估算加不确定性分析方法,该方法包含了一个结构化的模型不确定性量化方法.

子通道程序已被广泛应用于堆芯热工水力分析,相较于计算流体力学(CFD),子通道分析消耗的计算资源更少,能够快速提供分析所需的热工参数.由于子通道程序对于物理模型存在一定简化假设以及数值计算误差等因素的影响,程序直接计算出的结果存在一定的不确定性,而目前针对子通道程序的不确定性分析还较少.本研究使用基于输入参数不确定性传递的统计学方法,利用期望最大化的思想来反推输入模型参数不确定性的分布,对子通道程序COBRA-IV 的计算进行不确定性量化分析.

1 不确定性量化分析方法

不确定性分析方法包括对影响计算程序结果的所有不确定性因素的确认和描述,并用统计学方法将这些不确定性因素整合得到输出结果的总体不确定性,其一般过程如图1所示.首先从众多输入参数中选取对计算结果影响较大的输入参数;其次量化这些输入模型参数的范围或不确定性分布;再次通过蒙特卡洛抽样或拉丁超立方抽样对这些输入参数进行抽样,并将这些抽样的输入参数输入子通道程序进行计算;最后对大量目标参数值进行统计,以得到输出目标参数的不确定性.其中,输入参数不确定性的确定和对输入参数进行抽样是关键步骤.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 不确定性量化分析流程

Fig.1 Process of uncertainty quantitative analysis

1.1 输入模型参数不确定性量化

在分析过程中, 认为输出不确定性y是真实值y^r与程序计算值y^c之间的误差.实际可以得到的数据是实验值y^e与对应的程序计算值y^c,两者之差可以表示为

(1)y_w=y^e-y^c=(y^e-y^r)+(y^r-y^c)=e+y

式中:e=(e_j), j=1, 2,…, J 为实验误差,其中J为样本点数.

一般来说,模型参数的不确定性分析通常要确定模型参数基准值的无量纲乘数,记为k=(k_i), i=1, 2, …, p,其中p为模型参数的个数;将待评估的模型参数不确定性记为x=(x_i), i=1, 2, …, p.一般情况下, k_i与x_i存在以下关系:

(2)

\begin{array}{l} k_{i} = 1, & x_{i} = 0 \\ k_{i} \in (0, 1), & x_{i} < 0 \\ k_{i} > 1, & x_{i} > 0 \end{array}\}

因此可以采用k_i= $e^{x_{i}}$ 来表示模型参数系数和不确定性之间的转化关系^[8].

输入模型参数不确定性x和输出不确定性y之间的传递关系可简化为

(3)y=h(x, u)

式中:u为已知分布的输入参数不确定性.一般情况下,正态分布是最常见的分布方式,因此假设x和u均服从正态分布.同时认为样本之间实验误差互相独立,实验误差满足均值为0且方差已知的正态分布,即e_j~N(0, $σ_{e x p, j}^{2}$ ).为了简化分析,认为各模型参数之间相互独立.

近似认为x与y之间为线性关系,得到

(4)y_w=S_xx+S_uu+e

式中:S_x和S_u为样本点对应待求参数的敏感性矩阵,敏感性矩阵中的偏导数可以通过有限差分法求得^[11].

当存在数据缺失问题时,期望最大化(EM)算法是极大似然估计的一种常用迭代算法.但是实际计算过程中EM算法一般迭代次数过多,收敛较慢,因此使用EM算法的改进算法,即ECME算法^[13]进行计算.

将x的均值和方差记为μ_x和C_x,即待求参数,统一记为θ={μ_x, C_x}.完整数据的似然函数表示为L(θ; x¹, x², …, x^J, y_w),简化表示为^[11]

(5)L∝

{|C_{x}|}^{- \frac{J}{2}} \overset{J}{\prod_{j = 1}}

exp

[- \frac{1}{2} (x^{j} - μ_{x})^{T} C_{x}^{- 1} (x^{j} - μ_{x})]

式中:x^j为在第j个样本点对应的输入模型参数不确定性x的取值.由于L与 ln L 同时达到最大,所以求 ln L 达到最大值的点即可.考虑第m次迭代,令μ_x= $μ_{x}^{(m - 1)}$ ,求∂ln L/∂C_x=0可以得到

(6)

C_{x}^{(m)}

\frac{1}{J} \overset{J}{\sum_{j = 1}}

(x^j-

μ_{x}^{(m - 1)}

)(x^j-

μ_{x}^{(m - 1)}

)^T

再由μ_x= $μ_{x}^{(m - 1)}$ 和C_x= $C_{x}^{(m - 1)}$ ,对似然函数求数学期望可以最终得到

(7)$\begin{aligned}\boldsymbol{C}_{x}^{(m)}=& \boldsymbol{C}_{x}^{(m-1)}+\\& \frac{1}{J}{ }_{j=1}^{{ }^{J}}\left\{\frac{\boldsymbol{C}_{x}^{(m-1)} \boldsymbol{S}_{x j}^{\mathrm{T}} \boldsymbol{S}_{x j} \boldsymbol{C}_{x}^{(m-1)}}{\boldsymbol{S}_{x j} \boldsymbol{C}_{x}^{(m-1)} \boldsymbol{S}_{x j}^{\mathrm{T}}+\boldsymbol{S}_{u j} \boldsymbol{C}_{u} \boldsymbol{S}_{u j}^{\mathrm{T}}+\sigma_{\mathrm{exp}, j}^{2}} \times\right.\\& {\left.\left[\frac{\left(y_{\mathrm{w} j}-\boldsymbol{S}_{x j} \boldsymbol{\mu}_{x}^{(m-1)}-\boldsymbol{S}_{u j} \boldsymbol{\mu}_{u}\right)^{2}}{\boldsymbol{S}_{x j} \boldsymbol{C}_{x}^{(m-1)} \boldsymbol{S}_{x j}^{\mathrm{T}}+\boldsymbol{S}_{u j} \boldsymbol{C}_{u} \boldsymbol{S}_{u j}^{\mathrm{T}}+\sigma_{\exp, j}^{2}}-1\right]\right\} }\end{aligned}$

式中:y_w_i为y_w的第j个分量.最后最大化似然函数,可以得到

(8)

\overset{J}{\sum_{j = 1}} \frac{(y_{w j} - S_{x j} μ_{x}^{(m)} - S_{u j} μ_{u}) S_{x j}}{S_{x j} C_{x}^{(m)} {S^{T}}_{x j} + S_{u j} C_{u} {S^{T}}_{u j} + σ_{e x p, j}^{2}}

在实际计算过程中,给定初值 $μ_{x}^{(0)}$ 和 $C_{x}^{(0)}$ ,通过式(7)和式(8)循环迭代,当满足给定的收敛标准时,则可求得最终结果.其中,方差C_x可以直接显式计算得到,在求μ_x时需要求解线性方程组.为了保证具有较好的数值稳定性,可以采用高斯列主元消去法.

由于以上是基于正态分布假设的,所以为了证明结果的可靠性需要进行假设检验.对残差进行检验,对于每个实验样本点,残差为

(9)r_j=

\frac{y_{w j} - S_{x j} μ_{x} - S_{u j} μ_{u}}{\sqrt{S_{x j} C_{x}^{(m)} {S^{T}}_{x j} + S_{u j} C_{u} {S^{T}}_{u j} + σ_{e x p, j}^{2}}}

如果残差服从标准正态分布,则说明正态分布假设成立^[8].

为测试该方法的可靠性,建立简单的数学模型对该方法进行测试.在测试中给定70个样本点,令已知分布的输入参数不确定性u的维度为1,待评估的模型参数不确定性x的维度为2,敏感性系数由均匀分布U(5, 50)得到,已知分布参数服从 u₁~N(1.5, 0.4²),认为实验误差为e_j~N(0, 0.05²),用于生成y_w的真实分布满足x₁~N(-0.6, 0.3²), x₂~N(1.2, 0.2²),然后根据这些数据反推x的均值和方差,其计算结果如表1所示.可知,计算结果与真实值比较接近,相对误差不超过11%.

表1 评估所得参数与真实值的比较

Tab.1 Comparison of evaluated parameters and real values

参数	真实值	计算值	相对误差绝对值/%
$μ_{x_{1}}$	-0.6	-0.647 8	7.96
$σ_{x_{1}}$	0.3	0.281 7	6.23
$μ_{x_{2}}$	1.2	1.137 1	5.24
$σ_{x_{2}}$	0.2	0.221 3	10.65

新窗口打开| 下载CSV

1.2 输入参数抽样

不确定性的正向传递可以通过蒙特卡洛抽样进行.对确定的所有重要输入参数同时抽样,根据次序统计理论,抽样数目只与输出结果的容忍区间以及置信水平有关.满足特定容忍区间的最小抽样数目由Wilks公式^[14]确定,在双侧容忍区间的情况下,其形式为

(10)β=1-γ^Z+Z(1-γ)γ^Z^-1

式中:β为置信水平;γ为概率;Z为最小样本数目.对于统计方法,美国核管会(NRC)建议采用95%的置信水平,不确定性评估必须证明在β=95%时,95%的计算结果(容忍区间)在安全裕度内^[15].因此,令β=γ=95%,对于双侧容忍区间可得Z=93,即抽样计算93次后即可满足“95/95准则”, 得到的最大值和最小值可以认为是双95%置信区间的上下界.

2 PSBT空泡份额棒束基准

压水堆子通道和棒束实验(PSBT)是2010年发布的一套基准,主要用于验证现有子通道和计算流体力学程序模拟流体在单管和棒束的空泡份额、含气率以及偏离泡核沸腾(DNB)等.本研究计算对象为PSBT基准一阶段稳态棒束空泡份额分布问题.表2为本文计算涉及的3种组件具体参数^[16].其中,B5和B6组件的径向功率分布场为类型A,如图2(a)所示;B7组件的径向功率分布为类型B, 如图2(b)所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 径向相对功率分布^[8]

Fig.2 Distribution of radial relative power^[8]

表2 组件参数

Tab.2 Parameters of assemblies

参数	取值
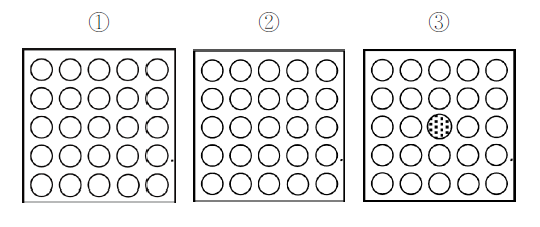
组件	B5(图示①)	B6(图示②)	B7(图示③)
棒束排列	5×5	5×5	5×5
加热棒数	25	25	24
套管数	0	0	1
加热棒外径/mm	9.50	9.50	9.50
套管外径/mm	-	-	12.24
加热棒间距/mm	12.60	12.60	12.60
轴向加热长度/mm	3 658	3 658	3 658
流道内宽度/mm	64.9	64.9	64.9
径向功率分布类型	A	A	B
轴向功率分布类型	均匀	余弦	余弦
搅混叶片格架数	7	7	7
非搅混叶片格架数	2	2	2
简单格架数	8	8	8
搅混叶片格架位置/mm	471, 925, 1 378, 1 832, 2 285, 2 739, 3 247
非搅混叶片格架位置/mm	2.5, 3 755
简单格架数位置/mm	237, 698, 1 151, 1 605, 2 059, 2 512, 2 993, 3 501

新窗口打开| 下载CSV

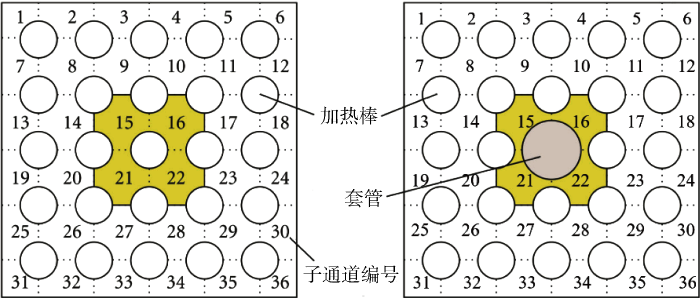
3为实验组件截面图和子通道的具体划分情况.实验数据为位于距离加热底端 2 216、2 669、3 177 mm共3个轴向位置的4个中心子通道的空泡份额平均值.在距离加热底端2 216 mm的底端测量点的空泡份额较低,空泡聚集在受热表面,因此实验确定的空泡份额将低于实际的空泡份额,具有较大误差.对此,仅选取 2 669、3 177 mm 两个轴向位置的测量值.根据计算,所选用稳态实验工况的数据范围为压力7.36~14.71 MPa、质量流量1 380.6~2 288.9 kg/(m²·s)、加热功率 1 920~3 536 kW、入口温度173.5~287.8 ℃.共选取30组工况,并从中选取25组工况进行输入模型参数的不确定性量化,利用另外5组对计算得到的不确定性分析结果进行评估,以验证计算结果的有效性.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 5×5棒束横截面示意图

Fig.3 Schematic diagram of cross section of rod bundle

从边界条件和计算模型两方面分析影响空泡份额分布的因素.对于边界条件,PSBT基准报告中给出了边界条件的测量精度,参照文献[17]的处理方式:压力、入口温度、质量流量、热流密度的不确定性的分布均为均值为0的正态分布,其标准差依次为0.333%、0.133%、0.5%、0.333%.

在子通道程序的计算过程中所选的重要模型和参数如表3所示.空泡份额模型采用滑移模型,滑速比可以设置.根据最小熵增原理^[18],在14 MPa下的滑速比计算结果为1.86,但是一般情况下计算值比大多数的实验值偏高^[19],而最典型的单相流模型是均相模型,其把两相流体看成某种单相混合物流体,认为气相与液相之间不存在相对速度,即滑速比为1,因此滑速比基准值最终取1.2.湍流交混模型中需要给定湍流交混系数,湍流交混系数主要与几何尺寸、棒束排布方式、流体类型以及雷诺数(Re)范围有关,根据与计算工况相近的Castellana等^[20]的实验所得湍流交混系数关系式,取湍流交混系数的基准值为0.008.

表3 PSBT基准题计算模型及参数选择

Tab.3 Calculation models and parameter selection for PSBT benchmark

模型或参数	内容
过冷空泡份额模型	Levy模型
空泡份额模型	滑移模型
两相摩擦倍增因子	Armand模型
湍流交混模型	EM模型
两相湍流交混倍增因子	Beus模型
单相湍流摩擦系数	0.184Re^-0.2
格架压降因子(MV/NMV/SS)	1.0/0.7/0.4
横流压降因子	0.5

新窗口打开| 下载CSV

模型参数使用基准值进行计算.如图4所示,横轴为空泡份额实验值v^e,纵轴为子通道程序空泡份额计算值v^c,越接近黑色实线代表计算值与测量值越符合,上、下两条虚线代表实验测量不确定性2σ(=0.08).可知,较多的计算值位于实验值的两倍标准差(2σ)范围之外,且整体预测值偏高,证明计算选用的模型过于保守,仍需要进一步改进.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 基准值计算结果

Fig.4 Calculation result of reference value

在进行模型参数不确定性量化过程中,计算敏感性矩阵是重要步骤.在使用有限差分法求偏导数的过程中,步长的选择并不是越小越好.因为步长太小可能会导致程序响应变化不明显,也会受到数值不稳定性的影响,步长过大又会导致误差过大.所以为了减小偏导数计算过程中的误差,需要进行平滑处理^[11].例如在求解滑速比和湍流交混系数对应的敏感性系数时,分别取步长为 ±0.01, ±0.03, ±0.1 来进行计算,对于每个样本点可以得到6个偏导数,然后舍掉最大值和最小值,求平均值作为最终的偏导数.

3 计算结果分析

将压力、入口温度、质量流量、热流密度当作已知分布参数,将滑速比和湍流交混系数作为待评估的模型参数,利用25组工况共50个实验样本点计算得到滑速比的均值和标准差分别为 0.440 5、0.259 9;湍流交混系数的均值和标准差分别为-0.103 4、0.048 8.可知,滑速比不确定性的标准差较大.根据最小熵增理论,滑速比的大小与压力密切相关,而在进行模型参数的不确定性分析时所选用的工况压力范围为7.36~14.71 MPa,因而滑速比也存在较大的不确定性.为了验证正态分布假设是否成立,使用卡方检验来验证残差是否满足标准正态分布,将残差划分为10个区间,有:

(11)χ²(=7.6)<

χ_{0.05}^{2}

(7)(=14.067)

则有95%的置信度认为参数服从正态分布.

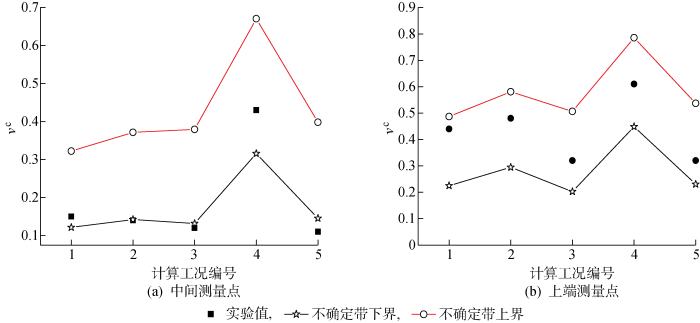
在得到了输入参数不确定性的具体分布之后,对另外5组工况进行不确定性的正向传播.将得到的模型参数及边界条件参数按照其分布进行93次抽样,并通过子通道程序进行计算,将得到的最大值和最小值当作双95%置信区间的上下界.图5为4个中心子通道的空泡份额平均值计算值不确定带对实验值的包络情况.可知,当空泡份额较高时,不确定带对实验值的包络性非常好;当空泡份额较低时,不确定带对实验数据的包络情况不够理想,有部分未包络,但不确定带下界也非常接近实验值.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不确定带上下界对实验值的包络情况

Fig.5 Envelope of experimental values with uncertain upper and lower bounds

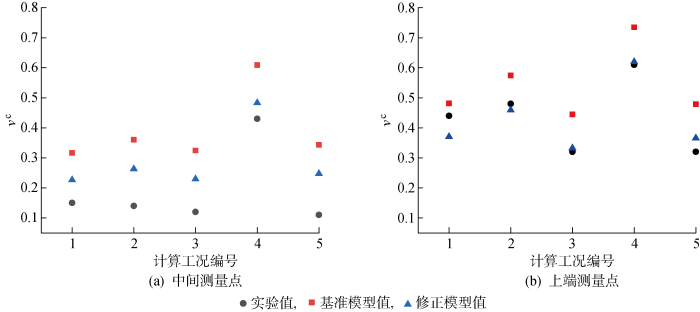
利用所求出的统计均值对模型系数进行修正,图6为基准模型修正前后4个中心子通道的空泡份额平均值计算结果对比.可知,样本点模型参数经过均值修正后,计算结果与实验值更接近,计算精度有了明显改善.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 均值对模型修正的效果

Fig.6 Effect of mean values on model calibration

4 结论

本文在假设输入参数不确定性与输出参数不确定性近似为线性关系的基础上,将边界条件压力、入口温度、质量流量、热流密度当作已知分布输入参数,对子通道程序COBRA-IV输入模型参数中滑速比和湍流交混系数的不确定性进行评估;然后进行输入参数不确定性的正向传递,得到了空泡份额的不确定带,并利用求得的模型参数不确定性统计均值对模型进行修正,计算结果表明:

(1) 在所选取的空泡分布实验工况范围内,滑速比存在较大的不确定性,而湍流交混系数的变化范围较小.

(2) 计算结果的不确定带对实验值的包络情况较好,尤其是当空泡份额较高时.

(3) 利用统计均值对模型进行修正后,可以得到比原模型更接近实验值的计算结果,对于输入模型参数的不确定性评估结果可以作为计算模型改进的重要参考.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

USNRC.

Best-estimate calculations of emergency core cooling system performance: RG 1.157[R]. Washington, USA: Office of Nuclear Regulatory Research, 1989.

[本文引用: 1]

[2]

BOYACK

B E

, CATTON

UCLA I

, DUFFEY

INEL R B

et al.

Quantifying reactor safety margins part 1: An overview of the code scaling, applicability, and uncertainty evaluation methodology

[J]. Nuclear Engineering and Design, 1990, 119(1): 1-15.

DOI:10.1016/0029-5493(90)90071-5 URL [本文引用: 1]

[3]

GLAESER

, HOFER

, KLOOS

et al.

Uncertainty and sensitivity analysis of a post-experiment calculation in thermal hydraulics

[J]. Reliability Engineering & System Safety, 1994, 45(1/2): 19-33.

DOI:10.1016/0951-8320(94)90073-6 URL [本文引用: 1]

[4]

D’AURIA

, DEBRECIN

, GALASSI

G M

Outline of the uncertainty methodology based on accuracy extrapolation

[J]. Nuclear Technology, 1995, 109(1): 21-38.

DOI:10.13182/NT109-21 URL [本文引用: 1]

[5]

POURGOL-MOHAMMAD

Thermal-hydraulics system codes uncertainty assessment: A review of the methodologies

[J]. Annals of Nuclear Energy, 2009, 36(11/12): 1774-1786.

[本文引用: 1]

[6]

D’AURIA

, GLAESER

, LEE

et al. Best estimate safety analysis for nuclear power plants: Uncertainty evaluation[R]. Vienna, Austria: IAEA, 2008.

[本文引用: 1]

[7]

GLAESER

, BAZIN

, BACCOU

et al.

Bemuse phase Ⅵ report: Status report on the area, classification of the methods, conclusions and recommendations

[R]. Paris, France: OECD Nuclear Energy Agency, 2011.

[本文引用: 1]

[8]

SKOREK

, DE

CRÉCY A

, KOVTONYUK

et al.

Quantification of the uncertainty of the physical models in the system thermal-hydraulic codes-PREMIUM benchmark

[J]. Nuclear Engineering and Design, 2019, 354: 110199.

DOI:10.1016/j.nucengdes.2019.110199 URL [本文引用: 6]

[9]

CELEUX

, GRIMAUD

, LEFÈBVRE

et al.

Identifying intrinsic variability in multivariate systems through linearized inverse methods

[J]. Inverse Problems in Science and Engineering, 2010, 18(3): 401-415.

DOI:10.1080/17415971003624330 URL [本文引用: 1]

[10]

HEO

, TURINSKY

P J

, DOSTER

J M

Optimization of thermal-hydraulic reactor system for SMRs via data assimilation and uncertainty quantification

[J]. Nuclear Science and Engineering, 2013, 173(3): 293-311.

DOI:10.13182/NSE11-113 URL [本文引用: 1]

[11]

李冬.

最佳估算模型的不确定性量化方法研究及再淹没模型评估的应用[D]. 上海: 上海交通大学, 2017.

[本文引用: 4]

Dong

Investigation of uncertainty quantification method on BE models and application of reflood model evaluation[D]. Shanghai: Shanghai Jiao Tong University, 2017.

[本文引用: 4]

[12]

XIONG

Q W

, GOU

J L

, CHEN

et al.

Investigation of uncertainty quantification methods for constitutive models and the application to LOFT LBLOCA

[J]. Annals of Nuclear Energy, 2019, 132: 119-133.

DOI:10.1016/j.anucene.2019.04.028 URL [本文引用: 1]

[13]

LIU

C H

, RUBIN

D B

The ECME algorithm: A simple extension of EM and ECM with faster monotone convergence

[J]. Biometrika, 1994, 81(4): 633-648.

DOI:10.1093/biomet/81.4.633 URL [本文引用: 1]

[14]

WILKS

S S

Determination of sample sizes for setting tolerance limits

[J]. The Annals of Mathematical Statistics, 1941, 12(1): 91-96.

DOI:10.1214/aoms/1177731788 URL [本文引用: 1]

[15]

FREPOLI

An overview of Westinghouse realistic large break LOCA evaluation model

[J]. Science and Technology of Nuclear Installations, 2008, 2008: 498737.

[本文引用: 1]

[16]

RUBIN

, SCHOEDEL

, AVRAMOVA

et al. OECD/NRC benchmark based on NUPEC PWR sub-channel and bundle tests (PSBT). Volume I: Experimental database and final problem specifications[R]. Paris, France: OECD Nuclear Energy Agency, 2012.

[本文引用: 1]

[17]

PANKA

, KERESZTÚRI

Assessment of the uncertainties of COBRA sub-channel calculations by using a PWR type rod bundle and the OECD NEA UAM and the PSBT benchmarks data

[J]. Kerntechnik, 2014, 79(4): 359-366.

DOI:10.3139/124.110460 URL [本文引用: 1]

[18]

ZIVIS

S M

Estimation of steady-state steam void-fraction by means of the principle of minimum entropy production

[J]. Journal of Heat Transfer, 1964, 86(2): 247-251.

DOI:10.1115/1.3687113 URL [本文引用: 1]

[19]

徐济鋆.

沸腾传热和气液两相流[M]. 第2版. 北京: 原子能出版社, 2001.

[本文引用: 1]

Jijun

Boiling heat transfer and gas-liquid two-phase flow[M]. 2nd ed. Beijing: Atomic Energy Press, 2001.

[本文引用: 1]

[20]

CASTELLANA

F S

, ADAMS

W T

, CASTERLINE

J E

Single-phase subchannel mixing in a simulated nuclear fuel assembly

[J]. Nuclear Engineering and Design, 1974, 26(2): 242-249.

[本文引用: 1]

1989

... 1989年美国发布管理导则RG 1.157^[1],允许在应急堆芯冷却系统分析中使用最佳估算程序.出于安全考虑,最佳估算程序必须与不确定性分析相结合,以判断计算与实际情况之间的差异.截至目前,国际上已有多种不同的不确定性分析方法,例如程序比例、适用性和不确定性分析方法(CSAU)^[2]、德国核安全中心方法(GRS)^[3]、基于精度外推的不确定性方法(UMAE)^[4]、先进统计学处理的不确定性方法(ASTRUM)^[5]等.这些不确定性分析方法大体可以分为两大类,一类是基于输入参数不确定性的传递,另一类是基于输出结果不确定性的外推^[6].基于输入参数不确定性传递的统计性方法的研究和应用相对更成熟和广泛,如在由经济合作与发展组织(OECD)发起的不确定性研究项目“最佳估算方法-不确定性和敏感性分析”阶段V中,14个参与者中有12个采用输入不确定性传递的方法^[7]. ...

Quantifying reactor safety margins part 1: An overview of the code scaling, applicability, and uncertainty evaluation methodology

1990

Uncertainty and sensitivity analysis of a post-experiment calculation in thermal hydraulics

1994

Outline of the uncertainty methodology based on accuracy extrapolation

1995

Thermal-hydraulics system codes uncertainty assessment: A review of the methodologies

2009

2008

Bemuse phase Ⅵ report: Status report on the area, classification of the methods, conclusions and recommendations

2011

Quantification of the uncertainty of the physical models in the system thermal-hydraulic codes-PREMIUM benchmark

2019

... 基于输入参数不确定性传递的方法需要知道输入参数的不确定性.然而,大多数热工水力程序都没有提供关于输入参数不确定性的足够信息,尤其是对于某些无法通过实验直接测量的输入模型参数,通常通过专家判断来进行量化.目前一些取代专家判断的评估方法被陆续提出,如比萨大学开发的基于快速傅里叶变换的方法(FFTBM)^[8],法国开发的输入参数经验确定方法(DIPE)^[8]和模型参数不确定性计算方法(CIRCÉ)^[9],韩国原子力研究院开发的通过数据同化进行模型标定方法(MCDA)^[10].李冬^[11]对CIRCÉ方法可评估参数有限和MCDA方法求解非线性问题耗时过长这两个缺点进行了改进;Xiong等^[12]开发了一种优化的最佳估算加不确定性分析方法,该方法包含了一个结构化的模型不确定性量化方法. ...

... [8]和模型参数不确定性计算方法(CIRCÉ)^[9],韩国原子力研究院开发的通过数据同化进行模型标定方法(MCDA)^[10].李冬^[11]对CIRCÉ方法可评估参数有限和MCDA方法求解非线性问题耗时过长这两个缺点进行了改进;Xiong等^[12]开发了一种优化的最佳估算加不确定性分析方法,该方法包含了一个结构化的模型不确定性量化方法. ...

... 因此可以采用k_i=

e^{x_{i}}

来表示模型参数系数和不确定性之间的转化关系^[8]. ...

... 如果残差服从标准正态分布,则说明正态分布假设成立^[8]. ...

... 压水堆子通道和棒束实验(PSBT)是2010年发布的一套基准,主要用于验证现有子通道和计算流体力学程序模拟流体在单管和棒束的空泡份额、含气率以及偏离泡核沸腾(DNB)等.本研究计算对象为PSBT基准一阶段稳态棒束空泡份额分布问题.表2为本文计算涉及的3种组件具体参数^[16].其中,B5和B6组件的径向功率分布场为类型A,如图2(a)所示;B7组件的径向功率分布为类型B, 如图2(b)所示.

10.16183/j.cnki.jsjtu.2021.068.F0002

图2 径向相对功率分布<sup>[<xref ref-type="bibr" rid="b8">8</xref>]</sup> Distribution of radial relative power<sup>[<xref ref-type="bibr" rid="b8">8</xref>]</sup>

Fig.2

10.16183/j.cnki.jsjtu.2021.068.T0002

表2

组件参数 ...

... [8]Fig.2

10.16183/j.cnki.jsjtu.2021.068.T0002

表2

组件参数 ...

Identifying intrinsic variability in multivariate systems through linearized inverse methods

2010

Optimization of thermal-hydraulic reactor system for SMRs via data assimilation and uncertainty quantification

2013

2017

... 式中:S_x和S_u为样本点对应待求参数的敏感性矩阵,敏感性矩阵中的偏导数可以通过有限差分法求得^[11]. ...

... 将x的均值和方差记为μ_x和C_x,即待求参数,统一记为θ={μ_x, C_x}.完整数据的似然函数表示为L(θ; x¹, x², …, x^J, y_w),简化表示为^[11] ...

... 在进行模型参数不确定性量化过程中,计算敏感性矩阵是重要步骤.在使用有限差分法求偏导数的过程中,步长的选择并不是越小越好.因为步长太小可能会导致程序响应变化不明显,也会受到数值不稳定性的影响,步长过大又会导致误差过大.所以为了减小偏导数计算过程中的误差,需要进行平滑处理^[11].例如在求解滑速比和湍流交混系数对应的敏感性系数时,分别取步长为 ±0.01, ±0.03, ±0.1 来进行计算,对于每个样本点可以得到6个偏导数,然后舍掉最大值和最小值,求平均值作为最终的偏导数. ...

2017

... 式中:S_x和S_u为样本点对应待求参数的敏感性矩阵,敏感性矩阵中的偏导数可以通过有限差分法求得^[11]. ...

... 将x的均值和方差记为μ_x和C_x,即待求参数,统一记为θ={μ_x, C_x}.完整数据的似然函数表示为L(θ; x¹, x², …, x^J, y_w),简化表示为^[11] ...

Investigation of uncertainty quantification methods for constitutive models and the application to LOFT LBLOCA

2019

The ECME algorithm: A simple extension of EM and ECM with faster monotone convergence

1994

... 当存在数据缺失问题时,期望最大化(EM)算法是极大似然估计的一种常用迭代算法.但是实际计算过程中EM算法一般迭代次数过多,收敛较慢,因此使用EM算法的改进算法,即ECME算法^[13]进行计算. ...

Determination of sample sizes for setting tolerance limits

1941

... 不确定性的正向传递可以通过蒙特卡洛抽样进行.对确定的所有重要输入参数同时抽样,根据次序统计理论,抽样数目只与输出结果的容忍区间以及置信水平有关.满足特定容忍区间的最小抽样数目由Wilks公式^[14]确定,在双侧容忍区间的情况下,其形式为 ...

An overview of Westinghouse realistic large break LOCA evaluation model

2008

... 式中:β为置信水平;γ为概率;Z为最小样本数目.对于统计方法,美国核管会(NRC)建议采用95%的置信水平,不确定性评估必须证明在β=95%时,95%的计算结果(容忍区间)在安全裕度内^[15].因此,令β=γ=95%,对于双侧容忍区间可得Z=93,即抽样计算93次后即可满足“95/95准则”, 得到的最大值和最小值可以认为是双95%置信区间的上下界. ...

2012

Assessment of the uncertainties of COBRA sub-channel calculations by using a PWR type rod bundle and the OECD NEA UAM and the PSBT benchmarks data

2014

... 从边界条件和计算模型两方面分析影响空泡份额分布的因素.对于边界条件,PSBT基准报告中给出了边界条件的测量精度,参照文献[17]的处理方式:压力、入口温度、质量流量、热流密度的不确定性的分布均为均值为0的正态分布,其标准差依次为0.333%、0.133%、0.5%、0.333%. ...

Estimation of steady-state steam void-fraction by means of the principle of minimum entropy production

1964

... 在子通道程序的计算过程中所选的重要模型和参数如表3所示.空泡份额模型采用滑移模型,滑速比可以设置.根据最小熵增原理^[18],在14 MPa下的滑速比计算结果为1.86,但是一般情况下计算值比大多数的实验值偏高^[19],而最典型的单相流模型是均相模型,其把两相流体看成某种单相混合物流体,认为气相与液相之间不存在相对速度,即滑速比为1,因此滑速比基准值最终取1.2.湍流交混模型中需要给定湍流交混系数,湍流交混系数主要与几何尺寸、棒束排布方式、流体类型以及雷诺数(Re)范围有关,根据与计算工况相近的Castellana等^[20]的实验所得湍流交混系数关系式,取湍流交混系数的基准值为0.008. ...

2001

Single-phase subchannel mixing in a simulated nuclear fuel assembly

1974

〈

〉