符号说明
制造企业中,设备维护成本是企业总成本的重要组成部分,与维护相关的支出(设备替换和停机成本等)最高可占据生产成本的70%[1].有效的设备维护策略可以减少设备故障时间,是降低维护成本,增强企业竞争力的重要举措.维护策略中,基于设备状态的维护(视情维护)策略根据设备退化的实时状态动态地制定维护决策,从而具有精确性和实时性,逐渐成为维护策略的主流.在视情维护策略研究中,沈南燕等[2]根据关键设备的状态监测数据预估故障概率,在此基础上建立数学模型,优化了设备的维护时间.De Jonge等[3]针对单零件系统,通过数值实验比较了视情维护策略和其余维护策略的有效性.侯文瑞等[4]基于相对劣化度建立了视情维护决策模型,并通过算例分析验证了模型有效性.
大多数维护文献都假设备件的库存量始终得到满足,忽略了备件库存决策[5].然而实际中,设备维护策略的实施依赖于备件库存.设备的维护频率和维护零件数量会根据备件库存量和订购量进行相应的调整.备件存量过少会导致缺货、设备维护频率降低和设备故障概率增加,存量过多将造成空间和资金的浪费,甚至导致维护频率增加.因此,企业应考虑设备维护和备件库存管理的联合优化.近年来,越来越多的文献关注两者的联合优化.针对单零件系统,文献[6⇓-8]考虑基于阈值的预防性维护与备件订购策略的联合优化,以成本最小化为目标建立数学模型,求解了预防性维护周期、阈值等参数.在单零件系统之外,很多文献也研究了多零件系统的联合优化问题.肖罗椿[9]考虑了同类型多零件系统的视情维修和备件供应联合决策优化,以最小化平均费用率为目标,通过仿真和遗传算法求解了预防性失效阈值等参数.Zhang等[10]针对视情维护和备件订购联合策略,基于阈值进行建模,通过遗传算法优化了检测间隔、维护阈值和安全库存.Olde Keizer等[5]将多台设备的视情维护和备件订购策略建模为马尔科夫决策过程,通过值迭代方法求解了最优的联合策略.
上述联合优化的文献均假设备件从单供应商处订购,但实际上备件订购往往面临价格和提前期不同的多个供应商,决策者需根据设备和库存状态选择有效的供应商进行补货.文献[11-12]分析了价格、提前期不同的双供应商(双源)订购模型对库存决策的影响,相比单源订购,双源订购在成本、补货速度等方面显示出了较高的优越性.但上述文献都忽略了维护对备件库存的影响.在考虑双供应商的设备维护策略中,决策者一方面需要平衡备件的订购成本和设备的故障成本.订购过多会增加总订购成本和持货成本,订货过少则易导致备件不足和设备故障.另一方面需要权衡供应商订购的提前期和价格,例如设备健康状态下可以向提前期长而订购价格低的供应商订购备件,而当设备的零件急需替换时则可以以更高的价格向提前期短的供应商补货.少数设备维护和备件订购联合优化的文献考虑了价格和提前期不同的双源订购模型[13-14],但均采用阈值控制策略,即当零件退化值或备件库存水平满足阈值条件时执行维护或订购决策.相比于阈值决策,马尔科夫决策模型能根据设备和库存状态信息进行动态决策,在降低成本上往往有更高的优越性[5].
针对以上问题,本文基于价格和提前期不同的双供应商(双源)订购模型研究设备维护与备件订购联合决策优化,以多台设备组成的并行制造系统为对象,以平均总成本最小化为目标,基于离散时间的马尔科夫决策过程进行建模,通过值迭代方法和启发式方法进行模型求解.本文创新可主要体现在两方面.一方面,本文的模型不仅考虑设备维护,还考虑备件的双供应商订购,实现了设备维护和备件订购两个系统的整体优化,有效降低总成本.而以往的文献,大多数只考虑设备维护或者双供应商订购,未曾考虑两者的结合.另一方面,本论文设计了启发式方法求解模型,有效降低了模型的求解时间.以往文献中针对于马尔科夫决策过程建立的模型多采用值迭代方法求解.但是,在多设备系统中,考虑双供应商和备件订购将导致状态和决策空间变大,使值迭代方法的求解时间变得很长.针对该问题,本文设计了启发式策略,有效缩短了求解时间.
1 问题描述
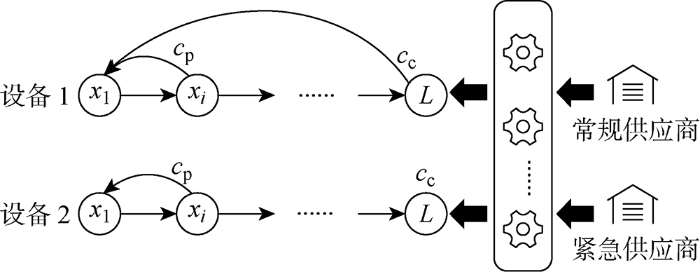
图1
每台设备都包含一个关键零件,零件服从退化率为α的泊松退化过程,彼此之间退化过程相互独立.零件的状态由退化值
本文的研究目标为最小化系统的长期平均总成本.总成本由替换成本、故障成本、订购成本和持货成本4个部分组成.替换成本包括替换的准备成本cs和每个零件的单位替换成本cp(预防性替换)和cc(故障后替换),其中替换的准备成本与替换的零件数量无关,当替换发生时发生[10].当设备因关键零件失效而故障时,会产生惩罚成本cd.订购导致的成本包括固定成本cF和每个零件的单位订购成本c1(常规供应商)或c2(紧急供应商).在决策后,仓库中的每个备件在下一个检测间隔间会产生持货成本ch.
2 维护与订购策略联合建模
介绍视情维护和备件订购联合决策模型和求解方法.首先通过马尔科夫决策过程对系统决策状态、转移概率等进行建模.之后采用值迭代算法求解最优策略.最后通过序列优化的启发式方法求得启发式策略,改进求解效率.
2.1 马尔科夫决策模型
马尔科夫决策模型是求解序列决策问题常用的方法之一[17].本文采用离散时间的马尔科夫决策模型对上述系统进行决策建模.根据图1的制造系统模型,马尔科夫决策过程可以用状态、决策、成本和转移概率表示.系统状态s由图1中各台设备关键零件的退化值、在库库存量和在途库存量组成,表示为s(x1, x2, …, xN, h0, h1, …, hl-1),缩写为s.其中(x1, x2, …, xN)表示系统退化状态,xi表示零件i(i=1, 2, …, N)的退化状态.(h0, h1, …, hl-1)表示系统库存状态, hj表示j(j=0, 1, …, l-1)个检测间隔后到达的备件数量,h0为在库库存量.
系统动作由替换和订购组成,表示为
C(s,a)为系统在状态s下执行动作a后导致的成本,由替换、故障、订购和持货成本组成.替换成本为替换的准备成本和预防性替换(或故障后替换)成本之和.假设总的替换零件数量为
在决策点执行动作后,系统状态将先根据动作更新,之后以概率转移到下一个状态.假设执行完动作
针对系统退化状态,假设单个关键零件的转移概率为
系统的状态转移和决策需满足相应的约束.根据问题描述,当在库库存不足时通过紧急订购补充库存,即
系统的总成本由值函数
式中:
2.2 求解算法
上述模型可以通过值迭代算法来求得最优的维护和订购联合策略以及最优的平均总成本.在本文中假定当迭代的误差
算法收敛后平均总成本由
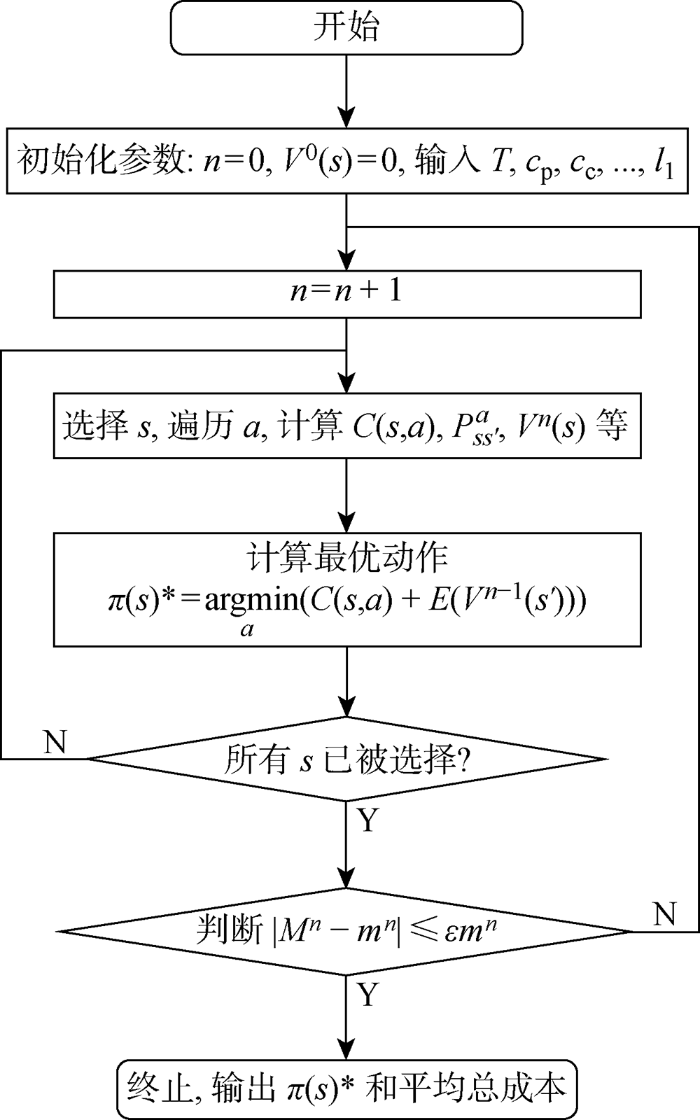
图2
值迭代方法是求解马尔科夫决策模型的最优化方法,可以获得最优的维护和订购联合决策.然而,算法需要大量的计算时间.为提高计算效率,本文采用了一种序列优化的启发式方法,在保证成本增加率低的同时减少计算时间.具体思想为:将维护决策和订购决策分离,先优化维护决策,在此基础上优化订购决策.对于维护,由于零件相同且相互独立,本文将系统状态(多个零件和库存状态)分为单个零件和库存状态,通过值迭代算法快速求出单个零件的最优维护决策.之后按照零件退化值降序判断单个零件是否维护.当决定完维护决策后通过枚举的方法选择最优的订购量,得到最终的维护和订购联合决策.具体的算法流程如下:
(1)初始化
(2) 根据图2的值迭代算法输出单个零件维护决策函数
(3) 对于所有系统状态s,从高到底降序遍历零件状态,计算维护决策
(4) 计算收敛误差.若
上述启发式算法对于计算效率的改进主要在于减少了计算联合决策时迭代的次数.值迭代算法中,最优联合决策通过遍历所有决策获得.由于设备维护仅考虑替换决策,每个零件的决策数量为2则N个零件的维护决策空间规模为
3 算例分析
为了验证本文所采用的启发式策略有效性,以2个零件和4个零件的系统进行算例分析.首先以2零件的系统分析最优策略和启发式策略的决策异同.之后以4零件的系统分析参数(持货成本、预防性替换成本、订购成本)的变化对成本和计算时间的影响.
3.1 决策和成本分析
表1 算例参数
Tab.1
| 参数 | 取值 | 参数 | 取值 |
|---|---|---|---|
| c1 | 120 | cp | 36 |
| c2 | 240 | cs | 30 |
| cc | 54 | l1 | 2 |
| cd | 200 | L | 9 |
| cF | 15 | T | 1 |
| ch | 0.48 | α | 0.5 |
| H | N+2 | ε | 0.0005 |
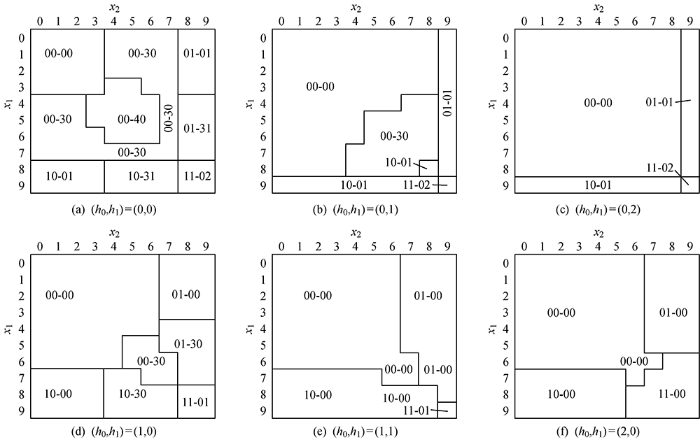
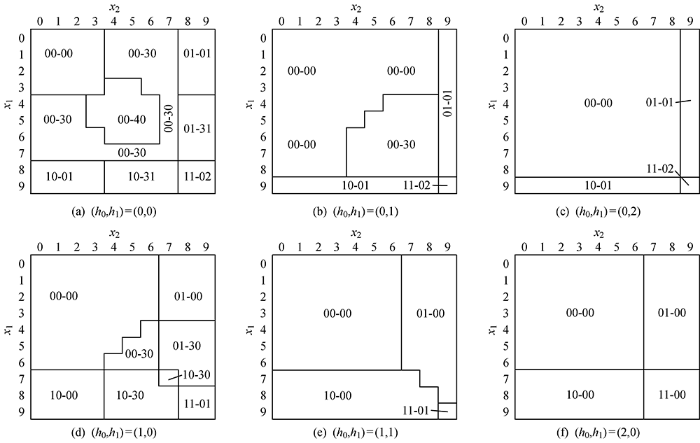
由图3(a)~3(c)和图4(a)~4(c)可知,当在库量为0时,最优策略和启发式策略的决策差异小.这是因为启发式策略主要改变了零件的替换策略.当系统无替换决策时,启发式策略将采取和最优策略相同的订购策略.当系统在库库存量不为0时,如图3(d)和图4(d)所示,随着零件退化值的增加,当两个零件的退化值都较高时,系统将会延迟零件的替换动作.零件1由替换变为不替换,而启发式策略则无延迟替换决策.这是因为多个零件共享备件,零件间的替换决策会相互影响.当备件数量有限且零件的退化值相同时,由于退化的随机性,难以确定下一决策点零件退化值的高低,此时将替换延迟到下一决策点可以减少设备失效的成本.随着在库备件数量的增加,延迟替换决策减少.如图3(f)和图4(f)所示,启发式策略和最优策略的差异逐渐减小,启发式策略优越性逐渐增加.因此在采用启发式策略时可以适当增加备件存量,从而减少与最优策略的差异,降低总成本.
图3
图4
表2 2零件和4零件系统平均总成本和计算时间
Tab.2
| N | 最优策略 | 阈值策略 | 启发式策略 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| f | g/s | f | g/s | q/% | f | g/s | q/% | |||
| 2 | 27.8 | 38 | 30.0 | 15 | 7.9 | 27.9 | 9 | 0.4 | ||
| 4 | 51.2 | 5 214 | 56.5 | 485 | 10.4 | 51.9 | 255 | 1.4 | ||
其中:
3.2 敏感性分析
表3
Tab.3
| ch | 最优策略 | 启发式策略 | q/% | |||
|---|---|---|---|---|---|---|
| f | g/s | f | g/s | |||
| 0.5 | 51.3 | 5 013 | 52.0 | 262 | 1.4 | |
| 1 | 52.1 | 4 608 | 52.9 | 215 | 1.5 | |
| 2 | 53.3 | 4 583 | 54.1 | 214 | 1.5 | |
| 3 | 54.2 | 4 645 | 55.1 | 226 | 1.7 | |
表4
Tab.4
| cp | 最优策略 | 启发式策略 | q/% | |||
|---|---|---|---|---|---|---|
| f | g/s | f | g/s | |||
| 12 | 45.2 | 4 714 | 46.0 | 264 | 1.8 | |
| 24 | 48.2 | 5 042 | 49.0 | 259 | 1.7 | |
| 36 | 51.2 | 5 214 | 51.9 | 255 | 1.4 | |
| 48 | 54.1 | 5 293 | 54.9 | 252 | 1.5 | |
表5
Tab.5
| c1 | 最优策略 | 启发式策略 | q/% | |||
|---|---|---|---|---|---|---|
| f | g/s | f | g/s | |||
| 50 | 32.5 | 5 236 | 33.7 | 293 | 3.7 | |
| 100 | 45.9 | 4 961 | 46.7 | 270 | 1.7 | |
| 150 | 58.9 | 5 222 | 59.7 | 249 | 1.4 | |
| 200 | 71.5 | 5 203 | 72.7 | 246 | 1.7 | |
表4显示了预防性替换成本cp如何影响启发式策略的优越性.设备替换存在准备成本,从而零件退化状态间存在依赖,同时替换多个零件会倾向于降低总成本.当cp较小时准备成本影响较大,维护的依赖性更强.启发式策略根据单台设备的状态判断是否维护,忽略了设备之间的依赖性,导致成本增加率较大.同时,当cp增加时,系统会减少备件库存,替换策略对总成本的影响增强,从而启发式策略的成本增加率将增加,优越性减弱.
表5显示了常规供应商的单位订购成本c1对启发式策略优越性的影响.备件的订购存在固定成本.当c1较小时,固定成本的影响较大,系统订购的频率降低,从而替换策略的影响增大,启发式策略有更大的成本增加率.当c1逐渐增加至靠近紧急供应商的订购成本c2时,系统会减少向常规供应商的订购频率,替换策略影响增强,启发式策略成本增加率会随着c1的增加再次增加.
4 结语
针对双供应商情形下的多零件设备维护和备件订购联合决策问题,建立了基于马尔科夫决策过程的预防性维护模型,基于设备状态和库存状态信息进行维护和订购联合决策优化,通过值迭代算法求取了最优的联合决策策略.在此基础上设计了启发式的设备维护和备件订购联合策略,在平均总成本增加率在一定范围(5%)内时减少了策略求解时间,通过算例分析验证了启发式策略的有效性.
针对拓展方向,将从以下两个方向拓展:① 本文仅考虑替换,在替换之外,可以引入小修、大修等维护动作,包括机会维护等策略;② 本文考虑并行的制造系统,在此基础上可以考虑串联以及k-out-of-n架构的制造系统.
参考文献
The analytic hierarchy process applied to maintenance strategy selection
[J].DOI:10.1016/S0951-8320(00)00047-8 URL [本文引用: 1]
自动化生产线中关键设备的预维护策略研究
[J].
DOI:10.3901/JME.2020.21.231
[本文引用: 1]

为了避免由于设备故障导致的生产线停产,首先研究生产线故障维修成本、预防性维护成本和停产损失的计算方法,建立生产线平均可靠度与维护总成本多目标优化模型,从而获得了最优的生产线周期性维护计划。针对关键设备,如数控机床、工业机器人,运行状态突然严重劣化的情况,基于时间延迟理论得到了关键设备子系统可靠度随时间变化的规律,根据设备运行状态的监测数据,采用支持向量机模型对设备子系统潜在故障的发生概率进行预测。由此建立了关键设备延迟维护最佳时刻优化模型,并通过粒子群优化算法求解关键设备的最佳维护时刻。最后,通过实例仿真分析验证了文本预维护策略的有效性,能够在保证可靠度要求的同时,有效降低维护成本。
Research on pre-maintenance strategy of key equipment in automatic production line
[J].
DOI:10.3901/JME.2020.21.231
[本文引用: 1]

In order to avoid the shutdown of production line caused by equipment failures, the optimal periodic maintenance plan is firstly obtained by solving a multi-objective optimization model of average reliability and total maintenance cost of the entire production line where the costs of downtime, breakdown repair and preventive maintenance are accurately evaluated based on equipment reliability. For the sudden and severe deterioration of key equipment, such as CNC machine tool and industrial robot, time delay theory is utilized to formulate subsystem reliability of key equipment and then the potential failure probability of equipment subsystem is predicted by using Support Vector Machine according to monitoring data on equipment operating status. And thus, the optimization model of delayed maintenance time of key equipment is established and solved by particle swarm optimization to search for the optimal maintenance time of key equipment. The case study conducted by simulation analysis shows the effectiveness of the proposed pre-maintenance strategy which can ensure the reliability and minimize maintenance cost of production line.
The influence of practical factors on the benefits of condition-based maintenance over time-based maintenance
[J].DOI:10.1016/j.ress.2016.10.002 URL [本文引用: 1]
基于相对劣化度的视情维修决策模型
[J].
Relative-deterioration degree based policy research of condition-based maintenance
[J].
Joint condition-based maintenance and inventory optimization for systems with multiple components
[J].DOI:10.1016/j.ejor.2016.07.047 URL [本文引用: 3]
Joint optimization of maintenance and inventory policies for a simple system
[J].DOI:10.1080/07408179608966288 URL [本文引用: 1]
设备视情预防维修与备件订购策略的联合优化
[J].
DOI:10.3901/JME.2015.11.150
[本文引用: 1]

研究设备的视情预防维修与备件订购策略的联合优化问题。在分析设备劣化与备件库存联合状态转换的基础上,给出了联合状态的稳态概率密度函数的显式表达式和数值求解方法。基于此联合概率密度函数,推导连续劣化的设备受备件库存状态影响的维修概率和备件的订购和持有概率,建立以设备的检测周期、备件订购阈值、预防维修阈值为决策变量,同时考虑维修和备件相关成本的长期平均费用率模型。通过数值试验验证了联合概率密度函数推导的正确性和所建立的模型的有效性。灵敏度分析结果表明维修成本和备件成本之间存在一定的权衡,只有将二者联合优化才能取得设备的全局最优联合策略。以氢气合成装置传输管道的变薄劣化为例验证了模型的实用性。
Joint optimization of condition-based preventive maintenance and spare parts provisioning policy for equipment maintenance
[J].
DOI:10.3901/JME.2015.11.150
[本文引用: 1]

A jointly condition-based preventive maintenance and spare parts provisioning policy is discussed for equipment maintenance. Based on analysis of all possible transitions of the joint state of equipment and its spare parts inventory, the explicit expression of stationary joint probability density function is derived and its numerical solution is deduced. On the basis of the joint probability density function, the maintenance probabilities of the equipment with the influence of spare parts inventory and the ordering and holding probabilities of its spare parts are derived. Then the expected long-run cost rate model is formulated for the joint policy using the renewal process, taking into account the costs incurred for performing maintenance and managing the spare parts inventory. A numerical experiment is carried out to identify the optimal values for the parameters of the policy, including the inspection interval, the ordering threshold, and the preventive maintenance threshold. The experiment results verify that the derivation of the joint probability density function is correct and the established model is effective. The results of the sensitivity analysis show that a trade-off exists between the maintenance related costs and the inventory related costs, and joint optimization of preventive maintenance and spare parts provisioning policy can ensure a global optimal policy. A practical case is provided to verify the effectiveness of the proposed method.
Joint optimization of condition-based opportunistic maintenance and spare parts provisioning policy in multiunit systems
[J].DOI:10.1016/j.ejor.2017.03.019 URL [本文引用: 2]
Structural properties of the optimal policy for dual-sourcing systems with general lead times
[J].DOI:10.1080/0740817X.2014.982839 URL [本文引用: 1]
Joint maintenance and spare parts inventory optimization for multi-unit systems considering imperfect maintenance actions
[J].
Joint optimization of spare parts ordering and maintenance policies for multiple identical items subject to silent failures
[J].DOI:10.1016/j.ejor.2013.10.065 URL [本文引用: 1]
Condition based spare parts supply
[J].DOI:10.1016/j.ress.2017.05.035 URL [本文引用: 1]
多元退化系统维修与备件订购策略优化模型
[J].
Optimization model of maintenance and spare parts ordering policy in multivariate degradation system
[J].
Optimization for condition-based maintenance with semi-Markov decision process
[J].DOI:10.1016/j.ress.2004.11.001 URL [本文引用: 1]
Markov decision processes: Discrete stochastic dynamic programming
[M].
Joint predictive maintenance and inventory strategy for multi-component systems using Birnbaum’s structural importance
[J].DOI:10.1016/j.ress.2017.05.034 URL [本文引用: 1]
A condition-based replacement and spare provisioning policy for deteriorating systems with uncertain deterioration to failure
[J].DOI:10.1016/j.ejor.2007.12.012 URL [本文引用: 1]
Joint optimization of condition-based maintenance and spare part inventory for two-component system
[J].