反向传播神经网络联合遗传算法对复合材料模量的预测

doi:10.16183/j.cnki.jsjtu.2021.126

反向传播神经网络联合遗传算法对复合材料模量的预测

王卓鑫¹, 赵海涛^,¹, 谢月涵², 任翰韬², 袁明清¹, 张博明³, 陈吉安¹

1.上海交通大学航空航天学院,上海 200240

2.中国商用飞机有限责任公司复合材料中心,上海 201210

3.北京航空航天大学材料科学与工程学院, 北京 100191

Prediction of Modulus of Composite Materials by BP Neural Network Optimized by Genetic Algorithm

WANG Zhuoxin¹, ZHAO Haitao^,¹, XIE Yuehan², REN Hantao², YUAN Mingqing¹, ZHANG Boming³, CHEN Ji’an¹

1. School of Aeronautics and Astronautics, Shanghai Jiao Tong University, Shanghai 200240, China

2. Composites Centre, Commercial Aircraft Corporation of China, Ltd., Shanghai 201210, China

3. School of Materials Science and Engineering, Beihang University, Beijing 100191, China

通讯作者: 赵海涛,男,副研究员,电话(Tel.):021-34207066;E-mail:zht@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2021-04-9

Received: 2021-04-9

作者简介 About authors

王卓鑫(1995-),女,山西省晋中市人,硕士生,从事复合材料性能的机器学习研究.

摘要

为减少测试成本和缩短设计周期,基于机器学习方法对树脂基复合材料模量的预报方法进行了研究.采用一种全新预测方法——神经网络联合遗传算法(GA-ANN),将T800/环氧复合材料的强度、泊松比和失效应变作为反向传播(BP)神经网络的3个输入变量,在遗传算法(GA)中得出最优阈值和权重,并将所得数值赋给对应的网络参数,更新BP神经网络以更高的准确率预测树脂基复合材料的模量;同等条件下,用Adam算法进行预测.对比这两种方法,结果充分证明了GA-ANN的可行性.

关键词： 机器学习; 反向传播神经网络; 遗传算法; 复合材料模量; Adam算法

Abstract

In order to reduce the cost of testing and shorten the design cycle, this paper studies the prediction method of the modulus of resin matrix composites based on the machine learning method. Using a new prediction method — the neural network in combination with the genetic algorithm (GA-ANN), the strength, the Poisson’s ratio, and the failure strain of the T800/epoxy composite material are used as three input variables of the back propagation (BP) neural network. Then, the optimal threshold and weight are obtained in the genetic algorithm (GA), which are assigned to the corresponding network parameters, and the BP neural network is updated for higher accuracy to predict the modulus of resin matrix composites. Under the same conditions, the Adam algorithm is used to predict. A comparison of these two methods fully proves the feasibility of the GA-ANN algorithm.

Keywords： machine learning; back propagation (BP) neural network; genetic algorithm; composite material modulus; Adam algorithm

PDF (2532KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王卓鑫, 赵海涛, 谢月涵, 任翰韬, 袁明清, 张博明, 陈吉安. 反向传播神经网络联合遗传算法对复合材料模量的预测[J]. 上海交通大学学报, 2022, 56(10): 1341-1348 doi:10.16183/j.cnki.jsjtu.2021.126

WANG Zhuoxin, ZHAO Haitao, XIE Yuehan, REN Hantao, YUAN Mingqing, ZHANG Boming, CHEN Ji’an. Prediction of Modulus of Composite Materials by BP Neural Network Optimized by Genetic Algorithm[J]. Journal of Shanghai Jiaotong University, 2022, 56(10): 1341-1348 doi:10.16183/j.cnki.jsjtu.2021.126

先进树脂基复合材料除了绿色环保、便于取得之外,其余优异性能不胜枚举.例如它在高温下不易变形、抗磨、防锈性能好,具有较高的比强度与比模量、出色的综合力学性能、可挠曲成形等^[1].因而,此类复合材料愈来愈受到宇航制造业的重视,甚至在各种客机的制造过程中被普遍应用.例如T800/环氧高温固化复合材料是民用飞机主受力结构、发动机叶轮结构等用于抵抗冲击力的常用材料.而现阶段面临的主要问题是如何提高树脂基复合材料的模量和强度、降低生产以及测试成本和减少设计周期等.

到目前为止,工业实验仍是树脂基复合材料模量数据获取的主要方式,而此种方式昂贵且耗时,需要对复合材料的所有参数都进行反复试验,大大提高了造价和放缓了进程.鉴于此,在大规模生产之前,以合理的精度预测材料的模量数据有助于制造企业和设计人员缩短周期同时降低成本.现今,机器学习已经可以为复杂的工业设计过程提供实时、快速和较高质量的预测.特别是在复合材料领域,机器学习已经成为分析材料属性的重要工具.Gelayol等^[2]曾针对碳纤维结构的力学性能采用支持向量回归(SVR)和人工神经网络(ANN)的方法进行预测,误差均低于5%.Zhang等^[3]曾用4种机器学习方法,即ANN、支持向量机(SVM)、决策树(DT)和K最邻近(KNN)研究石墨烯的3种力学性能,即弹性模量、断裂强度与应变,这项研究为发现和使用最新的计算方法探究机械性能提供了独特视角.Chen等^[4]为预测颗粒增强金属基复合材料的强度,分别用直接法和人工神经网络两种方式进行对比试验,发现人工神经网络能对材料的极限强度和耐久性极限作出比较准确的预测.Qi等^[5]在机器学习中使用回归树的方法建立了碳纤维单丝的性能变量和复合材料宏观参数之间的关系,分析了碳纤维的4种弹性性能,获得了具有较好泛化性能的模型. 杨红等^[6]采用反向传播(BP)、径向基函数神经网络(RBF)和SVR方法预测分析了木材的性能,通过比较得出SVR的泛化能力和准确率更高. 白晓明^[7]将张量分解的数据挖掘方法用于分析复合材料的宏观和微观性能,该方式在宏观性能上能够更贴切直接数值拟合. 张博^[8]采用梯度提升回归树(GBRT)的方法对稀土基化合物的磁熵变进行了机器学习预测分析,也得到了较准的预测结果.Qi等^[9]针对碳纤维单丝和复合材料的宏观参数使用分类回归树(CART)的方法对二者的关系展开预测,所得方法改进了测试误差,可以被借鉴应用到其他领域.

以上研究表明,近年来机器学习已遍及材料学应用的方方面面,并在材料性能预测分析方向具有非常大的潜力.BP神经网络(BP-ANN)被人们熟知且应用在各个领域.考虑到常规BP神经网络算法存在诸如不易找到全体中最佳解、准确度不高、收敛时间长等问题,本文采用一种全新的预测模量的方法——神经网络联合遗传算法(GA-ANN),该方法基于遗传算法(GA)修正BP神经网络的参数值,采用这种改进BP神经网络的方法对树脂基复合材料的拉伸模量和压缩模量同时预报和分析.比较各种性能指标之后发现,用GA改良后的BP神经网络的精度有了一定程度提高.

1 数据集与神经网络

1.1 数据集

本文所采用数据库中树脂基复合材料[0]₆铺层的强度、泊松比、失效应变以及拉伸模量的数据基于ASTM D 3039试验获得,压缩模量数据基于SACMA SRM 1R方式获取.其中,将数据库样本分为两类:一类是利用数据库形成模型,另一类是将数据库作为检验模型是否合格的“测试者”.利用sklearn将数据库随机分类为上述两种功能的样本,首先把164组数据库样本随机打乱,再分别按照75%、25%的比率划分出样本集,分别是训练、测试样本,即123个用于试验开发适于本文的模型,41个则用于测试已形成模型的性能.表1中列出了一些样本归一化作为示例,这些样本示例均来源于经过归一化处理后的试验数据库.表中: $x 为材料强度; y 为失效应变; ν 为泊松比; z_{1} 为拉伸模量; z_{2}$ 为压缩模量.其中将材料强度、泊松比和失效应变作为输入变量,两个输出变量为拉伸模量和压缩模量.同时,由于参与练习的数据属性较多且不同属性数据间大小迥异,为保证网络在训练过程中维持在一定范围且不溢出,并为能得到较为准确模量数值,在合适的模型确定前期,对输入变量和输出变量都执行数据预处理成为规则,以便处理后的值处在0~1之内^[10],并且输入变量的归一化值由下式确定:

（1）

\begin{matrix} X_{n} = (X_{i} - X_{i, m i n}) / (X_{i, m a x} - X_{i, m i n}) \end{matrix}

式中: $X_{i}$ 为未归一化的输入值; $X_{i, m i n}$ 为未进行归一化处理的最小输入值; $X_{i, m a x}$ 为未归一化的输入变量的最大输出值.

对输出变量归一化值进行类似预处理:

（2）

\begin{matrix} Y_{m} = (Y_{i} - Y_{i, m i n}) / (Y_{i, m a x} - Y_{i, m i n}) \end{matrix}

式中: $Y_{i} 为未归一化处理的输出值; Y_{i, m i n} 为初始最小输出值; Y_{i, m a x}$ 为初始变量的最大输出值.对于测试网络训练性能的结果也要经过式(1)和(2)加工后才能应用.经过规则化之后的局部数据样本如表1所示.

表1 数据集中的部分样本(归一化处理)

Tab.1 Some samples in the data set (normalized)

试验编号	x	ν	y	z₁	z₂
1	0.463 068	0.637 681	0.403 461	0.652 174	0.60
2	0.414 773	0.543 478	0.234 987	0.608 696	0.60
3	0.696 023	0.471 014	0.388 657	0.608 696	0.20
4	0.510 417	0.710 145	0.434 320	0.608 696	0.55
5	0.754 735	0.731 884	0.645 538	0.521 739	0.70
6	0.775 568	0.789 855	0.604 671	0.565 217	0.70
7	0.778 409	0.347 826	0.576 939	0.608 696	0.70

新窗口打开| 下载CSV

1.2 BP神经网络

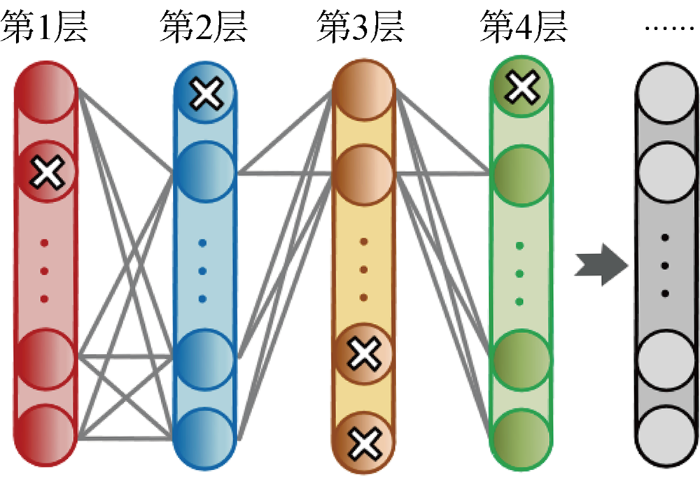
现如今,数据压缩、分类、函数逼近等问题都离不开BP-ANN,可以说,BP-ANN已成为最常用的机器学习方法之一,是ANN内包含的典型^[11].本文利用PyTorch构建上述BP-ANN模型.所用到的PyTorch是一种功能强大的Python库,类似于NumPy,利用它来构建深度学习模型容易理解、易于上手、灵活高效.本文采用PyTorch中模块化的方法构建BP神经网络,即在PyTorch中使用顺序容器torch.nn.Sequential迅速搭建网络.使用此方法时会自动将激励函数调入其中,并且在此模型中将激励表达式定义为relU.所构建的BP-ANN结构包括输入层、输出层和隐藏层^[12],隐藏层应由单个亦可以是若干层组成,有且仅有一个隐藏层的神经网络结构如图1所示.图中: $w_{i j} 为隐藏层与输入层之间的权值; w_{j k}$ 为隐藏层与输出层之间的权值.在网络训练过程中,网络结构对预测效果有十分重要的影响,例如不同的隐藏层层数,或者是单层中不同的神经元数都会影响神经网络模型的性能.试用不同的隐藏层,根据平均相对误差来选择适合本研究的模型.针对每种隐藏层结构,程序需要重复10次,这是因为对于具有随机初始点的模型,重复进行10次以上之后,误差就会基于某值上下浮动,很难再进一步减小^[2].为了提高预测效率,本文中设计的程序可以同时对材料的拉伸模量和压缩模量进行预报,因此两个输出模量共用一个神经网络结构.该神经网络有强度、泊松比和破坏应变这3个输入量,拉伸模量和压缩模量这两个输出量.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 BP神经网络

Fig.1 BP neural network

组成隐藏层的神经元从2开始依次变到6、10、14,结构从3-θ-2到3-θ-θ-2(θ为隐藏层神经元个数).对于选择的每种隐藏层,计算相应训练数据和测试数据的平均相对误差(e₁,e₂),得到的数据结果如表2和3所示.比较两个表,发现在3-10-2结构时所得模量的平均相对误差相对更小一些,因此选择一层具有10个神经元的隐藏层,并最终将3-10-2定义为网络的拓扑.同时在隐藏层引入relU激活函数来减少模型运行过程中的计算量,起到避免过拟合的作用.所选BP-ANN要进行 1 000 次重复反馈.图2中显示了训练过程中误差值和学习速率的变化曲线.图中:h为迭代次数;e为相对误差.由图可见,随着迭代次数的逐渐递增,相对误差最终收敛到一个较小的值,即证明所选择的网络结构可以正确地预测模量问题.

表2 一层隐藏层训练数据与测试数据平均相对误差

Tab.2 Mean relative error of training data and test data of a hidden layer%

隐藏层结构	e₁	e₂
2	2.087 7	2.765 7
6	2.094 0	2.739 1
10	2.076 5	2.533 3
14	2.068 1	2.647 5

新窗口打开| 下载CSV

表3 两层隐藏层训练数据与测试数据平均相对误差

Tab.3 Mean relative error of training data and test data of the two-layer hidden layer%

隐藏层结构	e₁	e₂
6, 6	2.062 4	2.568 7
10, 6	2.071 9	2.759 9
12, 10	2.070 3	2.667 9
14, 12	2.027 8	2.580 9

新窗口打开| 下载CSV

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 神经网络(3-10-2)学习曲线

Fig.2 Neural network (3-10-2) learning curves

2 神经网络优化算法

2.1 GA优化算法

BP-ANN的信号传递可以类比生物神经网络,它将模型信息存储在权重和阈值以及各个神经元中,根据误差减小的原理反向更进权值和阈值.BP-ANN的权重首次赋值和第一次确定的阈值对结果准确性影响较大,如果采取常规方式对BP-ANN模型参数随便进行赋值,那么在实行模型演练时陷入小部分最解中的现象时常发生^[13].而GA算法属于启发式算法,它基于概率方法完成连贯工作,包括选择(Select)、交叉(Cross)、变异(Mutate).历经几次迭代后,在种群后代中选择优秀的个体,从而高效地搜选总体中的最优解^[14].遗传算法不仅不用考虑误差函数的梯度信息就可以解决冗杂、大型、多峰分布和不可微问题,而且也不要求误差函数可微,因而可以显著地扩展误差函数选择规模,以降低BP-ANN的复杂度,提高其普遍应用价值.本文根据GA算法重新创建BP-ANN模型,其每一层权重初值与阈初值被重新修定,进一步在测得模量数据集时更接近于正确值.

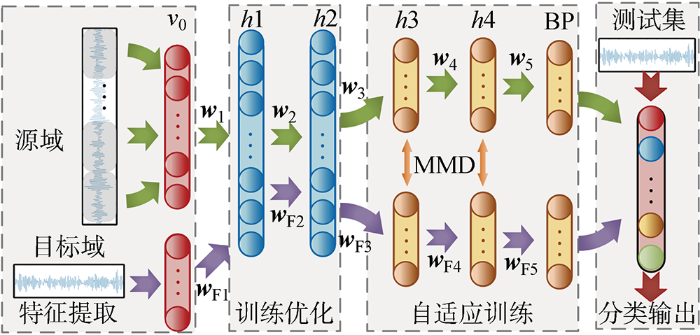
GA-ANN模型进行优化时首先需要大致构建网络框架,然后利用GA方法将参数修正改良,最后将更新后的BP-ANN替代原始结构开始预测^[15].网络结构部分是先按照模拟功能的输入、输出参数的数量来构建网络部分框架,通过提取材料的强度、泊松比和破坏应变特征值,采用之前预设8种隐藏层建立网络框架.将BP神经网络的参数信息编码于个体中,用遗传操作对各个参数进行选择、变异以及交叉,得到适应值最大的个体对应于网络的最佳参数.然后将参数初始数赋给相应权重和阀值,之后计算出8组ANN预测结果的平均误差,将差别最小组选成隐藏层,一旦设立了BP-ANN结构,对应需要被优化神经网络参数数量也随即得出,由此获得GA方法编码长度并确定需要的染色体具体数量.BP-ANN全部的权重和阀值都被编码在每一个个体,并且每个个体的适应度值(Fitness)都按照提前设定的Fitness表达式得出,种群经过Select、Cross、Mutate等一连串的运算过程,比较个体的Fitness并找到Fitness最大的个体,即适应度最好对应的个体^[16].表现最好的个体可用于确定BP-ANN每层权重和阀值的初始赋值,而后即可通过成形的样本的输出来完成BP神经网络的工作,从而推测材料两个模量值.

GA-ANN的示意图如图3所示,算法的修正过程如下.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 GA-ANN流程图

Fig.3 GA-ANN flow chart

步骤1 任意赋值给BP网络的全部初始参数,完成对BP-ANN的第一次构建.

步骤2 根据GA需要改良的参数设定初始种群,利用一连串遗传操作(Select、Cross、Mutate)使BP网络每一层的权重以及阀值得以充足优化.

步骤3 更新BP-ANN,首先用123组数据集塑造模型,接着用余下41组预测集证明模型的可行性.

初始化种群.选取0和1组成的计算机编码方式,所设种群总体里有200个个体,这些个体都有自己的独特编码,每个数值串都对应着网络参数的一套初始数值.初始数值由输入层与隐藏层之间的权重、隐藏层与输出层之间的权重以及隐藏层和输出层的阈值组成.

染色体设置.3-10-2结构的神经网络具有两组权重(Weights),输入层到隐藏层(30),隐藏层到输出层(20);两组阈值,输入层到隐藏层(10),隐藏层到输出层(2).由此共计有62个参数,每个参数自定义有18个基因位,初始化为由KaiMing确定的参数范围内的随机值.

适应度值计算.为使BP网络预测尽可能接近真实值,取误差的倒数为适应度,自定义种群总体规模为200,迭加300次,将经GA训练出的最佳参数代入到网络中运行.任意个体的适应值可以表示为

（3）

\begin{matrix} f (X_{i}) = l o s s (X_{i})^{- 1} \end{matrix}

（4）

\begin{array}{l} l o s s (X_{i}) = \frac{1}{m} \overset{m}{\sum_{j = 1}} ({\hat{Y}}_{j}^{i} - Y_{j})^{2} \end{array}

式中: $X_{i}$ 为第 $i$ 个个体, $i = 1, 2, \dots, 200$ ; $Y_{j}$ 为期望网络的输出; ${\hat{Y}}_{j}^{i}$ 为第 $j$ 个训练数据对应的预测值, $j = 1, 2, \dots, m$ ; $m$ 为训练数据样本数量;loss为损失函数.

选择运算.使用轮盘赌的方式,按照概率分配原则选择适应度性能强的个体组成新的种群,选择算子的计算方式如下:

（5）

\begin{matrix} P (X_{i}) = \frac{f (X_{i})}{\overset{N}{\sum_{k = 1}} f (X_{k})} \end{matrix}

式中:N为种群大小;k为个体数目.接着对每个个体累积选取概率 $Q_{i}$ 按照下式进行计算:

（6）

\begin{matrix} Q_{i} = \overset{i}{\sum_{k = 1}} P (X_{k}) \end{matrix}

随机生成一个均匀分布的数字 $r$ , $r \in [0, 1]$ .如果 $r \leq Q_{1}$ ,则选择个体1,如果 $Q_{k - 1} < r \leq Q_{k} (2 \leq k \leq N)$ ,那么选择第k个个体遗传至下一代种群.

交叉.从种群里任意筛出两组亲本染色体Cross,选择Single-point-cross,随机选择Cross处,交换两个染色体该点后面的全部基因.考虑到个体Fitness前后差异不大,因此选择默认固定交叉率为0.7.

变异.Mutate是种群多样性存在的一个最主要的方式.试验选择基本位Mutate策略.在这种遗传算法中,染色体较长(基因数为18×64=1 152),为此Mutate应选取多个基因位.在种群中随机选取个体之后,选择变异基因的任意位置进行Mutate操作,将概率设成0.1.

2.2 Adam优化算法

Adam在当今机器学习优化器中占有非常重要的地位,是目前应用最广泛且功能最强大的优化器之一.尤其在近年来已被应用到利用人工智能解决问题的各个领域中.它对传统单一的学习率进行了改进,能够自行更新调节,十分灵活高效.越是复杂的神经网络中越能够体现它的优越性能.在实际应用中,Adam方法延续了Adagrad和RMSprop两者的长处,即在非密集梯度问题和振荡浮动较大的数据中维持高能的预测效果.此外,除了达到收敛所用的时间更少,它还可以改善诸如学习率不稳定或是高方差参数幅度过大导致损失函数值波动等欠缺.总之,Adam已然成为最受欢迎的优化器^[17].另外,传统的机器学习算法如SVR是处理中小数据集监督训练的预测数据中比较典型的方式,但是在本论文研究内容下的平均预测误差却较大于神经网络,因此最终采用Adam优化神经网络的方法(Adam-ANN)与GA-ANN的性能进行对照.

为了评价GA-ANN优化方式预测数据的性能,采用Adam优化器建立了同样的神经网络模型,将两种优化方法预测数据得到的平均相对误差( $\bar{e}$ )、均方根误差(RMS)和标准误差(SEP)分别进行比较,从而得出本论文GA优化的普适、优越性能.RMS和SEP的计算公式如下:

（7）

\begin{matrix} R M S = \sqrt{\frac{1}{n} \overset{n}{\sum_{i = 1}} ({\hat{Y}}_{i} - Y_{i})^{2}} \end{matrix}

（8）

\begin{array}{l} S E P = \sqrt{\frac{1}{n} \overset{n}{\sum_{i = 1}} ({\hat{Y}}_{i} - E_{Y})^{2}} \end{array}

式中: ${\hat{Y}}_{i}$ 为模量的预测数据; $E_{Y}$ 为模量预测数据的期望; $n$ 为测试数据模本数量, $i = 1, 2, \dots, n$ .

3 结果与讨论

采用Anaconda平台下的软件Spyder编写Python(3.7)语言程序,分别对GA-ANN和Adam-ANN两种算法展开验证.为了防止模型过度拟合,任意划分模本集,其中75%为训练数据,25%为测试数据.本试验对训练数据和测试数据都进行了模量预报,由于测试数据组不参与模型训练,所以重点使用41组测试数据点进行分析和验证.表4是在GA和Adam优化网络模型下训练数据集的模量预测关于结果的比较情况.对于拉伸模量,Adam-ANN所得平均相对误差、RMS和SEP都略小于GA-ANN,值得注意的是,Adam-ANN和GA-ANN的平均相对误差分别为1.64%、1.66%.而压缩模量中,GA-ANN模型效果略优,Adam-ANN和GA-ANN的平均相对误差分别为2.50%、2.47%.由此可得,用这两类方式得到的训练模型均良好且差别甚小.表5对比GA和Adam所得训练模式下的测试数据预测情况.测试集的预测情况是考量最终模型泛化能力的标准,可以得出结论,GA-ANN模型预测性能好于Adam-ANN,GA-ANN的平均相对误差分别为1.83%、3.22%,Adam-ANN的平均相对误差为1.94%、3.71%.对于拉伸和压缩这两种模量,GA-ANN所得RMS、SEP都略小于Adam-ANN.为了更直观地说明,这些结论在图4中以三维图形的形式表示.由于图中仅有两个自变量,所以所作曲面应只对应一个泊松比的数值.本文选取一个预测效果比较好的测试数据,将其泊松比的数值固定为该测试数据对应的泊松比的定值,即0.318,

表4 GA-ANN和Adam-ANN训练集预测表

Tab.4 Comparison of GA-ANN and Adam-ANN training set prediction results

模型	$\bar{e}$ /%		RMS/GPa		SEP/GPa
模型	z₁	z₂	z₁	z₂	z₁	z₂
GA-ANN	1.66	2.47	3.939 9	4.614 8	3.939 9	4.614 3
Adam-ANN	1.64	2.50	3.847 3	4.674 7	3.847 2	4.673 7

新窗口打开| 下载CSV

表5 GA-ANN和Adam-ANN测试集预测表

Tab.5 Comparison of prediction results of GA-ANN and Adam-ANN test sets

模型	$\bar{e}$ /%		RMS/GPa		SEP/GPa
模型	z₁	z₂	z₁	z₂	z₁	z₂
GA-ANN	1.83	3.22	4.084 9	7.053 7	4.079 8	5.764 3
Adam-ANN	1.94	3.71	4.254 0	7.960 5	4.203 9	5.923 5

新窗口打开| 下载CSV

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 GA-ANN和Adam-ANN对拉伸模量和压缩模量的测试结果

Fig.4 Prediction results of GA-ANN and Adam-ANN models on tensile modulus and compressive modulus

然后画曲面.由图4可以得出,GA-ANN介于拉伸模量上下误差限制之间.同样,对于压缩模量也有相似的结论.这些结论证实了表5的结果.

将41个测试数据组的预测值按照 $\bar{e}$ 从小到大的顺序进行排列,选取误差最小的前15组数据作散点图.图5和图6分别描绘了基于3个输入参数开发的GA-ANN和Adam-ANN 经验模型得出的模量预测数据与真实数据对比效果.其中: $r_{1}$ 为拉伸模量的实际值; $o_{1}$ 为拉伸模量的预测值; $r_{2}$ 为压缩模量的实际值; $o_{2}$ 为压缩模量的预测值.二维图更加明显地表明,GA-ANN精度高于Adam-ANN.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 GA-ANN和Adam-ANN对拉伸模量的测试结果

Fig.5 Prediction results of GA-ANN and Adam-ANN models on tensile modulus

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 GA-ANN和Adam-ANN对压缩模量的测试结果

Fig.6 Prediction results of GA-ANN and Adam-ANN models on compressive modulus

4 结语

BP神经网络已经被广泛地应用到各个领域,特别是对于模糊模型的复杂问题,BP神经网络一般都能够很好地解决.但是关于参数初始值的选取环节,一般都是按照经验或者随机选取,目前并没有统一的定论来规范该操作.而GA可以改善BP关键参数于初始值获取的不足.相比而言,遗传算法擅长从总体上展开搜索,而BP算法通常在小范围搜索中更加有效,因此也常常被困在局部最小值中,经过测试发现,混合方式训练神经网络的效果比仅使用BP训练的方法更好.

本文通过传统试验的方式获得树脂基复合材料[0]₆铺层各个试验件的强度、泊松比、破坏应变、压缩模量和拉伸模量的真实数值.并利用强度、泊松比和破坏应变这3个特征值,采用GA优化BP神经网络,实现了对材料拉伸模量和压缩模量的回归预测,既避免了选取网络权重和阈值的不确定性,又提升了传统BP网络的预测功能.用GA优化之后的BP神经网络在测试集上进行验证检测,其平均相对误差不足3%,证明该算法性能良好.在与Adam-ANN的对比试验中,GA的平均相对误差、RMS、SEP值均较小,说明GA-ANN更具普适性、测试精度效果优,可以通过训练模型得到误差较小的复合材料模量值.本项工作为使用机器学习优化方法探索材料的模量特性提供了一些启示,可以应用到除了树脂基复合材料以外的各种材料中.

为了进一步增强预测模型的适应性和提高其预测数据的准确度,在未来的研究中,将采用机器学习与有限元相结合的方法扩充数据库,更大量的数据集将被用作模型的输入.再者,将思考使用更复杂机器学习模型与特征选择方式.最后,由于本研究是基于[0]₆试验件铺层对模量数据进行预测,所以不包括其他铺层情形,例如[90]₁₂、[45/-45]_4S、[45/0/-45/90]_2S等,后续研究将重点探索各种铺层的交错预测.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘陈续, 于桂兰.

基于神经网络的层状周期结构能量传输谱预测

[J]. 上海交通大学学报, 2021, 55(1): 88-95.